Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering
Abstract
1. Introduction
- (1)
- We develop an error propagation model of the Kalman filter that takes different sources of errors (quantization, unreliable memories) into account and allows us to derive new filter equations to minimize the estimation error. Moreover, these equations accurately predict the filter’s performance, depending on the considered sources of errors and on their parameters.
- (2)
- We propose a methodology for minimizing the energy of the unreliable memories used in the Kalman filter, under a given performance constraint. This methodology consists of computing the optimal number of quantization levels and bit energy allocation in two setups. The first setup considers that the B energy levels can be chosen freely, while the second one assumes that only energy levels can be set.
2. System Model
2.1. Kalman Filter
2.2. Quantized Implementation of the Filter
2.3. Implementation of the Filter by Using an Unreliable Memory
3. Error Analysis
3.1. Error Propagation Model
3.2. Quantization Error
3.3. Unreliable Memory Error
3.4. Total Error
4. Energy Optimization
4.1. Optimization across All the Bits
| Algorithm 1: Computing the optimal values for and m. |
| Input: , a, , , |
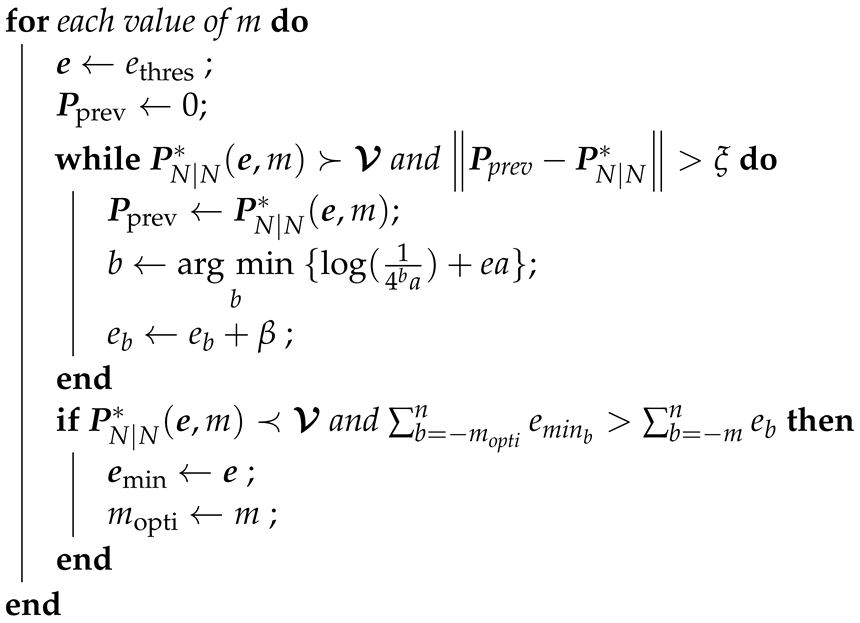 |
| Result: Optimal number of bits and optimal energy allocation vector |
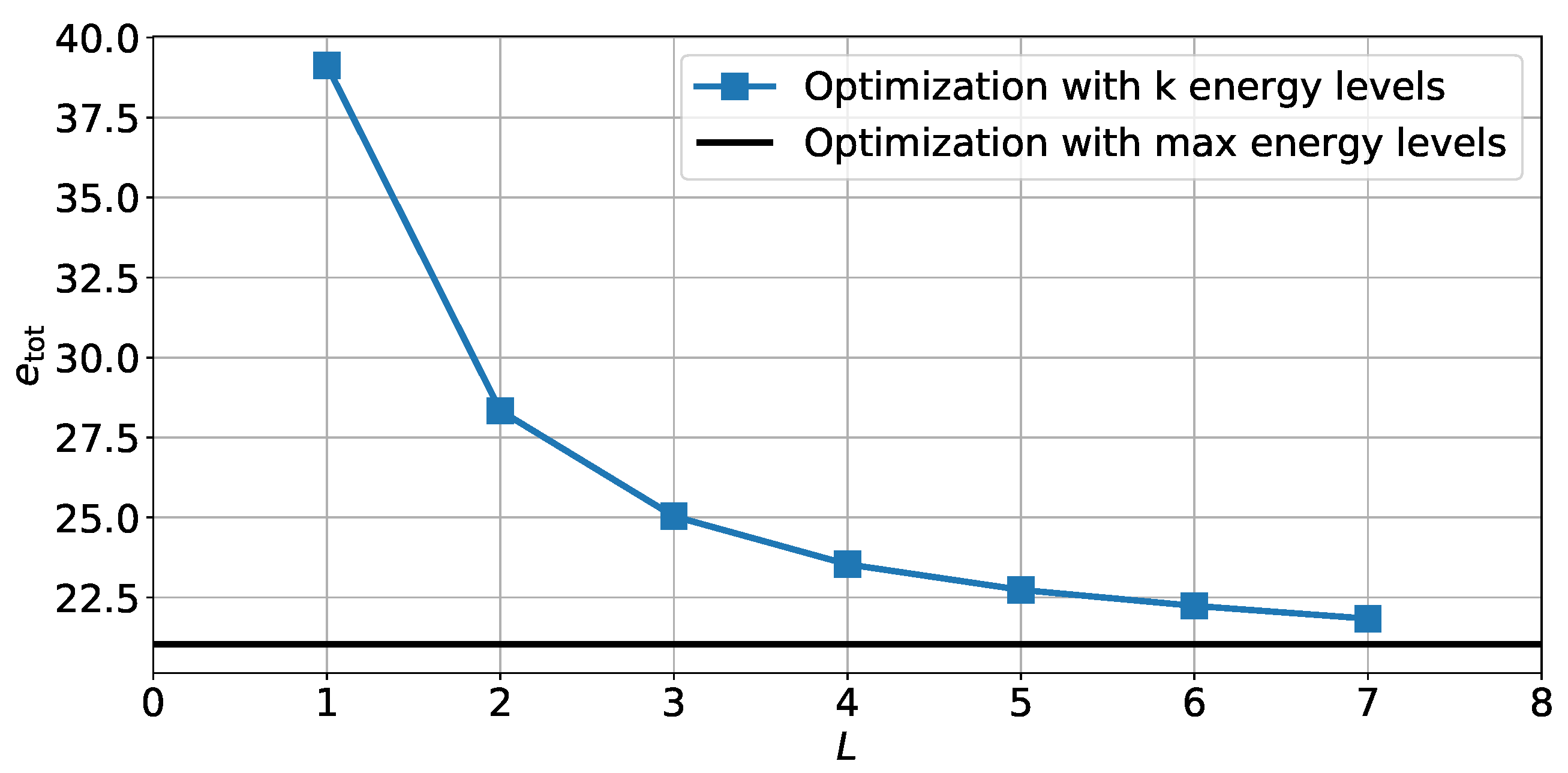
4.2. Optimization with a Limited Number of Energy Levels
5. Simulation Results
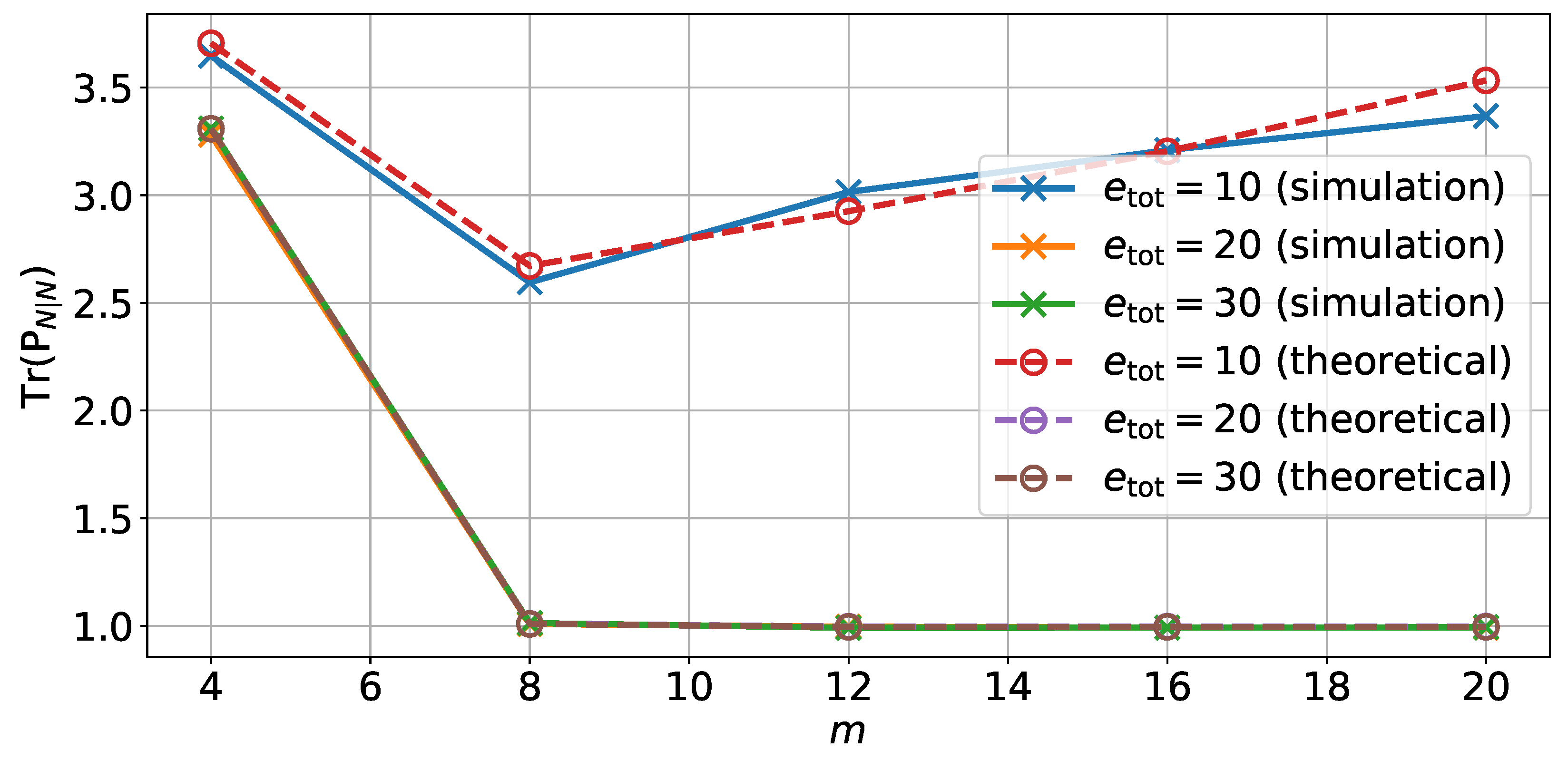
5.1. Accuracy of the Theoretical Analysis
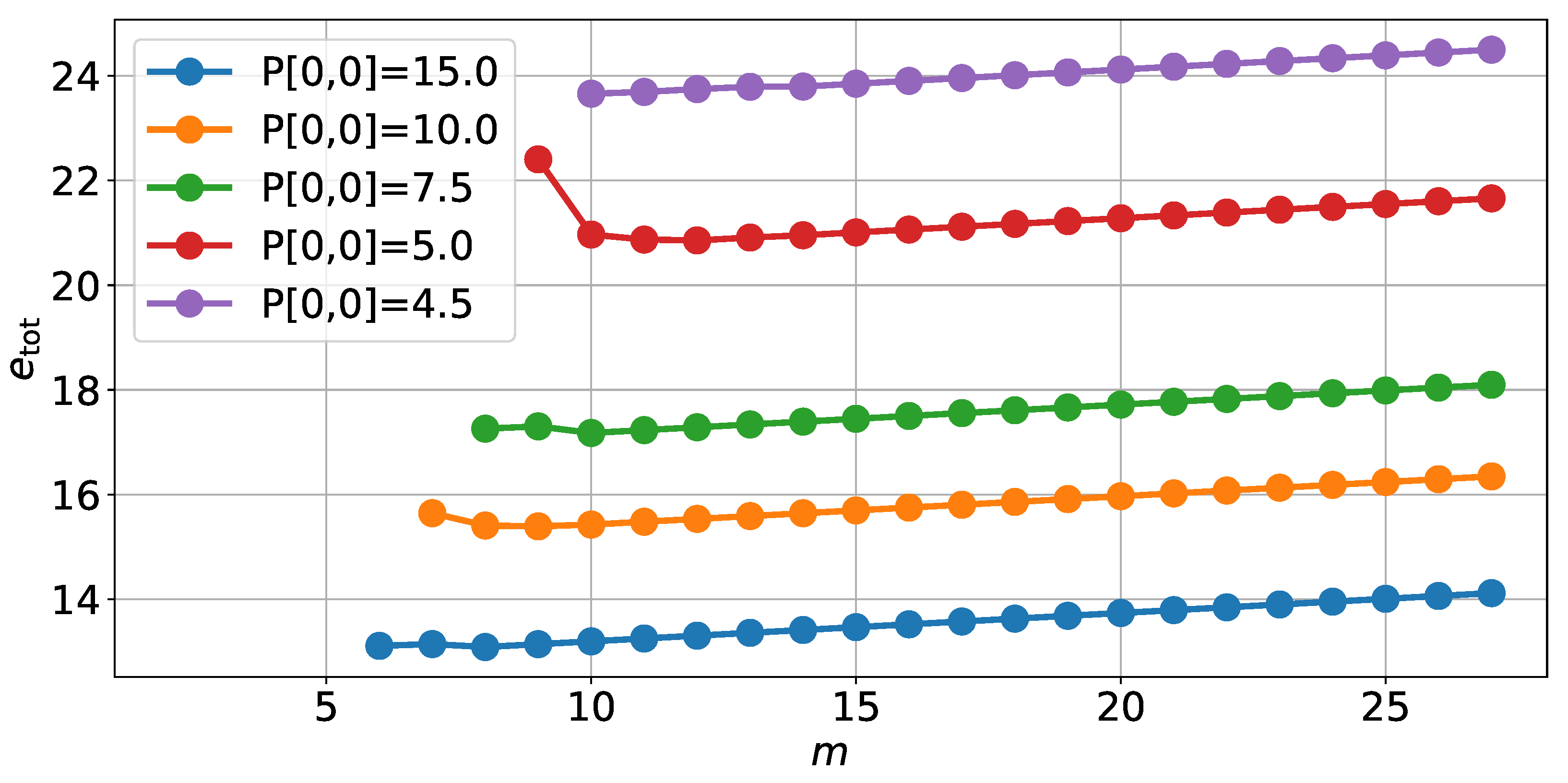
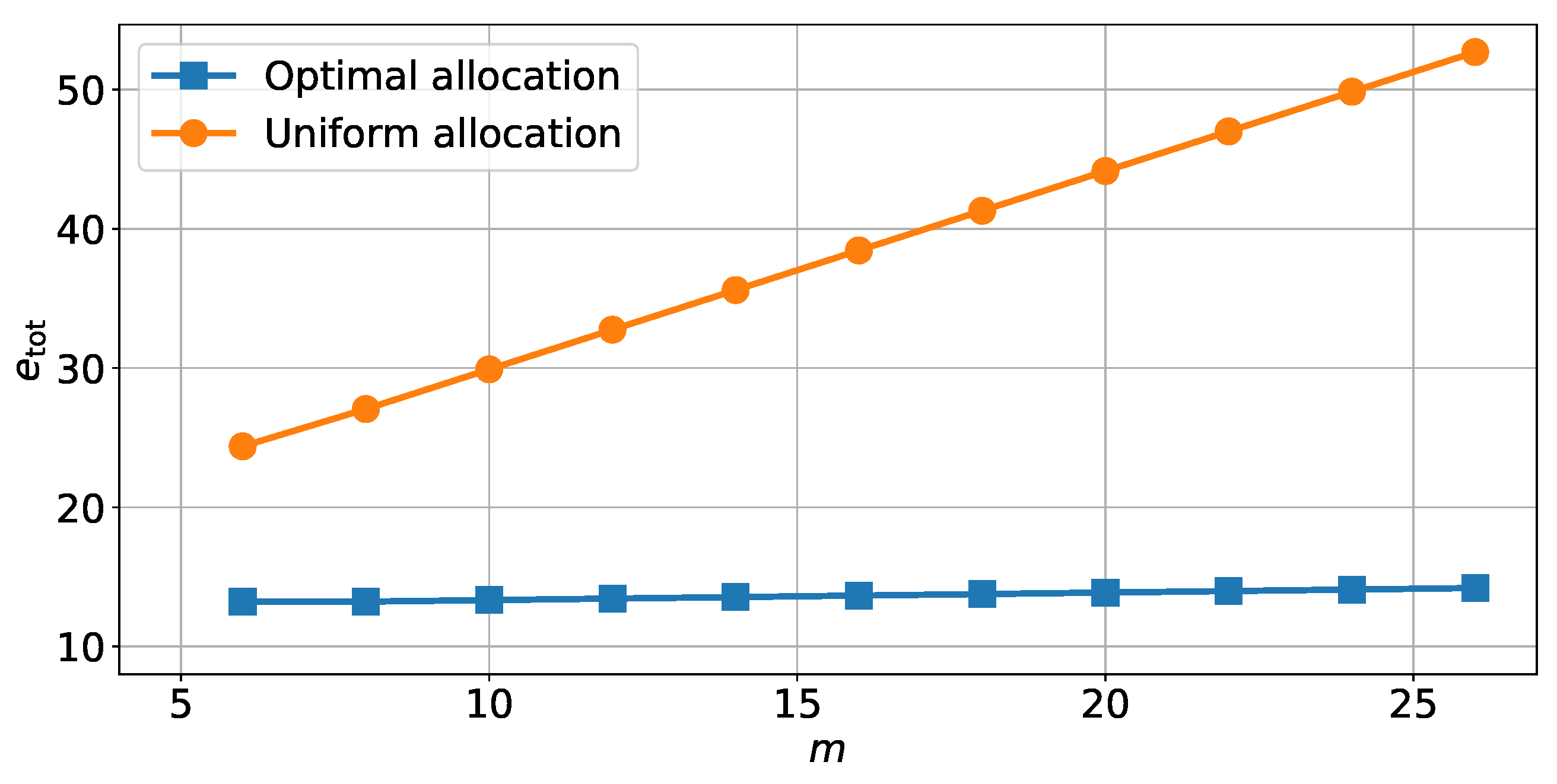
5.2. Solutions to the Optimization Problems
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Computation of
Appendix B. Computation of the Optimal Solution to Problem 1
References
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Lai, X.; Yang, T.; Wang, Z.; Chen, P. IoT Implementation of Kalman Filter to Improve Accuracy of Air Quality Monitoring and Prediction. Appl. Sci. 2019, 9, 1831. [Google Scholar] [CrossRef]
- Anania, G.; Tognetti, A.; Carbonaro, N.; Tesconi, M.; Cutolo, F.; Zupone, G.; Rossi, D.D. Development of a novel algorithm for human fall detection using wearable sensors. In Proceedings of the IEEE SENSORS, Lecce, Italy, 26–29 October 2008; pp. 1336–1339. [Google Scholar] [CrossRef]
- Wang, T.; Hu, J.; Ma, T.; Song, J. Forest fire detection system based on Fuzzy Kalman filter. In Proceedings of the 2020 International Conference on Urban Engineering and Management Science (ICUEMS), Zhuhai, China, 24–26 April 2020; pp. 630–633. [Google Scholar] [CrossRef]
- Sung, K.; Kim, H. Simplified KF-based energy-efficient vehicle positioning for smartphones. J. Commun. Netw. 2020, 22, 93–107. [Google Scholar] [CrossRef]
- Horowitz, M. 1.1 Computing’s energy problem (and what we can do about it). In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 10–14. [Google Scholar] [CrossRef]
- Dreslinski, R.G.; Wieckowski, M.; Blaauw, D.; Sylvester, D.; Mudge, T. Near-Threshold Computing: Reclaiming Moore’s Law Through Energy Efficient Integrated Circuits. Proc. IEEE 2010, 98, 253–266. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, M.; Varshney, L.R.; Shanbhag, N.R. Generalized Water-Filling for Source-Aware Energy-Efficient SRAMs. IEEE Trans. Commun. 2018, 66, 4826–4841. [Google Scholar] [CrossRef]
- Kim, Y.; Jeon, Y.; Guyot, C.; Cassuto, Y. Optimizing the Write Fidelity of MRAMs. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 792–797. [Google Scholar] [CrossRef]
- Dupraz, E.; Varshney, L.R. Binary Recursive Estimation on Noisy Hardware. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 877–881. [Google Scholar]
- Yang, Y.; Grover, P.; Kar, S. Computing Linear Transformations With Unreliable Components. IEEE Trans. Inf. Theory 2017, 63, 3729–3756. [Google Scholar] [CrossRef]
- Henwood, S.; Leduc-Primeau, F.; Savaria, Y. Layerwise Noise Maximisation to Train Low-Energy Deep Neural Networks. In Proceedings of the 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Genova, Italy, 31 August–2 September 2020; pp. 271–275. [Google Scholar] [CrossRef]
- Hacene, G.B.; Leduc-Primeau, F.; Soussia, A.B.; Gripon, V.; Gagnon, F. Training Modern Deep Neural Networks for Memory-Fault Robustness. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Shang, Y. Resilient consensus in multi-agent systems with state constraints. Automatica 2020, 122, 109288. [Google Scholar] [CrossRef]
- Yang, Y.; Grover, P.; Kar, S. Fault-tolerant distributed logistic regression using unreliable components. In Proceedings of the 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 940–947. [Google Scholar] [CrossRef]
- Hegde, R.; Shanbhag, N.R. Energy-efficient signal processing via algorithmic noise-tolerance. In Proceedings of the International Symposium on Low Power Electronics and Design (Cat. No. 99TH8477), San Diego, CA, USA, 17 August 1999; pp. 30–35. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Dolecek, L. ACOCO: Adaptive Coding for Approximate Computing on Faulty Memories. IEEE Trans. Commun. 2015, 63, 4615–4628. [Google Scholar] [CrossRef]
- Yaz, E.E.; Jeong, C.S.; Yaz, Y.I. An LMI approach to discrete-time observer design with stochastic resilience. J. Comput. Appl. Math. 2006, 188, 246–255. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, C.; Xue, A. Distributed non-fragile l2–l∞ filtering over sensor networks with random gain variations and fading measurements. Neurocomputing 2019, 338, 154–162. [Google Scholar] [CrossRef]
- Nahi, N. Optimal recursive estimation with uncertain observation. IEEE Trans. Inf. Theory 1969, 15, 457–462. [Google Scholar] [CrossRef]
- Hounkpevi, F.O.; Yaz, E.E. Robust minimum variance linear state estimators for multiple sensors with different failure rates. Automatica 2007, 43, 1274–1280. [Google Scholar] [CrossRef]
- Petersen, I.R.; McFarlane, D.C.; Rotea, M.A. Optimal Guaranteed Cost Control of Discrete-time Uncertain Linear Systems. IFAC Proc. Vol. 1993, 26, 35–38. [Google Scholar] [CrossRef]
- Yang, G.H.; Wang, J.L. Robust nonfragile Kalman filtering for uncertain linear systems with estimator gain uncertainty. IEEE Trans. Autom. Control 2001, 46, 343–348. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
- Jarrah, A. Optimized parallel architecture of Kalman filter for radar tracking applications. Jordan J. Electr. Eng. 2016, 2, 215–230. [Google Scholar]
- Sunil Kumar, T.; Duraiswamy, P. Optimization of Kalman Filter for Target Tracking Applications. In Advances in Multidisciplinary Analysis and Optimization; Salagame, R.R., Ramu, P., Narayanaswamy, I., Saxena, D.K., Eds.; Springer: Singapore, 2020; pp. 203–212. [Google Scholar] [CrossRef]
- Pereira, P.T.L.; Paim, G.; Ücker, P.; Costa, E.; Almeida, S.; Bampi, S. Exploring Architectural Solutions for an Energy-Efficient Kalman Filter Gain Realization. In Proceedings of the 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 650–653. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Verma, N. Reducing quantization error in low-energy FIR filter accelerators. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 1032–1036. [Google Scholar] [CrossRef]
- Xia, D.; Zhang, Y.; Cai, P.; Huang, L. An Energy-Efficient Signal Detection Scheme for a Radar-Communication System Based on the Generalized Approximate Message-Passing Algorithm and Low-Precision Quantization. IEEE Access 2019, 7, 29065–29075. [Google Scholar] [CrossRef]
- Marcastel, A.; Fijalkow, I.; Swindlehurst, L. Energy efficient downlink massive MIMO: Is 1-bit quantization a solution? In Proceedings of the 16th International Symposium on Wireless Communication Systems (ISWCS), Oulu, Finland, 27–30 August 2019; pp. 198–202. [Google Scholar] [CrossRef]
- Hashemi, S.; Anthony, N.; Tann, H.; Bahar, R.I.; Reda, S. Understanding the impact of precision quantization on the accuracy and energy of neural networks. In Proceedings of the Conference on Design, Automation & Test in Europe, Lausanne, Switzerland, 27–31 March 2017; pp. 1478–1483. [Google Scholar]
- Ding, R.; Liu, Z.; Blanton, R.D.S.; Marculescu, D. Quantized deep neural networks for energy efficient hardware-based inference. In Proceedings of the 23rd Asia and South Pacific Design Automation Conference (ASP-DAC), Jeju, Korea, 22–25 January 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Jain, S.; Venkataramani, S.; Srinivasan, V.; Choi, J.; Chuang, P.; Chang, L. Compensated-DNN: Energy efficient low-precision deep neural networks by compensating quantization errors. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Stripad, A.B. Performance Degradation in Digitally Implemented Kalman Filters. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 626–634. [Google Scholar] [CrossRef]
- Verhaegen, M.; Dooren, P.V. Numerical aspects of different Kalman filter implementations. IEEE Trans. Autom. Control 1986, 31, 907–917. [Google Scholar] [CrossRef]
- Sun, S.; Lin, J.; Xie, L.; Xiao, W. Quantized Kalman Filtering. In Proceedings of the IEEE 22nd International Symposium on Intelligent Control, Singapore, 1–3 October 2007; pp. 7–12. [Google Scholar] [CrossRef]
- Li, D.; Kar, S.; Cui, S. Distributed Kalman Filtering with quantized sensing state. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4040–4044. [Google Scholar] [CrossRef]
- Hu, X.; Bao, M.; Zhang, X.; Wen, S.; Li, X.; Hu, Y. Quantized Kalman Filter Tracking in Directional Sensor Networks. IEEE Trans. Mob. Comput. 2018, 17, 871–883. [Google Scholar] [CrossRef]
- You, K.; Xie, L.; Sun, S.; Xiao, W. Quantized filtering of linear stochastic systems. Trans. Inst. Meas. Control 2011, 33, 683–698. [Google Scholar] [CrossRef]
- You, K.; Zhao, Y.; Xie, L. Recursive quantized state estimation of discrete-time linear stochastic systems. In Proceedings of the 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 170–175. [Google Scholar]
- Dally, W.J.; Harting, R.C.; Aamodt, T.M. Digital Design Using VHDL: A Systems Approach; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Kern, J.; Dupraz, E.; Aïssa-El-Bey, A.; Leduc-Primeau, F. Improving the Energy-Efficiency of a Kalman Filter Using Unreliable Memories. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 5345–5349. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. State Estimation in Discrete-Time Linear Dynamic Systems. In Estimation with Applications to Tracking and Navigation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; pp. 199–266. [Google Scholar] [CrossRef]
- Thacker, N.; Lacey, A. Tutorial: The Kalman Filter; Imaging Science and Biomedical Engineering Division, Medical School, University of Manchester: Manchester, UK, 1998; p. 61. [Google Scholar]
- Ziv, J. On universal quantization. IEEE Trans. Inf. Theory 1985, 31, 344–347. [Google Scholar] [CrossRef]
- Sripad, A.; Snyder, D. A necessary and sufficient condition for quantization errors to be uniform and white. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 442–448. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mahmoodi, H.; Roy, K. Modeling of failure probability and statistical design of SRAM array for yield enhancement in nanoscaled CMOS. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2005, 24, 1859–1880. [Google Scholar] [CrossRef]
- Dupraz, E.; Declercq, D.; Vasić, B.; Savin, V. Analysis and Design of Finite Alphabet Iterative Decoders Robust to Faulty Hardware. IEEE Trans. Commun. 2015, 63, 2797–2809. [Google Scholar] [CrossRef]
- Kameni Ngassa, C.; Savin, V.; Dupraz, E.; Declercq, D. Density Evolution and Functional Threshold for the Noisy Min-Sum Decoder. IEEE Trans. Commun. 2015, 63, 1497–1509. [Google Scholar] [CrossRef][Green Version]
- Berberidis, D.; Giannakis, G.B. Data Sketching for Large-Scale Kalman Filtering. IEEE Trans. Signal Process. 2017, 65, 3688–3701. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Dolecek, L. Belief Propagation Algorithms on Noisy Hardware. IEEE Trans. Commun. 2015, 63, 11–24. [Google Scholar] [CrossRef]
- Shang, Y. Group consensus of multi-agent systems in directed networks with noises and time delays. Int. J. Syst. Sci. 2015, 46, 2481–2492. [Google Scholar] [CrossRef]

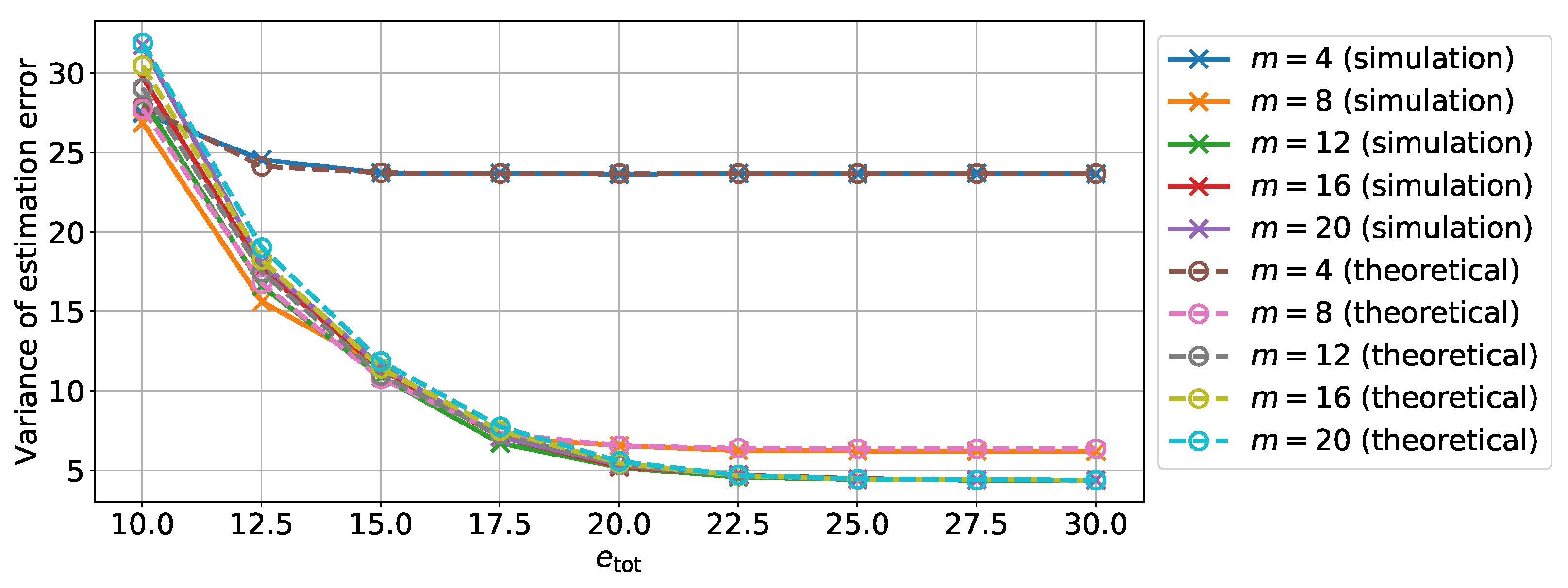
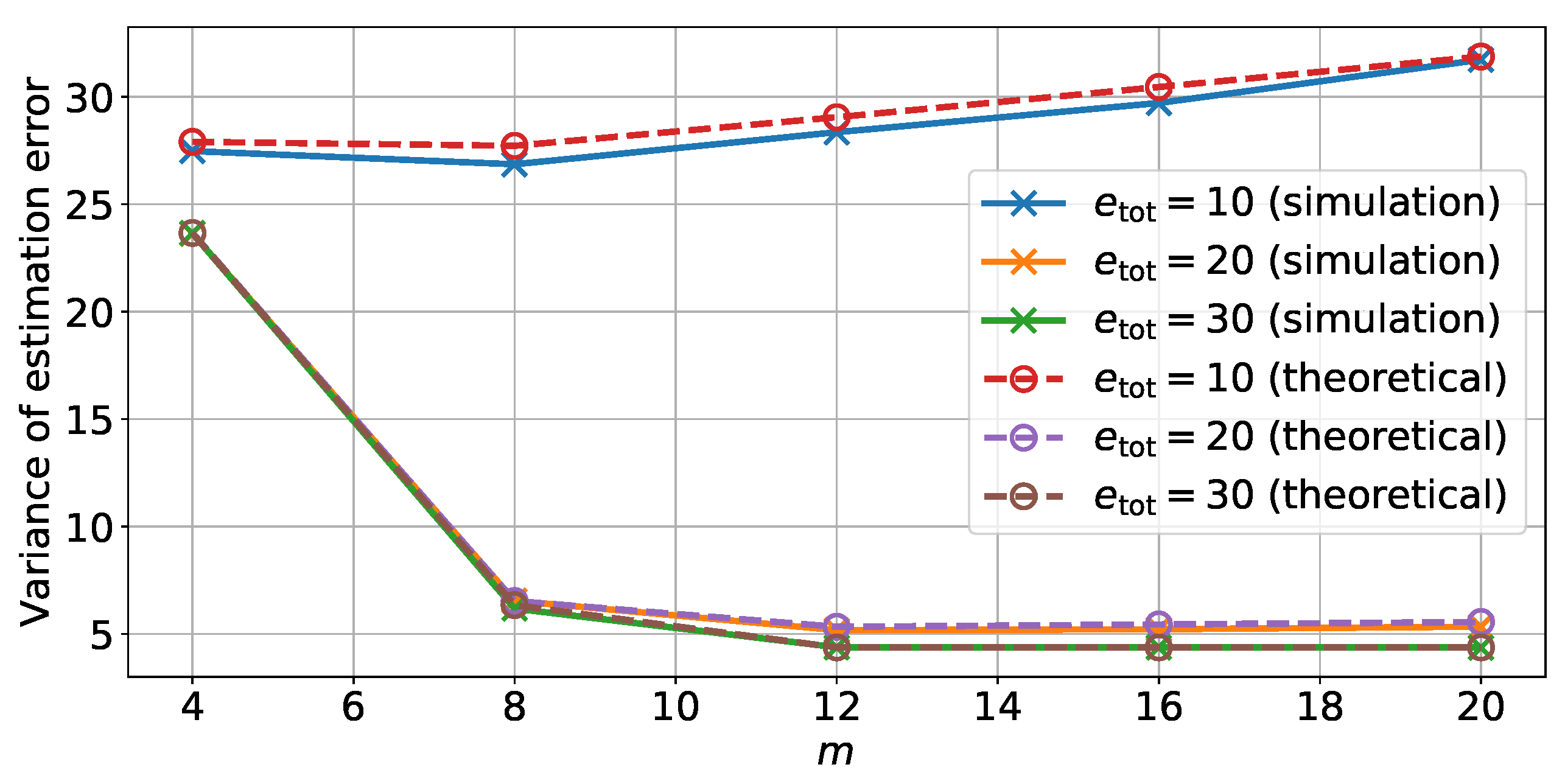
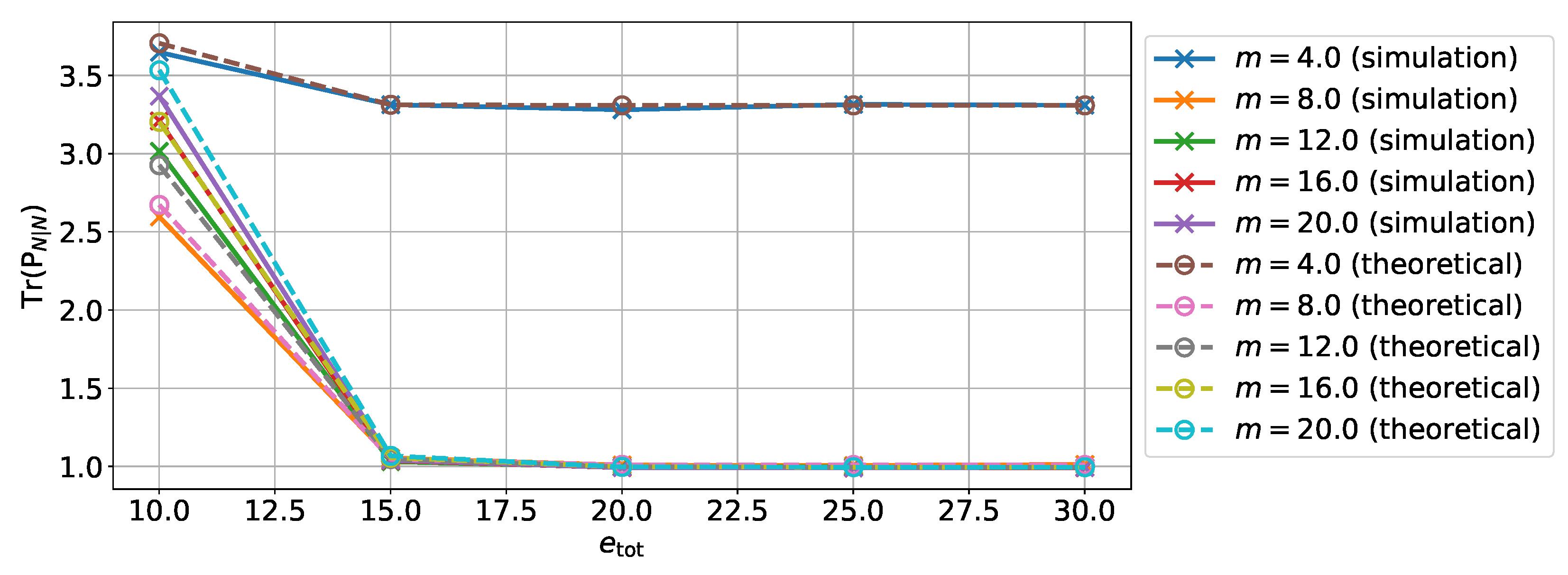
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kern, J.; Dupraz, E.; Aïssa-El-Bey, A.; Varshney, L.R.; Leduc-Primeau, F. Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering. Sensors 2022, 22, 853. https://doi.org/10.3390/s22030853
Kern J, Dupraz E, Aïssa-El-Bey A, Varshney LR, Leduc-Primeau F. Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering. Sensors. 2022; 22(3):853. https://doi.org/10.3390/s22030853
Chicago/Turabian StyleKern, Jonathan, Elsa Dupraz, Abdeldjalil Aïssa-El-Bey, Lav R. Varshney, and François Leduc-Primeau. 2022. "Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering" Sensors 22, no. 3: 853. https://doi.org/10.3390/s22030853
APA StyleKern, J., Dupraz, E., Aïssa-El-Bey, A., Varshney, L. R., & Leduc-Primeau, F. (2022). Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering. Sensors, 22(3), 853. https://doi.org/10.3390/s22030853





