1. Introduction
In the last decades, there has been a surge of interest regarding range imaging technologies. These devices typically provide depth images, showing the distance of each scene point from the camera sensors. The applications of these systems and devices are widespread, as they can be used for augmented reality, face identification, gesture recognition [
1], simultaneous localization and mapping [
2], 3D modeling and reconstruction [
3,
4,
5,
6,
7], autonomous driving [
8,
9] and even for navigation and landing on planetary bodies [
10].
Some of the most common technologies comprehend stereo devices [
11], that use the point of view of two different cameras to recover depth images, structured light scanners [
12], that compute distance information relying on light patterns and LIDARs [
13] and other Time-of-Flight (ToF) technologies [
14], which use the light travel time for the recovery of depth information.
In this work, we will mostly focus on time-of-flight based devices—a Time-of-Flight (ToF) camera is a range imaging device that captures depth information in real time. The working principle of ToF cameras consists of illuminating the scene with a light source and then computing the time it takes for the light to travel from the source to the scene and back to the sensor. Recovering depth from time is then a straightforward operation. If the time is measured directly, for example, with a time to digital converter (TDC), we are working with direct ToF (dToF) cameras, while in the case the time is calculated from intensity measurements through correlation of illumination and sensor modulation, we are dealing with indirect ToF (iToF) cameras. We will focus on iToF cameras, which, compared to dToF, can estimate the depth with a smaller maximum range but with a higher lateral resolution. These aspects make them the better option for indoor acquisitions and the most adopted solution for ToF image sensors today. In the following section, we will give a mathematical introduction to the iToF principles.
1.1. iToF Cameras
The main idea behind the retrieval of depth information in ToF imaging is to use the fact that the speed of light is fixed. In direct ToF a very short light pulse is emitted towards the scene, is reflected and is finally gathered by a sensor; the depth is then inferred from the travel time. Indirect ToF makes use of the same idea, but with a different kind of illumination signal. It uses a periodic light modulation and retrieves the depth information from the phase displacement
between the incoming light and an internal reference signal, according to the following relation:
where
is the modulation frequency and
c is the speed of light.
In practice, the emitter sends a modulated signal
with modulation frequency
towards the scene. At the sensor’s side, the reflected light
is correlated with the sensor sensitivity function
, that is, phase shifted by a factor
for ToF measurements as explained below; the raw measurements
of our camera are the result of these correlation operations. In the case of
being a sine wave, we can express the reflected light as an attenuated and delayed version of the original signal
, where we expressed the delay
in terms of phase displacement. If we then consider a sensor sensitivity of the form
and assume that the light bounces a single time inside the scene (quite a strong assumption as we will see) it holds that:
with
the integration time and
the phase displacement applied to the sensor sensitivity.
By assuming
(that is usually the case), we get the following closed-form solution of our integral [
15]:
where
I is the intensity of ToF signal,
A is its amplitude and
is the phase offset due to the scene depth by means of Equation (
1).
From the raw measurement in (
3), we want to recover
A,
I and
. As shown in [
15], it is sufficient to sample
at 4 different known phase displacements
of the sensor sensitivity
in order to get the following relations:
As introduced by Gupta et al. [
16], a quite convenient representation of the sinusoidal correlation function in (
3) is the phasor notation. In practice, we can express the raw measurements in the following alternative way:
where
X corresponds to the amplitude and
the phase of the original sinusoidal function.
We have considered the case in which the ToF signal is reflected only once inside the scene. However, in real scenarios it is highly likely for the light to be reflected multiple times, causing numerous light rays to arrive at the same pixel. This effect is called Multi-Path Interference (MPI). In this case, it is possible to generalize the above description by assuming that the resulting ToF signal is the summation of the different interfering signals, each one described as a phasor. Recall that sinusoidal signals with the same frequency, as well their phasor representation, are closed under summation [
16]. As a consequence, a ToF measurement originated by MPI can be described as
where
is the maximum time of flight of the considered interfering rays and
is the so called backscattering distribution function, describing the strength of the interfering rays, given their times of flight. The MPI phenomenon described above is a non-zero mean error in ToF depth measurements, usually leading to an overestimation of depth. A key aspect of MPI distortion is its dependency on the geometry of the considered scene, which heavily influences the backscattering distribution function
. While having been widely studied [
17,
18,
19,
20], the problem is still challenging.
Other noise sources affecting iToF devices are photon shot noise, linked to the random nature of light, thermal noise due to sensor electronics and signal distortion issues, which are a consequence of non-idealities of the emitted light signals [
12,
21,
22]. These errors, while still relevant, are easier to be tackled, and can be alleviated using calibration and filtering (e.g., bilateral filtering or total variation methods [
23,
24]).
As follows, we will introduce transient cameras, which are another range imaging technology strictly related to iToF; we will describe the relationship between the two and then continue by considering perks and limitations of transient sensors.
1.2. Transient Cameras
As previously remarked, the MPI effect is due to the multiple paths that single light rays follow after a reflection inside the scene. The integration done by an iToF sensor hides these multiple contributions and leads to an overestimation. As a matter of fact, if we were able to avoid such integration and instead capture the intensity of light arriving at the sensor at each time instant, we would be able to isolate the contributions due to different time of arrival of the incoming light reflections and therefore quickly understand what is the relevant information (the direct component) and what instead is noise (the global component).
Transient cameras are relatively new devices that do exactly this. In practice, transient sensors are able to capture the incoming intensity of light at extremely high temporal resolutions. As we are working with the speed of light, current sensors need a temporal resolution in the order of the tens of picoseconds [
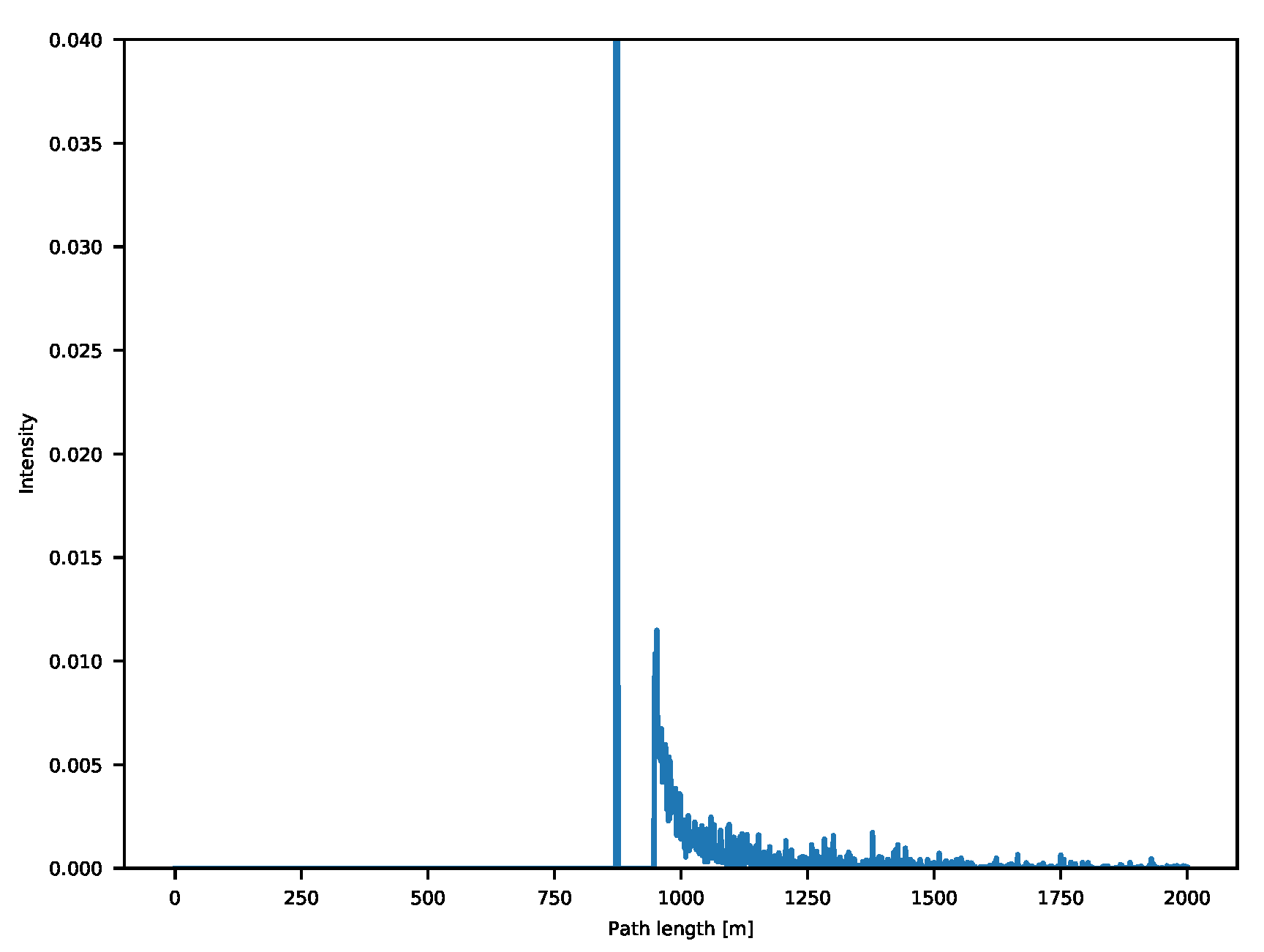
25] for millimeter distance resolution. What we are getting in this way is the behavior of light through time. For each of the sensor pixels, we record the backscattering vector, which makes it easy to avoid any interference-related issue and provides additional insights regarding scene geometry, reflective properties of the captured objects and in theory could even allow to retrieve information of elements out of line of sight [
26]. An example is shown in
Figure 1.
The mentioned perks, while certainly appealing, come at a cost as transient cameras currently have a low spatial resolution and higher prices w.r.t. their ToF counterpart [
25,
27]. The research on transient cameras is quite active—in [
28], the authors introduce a transient frequency transport equation, which helps simplifying transport analysis problems by tackling them in the frequency domain. More recently, in [
29] a co-focal scanning procedure is used to tackle the task of non-line-of-sight imaging, while [
30,
31] tackle the task using the concepts of Fermat paths and of phasor fields, respectively. Nowadays however, transient cameras are mostly limited to research grade instrumentation, while ToF cameras are available as off-the-shelf products.
In this work, we propose to employ the underlying structure of transient images as a prior for MPI denoising. In practice, we propose to train a deep learning model for MPI correction, with a solution following a simplified backscattering model. To our knowledge, this is the first time that transient information is used for the task of MPI correction in a deep learning framework. Many authors in the literature proposed methods to correct MPI starting from the raw data acquired by a ToF camera or from noisy depth measurements [
18,
19,
20,
32]. The focus of this work is the development of a completely new approach for MPI correction based on the underlying structure of the backscattering vectors. The deep learning pipeline we propose is split into two main blocks: a predictive model, which learns the relation between the noisy iToF measurements and the encoded version of our transient data and a fixed model which translates the encoded information into the corresponding transient vector. While the network was developed under the strongly simplifying assumption that MPI is related to a backscattering vector composed by two peaks, one for the direct light reflection and a second peak summarizing the global light, the approach still reaches competitive performance with state-of-the-art approaches. The proposed pipeline is to our knowledge the first data-driven approach going in the direction of transient image reconstruction from noisy ToF data.
The remainder of this paper is articulated in the following way—in
Section 2, we provide a review of the related literature. In
Section 3, we describe the training pipeline and the idea behind our model in depth, while in
Section 4 we show the datasets employed and then provide both qualitative and quantitative evaluation of our approach in
Section 5. Finally, in
Section 6 we draw our conclusions and mention some future developments.
2. Related Work
We will now describe some of the key works in the literature for MPI denoising, starting from approaches dealing with measurements at single or multiple frequencies, then focusing on some of the most recent deep learning methods which set the current state of the art and finally mentioning some other methods combining ToF with other 3D acquisition devices.
Many approaches rely only on standard measurements from ToF cameras. A single modulation frequency acquisition method is introduced by Fuchs et al. in [
33], where a two bounces scenario on ideal lambertian surfaces is considered. In [
34], they refine the approach by improving the reflection model and taking into account materials with multiple albedos. In [
35], Jiménez et al. start from a similar setting and then use an iterative optimization algorithm to find the image which best fits the ToF measurements. The cited approaches show a nice performance but prove to be quite slow due to the high computation time of the algorithms employed, which makes them unfeasible for real-time applications.
The method in [
36] by Freedman et al. is instead based on multi-frequency ToF acquisitions; they study MPI denoising as a LP minimization problem and propose an algorithm which works in real-time relying on a precomputed look-up table (LUT). The approach allows to estimate the backscattering information but the model is limited to a few peaks related to specular reflections. Bhandari et al. [
37] introduce instead a closed-form solution for light rays bouncing a maximum of
K times inside the scene, which however requires a high number of acquisitions at different frequencies (
) to be implemented.
All the mentioned approaches restrict themselves to a simplified model, limiting the maximum amount of bounces, or requiring only specular reflections inside the scene. The need of more general models and the creation of bigger ToF datasets [
19,
38], opened the way for data-driven models, which set the current state-of-the-art. In [
18] Son et al. designed a setup where a ToF camera is mounted on a robotic arm at acquisition time. They then employ two neural networks for the denoising, the first one
F for mapping the ToF measurements to the correct range and the second
G to correctly detect the object boundaries. Marco et al. [
19] proposed an encoder-decoder convolutional neural network (CNN) architecture where the encoder was trained in an unsupervised way over real data, while the decoder instead was trained with supervision on a synthetic dataset they introduced. However, the approach is limited to single frequency data, thus limiting the MPI removal capabilities. In the following years, different architectures and techniques were investigated—in [
24], the authors proposed a CNN for multi-frequency data with two separate branches: a coarse network analyzing the global structure of the scene at a low resolution and a fine one capturing the small details at a local level. In [
38], the authors propose a two-stage architecture combining an encoder-decoder pipeline with a kernel prediction network. Up to that point however, the evaluation of the models was carried out mainly on synthetic data, with only [
17,
38] showing a qualitative evaluation on real images, and [
24] showing the performance of their approach on a real dataset, but at the same time highlighting a clear gap between synthetic and real. Focusing on this issue, in 2019 Agresti et al. [
20] provided two novel realistic ToF datasets and devised an Unsupervised Domain Adaptation (UDA) strategy based on adversarial learning which showed impressive performance both on synthetic and real world data. In 2020, Dong et al. [
32] introduced a residual pyramid network, which focused on MPI patterns at different resolutions for a better prediction.
Table 1 shows a high-level of comparison between the main related works and the approach we introduce in this paper. To the best of our knowledge, this is the first work which exploits deep learning to reconstruct transient information starting from iToF data. The trend is to solve the MPI denoising task in the depth domain [
20,
24,
32], with only SRA [
36] trying to also predict the associated transient information. The proposed method is build on a sparse physical model for the MPI effect, similar to those adopted in [
33,
34,
35,
36,
37], but employs a CNN for the predictions. It relies on iToF data acquired at multiple modulation frequencies by a standard ToF camera, such as many of the most recent best performing works in the field [
17,
20,
24,
36,
38], and it turns out to be one of the simplest in terms of computational complexity.
On a different note, the works in [
39,
40,
41] combine stereo and ToF measurements for MPI denoising. In [
42,
43,
44], the authors propose a modified ToF light source which projects a set of different spatial patterns over the scene and use the additional spatial information to recover a clean ToF signal.
4. Training and Test Datasets
For the supervised optimization of the proposed approach we need a training set containing raw ToF data together with the corresponding ground truth transient data. Note that from geometrical considerations it is clear that the true depth value is always associated to the shortest returned path that corresponds to the direct component, and therefore depth information can be easily extracted from the transient scene. The acquisition of a real dataset with transient ground truth, however, is quite a complex and time consuming task; since no publicly available datasets of the kind exist, we had to rely on synthetic data.
For the training of the approach, we relied on the FLAT synthetic dataset introduced in [
38], which contains transient data. At first, we applied a depth equalization procedure, in order to obtain a final distribution that is as uniform as possible. Then, the data was processed as discussed in
Section 3.2.1 with the addition of a clipping operation for the intensity of the second peak, whose maximum value could be
, with
and
the intensity of the two peaks. Finally, the input iToF values were computed from the compressed transient information using the measurement model described in Equation (
10) with modulation frequencies of
and 60 MHz. After the processing the data was then split into a training and a validation set, made of 211200 and 2064
patches respectively. Note that no test set was built at this phase since the testing will be performed on real images.
The performance in the depth estimation provided by the proposed approach is evaluated on real-world scenes where no transient data is given. Since our objective is MPI denoising, transient data is not required at the testing phase, all that is needed are the raw measurements at the desired modulation frequencies and the corresponding ground truth depth maps. From the predictions on the selected dataset, we can focus on the first peak and use that to estimate the depth value of each pixel. The real-world datasets on which we carry out our analysis are the three real ToF datasets
provided by Agresti et al. in the works [
20,
24]. All three datasets have been captured in a laboratory environment without external illumination using the SoftKinetic ToF camera DS541 at multiple modulation frequencies. For each scene, they provide unwrapped phase, amplitude and intensity, as well as depth ground truth. The datasets are in the depth range between 58 and 203
.
In
Table 2 we can see the resolution, number of images and acquired modulation frequencies of the three datasets.
In particular, the dataset will be used for validation while and will be our test sets. Notice that, for all three considered datasets, we used only the data acquired at 20, 50 and 60 as input for the proposed method.
5. Experimental Results
In this Section we are going to present some experimental results obtained running the proposed approach for backscattering vector estimation.
The proposed network was trained on the simulated dataset described in
Section 4 using the Adam optimization algorithm. The entire dataset was divided into batches of 1024 samples each, and the gradient at each iteration was computed on a single batch. We run the training for a total number of
epochs on a Nvidia GeForce GTX 1060 GPU. The overall time required was around 6 h. To account for the noise always present in any real-world ToF measurements, at each iteration a gaussian zero-mean random noise is added to the real and imaginary parts of the simulated raw ToF data:
The Gaussian noise is independent and identically distributed across all the samples and across all the acquired phasors at the different modulation frequencies. It is also independently added to the real and complex component. Changing the noise at each iteration helps avoiding overfitting and acts as a form of regularization. The network never sees the same exact input data more than once. Moreover, it helps the network in learning to denoise the input data, giving more importance to the more stable relationships between the acquired phasors and less to small fluctuations around the average. In
Section 5.1 we will show this in more detail; for all other experiments, unless otherwise stated, we will use noise with a standard deviation
. The choice of this value was performed as mentioned in
Section 5.1.
The best set of weights are chosen according to the network performance on the real dataset
, which we employ as a realistic validation set. The testing is then carried out from a qualitative and quantitative point of view on the two real datasets
and
provided by Agresti et al. [
20,
24]. As anticipated in
Section 4, the evaluations focus on the degree of MPI correction, while a few comparisons concerning the reconstruction of the transient component are reported in
Section 5.1. The metric used to quantify the error in the depth domain is the Mean Absolute Error (MAE).
Figure 5 reports the depth error maps obtained applying our method on the real datasets
and
. The average MAEs for raw ToF measurements at 60
are respectively
and
for
and
; these errors are reduced to
and
for the two datasets by the proposed method.
Even if we are considering only two reflections, experimental results show good MPI compensation capabilities, confirming that many real-world cases can be well approximated by a two components reflection model. This is due to the fact that, since the light power decays with the square of the distance, higher order reflections reaching the camera are very dim. Moreover, real lambertian surfaces present always a fraction of specular reflections and thus our assumption in first approximation holds also for those surfaces. From
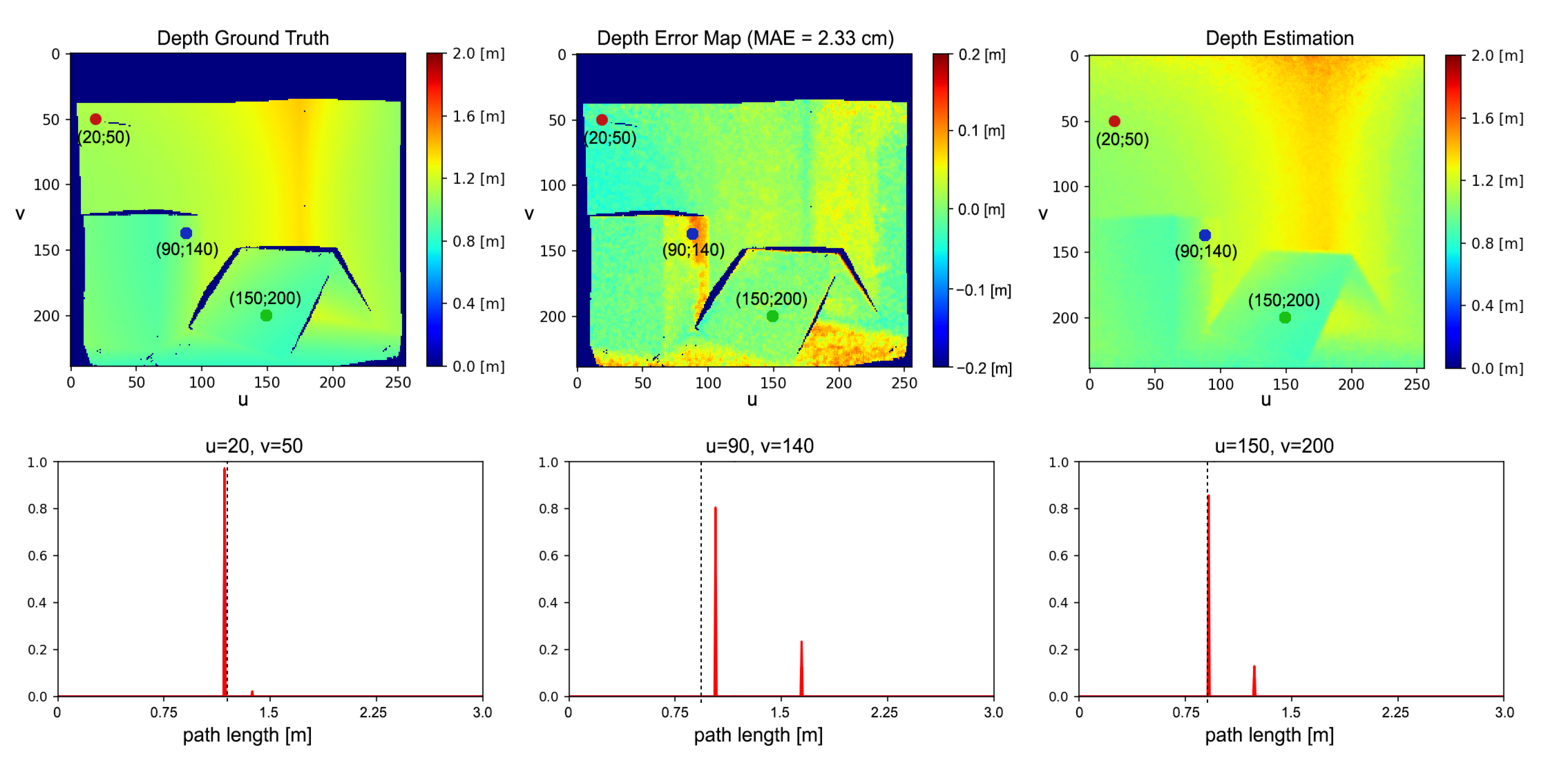
Figure 5 it is possible to see how our approach removes most of the MPI on wall surfaces and reduces it in proximity of edges. The large amount of MPI on the floor surfaces is also consistently reduced even if some depth reconstruction errors are still present. These areas are probably subject to more complex reflection patterns and are therefore more error prone. Looking at the network output at some significant points (
Figure 6), it is evident that it has learnt to discriminate between MPI-free and MPI-affected pixels, introducting the global component only when it is necessary to compensate for the MPI effect and providing a more reliable depth estimation.
We have performed a thorough consistent comparison between different state-of-the-art algorithms for MPI compensation, studying how our approach behaves with respect to the others techniques. The compared algorithms are the SRA method proposed by Freedman et al. [
36], DeepToF proposed by Marco et al. [
19] and the two methods proposed by Agresti et al. [
20,
24].
Table 3 reports the MAEs and the relative errors for the compared algorithms on the real datasets
and
, while
Figure 7 shows a qualitative comparison between the competing approaches. The relative errors are computed as the ratio between the MAE of the approach and that of the reconstruction based on the highest input frequency (60 MHz for all the approaches but for DeepToF [
19], which uses 20 MHz). From
Figure 7 it is possible to notice how our approach achieves a much better MPI reduction on the floor and wall surfaces if compared with SRA and DeepToF. It also outperforms [
24] and achieves results very similar to [
20] even if no real depth acquisitions have been used for the training.
On real-world scenes our approach achieves performance comparable to the other state-of-the-art algorithms. It produces an error of
on
and an error of
on
, performing better than all other methods, with the exception of the unsupervised domain adaptation technique of Agresti et al. [
20] which produces test errors of respectively
and
. We stress the fact that the unsupervised domain adaptation technique has been adapted using unsupervised real data similar to the one in
and
, while our approach relies only on a completely different synthetic training dataset. It is remarkable to notice that our method clearly outperforms the SRA method [
36], which is the one adopting the most similar setup to ours. We both acquire data at three modulation frequencies and use a physical model to describe the MPI effect under the specular reflections assumption. The MAEs on datasets
and
obtained by SRA are respectively
and
.
Figure 8 shows the depth profiles estimated in proximity of a corner using the compared algorithms. Also in this case our network is able to reconstruct depth values which closely resemble the ground truth.
Concerning the complexity of the compared algorithms, note that our approach is able to achieve state-of-the-art performance using around 22k learnable parameters (14k in the version without the exploitation of the spatial correlation), approximately an order of magnitude less with respect to the 145k parameters required by the two works of Agresti et al. [
20,
24]. The DeepToF method [
19] requires even more parameters (330k). For SRA [
36] the complexity is estimated by the size of the associated look-up table (LUT). Fixed the number
L of discretization steps for the input raw iToF measurements, the size of the LUT grows as
.
As a final study, we decided to investigate the goodness of the prediction of our network for the intensity and time components of the two predicted peaks (corresponding to direct and global component). Since the
and
dataset do not have transient information, we relied on the synthetic validation dataset we introduced in
Section 4 in order to compare our approach to [
36], which is the only one among the compared approaches that estimates the second peak. Comparing the accuracy of the reconstruction of the global component is quite straightforward—from
Table 3 we can retrieve the depth information (which is linked to the time displacement) and we can see that our method reaches significantly better results (
and
on the
and
datasets respectively vs.
and
of [
36]), while concerning the intensity values of the first peak we obtained a MAE of
for our method against
for SRA. For the second peak, since it is not always present, we considered the capability of the approaches to correctly detect its presence with the well known precision-recall measures. The precision (number of pixels correctly identified as having a second peak over the total amount that have it), is
for our approach against 1 for SRA. However, these results are due to the fact that SRA overestimates the presence of the second peak as shown by the recall measure (number of pixels correctly identified as having a second peak divided by the total amount of peaks identified), with a result of
for our approach against
for SRA. Our approach also better estimates the intensity of the second peak with a MAE of
against
of SRA [
36].
5.1. Ablation Studies
In this section, we present some ablation studies to evaluate the impact of some of the employed design choices. In particular we focus on the addition of noise during training, on the exploitation of the spatial correlation between pixels and finally on the choice of the loss function.
Firstly, we will consider the addition of noise to the simulations. As we have mentioned, there is a loss in performance when switching from synthetic to realistic data, due to the different characteristics of the two sets. The addition of noise helps the generalization capabilities of the network and reduces the gap.
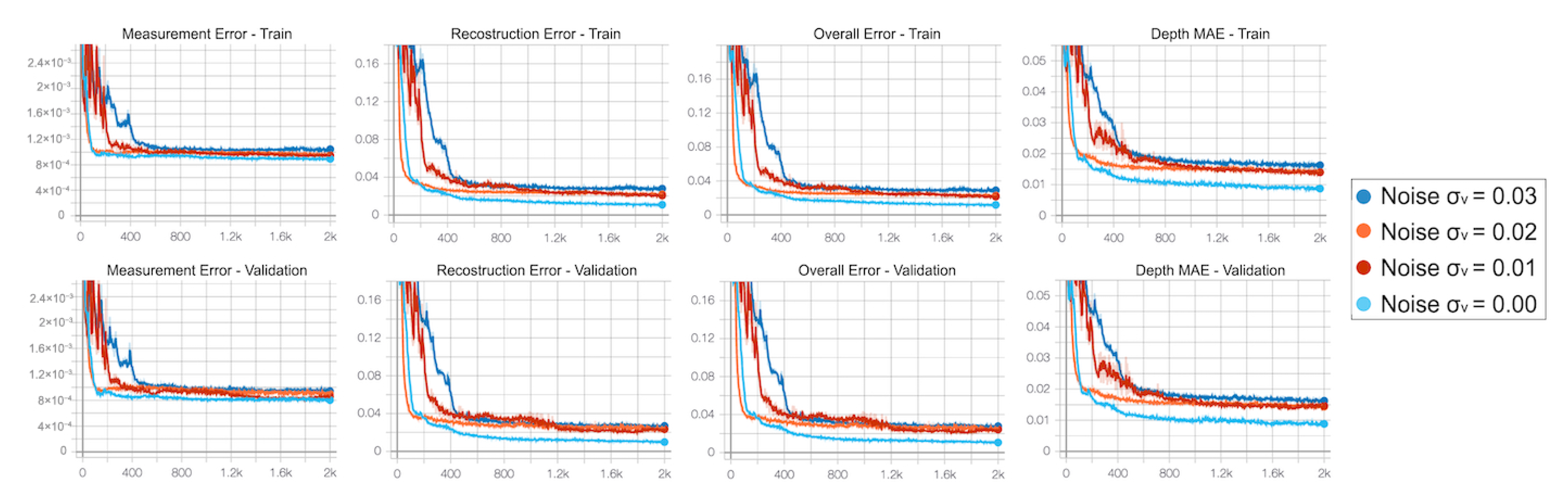
We repeated the training multiple times, varying the standard deviation of the noise
added to the input data. At each epoch we monitored the behaviour of measurement error
, reconstruction error
and overall error
, as well as the MAE on the depth estimated using the predicted output backscattering vector.
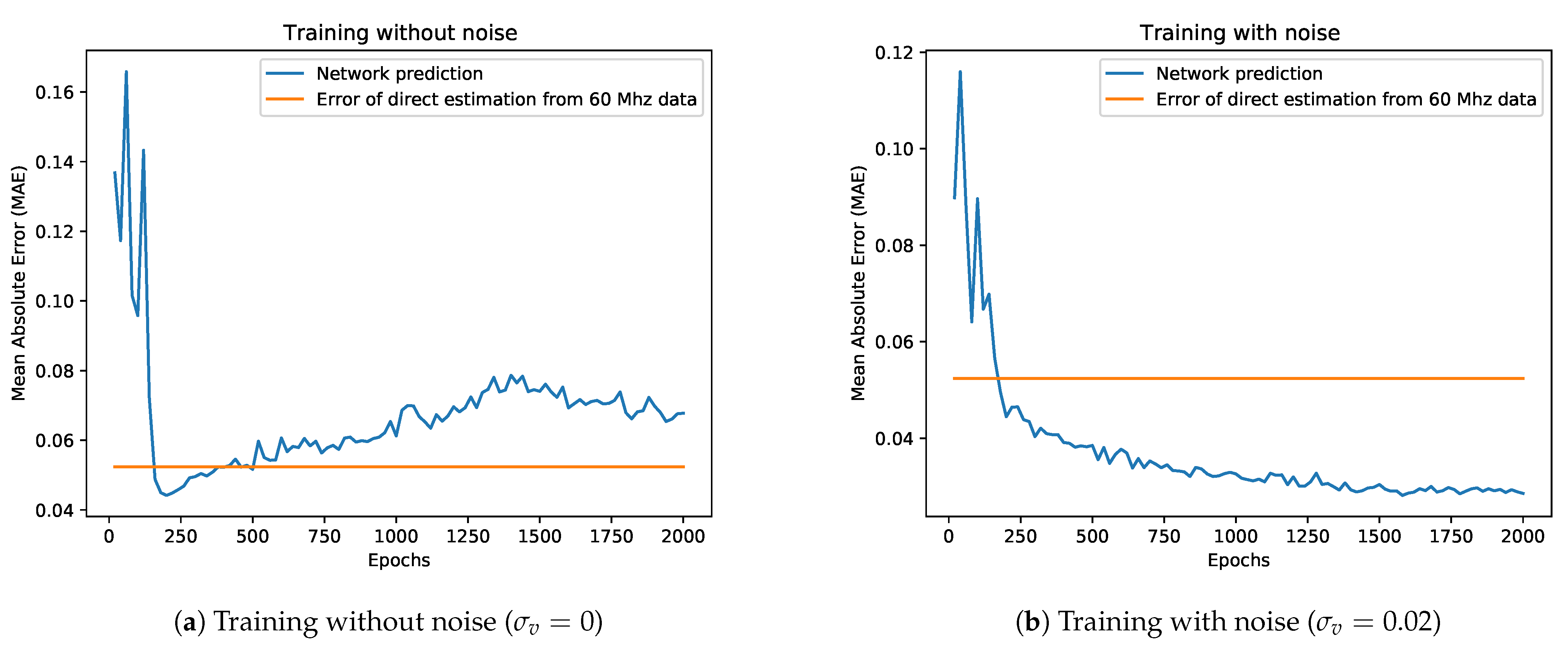
Figure 9 reports the behaviour of the considered metrics during the optimization on both the synthetic training and validation sets. As expected, the higher the noise level, the larger the errors of the predictive model will be for the synthetic data. More interesting is instead the behaviour on real data: in
Figure 10a we show the performance of the network trained without noise on the dataset
compared to a direct estimation of the depth from the component at 60 MHz. It is clear that, after a promising start, the network performance starts quickly degrading as it better learns the synthetic dataset; as the trend goes on we quickly get to the point where its performance gets worse with respect even to a rough estimation based on a single frequency component. The opposite trend is instead shown in
Figure 10b, where we display the network performance over the
dataset after training the model with a noise std of
. The network quickly outperforms the naive reconstruction based on a single modulation frequency while showing an overall better behaviour.
In
Table 4, we show the performance of our network on the
dataset for different noise levels. While a small amount of noise helps with the generalization, if it gets too high we instead make the task too hard to solve. Experimentally, a noise std of
turned out to be the best compromise, as can be seen in the table.
Another line of investigation is the relevance of the spatial correlation in the final prediction. The idea is that the network should take advantage also from the local information coming from a small neighbourhood around each pixel to produce a more reliable result. To this end, we trained our network for increasing kernel sizes and evaluated its performance on the real datasets. In
Table 5 we can see that we have the best results for a window size of
pixels around the central one, while they get worse for increasing sizes. Focusing on the network trained without spatial correlation (
windows) the average MAEs obtained over
and
are respectively 3.43 and 2.52 cm, which turn into 2.99 and 1.88 cm after some bilateral filtering. Experimental results confirm our intuition. In the noise-free case the two networks converge to very similar results, while in the case of noise the spatial correlation helps providing a smoother prediction making the network more resilient against noise.
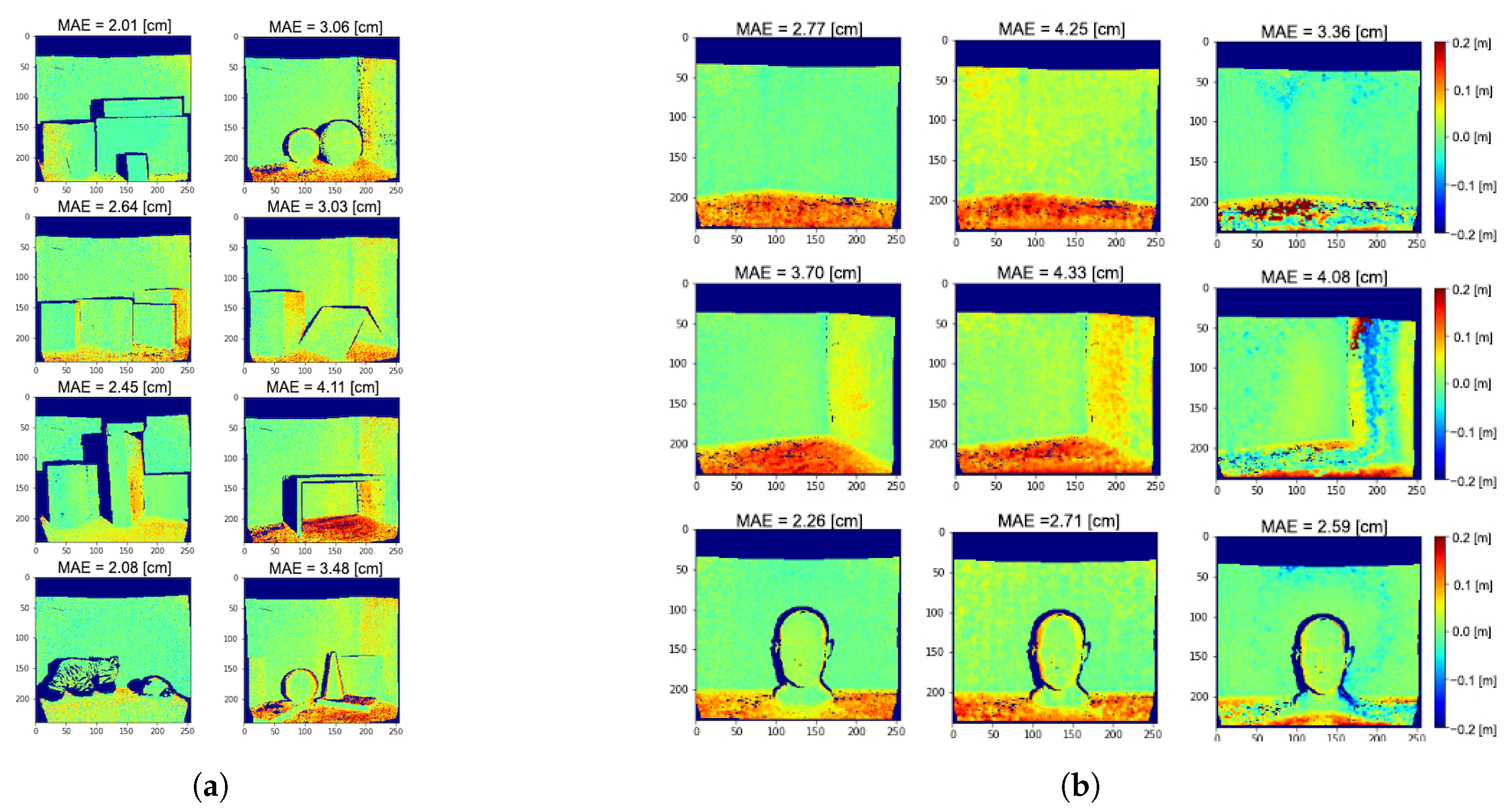
Figure 11a reports the depth error maps we get on dataset
without exploiting the spatial correlation.
In
Figure 11b, we show the results obtained on three real scenes for values of
and 3 (corresponding to windows of size
,
and
). It is quite clear how a bigger window size generates some strong artifacts and leads to over-correcting MPI. One more time we stress the importance of linking the final prediction for each pixel to the corresponding input pixel since it is the one which carries the most information, using only a small amount of spatial correlation to refine the estimation.
To conclude the discussion on spatial information, notice that considering only a very small window size around each pixel also improves the generalization capabilities of the network. As pointed out by the ablation, a direct approach such as the one we attempted (increasing the window size) leads to not very satisfactory performances, but probably the spatial information could be exploited by using a more refined branch (e.g., a second architecture in parallel with a large window size, that only considers the high level structure of the scene, similarly to [
24]).
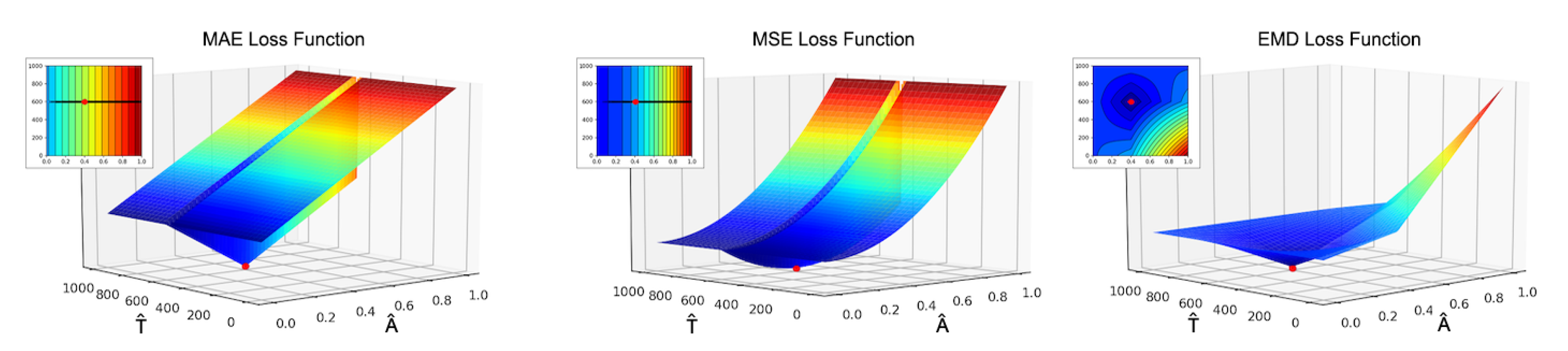
The choice of a proper loss function is a crucial point in the machine learning pipeline. As already stated, some problems arise with the reconstruction loss function
since we are dealing with highly sparse vectors and in this case the gradient likely vanishes. In our study we evaluated many different loss function models in order to identify the best suitable one for our task. We started from the common MAE and MSE but they produce an all-zero output backscattering vector in most of the cases. Intuitively, looking at the behaviour of these loss functions in
Figure 12 it is evident that applying the gradient descent algorithm the solution easily gets stuck on bad local minima. Then, we shifted to cross-correlation based loss functions obtaining a significant improvement in the final prediction but they still are subjected to numerical instabilities during the optimization phase. The best results came from the weighted Earth Mover Distance introduced in
Section 3.2.3 which exhibits good convergence properties and turns out to be able to drive the algorithm towards the optimal solution in a smooth fashion.
6. Conclusions
In this paper, we have presented a novel approach for MPI denoising based on transient information. Since neural networks have issues when handling high dimensional data, which is exactly what backscattering vectors are, we split the problem in two parts—a predictive model and a backscattering model. The predictive model takes the input iToF measurements and predicts an encoded version of the transient information, while the backscattering model links each encoded representation to the respective transient one. In this work, the backscattering model has been kept fixed since our aim was MPI denoising rather than transient data reconstruction. In practice, while the direct component has been kept, the global component has instead been summarized into a single peak. This allowed to build a simple but effective model where the neural network only had to predict two peaks from the input raw measurements.
Even if all the trainings have been performed on synthetic data, the testing has been done on real iToF data. Our approach showed close to state of the art performance, without the need of a heavy or complex structure or of a large amount of training data (our model contains only a few thousands parameters).
Our work leaves open several future research directions, first of all an extension of the backscattering model which as of now is quite simple and an extension of the approach employing a similar model for transient data reconstruction. We will also consider more advanced architectures in order to exploit the spatial context in the backscattering estimation.