Abstract
Vehicular sensor networks (VSNs) have emerged as a paradigm for improving traffic safety in urban cities. However, there are still several issues with VSNs. Vehicles equipped with sensing devices usually upload large amounts of data reports to a remote cloud center for processing and analyzing, causing heavy computation and communication costs. Additionally, to choose an optimal route, it is required for vehicles to query the remote cloud center to obtain road conditions of the potential moving route, leading to an increased communication delay and leakage of location privacy. To solve these problems, this paper proposes an efficient privacy-preserving data sharing (EPDS) scheme for fog-assisted vehicular sensor networks. Specifically, the proposed scheme utilizes fog computing to provide local data sharing with low latency; furthermore, it exploits a super-increasing sequence to format the sensing data of different road segments into one report, thus saving on the resources of communication and computation. In addition, using the modified oblivious transfer technology, the proposed scheme can query the road conditions of the potential moving route without disclosing the query location. Finally, an analysis of security suggests that the proposed scheme can satisfy all the requirements for security and privacy, with the evaluation results indicating that the proposed scheme leads to low costs in computation and communication.
1. Introduction
Vehicular sensor networks (VSNs) [1,2,3], that is, a combination of wireless communication given by vehicular ad hoc networks [4] and the sensing devices installed in the vehicle, can improve traffic conditions in urban cities, and have recently received considerable attention. In VSNs, the vehicles equipped with sensing devices can record a myriad of data reports on the road conditions and environment situations, and these data reports need be uploaded to the remote cloud center [5,6] for processing and analyzing. In addition, vehicles often need to query the road conditions of potential moving routes at remote cloud centers. However, uploading a large amount of data reports to the cloud data center consumes heavy bandwidth, and leads to an increased communication delay.
Recently, fog computing [7] has been proposed to extend the capabilities of cloud computing [8] near vehicles [9], which can locally handle the data reports uploaded by vehicles. These new properties will bring about benefits such as location awareness and low latency. Fog computing has already been used to provide low latency services in vehicular sensor networks, such as navigation services [10] and surface condition monitoring [11].
A typical architecture of fog-assisted vehicular sensor networks (F-VSNs) [12,13,14] contains the trusted authority, cloud center, fog nodes, and vehicles. The trusted authority is responsible for generating system parameters, and the registration of all entities (cloud center, fog nodes and vehicles). The cloud center provides centralized control with strong computing power and large storage capacity from a remote location. Fog nodes have available computing, storage, and communication resources [15], which is deployed at the edge of networks with physical proximity to vehicles, playing as the bridge across the vehicles and the cloud center. Vehicles are installed with a variety of smart sensors that can sense road conditions and environmental parameters. F-VSNs allows some computations and processing to be performed at the fog nodes, greatly reducing the consumption of communication time and energy.
Although F-VSNs brings a great deal of benefits and conveniences, there still exist several issues in terms of data collection and data query. Specifically, vehicles generate a large amount of sensory data reflecting the road conditions and environment situations, and need to upload the sensory data to cloud center for further processing and analyzing, which brings heavy computation and communication costs. To solve this problem, data aggregation technology, which is designed to aggregate multiple data into one report, has recently received more and more attention.
However, using the existing data aggregation schemes [16,17,18,19,20,21,22] cannot determine the number of data reports produced in each road segment, and cannot compute the average sensory data in each road segment. To solve the problem, the scheme [23] exploits the Chinese remainder theorem and Paillier cryptosystem to calculate the average sensory data in each segments; however, it brings heavy computation and communication costs. In addition, to choose an optimal route, vehicles often query about the road conditions of the potential moving routes, but the query reports uploaded by vehicles are tightly associated with the query location, and thus the query location could be disclosed.
The oblivious transfer [24,25], homomorphic encryption technology [26,27], and proxy re-encryption technique [23] have been exploited to hide the query location. However, it is worth noting that the computation and communication costs by the schemes [24,25] is directly proportional to the data dimension, the schemes [26,27] do not support the scenario with high vehicle density, and the scheme [23] needs heavy computation and communication costs.
1.1. Our Contributions
To solve the aforementioned problems, this paper proposes an efficient privacy-preserving data sharing (EPDS) scheme for fog-assisted vehicular sensor networks. The main contributions of this paper are as follows:
- First, the proposed EPDS scheme exploits the super-increasing sequence [20] for achieving multi-dimensional data aggregation, while calculating the average sensory data in each road segment, greatly saving on the resources of communication and computation.
- Secondly, by utilizing the modified oblivious transfer [28], the proposed EPDS scheme is able to query about the road conditions of the potential moving routes without disclosing the query location.
- Thirdly, an analysis of security indicates that the proposed EPDS scheme is proven to be secure under elliptic curve discrete logarithm (ECDL) assumption in the random oracle model and satisfies all the requirements for security and privacy.
- Finally, the performances of computation and communication in costs are evaluated through quantitative calculations, with the results that the proposed EPDS scheme is of more efficiency than others.
1.2. Organization
This paper is organized as follows. The related work is surveyed in Section 2. We introduce the background in Section 3. The concrete scheme is proposed in Section 4. Section 5 provides an analysis of the security. In Section 6, the performance evaluation is performed. Section 7 concludes the paper.
2. Related Works
Some works closely related to this paper are briefly reviewed below.
In F-VSNs, massive sensory data is produced in each data dimension, and needs to be uploaded for further processing and analysis; data aggregation schemes [16,17,18,19,20,21,22,23] have received considerable attention recently, and are roughly classified into two categories: single-dimensional data aggregation [16,17,18,19] and multi-dimensional data aggregation [20,21,22,23]. Zhuo et al. [16] introduced a data aggregation scheme, which protects each involved entity’s identity privacy, and allows the requester to examine the correctness of the obtained results. Rabieh et al. [17] employed the data aggregation technique to find out the routes for the vehicle to be in each road segment; however, it only can calculate the data aggregation result, and cannot recover the content in each data dimension.
Xu et al. [18] constructed a privacy-preserving data aggregation scheme that can classify messages based on where and when the sensor data is collected, and aggregate the data collected in the same area and period. Sun et al. [19] designed a data aggregation mechanism considering data integrity and access control. However, the schemes [16,17,18,19] are unable to determine the number of the data reports produced in each data dimension, and further fail to calculate the average sensory data in each data dimension. Lin et al. [20] integrated the perturbation technique and super-increasing sequence to combine multiple aggregated data into one data report to improve the energy efficiency.
Lu et al. [21] employed the homomorphic Paillier encryption, one-way hash chain technique and Chinese remainder theorem to achieve lightweight multi-dimensional data aggregation. On the basis of the super-increasing sequence and modified homomorphic Paillier encryption, Wang et al. [22] introduced a multi-subtasks aggregation scheme, in which each aggregated datum is mapped to a specific area and period. Kong et al. [23] designed a privacy-preserving multi-dimensional data sharing scheme using the Chinese remainder theorem and modified Paillier encryption, with counting the number of the sensory data collected at each segments and calculating the average sensory data in each segment.
Although schemes [20,21,22,23] are able to calculate the average sensory data in each data dimension, they bring heavy computation costs and communication overhead. In addition, the query vehicle usually wants to know the road conditions of the potential moving route, which could lead to that the query location being disclosed in the data query process, the schemes in [23,24,25,26,27] have been proposed to solve this problem.
Ghinita et al. [24] and Paulet et al. [25] employed the oblivious transfer to hide query location in the data query process, but the communication cost of schemes [24,25] is directly proportional to the data dimension. Zhu et al. [25,26] utilized an improved homomorphic encryption technology to protect the query location in location-based services, but it do not support scenarios with a high vehicle density. Kong et al. [23] utilized the proxy re-encryption technique to hide the query location, but it does not support queries of whole network sensory data during the data query phase.
To sum up, from the review above, the available data aggregation schemes [16,17,18,19,20,21,22,23] either fail to determine the number of data reports produced in each data dimension or bring heavy computation and communication costs. In addition, the communication costs of the existing schemes [23,24,25,26,27] are either directly proportional to the data dimension or bring heavy communication costs in the data query process.
To address the issues above, we propose an EPDS scheme for fog-assisted vehicular sensor networks, which can not only reduce the computation and communication costs, but also calculate the average sensory data in each road segment. Additionally, the proposed EPDS scheme can query the road conditions of potential moving routes without disclosing the query location.
3. Background
3.1. System Model
The system model is presented in Figure 1, which is composed of five entities: trusted authority (), cloud center (), the data collection vehicle , fog node , and the data query vehicle . The road area is divided into m segments, and each segment k is represented by a unique two-dimensional identifier , approximating of the location coordinates [23]. As to readability, the definitions of notations employed in this study are illustrated in Table 1.
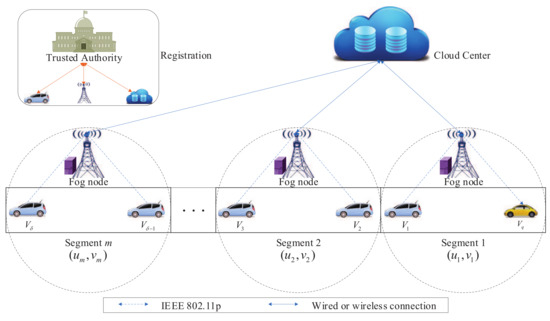
Figure 1.
System model.

Table 1.
Notations
The wireless connections between the vehicles and the fog nodes are brought about by the Institute of Electrical and Electronics Engineers (IEEE) 802.11p standard [29]. The connections between the fog nodes and are achieved via either the wired links or other links with low transmission delay and high bandwidth.
: A fully trusted entity, which is responsible for the management of the security parameters for the system and the registration of the cloud center, fog nodes, and vehicles, and periodically updates the system information.
: An honest-but-curious entity, which is responsible for providing centralized control with powerful storage and computing capabilities from a remote location. In addition, it can perform computational analytics from data reports uploaded by the fog nodes, and distribute data to all fog nodes for further sharing with vehicles [30].
: It is equipped with smart sensors, periodically formatting a data report from the collected sensory data and uploading the data report towards the fog node.
: This consists of a road side unit and an edge server [13], and aggregates the data reports uploaded by the data collection vehicles under its communication range and transmits the aggregated data report towards . Meanwhile, each fog node manages one or more segments, and can assist in sharing the sensory data to the query vehicle [31].
: To choose an optimal route, usually sends a query report to the fog node, then the fog node returns a response report to .
In our system model, we assume the fog node is honest-but-curious, i.e., it is able to correctly execute the operations defined in the protocol; however, it also can try to violate the privacy of the vehicle through analyzing the vehicle’s data report and query report; meanwhile, we assume neither the fog nodes nor the query vehicles can collude with each other in the proposed EPDS scheme. Additionally, we assume there exists an attacker, which can eavesdrop on the data transmission and launch attacks.
3.2. Security Requirement
The following security requirements should be achieved.
Authentication and data integrity: The proposed EPDS scheme should guarantee that any reports are not modified during the transmission process, and can detect any modification of the reports; moreover, any entity in F-VSNs should be able to be authenticated to ensure the reliability of the data source.
Confidentiality: To ensure the privacy of sensory data, the proposed EPDS scheme should provide confidentiality, i.e., no attacker can obtain the sensory data from data report.
Location privacy preservation: To protect vehicle’s query location, it is important not to disclose the query location to fog nodes that provide location-based services in the data query process.
Identity privacy preservation: Apart from the , any entities should not trace or recognize the identity of the data collection vehicle by analyzing the received data reports.
Traceability: should be able to reveal the identity of the malicious vehicle uploading the bogus data report.
Unlinkability: Apart from the , neither fog nodes nor the malicious vehicles can determine whether the two data reports are from the same vehicle.
Resistance to attacks: The proposed EPDS scheme should be able to withstand various popular attacks such as the modification attack, replay attack, impersonation attack, and man-in-the-middle attack.
3.3. Elliptic Curve
Let be a finite field with a prime number p. The elliptic curve E over defined as the set of all points meeting , where and [32,33].
An infinity point O, and other points on E, form an additive cyclic group with the order q and generator P. Let and , the scalar multiplication over is described as (k times).
3.4. Security Assumption
ECDL problem [34,35]: Given two elements , the ECDL problem is to find an integer such that .
ECDL assumption [34,35]: It is hard for any probabilistic polynomial-time algorithm to solve ECDL problem with non-negligible probability.
4. The Proposed Scheme
The proposed EPDS scheme includes system initialization, registration, data collection, and data query phases. Note that the data flows in the data collection and data query phases are shown in Figure 2.
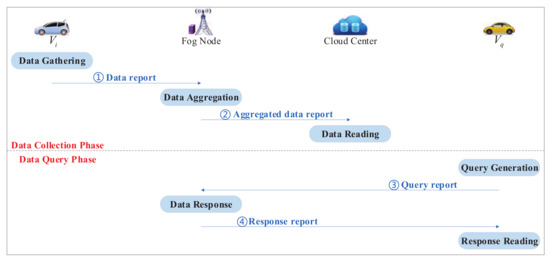
Figure 2.
Data flows in the data collection and data query phases.
4.1. System Initialization
produces all system parameters through executing the following steps.
- (1)
- randomly chooses a large prime number p, and selects a non-singular elliptic curve E defined by , where .
- (2)
- picks a group of E with the prime order q and a generator P.
- (3)
- randomly chooses as its master key and computes its public key .
- (4)
- chooses eight one-way hash functions , , .
- (5)
- chooses a super-increasing sequence , such that , (), where are large prime numbers and d is the maximum value of the data. Then, assigns prime number towards segment k.
- (6)
- publishes the system parameters .
4.2. Registration
All vehicles, fog nodes, and cloud centers register with .
4.2.1. Registers with
- (1)
- sends the identity to the in secure channel.
- (2)
- After confirming the identity , randomly chooses and computesand sets , where represents the valid period of .
- (3)
- randomly chooses and computes
- (4)
- randomly chooses a sharing key , and transmits the pseudo identity , the private key and the sharing key to in a secure channel.
4.2.2. Registers with
- (1)
- sends the identity to the in a secure channel.
- (2)
- randomly chooses and computes
- (3)
- sends the private key to in a secure channel.
4.2.3. Registers with
- (1)
- randomly chooses and computes .
- (2)
- sends the private key x and public key to in a secure channel.
4.3. Data Collection
The data collection phase includes three processes: data gathering, data aggregation, and data reading.
4.3.1. Data Gathering
gathers sensory data in a short period of time, e.g., every five minutes: (i) if there is a sensory data obtained at road segment k under , i.e., , then ; (ii) if there is no sensory data obtained at road segment k under , i.e., , then .
produces a data report through executing the following steps:
- (1)
- formats and into and .
- (2)
- randomly selects , and computes
- (3)
- randomly picks and calculateswhere is current timestamp.
- (4)
- transmits the data report towards , as shown in Figure 2 (①).
4.3.2. Data Aggregation
Supposing w vehicles upload the data reports to , where . can aggregate data reports through executing the following steps:
- (1)
- checks whether is valid and is fresh for each . If is not valid or is not fresh, will be rejected. Otherwise, performs the batch verification using small exponent test [36]. randomly selects a set of small numbers and checks whether the following equation holdsIf it does hold, computes
- (2)
- randomly picks and calculateswhere is current timestamp.
- (3)
- transmits the aggregated data report towards , as shown in Figure 2 (②).
4.3.3. Data Reading
After receiving from respectively, executes the following steps:
- (1)
- checks whether is fresh for each . If is not fresh, will be rejected. Otherwise, randomly chooses a set of small numbers and performs the batch verification using small exponent test [36]. verifies whether the following equation holdsIf it does hold, calculatesBy solving the discrete log of and with the base P, utilizing the Pollard’s lambda algorithm [37], can obtain
- (2)
- distributes and to all fog nodes for further sharing with vehicles.
4.4. Data Query
The data query vehicle intends to query the data captured at segment c with the identifier at the . The phase includes three processes: query generation, data response, and response reading.
4.4.1. Query Generation
- (1)
- selects two random numbers and calculates
- (2)
- randomly picks and calculateswhere is the current timestamp.
- (3)
- transmits the query report towards , as shown in Figure 2 (③).
4.4.2. Data Response
- (1)
- After receiving , checks whether is valid and is fresh. If is not valid or is not fresh, will be rejected. Otherwise, verifies whether the following equation holdsIf it does hold, selects two random numbers and calculates
- (2)
- randomly picks and calculateswhere is the current timestamp.
- (3)
- transmits the response report towards , as shown in Figure 2 (④).
4.4.3. Response Reading
- (1)
- After receiving , checks whether is fresh. If is not fresh, will be rejected. Otherwise, verifies whether the following equation holdsIf it does hold, calculatesBy solving the discrete log of with the base P, utilizing the Pollard’s lambda algorithm [37], can obtain .
- (2)
- By calling the Algorithm 1, can achieve the average sensing data captured at segment c.
| Algoruthm 1 Recovery captured at segment c |
| Input: , , , , and |
| Output: |
| begin: |
| set , ; |
| for to c do |
| , ; |
| , ; |
| return . |
| end |
5. Security
This section depicts the security proof of the proposed EPDS scheme in the random oracle model. Additionally, a security evaluation and comparison on the proposed EPDS scheme and schemes of [17,19,23,25,26] is conducted.
5.1. Security Model
The security model of the proposed EPDS scheme can be found in the Appendix A.
5.2. Security Proof
The security proof of the proposed EPDS scheme can be found in the Appendix B.
5.3. Analysis and Comparison of Security Requirement
Authentication and data integrity: Based on Theorem 2, no polynomial-time attacker is able to fake a valid data report owing to the ECDL assumption. Therefore, authentication and data integrity can be ensured in the proposed EPDS scheme.
Confidentiality: Based on Theorem 1, without the cloud center’s private key x, any attacker is unable to compute the sensing data and , and thus confidentiality can be ensured in the proposed EPDS scheme.
Location privacy preservation: Based on Theorem 1, without the the data query vehicle’s private key , no attacker can obtain the query location from , , , , and hence the location privacy can be guaranteed in the proposed EPDS scheme.
Identity privacy preservation: On the basis of the proposed EPDS scheme, the identity of is only contained in the pseudo identity , where , and . To extract the identity of , the attacker has to compute . However, it is impossible to solve for any attacker to obtain without knowing and s. Therefore, the identity privacy is guaranteed in the proposed EPDS scheme.
Traceability: In accordance with the proposed EPDS scheme, can adopt its own master key s to calculate , and find out the identity of from the pseudo identity involved in the data report, with the proposed EPDS scheme satisfying the traceability.
Unlinkability: On the basis of the proposed EPDS scheme, the data reports generated by any vehicle are random, and any attacker cannot link the two data reports sent by the same vehicle, with the proposed EPDS scheme realizing the traceability.
Resistance to attacks: The proposed EPDS scheme is able to withstand the networks attacks in the following:
- Modification attack: Based on Theorem 2, any polynomial attacker is unable to forge a valid data report with modification on data reports found.
- Replay attack: On the basis of the proposed EPDS scheme, the timestamp is contained in the data report. By examining freshness of the timestamp, the verifier is able to bear any replay attacks.
- Impersonation attack: From Theorem 2, no attacker can fabricate a legal data report without vehicle’s private key.
- Man-in-the-middle attack: The analysis of the modification attack shows that any modification of the data reports on transmission is able to be found.
Security comparisons of schemes [17,19,23,25,26] and the proposed EPDS scheme are displayed in Table 2. S1, S2, S3, S4, S5, S6, S7, S8, S9, and S10 are used to represent authentication and data integrity, confidentiality, location privacy preservation, identity privacy preservation, traceability, unlinkability, the modification attack, the replay attack, the impersonation attack, and the man-in-the-middle attack, respectively.

Table 2.
Security comparisons. Efficient privacy-preserving data sharing (EPDS), √ represents “satisfy” and × denotes “does not satisfy”.
In accordance with Table 2, Rabieh et al.’s scheme [17] is able to provide location privacy preservation, identity privacy preservation, and traceability. Sun et al.’s scheme [19] cannot achieve location privacy preservation. Kong et al.’s scheme [23] cannot achieve identity privacy preservation, traceability, the replay attack, and the man-in-the-middle attack. Paulet et al.’s scheme [25] cannot achieve authentication and data integrity, identity privacy preservation, traceability, the modification attack, the replay attack, the impersonation attack, and the man-in-the-middle attack. Zhu et al.’s scheme [26] cannot achieve identity privacy preservation and traceability, the replay attack, and the man-in-the-middle attack. In contrast, all security requirements are able to be satisfied in the proposed EPDS scheme.
6. Performance Evaluation
We analyze the computation and communication costs of these schemes [17,19,23,25,26] and the proposed EPDS scheme, and evaluate their performance.
To realize a fair comparison, we compare these schemes [17,19,23,25,26] with the proposed EPDS scheme under the 80-bit security level [38]. Regarding the pairing-based schemes [17,19,23,25,26], we choose a bilinear pairing , where is an additive group defined by the generator P with order q on the super singular elliptic curve with the embedding degree 2, q is 160-bit Solinas prime number and p is 512-bit primer number meeting . With regard to the proposed EPDS scheme, we pick a group , where is produced by the generator P with the order q on an elliptic curve with a prime order q, where q, p are 160 bits prime number and , b is 160-bits random prime number.
The running time of the operations is able to be derived by making use of the MIRACL Crypto SDK [39]. We run the experiment on a 64-bit Windows 10 operating system with 2.53 GHz, an i7 CPU and 4 GB memory. Table 3 lists the average running time for these operations.

Table 3.
Runtime of cryptographic operation (millisecond).
6.1. Computation Costs
The computation costs of the proposed EPDS scheme and these schemes [17,19,23,25,26] are displayed in Table 4.

Table 4.
Comparison of computation costs.
In the data collection phase, for Rabieh et al.’s scheme [17], requires running two multiplication operations in and two exponentiation operations in , thus the total time is = 6.9164 ms. requires executing one multiplication operation in , one exponentiation operation in , and bilinear pairing operations in , and thus the total time is = 10.3092w+13.7674 ms. requires executing one exponentiation operation in and bilinear pairing operations in , and hence the total time is ms.
For Sun et al.’s scheme [19], requires running two multiplication operations in and one exponentiation operation in and one map to point hash function operation, thus the total time is = 15.1967 ms. requires executing multiplication operations in and four bilinear pairing operations in , so the total time is = 1.4293w +45.5247 ms. requires executing one multiplication operation in , n exponentiation operations in and two multiplication operations in , and hence the total time is ms.
For Kong et al.’s scheme [23], requires running four multiplication operations in and four exponentiation operations in , thus the total time is = 13.8328 ms. requires executing multiplication operations in , so the total time is = 2.8586w ms. requires executing multiplication operations in and exponentiation operations in , and hence the total time is ms.
For the proposed EPDS scheme, needs to run five scalar multiplication operations in , and therefore the total time is = 1.9255 ms. requires executing scalar multiplication operations in ; accordingly, the total time is = 0.3851w+1.1553 ms. requires executing scalar multiplication operations in and two solving the DL operations; therefore, the total time is = 0.3851n+2.4429 ms.
In the data query phase, for Kong et al.’s scheme [23], requires running ten multiplication operations in and seven exponentiation operations in , so the total time is = 28.4953 ms. needs to run nine multiplication operations in and seven exponentiation operations in , the total time is thus = 27.0660 ms. For Paulet et al.’s scheme [25], requires running five multiplication operations in and nine exponentiation operations in , the total time is thus = 25.4066 ms. needs to run multiplication operations in and exponentiation operations in , the total time is thus = 24.8070m +6.0867 ms.
For Zhu et al.’s scheme [26], requires running five exponentiation operations in and two bilinear pairing operation in , the total time is thus = 30.7629 ms. needs to run four multiplication operations in and four bilinear pairing operation in , the total time is thus = 46.9540 ms.
For the proposed EPDS scheme, needs to run eleven scalar multiplication operations in and two solving the DL operations, and hence the total time is = 5.5237 ms. needs to run eight scalar multiplication operations in , thus the total time is = 3.0808 ms.
Figure 3 clearly demonstrates the comparison result of computation costs in the data collection phase. Figure 3a shows that the computation costs of is 1.9255 ms, which decreases by 72.2%, 87.3%, and 86.1% compared with that by Rabieh et al.’s scheme [17], Sun et al.’s scheme [19], and Kong et al.’s scheme [23], respectively. As shown in Figure 3b, the computation costs of increase linearly with the number of vehicles, with the proposed EPDS scheme having a lower slope compared with Rabieh et al.’s scheme [17], Sun et al.’s scheme [19], and Kong et al.’s scheme [23]. From Figure 3c, we can see that the computation costs of grows linearly with the number of fog nodes, and the proposed EPDS scheme has a lower slope compared with Rabieh et al.’s scheme [17], Sun et al.’s scheme [19], and Kong et al.’s scheme [23].
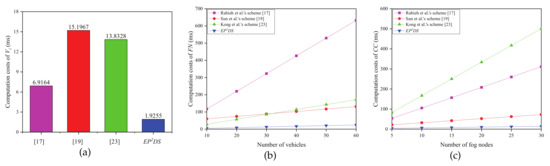
Figure 3.
Computation costs in the data collection phase. (a) Computation costs of (b) Computation costs of vs. number of vehicles; (c) Computation costs of vs. number of .
Figure 4 clearly indicates the comparison result of the computation costs in the data query phase. From Figure 4a, we can know that the computation costs of in the proposed EPDS scheme are 5.5237 ms, which decreases by 80.6%, 78.3%, and 82.0% compared with that by Kong et al.’s scheme [23], Paulet et al.’s scheme [25], and Zhu et al.’s scheme [26], respectively. Figure 4b shows the correlation between the computation cost of and the number of segments m, we can see that the computation cost of in the EPDS scheme is the smallest compared with Kong et al.’s scheme [23], Paulet et al.’s scheme [25], and Zhu et al.’s scheme [26]. The computation costs of in the proposed EPDS scheme are 3.0808 ms, which decreases by 88.6% and 93.4% compared with Kong et al.’s scheme [23] and Zhu et al.’s scheme [26]. Furthermore, unlike Paulet et al.’s scheme [25], the computation cost of in the EPDS scheme does not increase with the number of segments m.
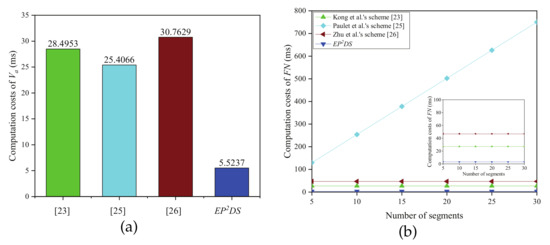
Figure 4.
Computation costs in the data query phase. (a) Computation costs of (b) Computation costs of vs. number of segments.
6.2. Communication Costs
The communication costs of the proposed EPDS scheme and these schemes [17,19,23,25,26], are evaluated in this subsection. We mainly consider the data report size, query report size, and response report size. As mentioned above, the lengths of the elements in , , and are 160 bits (20 bytes), 160 bits (20 bytes), 1024 bits (128 bytes), and 2048 bits (256 bytes), respectively, assuming that the length of timestamp and identity are 32 bits (4 bytes). The comparison results of communication costs are illustrated in Table 5.

Table 5.
Comparison of the communication costs.
In the data collection phase, for Rabieh et al.’s scheme [17], the data report size is 260 bytes, as
For Sun et al.’s scheme [19], the data report size is 516 bytes, as
For Kong et al.’s scheme [23], the data report size is 1152 bytes, as
For the proposed EPDS scheme, the data report size is 172 bytes, as
In the data query phase, for Kong et al.’s scheme [23], the query report size is 1152 bytes, as
The response report size is 1664 bytes, as
For Paulet et al.’s scheme [25], the query report size is 256 bytes, as
The response report size is 256m+128 bytes, as
For Zhu et al.’s scheme [26], the query report size is 324 bytes, as
The response report size is 320 bytes, as
For the proposed EPDS scheme, the query report size is 172 bytes, as
The response report size is 148 bytes, as
The results from the comparison of communication costs in the data collection phase are illustrated in Figure 5. In terms of the data report size, the proposed EPDS scheme requires 172 bytes, which is decreased by 33.8%, 66.7%, and 85.1% compared with that for Rabieh et al.’s scheme [17], Sun et al.’s scheme [19], and Kong et al.’s scheme [23], respectively.
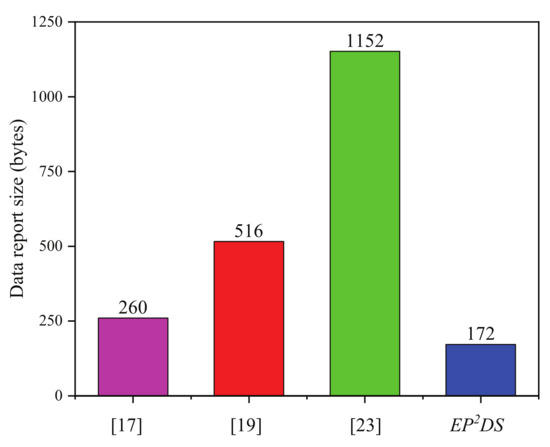
Figure 5.
Comparison of the data report size.
The result from the comparison of communication costs in the data query phase is shown in Figure 6. Regarding the query report size, from Figure 6a, we can see that the proposed EPDS scheme requires 172 bytes, a decrease of 85.1%, 32.8%, and 46.9% compared with that by Kong et al.’s scheme [23], Paulet et al.’s scheme [25], and Zhu et al.’s scheme [26], respectively. Figure 6b shows the correlation between the response report size and the number of segments m, and we can see that the response report size in the EPDS scheme is the smallest compared with Kong et al.’s scheme [23], Paulet et al.’s scheme [25], and Zhu et al.’s scheme [26]. The proposed EPDS scheme requires 148 bytes, which is decreased by 91.1% and 53.8% compared with that of Kong et al.’s scheme [23] and Zhu et al.’s scheme [26], respectively. Furthermore, unlike Paulet et al.’s scheme [25], the response report size in the EPDS scheme does not increase with the number of segments m.
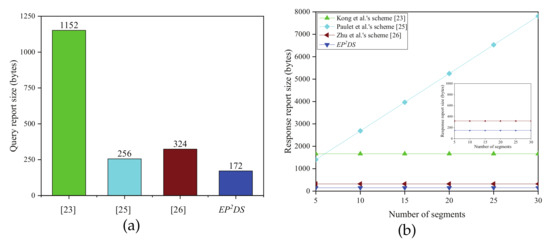
Figure 6.
(a) Comparison of the query report size; (b) Comparison of the response report size.
7. Conclusions
This paper proposes an efficient privacy-preserving data sharing scheme for fog-assisted vehicular sensor networks. Based on the super-increasing sequence, the proposed EPDS scheme is able to format the data reports captured at different road segments into one report, while calculating the average sensory data in each road segment, greatly saving on the resources of communication and computation. Furthermore, by exploiting the modified oblivious transfer technology, the proposed EPDS scheme also can query the road conditions of the potential moving route in the data query phase without disclosing the query location. Finally, an analysis of security displays that the proposed EPDS scheme can satisfy all the requirements for security and privacy, with the performance evaluation suggesting that the proposed EPDS scheme is more efficient in computation and communication costs compared to the existing schemes of [17,19,23,25,26]. Accordingly, the proposed EPDS scheme is more appropriate for achieving data sharing in fog-assisted vehicular sensor networks. In future work, we will consider using blockchain technology to achieve decentralization and privacy protection.
Author Contributions
Y.M. and X.Y. conceived of the work, designed the concrete scheme, and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Science Foundation of Shaanxi Province under Grant 2018JM6081, and in part by the Fundamental Research Funds for the Central Universities, CHD, under Grant 300102249204.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions which helped us to improve the organization and presentation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Security Model
The proposed EPDS scheme should satisfy the confidentiality and unforgeability. The security is defined by the following two interaction games executed by a challenger and an attacker . could make the following queries.
- Hash queries: Upon receiving the query, returns a random value to .
- Extract queries: Upon receiving the query on the pseudo identity , returns a private key to .
- Signcryption queries: Upon receiving the query on the message under , returns a ciphertext to .
Definition A1
(Confidentiality). The proposed scheme is secure against indistinguishability under the chosen plaintext attack (IND-CPA), if any probabilistic polynomial-time attacker does not have the ability to win the below game with a non-negligible advantage.
The IND-CPA is defined by the following game.
Setup: generates the system parameters and returns to .
Phase 1: adaptively makes the hash, extract, and signcryption queries with polynomial bounded times.
Challenge: chooses a challenging identity , picks two messages and and sends to . randomly picks and produces the ciphertext of message under . Finally, returns the ciphertext to .
Phase 2: is able to adaptively perform the query in Phase 1 apart from that, it cannot make extract queries on .
Guess: produces a guess . The advantage that wins the game is
Definition A2
(Unforgeability). The proposed scheme can achieve existential unforgeability against adaptive chosen message attacks (EUF-CMA), if any probabilistic polynomial-time attacker does not have the ability to win the below game with a non-negligible advantage.
The EUF-CMA is defined by the following game.
Initialization: selects a challenging pseudo identity and transmits to .
Setup: generates the system parameters and returns to .
Queries: adaptively makes hash, extract and signcryption queries.
Forgery: outputs a ciphertext on under , such that
- The ciphertext on under is valid.
- has not been requested in the extract queries.
Appendix B
Security Proof
Theorem A1.
The proposed EPDS scheme can provide confidentiality if ElGamal encryption is secure against the IND-CPA.
Supposing there is an attacker is able to win the game defined in Definition 1 with a non-negligible probability , we can construct an algorithm that could break the IND-CPA of ElGamal encryption with probability .
Initialization: The simulator for ElGamal encryption generates the and transmits to .
Setup: chooses hash functions : and a super-increasing sequence . Finally, returns to .
To keep the rapidly response and consistency, maintains the following list:
- : It consists of tuples .
- : It consists of tuples .
- : It consists of tuples .
Phase 1: adaptively is able to adaptively perform the following polynomial bounded times queries.
queries: performs a query on , executes as follows:
- If contains , responds with the previous value to .
- If does not contain , randomly chooses a number , adds into and returns to .
queries: performs a query on , executes as follows:
- If contains , responds with the previous value to .
- If does not contain , randomly chooses a number , adds into and returns to .
Extract queries: performs a query on , executes as follows:
- If , aborts the game.
- If , executes:
- -
- If contains , returns to .
- -
- If does not contain , randomly chooses and makes . If already appear in , chooses another and tries again. inserts and into and , respectively. Finally, returns the to .
Signcryption queries: makes a query on the message under , returns to . randomly chooses and computes , ,and returns them to . produces a ciphertext in accordance with the proposed scheme. Finally, returns the ciphertext to .
Challenge: selects a challenging identity , picks two same length message and and sends them to . Then transmits them to . randomly chooses , and computes , , and returns them to . produce a ciphertext in accordance with the proposed scheme. Finally, returns the ciphertext to .
Phase 2: is able to adaptively perform the query in Phase 1 apart from it cannot make a extract queries on .
Guess: can output as its guess against the IND-CPA of ElGamal encryption.
Probability analysis: Supposing that is able to make at most times queries, times queries, times extract queries and times signcryption queries. We define two events as follows:
- : does not abort above game in extract queries.
- : is able to correctly output the value of b.
According to the above simulation, we could obtain that and , and hence the advantage that is able to break the IND-CPA of ElGamal encryption is
In accordance with the above analysis, we can conclude that can break the IND-CPA of ElGamal encryption with a non-negligible probability, this is contradicts with the security of ElGamal encryption, so the proposed EPDS scheme could provide confidentiality.
Theorem A2.
The proposed EPDS scheme can provide the unforgeability if the ECDL problem is hard.
Assuming that there is an attacker can break the unforgeability of the proposed EPDS scheme with a non-negligible advantage , we can construct an algorithm for solving the ECDL problem with probability .
Initialization: picks a challenging identity and returns to .
Setup: Given an instance of the ECDL problem, then sets and returns to .
queries: It is the same as Theorem 1.
queries: It is the same as Theorem 1.
Extract queries: It is the same as Theorem 1.
Signcryption queries: makes a query on the message under , executes as follows:
- If , randomly selects and calculates , , . If the already appears in or already appears in , chooses another and tries again. Then, returns the ciphertext to , and inserts and into and , respectively.
- If , generates a ciphertext in accordance with the proposed scheme. Then, returns the ciphertext to .
Forgery: outputs a forged ciphertexts on under . On the basis of the forking lemma [40,41], is able to output another valid ciphertext on under by choosing a different . Since both ciphertexts are valid, we are able to gain the following two equations
We can gain the equations:
outputs as a solution of ECDL problem.
Probability analysis: Supposing that is able to make at most times queries, times queries, times extract queries, and times signcryption queries. We define three events as follows:
- : never abort above game in extract and signcryption queries.
- : is able to output a valid ciphertext.
- : .
According to the above simulation, we could obtain that , , and . Thus, the probability that is able to solve the ECDL problem is shown as:
Due to the non-negligibility of , we are able to know that is non-negligible. In accordance with the above analysis, we are able to conclude that can solve the ECDL problem with a non-negligible probability. This contradicts with the hardness of the ECDL problem [42], and hence the proposed EPDS scheme can provide unforgeability.
References
- Lee, U.; Magistretti, E.; Zhou, B.; Gerla, M.; Bellavista, P.; Corradi, A. MobEyes: Smart mobs for urban monitoring with a vehicular sensor network. IEEE Trans. Commun. Mag. 2006, 13, 52–57. [Google Scholar] [CrossRef]
- Placzek, B. Selective data collection in vehicular networks for traffic control applications. Transp. Res. Part C Emerging Technol. 2012, 23, 14–28. [Google Scholar] [CrossRef]
- Mednis, A.; Elsts, A.; Selavo, L. Embedded solution for road condition monitoring using vehicular sensor networks. In Proceedings of the 2012 6th International Conference on Application of Information and Communication Technologies (AICT), Tbilisi, Georgia, 17–19 October 2012; pp. 1–5. [Google Scholar]
- Fiebig, B. European traffic accidents and purposed solutions. In Proceedings of the ITU-Workshop on Standardization in Telecommunication for Motor Vehicles, Geneva, Switzerland, 24–25 November 2003; pp. 24–25. [Google Scholar]
- Yu, R.; Huang, X.; Kang, J.; Ding, J.; Maharjan, S.; Gjessing, S.; Zhang, Y. Cooperative resource management in cloud-enabled vehicular networks. IEEE Trans. Ind. Electron. 2015, 62, 7938–7951. [Google Scholar] [CrossRef]
- Ni, J.; Lin, X.; Zhang, K.; Shen, X.M. Privacy-preserving real-time navigation system using vehicular crowdsourcing. In Proceedings of the IEEE 84th Vehicular Technology Conference: VTC2016-Fall, Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog computing and its role in the internet of things. In Proceedings of the Mobile Cloud Computing Workshop, Helsinki, Finland, 13–17 August 2012; pp. 13–16. [Google Scholar]
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.D.; Katz, R.H.; Konwinski, A.; Lee, G.; Patterson, D.A.; Rabkin, A.; Stoica, I.; et al. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, D.; Maharjan, S.; Zhang, Y. Joint offloading and resource allocation in vehicular edge computing and networks. In Proceedings of the IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Ni, J.; Zhang, K.; Yu, Y.; Lin, X.; Shen, X.S. Privacy-preserving smart parking navigation supporting efficient driving guidance retrieval. IEEE Trans. Veh. Technol. 2018, 67, 6504–6517. [Google Scholar] [CrossRef]
- Basudan, S.; Lin, X.; Sankaranarayanan, K. A privacy-preserving vehicular crowdsensing based road surface condition monitoring system using fog computing. IEEE Internet Things J. 2017, 4, 772–782. [Google Scholar] [CrossRef]
- Chun, S.; Shin, S.; Seo, S.; Eom, S.; Jung, J.; Lee, K. A pubsub-based fog computing architecture for Internet-of-vehicles. In Proceedings of the 8th International Conference on Cloud Computing Technology and Science, Luxembourg, 12–15 December 2016; pp. 90–93. [Google Scholar]
- Ni, J.; Zhang, A.; Lin, X.; Shen, X.S. Security, privacy, and fairness in fog-based vehicular crowdsensing. IEEE Commun. Mag. 2017, 55, 146–152. [Google Scholar] [CrossRef]
- Wei, J.; Wang, X.; Li, N. A privacy-preserving fog computing framework for vehicular crowdsensing betworks. IEEE Access 2018, 6, 43776–43784. [Google Scholar] [CrossRef]
- Omoniwa, B.; Hussain, R.; Javed, M.A. Fog/Edge computing-based IoT (FECIoT): Architecture, applications, and research issues. IEEE Internet Things 2019, 6, 4118–4149. [Google Scholar] [CrossRef]
- Zhuo, G.; Jia, Q.; Guo, L.; Li, M.; Li, P. Privacy-preserving verifiable data aggregation and analysis for cloud-assisted mobile crowdsourcing. In Proceedings of the 35th IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Rabieh, K.; Mahmoud, M.M.E.A.; Younis, M. Privacy-preserving route reporting schemes for traffic management systems. IEEE Trans. Veh. Technol. 2017, 66, 2703–2713. [Google Scholar] [CrossRef]
- Xu, C.; Lu, R.; Wang, H.; Zhu, L.; Huang, C. PAVS: A new privacy-preserving data aggregation scheme for vehicle sensing systems. Sensors 2017, 17, 500. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Sun, S.; Sun, J.; Yu, H.; Du, X.; Guizani, M. Security and privacy preservation in fog-based crowd sensing on the internet of vehicles. J. Network Comput. Appl. 2019, 134, 89–99. [Google Scholar] [CrossRef]
- Lin, X.; Lu, R.; Shen, X. MDPA: Multidimensional privacy-preserving aggregation scheme for wireless sensor networks. Wirel. Commun. Mob. Comput. 2010, 10, 843–856. [Google Scholar] [CrossRef]
- Lu, R.; Heung, K.; Lashkari, A.H.; Ghorbani, A.A. A light-weight privacy-preserving data aggregation scheme for fog computing-enhanced IoT. IEEE Access 2017, 5, 3302–3312. [Google Scholar] [CrossRef]
- Wang, B.; Chang, Z.; Zhou, Z.; Ristaniemi, T. Reliable and privacy-preserving task recomposition for crowdsensing in vehicular fog computing. In Proceedings of the 87th Vehicular Technology Conference, Porto, Portugal, 3–6 June 2018; pp. 6–11. [Google Scholar]
- Kong, Q.; Lu, R.; Ma, M.; Bao, H. A privacy-preserving sensory data sharing scheme in internet of vehicles. Future Gener. Comput. Syst. 2019, 92, 644–655. [Google Scholar] [CrossRef]
- Ghinita, G.; Kalnis, P.; Kantarcioglu, M.; Bertino, E. A hybrid technique for private location-based queries with database protection. In Proceedings of the 11th International Symposium on Spatial and Temporal Databases, Aalborg, Denmark, 8–10 July 2009; pp. 98–116. [Google Scholar]
- Paulet, R.; Kaosar, M.G.; Yi, X.; Bertino, E. Privacy-preserving and content protecting location based queries. IEEE Trans. Knowl. Data Eng. 2014, 26, 1200–1210. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, R.; Huang, C.; Chen, L.; Li, H. An efficient privacy-preserving location-based services query scheme in outsourced cloud. IEEE Trans. Veh. Technol. 2016, 65, 7729–7739. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, F.; Li, H. Efficient and privacy-preserving polygons spatial query framework for location-based services. IEEE Internet Things J. 2017, 4, 536–545. [Google Scholar] [CrossRef]
- Naor, M.; Pinkas, B. Oblivious transfer with adaptive queries. In Proceedings of the Advances in Cryptology-CRYPTO’99, Santa Barbara, CA, USA, 15–19 August 1999; pp. 573–590. [Google Scholar]
- IEEE, 802.11p-2010-IEEE Standard for Information technology. Available online: https://ieeexplore.ieee.org/document/5514475/versions#versions (accessed on 14 January 2020).
- Jiang, S.; Liu, J.; Duan, M.; Wang, L.; Fang, L. Secure and privacy-preserving report de-duplication in the fog-based vehicular crowdsensing system. In Proceedings of the IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Zhu, L.; Li, M.; Zhang, Z. Secure fog-assisted crowdsensing with collusion resistance: From data reporting to data requesting. IEEE Internet Things J. 2019, 6, 5473–5484. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Advances in Cryptology-CRYPTO’85, Santa Barbara, CA, USA, 18–22 August 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystem. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Ming, Y.; Zhang, X.; Shen, X. Efficient privacy-preserving multi-dimensional data aggregation scheme in smart grid. IEEE Access 2019, 7, 32907–32921. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Xu, B.; Huang, X. An efficient identity-based conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2681–2690. [Google Scholar] [CrossRef]
- Liu, J.K.; Yuen, T.H.; Au, M.H.; Susilo, W. Improvements on an authentication scheme for vehicular sensor networks. Expert Syst. Appl. 2014, 41, 2559–2564. [Google Scholar] [CrossRef]
- Boneh, D.; Goh, E.; Nissim, K. Evaluating 2-DNF formulas on ciphertexts. In Proceedings of the 2nd Theory of Cryptography Conference, Cambridge, MA, USA, 10–12 February 2005; pp. 325–341. [Google Scholar]
- Ming, Y.; Cheng, H. Efficient certificateless conditional privacy-preserving authentication scheme in VANETs. Mob. Inf. Syst. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Shamus Software Ltd. Multi precision integer and rational arithmetic cryptographic library (MIRACL). Available online: http://www.certivox.com/miracl/ (accessed on 1 December 2019).
- Pointcheval, D.; Stern, J. Security proofs for signature schemes. In Proceedings of the Advances in Cryptology-EUROCRYPT’96, Saragossa, Spain, 12–16 May 1996; pp. 387–398. [Google Scholar]
- Ming, Y.; Shen, X. PCPA: A practical certificateless conditional privacy preserving authentication scheme for vehicular ad hoc networks. Sensors 2018, 18, 1573. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Kumar, N.; Zeadally, S.; Vinel, A.; Yang, L.T. Efficient and privacy-preserving data aggregation scheme for smart grid against internal adversaries. IEEE Trans. Smart Grid 2017, 13, 1–9. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).