Abstract
Secure communication is a significant issue in wireless sensor networks. User authentication and key agreement are essential for providing a secure system, especially in user-oriented mobile services. It is also necessary to protect the identity of each individual in wireless environments to avoid personal privacy concerns. Many authentication and key agreement schemes utilize a smart card in addition to a password to support security functionalities. However, these schemes often fail to provide security along with privacy. In 2015, Chang et al. analyzed the security vulnerabilities of previous schemes and presented the two-factor authentication scheme that provided user privacy by using dynamic identities. However, when we cryptanalyzed Chang et al.’s scheme, we found that it does not provide sufficient security for wireless sensor networks and fails to provide accurate password updates. This paper proposes a security-enhanced authentication and key agreement scheme to overcome these security weaknesses using biometric information and an elliptic curve cryptosystem. We analyze the security of the proposed scheme against various attacks and check its viability in the mobile environment.
1. Introduction
Wireless sensor networks (WSNs) are ad hoc networks composed of a number of sensor nodes with limited power, computation, storage and communication capabilities [1]. They provide effective solutions to a wide array of monitoring problems in various environments, such as battlefields, healthcare services and the smart grid [2]. Recently, sensor-attached things that communicate with neighboring things are enabling the development of the Internet of Things (IoT) environment [3]. For these reasons, WSNs have gained wide attention, in both the academic and industrial fields. However, the issue of securing and authenticating communication is problematic, because the nodes are vulnerable to attacks and do not have enough capacity for the secure storage of keys [4,5,6]. To solve these security issues, authentication and key agreement schemes using two-factor security, passwords and smart cards have attracted attention and have been studied widely in an effort to guarantee secure communication [7,8,9,10,11,12,13,14]. Unfortunately, many of them still suffer from various attacks and do not provide secure communication.
Several authentication and key agreement schemes for WSNs have been proposed. In 2010, Das [8] proposed a two-factor user authentication protocol for WSNs. He insisted the scheme withstood various attacks from users with the same identity, as well as from stolen-verifier attacks. However, He et al. [9], Khan and Alghathbar [10] and Chen and Shih [11] pointed out that Das’s scheme was vulnerable to insider and impersonation attacks, gateway node bypassing attacks and privileged-insider attacks and did not provide mutual authentication. Subsequently, each proposed their own authentication scheme to provide secure user authentication in WSNs. In 2012, Vaidya et al. [12] demonstrated that Das’s scheme [8], Khan and Alghathbar’s scheme [10] and Chen and Shih’s scheme [11] had security problems and that none of them provided key agreement. Vaidya et al. proposed a two-factor mutual user authentication scheme with key agreement for WSNs. In 2014, Kim et al. [13] presented that both gateway node bypassing attacks and user impersonation attacks were possible in Vaidya et al.’s scheme [12]. They proposed an authentication and key agreement scheme that resisted user impersonation and gateway node bypassing attacks. However, in 2015, Chang et al. [14] analyzed Kim et al.’s scheme [13] and found it had security vulnerabilities in the following areas: impersonation attacks, lost smart card attacks, man-in-the-middle attacks, violation of session key security and failure to protect user privacy. To solve these problems, Chang et al. [14] proposed a scheme that provided user privacy by using dynamic identities and provided better security functionality than Kim et al.’s scheme. However, we point out that Chang et al.’s scheme does not withstand several types of attacks and fails to provide a password update.
Recently, to improve the security of two-factor authentication schemes that are vulnerable to guessing attacks and subject to inefficient password change policies in WSNs, biometric-based user authentication schemes, combined with smart cards and passwords, have drawn considerable attention in research [15,16,17,18,19]. Biometric-based user authentication in the WSN becomes inherently more reliable and secure than traditional two-factor user authentication schemes [20]. Several advantages can be derived from the use of biometric keys over traditional passwords because they cannot be lost; they are unforgettable, difficult to copy, hard to forge and difficult to break. Therefore, biometric-based user authentication is considered to be more secure and reliable than conventional authentication schemes [20].
In this paper, we cryptanalyze Chang et al.’s scheme [14] and demonstrate the security weaknesses, such as password guessing attacks, lack of forward secrecy and inaccurate password updates. Further, we propose a biometric-based user authentication and key agreement scheme for WSNs using fuzzy extraction and an elliptic curve cryptosystem (ECC). The proposed scheme withstands security threats from malicious adversaries and insider users by using an ECC-based session key. Our scheme is also suitable for WSNs when compared to traditional authentication and key agreement schemes because it performs simple ECC operations, hash functions and exlusive OR (XOR) operations. We prove that our scheme provides mutual authentication using Burrows-Abadi-Needham (BAN) logic [21].
The remainder of this paper is organized as follows: In Section 2, we present our preliminary details, and Chang et al.’s scheme is reviewed in Section 3. In Section 4, we cryptanalyze Chang et al.’s scheme, and our proposed scheme is presented in Section 5. Finally, we analyze our proposed scheme in Section 6 and conclude with the findings of this work in Section 7.
2. Preliminaries
In this section, we introduce the notations used in this paper and then define the cryptographic system and primitives used as building blocks in our security system. Finally, we define security requirements for user authentication in WSNs.
2.1. Notations
The notations used throughout this paper are described in Table 1.

Table 1.
Notations.
2.2. Elliptic Curves Cryptosystem
Let be two large primes, and indicates an elliptic curve over the finite field . We denote by a q-order subgroup of the additive group of points of . The discrete logarithm problem (DLP) is required to be hard in . Mathematical problems in ECC are given as follows [22]:
Definition 1 (Elliptic curve discrete logarithm (ECDL) problem).
Given a point element , find an integer , such that , where indicates that the point P is added to itself for a times by the elliptic curve operation.
Definition 2 (Elliptic curve computational Diffie–Hellman (ECDH) problem).
For , given two point elements , compute .
Definition 3 (Elliptic curve decisional Diffie–Hellman (ECDDH) problem).
For , given three point elements , decide whether or not.
We assume that the ECDDH problem is intractable, which may guarantee that there is no probabilistic polynomial time (PPT) algorithm to solve ECDDHP, ECCDHP and ECDDLP with non-negligible probability.
2.3. Fuzzy Extraction
We briefly describe the extraction process of key data from the given biometrics of a user using a fuzzy extractor. The output of a conventional hash function is sensitive, and it may also return completely different outputs even if there is little variation in the inputs. Note that the biometric information is prone to various noises during data acquisition, and the reproduction of the actual biometrics is hard in common practice. To avoid such a problem, a fuzzy extractor method [23] is preferred, which can extract a uniformly-random string and public information from the biometric template with a given error tolerance. In the reproduction process, the fuzzy extractor recovers the original biometric key data for noisy biometrics using a helper string. The fuzzy extractor consists of Gen (generate) and Rep (reproduce).
- This probabilistic algorithm takes a biometric template as an input and then outputs a biometric key , which is a uniform and random string, and a helper string . can be the same under the assistance of even if the biometric information changes slightly.
- This deterministic algorithm takes noisy biometric information and a helper string as inputs, then reproduces the biometric key . To reproduce the same , the metric space distances between and have to meet the given verification threshold.
2.4. Network Model
- : A user who receives a smart card from and uses it to access multiple servers. After a successful authentication process with , the user is given access to mobile services. Furthermore, the user’s smart card is not tamper-resistant and can be lost or stolen by an adversary.
- : A sensor node that collects information and provides services to users who successfully complete the authentication process. Sensors are not equipped with tamper-resistant hardware due to cost constraints, thus an adversary will know all of the keying materials stored in that sensor’s memory.
- : A trusted third-party that generates system parameters. It provides smart cards to users and pre-shared keys to sensors. is assumed to be trustworthy and never compromised by an adversary.
2.5. Security Requirements
According to recent studies [24,25], the user authentication scheme for WSNs should satisfy the following security requirements: (1) mutual authentication: the user and the sensor node should authenticate each other with the help of the gateway node ; (2) anonymity: any adversary should not be able to obtain the real identity of the user ; (3) session key generation: after executing the authentication and key agreement phase, the user and the sensor node should generate a session key; (4) unconstrained by : the should not have or be able to compute the registered user’s information, such as the password and biometric template; (5) attack resistance: the scheme should withstand various attacks, such as off-line identity/password guessing, impersonation, smart card loss, man-in-the-middle and reply attacks; (6) efficient password update: it is required to change or update the users’ password without the participation of .
3. Review of Chang et al.’s Authentication and Key Agreement Scheme
In this section, we review Chang et al.’s authenticated key agreement scheme. It comprises four phases: registration, login, authentication and key agreement, as well as password change.
3.1. Registration Phase
- Step 1:
- chooses and a random number , then computes and sends to via a secure channel.
- Step 2:
- computes , , , , . Then, sends the smart card to via a secure channel. stores in its storage, where , is a nonce, and , where means contains nothing.
- Step 3:
- computes and inserts it into .
3.2. Login Phase
- Step 1:
- inputs and into .
- Step 2:
- computes , , , . Then, verifies . If it is valid, computes , , , where is the timestamp.
- Step 3:
- sends to .
3.3. Authentication and Key Agreement Phase
- Step 1:
- checks the validity of and retrieves from . Then, computes , , , , then checks . If it is correct, computes , , then sends to , where is the timestamp.
- Step 2:
- checks the validity of and computes , then checks . If it is successful, computes , , , , then sends to , where is the timestamp.
- Step 3:
- checks the validity of and computes , , , then checks . If it is correct, computes , , , then sends , where is the timestamp. Additionally, updates as .
- Step 4:
- checks the validity of and computes , , then checks If it is correct, computes and updates as .
3.4. Password Change Phase
- Step 1:
- inputs into , where is a new password.
- Step 2:
- The smart card computes , , , , then checks . If it is correct, computes updated values , , , . Then, replaces with .
4. Security Weaknesses of Chang et al.’s Scheme
In this section, we analyze the security weaknesses of Chang et al.’s scheme [14]. Chang et al. cryptanalyzed Kim et al.’s scheme [13] and improved it by providing enhanced security properties. They claimed that their protocol could withstand various attacks. However, we show that their protocol is vulnerable to off-line password guessing attacks and does not provide perfect forward secrecy. We also show that their protocol cannot satisfy accurate password change. The capabilities of an adversary [25] throughout this paper are as follows:
- An adversary can be either a user or a sensor node, but not a gateway node [26].
- An adversary has total control over the public communication channel. Thus, the adversary can intercept, insert, delete or modify any message transmitted via a public channel.
- An adversary may steal a user’s smart card and extract the information stored in it by means of analyzing the power consumption [27].
- An adversary can easily guess low-entropy passwords in an off-line manner, but the guessing of two secret parameters is computationally infeasible in polynomial time [28].
4.1. Off-Line Password Guessing Attack
Previous works [27] demonstrated that smart cards could be vulnerable to side channel attack, i.e., could extract the information stored in the smart card . chooses an arbitrary password , then computes to guess a correct password as follows:
If they are equal, finds the correct password. Otherwise, guesses another and repeats the steps listed above until the correct password is found. In practical applications, people usually choose an easy-to-remember password for convenience, thus passwords could come from a very small dictionary. Therefore, could find the correct password using a brute-force attack.
Even though Chang et al. has claimed that it is secure, once guesses the password correctly, can launch various attacks, such as impersonation, stolen verifier and lost smart card attacks. This is due to the fact that the scheme uses only a password to check the validity of users. Therefore, it is crucial to protect password guessing attacks and use various authentication factors to check the validity of users.
4.2. Lack of Perfect Forward Secrecy
In Chang et al.’s scheme, session key is computed as . Once a long-term key of , , is disclosed to , can compute previous session keys as follows:
- Step 1:
- intercepts and stores all messages exchanged in previous sessions, such as and .
- Step 2:
- computes , then finally retrieves a previous session key .
This result indicates that Chang et al.’s scheme does not provide perfect forward secrecy. Furthermore, who knows also can compute present and future session keys by intercepting messages via the public channel, indicating that Chang et al.’s scheme does not provide backward secrecy.
4.3. Incorrectness of Password Change
Chang et al.’s adopted Kim et al.’s password change phase; however, we found out that Kim et al.’s password update is not suitable for Chang et al.’s scheme. We demonstrate the incorrectness of the password change phase as follows:
- Step 1:
- Once the user performs the password change phase, the previous password is changed into , and information in the smart card, , is replaced with .
- Step 2:
- Then, the user performs the login phase using the new password ; however, is not allowed to access for not computing the proper from . is not updated in the password change phase; therefore, and, finally, .
In addition, it is of no use to update the password if the password is revealed even one time because no other information, such as identity, is required to login and change the password. Therefore, regardless of whether a user changes the password, can also change the password and be verified by the smart card.
5. The Proposed Three-Factor Authentication and Key Agreement Scheme
In this section, we propose a secure three-factor authentication and key agreement scheme for WSNs to overcome the security weaknesses in Chang et al.’s scheme. Based on Kim et al. and Chang et al.’s schemes, the proposed scheme provides better security functionality by using biometric information of the user and makes up for the password update inaccuracy. The proposed scheme consists of four phases: registration, login, authentication and key agreement and password change. The details of each phase are presented as follows.
5.1. Registration Phase
A user registers the identity and password to , then generates a smart card for and sends it to through a secure channel. Likewise, a sensor node is distributed with , where . Figure 1 illustrates the registration phase, which is performed as follows:
- Step 1:
- :chooses and and imprints , then computes and and sends to through a secure channel.
- Step 2:
- :computes , , , , .
- Step 3:
- stores parameters , where ( is a nonce); . is empty at first time because has not been updated; however, this parameter is required to check the correctness of the received and retrieve safely when does not find a proper updated in the case of an unsuccessful update process.Then, issues the smart card and sends it to through a secure channel.
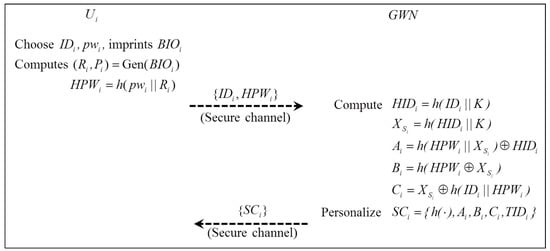
Figure 1.
Registration phase.
5.2. Login Phase
When tries to access the , the login request is launched at first by with . Figure 2 illustrates the login phase, which is performed as follows:
- Step 1:
- inserts , inputs , and imprints .
- Step 2:
- computes , , , . Then, verifies . If it is correct, generates a random number and computes , , , , where is the current timestamp.
- Step 3:
- sends the login request message to .
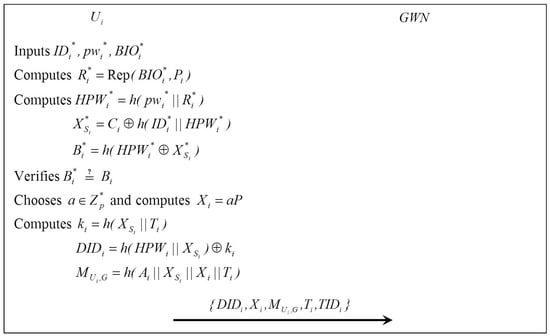
Figure 2.
Login phase.
5.3. Authentication and Key Agreement Phase
In this phase, and authenticate each other and generate a common session key by the help of . The trusted party is interconnected with and , respectively, and helps to establish a session key between and ; however, is not able to derive the session key. Figure 3 illustrates the authentication and key agreement phase, which is performed as follows:
- Step 1:
- :After receiving , checks the validity of and retrieves from . If no is found, checks . If it still is not found, rejects the login request; otherwise, computes and . Then, verifies . If it is valid, authenticates and computes , then sends to , where is the current timestamp.
- Step 2:
- :After receiving , checks the validity of and verifies using its stored secret value . If it is valid, authenticates and computes , , where is the current timestamp. Then, generates a random number and computes and a session key . Finally, computes and sends to .
- Step 3:
- :After receiving , checks the validity of , computes , and verifies . If it is valid, authenticates and computes , , , where is the current timestamp. Then, sends to and updates as in its storage.
- Step 4:
- After receiving , checks the validity of , computes and verifies . If it is valid, computes the session key . Finally, updates as .

Figure 3.
Authentication and key agreement phase.
5.4. Password Change Phase
When wants to change with the new , performs the password change phase. Figure 4 illustrates the password change phase, which is performed as follows:
- Step 1:
- imprints and computes , then inputs into .
- Step 2:
- computes , , . Then, verifies to check the validity of . If it is correct, computes updated values , , , . Then, replaces with .

Figure 4.
Password change phase.
6. Analysis
In this section, we describe an analysis of our proposed authentication and key agreement scheme with respect to security and efficiency. We assume that the capabilities of the adversary are the same as those from our cryptanalysis of Chang et al.’s scheme in Section 4. We first prove the security of our scheme with BAN logic [21], then analyze the proposed scheme based on the security requirements for WSNs.
6.1. Proof of Authentication and Key Agreement Based on BAN Logic
Recently, security analyses about authentication and key agreement schemes in WSNs have been conducted using the BAN logic, which is a method to prove the security of mutual authentication and a session key [25,29]. In this section, we analyze the security of our proposed authentication scheme with BAN logic [21]. Table 2 illustrates notations used in BAN logic.

Table 2.
BAN logic notations.
- The BAN logic postulates:
- (a)
- Message meaning rule:
- (b)
- Nonce-verification rule:
- (c)
- Jurisdiction rule:
- (d)
- Freshness-conjuncatenation rule:
- Security goals:The proposed scheme should satisfy the following goals:
- g1.
- g2.
- g3.
- g4.
- Idealized scheme:We transform our scheme into the idealized form as follows:
- Msg1.
- Msg2.
- Msg3.
- Msg4.
- Initiative premises:We make the assumptions about the initial state of the scheme to analyze the proposed scheme as follows.
- p1.
- p2.
- p3.
- p4.
- p5.
- p6.
- p7.
- p8.
- p9.
- p10.
- (The meanings of and are different from and . and are not the goals that we want to deduce. These are widely-used premises as done in [29,30,31,32].)
- Security analysis of the idealized form of the proposed scheme:
- a1.
- According to , we could get:
- a2.
- According to , we apply the message-meaning rule to obtain:
- a3.
- According to , we apply the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a4.
- According to , we could get:
- a5.
- According to , we apply the message-meaning rule to obtain:
- a6.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a7.
- According to , we could get:
- a8.
- According to , we apply the message-meaning rule to obtain:
- a9.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a10.
- According to , we could get:
- a11.
- According to , we apply the message-meaning rule to obtain:
- a12.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a13.
- Because , according to and , we could produce:Likewise, , according to and , we could produce:
- a14.
- According to and , we apply the jurisdiction rule to produce:Likewise, according to and , we apply the jurisdiction rule to produce:
According to Goal 1, Goal 2, Goal 3 and Goal 4, we conclude that both and believe they share the session key.
6.2. Security Analysis against Various Attacks
- •
- User anonymity and untraceability: Our scheme provides anonymity of users. The user does not reveal a real identity in open channels; instead, generates and sends a pseudonym identity to in the registration phase and updates it as before finalizing the session. The identity is dynamic for every session; thus, an adversary cannot obtain the user’s true identity. The proposed scheme also provides untraceability by having all messages used in the session satisfy a freshness requirement. Therefore, cannot trace the user.
- •
- Perfect forward secrecy: A session key is computed as . Even though the long-term private keys and are disclosed to , he/she cannot compute previous session keys, because it is hard to compute using and due to the difficulty of ECDH. Thus, cannot compute previous session keys using long-term private keys. Therefore, our scheme provides forward secrecy.
- •
- Mutual authentication: In our scheme, and authenticate each other, and and authenticate each other, respectively. authenticates by checking . needs to compute and to reconstruct ; however, only a legal user can compute those values. authenticates by checking . needs to compute and to reconstruct ; however, only a legal can compute those values. Therefore, and mutually authenticate. Similarly, authenticates by checking , and authenticates by checking . Additionally, only legal and can reconstruct them, then authenticate mutually. Therefore, our scheme provides proper mutual authentication.
- •
- Off-line password guessing attack: may attempt to guess the password by extracting the values stored in the smart card . could guess correctly if he/she generates a series of equations and computes the valid using guessing passwords. However, is required to know the biometric information of the user, which cannot be forged, for generating equations. Therefore, it is infeasible to correctly guess the user’s password in our scheme.
- •
- Smart card loss attack: can extract values in the smart card by means of power analysis and other techniques. Suppose obtains the user’s smart card and extracts stored parameters . From these values, cannot obtain any useful information because the parameters are safeguarded with a one-way hash function, and is just a nonce. Furthermore, may attempt to log in by generating a login request message. However, cannot even pass the login phase and generate a valid login request message without proper , and . Therefore, the proposed scheme withstands smart card loss attacks.
- •
- User impersonation attack: who somehow possesses a valid smart card of and wants to access is required to generate and send a valid login request message to . must know and to compute these values. However, in our scheme, and are not revealed. Thus, cannot compute the temporal key and generate a valid login request message. Therefore, our scheme is secure against the user impersonation attack.
- •
- Man-in-the-middle attack and replay attack: who knows public channel information and has the smart card of may attempt to establish a secure channel with . However, cannot authenticate with because cannot generate a valid login request message, as mentioned above. In addition, those messages captured in a public channel are refreshed in every session, so that cannot use them repeatedly. Therefore, our scheme withstands man-in-the-middle and replay attacks.
- •
- Stolen verifier attack: who obtains the verifier table of may attempt to attack users to gain some advantages. However, still cannot compute , and and will fail to pass the login phase. Of course, will fail to compute a login request message without and . Therefore, even if has the verifier table, our protocol withstands stolen verifier attacks.
- •
- Known-key attack: A session key is computed as , and , and are independent in each session. Though , who somehow possesses each value, attempts to generate other session keys, he/she will find that they cannot successfully derive valid session keys. Therefore, our proposed scheme withstands known-key attacks.
We compare the functionality features of the proposed scheme with related user authentication schemes for WSNs in Table 3. ∘ denotes that the scheme provides the property; × denotes that the scheme does not provide the property; Δ denotes that the scheme does not provide the property when off-line password guessing attacks succeed; − denotes that the scheme does not concern the property.

Table 3.
Comparisons of the functionality features. ECC, elliptic curve cryptosystem.
6.3. Performance Comparisons
In Table 4, we compare the computational cost with related schemes. denotes the computation time for the hash function; denotes the XOR operation; denotes the fuzzy extraction; denotes the ECC multiplication; denotes the encryption/decryption. The computation cost of ours is a bit higher than [13,14] because of the usage of biometrics and ECC, but it is considered to be operationally viable in WSNs [15,18]. Additionally, our proposed scheme provides the enhanced security functionalities and is secure against various attacks.

Table 4.
Comparisons of the computation costs.
7. Conclusions
To provide improved security functionality for mobile services in WSNs, several user authentication and key agreement schemes have been proposed in the last few years. However, most of them cannot provide secure authentication and are vulnerable to security attacks.
In this paper, we analyzed the security weaknesses of Chang et al.’s scheme and found that it is vulnerable to off-line password guessing attacks and does not provide forward secrecy and accurate password updates. To address the security problems, we proposed a biometric-based user authentication and key agreement scheme. The proposed scheme withstands the security attacks described above and provides better security functionality than previous schemes by using biometric information and ECC. In addition, we provided security and efficiency analyses, which demonstrated that the proposed protocol is more secure than the previous schemes and operationally viable in WSNs.
Acknowledgments
This study was supported by the BK21 Plus project funded by the Ministry of Education, Korea (21A20131600011).
Author Contributions
YoHan Park and YoungHo Park found the problems in the related schemes for WSNs, analyzed the vulnerabilities of the related schemes, designed the improved scheme, proved the security of proposed scheme and wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 102–114. [Google Scholar] [CrossRef]
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Futur. Gene Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Pathan, A.S.K.; Lee, H.W.; Hong, C.S. Security in wireless sensor networks: Issues and challenges. In Proceedings of the 8th International Conference Advanced Communication Technology (ICACT), Phoenix Park, Korea, 20–22 February 2006; pp. 1043–1048.
- Perrig, A.; Stankovic, J.; Wagner, D. Security in wireless sensor networks. ACM Commun. 2004, 47, 53–57. [Google Scholar] [CrossRef]
- Al Ameen, M.; Liu, J.; Kwak, K. Security and privacy issues in wireless sensor networks for healthcare applications. J. Med. Syst. 2012, 36, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.H.; Zheng, Y.; Cao, J.; Wang, S. A dynamic user authentication scheme for wireless sensor networks. In Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Taichung, Taiwan, 5–7 June 2006; pp. 1–8.
- Das, M.L. Two-factor user authentication scheme in wireless sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1086–1090. [Google Scholar] [CrossRef]
- He, D.; Gao, Y.; Chan, S.; Chen, C.; Bu, J. An enhanced two-factor user authentication scheme in wireless sensor networks. Ad Hoc Sens. Wirel. Netw. 2010, 10, 361–371. [Google Scholar]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and security improvements of two-factor user authentication in wireless sensor networks. Sensors 2010, 10, 2450–2459. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.H.; Shih, W.K. A robust mutual authentication protocol for wireless sensor networks. ETRI J. 2010, 32, 704–712. [Google Scholar] [CrossRef]
- Vaidya, B.; Makrakis, D.; Mouftah, H. Two-factor mutual authentication with key agreement in wireless sensor networks. Secur. Commun. Netw. 2016, 9, 171–183. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Jeon, W.; Lee, Y.; Won, D. Security analysis and improvements of two-factor mutual authentication with key agreement in wireless sensor networks. Sensors 2014, 14, 6443–6462. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.P.; Lee, T.F.; Lin, T.H.; Liu, C.M. Enhanced two-factor authentication and key agreement using dynamic identities in wireless sensor networks. Sensors 2015, 15, 29841–29854. [Google Scholar] [CrossRef] [PubMed]
- Yoon, E.J.; Yoo, K.Y. A biometric-based authenticated key agreement scheme using ECC for wireless sensor networks. In Proceedings of the 29th Annual ACM Symposium on Applied Computing, Gyeongju, Korea, 24–28 March 2014; pp. 699–705.
- Das, A.K. A secure and efficient user anonymity-preserving three-factor authentication protocol for large-scale distributed wireless sensor networks. Wirel. Pers. Commun. 2015, 82, 1377–1404. [Google Scholar] [CrossRef]
- Das, A.K. A secure and effective biometric-based user authentication scheme for wireless sensor networks using smart card and fuzzy extractor. Int. J. Commun. Syst. 2015, 2015, 1–25. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, Y.; Won, D. Security improvement on biometric based authentication scheme for wireless sensor networks using fuzzy extraction. Int. J. Dist. Sens. Netw. 2016, 8572410, 1–16. [Google Scholar] [CrossRef]
- Park, Y.; Lee, S.; Kim, C.; Park, Y. Secure biometric-based authentication scheme with smart card revocation/reissue for wireless sensor networks. Int. J. Dist. Sens. Netw. 2016, 12, 1–11. [Google Scholar] [CrossRef]
- Li, C.T.; Hwang, M.S. An efficient biometric-based remote authentication scheme using smart cards. J. Netw. Comp. Appl. 2010, 33, 1–5. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R.M. A logic of authentication. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1989, 426, 233–271. [Google Scholar] [CrossRef]
- Lu, R.; Cao, Z.; Chai, Z.; Liang, X. A Simple User Authentication Scheme for Grid Computing. IJ Netw. Sec. 2008, 7, 202–206. [Google Scholar]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; pp. 523–540.
- Tan, Z. A user anonymity preserving three-factor authentication scheme for telecare medicine information systems. J. Med. Syst. 2014, 38, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Kim, J.; Choi, Y.; Won, D. An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors 2016, 16, 1299. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H.L.; Chen, T.H.; Liu, P.C.; Kim, T.H.; Wei, H.W. A secured authentication protocol for wireless sensor networks using elliptic curves cryptography. Sensors 2011, 11, 4767–4779. [Google Scholar] [CrossRef] [PubMed]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Proceedings of the Advances in Cryptology-CRYPTO’99, Santa Barbara, CA, USA, 15–19 August 1999; Volume 1666, pp. 388–397.
- Amin, R.; Biswas, G.P. A secure light weight scheme for user authentication and key agreement in multi-gateway based wireless sensor networks. Ad Hoc Netw. 2016, 36, 58–80. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Chilamkurti, N. A secure temporal-credential-based mutual authentication and key agreement scheme with pseudo identity for wireless sensor networks. Inf. Sci. 2015, 321, 263–277. [Google Scholar] [CrossRef]
- Jiang, Q.; Kumar, N.; Ma, J.; Shen, J.; He, D.; Chilamkurti, N. A privacy-aware two-factor authentication protocol based on elliptic curve cryptography for wireless sensor networks. Int. J. Netw. Manag. 2016. [Google Scholar] [CrossRef]
- Lu, Y.; Li, L.; Yang, X.; Yang, Y. Robust biometrics based authentication and key agreement scheme for multi-server environments using smart cards. PLoS ONE 2015, 10, e0126323. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, Q.; Yan, R.; Sun, R. Efficient authenticated key exchange protocols for wireless body area networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).