Genomic Prediction of Adaptation in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Hybrids
Abstract
1. Introduction
2. Results
2.1. Yield Components and Biomass Variables Were Correlated and Differed Across Localities
2.2. BayesC Was the Model with the Best Performance Across Traits and Localities
2.3. All Markers Conveyed Greater Precision and Heritability than Only Associated Markers
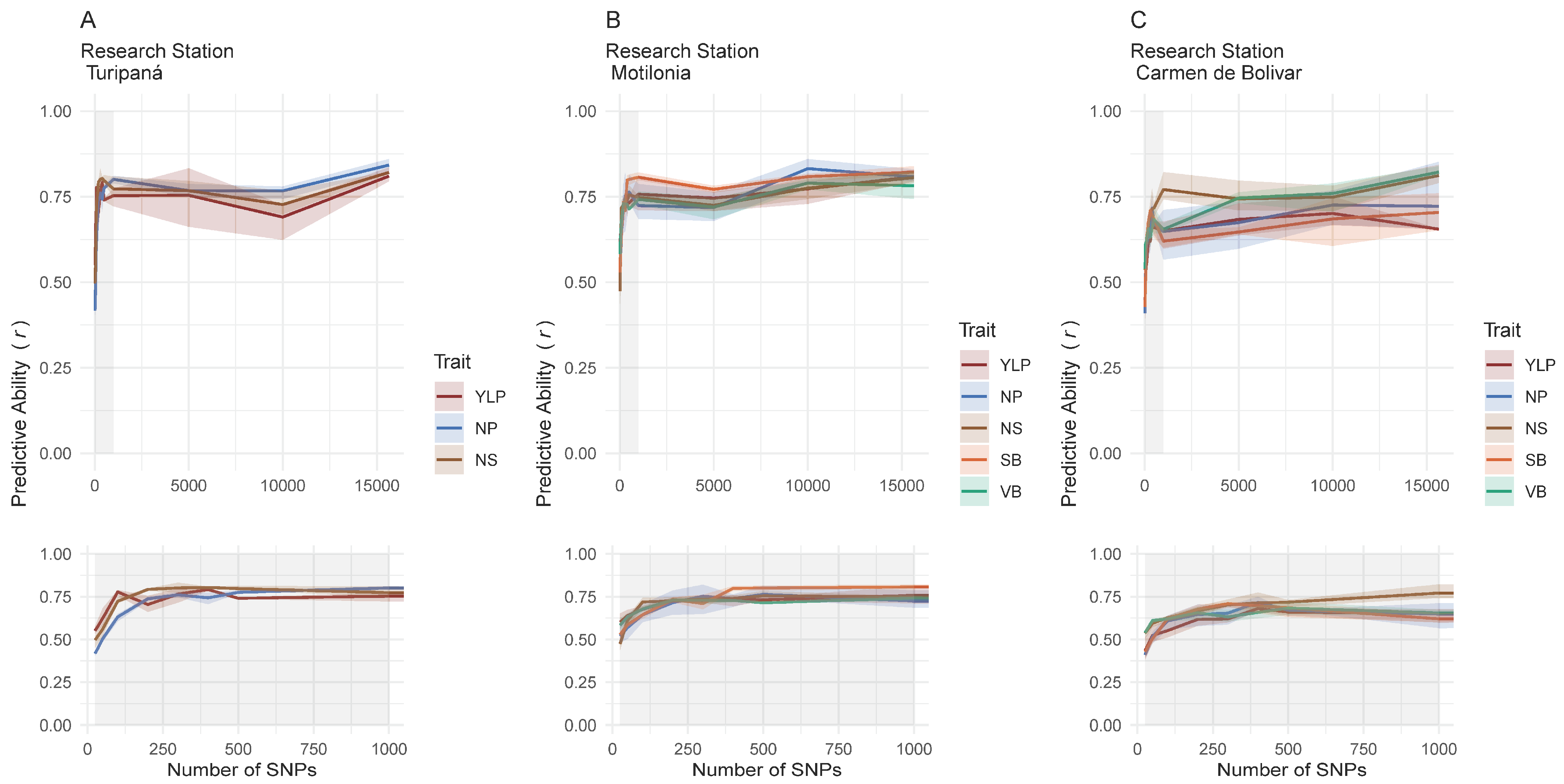
2.4. Genomic Heritability Differed Among Localities While Predictive Ability Was Consistent
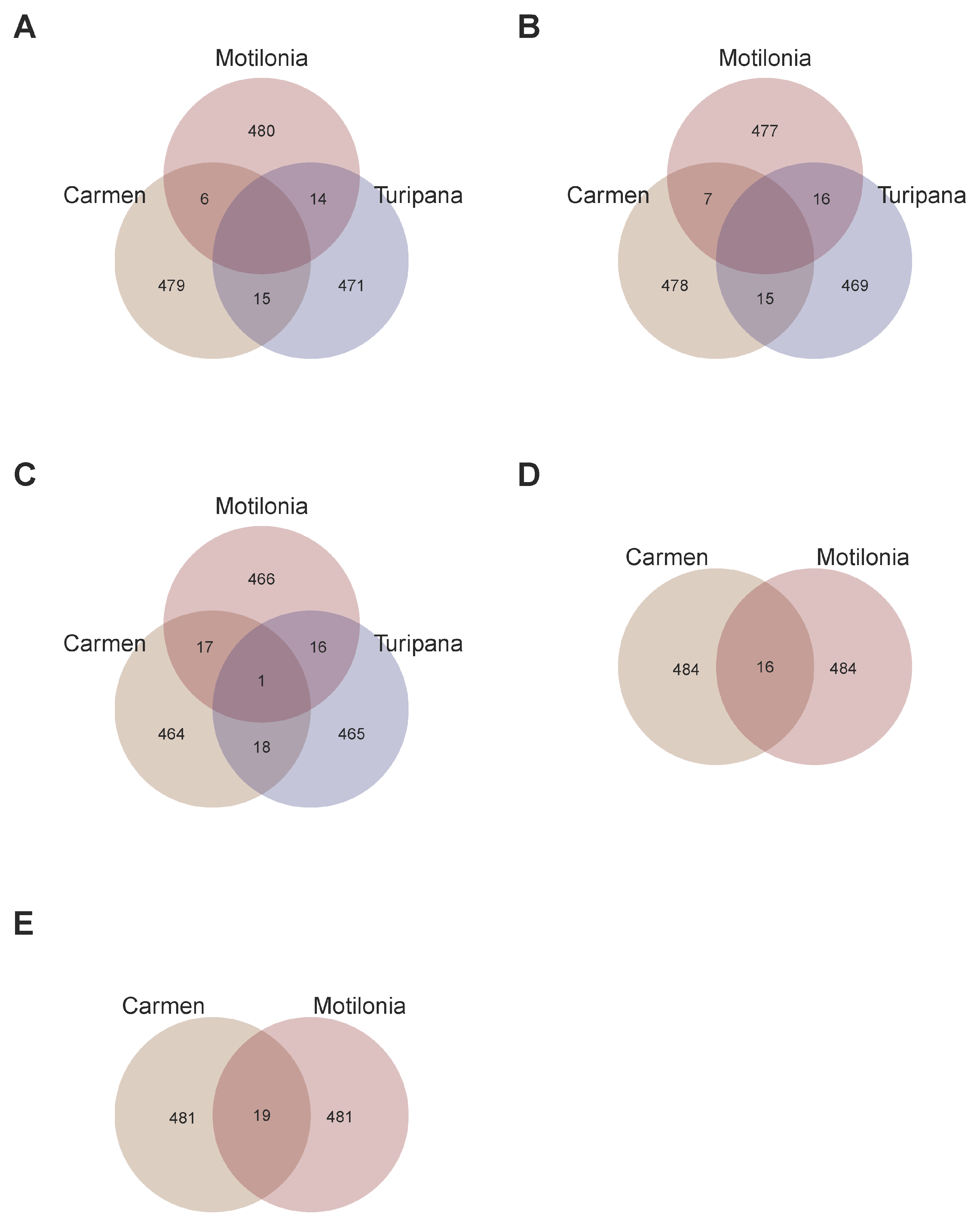
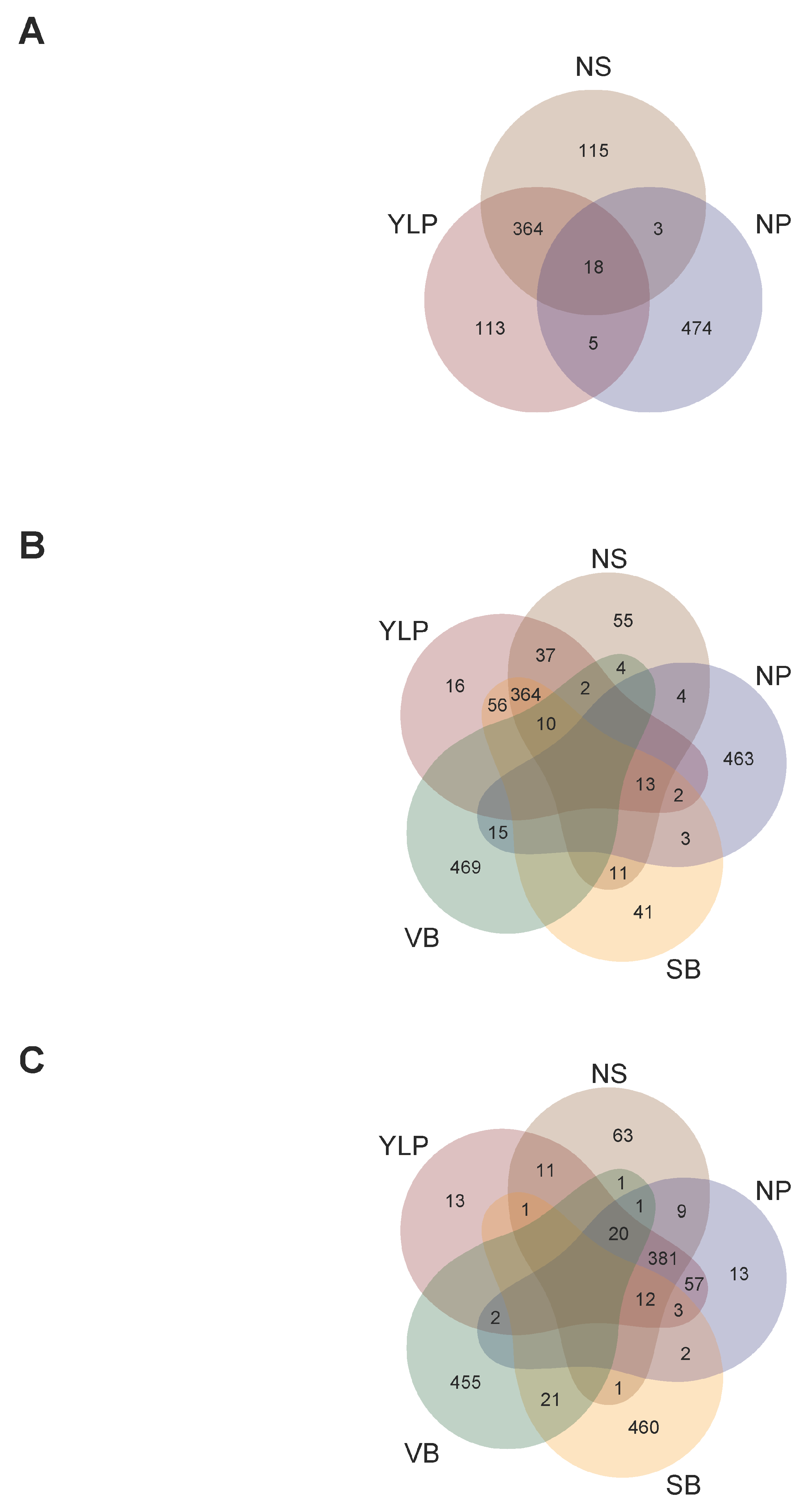
2.5. A Total of 13 Customized SNP-Chips Captured Trait Variation Across Localities
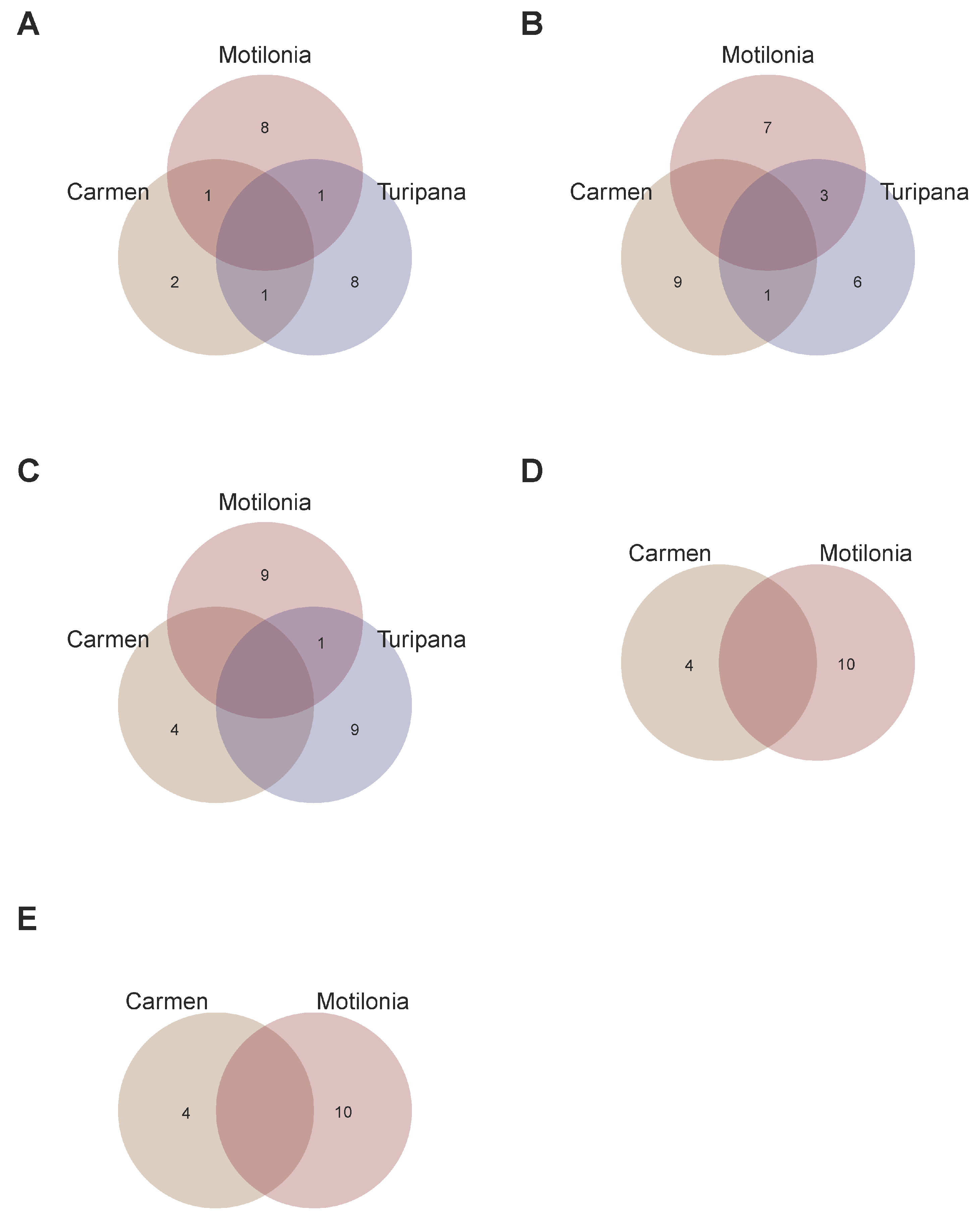
2.6. Recommendation Domains for Adaptation of Interspecific Genotypes
3. Discussion
3.1. Genomic Prediction Assists Introgression Breeding
3.2. Genomic Prediction Captures Missing Heritability and Locality-Dependent Effects
3.3. Candidate Customized SNP-Chips for Genotype Ranking May Optimize Genomic Selection
3.4. Enhancing the Predictive Ability of GP for Interspecific Panels
3.5. Perspectives
4. Materials and Methods
4.1. Plant Material and Multi-Locality Field Trials
4.2. Experimental Design and Phenotypic Segregation Across Localities
4.3. Genotyping by Sequencing and SNP Calling
4.4. Genomic Datasets from GBS and GWAS
4.5. Genomic Prediction Analyses
4.6. Predictive Ability and Genomic Heritability
4.7. Candidate Markers for Customized SNP-Chips per Trait and Locality
4.8. Top Genotypes per Locality
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Tai, A.P.K.; Martin, M.V.; Heald, C.L. Threat to Future Global Food Security from Climate Change and Ozone Air Pollution. Nat. Clim. Change 2014, 4, 817–821. [Google Scholar] [CrossRef]
- FAO. The State of Food Security and Nutrition in the World 2024; FAO: Rome, Italy, 2024; ISBN 2663-8541. [Google Scholar]
- FAO. Panorama de La Seguridad Alimentaria y Nutricional; FAO: Rome, Italy, 2020. [Google Scholar]
- Sgarbieri, V.C.; Whitaker, J.R. Physical, Chemical, and Nutritional Properties of Common Bean (Phaseolus) Proteins. Adv. Food Res. 1982, 28, 93–166. [Google Scholar] [CrossRef] [PubMed]
- Uebersax, M.A.; Porch, T.G.; Snapp, S.S.; Cichy, K.A.; Gomez, F.E.; Heitholt, J.; Bales, S.; Osorno, J.M.; Kamfwa, K. Dry Beans (Phaseolus vulgaris L.) as a Vital Component of Sustainable Agriculture and Food Security—A Review. Legume Sci. 2022, 5, e155. [Google Scholar] [CrossRef]
- FAO. Crop Production and Trade Data. Available online: http://www.fao.org/faostat/en/#data (accessed on 19 June 2025).
- Abberton, M.; Batley, J.; Bentley, A.; Bryant, J.; Cai, H.; Cockram, J.; Costa de Oliveira, A.; Cseke, L.J.; Dempewolf, H.; De Pace, C.; et al. Global Agricultural Intensification during Climate Change: A Role for Genomics. Plant Biotechnol. J. 2016, 14, 1095–1098. [Google Scholar] [CrossRef]
- Teichmann, C.; Eggert, B.; Elizalde, A.; Haensler, A.; Jacob, D.; Kumar, P.; Moseley, C.; Pfeifer, S.; Rechid, D.; Remedio, A.R.; et al. How Does a Regional Climate Model Modify the Projected Climate Change Signal of the Driving GCM: A Study over Different CORDEX Regions Using REMO. Atmosphere 2013, 4, 214–236. [Google Scholar] [CrossRef]
- Molina, O.D.; Bernhofer, C. Projected Climate Changes in Four Different Regions in Colombia. Environ. Syst. Res. 2019, 8, 33. [Google Scholar] [CrossRef]
- Cortés, A.J.; Monserrate, F.A.; Ramírez-Villegas, J.; Madriñán, S.; Blair, M.W. Drought Tolerance in Wild Plant Populations: The Case of Common Beans (Phaseolus vulgaris L.). PLoS ONE 2013, 8, e62898. [Google Scholar] [CrossRef]
- Cortés, A.J.; López-Hernández, F. Harnessing Crop Wild Diversity for Climate Change Adaptation. Genes 2021, 12, 783. [Google Scholar] [CrossRef]
- Cortés, A.J.; López-Hernández, F.; Blair, M.W. Genome–Environment Associations, an Innovative Tool for Studying Heritable Evolutionary Adaptation in Orphan Crops and Wild Relatives. Front. Genet. 2022, 13, 910386. [Google Scholar] [CrossRef]
- Tofiño Rivera, A.; Ospina Cortés, D.A.; Rozo Leguizamón, Y. Compatibility of Ancestral and Innovative Agricultural Practices in the Kankuamo People of Colombia. Ambient. Soc. 2021, 24, e00781. [Google Scholar] [CrossRef]
- Buitrago-Bitar, M.A.; Cortés, A.J.; López-Hernández, F.; Londoño-Caicedo, J.M.; Muñoz-Florez, J.E.; Carmenza Muñoz, L.; Blair, M.W. Allelic Diversity at Abiotic Stress Responsive Genes in Relationship to Ecological Drought Indices for Cultivated Tepary Bean, Phaseolus acutifolius A. Gray, and Its Wild Relatives. Genes 2021, 12, 556. [Google Scholar] [CrossRef] [PubMed]
- Mhlaba, Z.B.; Mashilo, J.; Shimelis, H.; Assefa, A.B.; Modi, A.T. Progress in Genetic Analysis and Breeding of Tepary Bean (Phaseolus acutifolius A. Gray): A Review. Sci. Hortic. 2018, 237, 112–119. [Google Scholar] [CrossRef]
- Jiri, O.; Mafongoya, P.L.; Chivenge, P. Climate Smart Crops for Food and Nutritional Security for Semi-Arid Zones of Zimbabwe. Afr. J. Food Agric. Nutr. Dev. 2017, 17, 12280–12294. [Google Scholar] [CrossRef]
- Moghaddam, S.M.; Oladzad, A.; Koh, C.; Ramsay, L.; Hart, J.P.; Mamidi, S.; Hoopes, G.; Sreedasyam, A.; Wiersma, A.; Zhao, D.; et al. The Tepary Bean Genome Provides Insight into Evolution and Domestication under Heat Stress. Nat. Commun. 2021, 12, 2638. [Google Scholar] [CrossRef] [PubMed]
- Mwale, S.E.; Shimelis, H.; Mafongoya, P.; Mashilo, J. Breeding Tepary Bean (Phaseolus acutifolius) for Drought Adaptation: A Review. Plant Breed. 2020, 139, 821–833. [Google Scholar] [CrossRef]
- Muñoz, L.C.; Duque, M.C.; Debouck, D.G.; Blair, M.W. Taxonomy of Tepary Bean and Wild Relatives as Determined by Amplified Fragment Length Polymorphism (AFLP) Markers. Crop Sci. 2006, 46, 1744–1754. [Google Scholar] [CrossRef]
- Migicovsky, Z.; Myles, S. Exploiting Wild Relatives for Genomics-Assisted Breeding of Perennial Crops. Front. Plant Sci. 2017, 8, 460. [Google Scholar] [CrossRef]
- Burbano-Erazo, E.; León-Pacheco, R.I.; Cordero-Cordero, C.C.; López-Hernández, F.; Cortés, A.J.; Tofiño-Rivera, A.P. Multi-Environment Yield Components in Advanced Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Interspecific Lines for Heat and Drought Tolerance. Agronomy 2021, 11, 1978. [Google Scholar] [CrossRef]
- Souter, J.R.; Gurusamy, V.; Porch, T.G.; Bett, K.E. Successful Introgression of Abiotic Stress Tolerance from Wild Tepary Bean to Common Bean. Crop Sci. 2017, 57, 1160–1171. [Google Scholar] [CrossRef]
- Belivanis, T.; Doré, C. Interspecific Hybridization of Phaseolus vulgaris L. and Phaseolus angustissimus A. Gray Using in Vitro Embryo Culture. Plant Cell Rep. 1986, 5, 329–331. [Google Scholar] [CrossRef]
- López-Hernández, F.; Burbano-Erazo, E.; León-Pacheco, R.I.; Cordero-Cordero, C.C.; Villanueva-Mejía, D.F.; Tofiño-Rivera, A.P.; Cortés, A.J. Multi-Environment Genome-Wide Association Studies of Yield Traits in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Interspecific Advanced Lines in Humid and Dry Colombian Caribbean Subregions. Agronomy 2023, 13, 1396. [Google Scholar] [CrossRef]
- Grattapaglia, D.; Silva-Junior, O.B.; Resende, R.T.; Cappa, E.P.; Müller, B.S.F.; Tan, B.; Isik, F.; Ratcliffe, B.; El-Kassaby, Y.A. Quantitative Genetics and Genomics Converge to Accelerate Forest Tree Breeding. Front. Plant Sci. 2018, 9, 1693. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for Classification and Analysis of Multivariate Observations; Lucien Marie Le Cam, J.N., Ed.; University of California: Berkeley, CA, USA, 1967; pp. 281–298. [Google Scholar]
- Gianola, D.; Fernando, R.L.; Stella, A. Genomic-Assisted Prediction of Genetic Value With Semiparametric Procedures. Genetics 2006, 1776, 1761–1776. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.; Hayes, B.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Arenas, S.; Cortés, A.J.; Mastretta-Yanes, A.; Jaramillo-Correa, J.P.; Jaramillo-Correa, J.P. Evaluating the Accuracy of Genomic Prediction for the Management and Conservation of Relictual Natural Tree Populations. Tree Genet. Genomes 2021, 17, 12. [Google Scholar] [CrossRef]
- de los Campos, G.; Hickey, J.M.; Pong-Wong, R.; Daetwyler, H.D.; Calus, M.P.L. Whole-Genome Regression and Prediction Methods Applied to Plant and Animal Breeding. Genetics 2013, 193, 327–345. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic Selection in Plant Breeding: Methods, Models, and Perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- Baek, E.; Beretvas, S.N.; Van den Noortgate, W.; Ferron, J.M. Brief Research Report: Bayesian Versus REML Estimations With Noninformative Priors in Multilevel Single-Case Data. J. Exp. Educ. 2020, 88, 698–710. [Google Scholar] [CrossRef]
- De los Campos, G.; Gianola, D.; Rosa, G.J.M.; Weigel, K.A.; Crossa, J. Semi-Parametric Genomic-Enabled Prediction of Genetic Values Using Reproducing Kernel Hilbert Spaces Methods. Genet. Res. 2010, 92, 295–308. [Google Scholar] [CrossRef]
- Keller, B.; Ariza-Suarez, D.; de la Hoz, J.; Aparicio, J.S.; Portilla-Benavides, A.E.; Buendia, H.F.; Mayor, V.M.; Studer, B.; Raatz, B. Genomic Prediction of Agronomic Traits in Common Bean (Phaseolus vulgaris L.) Under Environmental Stress. Front. Plant Sci. 2020, 11, 1001. [Google Scholar] [CrossRef]
- Tan, B.; Grattapaglia, D.; Martins, G.S.; Ferreira, K.Z.; Sundberg, B.; Ingvarsson, P.K. Evaluating the Accuracy of Genomic Prediction of Growth and Wood Traits in Two Eucalyptus Species and Their F1 Hybrids. BMC Plant Biol. 2017, 17, 110. [Google Scholar] [CrossRef]
- Zhang, Z.; Ober, U.; Erbe, M.; Zhang, H.; Gao, N.; He, J.; Li, J.; Simianer, H. Improving the Accuracy of Whole Genome Prediction for Complex Traits Using the Results of Genome Wide Association Studies. PLoS ONE 2014, 9, e93017. [Google Scholar] [CrossRef]
- Bian, Y.; Holland, J.B. Enhancing Genomic Prediction with Genome-Wide Association Studies in Multiparental Maize Populations. Heredity 2017, 118, 585–593. [Google Scholar] [CrossRef] [PubMed]
- Denning-James, K.E.; Chater, C.; Cortes, A.J.; Blair, M.W.; Peláez, D.; Hall, A.; De Vega, J.J. Genome-wide association mapping dissects the selective breeding of determinacy and photoperiod sensitivity in common bean (Phaseolus vulgaris L.). G3 Genes Genomes Genet. 2025, 15, jkaf090. [Google Scholar] [CrossRef]
- Patil, I. Visualizations with Statistical Details: The “ggstatsplot” Approach. J. Open Source Softw. 2021, 6, 3167. [Google Scholar] [CrossRef]
- Rogers, A.R.; Turnbull, C.; Bian, Y.; Nelson, P.; Krakowsky, M.; Holland, J.B.; Peters, D. Genomic Prediction for the Germplasm Enhancement of Maize Project. Plant Genome 2022, 15, e20267. [Google Scholar] [CrossRef]
- Yu, P.; Ye, C.; Li, L.; Yin, H.; Zhao, J.; Wang, Y.; Zhang, Z.; Li, W.; Long, Y.; Hu, X.; et al. Genome-Wide Association Study and Genomic Prediction for Yield and Grain Quality Traits of Hybrid Rice. Mol. Breed. 2022, 42, 16. [Google Scholar] [CrossRef] [PubMed]
- Hybrids, S.; Islam, S.; Mccord, P.; Read, Q.D.; Qin, L.; Lipka, A.E.; Sood, S.; Todd, J.; Olatoye, M. Accuracy of genomic prediction of yield and sugar traits in Saccharum spp. hybrids. Agriculture 2022, 12, 1436. [Google Scholar] [CrossRef]
- Garzón-Martínez, G.A.; Osorio-Guarín, J.A.; Moreno, L.P.; Bastidas, S.; Barrero, L.S.; Lopez-Cruz, M.; Enciso-Rodríguez, F.E. Genomic Selection for Morphological and Yield-Related Traits Using Genome-Wide SNPs in Oil Palm. Mol. Breed. 2022, 42, 71. [Google Scholar] [CrossRef]
- Barili, L.D.; do Vale, N.M.; e Silva, F.F.; de Souza Carneiro, J.E.; de Oliveira, H.R.; Vianello, R.P.; Valdisser, P.A.M.R.; Nascimento, M. Genome Prediction Accuracy of Common Bean via Bayesian Models. Ciência Rural 2018, 48, e20170497. [Google Scholar] [CrossRef]
- Ewens, W.J. Additive Genetic Variance. In Brenner’s Encyclopedia of Genetics, 2nd ed.; Academic Press: Cambridge, MA, USA, 2013; pp. 19–20. [Google Scholar] [CrossRef]
- Rasheed, A.; Hao, Y.; Xia, X.; Khan, A.; Xu, Y.; Varshney, R.K.; He, Z. Crop Breeding Chips and Genotyping Platforms: Progress, Challenges, and Perspectives. Mol. Plant 2017, 10, 1047–1064. [Google Scholar] [CrossRef] [PubMed]
- Varshney, R.K.; Nayak, S.N.; May, G.D.; Jackson, S.A. Next-Generation Sequencing Technologies and Their Implications for Crop Genetics and Breeding. Trends Biotechnol. 2009, 27, 522–530. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Cao, Y.; Wang, Y.; Ding, Y. Development of the Maize 5.5K Loci Panel for Genomic Prediction through Genotyping by Target Sequencing. Front. Plant Sci. 2022, 13, 972791. [Google Scholar] [CrossRef]
- Yu, G.; Cui, Y.; Jiao, Y.; Zhou, K.; Wang, X.; Yang, W.; Xu, Y.; Yang, K.; Zhang, X.; Li, P.; et al. Comparison of Sequencing-Based and Array-Based Genotyping Platforms for Genomic Prediction of Maize Hybrid Performance. Crop J. 2022, 11, 490–498. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, Y.H.; Su, S.S.; Reif, J.C.; Qi, Z.M.; Wang, X.B.; Wang, X.; Tian, Y.; Li, D.L.; Sun, R.J.; et al. SoySNP618K Array: A High-Resolution Single Nucleotide Polymorphism Platform as a Valuable Genomic Resource for Soybean Genetics and Breeding. J. Integr. Plant Biol. 2022, 64, 632–648. [Google Scholar] [CrossRef]
- Satpathy, S.; Shahi, D.; Blanchard, B.; Pontif, M.; Gravois, K.; Kimbeng, C.; Hale, A.; Todd, J.; Rao, A.; Baisakh, N. Evaluation of Models for Utilization in Genomic Prediction of Agronomic Traits in the Louisiana Sugarcane Breeding Program. Agriculture 2022, 12, 1330. [Google Scholar] [CrossRef]
- Spindel, J.E.; McCouch, S.R. When More Is Better: How Data Sharing Would Accelerate Genomic Selection of Crop Plants. New Phytol. 2016, 212, 814–826. [Google Scholar] [CrossRef]
- Sehgal, D.; Rosyara, U.; Mondal, S.; Singh, R.; Poland, J.; Dreisigacker, S. Incorporating Genome-Wide Association Mapping Results Into Genomic Prediction Models for Grain Yield and Yield Stability in CIMMYT Spring Bread Wheat. Front. Plant Sci. 2020, 11, 197. [Google Scholar] [CrossRef]
- Shi, A.; Gepts, P.; Song, Q.; Xiong, H.; Michaels, T.E.; Chen, S. Genome-Wide Association Study and Genomic Prediction for Soybean Cyst Nematode Resistance in USDA Common Bean (Phaseolus vulgaris) Core Collection. Front. Plant Sci. 2021, 12, 624156. [Google Scholar] [CrossRef]
- Wu, J.; Wang, L.; Fu, J.; Chen, J.; Wei, S.; Zhang, S.; Zhang, J.; Tang, Y.; Chen, M.; Zhu, J.; et al. Resequencing of 683 Common Bean Genotypes Identifies Yield Component Trait Associations across a North–South Cline. Nat. Genet. 2020, 52, 118–125. [Google Scholar] [CrossRef]
- Blair, M.W.; Cortés, A.J.; Farmer, A.D.; Huang, W.; Ambachew, D.; Penmetsa, R.V.; Carrasquilla-Garcia, N.; Assefa, T.; Cannon, S.B. Uneven recombination rate and linkage disequilibrium across a reference SNP map for common bean (Phaseolus vulgaris L.). PLoS ONE 2018, 13, e0189597. [Google Scholar] [CrossRef] [PubMed]
- Cortés, A.J.; Chavarro, M.C.; Blair, M.W. SNP Marker Diversity in Common Bean (Phaseolus vulgaris L.). Theor. Appl. Genet. 2011, 123, 827–845. [Google Scholar] [CrossRef]
- Li, B.; Zhang, N.; Wang, Y.G.; George, A.W.; Reverter, A.; Li, Y. Genomic Prediction of Breeding Values Using a Subset of SNPs Identified by Three Machine Learning Methods. Front. Genet. 2018, 9, 237. [Google Scholar] [CrossRef]
- Azodi, C.B.; Bolger, E.; McCarren, A.; Roantree, M.; de los Campos, G.; Shiu, S.H. Benchmarking Parametric and Machine Learning Models for Genomic Prediction of Complex Traits. G3 Genes Genomes Genet. 2019, 9, 3691–3702. [Google Scholar] [CrossRef] [PubMed]
- Abdollahi-Arpanahi, R.; Gianola, D.; Peñagaricano, F. Deep Learning versus Parametric and Ensemble Methods for Genomic Prediction of Complex Phenotypes. Genet. Sel. Evol. 2020, 52, 12. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A Review of Deep Learning Applications for Genomic Selection. BMC Genomics 2021, 22, 19. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer Nature: Berlin/Heidelberg, Germany, 2022; ISBN 9783030890094. [Google Scholar]
- Cortés, A.J. Unlocking genebanks for climate adaptation. Nat. Clim. Change 2025, 15, 590–592. [Google Scholar] [CrossRef]
- Blair, M.W.; Soler, A.; Cortés, A.J. Diversification and Population Structure in Common Beans (Phaseolus vulgaris L.). PLoS ONE 2012, 7, e49488. [Google Scholar] [CrossRef]
- Elshire, R.J.; Glaubitz, J.C.; Sun, Q.; Poland, J.A.; Kawamoto, K.; Buckler, E.S.; Mitchell, S.E. A Robust, Simple Genotyping-by-Sequencing (GBS) Approach for High Diversity Species. PLoS ONE 2011, 6, e19379. [Google Scholar] [CrossRef]
- Cortés, A.J.; Blair, M.W. Genotyping by Sequencing and Genome–Environment Associations in Wild Common Bean Predict Widespread Divergent Adaptation to Drought. Front. Plant Sci. 2018, 9, 128. [Google Scholar] [CrossRef]
- López-Hernández, F.; Cortés, A.J. Last-Generation Genome–Environment Associations Reveal the Genetic Basis of Heat Tolerance in Common Bean (Phaseolus vulgaris L.). Front. Genet. 2019, 10, 954. [Google Scholar] [CrossRef] [PubMed]
- McKenna, A.; Hanna, M.; Banks, E.; Sivachenko, A.; Cibulskis, K.; Kernytsky, A.; Garimella, K.; Altshuler, D.; Gabriel, S.; Daly, M.; et al. The Genome Analysis Toolkit: A MapReduce Framework for Analyzing next-Generation DNA Sequencing Data. Genome Res. 2010, 20, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Li, H. Aligning Sequence Reads, Clone Sequences and Assembly Contigs with BWA-MEM. arXiv 2013, arXiv:1303.3997. [Google Scholar]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The Sequence Alignment/Map Format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef] [PubMed]
- Afgan, E.; Baker, D.; Batut, B.; Van Den Beek, M.; Bouvier, D.; Ech, M.; Chilton, J.; Clements, D.; Coraor, N.; Grüning, B.A.; et al. The Galaxy Platform for Accessible, Reproducible and Collaborative Biomedical Analyses: 2018 Update. Nucleic Acids Res. 2018, 46, W537–W544. [Google Scholar] [CrossRef]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for Association Mapping of Complex Traits in Diverse Samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef]
- Money, D.; Gardner, K.; Migicovsky, Z.; Schwaninger, H.; Zhong, G.Y.; Myles, S. LinkImpute: Fast and Accurate Genotype Imputation for Nonmodel Organisms. G3 Genes Genomes Genet. 2015, 5, 2383–2390. [Google Scholar] [CrossRef]
- Villordo-Pineda, E.; González-Chavira, M.M.; Giraldo-Carbajo, P.; Acosta-Gallegos, J.A.; Caballero-Pérez, J. Identification of Novel Drought-Tolerant-Associated SNPs in Common Bean (Phaseolus vulgaris). Front. Plant Sci. 2015, 6, 546. [Google Scholar] [CrossRef]
- Mir, R.R.; Reynolds, M.; Pinto, F.; Khan, M.A.; Bhat, M.A. High-Throughput Phenotyping for Crop Improvement in the Genomics Era. Plant Sci. 2019, 282, 60–72. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the Bayesian Alphabet for Genomic Selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- de los Campos, G.; Gianola, D.; Rosa, G.J. Reproducing Kernel Hilbert Spaces Regression: A General Framework for Genetic Evaluation. J. Anim. Sci. 2009, 87, 1883–1887. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. Genomic Selection Using Low-Density Marker Panels. Genetics 2009, 182, 343–353. [Google Scholar] [CrossRef]
- Ferrão, L.F.V.; Ferrão, R.G.; Ferrão, M.A.G.; Fonseca, A.; Carbonetto, P.; Stephens, M.; Garcia, A.A.F. Accurate Genomic Prediction of Coffea Canephora in Multiple Environments Using Whole-Genome Statistical Models. Heredity 2019, 122, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D. Priors in Whole-Genome Regression: The Bayesian Alphabet Returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef]
- Cuevas, J.; Crossa, J.; Soberanis, V.; Pérez-Elizalde, S.; Pérez-Rodríguez, P.; de los Campos, G.; Montesinos-López, O.A.; Burgueño, J. Genomic Prediction of Genotype × Environment Interaction Kernel Regression Models. Plant Genome 2016, 9, 1–20. [Google Scholar] [CrossRef]
- Pérez, P.; De los Campos, G. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- de los Campos, G.; Sorensen, D.; Gianola, D. Genomic Heritability: What Is It? PLoS Genet. 2015, 11, e1005048. [Google Scholar] [CrossRef]
- Sousa, T.V.; Caixeta, E.T.; Alkimim, E.R.; Oliveira, A.C.B.; Pereira, A.A.; Sakiyama, N.S.; Zambolim, L.; Resende, M.D.V. Early Selection Enabled by the Implementation of Genomic Selection in Coffea Arabica Breeding. Front. Plant Sci. 2019, 9, 1934. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Wang, H.; Beyene, Y.; Semagn, K.; Liu, Y.; Cao, S.; Cui, Z.; Ruan, Y.; Burgueño, J.; Vicente, F.S.; et al. Effect of Trait Heritability, Training Population Size and Marker Density on Genomic Prediction Accuracy Estimation in 22 Bi-Parental Tropical Maize Populations. Front. Plant Sci. 2017, 8, 1916. [Google Scholar] [CrossRef] [PubMed]
- Cortés, A.J. Abiotic stress tolerance boosted by genetic diversity in plants. Int. J. Mol. Sci. 2024, 25, 5367. [Google Scholar] [CrossRef]
- Peláez, D.; Aguilar, P.A.; Mercado, M.; López-Hernández, F.; Guzmán, M.; Burbano-Erazo, E.; Denning-James, K.; Medina, C.I.; Blair, M.W.; De Vega, J.J.; et al. Genotype selection, and seed uniformity and multiplication to ensure common bean (Phaseolus vulgaris L.) var. Liborino. Agronomy 2022, 12, 2285. [Google Scholar] [CrossRef]


| Variable | Locality | SNP Dataset | Best-Performing Model | Prediction Ability ry | Genomic Heritability h2g | MSE |
|---|---|---|---|---|---|---|
| YLP | Carmen de Bolivar | All markers | BayesC | 0.83 ± 0.17 | 0.487 ± 0.015 | 0.038 |
| YLP | Carmen de Bolivar | Associated markers | BayesC | 0.67 ± 0.18 | 0.378 ± 0.004 | 0.055 |
| YLP | Motilonia | All markers | BayesC | 0.81 ± 0.10 | 0.776 ± 0.009 | 0.010 |
| YLP | Motilonia | Associated markers | BayesC | 0.80 ± 0.12 | 0.719 ± 0.003 | 0.010 |
| YLP | Turipaná | All markers | BayesC | 0.79 ± 0.10 | 0.289 ± 0.016 | 0.093 |
| YLP | Turipaná | Associated markers | BayesC | 0.53 ± 0.20 | 0.175 ± 0.003 | 0.169 |
| NP | Carmen de Bolivar | All markers | BayesA | 0.47 ± 0.12 | 0.466 ± 0.008 | 0.093 |
| NP | Carmen de Bolivar | Associated markers | BayesC | 0.49 ± 0.12 | 0.251 ± 0.003 | 0.093 |
| NP | Motilonia | All markers | BayesC | 0.82 ± 0.10 | 0.760 ±0.009 | 0.015 |
| NP | Motilonia | Associated markers | BayesC | 0.77 ± 0.11 | 0.601 ± 0.004 | 0.018 |
| NP | Turipaná | All markers | BayesC | 0.84 ± 0.13 | 0.597 ± 0.016 | 0.033 |
| NP | Turipaná | Associated markers | BayesC | 0.46 ± 0.18 | 0.345 ± 0.003 | 0.067 |
| NS | Carmen de Bolivar | All markers | BayesC | 0.83 ± 0.18 | 0.402 ± 0.015 | 0.037 |
| NS | Carmen de Bolivar | Associated markers | BayesC | 0.70 ± 0.18 | 0.340 ± 0.004 | 0.053 |
| NS | Motilonia | All markers | BayesC | 0.81 ± 0.09 | 0.670 ± 0.012 | 0.010 |
| NS | Motilonia | Associated markers | BayesC | 0.79 ± 0.12 | 0.727 ± 0.005 | 0.010 |
| NS | Turipaná | All markers | BayesC | 0.85 ± 0.08 | 0.224 ± 0.011 | 0.097 |
| NS | Turipaná | Associated markers | BayesC | 0.48 ± 0.20 | 0.181 ± 0.002 | 0.168 |
| SB | Carmen de Bolivar | All markers | BayesC | 0.84 ± 0.17 | 0.680 ± 0.013 | 0.030 |
| SB | Carmen de Bolivar | Associated markers | BayesC | 0.71 ± 0.18 | 0.388 ± 0.004 | 0.039 |
| SB | Motilonia | All markers | BayesC | 0.83 ± 0.10 | 0.744 ± 0.007 | 0.018 |
| SB | Motilonia | Associated markers | BayesC | 0.81 ± 0.12 | 0.513 ± 0.006 | 0.021 |
| VB | Carmen de Bolivar | All markers | BayesC | 0.75 ± 0.10 | 0.455 ± 0.012 | 0.018 |
| VB | Carmen de Bolivar | Associated markers | BayesC | 0.47 ± 0.20 | 0.256 ± 0.002 | 0.256 |
| VB | Motilonia | All markers | BayesC | 0.83 ± 0.08 | 0.874 ± 0.006 | 0.018 |
| VB | Motilonia | Associated markers | BayesC | 0.83 ± 0.11 | 0.793 ± 0.004 | 0.019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Hernández, F.; Villanueva-Mejía, D.F.; Tofiño-Rivera, A.P.; Cortés, A.J. Genomic Prediction of Adaptation in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Hybrids. Int. J. Mol. Sci. 2025, 26, 7370. https://doi.org/10.3390/ijms26157370
López-Hernández F, Villanueva-Mejía DF, Tofiño-Rivera AP, Cortés AJ. Genomic Prediction of Adaptation in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Hybrids. International Journal of Molecular Sciences. 2025; 26(15):7370. https://doi.org/10.3390/ijms26157370
Chicago/Turabian StyleLópez-Hernández, Felipe, Diego F. Villanueva-Mejía, Adriana Patricia Tofiño-Rivera, and Andrés J. Cortés. 2025. "Genomic Prediction of Adaptation in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Hybrids" International Journal of Molecular Sciences 26, no. 15: 7370. https://doi.org/10.3390/ijms26157370
APA StyleLópez-Hernández, F., Villanueva-Mejía, D. F., Tofiño-Rivera, A. P., & Cortés, A. J. (2025). Genomic Prediction of Adaptation in Common Bean (Phaseolus vulgaris L.) × Tepary Bean (P. acutifolius A. Gray) Hybrids. International Journal of Molecular Sciences, 26(15), 7370. https://doi.org/10.3390/ijms26157370









