Efficient Control of DC Microgrid with Hybrid PV—Fuel Cell and Energy Storage Systems

Abstract

Direct current microgrids are attaining attractiveness due to their simpler configuration and high-energy efficiency. Power transmission losses are also reduced since distributed energy resources (DERs) are located near the load. DERs such as solar panels and fuel cells produce the DC supply; hence, the system is more stable and reliable. DC microgrid has a higher power efficiency than AC microgrid. Energy storage systems that are easier to integrate may provide additional benefits. In this paper, the DC micro-grid consists of solar photovoltaic and fuel cell for power generation, proposes a hybrid energy storage system that includes a supercapacitor and lithium–ion battery for the better improvement of power capability in the energy storage system. The main objective of this research work has been done for the enhanced settling point and voltage stability with the help of different maximum power point tracking (MPPT) methods. Different control techniques such as fuzzy logic controller, neural network, and particle swarm optimization are used to evaluate PV and FC through DC–DC boost converters for this enhanced settling point. When the test results are perceived, it is evidently attained that the fuzzy MPPT method provides an increase in the tracking capability of maximum power point and at the same time reduces steady-state oscillations. In addition, the time to capture the maximum power point is 0.035 s. It is about nearly two times faster than neural network controllers and eighteen times faster than for PSO, and it has also been discovered that the preferred approach is faster compared to other control methods.

1. Introduction

The global energy demand is steadily increasing. Traditional energy sources emit greenhouse gases, so non-traditional energy sources such as solar PV and wind turbines were developed to be renewable, abundant in nature, cost-efficient, and widely used. Instead, use a source as FC has in this ever-increasing power demand. The majority of rural areas do not have access to reliable electricity. The initial investment cost to electrify rural areas was very high. Still, with the aid of DC microgrids based on renewable energy sources (RES) such as solar PV and FC with energy storage systems (ESS), implementation is simple and cost-effective [1,2]. In this current scenario, DC microgrids are more popular because of easy interfacing with distribution generation without interlinking AC/DC and DC/AC transformation stages. They do not have any reactive power and complex frequency issues. DC/DC converters are important for the integration of distribution generation in DC microgrids [3]. Buck converters, boost converters, and buck-boost converters [4] are the three types of DC/DC converters commonly used. Buck converter produces a controlled output voltage, which is lesser than the input voltage; for a boost converter, the controlled output voltage is greater than the input voltage; similarly, for a buck-boost converter, the controlled output voltage is lesser or greater than the input voltage. Compared to an AC micro-grid, connecting RESs to a common DC bus has many advantages, including greater performance and accuracy and the elimination of frequency and phase control requirements [5,6]. Similarly, bi-directional DC/DC converters are used in this dc microgrid to maintain high reliability and load power supply [7]. The ultra-capacitor is preferred with battery combinations because of low power density battery cannot reimburse for fast power fluctuation [8,9]. Mohammed T. Arif proposed a significance of storage on solar PV system for residential load considering PV as renewable energy generator [10].

In the FC, an electrolyzer produces hydrogen gas by the process called electrolysis. The gas tanks and metal hydride tanks are used to store the hydrogen gas in the FC. Compared to gas tanks, metal hydride is more expensive and bigger in size, but the safety against accidents is high, and that’s why it is essential for self-governing systems installed in remote areas [11]. In this paper, the maximum power point tracking (MPPT) of solar PV and FC are achieved. To track the maximum power, different types of MPPT techniques are used, namely perturb and observe (P and O), incremental conductance (INC), FLC, ANN, and the particle swarm optimization (PSO) algorithm. In these different MPPT methods, P and O MPPT technique is most frequently used, and it is proposed for both PV and FC systems [12,13]. In this paper, different types of MPPT [14,15,16] techniques (FLC, ANN and PSO) are used for attaining the maximum power of PV and FC system and embrace all hybrid power (PV-FC) with battery and ultra-capacitor power at DC link. Saleh Elkelani Babaa [17] has presented an overview of different MPPT methods for PV systems. Luigi Costano and Massimo Vitelli [18] have designed a single-stage grid-connected PV system in mind. Its efficiency is compared numerically to that of the commonly used perturb and observe (P and O) MPPT technique. Mohammed Junaid Khan [19] has designed a fuzzy logic–based MPPT controller for PV and FC applications.

Figure 1 shows the distributed RES, ESS, DC load with grid-connected voltage source converter. DC microgrids have more advantages such as high efficiency, reliability, and low environmental pollution than AC microgrid and do not have frequency, reactive power issues. Hence, it is easy to link with DC micro sources.

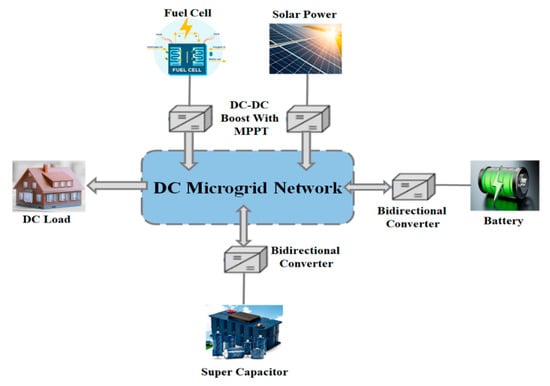
Figure 1. Schematic Diagram of DC Microgrid consists of Renewable Energy Sources (RESs) and Energy Storage Systems (ESS).

A study of different controllers such as FLC, NN, and PSO algorithm for hybrid DC microgrid has been made in this paper. With the assistance of various controllers, the settling time of power is observed. It is determined that fuzzy provides the most effective MPPT system compared to other control techniques. The organization of this research is as follows. Section 2 presents the solar PV and FC mathematical modeling. Section 3 explains the different MPPT control techniques such as FLC, ANN, and PSO algorithm to control the DC bus voltage, and the simulation results are presented in Section 4. Section 5 illustrates the conclusion and future scope of the hierarchical control structure.

2. Mathematical Model of Solar PV and Fuel Cell

The mathematical equations are modeled and designed using MATLAB/Simulink (2019a, The Mathwork, Inc., Natick, MA, USA) for PV and FC, which is illuminated as follows:

2.1. Modelling of Solar PV

PV cells are electrical devices that transform solar energy into electricity using semiconducting devices that demonstrate the photovoltaic effect. The photovoltaic cell is used to describe electrical variables such as current, voltage, and resistance as they change in response to sunlight. The equivalent circuit of a solar cell is shown in Figure 2. When an electron collides with another electron in its bound state, electron conduction occurs, and these electrons are energized by the base energy provided by the semiconductor’s bandgap. The equivalent circuit of PV [20] module contains a diode, light-created source, and resistance connected in parallel. Figure 3 shows the P-V and I-V characteristics [21,22,23] of solar cell, which is conditioned and screened for various irradiances at T = 25 °C. The following Equations (1)–(4) represent the mathematical equations for modeling solar cells.

$$\mathrm{I}={\mathrm{I}}_{\mathrm{ph}}-{\mathrm{I}}_{\mathrm{d}}\left[\exp \left(\frac{\mathrm{qV}}{{\mathrm{k}}_{\mathrm{b}}\mathrm{TA}}\right)-1\right]$$

(1)

$${\mathrm{I}}_{\mathrm{sh}}=\frac{\left[\mathrm{V}+\left({\mathrm{I}\ast \mathrm{R}}_{\mathrm{s}}\right)\right]}{{\mathrm{R}}_{\mathrm{sh}}}$$

(2)

$${\mathrm{I}}_{\mathrm{ph}}={\mathrm{I}}_{\mathrm{rr}}\left[{\mathrm{I}}_{\mathrm{sc}}+{\mathrm{k}}_{\mathrm{i}}\left({\mathrm{T}}_{\mathrm{op}}-{\mathrm{T}}_{\mathrm{ref}}\right)\right]$$

(3)

$${\mathrm{I}}_{\mathrm{d}}={\mathrm{I}}_{\mathrm{rr}}{\left[\frac{{\mathrm{T}}_{\mathrm{op}}}{{\mathrm{T}}_{\mathrm{ref}}}\right]}^3\exp \left(\frac{{\mathrm{qE}}_{\mathrm{g}}}{\mathrm{kQA}}\left[\frac{1}{{\mathrm{T}}_{\mathrm{ref}}}-\frac{1}{{\mathrm{T}}_{\mathrm{op}}}\right]\right)$$

(4)

where, I = total current (A); V = output voltage (V); T = temperature (°C); q = electron charge; k_i = short-circuit temperature coefficient; I_sh = shunt resistance current; R_s = Series Resistance; R_sh = Shunt Resistance; k_b = open-circuit voltage temperature coefficient and k = Boltzmann’s constant; A = ideality factor; I_ph = load current; I_d = diode current; I_rr = saturation current at T_ref; I_sc = short-circuit current at reference condition; T_ref = reference temperature; Q = total electron charge; E_g = band-gap energy.

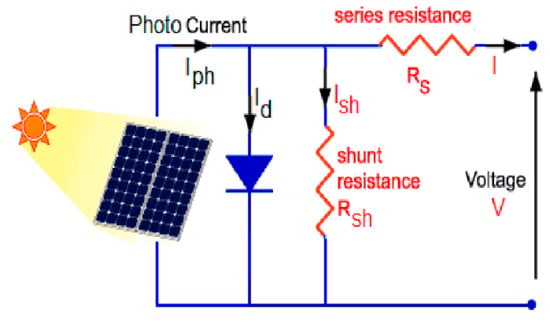
Figure 2. Solar Cells equivalent circuit.

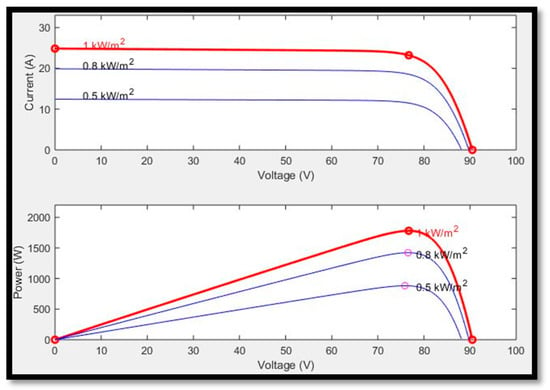
Figure 3. P–V and I–V Characteristics of solar cell for Different Irradiance for constant T = 25 °C.

2.2. FC Mathematical Model

The FC [24] consists of Proton exchange membrane (PEM) [25,26,27], catalyst layer (CL), gas diffusion layer (GDL), gas channel (GC), and current collector (CC) of both anode and cathode. Figure 4 illustrates the proton exchange membrane fuel cell (PEMFC).

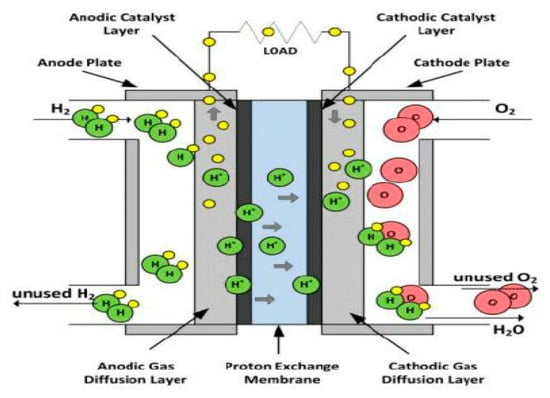
Figure 4. Schematic illustration of proton exchange membrane fuel cell (PEMFC).

2.2.1. Model Equations of FC

FC’s fundamental model includes mass, thermal energy, momentum, organisms, and charge. This FC model is based on five equations. These equations are combined to form an electrochemical process to express reaction kinetics and electro-osmotic drag during the polymer electrolyte process. Equations (5)–(10) represent the five equations for this FC model in vector form.

2.2.2. Continuity Equation

The electrodes present in the FC are made up of carbon fiber or carbon cloth. The reactant gases are spread over the CL, and the electrodes are restrained as a porous medium everywhere. The continuity equation for the porosity with the help of electrodes (ε) has given in Equation (5).

$$\left(\frac{\partial \mathsf{\epsilon }\mathsf{\rho }}{\partial \mathrm{t}}\right)+\nabla \times \left(\mathsf{\epsilon }\mathsf{\rho }\mathrm{U}\right)=0$$

(5)

where ∇ = differential operator of a vector, ρ = liquid density, ε = porosity, U = floating speed vector and t = time.

2.2.3. Momentum Conservation

Navier–Stokes equation has given in Equation (6) and designed for a Newtonian fluid.

$$\left(\frac{\partial \left(\mathsf{\epsilon }\mathsf{\rho }\mathrm{U}\right)}{\partial \mathrm{t}}\right)+\nabla ·\left({\mathsf{\epsilon }\mathsf{\rho }\mathrm{U}}^2\right)=-\mathsf{\epsilon }\nabla \mathrm{p}+\mathsf{\epsilon }\mathrm{F}+\nabla ·\left(\mathsf{\epsilon }\mathsf{\tau }\right)-\frac{{\mathsf{\epsilon }}^2\mathsf{\mu }\mathrm{U}}{\mathrm{k}}$$

(6)

where $\mathsf{\rho }$ = pressure; τ = stress tensor; F = floating mass vector; μ = liquid viscidity degree; k = permeate ratio of the liquid by porous medium.

2.2.4. Conversion of Charge Equation

PEMFC is used in CL to conduct electrochemical reactions. The charge equations are an integral part of the FC, and this equation consists of two equations: electron removal above conductive solid phase and proton transference above the membrane. The oxygen diffusion flux (ODF) on the catalyst surface is used to calculate the current density (CD) that circulates along with CL. The CL’s two-dimensional Poisson’s equation is as follows:

$$\nabla ·\mathrm{i}=0$$

(7)

The sum of phase currents of solid (i_s) and membrane (i_m) during CL is equal to the total current (i), which is given in the following equation,

$$\mathrm{i}={\mathrm{i}}_{\mathrm{s}}+{\mathrm{i}}_{\mathrm{m}}$$

(8)

Using Ohm’s law, the transfer current density (J_t) with solid surface tension is given by,

$${\mathrm{J}}_{\mathrm{t}}=-\nabla ·-\left({\mathsf{\sigma }}_{\mathrm{s}}\nabla {\mathsf{\phi }}_{\mathrm{s}}\right)=\nabla ·\left(-{\mathsf{\sigma }}_{\mathrm{m}}\nabla {\mathsf{\phi }}_{\mathrm{m}}\right)$$

(9)

where J_t = transfer current density at time t, σ_s = solid phase surface tension, σ_m = membrane phase surface tension, ${\mathsf{\phi }}_{\mathrm{s}}$ = solid phase flux, ${\mathsf{\phi }}_{\mathrm{m}}$ = membrane phase flux.

2.2.5. Electrochemical Reaction Dynamics equation

The current density at time (J_t) is a classification of electrochemical reaction velocity, the concentration of species, and potential among the phase of the membrane and solid. The expression for Butler–Volmer (B–V) has expressed below,

$${\mathrm{J}}_{\mathrm{t}}={\mathrm{J}}_{\mathrm{o}}\left\{\exp \left[\frac{{\mathsf{\alpha }}_{\mathrm{a}}\mathrm{F}}{\mathrm{RT}}\left({\mathsf{\Phi }}_{\mathrm{s}}-{\mathsf{\Phi }}_{\mathrm{m}}\right)\right]-\exp \left[\frac{{\mathsf{\alpha }}_{\mathrm{c}}\mathrm{F}}{\mathrm{RT}}\left({\mathsf{\Phi }}_{\mathrm{s}}-{\mathsf{\Phi }}_{\mathrm{m}}\right)\right]\right\}{\displaystyle \prod }_{\mathrm{j}=1}^{\mathrm{N}}{[ᴧ]}^{\mathsf{\alpha }\mathrm{j}}$$

(10)

where, F = Faraday’s constant, R = electrical resistance, J₀ = exchange current density, αj = charge transfer coefficient, α_a and α_c = transfer coefficients of cathode and anode. ᴧ = mol concentration of the reactant.

3. MPPT Techniques

The efficient yield of solar PV and FC has developed via different MPPT methods. Various types of MPPT techniques are there. From that, the utmost familiar MPPT methods are perturb and observe (P and O), incremental conductance technique (INC), the FLC, ANN, and particle swarm optimization (PSO) control methods. In this paper, power has been transferred to load with the help of MPPT to extract maximum power from hybrid (PV-FC) DC microgrid. DC/DC boost converter performs as an interface among load and hybrid (PV-FC) sources. The maximum power has been obtained by changing the duty cycle of the DC/DC converter with respect to the load impedance. Hence, the MPPT techniques for solar PV and FC are necessary to sustain the module functioning at its MPPT.

3.1. Particle Swarm Optimization (PSO)

Kennedy and Eberhart founded PSO [28,29,30] as an evolutionary computation strategy. Birds penetrating for food stimulate the PSO. Flocking is a mechanism through which birds classify their food sources, and it was through these flock activities, the PSO process was discovered. The search space directs moving particles to their known positions. When a better position is found, it will be used to direct the flock’s movement. Since the method is ongoing, as is the execution, the appropriate outcome can be trusted but not guaranteed. The difference between PSO and conventional evolutionary computation approaches is that particle velocities are tuned while individual evolutionary positions are replaced; it’s as if the particle swarm individual’s “fate” is changed rather than their “state.” Furthermore, PSO experiences partial optimism, which results in less precise measurements of its position and velocity in its Control. However, this algorithm does not solve the optimization or scattering problems. The flowchart for the PSO algorithm is shown in Figure 5.

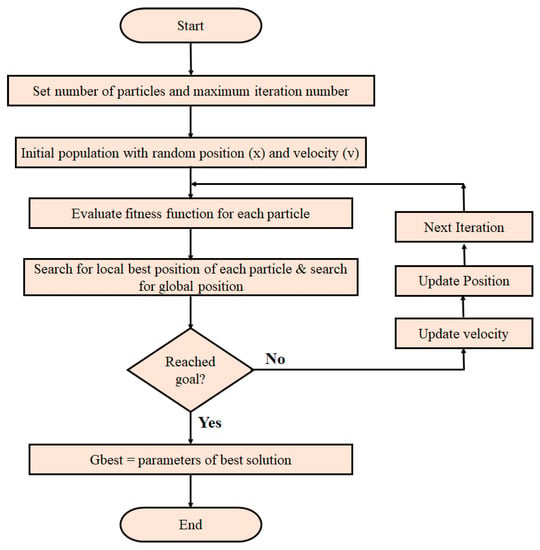
Figure 5. Flowchart of particle swarm optimization (PSO) Algorithm.

3.2. Artificial Neural Network

The computational tool that represents nonlinear systems has been said to be ANN [31,32,33]. ANN consists of biological neurons, which contain weight and bias to interconnect each other by transferring signals. The weights related to input values go together with the learning rule in the training process. The output y_j of ANN has given in Equation (11),

$${\mathrm{y}}_{\mathrm{i}}=\mathrm{f}\left({\displaystyle \sum }{\mathrm{w}}_{\mathrm{ij}}{\mathrm{x}}_{\mathrm{i}}+\mathrm{b}\right)$$

(11)

where f = activation function, x_i = input signal and w_ij = weight between input and output, b = bias value. The output neuron E, obtained as follows,

$$\mathrm{E}=\frac{1}{2}{\displaystyle \sum }_{\mathrm{i}}{\left({\mathrm{y}}_{\mathrm{di}}-{\mathrm{y}}_{\mathrm{i}}\right)}^2$$

(12)

where y_di = desired value of output neuron i and y_i = actual output.

In this paper, a quasi-Newton back propagation algorithm has been used for weight mean square error (MSE). With the help of a minimum number of neurons per layer, maximum accuracy has been obtained by carrying out more trials. The ANN that is developed in this paper, the input layer contains 1 neuron, the hidden layer has 10 neurons, and the output layer has 1 neuron. The neurons in the input layer and the hidden layers’ sigmoidal activation functions are used, and the neurons in the output layer linear activation function are used. The structure of ANN used in this paper is shown in Figure 6 and Figure 7.

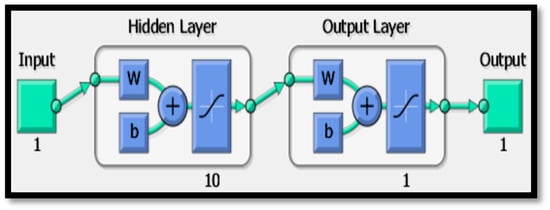
Figure 6. Design of ANN controller for the boost converter.

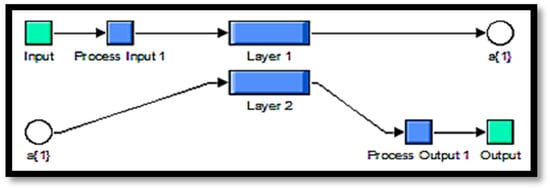
Figure 7. Simulink model of artificial neural network (ANN) chosen for the boost converter.

3.3. Fuzzy Logic Controller

The linguistic variables and their ranges are determined with the help of the main control variables. With the help of these control variables, the fuzzy logic controller (FLC) [34,35,36,37] is designed. The human’s specific intellect and understanding for developing the membership functions are essential for making the perception. Figure 8 and Figure 9 depict an FLC-based MPPT controller and an FLC rule viewer and sur-face viewer, respectively. Consider the input variables error E (k) and shift in error DE when determining the fuzzy membership functions (k). As a result of these input signals, linguistic variables are obtained. Change of Control (Duty cycle D (k)) is the contribution of the fuzzy membership function. Figure 10 shows the proposed MPPT [38] control scheme with membership feature fuzzy controller for E (k), DE (k), and D (k). With the use of the intuition method, a triangular membership function was used to obtain E (k) membership values and DE (k). The E (k) and DE (k) (−2, 2) intervals are set. To classify some unique input, a triangular style membership feature is proposed for an individual dominant fuzzy subset. Fuzzy rules for the hybrid (PV–FC) scheme are presented in Table 1.

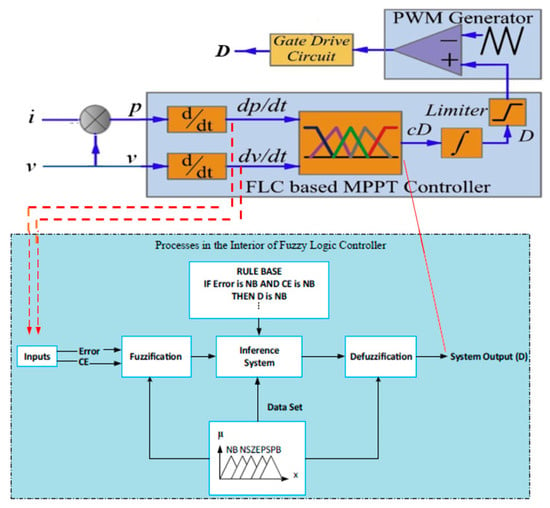
Figure 8. Fuzzy logic-based maximum power point tracking (MPPT) controller for boost converter.

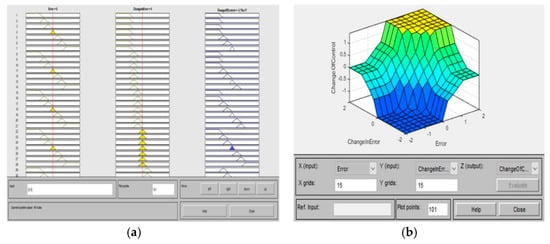
Figure 9. Fuzzy logic controller (a) rule viewer (b) surface viewer.

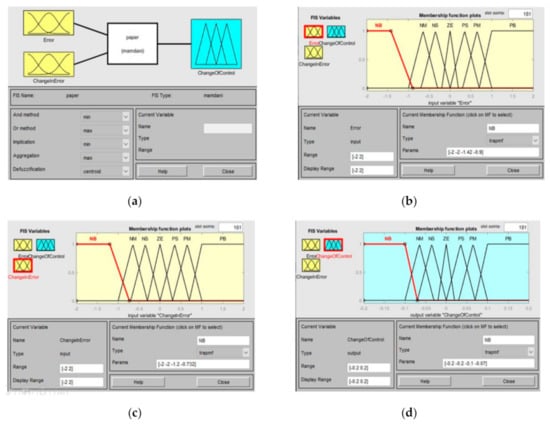
Figure 10. (a) Design of fuzzy (b) membership functions of input variable E (k) (c) membership functions for input variables DE (k) (d) membership functions of output change in duty cycle.

Table 1. Rules table of the fuzzy logic controller (FLC).

E(k)	NB	NM	NS	ZE	PS	PM	PB
∆E(k)
NB	ZE	ZE	NS	NM	PM	PM	PB
NM	ZE	ZE	ZE	NS	PS	PM	PB
NS	ZE	ZE	ZE	ZE	PS	PM	PB
ZE	NB	NM	NM	ZE	PS	PM	PB
PS	PB	NM	NM	ZE	ZE	ZE	ZE
PM	NB	NM	NM	PS	ZE	ZE	ZE
PB	NB	NM	NM	PM	PS	ZE	ZE

4. Simulink model of DC Microgrid

The hybrid DC microgrid Simulink model using MATLAB comprises DC–DC boost converters, PV, FC, FLC, ANN, PSO-based MPPT method, and resistive load. This proposed hybrid DC microgrid has been developed with the help of MATLAB simulation software. The system parameters for PV, FC, boost converter, DC–DC bidirectional converter, supercapacitor, and battery are illustrated in Table 2. Figure 11 illustrates MATLAB Simulink model of hybrid DC microgrid, and Figure 12, Figure 13 and Figure 14 show the subsystem of FC, DC–DC bidirectional converter and boost converter, model of FLC.

Table 2. Renewable Energy Parameters Used for DC Microgrid.

Parameters	Values	Name of the Component
Temperature	25 °C	Solar PV Module
Irradiance	1000 W/m2
Series Connected Modules Per String	2
Parallel Strings	4
Open Circuit Voltage	21 V
Short Circuit Current	8 A
Number of Cells	65	Fuel Cell
Nominal Stack Efficiency	55%
Operating Temperature	65 °C
Nominal Air Flow Rate	300 1pm
Nominal Supply Pressure	Fuel—1.5 bar
	Air—1 bar
Nominal Composition	99.95 H2, 21 O2, 1 H2O in %
Fuel Cell Resistance	0.07833 Ω
Nerst Voltage of one Cell	1.1288 V
Input Resistance	0.005 Ω	Boost Converter
Inductor	3 mH
Input Capacitor	0.02 μF
IGBT	1 No.
DC–Link	300 μF
Input Inductance	1.5 mH	DC-DC Bidirectional Converter
IGBT	2 Nos.
Output Resistance	0.5 Ω
Output Inductance	0.35 mH
Rated Capacitance	29 F	Super Capacitor
Equivalent DC Series Resistance	0.03 Ω
Rated Voltage	32 V
Number Series Capacitor	1
Number of Parallel Capacitor	1
Initial Voltage	32 V
Operating Temperature	25 °C
Type	lithium-Ion	Battery
Nominal Voltage	24 V
Rated capacity	14 Ah
Initial state-of-charge	50%
Cut-off voltage	18 V

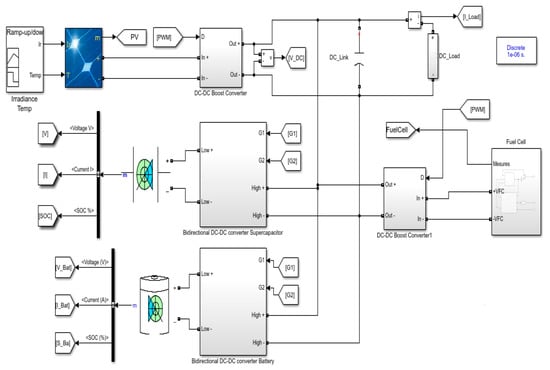
Figure 11. MATLAB/Simulink model for hybrid DC microgrid.

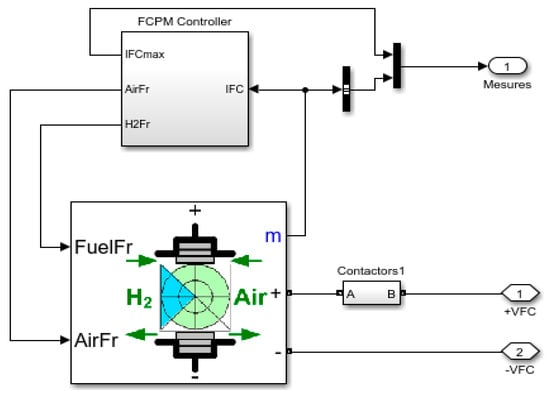
Figure 12. Fuel cell model of a DC microgrid.

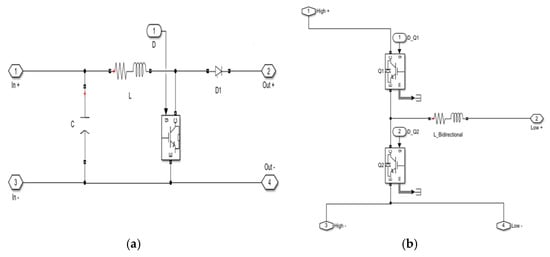
Figure 13. (a) The subsystem of boost converter (b) Subsystem of bidirectional converter for ESS.

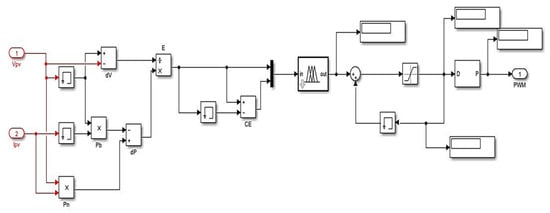
Figure 14. The subsystem of FLC.

Figure 15a,b shows the solar PV irradiance of 980 W/m² for t < 1 s and 800 W/m² for t > 1 s with constant temperature T = 25 °C and nominal charging and discharging characteristics of an energy storage system.

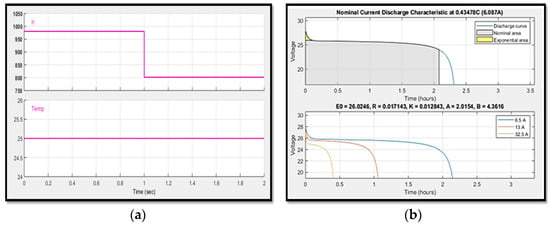
Figure 15. (a) Irradiance and temperature for solar PV (b) nominal current discharging of a battery.

In this proposed system, the hybrid DC microgrid comprises solar PV with a boost converter, FC with a boost converter, Supercapacitor with bidirectional converter, and battery with bidirectional converter. The aforementioned simulations comprise FLC, ANN, and PSO-based MPPT. Figure 16, Figure 17 and Figure 18 illustrate solar PV power with (FLC, ANN, and PSO) and without MPPT controller.

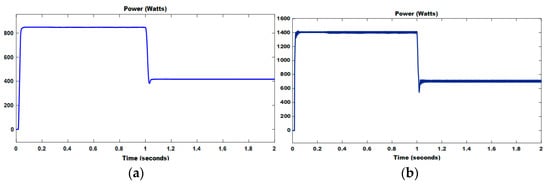
Figure 16. (a) PV power without MPPT controller (b) PV power with FLC.

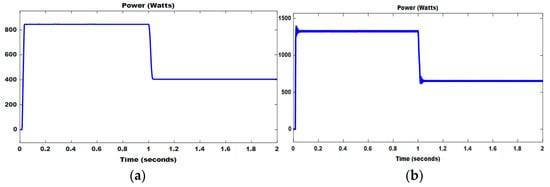
Figure 17. (a) PV power without MPPT controller (b) PV power with ANN.

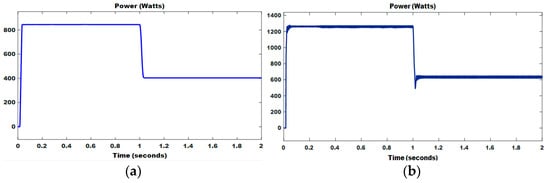
Figure 18. (a) PV power without MPPT controller (b) PV power with PSO.

Similarly, Figure 19 shows the output power of FC with (FLC, ANN and PSO) and without an MPPT controller. Figure 20 and Figure 21 show the output voltage, current, power, and state of charge (SOC) of battery and supercapacitor with the use of a bidirectional converter. Using FLC, the performance of solar PV has risen to 1402 W from 845 W, which is a rise of 66%, then FC has raised to 1278 W from 787 W, which is a rise of 62%. Using ANN, the performance of solar PV has risen to 1335 W to 845 W, which is a rise of 58% then FC has raised to 1208 W from 787 W, which is a rise of 53%. Similarly, by using the PSO algorithm, the performance of solar PV has raised to 1260 W from 845 W, which is a rise of 49% then FC has raised to 1188 W from 787 W, which is a rise of 51%.

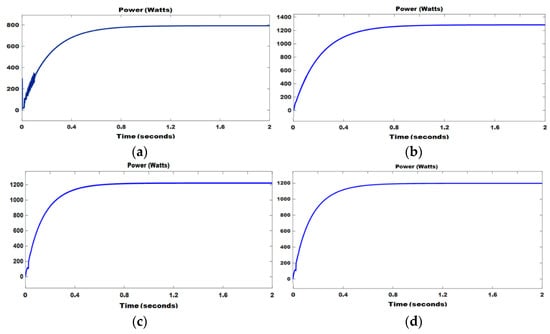
Figure 19. (a) Output power of FC without MPPT (b) Output power of FC with FLC-based MPPT (c) Output power of FC with ANN-based MPPT (d) Output power of FC with PSO-based MPPT.

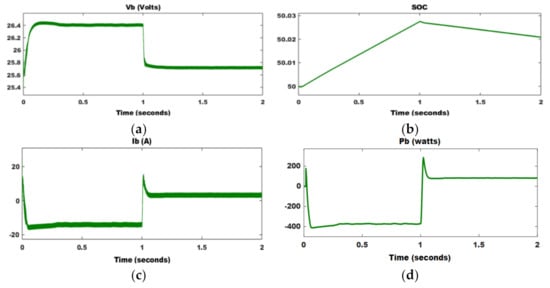
Figure 20. (a) Battery output voltage (b) SOC of battery (c) battery output current (d) battery output power.

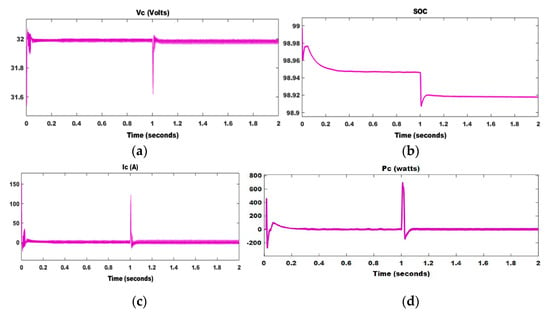
Figure 21. (a) The voltage of Supercapacitor (b) SOC of Super Capacitor (c) Current of Super Capacitor (d) Power of Super Capacitor.

It clears that FLC gives the best performance for this proposed hybrid Dc microgrid when compared to ANN and PSO algorithm. Table 3 gives the comparative analysis of power for PV and FC without MPPT and with FLC, ANN, and PSO algorithm-based MPPT.

Table 3. Comparison table for hybrid (PV–FC) power with and without MPPT techniques.

Sources	Power (Watt)
	Without MPPT	With MPPT Control
		FLC	ANN	PSO
PV	845	1402	1335	1260
FC	787	1278	1208	1194

Figure 22, Figure 23 and Figure 24 show the Simulink output voltage of 150 V, current of 15 A and power of 2250 W for hybrid DC microgrid with a comparative analysis of FLC, ANN and PSO algorithm-based MPPT controller. Table 4 shows the comparison of settling time, overshoot, and undershoot for the proposed hybrid DC microgrid with the help of FLC, ANN, and PSO algorithm. The simulation results, which were obtained for the hybrid DC microgrid, tabulated in Table 4. Hence, with the help of different controllers, the enactment of the hybrid structure has been detected and analyzed. The Simulation analysis for hybrid DC microgrid using MATLAB/Simulink has been done to compute the maximum power of the DC load (resistive load) with different controllers.

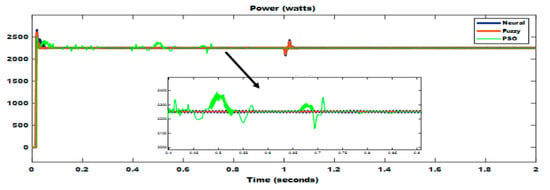
Figure 22. Load power with fuzzy, neuro and PSO.

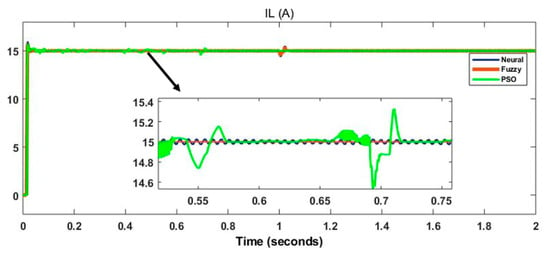
Figure 23. Load current with fuzzy, neuro, and PSO.

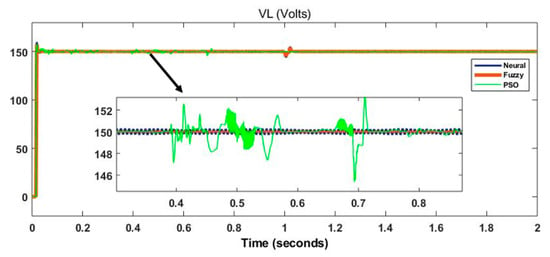
Figure 24. Load voltage with fuzzy, neuro, and PSO.

Table 4. Performance of load parameters with different controllers (FLC, ANN, and PSO).

Control Technique	Performance Parameters after MPPT
	Under Shoot (W)	Over Shoot (W)	Settling Time (s)
PSO	1442	1667	0.650
Neural Network	1490	1775	0.054
Fuzzy	1491	1735	0.035

5. Conclusions

In this paper, a hybrid DC microgrid with various control techniques has been proposed to achieve maximum power point in solar PV and FC. The MPPT method improves the settling time of the proposed hybrid DC microgrid, according to the results obtained using different control techniques such as FLC, ANN, and PSO algorithm. When compared to other control methods, FLC has a higher efficiency rating. The results show that the fuzzy MPPT approach for forecasting hybrid DC microgrid output has a high level of precision, effectiveness, and reliability. This research has been applied to both grid and stand-alone systems. As a result of this research into different control techniques for MPPT systems, it is now possible to choose a particular MPPT process for various applications. We will investigate the possibility of implementing the appropriate control methods to other types of DC-DC converters as well as to control a DC microgrid with advanced DC-DC converter topologies in future research.