Abstract
We study non-Markovian dynamics of an open quantum system system interacting with a nonstationary squeezed bosonic reservoir. We derive exact and approximate descriptions for the open system dynamics. Focusing on the spin boson model, we compare exact dynamics with Redfield theory and a quantum optical master equation for both short and long time dynamics and in non-Markovian and Markov regimes. The squeezing of the bath results in asymptotic oscillations in the stationary state, which are captured faithfully by the Redfield master equation in the case of weak coupling. Furthermore, we find that the bath squeezing direction modifies the effective system–environment coupling strength and, thus, the strength of the dissipation.
1. Introduction
In 1926 and 1927, two families of quantum states for the quantum harmonic oscillator were proposed by Schrödinger [1] and Kennard [2], respectively. The first family of states included coherent states [3,4,5] and the second family included squeezed states [6]. These can be distinguished by considering the Heisenberg uncertainty principle:
which was discovered also in 1927 [7]. The coherent states saturate this uncertainty principle with equal variances in both quadratures. This makes them the closest to points in phase space; therefore, coherent states are often considered the most classical quantum states. In contrast, for a squeezed state, the variances of one of the quadratures can be smaller that . The state is, thus, squeezed along a certain direction in phase space. According to the Heisenberg uncertainty principle, the variance of the other quadrature must then be larger than . Often, squeezed states are regarded as nonclassical states [8,9]. In fact, so-called two mode squeezing generates entanglement between two oscillators [10]. In contrast to coherent states, squeezed states are not stationary states of the harmonic oscillator.
Ensembles of harmonic oscillators are commonly considered as quantum environments of open quantum systems. In most applications, these environments are stationary, meaning that the initial state of the reservoir oscillators is a stationary state, for instance, a thermal state (which becomes a coherent state for zero temperature). In a large thermal bath, the system is expected to reach thermal equilibrium [11]. If instead the bath can be prepared in a squeezed state, one directly violates stationarity, resulting in a a breakdown of equilibration.
This can have a drastic impact on the dissipation induced by the bath. In 1986, it was proposed that a nonstationary reservoir consisting of harmonic oscillators prepared in squeezed states can lead to an inhibition of phase decay of an atom [12]. Only in 2013, this prediction was experimentally verified using superconducting qubits [13].
Previous theoretical works on squeezed reservoirs were based on quantum master equations with constant coefficients [14,15,16,17,18,19]. The validity of these equations requires severe assumptions on the system and bath coupling strength and possibly also a separation of time scales such that a rotating wave approximation can be performed. For this reason, such master equations are unable to capture certain phenomena in an exact manner. For instance, they can predict that the very short time dynamics of an observable is linear in time, whereas the Schrödinger equation actually yields quadratic short time dynamics [20,21].
In this article, we investigate open quantum system dynamics in a non-stationary reservoir consisting of oscillators prepared in two-mode squeezed states (broad band squeezed reservoir) [18]. We derive an exact description of the reduced state dynamics using non-Markovian quantum state diffusion (NMQSD) [22,23,24]. Then, using NMQSD as a starting point, we derive a Hierarchy of Equations of Motion [25] (HEOM) for the density matrix of the open system based on the Hierarchy of stochastic Pure States (HOPS) [26]. For the example of a single two level system, we compare the short and long time dynamics of the numerically exact HEOM theory with a weak coupling perturbation theory, so-called Redfield theory, and the commonly used standard master equation with time independent coefficients. Our main findings are that, in a parameter regime where a quantum optical master equation would work fine for stationary reservoirs, it can not capture accurately short and long time dynamics. Remarkably, if the bath memory time is short the Redfield theory performs extremely well, matching with exact dynamics and predicting accurate long time dynamics.
2. Model
We consider the following commonly used model for open quantum systems:
where the environment consists of independent harmonic oscillators (bosonic modes) [19]. The system Hamiltonian and the system coupling operator are left arbitrary, except that we demand . Moving to an interaction representation with respect to the free bath Hamiltonian, one obtains the following.
If the bath’s initial state is Gaussian and the coupling of the system to the bath is linear, the response of the bath to the system is fully characterized by the first and second moment of the bath response operator . Typically, and without loss of generality, one considers . Then, the so-called bath correlation function (BCF) is the only relevant quantity describing the influence of the bath [27]:
where the expectation value is with respect to the bath initial state. As an initial condition, for the bath, usually a stationary state of the free bath Hamiltonian is considered. For example, a zero temperature bath is described by vacuum state , which is a Gaussian state; hence, it is fully characterized by the following correlations.
This results in a stationary BCF that depends on the time difference only.
An alternative characterization of a stationary bath is given in terms of spectral density:
which is the Fourier transform of the stationary BCF.
In this article, we are interested in the situation where the initial state of the bath is a squeezed vacuum. In particular, we consider two-mode squeezing which is symmetric around a reference frequency . We denote our squeezed vacuum state by , where S is a unitary squeezing operator. If we order the bath modes according to , the state is characterized by the following correlations.
Because S is a unitary operator, the squeezing parameters and satisfy . We also have assumed that the two mode squeezing is homogeneous, i.e., u and v are the same for all modes . This is often called broadband squeezing. In order to parametrize the squeezing, we introduce real variables r and and write
where r is squeezing strength, and is the squeezing direction in phase space. corresponds to squeezing the p-quadrature, whereas corresponds to squeezing the x-quadrature. In case of no squeezing , we recover the vacuum correlations (4). To continue, we further assume that coupling constants have a symmetry property , which implies that the spectral density is symmetric around . From this, we obtain that the bath correlation function has the following structure:
where is the zero temperature bath correlation function from Equation (5). It is easy to check that this is a valid BCF obeying . Note that this function does depend explicitly on both t and s and not only on their difference. This is because the bath initial state is not stationary with respect to the bath Hamiltonian. We assume the following model for the vacuum BCF:
which corresponds to a continuous bath with Lorentzian spectral density.
This bath satisfies the required symmetry if , which we assume in the following. Notably, for such a bath, the white noise limit exits when .
The non-Markovian open system dynamics of this model can be described with non-Markovian quantum state diffusion (NMQSD) [22,24,28]. NMQSD is a stochastic unraveling of reduced open system dynamics in terms of a Gaussian colored noise process with statistics and . The system state is obtained as the ensemble average of stochastic pure states , which depend on this noise process.
The stochastic states obey the NMQSD evolution equation.
Different solution strategies for this equation exits, notably the O-operator method [23,29] and the exact HOPS method [26,30,31]. Here, we use NMQSD as a tool to derive perturbative and exact master equations for the squeezed bath problem (9).
Although most results are very general, an example we will consider is the spin boson model. For this model, the system is a simple two level system with the following operators
3. Perturbative Master Equations
If the coupling to the bath is weak and/or the BCF decays rapidly, we can make a perturbative approximation to NMQSD. The lowest order perturbative equation is given by the following.
Because in this approximation the operator does not depend on the stochastic process, a master equation can be directly derived from NMQSD as follows [23].
This is the well known Redfield master equation [32].
Under certain conditions and in a frame rotating with the frequency , one can derive a master equation with constant coefficients starting from the Redfield equation. The resulting equation is well known from quantum optics textbooks [17,18]. For a derivation, we assume the spin boson model with and . In particular, we consider the case where and defines the fastest timescale and . The state in the rotating frame is given by the following.
To obtain a master equation with constant coefficients, analogous to the standard quantum optical master equation [32], one explicitly computes the integral in (15) and neglects exponentially decaying terms as well as terms of order . Plugging the result into the Redfield Equation (16) in the rotating frame, one can identify counter-rotating terms that oscillate at frequency . Under the above assumptions, these terms can be neglected and one obtains a master equation with time-independent coefficients.
Note that the coefficients of the last two terms become time dependent if one moves back to the laboratory frame.
In order to assess the validity of these perturbative master equations, we have to compare their predictions with exact results. We discuss in the following how the exact reduced dynamics can be computed using non-Markovian open system methods.
4. Exact Method
We can utilize non-Markovian open system methods to compute the exact reduced dynamics in the squeezed reservoir. In particular, due to the exponential form of the bath correlation function, we can easily generalize hierarchical methods for the squeezed bath. To this aim, we decompose the BCF in the following manner:
To solve the linear NMQSD Equation (13), we further define the corresponding functional differential operators:
so that (13) becomes the following.
Because of the exponential form of the kernels (20), we can compute the time derivative of the functional differential operators.
This allows employing the hierarchy of pure states (HOPS) scheme to solve NMQSD. In particular, one defines an ’auxiliary state’ for every double-index .
These states obey the hierarchy of pure states equation of motion.
In this equation, we set . The exact NMQSD solution is simply the ’root’ state of the hierarchy . Truncating the hierarchy at a finite depth yields a closed set of equations, which can be numerically integrated. Typically, for a weak coupling, only a few auxiliary states have to be taken into account to achieve convergence. There also exists a hierarchy of operators complementary to HOPS, which is known as the hierarchy of equations of motions (HEOM) [25,30]. We define auxilliary operators with two multiindices as follows.
Upon employing the HOPS Equation (26) with relation , we find the hierarchical equations of motion:
where the reduced state of the system is simply given by . We can use a truncated hierarchy to accurately describe the non-Markovian open system dynamics of the model, even for strong coupling (large ) and long memory time (small ).
5. Dynamics
The fidelity of time-evolved state with an initial pure system state can be used to investigate how master equations capture short time dynamics. In general, the fidelity behaves for short times as [20]:
where and are the variances of operator X.
A quantum optical master equation that has constant coefficients, such as Equation (18), instead, leads to a linear short time behavior for the fidelity of the state of the system alone [21]:
where . Here, operators are the operators, which act on the left or on the right, respectively, in the sandwich term of the master equation.
The quadratic short time behavior is captured exactly by the Redfield theory, which is the lowest order perturbation theory.
In Figure 1, we compare the short time linear rate computed for master Equation (18) and the quadratic rate for the full system. We observe that the full rate has a maximum at , which corresponds to squeezing along the x-direction. The two-level system is coupled to the x-quadrature of the bath, and squeezing in this direction increases the coupling strength which should lead to faster decay. In contrast, the master equation predicts a minimum for , which is not in line with the microscopic theory.
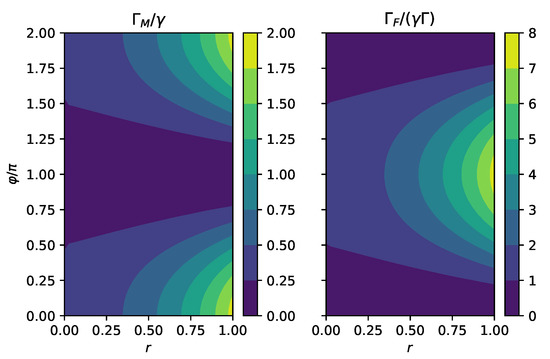
Figure 1.
(Left): Linear rate for short time dynamics due to the Markov master equation divided by the overall coupling strength . (Right): Quadratic rate for short time dynamics for the total system divided by , where is the inverse bath correlation time scale. is proportional to , which has a maximum when . is proportional to , which has a minimum at . Here, we consider the spin boson model (14) in a squeezed bath (9) with and and initial state , where and are the eigenstates of . We have chosen the following parameters: , , and .
In Figure 2, we compare the logarithm of the fidelity computed using the HEOM (28), the Redfield theory (16), and the master equation (18) with quadratic short time estimates (29), (31) and the linear estimate (30).
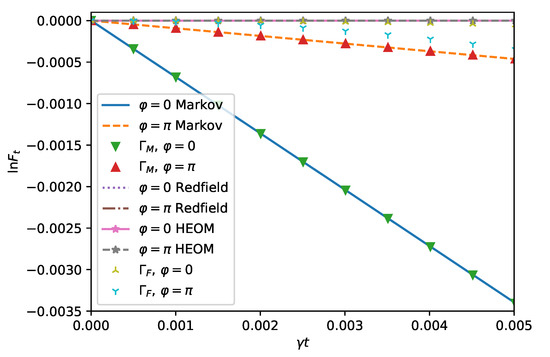
Figure 2.
Short time dynamics of the spin boson model (14) in the squeezed bath (9) with , , , and . The logarithm of the fidelity is displayed for short times within different approximate and exact descriptions. The quadratic short time dynamics holds up to for as the HEOM and the Redfield theory start to deviate from the short time expansion. For , the quadratic short time dynamics, HEOM, and the Redfield agree well in the range of the plot. This is explained by the effectively strong system environment coupling for , which sets a different regime of validity for the short time expansion. The parameters are chosen as in Figure 1.
The quadratic estimates; the HEOM and the Redfield curves are in line with each other for both squeezing directions and . The linear prediction and the master equation curves also are on top of each other but show a different behavior for different . For , the decay of the fidelity is faster than for , as expected from Figure 1.
For longer times, the fidelity is still captured correctly by the Redfield equation, while the Markovian equation becomes valid only asymptoically, as seen in Figure 3.
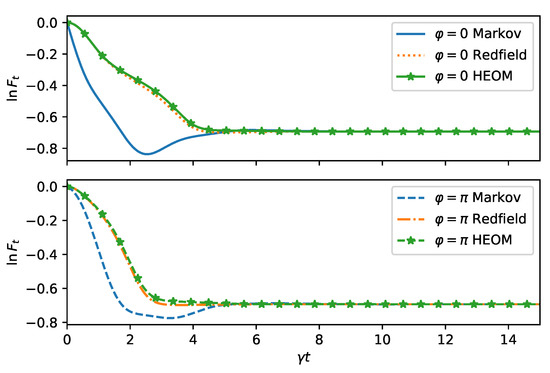
Figure 3.
Dynamics of the fidelity as in Figure 2 but for long times and for two squeezing directions (top) and for (bottom). The decay of the fidelity is faster for for HEOM and Redfield as expected from the microscopic model. Predictions from the quantum optical master equation (Markov) show an opposite behavior and the fidelity even has a positive slope at intermediate times.
We now turn to the long time dynamics, which reveals the steady state properties. In Figure 4, we compare the time evolution computed from HEOM, Redfield, and master equation for . We do the same for in Figure 5. The same conclusions hold as before: For , the decay is faster, as can be observed from HEOM and Redfield curves. The steady state prediction of the master equation is far-off from the Refield and HEOM computations, which both agree exptremely well for the choosen parameters. This is because the memory time of the bath is chosen to be very short. As expected for a spin boson model, the steady state reaches a finite value. However, due to the non-stationary bath, some residual oscillations remain indefinitely in long time dynamics.
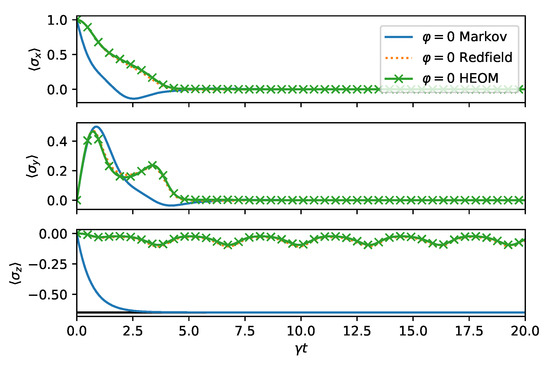
Figure 4.
Long time dynamics of the spin boson model (14) in the squeezed bath (9) as in Figure 2 with . Both approximate methods describe correctly that the x and y Bloch sphere components decay to zero. The expectation value asymptotically acquires a finite value modulated by weak oscillations which are captured properly in the Redfield theory.
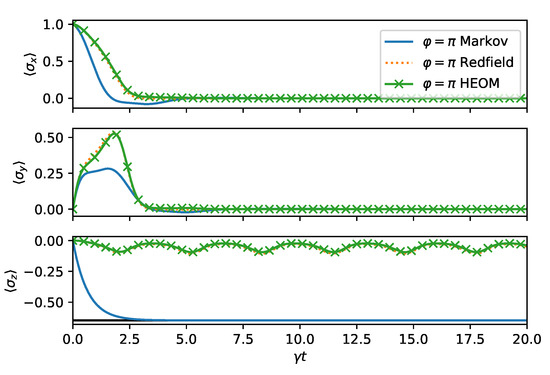
Figure 5.
Long time dynamics as in Figure 4, except .
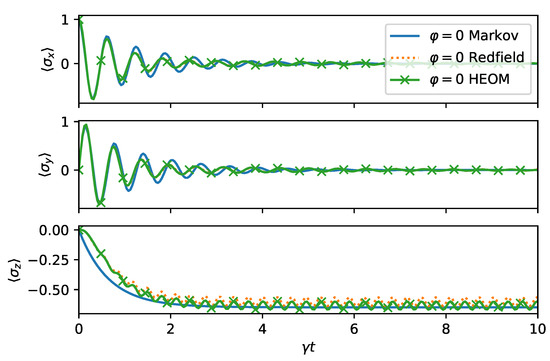
Next, we investigate the Markov limit where we expect the master Equation (18) to be applicable. We chose , , which is in a regime where the assumptions for the rotating wave approximation are satisfied. Moreover, since , the BCF decays faster than the time scale set for system bath interaction by . As we can observe from Figure 6, the master equation, the Redfield theory, and HEOM are in good qualitative agreement. The rapid oscillations present in HEOM and Redfield solutions are removed by the secular approximation behind the Markovian master equation.
When we change the direction of the squeezing to , hence effectively coupling the system and the environment more strongly, the agreement is not as good, as shown in Figure 7. This in particularly visible for the expectation value . The asymptotic values are, however, captured accurately.
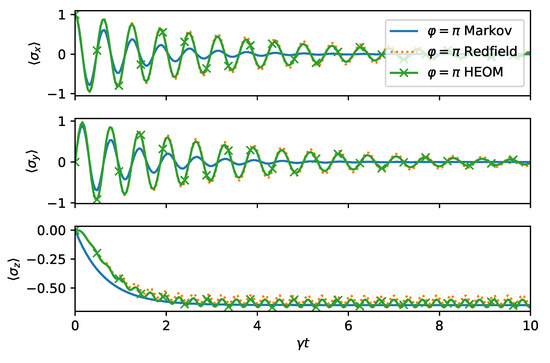
Figure 7.
Dynamics of the spin boson model as in Figure 6, except .
Lastly, we investigate a regime for non-Markovian dynamics. The Redfield theory is a weak system–environment coupling theory. We expect it to fail when the bath correlation function decays on a slower time scale than the system environment interactions; that is, when . For short times, the Redfield theory agrees with the exact results. We confirm these statements in Figure 8, where one observes that the Redfield and the quantum optical master equation are both far-off from the exact solution. In fact, in this regime, the solution of the Redfield equation ceases to be positive, as can be observed from . To compute the exact dynamics, we have estimated convergence of HEOM by increasing the hierarchy depth until the relative change in the solution is less than .
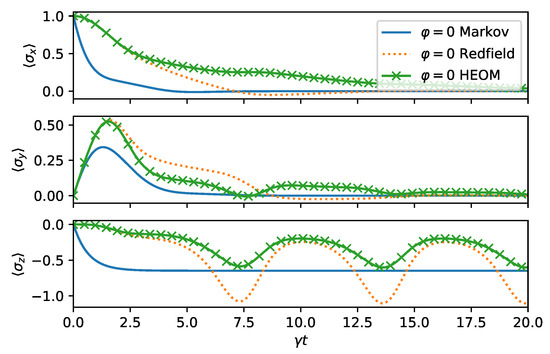
Figure 8.
Highly non-Markovian dynamics in the spin boson model. We have chosen , , , and . We are in the strong system–envinronment coupling regime since . This means that system–environment dynamics occurs on a faster time scale than the bath correlation function decay time. The failure of weak coupling master equations is expected.
6. Conclusions
In this article, we have revisited an old quantum optical model, namely, the decay to a squeezed reservoir [12]. This model has been realized experimentally using superconducting qubits [13] and is an interesting example of non-stationary open system dynamics. We investigated the short and long time dynamics of the model using textbook master equations [17,18,19], perturbative Redfield theory [32], and exact hierarchical methods [25,26], which we generalize to treat our non-Markovian squeezed bath model. Assuming broadband two mode squeezing, a model for the bath correlation function can be proposed where the bath memory time can be easily controlled by a single parameter . This corresponds to a Lorentzian spectral density, which yields an exponentially decaying bath correlation function. We showed how in the limit where , where is the overall system environment coupling, the Redfield theory performs extremely well. However, the dynamics is far from a regime where a usual “quantum optical master equation” is valid. This is due to the fact that there are other time scales involved which need to satisfy a strict hierarchical order so that the Markov approximation can be justified. These timescales are determined by the free system evolution and the bath resonance (). The quantum optical master equation is valid only in a regime where is by far the fastest time-scale. All in all, the Redfield theory, which is based on weak coupling approximation only, produces the correct short and long time dynamics in a wide parameter range and is conceptually and numerically much simpler then more advanced methods such as HEOM. To those concerned about the possible positivity violations when using the Redfield theory, we would like to point out that this should be seen merely as a symptom of the breakdown of the weak coupling perturbation theory [32].
Author Contributions
V.L. and K.L. contributed equally to this work. W.T.S. contributed to the development of the concept and initial ideas behind this project. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NMQSD | Non-Markovian quantum state diffusion; |
| HEOM | Hierarchical equations Of motion; |
| HOPS | Hierarchy of pure states; |
| BCF | Bath correlation function. |
References
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Klauder, J.R. The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers. Ann. Phys. 1960, 11, 123–168. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Plebanski, J. Wave Functions of a Harmonic Oscillator. Phys. Rev. 1956, 101, 1825–1826. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Dodonov, V.; Man’ko, V. Theory of Nonclassical States of Light; Taylor & Francis: London, UK, 2003. [Google Scholar]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: Recent advances and current perspectives. J. Phys. A Math. Theor. 2007, 40, 7821–7880. [Google Scholar] [CrossRef]
- Bach, V.; Fröhlich, J.; Sigal, I.M. Return to equilibrium. J. Math. Phys. 2000, 41, 3985–4060. [Google Scholar] [CrossRef]
- Gardiner, C.W. Inhibition of Atomic Phase Decays by Squeezed Light: A Direct Effect of Squeezing. Phys. Rev. Lett. 1986, 56, 1917–1920. [Google Scholar] [CrossRef]
- Murch, K.W.; Weber, S.J.; Beck, K.M.; Ginossar, E.; Siddiqi, I. Reduction of the radiative decay of atomic coherence in squeezed vacuum. Nature 2013, 499, 62–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Dum, R.; Parkins, A.S.; Zoller, P.; Gardiner, C.W. Monte Carlo simulation of master equations in quantum optics for vacuum, thermal, and squeezed reservoirs. Phys. Rev. A 1992, 46, 4382–4396. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Walls, D.; Milburn, G. Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Breuer, H.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Braun, D.; Haake, F.; Strunz, W.T. Universality of Decoherence. Phys. Rev. Lett. 2001, 86, 2913–2917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beau, M.; Kiukas, J.; Egusquiza, I.L.; del Campo, A. Nonexponential Quantum Decay under Environmental Decoherence. Phys. Rev. Lett. 2017, 119, 130401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strunz, W.T. Linear quantum state diffusion for non-Markovian open quantum systems. Phys. Lett. A 1996, 224, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Strunz, W.T.; Yu, T. Convolutionless Non-Markovian master equations and quantum trajectories: Brownian motion. Phys. Rev. A 2004, 69, 052115. [Google Scholar] [CrossRef] [Green Version]
- Megier, N.; Strunz, W.T.; Viviescas, C.; Luoma, K. Parametrization and Optimization of Gaussian Non-Markovian Unravelings for Open Quantum Dynamics. Phys. Rev. Lett. 2018, 120, 150402. [Google Scholar] [CrossRef] [Green Version]
- Tanimura, Y. Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM). J. Chem. Phys. 2020, 153, 020901. [Google Scholar] [CrossRef]
- Suess, D.; Eisfeld, A.; Strunz, W.T. Hierarchy of Stochastic Pure States for Open Quantum System Dynamics. Phys. Rev. Lett. 2014, 113, 150403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mascherpa, F.; Smirne, A.; Somoza, A.D.; Fernández-Acebal, P.; Donadi, S.; Tamascelli, D.; Huelga, S.F.; Plenio, M.B. Optimized auxiliary oscillators for the simulation of general open quantum systems. Phys. Rev. A 2020, 101, 052108. [Google Scholar] [CrossRef]
- Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum state diffusion. Phys. Rev. A 1998, 58, 1699–1712. [Google Scholar] [CrossRef] [Green Version]
- Roden, J.; Strunz, W.T.; Eisfeld, A. Non-Markovian quantum state diffusion for absorption spectra of molecular aggregates. J. Chem. Phys. 2011, 134, 034902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suess, D.; Strunz, W.T.; Eisfeld, A. Hierarchical Equations for Open System Dynamics in Fermionic and Bosonic Environments. J. Stat. Phys. 2015, 159, 1408–1423. [Google Scholar] [CrossRef]
- Hartmann, R.; Strunz, W.T. Exact Open Quantum System Dynamics Using the Hierarchy of Pure States (HOPS). J. Chem. Theory Comput. 2017, 13, 5834–5845. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, R.; Strunz, W.T. Accuracy assessment of perturbative master equations: Embracing nonpositivity. Phys. Rev. A 2020, 101, 012103. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).