Entanglement and Fisher Information for Atoms–Field System in the Presence of Negative Binomial States
Abstract
1. Introduction
2. Hamiltonian and Dynamics
3. Quantumness Measures
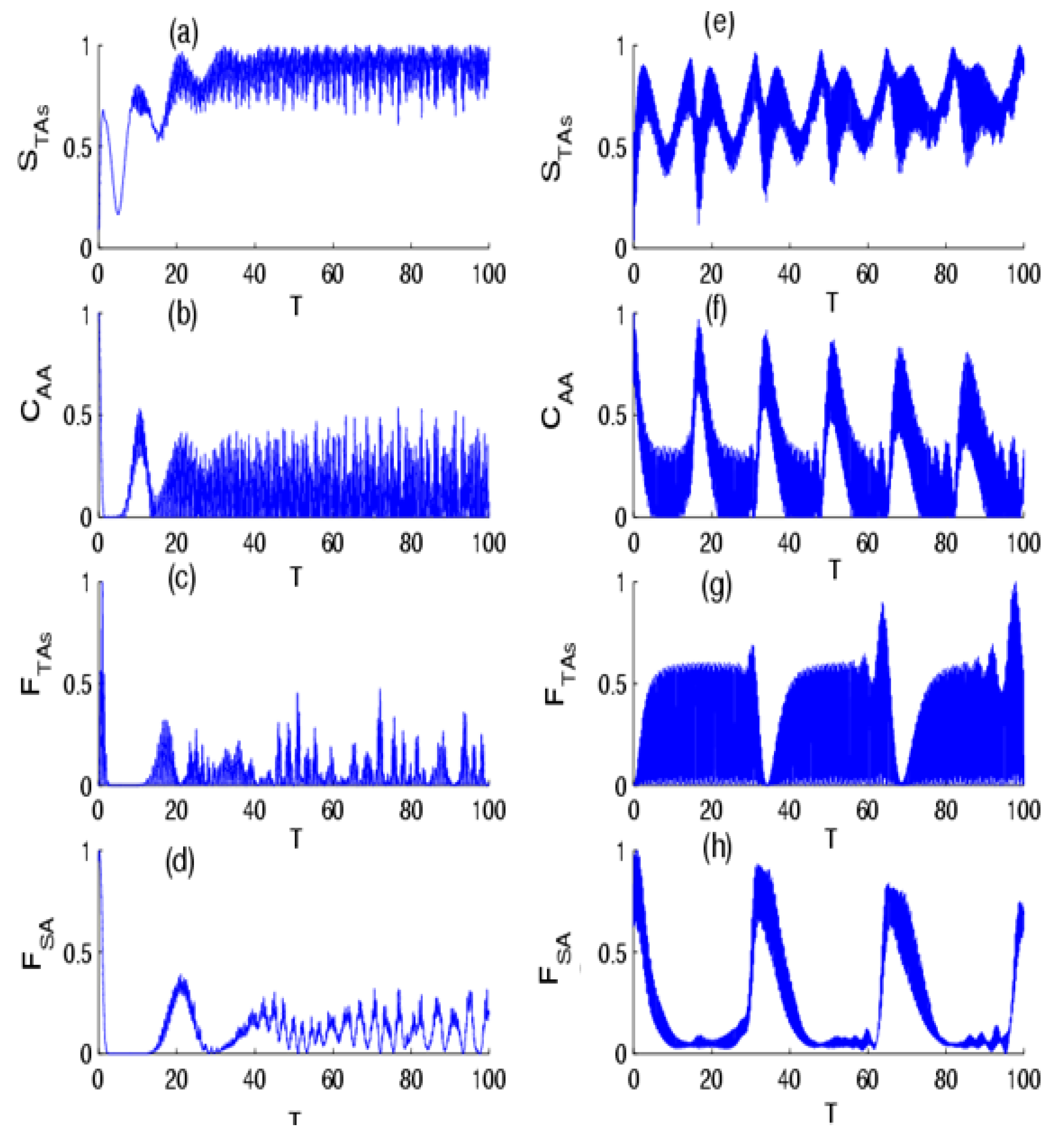
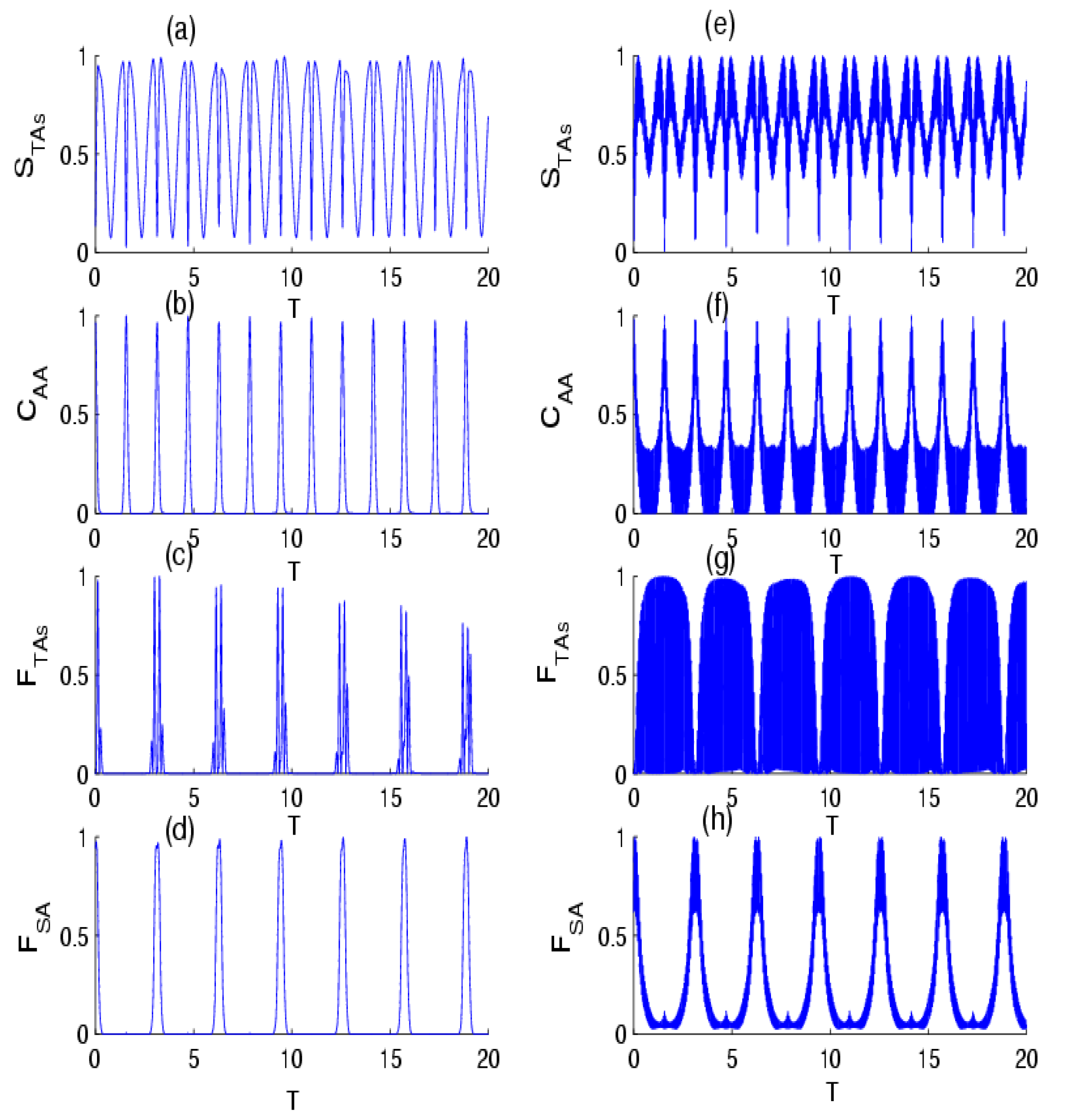
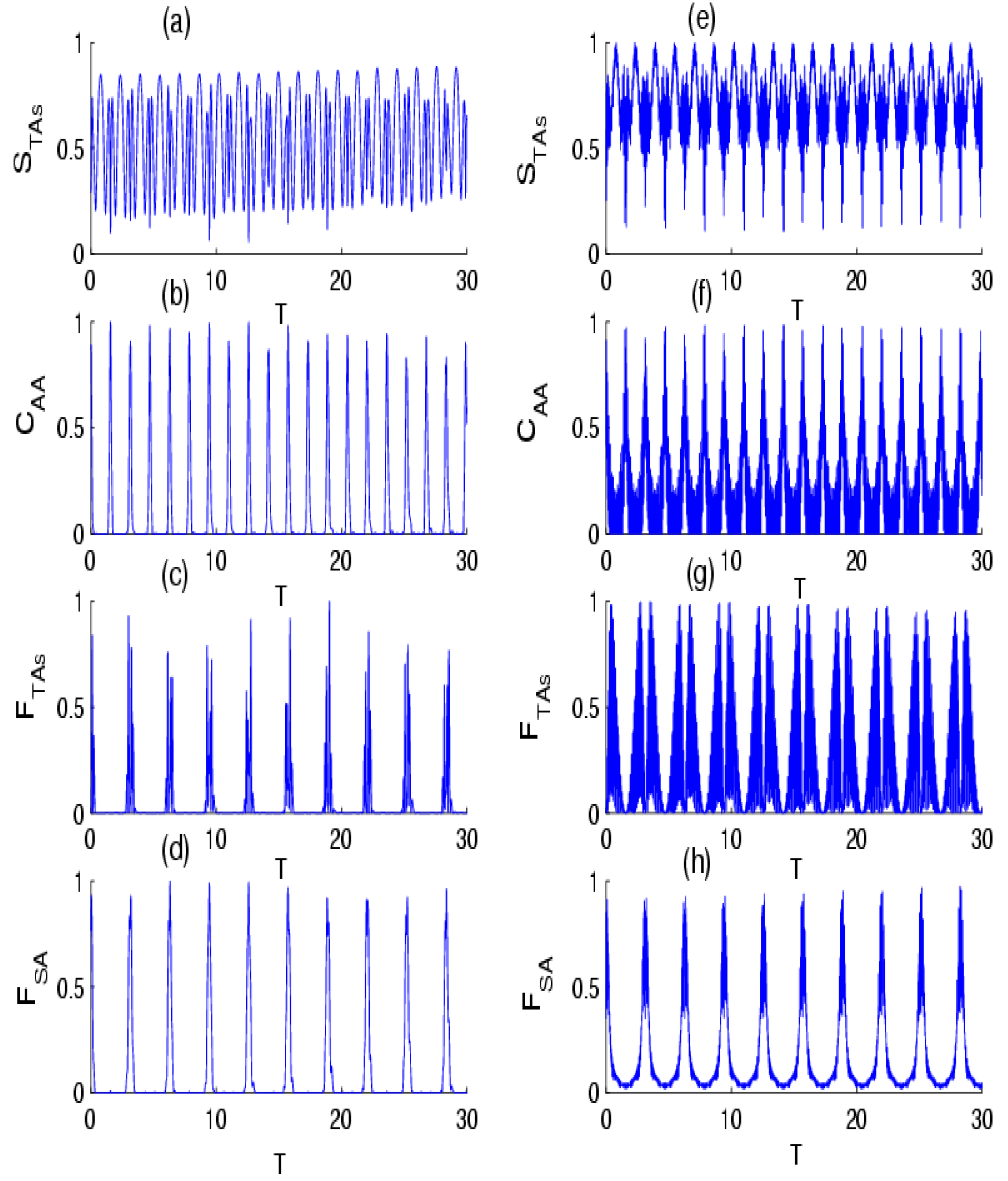
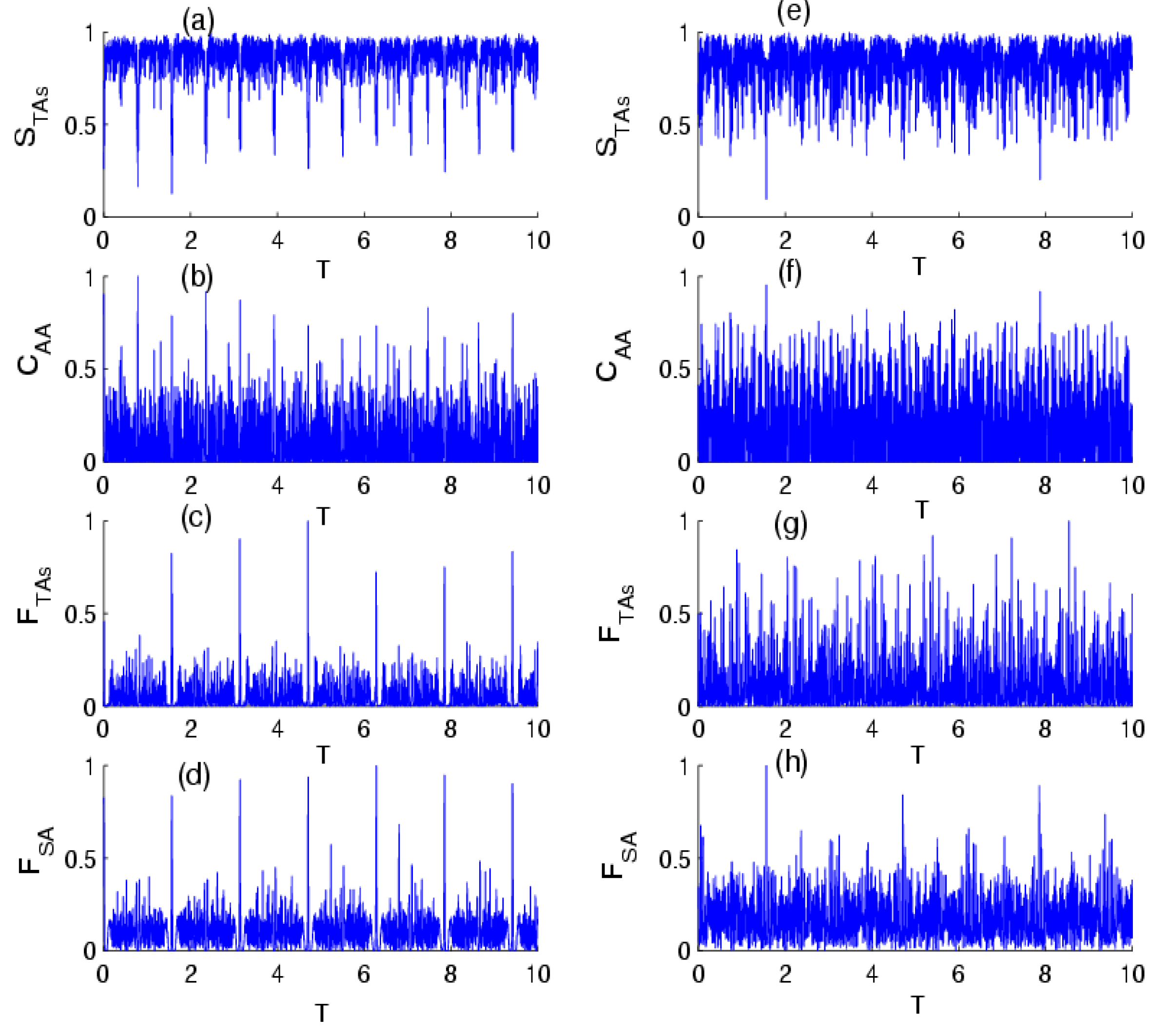
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Cummings, F.W. Stimulated Emission of Radiation in a Single Mode. Phys. Rev. 1965, 140, A1051. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez-Mondragon, J.J. Periodic spontaneous collapse and revival in a simple quantum model. Phys. Rev. Lett. 1980, 44, 1323. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353. [Google Scholar] [CrossRef]
- Boukobza, E.; Tannor, D.J. Entropy exchange and entanglement in the Jaynes-Cummings model. Phys. Rev. A 2005, 71, 063821. [Google Scholar] [CrossRef]
- van Wonderen, A.J.; Lendi, K. Unification of the Jaynes–Cummings model and Planck’s radiation law. J. Math. Phys. 2002, 43, 4692–4720. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-Time Disentanglement Via Spontaneous Emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef]
- Masood, S.S.; Miller, A. Entanglement in a Jaynes-Cummings Model with Two Atoms and Two Photon Modes. Univ. J. Phys. Appl. 2014, 2, 237. [Google Scholar] [CrossRef]
- Wang, F.Q.; Liu, W.C.; Liang, R.S. Decoherence of two qubits coupled with one-mode cavity without rotating-wave approximation. arXiv 2008, arXiv:0806.3884. [Google Scholar]
- Chan, S.; Reid, M.D.; Ficek, Z. Entanglement evolution of two remote and non-identical Jaynes–Cummings atoms. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 065507. [Google Scholar] [CrossRef]
- Vieira, A.R.; G de Oliveira Junior, J.G.; Peixoto de Faria, J.G.; Nemes, M.C. Geometry in the entanglement dynamics of the double Jaynes–Cummings model. Braz. J. Phys. 2014, 44, 19–29. [Google Scholar] [CrossRef][Green Version]
- Algarni, M.; Berrada, K.; Abdel-Khalek, S.; Eleuch, H. Parity Deformed Tavis-Cummings Model: Entanglement, Parameter Estimation and Statistical Properties. Mathematics 2022, 10, 3051. [Google Scholar] [CrossRef]
- Aldaghfag, S.A.; Berrada, K.; Abdel-Khalek, S. Entanglement and photon statistics of two dipole–dipole coupled superconducting qubits with Kerr-like nonlinearities. Results Phys. 2020, 16, 102978. [Google Scholar] [CrossRef]
- Yönaç, M.; Yu, T.; Eberly, J.H. Sudden death of entanglement of two Jaynes–Cummings atoms. J. Phys. B At. Mol. Opt. Phys. 2006, 39, S621. [Google Scholar] [CrossRef]
- Sainz, I.; Björk, G. Entanglement invariant for the double Jaynes-Cummings model. Phys. Rev. A 2007, 76, 042313. [Google Scholar] [CrossRef]
- Hu, Y.H.; Fang, M.F.; Cai, J.W.; Jiang, C.L. Sudden death and long-lived entanglement between two atoms in a double JC model system. Int. J. Theor. Phys. 2008, 47, 2554–2565. [Google Scholar] [CrossRef]
- Chen, Q.H.; Yang, Y.; Liu, T.; Wang, K.L. Entanglement dynamics of two independent Jaynes-Cummings atoms without the rotating-wave approximation. Phys. Rev. A 2010, 82, 052306. [Google Scholar] [CrossRef]
- Tanas, R. Quantum Dynamics and Information; Olkiewicz, R., Cegła, W., Frydryszak, A., Garbaczewski, P., Jakóbczyk, L., Eds.; World Scientific: Singapore, 2010; p. 179. [Google Scholar]
- Zhang, G.F.; Xie, X.C. Entanglement between two atoms in a damping Jaynes-Cummings model. Eur. Phys. J. D 2010, 60, 423–427. [Google Scholar] [CrossRef]
- Shen, L.T.; Shi, Z.C.; Wu, H.Z.; Yang, Z.B. Dynamics of entanglement in Jaynes–Cummings nodes with nonidentical qubit-field coupling strengths. Entropy 2017, 19, 331. [Google Scholar] [CrossRef]
- Pandit, M.; Das, S.; Roy, S.S.; Dhar, H.S.; Sen, U. Effects of cavity–cavity interaction on the entanglement dynamics of a generalized double Jaynes–Cummings model. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 045501. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Eleuch, H.; Abel-Aty, M. Dynamics of Wehrl entropy of a degenerate two-photon process with a nonlinear medium. Opt. Quantum Electron. 2011, 42, 887–897. [Google Scholar] [CrossRef]
- Singh, S. Field statistics in some generalized Jaynes-Cummings models. Phys. Rev. A 1982, 25, 3206. [Google Scholar] [CrossRef]
- Tavis, M.; Cummings, F.W. Exact solution for an N-molecule—Radiation-field Hamiltonian. Phys. Rev. 1968, 170, 379. [Google Scholar] [CrossRef]
- Tessier, T.E.; Deutsch, I.H.; Delgado, A.; Fuentes-Guridi, I. Entanglement sharing in the two-atom Tavis-Cummings model. Phys. Rev. A 2003, 68, 062316. [Google Scholar] [CrossRef]
- López, C.E.; Lastra, F.; Romero, G.; Retamal, J.C. Entanglement properties in the inhomogeneous Tavis-Cummings model. Phys. Rev. A 2007, 75, 022107. [Google Scholar] [CrossRef]
- Guo, J.-L.; Song, H.-S. Entanglement between two Tavis–Cummings atoms with phase decoherence. J. Mod. Opt. 2009, 56, 496. [Google Scholar] [CrossRef]
- Bashkirov, E.K.; Rusakova, M.S. Entanglement for two-atom Tavis–Cummings model with degenerate two-photon transitions in the presence of the Stark shift. Optik 2012, 123, 1694. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Alber, G.; Beth, T.; Horodecki, M.; Horodecki, P.; Horodecki, R.; Rotteler, M.; Weinfurter, H.; Zeilinger, R.A. Quantum Information; Springer: Berlin/Heidelberg, Germany, 2001; Chapter 5. [Google Scholar]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Kibe, T.; Mukhopadhyay, A.; Roy, P. Quantum Thermodynamics of Holographic Quenches and Bounds on the Growth of Entanglement from the Quantum Null Energy Condition. Phys. Rev. Lett. 2022, 128, 191602. [Google Scholar] [CrossRef]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Raymond Ooi, C.H. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86, 033823. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with SU (1, 1) coherent states in the presence of nonlinear phase shifts. Phys. Rev. A 2013, 88, 013817. [Google Scholar] [CrossRef]
- Liu, C.; Tu, T.; Li, P.-Y.; Liu, X.; Zhu, X.-Y.; Zhou, Z.-Q.; Li, C.-F.; Guo, G.-C. Towards entanglement distillation between atomic ensembles using high-fidelity spin operations. Commun. Phys. 2022, 5, 67. [Google Scholar] [CrossRef]
- Castelano, L.K.; Fanchini, F.F.; Berrada, K. Open quantum system description of singlet-triplet qubits in quantum dots. Phys. Rev. B 2016, 94, 235433. [Google Scholar] [CrossRef]
- Pfaff, W.; Taminiau, T.H.; Robledo, L.; Bernien, H.; Markham, M.; Twitchen, D.J.; Hanson, R. Demonstration of entanglement-by-measurement of solid-state qubits. Nat. Phys. 2013, 9, 29. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Khalil, E.M.; Eleuch, H.; Obada, A.S.F.; Reda, E. Tavis–Cummings Model with Moving Atoms. Entropy. 2021, 23, 452. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Aldaghfag, S.A. Quantum correlations and non-classical properties for two superconducting qubits interacting with a quantized field in the context of deformed Heisenberg algebra. Chaos Solitons Fractals 2021, 143, 110466. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Eberly, J.H.; Yu, T. The end of an entanglement. Science 2007, 316, 555. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden Death of Entanglement: Classical Noise Effects. Opt. Commun. 2006, 264, 393. [Google Scholar] [CrossRef]
- Scheie, A.; Laurell, P.; Samarakoon, A.M.; Lake, B.; Nagler, S.E.; Granroth, G.E.; Okamoto, S.; Alvarez, G.; Tennant, D.A. Witnessing entanglement in quantum magnets using neutron scattering. Phys. Rev. B 2021, 103, 224434. [Google Scholar] [CrossRef]
- Gabbrielli, M.; Smerzi, A.; Pezzè, L. Multipartite entanglement at finite temperature. Sci. Rep. 2018, 8, 15663. [Google Scholar] [CrossRef] [PubMed]
- Akbari-Kourbolagh, Y.; Azhdargalam, M. Entanglement criterion for multipartite systems based on quantum Fisher information. Phys. Rev. A 2019, 99, 012304. [Google Scholar] [CrossRef]
- Hong, Y.; Qi, X.; Gao, T.; Yan, F. Detection of multipartite entanglement via quantum Fisher information. Europhys. Lett. 2021, 134, 60006. [Google Scholar] [CrossRef]
- Chen, L.-P.; Guo, Y.-N. Dynamics of local quantum uncertainty and local quantum fisher information for a two-qubit system driven by classical phase noisy laser. J. Mod. Opt. 2021, 68, 217–223. [Google Scholar] [CrossRef]
- Almarashi, A.M.; Algarni, A.; Abdel-Khalek, S.; Ng, H.K.T. Quantum Fisher information and tomographic entropy of a single qubit in excited binomial and negative binomial distributions. J. Russ. Laser Res. 2019, 40, 313–320. [Google Scholar] [CrossRef]
- Luo, S. Wigner-Yanase skew information vs. quantum Fisher information. Proc. Am. Math. Soc. 2004, 132, 885–890. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef]
- Kim, S.; Li, L.; Kumar, A.; Wu, J. Characterizing nonclassical correlations via local quantum Fisher information. Phys. Rev. A 2018, 97, 032326. [Google Scholar] [CrossRef]
- Sbiri, A.; Mansour, M.; Oulouda, Y. Local quantum uncertainty versus negativity through Gisin states. Int. J. Quantum Inf. 2021, 19, 2150023. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Stoler, D.; Saleh, B.E.A.; Teich, M.C. Binomial states of the quantized radiation field. Opt. Acta 1985, 32, 345–355. [Google Scholar] [CrossRef]
- Fu, H.-C.; Sasaki, R. Negative binomial and multinomial states: Probability distributions and coherent states. J. Math. Phys. 1997, 38, 3968–3987. [Google Scholar] [CrossRef]
- Bergeron, H.; Curado, E.M.F.; Gazeau, J.P.; Rodrigues, L.M. Symmetric generalized binomial distributions. J. Math. Phys. 2013, 54, 123301. [Google Scholar] [CrossRef]
- Popov, D.; Pop, N.; Maria, R. Excited binomial states for the pseudoharmonic oscillator. AIP Conf. Proc. 2012, 1472, 77–82. [Google Scholar]
- Stoler, D. Generalized Coherent States. Phys. Rev. D 1971, 4, 2309. [Google Scholar] [CrossRef]
- Lee, C.T. Photon antibunching in a free-electron laser. Phys. Rev. A 1985, 31, 1213. [Google Scholar] [CrossRef]
- Dattoli, G.; Gallardo, J.; Torre, A. Binomial states of the quantized radiation field: Comment. J. Opt. Soc. Am. B 1987, 2, 185–187. [Google Scholar] [CrossRef]
- Joshi, A.; Puri, R.R. Effects of Atomic Coherence on Collapses and Revivals in the Binomial State of the Field. J. Mod. Opt. 1989, 36, 557–570. [Google Scholar] [CrossRef]
- Vidiella-Barranco, A.; Roversi, J.A. Statistical and phase properties of the binomial states of the electromagnetic field. Phys. Rev. A 1994, 50, 5233. [Google Scholar] [CrossRef]
- Baseia, B.; De Lima, A.F.; Da Silva, A.J. Intermediate number-squeezed state of the quantized radiation field. Mod. Phys. Lett. B 1995, 9, 1673–1683. [Google Scholar] [CrossRef]
- Fu, H.C.; Sasaki, R. Hypergeometric states and their nonclassical properties. J. Math. Phys. 1997, 38, 2154–2166. [Google Scholar] [CrossRef]
- Fan, H.-Y.; Jing, S.-C. Connection of a type of q-deformed binomial state with q-spin coherent states. Phys. Rev. A 1994, 50, 1909. [Google Scholar]
- Baseia, B.; De Lima, A.F.; Marques, G.C. Intermediate number-phase states of the quantized radiation field. Phys. Lett. A 1995, 204, 1–6. [Google Scholar] [CrossRef]
- Fu, H.-C.; Sasaki, R. Negative Binomial States of Quantized Radiation Fields. J. Phys. Soc. Jpn. 1997, 66, 1989–1994. [Google Scholar] [CrossRef][Green Version]
- Popov, D.; Pop, N.; Davidovic, M. Negative binomial states for the pseudoharmonic oscillator. Phys. Scr. 2013, 014051. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation and concurrence. Quant. Inform. Comput. 2001, 1, 27–44. [Google Scholar] [CrossRef]
- Berrada, K. Protecting the precision of estimation in a photonic crystal. J. Opt. Soc. Am. B 2015, 32, 571–576. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Eleuch, H.; Ooi, C.R. Quantum coherence and entanglement partitions for two driven quantum dots inside a coherent micro cavity. Phys. Lett. A 2019, 383, 125905. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with classical light states in non-Markovian lossy channels. J. Opt. Soc. Am. B 2017, 34, 1912–1917. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrada, K.; Abdel-Khalek, S.; Algarni, M.; Eleuch, H. Entanglement and Fisher Information for Atoms–Field System in the Presence of Negative Binomial States. Entropy 2022, 24, 1817. https://doi.org/10.3390/e24121817
Berrada K, Abdel-Khalek S, Algarni M, Eleuch H. Entanglement and Fisher Information for Atoms–Field System in the Presence of Negative Binomial States. Entropy. 2022; 24(12):1817. https://doi.org/10.3390/e24121817
Chicago/Turabian StyleBerrada, Kamal, Sayed Abdel-Khalek, Mariam Algarni, and Hichem Eleuch. 2022. "Entanglement and Fisher Information for Atoms–Field System in the Presence of Negative Binomial States" Entropy 24, no. 12: 1817. https://doi.org/10.3390/e24121817
APA StyleBerrada, K., Abdel-Khalek, S., Algarni, M., & Eleuch, H. (2022). Entanglement and Fisher Information for Atoms–Field System in the Presence of Negative Binomial States. Entropy, 24(12), 1817. https://doi.org/10.3390/e24121817





