Abstract
In this paper, we have analyzed the mathematical model of various nonlinear oscillators arising in different fields of engineering. Further, approximate solutions for different variations in oscillators are studied by using feedforward neural networks (NNs) based on the backpropagated Levenberg–Marquardt algorithm (BLMA). A data set for different problem scenarios for the supervised learning of BLMA has been generated by the Runge–Kutta method of order 4 (RK-4) with the “NDSolve” package in Mathematica. The worth of the approximate solution by NN-BLMA is attained by employing the processing of testing, training, and validation of the reference data set. For each model, convergence analysis, error histograms, regression analysis, and curve fitting are considered to study the robustness and accuracy of the design scheme.
1. Introduction
The study of nonlinear problems is of great importance in all areas of applied mathematics, engineering, and physics. Most of the phenomena occurring in these fields are modeled as nonlinear differential equations. In general, exact or analytical solutions of highly nonlinear differential equations do not always exist and hence most of the researchers have used either approximate analytical techniques or numerical methods to obtain approximate solutions. Only a few nonlinear systems can be directly solved; thus, numerical methods, particularly the well-known Runge–Kutta method of the fourth order, are commonly employed to derive approximate solutions [1]. Nonlinear oscillators are considered fundamental equations that have gained the attention of researchers, and many methods have been used to find approximate and numerical solutions to various nonlinear oscillators [2,3,4]. Ji-Huan [5] proposed a new perturbation in contrast to other traditional perturbation techniques for the solution of the Duffing equation with a high order of nonlinearity. In their study, they constructed the homotopy with an imbedding parameter p, which is used as a small parameter. Oliveira in [6] deal with the problems in nonlinear mechanics by using the method of averaging. They discuss the developments of the method of averaging and construct the approximate solutions for oscillatory models with small and large parameters. Amol Marathe [7] investigated the attenuation of harmonic waves through a periodic and discrete structure with a frequency ostensibly within the propagation zone due to mild damping. They used the matrix transform method and adopted harmonic balance to study the linear and nonlinear damping. Hui Li [8] developed an energy balance approach for calculating the frequency–amplitude relationships of nonlinear oscillators with large nonlinearities and discontinuous terms. M. Heydari [9] combined the spectral method and variational iteration method to investigate the famous strongly nonlinear oscillators. Liu Ming studied the oscillations in a pendulum by modifying the Adomian decomposition method (ADM) [10].
In recent years, different nonlinear oscillatory problems have gained the attention of the research community due to the stiffness and rigidness in the behavior of the mathematical models [11,12]. Akuro [13] investigated the periodic oscillation and performed bifurcation analysis of a pendulum with spinning support using the modified continuous piecewise linearization method. Kargar [14] used He’s Energy Balance Method (HEBM) and He’s Amplitude-Frequency Formulation method (HFAF) to perform the frequency analysis of a rotational pendulum system with large-amplitude oscillation. Nonlinear oscillation typified as a mass attached to an elastic wire was studied by [15]. S. Li [16] used the harmonic balance method to analyze the Duffing oscillation of van der Pol oscillators. An analysis of large-amplitude oscillations in triple wells of a non-natural system was conducted by S. Lai [17]. Razzak [18] studied the phenomena of Duffing oscillators with rational and irrational forces, while A. Koochi [19] investigated the nonlinear oscillations of a CNT Nano-resonator based on nonlocal electricity using the energy balance method. Qian and Liu [20,21] used the residue harmonic method to study the vibrations of a system of cantilever beams carrying an intermediate lumped mass. All the above-discussed techniques were developed to analyze the mathematical models under different scenarios.
Oscillators are extremely important in physics because of their mathematical properties as expressed in the Fourier theorem. It represents the regular periodic change in a system. Oscillations occur not only in mechanical systems but also in dynamical systems and virtually in every area of science—for example, the periodic firing of nerve cells in the brain, the beating of the human heart (for circulation), predator–prey population cycles in ecology, business cycles in economics, the vibration of strings in guitars and other string instruments, geothermal geysers in geology, and the periodic swelling of Cepheid variable stars in astronomy. Testing and correctly interpreting the results of such nonlinear oscillatory systems is inherently complex. Preconceived notions about how the system would respond must be avoided at all costs, as this will often influence the types of tests and processing techniques used. Due to the nonlinear and stiff nature of the mathematical model of nonlinear oscillators, a number of semi-analytic methods, such as the iteration perturbation method (IPM), modified differential transform method (MDTM) [22], max-min approach [23], linearized perturbation method (LPM) [24], modified simple equation (MSE) scheme [25], Lindstedt–Poincare method [26], extended BKP–Boussinesq equation [27], and homotopy analysis method (HAM) [28], have been developed. Besides their advantages, these techniques are deterministic approaches and mostly require prior information about the gradient and other essential parameters. In this study, a stochastic approach based on supervised machine learning is utilized to find numerical solutions for various nonlinear oscillators. These stochastic algorithms have various applications in different areas, including biomathematics [29], civil engineering [30], petroleum engineering [31], wireless communications [32], electrical engineering [33,34], and wire coating dynamics [35]. These facts and their significance inspired the authors to exploit and explore the architecture of neural networks to solve stiff and strongly nonlinear models of oscillators. Some potential outcomes of the given study are summarized below.
- The main purpose of this study is to formulate mathematical models and investigate the influence of variations in certain parameters of nonlinear oscillators such as a rotational pendulum system, mass attached to an elastic wire, a uniform beam carrying an intermediate lumped mass, a two-mass system with three springs, the van der Pol equation, and a two-mass system with small damping.
- An integrated novel design of soft computing based on neural networks and the backpropagated Levenberg–Marquardt algorithm is utilized to study the displacement, velocity, and acceleration of the models.
- The supervised learning of the NNs-BLM algorithm works effectively on the data set generated by a numerical solution using the Runge–Kutta method.
- The performance of the design scheme is validated by conducting convergence analysis based on mean square error, regression analysis, error histogram, and curve fitting with reference data. Results demonstrate that the proposed algorithm is smooth and easy to implement.
2. Proposed Methodology
In this section, a novel machine learning technique based on the supervised learning of neurons in artificial neural networks (ANNs) is utilized to study the oscillations in various systems. The control of oscillations in nonlinear systems is a serious challenge for engineers. The destabilization in the oscillatory systems can create a serious thread. Therefore, an automatic oscillation detection tool is required to quickly detect the frequency and amplitude of oscillations in the systems. In this work, a new approach based on machine learning for periodic solutions of the oscillatory systems has been proposed using ANNs, in a multi-layer perceptron (MLP) configuration. The MLP, also known as the Feed-Forward Neural Network (FNN), is a type of neural network that has a hidden layer between the input and output layers. The ANN controller for a single neuron is shown in Figure 1. Mathematically, an ANN model can be written as
where Y and are the output and input data, is the output bias, m and n denote the number of hidden and input neurons, respectively, is the hidden unit biases, and are weights. h and f are activation functions at the hidden input layer and hidden output layer, respectively. In this study, Log-sigmoid is used as an activation function between the hidden and output layers, which is given as
Further, the Feed-Forward Neural Network is optimized with a training algorithm such as the backpropagated Levenberg–Marquardt algorithm. It is also known as the damped least-squares (DLS) method and is used to minimize the nonlinear minimization problem by using the least square fitting. The LM algorithm is used as a built-in function in various applications to find a local minimum. It interpolates between the method of gradient descent (GD) and Gauss–Newton method (GNM). Some recent applications of the LM algorithm are the speed control of an induction motor drive [36] and short-term wind speed prediction [37].

Figure 1.
Architecture of the basic ANN.
Moreover, the implementation of NN-BLMA works in two phases. The detailed workflow of the design algorithm is presented in Figure 2.
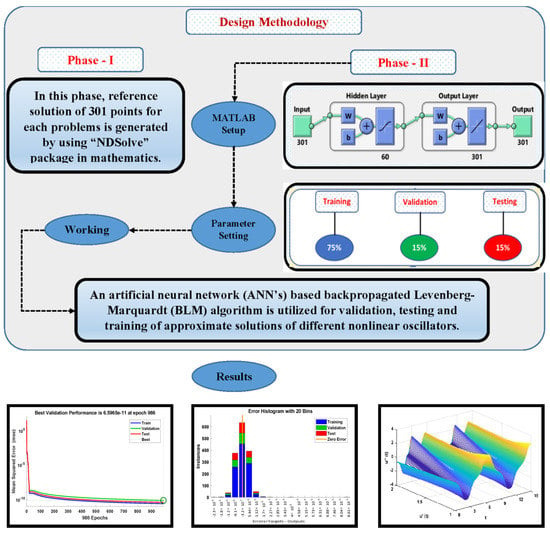
Figure 2.
Working mechanism of NN-BLMA for solving strongly nonlinear oscillators.
- An initial data set is generated by using an analytical solution or calculating a numerical solution by using the Runge–Kutta method of order 4 (RK-4), with the ND Solve package in Mathematica.
- In the second phase, the BLM algorithm is executed by using “nftool” in the MATLAB package with appropriate settings of hidden neurons and testing data. Further, BLM uses a reference solution and implements the process of testing, training, and validation to obtain approximate solutions for different cases of nonlinear oscillators. Table 1 shows the parameter setting for the execution of the design scheme.
 Table 1. Parameter setting for the implementation of the designed NN-BLM algorithm.
Table 1. Parameter setting for the implementation of the designed NN-BLM algorithm.
The NN-BLM algorithm has a simple structure and is easy to use in handling and processing the nonlinear problems. The NN-BLM algorithm is a gradient-free technique and its speed of convergence is much higher than that of other machine learning algorithms and state-of-the-art techniques. Further, to study the efficiency, stability, and convergence, the following performance indices are defined:
where , , and denote the reference, approximate, and mean of solution. m denotes the grid points. For the perfect modeling of approximate solutions, values of MSE and AE approach zero while the value of is 1.
3. Numerical Experimentation and Discussion
In order to study the performance and efficiency of the design algorithm, various cases of strongly nonlinear oscillators are formulated. Figure 3 presents a complete overview of the different problems and cases studied in this paper.
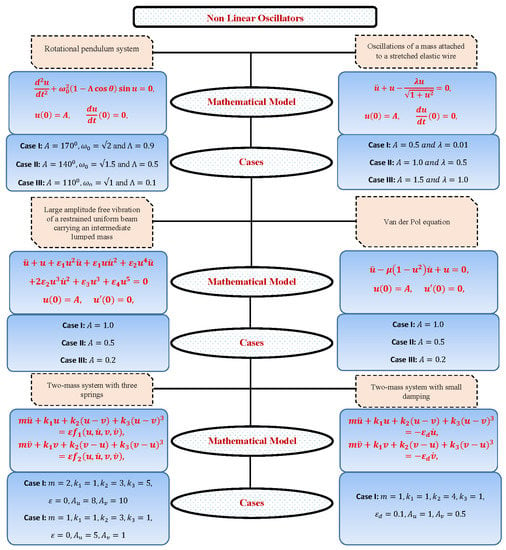
Figure 3.
A general view of different cases of nonlinear oscillators discussed in this paper.
3.1. Rotational Pendulum
Consider a mechanical model that represents a simple pendulum as shown in Figure 4. For large oscillation, at the neutral axis, a body of mass is attached to a rotating base. This system’s equation for the motion is modeled as a second-order differential equation, which is given as [38]
where u represents the angular displacement of the mass in relation to time , and A denotes the initial amplitude of oscillation. and are defined as
where , l, and g represent the angular velocity, length of weightless rod, and gravitational acceleration, respectively. A simple pendulum oscillates between the symmetric intervals when the revolver is pushed as a constant velocity. The range of values for is assumed to be taken from . To study the effect of variations in Equation (5), the following cases are considered based on the increase in the amplitude of oscillation. Case I: , , and . Case II: , , and , Case III: , , and .
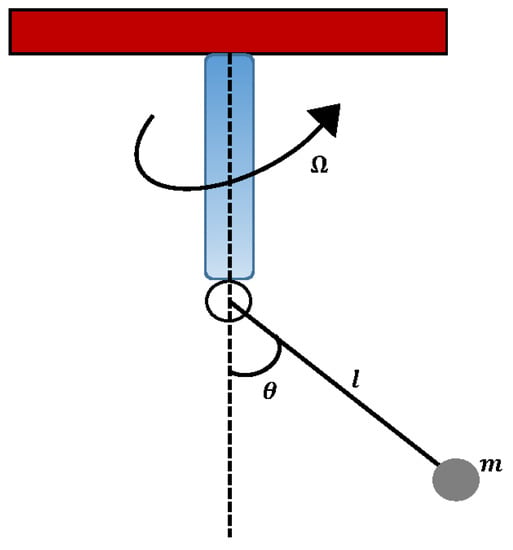
Figure 4.
A schematic of a rotational simple pendulum.
In this problem, the influence of variations in different parameters of the rotational pendulum system has been investigated by using the NN-BLM algorithm. Approximate solutions obtained by the proposed algorithm are compared with He’s Energy Balance Method (HEBM) [39], as shown in Table 2. The results for displacement, velocity, and acceleration are given in Table 3 and graphically shown in Figure 5. Periodic results show that displacement decreases with the increase in time. To study the relation of velocity and acceleration with time, three-dimensional surface graphs were plotted and are shown in Figure 6. The results show that a decrease in the amplitude of oscillation causes a decrease in the velocity and acceleration of the pendulum. Further, to study the effectiveness of the solutions and the efficiency of the design algorithm, error histogram graphs and performance graphs were plotted, as shown in Figure 7 and Figure 8, respectively. The results obtained by the design algorithm overlap with the analytical solution with minimum absolute errors. The absolute error for each case lies around to , to , and to , respectively. In addition, the values of performance function show the perfect modeling of solutions as they lie around , , and , respectively. Statistics of validation, testing, and training of the reference solution are provided in Table 4. Regression analysis is given in Figure 9, which shows the accuracy of the proposed algorithm in calculating approximate solutions.

Table 2.
Comparison of approximate solutions obtained by NN-BLM algorithm with He’s Energy Balance Method, Homotopy Analysis Method, Residue Harmonic Balance Method, and Homotopy Perturbation Method.

Table 3.
Approximate solutions for angular displacements of problems 1, 2, and 3.

Figure 5.
(a) Approximate solutions by the design scheme for different cases of rotational pendulum system, while (b) illustrates the phase plane between velocity and displacement of the system.

Figure 6.
Three-dimensional plots to study the influence of time in velocity and acceleration of rotational pendulum system.

Figure 7.
Error histogram analysis for each case of rotational pendulum.
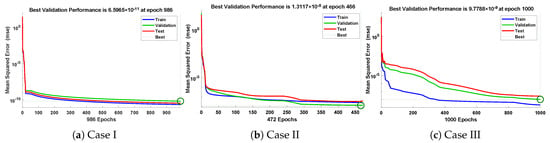
Figure 8.
Convergence of performance function in terms of MSE for each case of problem 1.

Table 4.
Statistics of performance measures for obtaining solutions to problems 1 and 2.
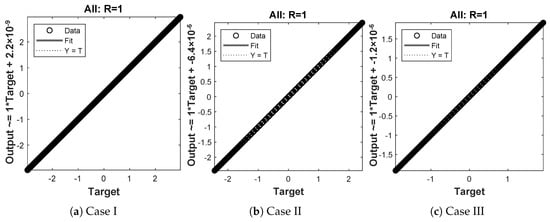
Figure 9.
Regression analysis for different cases of problem 1.
3.2. Oscillations of a Mass Attached to a Stretched Elastic Wire
Consider the particle of mass (m) attached to the center of a stretched elastic wire, as shown in Figure 10. The one-dimensional equation of motion for the mass moving in the horizontal direction is given as [15]
subject to the initial conditions
and dimensionless variables are defined in terms of u and t as
where k is the coefficient of stiffness and 2d denotes the length of the elastic wire. Substituting Equation (9) into Equation (7), we obtain
where and . Further, the variations in A and are studied by considering the following cases. Case I: and , Case II: A = 1.0 and and Case III: and .
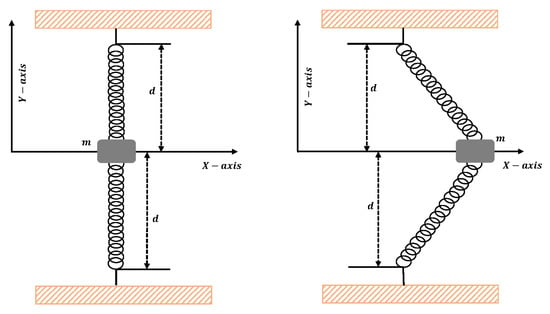
Figure 10.
Mass attached to the center of elastic wire.
The design algorithm NN-BLMA is executed to study the influence of variations in oscillations of a mass attached to an elastic wire. Statistics of approximate solutions for angular displacement, velocity, and acceleration obtained by the proposed algorithm are given in Table 3. Approximate solutions and the phase plane curves between the angular velocity and displacement are shown in Figure 11. Moreover, from Figure 12, it can be observed that the amplitude of oscillations increases but the periodic curves decrease with an increase in time, which causes the decreases in angular displacement and velocity of the system. Further, to study the effectiveness of the solutions, convergence, error histogram, and regression analysis were carried out, as shown in Figure 13 and Figure 14, respectively. Numerical results show that the NN-BLM algorithm overlaps with the analytical solution with minimum absolute errors that lie around to , to , and to , respectively. Table 4 represents the states of computational complexity of the design scheme in obtaining results for the nonlinear oscillator.
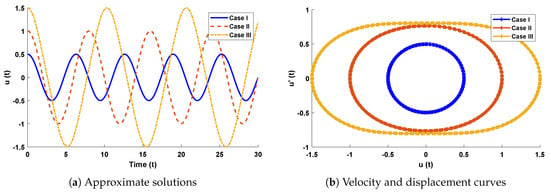
Figure 11.
(a) Approximate solutions obtained by proposed algorithm for the system. (b) shows the phase plane between velocity and displacement of the stretched elastic wire.
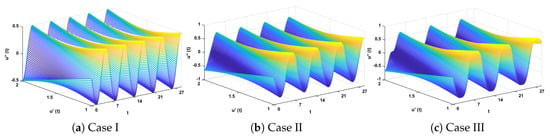
Figure 12.
Three-dimensional plots to study the influence of time in velocity and acceleration of mass attached to a stretched elastic wire.

Figure 13.
Error histogram analysis for each case of mass attached to stretched elastic wire.
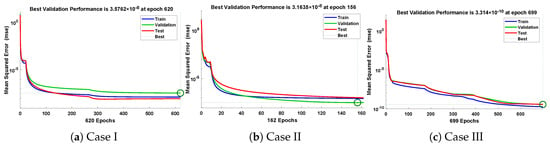
Figure 14.
Convergence of performance function in terms of mean square error for each case of problem 2.
3.3. Large-Amplitude Free Vibration of a Restrained Uniform Beam Carrying an Intermediate Lumped Mass
In this problem, we consider a beam with uniform length l and mass per unit length, hinged at the bottom of a rotational spring with stiffness , as shown in Figure 15. The thickness of the beam is considered to be significantly smaller than the length of the beam; therefore, the effects of shear deformation and rotational inertia are neglected [20]. Inclination in the beam due to lumped mass in denoted by and displacement of the beam is given by . Euler–Lagrange differential equations are used to derive a fifth-order Duffing-type model for the motion of the uniform beam carrying an intermediate lumped mass, which is given as
with initial conditions
where u denotes the dimensionless deflection of the beam at the tip, A is the maximum amplitude, and are positive constants. Table 5 represents different cases of Equation (11) depending on the values of A and positive constants.
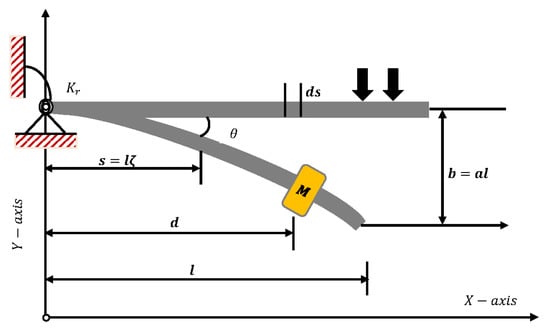
Figure 15.
Geometry and coordinate system for a beam with rotational spring and a lumped mass.

Table 5.
Values of parameters involved in mathematical model of restrained uniform beam carrying an intermediate lumped mass.
In this problem, the designed technique is applied to study the variations in amplitude and positive parameters on the deflection of uniform beam carrying an intermediate lumped mass. Table 3 lists the statistics of the approximate solutions in terms of displacement for each case of problem 3. Phase plane analysis of velocity against displacement is shown in Figure 16. The results show that deflection in the beam increases with an increase in the amplitude A. In addition, the oscillation in acceleration and velocity also increases, as shown in Figure 17. Absolute errors between targeted data and results obtained by the NN-BLM algorithm for different cases of Equation (11) are shown in Figure 18. The values of AE for each case lie around to , to , and to , respectively. Table 6 presents the measure of convergence for each testing, validation, training, gradient, and mu. Complexity analysis in terms of the time taken by the system to achieve the desired results shows the robustness of the designed technique. It can be seen that the values for the gradient for each case lie around to . Values of mu lie around to . It can be seen from Figure 19 that the MSE for each case is approaching zero, which shows the accuracy of the proposed algorithm.
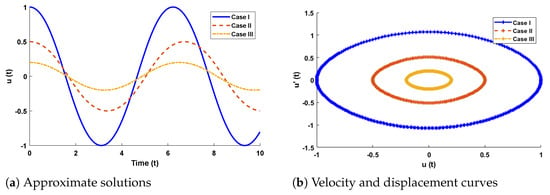
Figure 16.
(a) Approximate solutions obtained by proposed algorithm for the system. (b) Phase plane analysis between velocity and displacement for mathematical model of restrained uniform beam carrying an intermediate lumped mass.
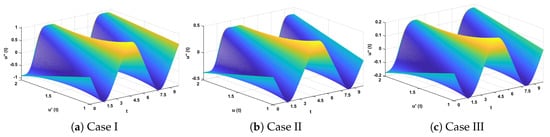
Figure 17.
Three-dimensional plots to study the influence of time in velocity and acceleration of mathematical model given in Equation (6).

Figure 18.
Error histogram analysis for each case of restrained uniform beam carrying an intermediate lumped mass.

Table 6.
Statistics of performance measures for obtaining solutions to problems 3 and 4.
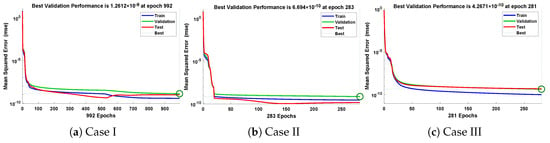
Figure 19.
Convergence of performance function in terms of mean square error for each case of problem 3.
3.4. Van der Pol Equations
In this problem, we have considered van der Pol equations, which were introduced in 1920 by van der Pol to study the triode electric circuit and their self-sustained oscillations. The mathematical model for self-excited oscillations is given as
where is a scaling parameter that represents the length of damping and degree of nonlinearity. For , Equation (13) reduces to the equation of simple harmonic motion. Moreover, for and , the system behaves as a damped one. To study the mathematical model of van der Pol oscillators, we have considered the following cases depending on different values of the scaling parameter, i.e., and 10.
In this problem, the effect of variations in has been investigated by the NN-BLM algorithm. Results obtained by the designed scheme for displacement, velocity, and acceleration are compared with RK-4, as shown in Figure 20. The results of the designed scheme overlap with the analytical solutions, with AEs that lie around to . The performance of the fitness function in terms of mean square error is given in Table 7. The best values of the fitness function for each case are , , and at epoch 100, 1000, and 340, respectively. Values of the gradient and mu for each case lie around to and to , respectively. Regression values for each case are exactly 1, as shown in Figure 21.
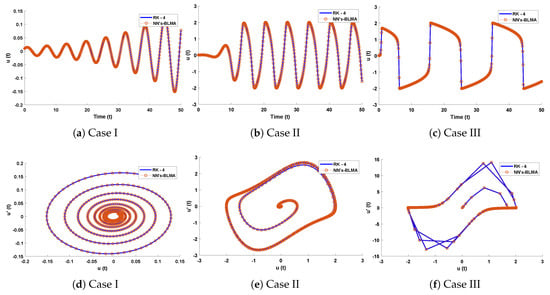
Figure 20.
(a–c) Comparison of approximate solutions obtained by designed algorithm with RK-4. (d–f) show the analysis of phase plane between velocity and acceleration for van der Pol equation.

Table 7.
Approximate solutions for displacement of problems 4, 5, and 6.
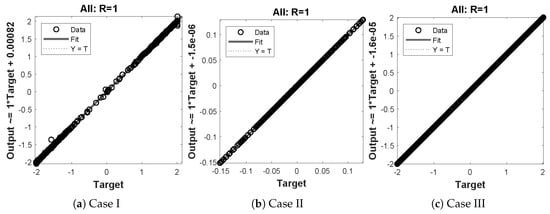
Figure 21.
Regression analysis for different cases of problem 4.
3.5. Two-Mass System with Three Springs
In this problem, we consider a system of two equal masses (m) attached with fixed support and three springs with stiffness , as shown in Figure 22. The equation for the motion of this system in generalized coordinates u and v is given as
subject to the initial conditions
where and are the spring elasticity and cubic nonlinearity, respectively, while and are small nonlinearities. To briefly study the system, the following two cases are considered. Case I: . Case II: .

Figure 22.
Schematic of two masses attached with three springs and fixed support.
In this problem, the influence of variations in different parameters of mass attached to three springs has been investigated by using the NN-BLM algorithm. Approximate solutions obtained by the designed scheme are compared with targeted data generated from RK-4, as shown in Figure 23. It can be seen that the analytical solution overlaps with the approximate solutions, with minimum absolute errors that lie around to . The results show that a decrease in mass increases the oscillations in the spring. Furthermore, the convergence plots for each case of problem 5 in terms of validation, testing, and training are shown in Figure 24. Statistics of the training parameters are provided in Table 8. Values of performance function for each case are , , , and at epoch 520 and 1000, respectively. Analysis based on regression for each case is shown in Figure 25.
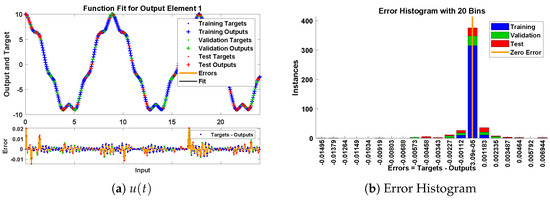
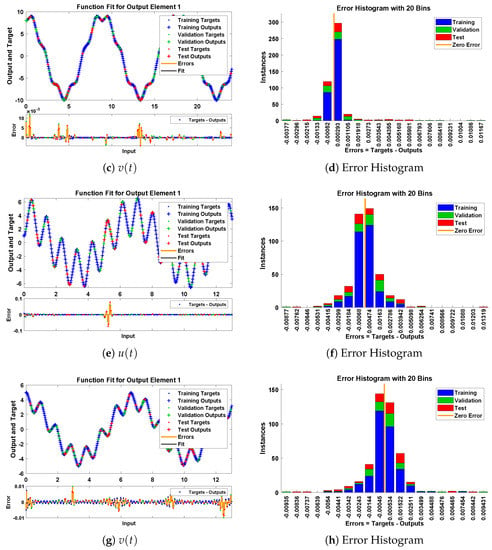
Figure 23.
Approximate solution and histograms of and for Case I and II of problem 5.
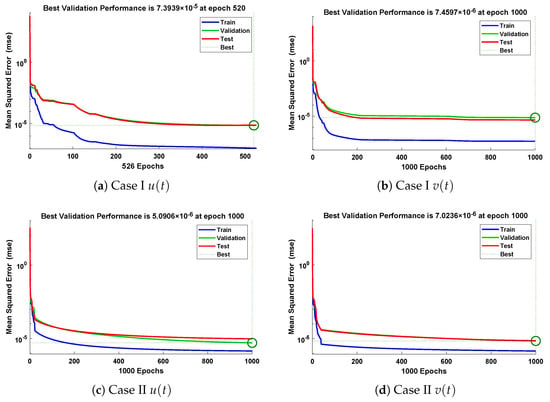
Figure 24.
Analysis of performance function in terms of mean square error for different cases of problem 5.

Table 8.
Statistics of performance measures by NN-BLMA for obtaining solutions to problems 5 and 6.

Figure 25.
Regression plots for different cases of mass attached to three springs.
3.6. Two-Mass System with Small Damping
In this problem, we consider the special case of problem 5 when there exists small damping. The model of the scenario is shown in Figure 26. The governing equations of motion for the system are given as
with initial conditions
To find approximate solutions, we consider the case when .
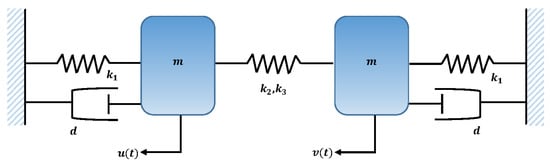
Figure 26.
Schematic of two masses attached with three springs and fixed support.
The designed scheme is exploited to determine the fitting of the approximate solutions with numerical results. The curve fitting of the approximate solutions by NN-BLMA for example 6 is plotted in Figure 27. The results are in good agreement with the analytical solutions as the absolute errors of and lie around to , respectively. The performance of the objective function in terms of MSE for obtaining the best fitting is shown in Figure 28. The best validated performance of MSE is , , respectively. It is observed that the value of regression is one, which reflects the accuracy of the solutions obtained by the designed algorithm.
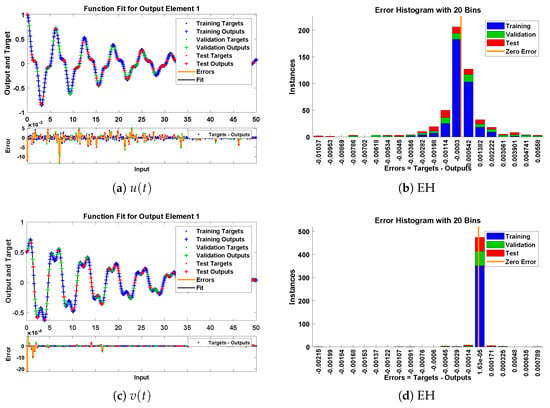
Figure 27.
Approximate solution and histograms of and for problem 6.
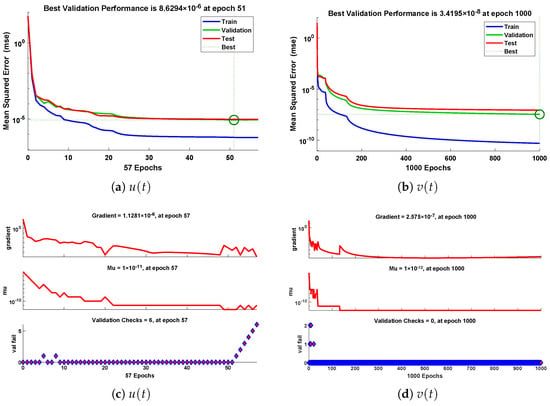
Figure 28.
Performance state of training parameters and convergence of fitness function for example 6.
4. Conclusions
In this paper, an intelligent technique based on artificial neural networks is utilized to investigate the mathematical models of various nonlinear oscillators arising in physics, mechanics, and applied mathematics, such as a rotational pendulum system, mass attached to an elastic wire, a uniform beam carrying an intermediate lumped mass, van der Pol equation, a two-mass system with three springs, and a two-mass system with small damping. Furthermore, soft computing based on supervised learning of neural networks in used to calculate the displacements, velocity, and acceleration of nonlinear oscillators under the influence of different variations. A reference solution is generated by using the RK-4 method, which is then evaluated by the training, testing, and validation process of the Levenberg–Marquardt algorithm. The results obtained by the proposed algorithm are compared with He’s Energy Balance Method, Homotopy Analysis Method, Residue Harmonic Balance Method, and Homotopy Perturbation Method. Extensive graphical and statistical analysis shows that the designed algorithm is accurate and efficient as the approximate solutions overlap with the analytical solutions, with minimum absolute errors as compared to the state-of-the-art techniques. In addition, the values of performance indicators are approaching zero, which shows the perfect modeling of the results.
Author Contributions
Data curation, N.A.K.; Formal analysis, N.A.K.; Funding acquisition, F.S.A. and C.A.T.R.; Investigation, N.A.K. and M.S.; Methodology, N.A.K. and M.S.; Project administration, M.S.; Resources, F.S.A. and C.A.T.R., M.S.; Software, M.S.; Supervision, M.S.; Visualization, N.A.K.; Writing—original draft, N.A.K.; Writing—review and editing, F.S.A., C.A.T.R., M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Dirección General de Investigaciones of Universidad Santiago de Cali under call No. 01-2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
This research has been funded by Dirección General de Investigaciones of Universidad Santiago de Cali under call No. 01-2021.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Hosen, M.A.; Chowdhury, M.; Ali, M.Y.; Ismail, A.F. An analytical approximation technique for the duffing oscillator based on the energy balance method. Ital. J. Pur. Appl. Math. 2017, 37, 455–466. [Google Scholar]
- Gottlieb, H. Harmonic balance approach to periodic solutions of non-linear jerk equations. J. Sound Vib. 2004, 271, 671–683. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lin, J.; Hu, Z.; Khan, N.A.; Sulaiman, M. Analysis of Third-Order Nonlinear Multi-Singular Emden–Fowler Equation by Using the LeNN-WOA-NM Algorithm. IEEE Access 2021, 9, 72111–72138. [Google Scholar] [CrossRef]
- Hu, H.; Zheng, M.; Guo, Y. Iteration calculations of periodic solutions to nonlinear jerk equations. Acta Mech. 2010, 209, 269–274. [Google Scholar] [CrossRef]
- He, J.H. Iteration perturbation method for strongly nonlinear oscillations. J. Vib. Control 2001, 7, 631–642. [Google Scholar] [CrossRef]
- Oliveira, A.R. History of Krylov-Bogoliubov-Mitropolsky Methods of Nonlinear Oscillations. Adv. Hist. Stud. 2017, 6, 40. [Google Scholar] [CrossRef] [Green Version]
- Marathe, A.; Chatterjee, A. Wave attenuation in nonlinear periodic structures using harmonic balance and multiple scales. J. Sound Vib. 2006, 289, 871–888. [Google Scholar] [CrossRef]
- He, J.H. Preliminary report on the energy balance for nonlinear oscillations. Mech. Res. Commun. 2002, 29, 107–111. [Google Scholar] [CrossRef] [Green Version]
- Heydari, M.; Loghmani, G.; Hosseini, S. An improved piecewise variational iteration method for solving strongly nonlinear oscillators. Comput. Appl. Math. 2015, 34, 215–249. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method, with a Preface by Yves Cherruault; Fundamental Theories of Physics; Kluwer Academic: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Big-Alabo, A.; Ekpruke, E.O.; Ossia, C.V. Equivalent oscillator model for the nonlinear vibration of a porter governor. J. King Saud-Univ.-Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Big-Alabo, A.; Ogbodo, C.O.; Ossia, C.V. Semi-analytical treatment of complex nonlinear oscillations arising in the slider-crank mechanism. World Sci. News 2020, 142, 1–24. [Google Scholar]
- Big-Alabo, A.; Ossia, C.V. Periodic oscillation and bifurcation analysis of pendulum with spinning support using a modified continuous piecewise linearization method. Int. J. Appl. Comput. Math. 2019, 5, 1–16. [Google Scholar] [CrossRef]
- Kargar, A.; Akbarzade, M. Frequency Analysis of Large-Amplitude Oscillation of a Rotational Pendulum System Using He’s Amplitude-Frequency Formulation (HFAF) and He’s Energy Balance Method (HEBM). Int. J. Math. Anal. 2012, 6, 1147–1152. [Google Scholar]
- Bataineh, A.S. Application of adaptation HAM for nonlinear oscillator typified as a mass attached to a stretched elastic wire. Commun. Math. Appl. 2017, 8, 157–165. [Google Scholar]
- Li, S.; Niu, J.; Li, X. Primary resonance of fractional-order Duffing–van der Pol oscillator by harmonic balance method. Chin. Phys. B 2018, 27, 120502. [Google Scholar] [CrossRef]
- Lai, S.; Yang, X.; Gao, F. Analysis of large-amplitude oscillations in triple-well non-natural systems. J. Comput. Nonlinear Dyn. 2019, 14, 091002. [Google Scholar] [CrossRef]
- Razzak, M.A. A simple new iterative method for solving strongly nonlinear oscillator systems having a rational and an irrational force. Alex. Eng. J. 2018, 57, 1099–1107. [Google Scholar] [CrossRef]
- Koochi, A.; Goharimanesh, M. Nonlinear Oscillations of CNT Nano-resonator Based on Nonlocal Elasticity: The Energy Balance Method. Rep. Mech. Eng. 2021, 2, 41–50. [Google Scholar]
- Qian, Y.; Pan, J.; Chen, S.; Yao, M. The spreading residue harmonic balance method for strongly nonlinear vibrations of a restrained cantilever beam. Adv. Math. Phys. 2017, 2017, 5214616. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.X.; Yan, Y.; Wang, W.Q. Primary and secondary resonance analyses of a cantilever beam carrying an intermediate lumped mass with time-delay feedback. Nonlinear Dyn. 2019, 97, 1175–1195. [Google Scholar] [CrossRef]
- Momani, S.; Ertürk, V.S. Solutions of non-linear oscillators by the modified differential transform method. Comput. Math. Appl. 2008, 55, 833–842. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. Max-min approach to nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9, 207–210. [Google Scholar] [CrossRef]
- He, J.H. Modified straightforward expansion. Meccanica 1999, 34, 287–289. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ali, M.Z.; Noor, N. Novel dynamics of wave solutions for Cahn–Allen and diffusive predator–prey models using MSE scheme. Partial Differ. Equ. Appl. Math. 2021, 3, 100017. [Google Scholar] [CrossRef]
- He, J.H. Modified Lindstedt–Poincare methods for some strongly non-linear oscillations: Part I: Expansion of a constant. Int. J. Non-Linear Mech. 2002, 37, 309–314. [Google Scholar] [CrossRef]
- Roshid, H.O.; Khatun, M.S.; Baskonus, H.M.; Belgacem, F.B.M. Breather, multi-shock waves and localized excitation structure solutions to the Extended BKP–Boussinesq equation. Commun. Nonlinear Sci. Numer. Simul. 2021, 101, 105867. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, S.; Li, Z. Symbolic computation of strongly nonlinear periodic oscillations. J. Symb. Comput. 2013, 55, 72–95. [Google Scholar] [CrossRef]
- Ali, A.; Hamraz, M.; Kumam, P.; Khan, D.M.; Khalil, U.; Sulaiman, M.; Khan, Z. A k-nearest neighbours based ensemble via optimal model selection for regression. IEEE Access 2020, 8, 132095–132105. [Google Scholar] [CrossRef]
- Huang, W.; Jiang, T.; Zhang, X.; Khan, N.A.; Sulaiman, M. Analysis of beam-column designs by varying axial load with internal forces and bending rigidity using a new soft computing technique. Complexity 2021, 2021, 6639032. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Aljohani, A.J.; Kumam, P.; Alrabaiah, H. Analysis of multi-phase flow through porous media for imbibition phenomena by using the LeNN-WOA-NM algorithm. IEEE Access 2020, 8, 196425–196458. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Aljohani, A.J.; Bakar, M.A. Mathematical models of CBSC over wireless channels and their analysis by using the LeNN-WOA-NM algorithm. Eng. Appl. Artif. Intell. 2022, 107, 104537. [Google Scholar] [CrossRef]
- Khan, N.A.; Khalaf, O.I.; Romero, C.A.T.; Sulaiman, M.; Bakar, M.A. Application of Euler Neural Networks with Soft Computing Paradigm to Solve Nonlinear Problems Arising in Heat Transfer. Entropy 2021, 23, 1053. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Kumam, P.; Bakar, M.A. Thermal analysis of conductive-convective-radiative heat exchangers with temperature dependent thermal conductivity. IEEE Access 2021, 9, 138876–138902. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Kumam, P.; Aljohani, A.J. A new soft computing approach for studying the wire coating dynamics with Oldroyd 8-constant fluid. Phys. Fluids 2021, 33, 036117. [Google Scholar] [CrossRef]
- Reddy, V.R.; Reddy, V.; Mohan, V.C.J. Speed control of induction motor drive using artificial neural networks-Levenberg-Marquardt Backpropogation algorithm. Int. J. Appl. Eng. Res. 2018, 13, 80–85. [Google Scholar]
- Multazam, T.; Putri, R.I.; Pujiantara, M.; Lystianingrum, V.; Priyadi, A.; Heryp, M. Short-Term Wind Speed Prediction Base on Backpropagation Levenberg-Marquardt Algorithm; Case Study Area Nganjuk. In Proceedings of the 2017 5th International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 6–7 November 2017; pp. 163–166. [Google Scholar] [CrossRef]
- Wu, S.T. Active pendulum vibration absorbers with a spinning support. J. Sound Vib. 2009, 323, 1–16. [Google Scholar] [CrossRef]
- Khan, Y.; Mirzabeigy, A.; Arjmand, H. Nonlinear oscillation of the bifilar pendulum: An analytical approximation. Multidiscip. Model. Mater. Struct. 2017. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).