Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System
Abstract
1. Introduction
2. Mathematical Preliminaries
3. Description of the Hardware Testing Platform
4. Implementation of the Grünwald–Letnikov Fractional-Order Operator
4.1. Memory Limitations
4.2. Compiler Settings
4.3. Measuring the Performance
- TRCENA bit [24] in the Debug Exception and Monitor Control Register (DEMCR) set to 1 to enable use of the trace and debug blocks.
- CYCCNTENA bit [0] in the DWT Control Register (DWT_CTRL) set to 1 to enable the CYCCNT counter.
- Value of the DWT_CYCCNT register initialized to 0.
4.4. Implementation of Fractional-Order Backward Difference
5. Optimization
5.1. SIMD and DSP Instructions in the CMSIS Library
5.2. Enabling the Hardware Floating-Point Unit
5.3. Other Optimizations
5.4. Implementation
- The appropriate linked CMSIS-DSP lib file: arm_cortexM3l_math.lib for STM32L152RCT6 (little-endian) and arm_cortexM7lfsp_math.lib for STM32F746ZG (little-endian, single-precision FPU). Required macros defined.
6. Fixed-Point Arithmetic
- The vector of the predefined floating-point input samples, initial fractional-order , and the sampling time h were converted to Q11.21 format by multiplying the values by and rounding to the nearest integer.
- The recursive function for calculating and fractional differintegral algorithm were modified for handling fixed-point arithmetic in Q11.21 notation.
- In the main loop, the order was incremented by one each step and the vectors of the coefficients, as well as the variable fractional-order backward difference and derivative responses, were recalculated.
7. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
Abbreviations
| ABI | Application Binary Interface |
| CPACR | Coprocessor Access Control Register |
| DEMCR | Debug Exception and Monitor Control Register |
| DFT | Discrete Fourier Transform |
| DWT | Data Watchpoint and Trace unit |
| DWT_CTRL | DWT Control Register |
| DWT_CYCCNT | DWT Cycle Count Register |
| FIR | Finite Impulse Response |
| FPU | Floating-Point Unit |
| GL | Grünwald–Letnikov |
| IIR | Infinite Impulse Response |
| MAC | Multiply-Accumulate |
| PID | Proportional-Integral-Derivative Controller |
| SIMD | Single Instruction Multiple Data |
| (V)FOBD/S | (Variable) Fractional-Order Backward Difference/Sum |
| (V)FOD/I | (Variable) Fractional-Order Differintegral |
| (V)FOPID | (Variable) Fractional-Order Proportional-Integral-Derivative Controller |
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus - Theory and Applications of Differentiation and Integration to Arbitrary Order. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1974; Volume 111, ISBN 978-0-12-525550-9. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations, 1st ed.; John Wiley & Sons: New York, NY, USA, 1993; ISBN 978-04-7158-884-9. [Google Scholar]
- Podlubny, I. Fractional Differential Equations—An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198, ISBN 978-01-2558-840-9. [Google Scholar] [CrossRef]
- Parsa Moghaddam, B.; Dabiri, A.; Tenreiro Machado, J.A. Application of variable-order fractional calculus in solid mechanics. In Handbook of Fractional Calculus with Applications. Applications in Engineering, Life and Social Sciences, Part A; Bǎleanu, D., Mendes Lopes, A., Tenreiro Machado, J.A., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 7, pp. 207–224. ISBN 978-3-11-057091-5. [Google Scholar] [CrossRef]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef]
- MacDonald, C.L.; Bhattacharya, N.; Sprouse, B.P.; Silva, G.A. Efficient computation of the Grünwald–Letnikov fractional diffusion derivative using adaptive time step memory. J. Comput. Phys. 2015, 297, 221–236. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Tejado, I.; Pérez, E.; Valério, D. Fractional Derivatives for Economic Growth Modelling of the Group of Twenty: Application to Prediction. Mathematics 2020, 8, 50. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sarimveis, H. Controlled Drug Administration by a Fractional PID. IFAC Proc. Vol. 2014, 47, 8421–8426. [Google Scholar] [CrossRef]
- Valentim, C.A.; Oliveira, N.A.; Rabi, J.A.; David, S.A. Can fractional calculus help improve tumor growth models? J. Comput. Appl. Math. 2020, 379, 112964. [Google Scholar] [CrossRef]
- Aliyu, A.I.; Alshomrani, A.S.; Li, Y.; Inc, M.; Baleanu, D. Existence theory and numerical simulation of HIV-I cure model with new fractional derivative possessing a non-singular kernel. Adv. Differ. Equ. 2019, 2019, 408. [Google Scholar] [CrossRef]
- Al-Shamasneh, A.R.; Jalab, H.A.; Shivakumara, P.; Ibrahim, R.W.; Obaidellah, U.H. Kidney segmentation in MR images using active contour model driven by fractional-based energy minimization. Signal Image Video Process. 2020, 1–8. [Google Scholar] [CrossRef]
- Lv, T.; Tong, L.; Zhang, J.; Chen, Y. A real-time physiological signal acquisition and analyzing method based on fractional calculus and stream computing. Soft Comput. 2020, 1–7. [Google Scholar] [CrossRef]
- Huang, L.L.; Park, J.H.; Wu, G.C.; Mo, Z.W. Variable-order fractional discrete-time recurrent neural networks. J. Comput. Appl. Math. 2020, 370, 112633. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190498. [Google Scholar] [CrossRef] [PubMed]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4, 9:1–9:7. [Google Scholar] [CrossRef]
- Lewandowski, M.; Orzyłowski, M. Fractional-order models: The case study of the supercapacitor capacitance measurement. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 449–457. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Shang, Y.; Duan, B.; Cui, N.; Zhang, C. A Fractional-Order Kinetic Battery Model of Lithium-Ion Batteries Considering a Nonlinear Capacity. Electronics 2019, 8, 394. [Google Scholar] [CrossRef]
- Majka, L.; Klimas, M. Diagnostic approach in assessment of a ferroresonant circuit. Electr. Eng. 2019, 101, 149–164. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. IFAC-PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Ostalczyk, P.; Brzezinski, D.; Duch, P.; Łaski, M.; Sankowski, D. The variable, fractional-order discrete-time PD controller in the IISv1.3 robot arm control. Cent. Eur. J. Phys. 2013, 11, 750–759. [Google Scholar] [CrossRef][Green Version]
- El-Khazali, R. Fractional-order PIλDμ controller design. Comput. Math. Appl. 2013, 66, 639–646. [Google Scholar] [CrossRef]
- Petráš, I.; Vinagre, B.M. Practical application of digital fractional-order controller to temperature control. Acta Montan. Slovaca 2002, 7, 131–137. Available online: https://actamont.tuke.sk/pdf/2002/n2/11petras.pdf (accessed on 11 March 2020).
- Brzeziński, D.W. Fractional Order Derivative and Integral Computation with a Small Number of Discrete Input Values Using Grünwald–Letnikov Formula. Int. J. Comput. Methods 2019, 17, 1940006. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Ostalczyk, P. On simplified forms of the fractional-order backward difference and related fractional-order linear discrete-time system description. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 423–433. [Google Scholar] [CrossRef][Green Version]
- Oustaloup, A. La commande CRONE: Commande Robuste D’Ordre non Entier; Hermes Science Publications: Paris, France, 1991; ISBN 978-28-6601-289-2. [Google Scholar]
- Oprzȩdkiewicz, K.; Podsiadło, M.; Dziedzic, K. Integer order vs fractional order temperature models in the forced air heating system. Przegla̧d Elektrotechniczny 2019, 95, 35–40. [Google Scholar] [CrossRef]
- Baranowski, J.; Bauer, W.; Zagórowska, M.; Pia̧tek, P. On Digital Realizations of Non-integer Order Filters. Circuits Syst. Signal Process. 2016, 35, 2083–2107. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-order Systems and Controls. Fundamentals and Applications; Advances in Industrial Control; Springer: London, UK, 2010; ISBN 978-1-84996-334-3. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Caponetto, R.; Machado, J.T.; Murgano, E.; Xibilia, M.G. Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy 2019, 21, 876. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Implementation and real-time simulation of a fractional-order controller using a MATLAB based prototyping platform. In Proceedings of the 13th Biennial Baltic Electronics Conference, Tallinn, Estonia, 3–5 October 2012; pp. 145–148. [Google Scholar] [CrossRef]
- Pyeatt, L.D.; Ughetta, W. Non-Integral Mathematics. In Modern Assembly Language Programming with the ARM Processor; Pyeatt, L.D., Ughetta, W., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 8; pp. 239–292. ISBN 978-01-2819-221-4. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific Publishing Co., Inc.: Singapore, 2016; ISBN 978-98-1472-566-8. [Google Scholar]
- Mozyrska, D.; Ostalczyk, P. Variable-, fractional-order Grünwald-Letnikov backward difference selected properties. In Proceedings of the 39th International Conference on Telecommunications and Signal Processing (TSP 2016), Vienna, Austria, 27–29 June 2016; pp. 634–637. [Google Scholar] [CrossRef]
- STMicroelectronics. STM32L15xCC STM32L15xRC STM32L15xUC STM32L15xVC Ultra-low-power 32-bit MCU ARM-based Cortex-M3, 256KB Flash, 32KB SRAM, 8KB EEPROM, LCD, USB, ADC, DAC. Datasheet—Production Data. DocID022799 Rev 13. 2017. Available online: https://www.st.com/resource/en/datasheet/stm32l152rc.pdf (accessed on 11 March 2020).
- STMicroelectronics. STM32F745xx STM32F746xx ARM-based Cortex-M7 32b MCU+FPU, 462DMIPS up to 1MB Flash/320+16+4KB RAM, USB OTG HS/FS, ethernet, 18TIMs, 3ADCs, 25 com itf, cam & LCD Datasheet—Production Data. DocID027590 Rev 4. 2016. Available online: https://doi.org/https://www.st.com/resource/en/datasheet/stm32f746zg.pdf (accessed on 11 March 2020).
- STMicroelectronics. UM1079 User Manual. Discovery kits with STM32L152RCT6 and STM32L152RBT6 MCUs. 2017. Available online: http://www.st.com/resource/en/user_manual/dm00093903.pdf (accessed on 11 March 2020).
- STMicroelectronics. UM1974 User Manual STM32 Nucleo-144 Boards. 2017. Available online: http://www.st.com/content/ccc/resource/technical/document/user_manual/group0/26/49/90/2e/33/0d/4a/da/DM00244518/files/DM00244518.pdf/jcr:content/translations/en.DM00244518.pdf (accessed on 11 March 2020).
- Arm Ltd. Using Common Compiler Options. Selecting optimization options. In Arm® Compiler Version 6.12 User Guide; Arm Ltd.: Cambridge, UK, 2019; pp. 35–37. Available online: https://developer.arm.com/docs/100748/0612 (accessed on 11 March 2020).
- Arm Ltd. Data Watchpoint and Trace Unit. In Arm® Cortex®-M7 Processor Technical Reference Manual, r1p2 ed.; Arm Ltd.: Cambridge, UK, 2018; pp. 139–143. Available online: https://developer.arm.com/docs/ddi0489/d (accessed on 11 March 2020).
- Arm Ltd. CMSIS-Core (Cortex-M) Intrinsic Functions for SIMD Instructions [only Cortex-M4 and Cortex-M7]; Arm Ltd.: Cambridge, UK, 2019; Available online: https://www.keil.com/pack/doc/CMSIS/Core/html/group__intrinsic__SIMD__gr.html (accessed on 11 March 2020).
- Arm Ltd. CMSIS-DSP Software Library; Arm Ltd.: Cambridge, UK, 2019; Available online: https://www.keil.com/pack/doc/CMSIS/DSP/html/index.html (accessed on 11 March 2020).
- STMicroelectronics. AN4841 Application Note. Digital Signal Processing for STM32 Microcontrollers Using CMSIS. Rev 2. 2018. Available online: https://www.st.com/content/ccc/resource/technical/document/application_note/group0/c1/ee/18/7a/f9/45/45/3b/DM00273990/files/DM00273990.pdf/jcr:content/translations/en.DM00273990.pdf (accessed on 11 March 2020).
- ARM Ltd. Arm Cortex-M7 Processor Technical Reference Manual, r1p2 ed.; ARM Ltd.: Cambridge, UK, 2018; Available online: https://static.docs.arm.com/ddi0489/f/DDI0489F_cortex_m7_trm.pdf (accessed on 11 March 2020).
- Noronha, D.H.; Leong, P.H.; Wilton, S.J. Kibo: An Open-Source Fixed-Point Tool-kit for Training and Inference in FPGA-Based Deep Learning Networks. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW 2018), Vancouver, BC, Canada, 21–25 May 2018; pp. 178–185. [Google Scholar] [CrossRef]
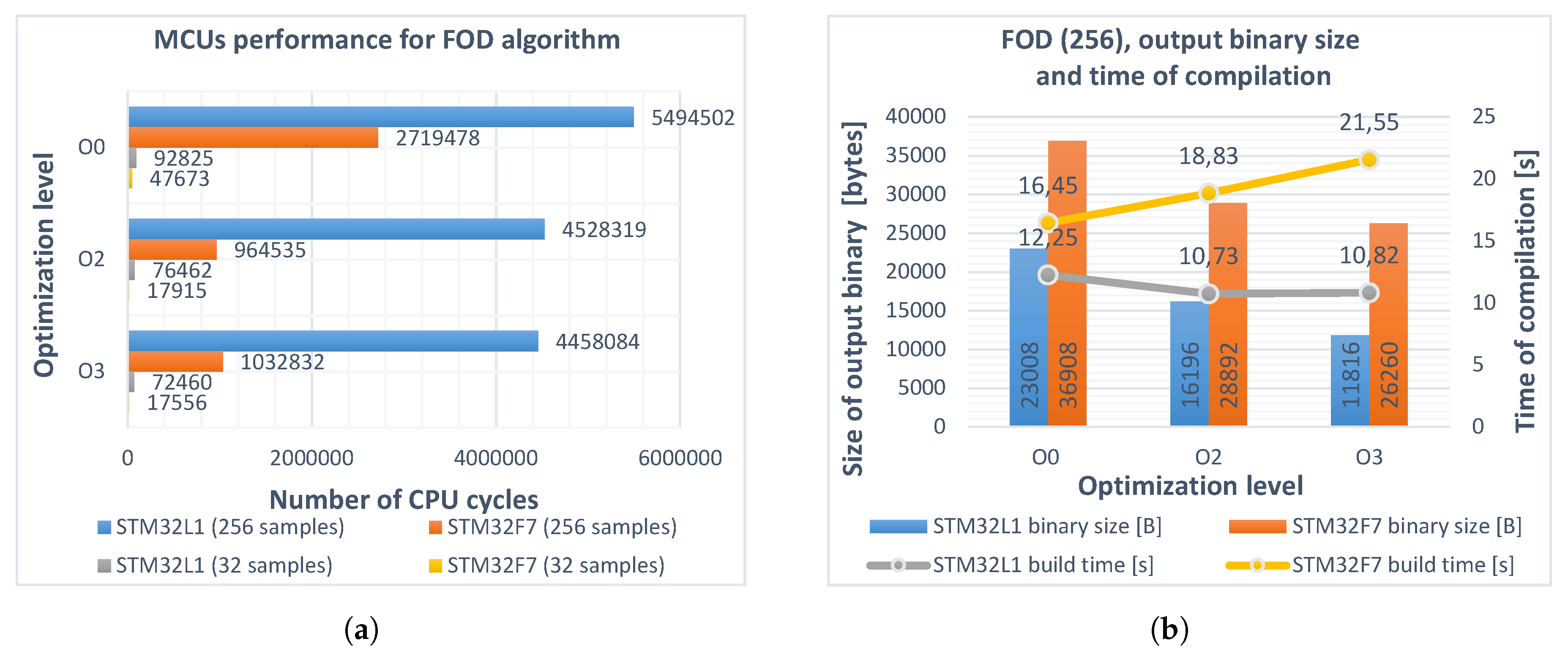
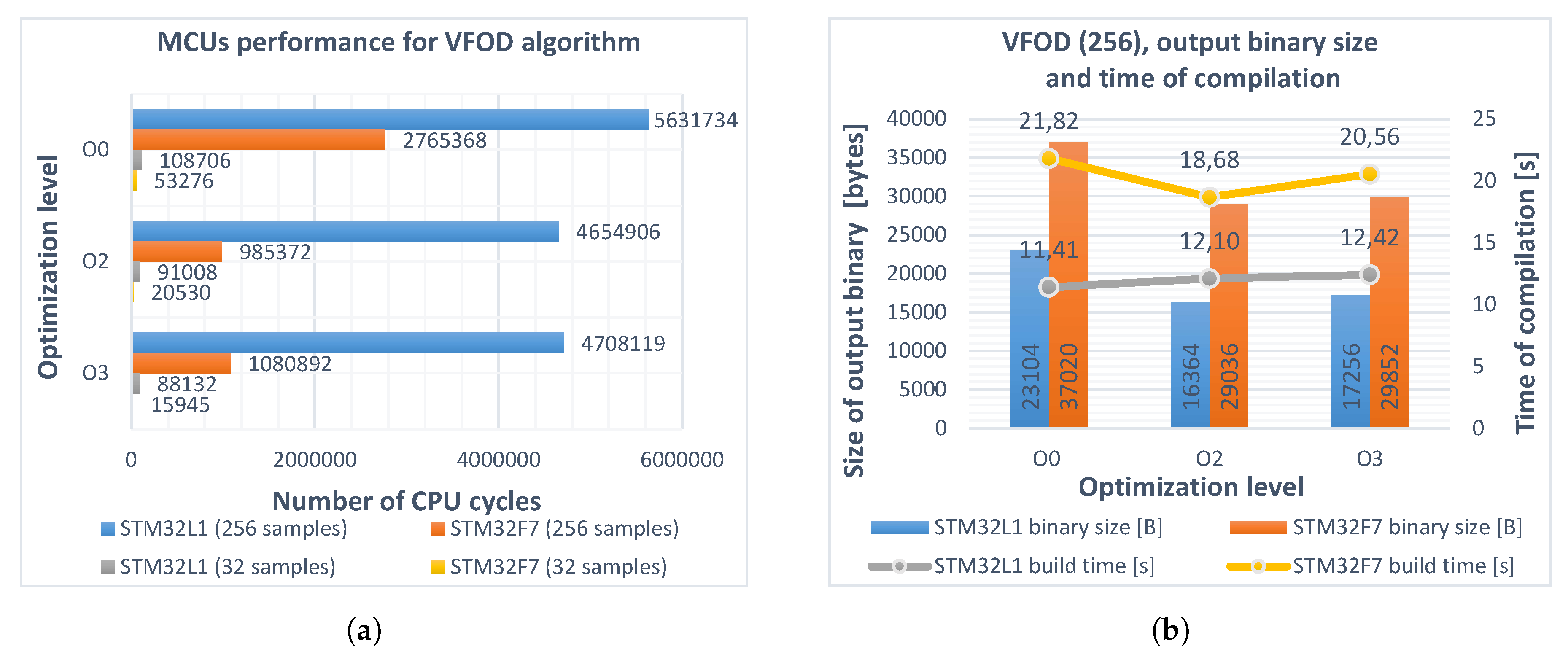
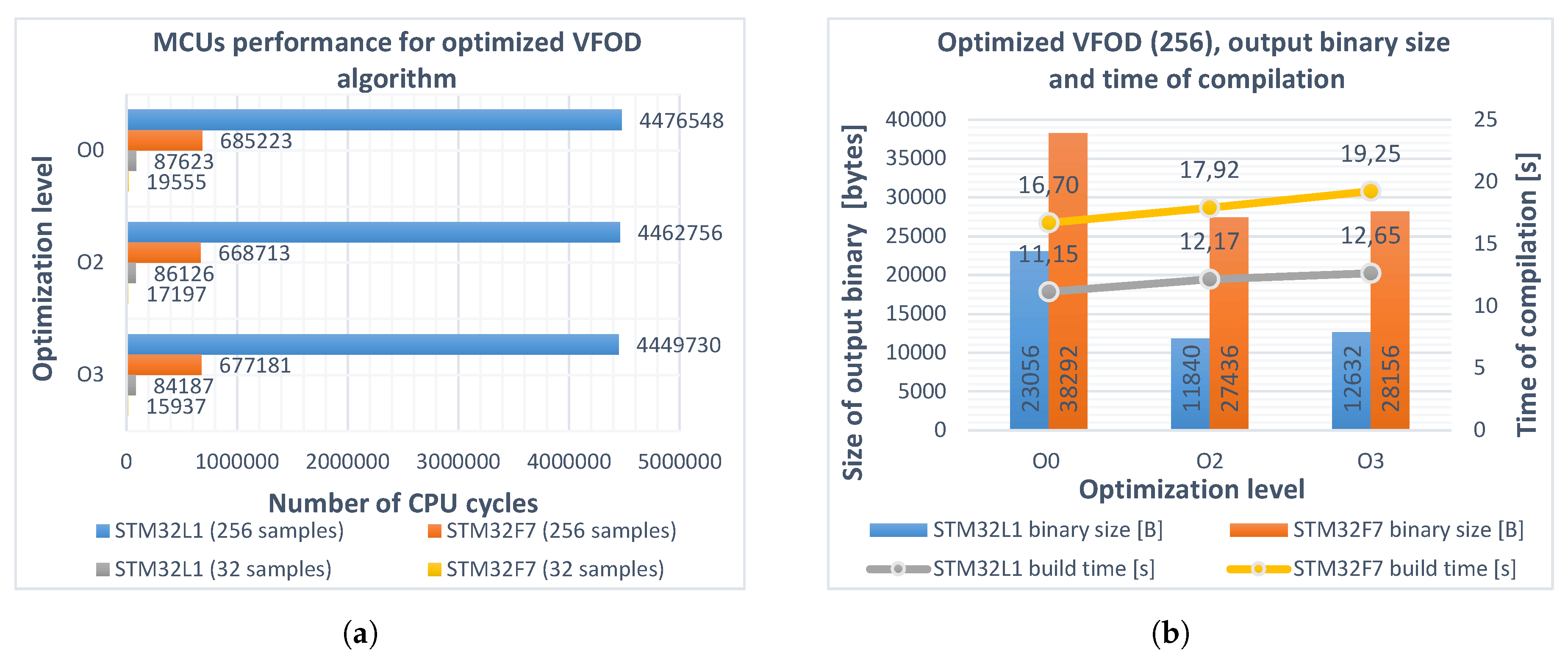
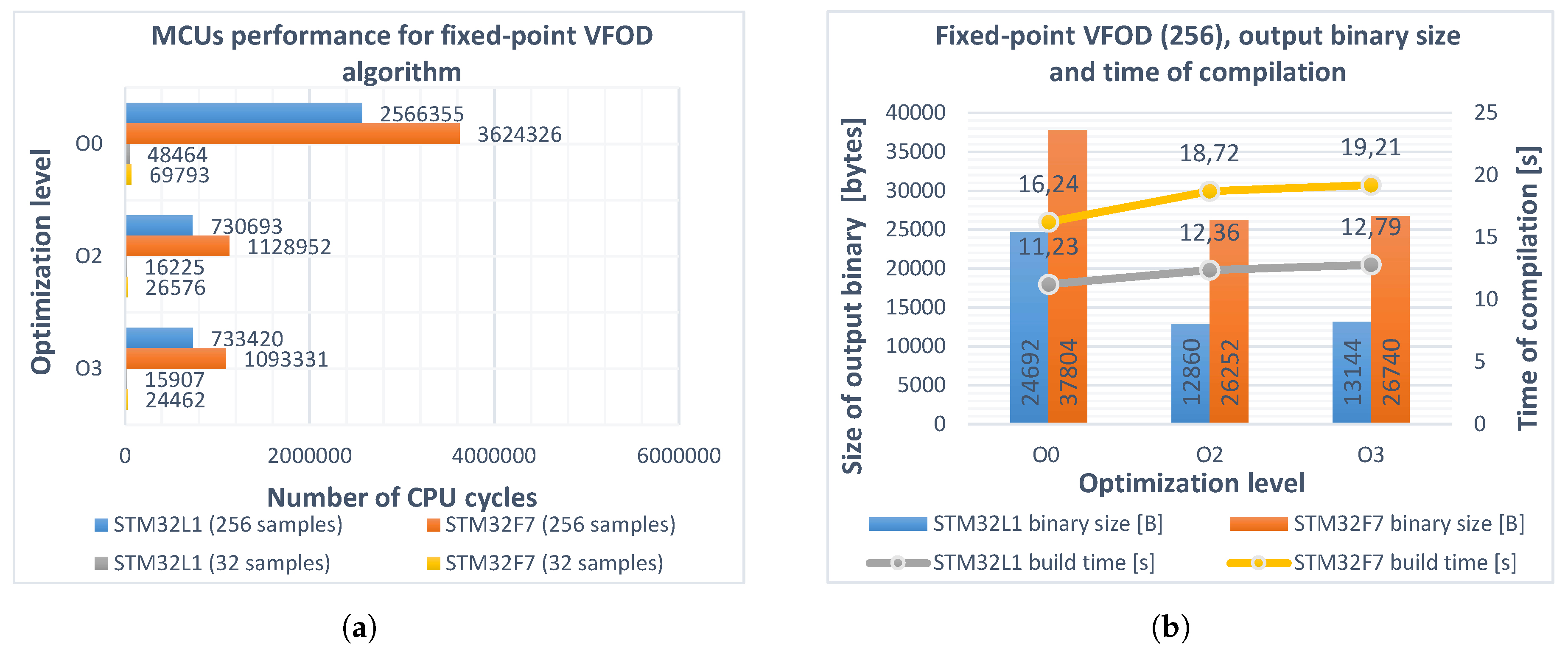
| Parameter Name | STM32L152RCT6 (Arm® Cortex®-M3) | STM32F746ZG (Arm® Cortex®-M7) |
|---|---|---|
| CPU clock frequency () | up to 32 MHz | up to 216 MHz |
| Memory () | 256 KB Flash + 32 KB SRAM + 8 KB EEPROM | 1024 KB Flash + 320 KB SRAM |
| Converters () | 12-bit 1 MSPS ADC, 12-bit DAC | 3× 12-bit 2.4 MSPS ADC, 2× 12-bit DAC |
| Power supply () | 1.65–3.6 V | 1.8–3.6 V |
| Other features | ultra-low-power technology, LCD driver, touch sensor channels | floating-point unit real-time accelerator, DSP instructions, LCD and cam interface |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matusiak, M. Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System. Entropy 2020, 22, 566. https://doi.org/10.3390/e22050566
Matusiak M. Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System. Entropy. 2020; 22(5):566. https://doi.org/10.3390/e22050566
Chicago/Turabian StyleMatusiak, Mariusz. 2020. "Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System" Entropy 22, no. 5: 566. https://doi.org/10.3390/e22050566
APA StyleMatusiak, M. (2020). Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System. Entropy, 22(5), 566. https://doi.org/10.3390/e22050566





