Endoreversible Modeling of a Hydraulic Recuperation System
Abstract
1. Introduction
2. Endoreversible Formalism
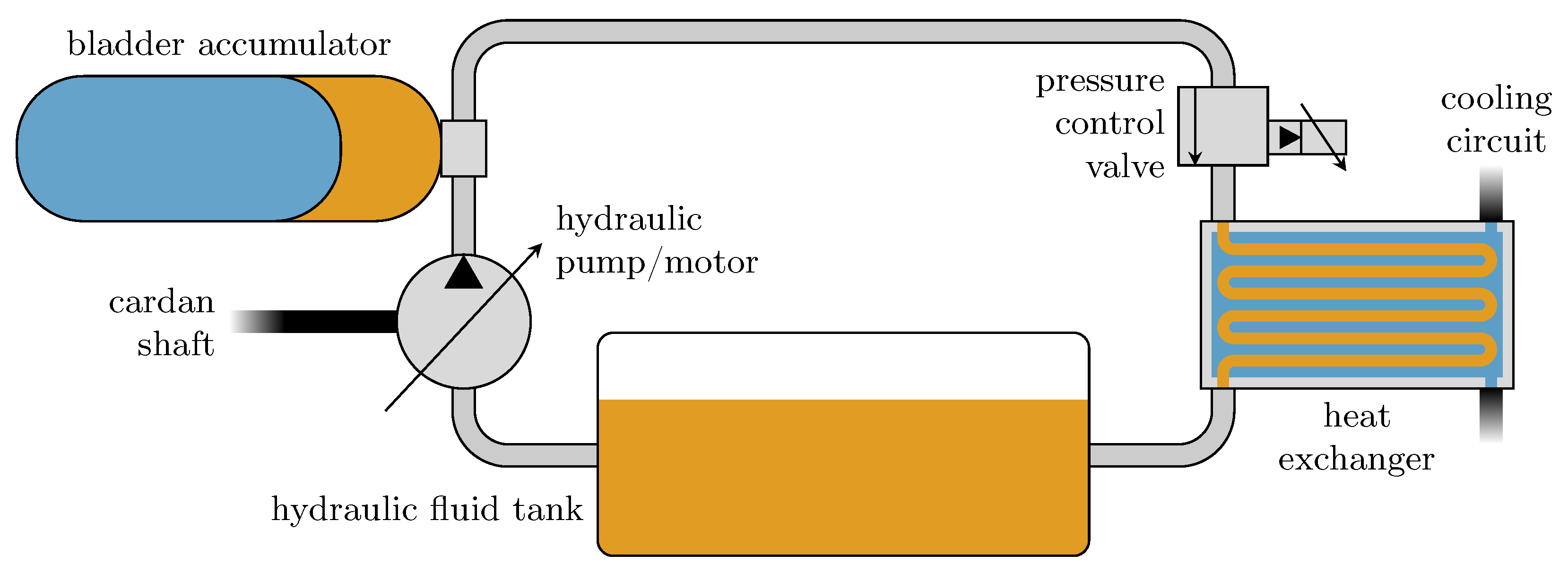
3. Model Description
3.1. Hydraulic Fluid
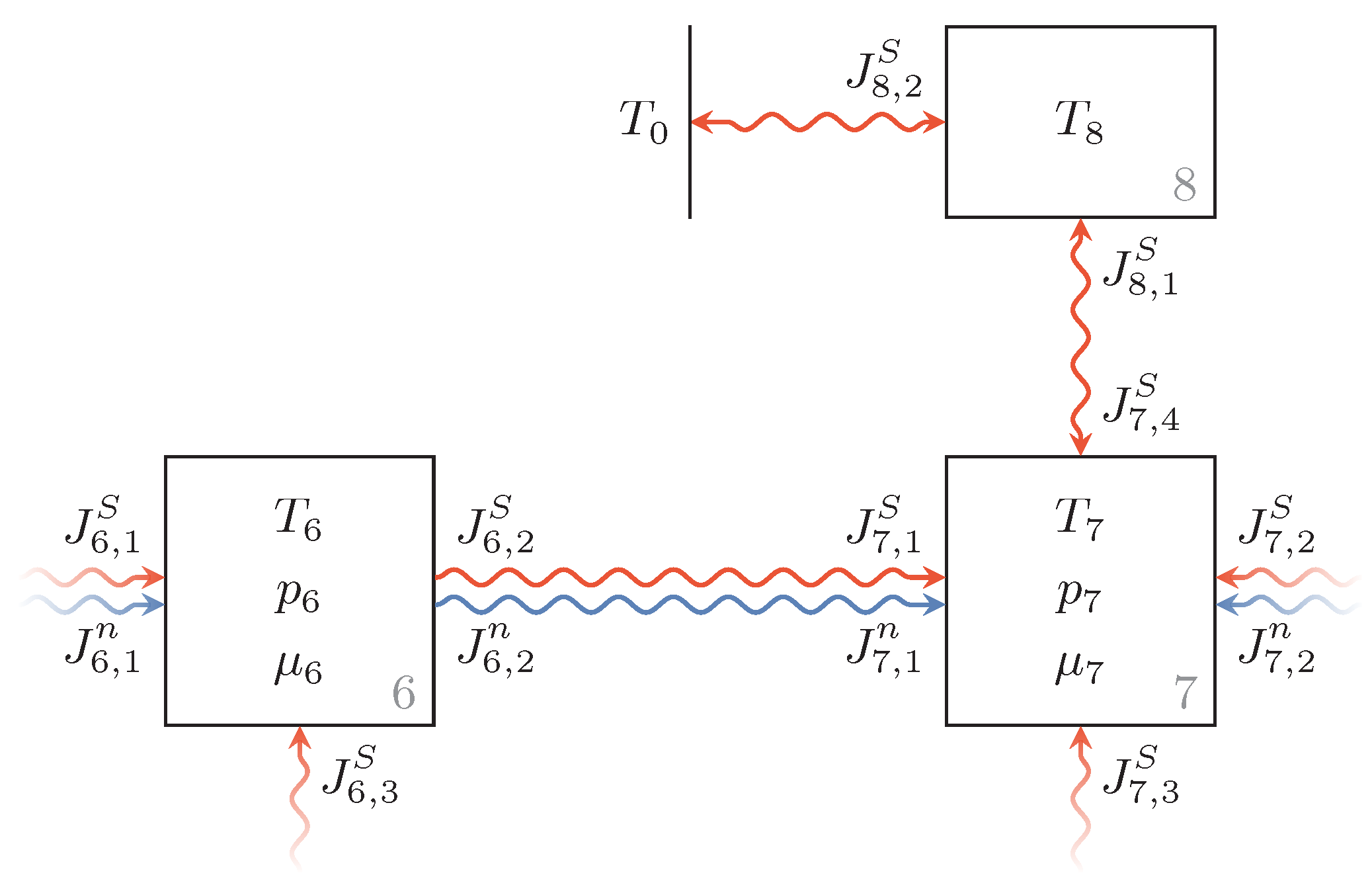
3.2. Pipes and Hydraulic Fluid Tank
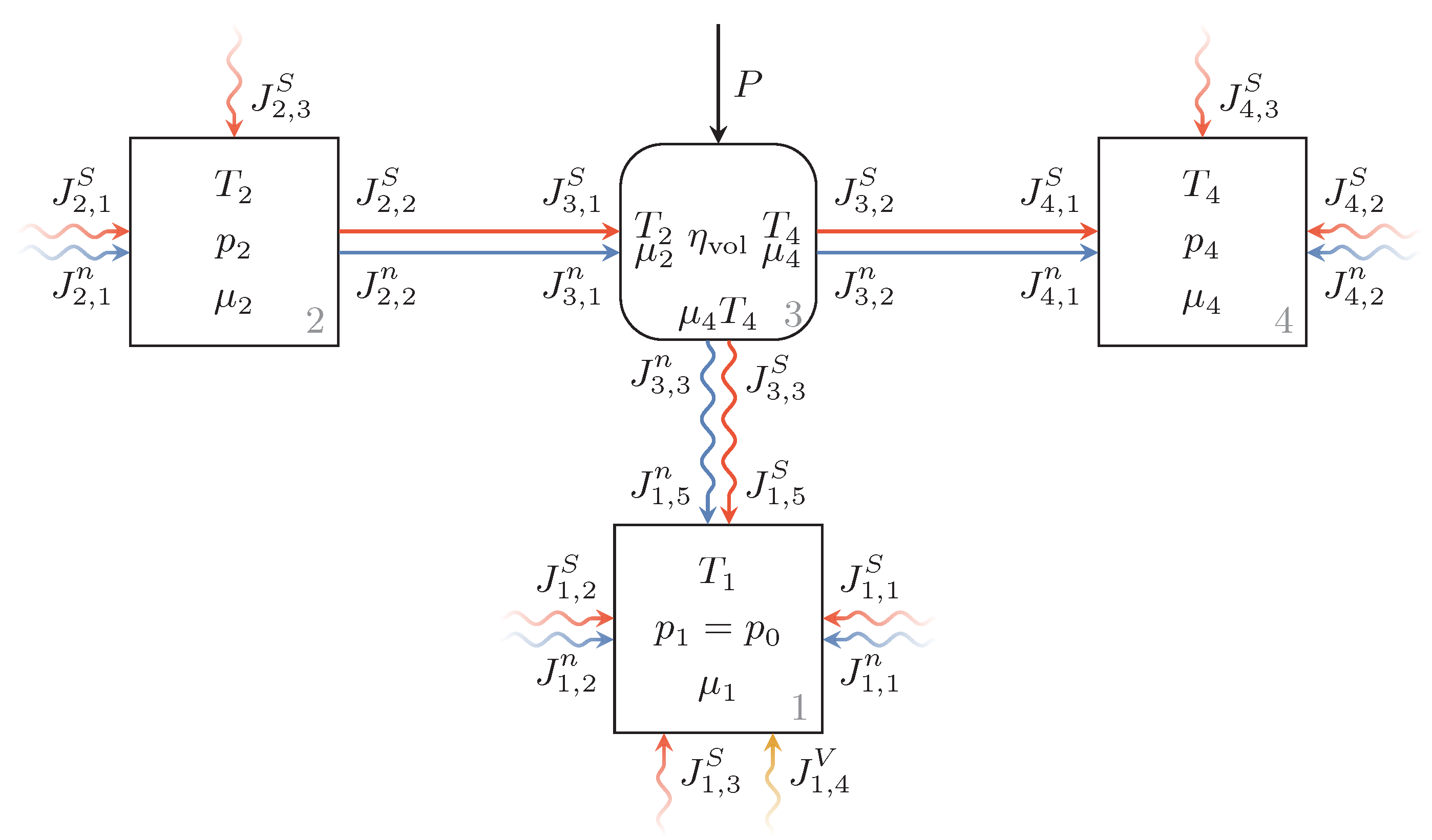
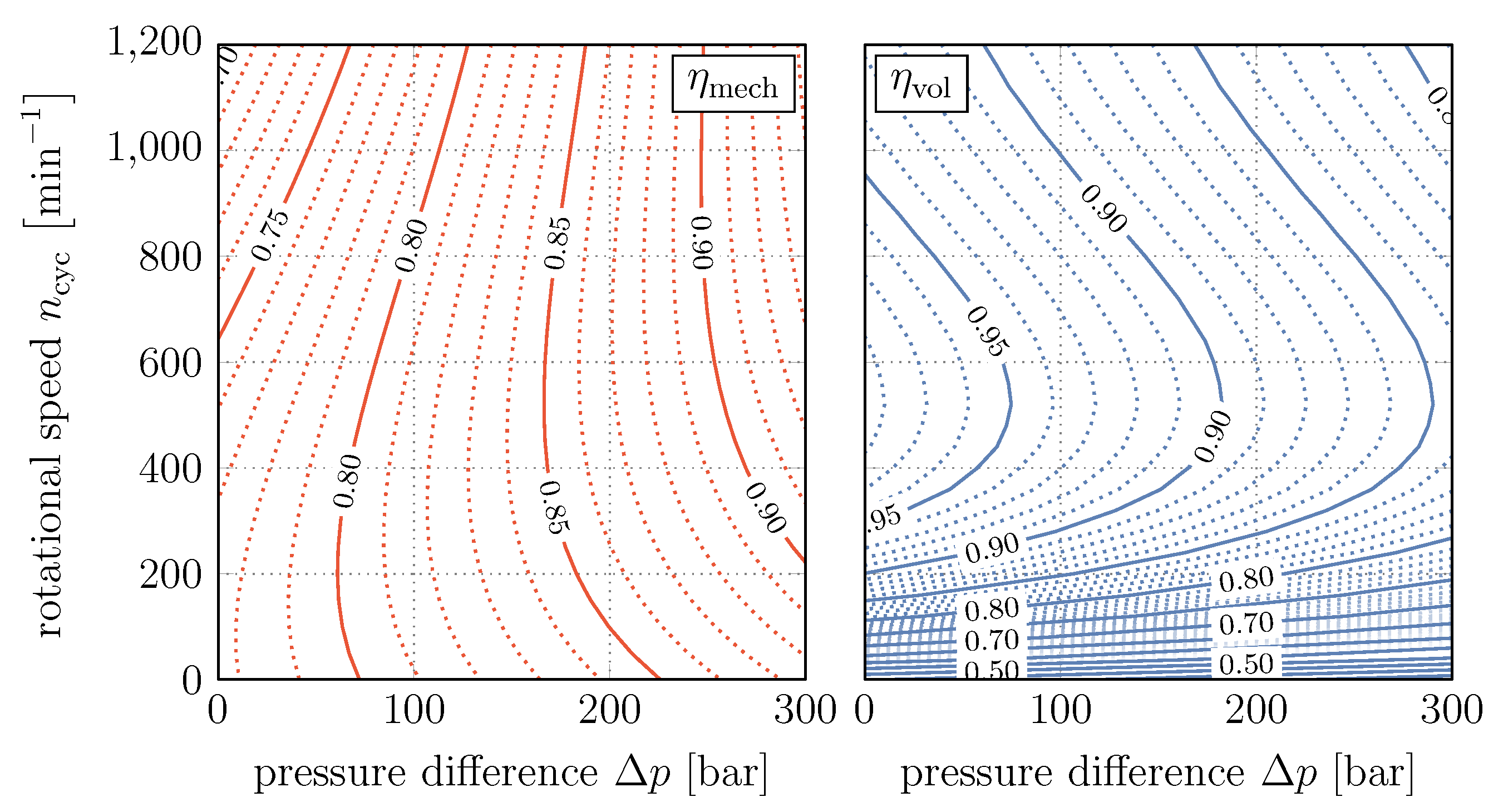
3.3. Hydraulic Unit
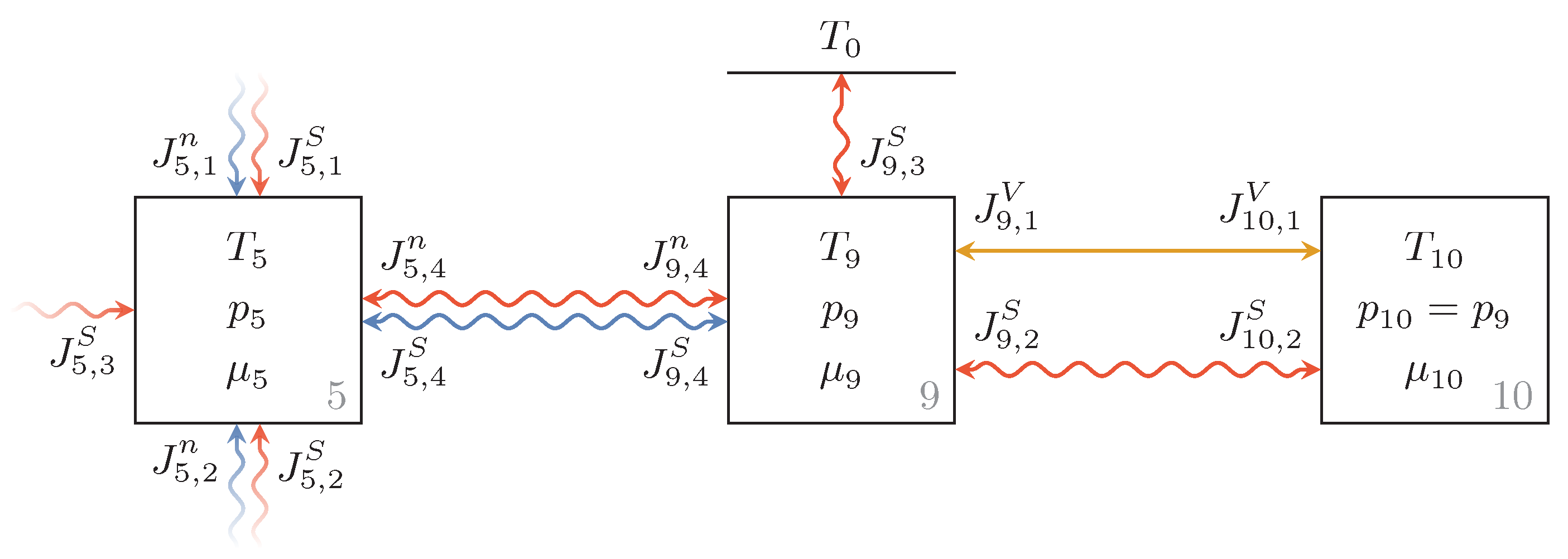
3.4. Bladder Accumulator
3.5. Pressure Control Valve
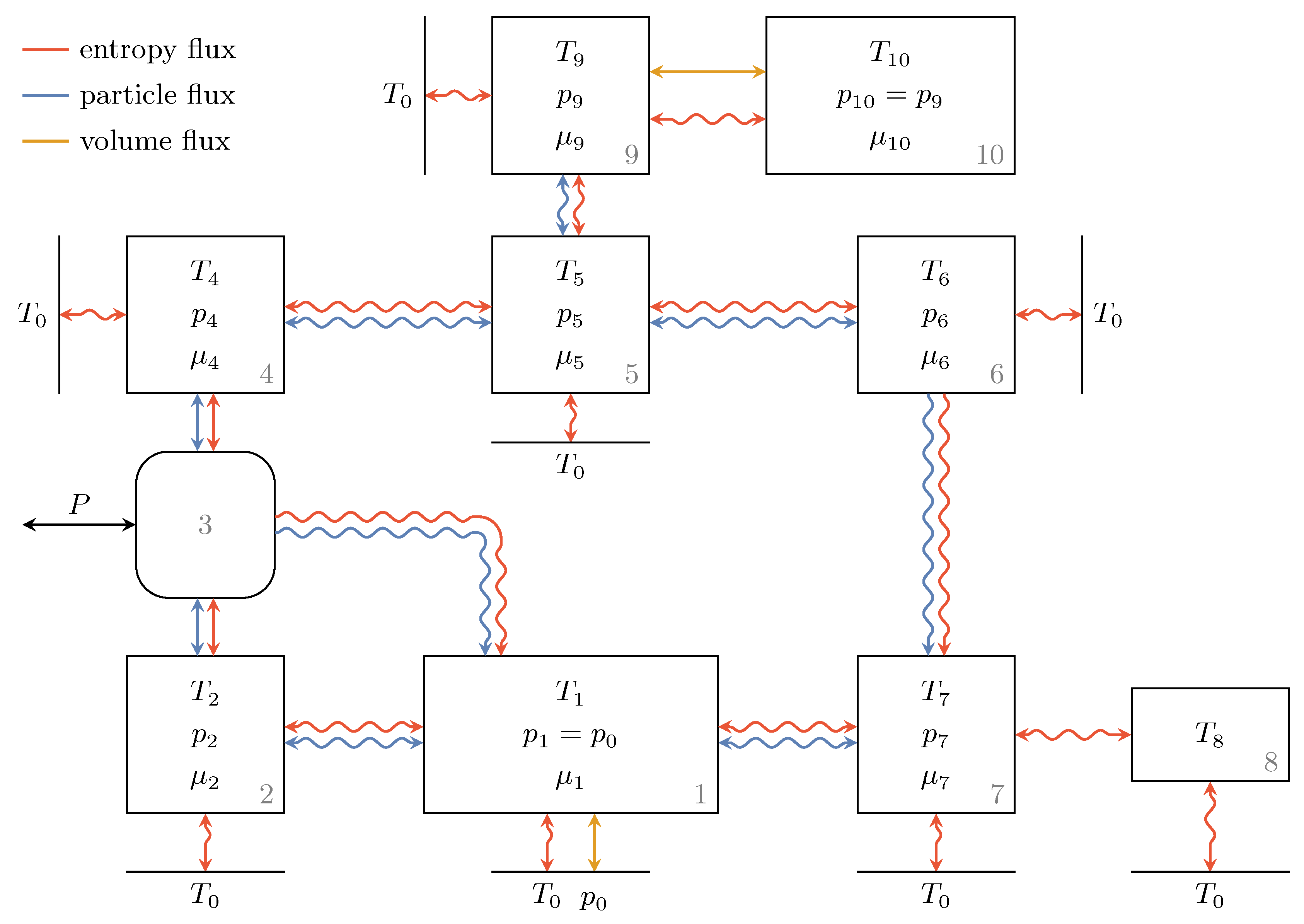
3.6. Composite Model
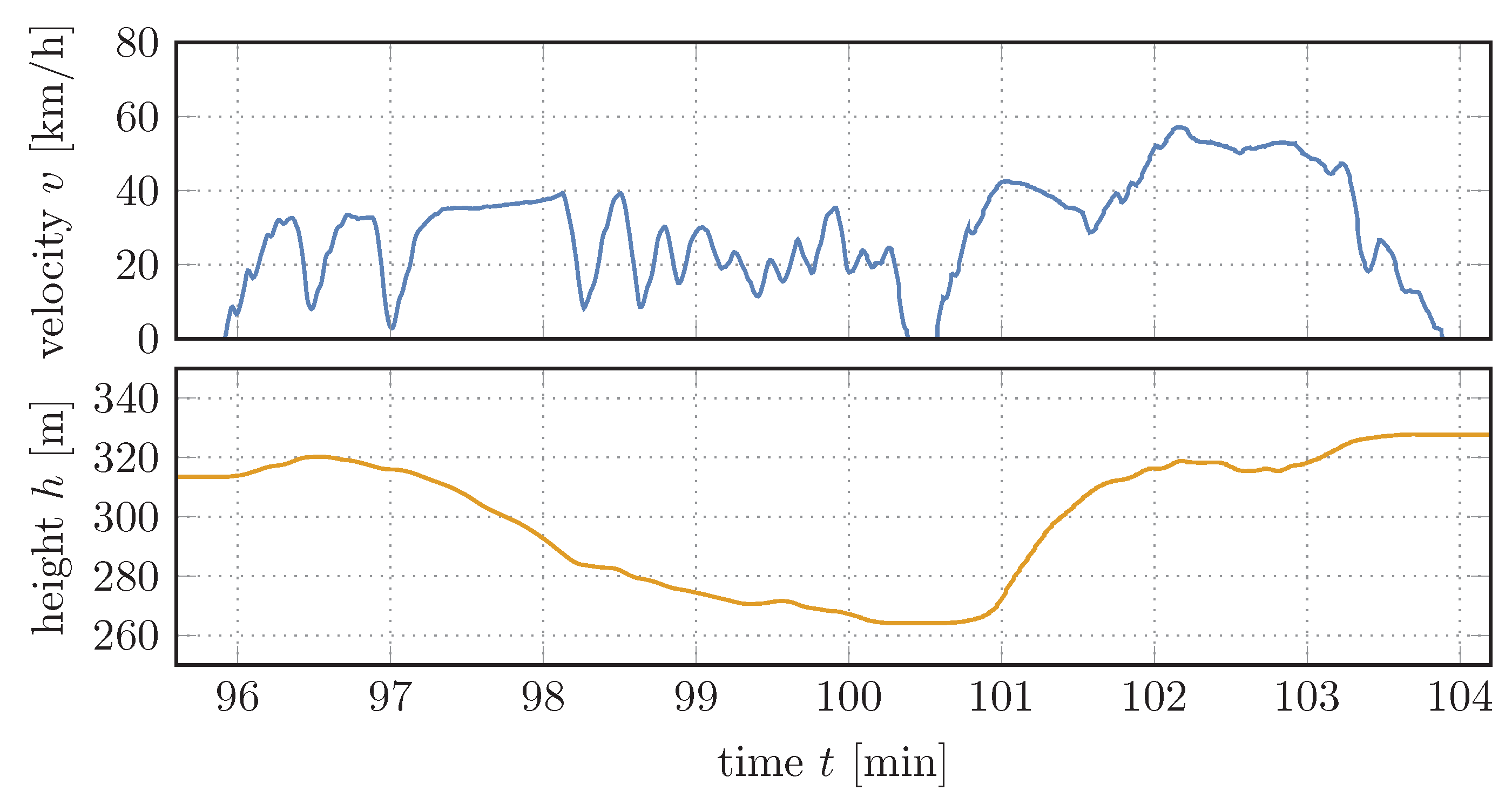
3.7. Driving Dynamics of the Truck
4. Energy Savings
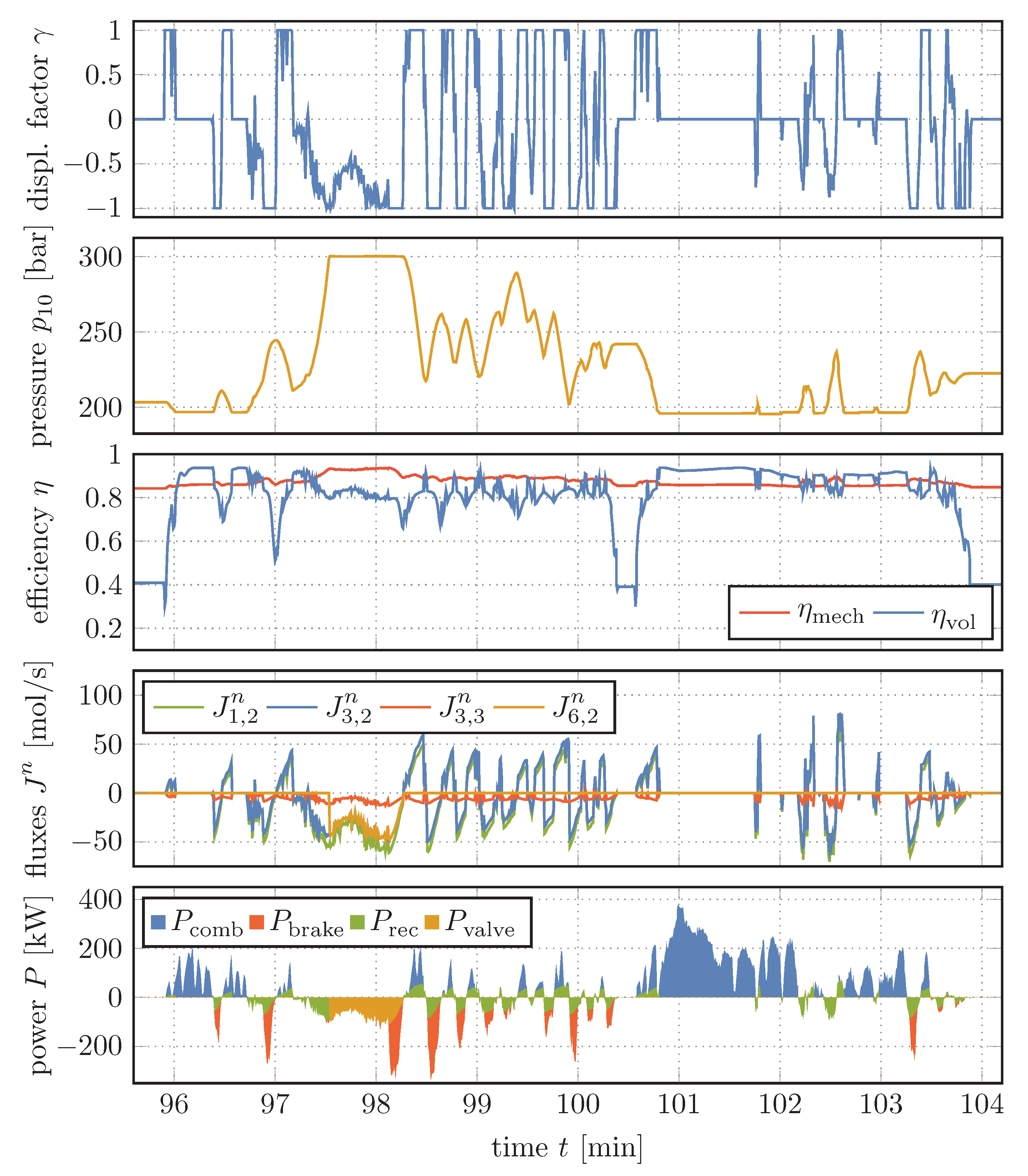
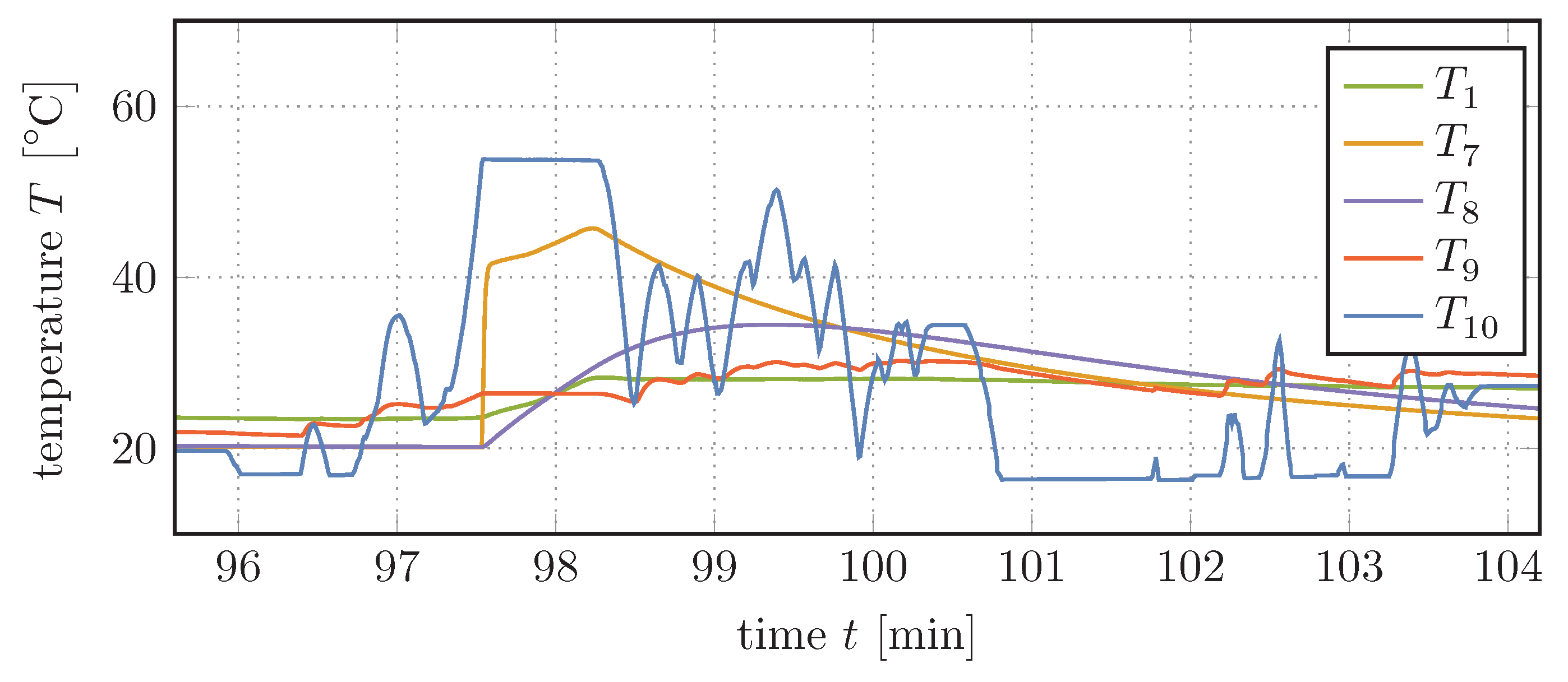
4.1. Dynamical Behavior of the System
4.2. Variation of Selected Parameters
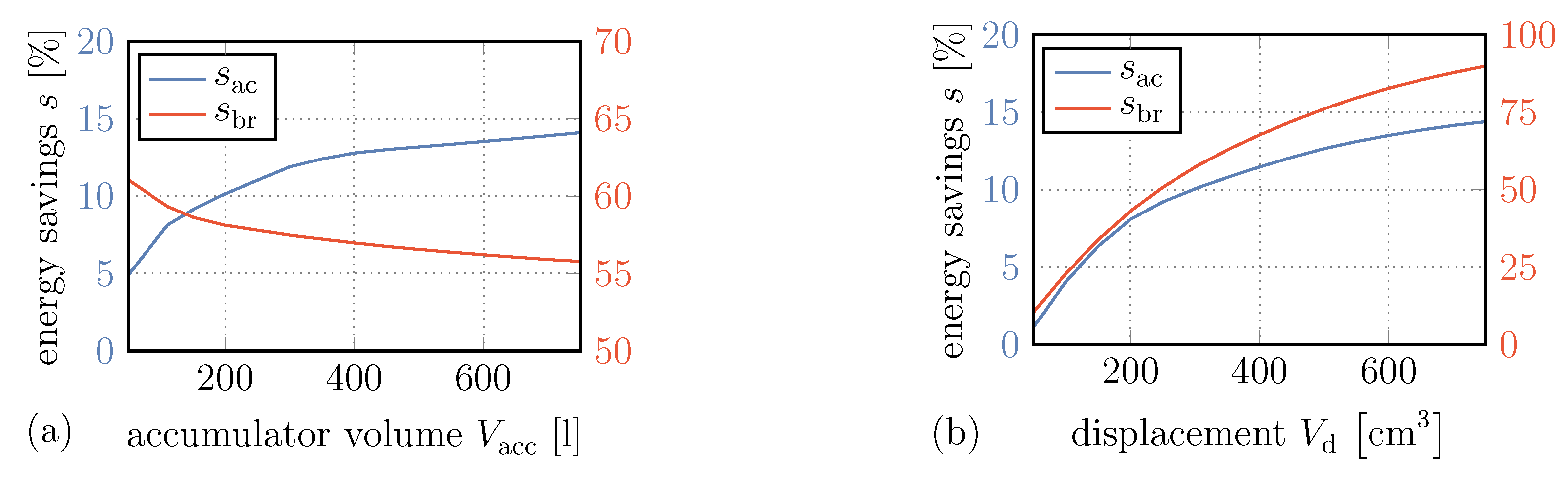
4.2.1. Bladder Accumulator Volume and Displacement of Hydraulic Unit
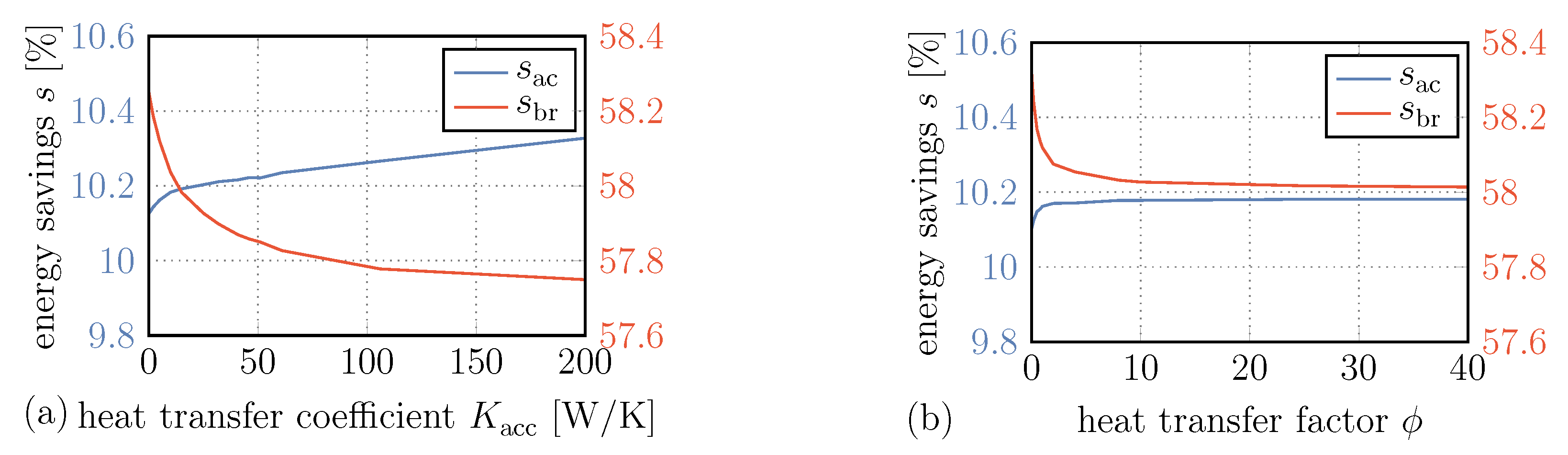
4.2.2. Heat Transfer within the Bladder Accumulator
4.2.3. Heat Transfer to the Environment
4.2.4. Pipe Diameter
5. Summary
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| inclination of the street | ° | |
| coefficient of volumetric thermal expansion | k−1 | |
| compressibility | Pa−1 | |
| displacement factor | - | |
| relief flux coefficient | m3 s−1 | |
| efficiency | - | |
| thermal conductivity | W K−1 | |
| chemical potential | J mol−1 | |
| kinematic viscosity | m2 s−1 | |
| density | kg m−3 | |
| a | cohesion pressure | Pa m6 mol−2 |
| A | area | m2 |
| b | co-volume | m3 mol−1 |
| drag coefficient | - | |
| specific heat capacity at constant pressure | J kg−1 K−1 | |
| coefficient of rolling resistance | - | |
| specific heat capacity at constant volume | J kg−1 K−1 | |
| dimensionless heat capacity at constant volume | - | |
| heat capacity at constant pressure | J K−1 | |
| heat capacity at constant volume | J K−1 | |
| Darcy friction factor | - | |
| mass factor | - | |
| g | gravitational acceleration | m s−2 |
| h | specific heat transfer coefficient | W K−1 m−1 |
| I | energy flux | W |
| J | extensity flux | * |
| k | heat transfer coefficient | W K−1 m−2 |
| K | overall heat transfer coefficient | W K−1 |
| l | length | m |
| m | mass | kg |
| M | molar mass | kg mol−1 |
| n | mole number | mol |
| rotational speed | s−1 | |
| p | pressure | Pa |
| P | power | W |
| Q | volumetric flow rate | m3 s−1 |
| R | universal gas constant | J mol−1 K−1 |
| Re | Reynolds number | - |
| s | energy savings | - |
| t | time | s |
| T | temperature | K |
| u | mean velocity of the fluid | m s−1 |
| U | internal energy | J |
| v | velocity | m s−1 |
| V | volume | m3 |
| molar volume | m3 mol−1 | |
| displacement | m3 | |
| X | extensity | * |
| Y | intensity | * |
| * varying unit |
References
- Sciarretta, A.; Guzzella, L. Control of hybrid electric vehicles. IEEE Contr. Syst. Mag. 2007, 27, 60–70. [Google Scholar]
- Peng, D.; Zhang, Y.; Yin, C.L.; Zhang, J.W. Combined control of a regenerative braking and anti-lock braking system for hybrid electric vehicles. Int. J. Automot. Technol. 2008, 9, 749–757. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Danyali, S.; Hosseini, S.H.; Sabahi, M.; Niapour, S.M. Modeling and Control of a New Three-Input DC-DC Boost Converter for Hybrid PV/FC/Battery Power System. IEEE T. Power Electr. 2012, 27, 2309–2324. [Google Scholar] [CrossRef]
- Moreno, J.; Ortúzar, M.E.; Dixon, J.W. Energy-Management System for a Hybrid Electric Vehicle, Using Ultracapacitors and Neural Networks. IEEE Trans. Ind. Electron. 2006, 53, 614–623. [Google Scholar] [CrossRef]
- Ahn, J.K.; Jung, K.H.; Kim, D.H.; Jin, H.B.; Kim, H.S.; Hwang, S.H. Analysis of a regenerative breaking system for hybrid electric vehicles using an electro-mechanical brake. Int. J. Automot. Technol. 2009, 10, 229–234. [Google Scholar] [CrossRef]
- Pourmovahed, A.; Beachley, N.H.; Fronczak, F.J. Modeling of a Hydraulic Energy Regeneration System: Part I— Analytical Treatment. J. Dyn. Syst. Meas. Control 1992, 114, 155–159. [Google Scholar] [CrossRef]
- Shan, M. Modeling and Control Strategy for Series Hydraulic Hybrid Vehicles. Ph.D. Thesis, University of Toledo, Toledo, Spain, 2009. [Google Scholar]
- Hui, S.; Ji-hai, J.; Xin, W. Torque control strategy for a parallel hydraulic hybrid vehicle. J. Terramech. 2009, 46, 259–265. [Google Scholar] [CrossRef]
- Hui, S.; Junqing, J. Research on the system configuration and energy control strategy for parallel hydraulic hybrid loader. Automat. Constr. 2010, 19, 213–220. [Google Scholar] [CrossRef]
- Chen, Y.L.; Liu, S.A.; Jiang, J.H.; Shang, T.; Zhang, Y.K.; Wei, W. Dynamic analysis of energy storage unit of the hydraulic hybrid vehicle. Int. J. Automot. Technol. 2013, 14, 101–112. [Google Scholar] [CrossRef]
- Rupprecht, K.R. Hydrospeicher, Experimentelle und Analytische Untersuchungen zur Energiespeicherung. Ph.D. Thesis, Technische Hochschule Aachen, Aachen, Germany, 1988. [Google Scholar]
- Pourmovahed, A.; Baum, S.A.; Fronczak, F.J.; Beachley, N.H. Experimental Evaluation of Hydraulic Accumulator Efficiency With and Without Elastomeric Foam. J. Propulsion 1988, 4, 185–192. [Google Scholar] [CrossRef]
- Pourmovahed, A.; Otis, D.R. An Experimental Thermal Time-Constant Correlation for Hydraulic Accumulators. J. Dyn. Syst. Meas. Control 1988, 112, 116–121. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Lebon, G. Heat conduction at micro and nanoscales: A review through the prism of Extended Irreversible Thermodynamics. J. Non-Equilib. Thermodyn. 2014, 39, 35–39. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Grmela, M. Extended Reversible and Irreversible Thermodynamics: A Hamiltonian Approach with Application to Heat Waves. J. Non-Equilib. Thermodyn. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Truesdell, C.; Bharatha, S. The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines; Springer Science & Business Media: Berlin, Germany, 1977. [Google Scholar]
- Matolcsi, T. Ordinary Thermodynamics; Society for the Unity of Science and Technology: Budapest, Hungary, 2017. [Google Scholar]
- Janečka, A.; Pavelka, M. Gradient Dynamics and Entropy Production Maximization. J. Non-Equilib. Thermodyn. 2018, 43, 1–19. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible Thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- Salamon, P.; Nitzan, A.; Andresen, B.; Berry, R.S. Minimum Entropy Production and the Optimization of Heat Engines. Phys. Rev. A 1980, 21, 2115–2129. [Google Scholar] [CrossRef]
- Rubin, M.H.; Andresen, B. Optimal Staging of Endoreversible Heat Engines. J. Appl. Phys. 1982, 53, 1–7. [Google Scholar] [CrossRef]
- De Vos, A. Reflections on the power delivered by endoreversible engines. J. Phys. D Appl. Phys. 1987, 20, 232–236. [Google Scholar] [CrossRef]
- Gordon, J.M. Observations on Efficiency of Heat Engines Operating at Maximum Power. Am. J. Phys. 1990, 58, 370–375. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Fischer, A.; Schaller, M.; Schubert, S. Optimal Process Paths for Endoreversible Systems. J. Non-Equilib. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Fischer, A.; Hoffmann, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Huleihil, M.; Andresen, B. Optimal piston trajectories for adiabatic processes in the presence of friction. J. Appl. Phys. 2006, 100, 114914. [Google Scholar] [CrossRef]
- Aragón-González, G.; Canales-Palma, A.; León-Galicia, A.; Morales-Gómez, J.R. Maximum Power, Ecological Function and Efficiency of an Irreversible Carnot Cycle. A Cost and Effectiveness Optimization. Braz. J. Phys. 2008, 38, 1–8. [Google Scholar] [CrossRef]
- Kojima, S. Maximum Work of Free-Piston Stirling Engine Generators. J. Non-Equilib. Thermodyn. 2017, 42, 169–186. [Google Scholar] [CrossRef]
- Paéz-Hernández, R.T.; Chimal-Eguía, J.C.; Sánchez-Salas, N.; Ladino-Luna, D. General Properties for an Agrowal Thermal Engine. J. Non-Equilib. Thermodyn. 2018, 43, 131–139. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P. Distillation by Thermodynamic Geometry. In Thermodynamics of Energy Conversion an Transport; Sieniutycz, S., De Vos, A., Eds.; Springer: New York, NY, USA, 2000; chapter 12; pp. 319–331. [Google Scholar]
- Gordon, J.M. Generalized Power Versus Efficiency Characteristics of Heat Engines: The Thermoelectric Generator as an Instructive Illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Wu, C. Maximum Obtainable Specific Cooling Load of a Refrigerator. Energy Convers. Manag. 1995, 36, 7–10. [Google Scholar] [CrossRef]
- Chen, J.; Andresen, B. The Maximum Coefficient of Performance of Thermoelectric Heat Pumps. Int. J. Power Energy Syst. 1996, 17, 22–28. [Google Scholar] [CrossRef]
- Wagner, K.; Hoffmann, K.H. Endoreversible modeling of a PEM fuel cell. J. Non-Equilib. Thermodyn. 2015, 40, 283–294. [Google Scholar] [CrossRef]
- Marsik, F.; Weigand, B.; Thomas, M.; Tucek, O.; Novotny, P. On the Efficiency of Electrochemical Devices from the Perspective of Endoreversible Thermodynamics. J. Non-Equilib. Thermodyn. 2019, 44, 425–437. [Google Scholar] [CrossRef]
- De Vos, A. Is a solar cell an edoreversible engine? Sol. Cells 1991, 31, 181–196. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Optimal Control of an Endoreversible Solar Power Plant. J. Non-Equilib. Thermodyn. 2018, 43, 255–271. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Stochastic Novikov engine with time dependent temperature fluctuations. Appl. Thermal Eng. 2018, 142, 483–488. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Performance Features of a Stationary Stochastic Novikov Engine. Entropy 2018, 20, 52. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Novikov engine with fluctuating heat bath temperature. J. Non-Equilib. Thermodyn. 2018, 43, 141–150. [Google Scholar] [CrossRef]
- Schwalbe, K.; Fischer, A.; Hoffmann, K.H.; Mehnert, J. Applied endoreversible thermodynamics: Optimization of powertrains. In Proceedings of the ECOS 2014—27th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Turku, Finland, 15–19 June 2014; pp. 45–55. [Google Scholar]
- Wagner, K.; Hoffmann, K.H. Chemical reactions in endoreversible thermodynamics. Eur. J. Phys. 2016, 37, 015101. [Google Scholar] [CrossRef]
- Masser, R.; Hoffmann, K.H. Dissipative Endoreversible Engine with Given Efficiency. Entropy 2019, 21, 1117. [Google Scholar] [CrossRef]
- Muschik, W.; Hoffmann, K.H. Endoreversible Thermodynamics: A Tool for Simulating and Comparing Processes of Discrete Systems. J. Non-Equilib. Thermodyn. 2006, 31, 293–317. [Google Scholar] [CrossRef]
- Wagner, K. An Extension to Endoreversible Thermodynamics for Multi-Extensity Fluxes and Chemical Reaction Processes. Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2014. [Google Scholar]
- Essex, C.; Andresen, B. The principal equation of state for classical particles, photons, and neutrinos. J. Non-Equilib. Thermodyn. 2013, 38, 293–312. [Google Scholar] [CrossRef]
- Ho, T.H.; Ahn, K.K. Modeling and simulation of hydrostatic transmission system with energy regeneration using hydraulic accumulator. J. Mech. Sci. Technol. 2010, 24, 1163–1175. [Google Scholar] [CrossRef]
- Stephan, P.; Kabelac, S.; Kind, M.; Mewes, D.; Schaber, K.; Wetzel, T. VDI-Wärmeatlas; Springer: Berlin/Heidelberger, Germany, 2013. [Google Scholar]
- Schweizer, A. Formelsammlung und Berechnungsprogramme Anlagenbau. Available online: https://www.schweizer-fn.de/ (accessed on 18 February 2019).
- Addinol. Sicherheitsdatenblatt ADDINOL Hydrauliköl HLP 46. Available online: http://addinol.oilfinder.net/show_msds.php?id=64764&download=1 (accessed on 18 February 2019).
- Bosch Rexroth AG. Drehzahlvariables Druck- und Förderstrom-Regelsystem Sytronix DFEn 5000. Available online: http://static.mercateo.com/c0/986f0946fb5c4a09a9ec8ea992d97080/pdf/boschrexroth-rd62241.pdf?v=2 (accessed on 18 February 2019).
- Hydac. Proportional-Druckbegrenzungsventil Schieberausführung, vorgesteuert Einschraubventil UNF - 350 bar. Available online: https://www.hydac.com/fileadmin/pdb/pdf/PRO0000000000000000000059913010011.pdf (accessed on 18 February 2019).


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masser, R.; Hoffmann, K.H. Endoreversible Modeling of a Hydraulic Recuperation System. Entropy 2020, 22, 383. https://doi.org/10.3390/e22040383
Masser R, Hoffmann KH. Endoreversible Modeling of a Hydraulic Recuperation System. Entropy. 2020; 22(4):383. https://doi.org/10.3390/e22040383
Chicago/Turabian StyleMasser, Robin, and Karl Heinz Hoffmann. 2020. "Endoreversible Modeling of a Hydraulic Recuperation System" Entropy 22, no. 4: 383. https://doi.org/10.3390/e22040383
APA StyleMasser, R., & Hoffmann, K. H. (2020). Endoreversible Modeling of a Hydraulic Recuperation System. Entropy, 22(4), 383. https://doi.org/10.3390/e22040383



