What Is Temperature? Modern Outlook on the Concept of Temperature
Abstract
1. Introduction
2. Results and Discussion
2.1. Temperature as an Average of the Kinetic Energy and the Metrics of Configurational Space
2.2. Temperature, Energy, and Entropy: An Alternative Glance on the Temperature
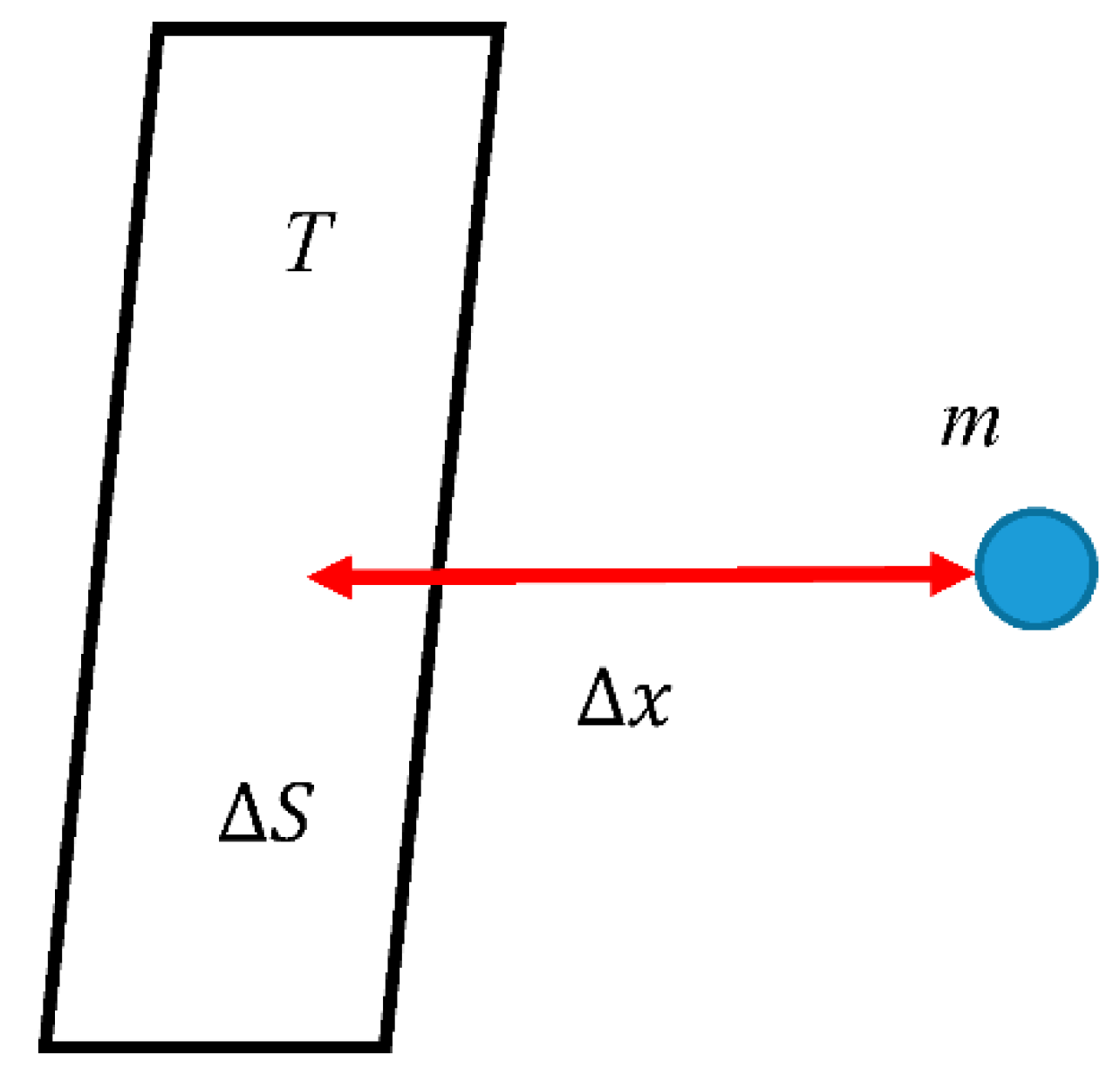
2.3. Entropy Forces and Fundamental Role of Temperature
2.4. The Landauer Principle and Informational Interpretation of the Temperature
2.5. Fundamental Role of the Cosmic Background Temperature
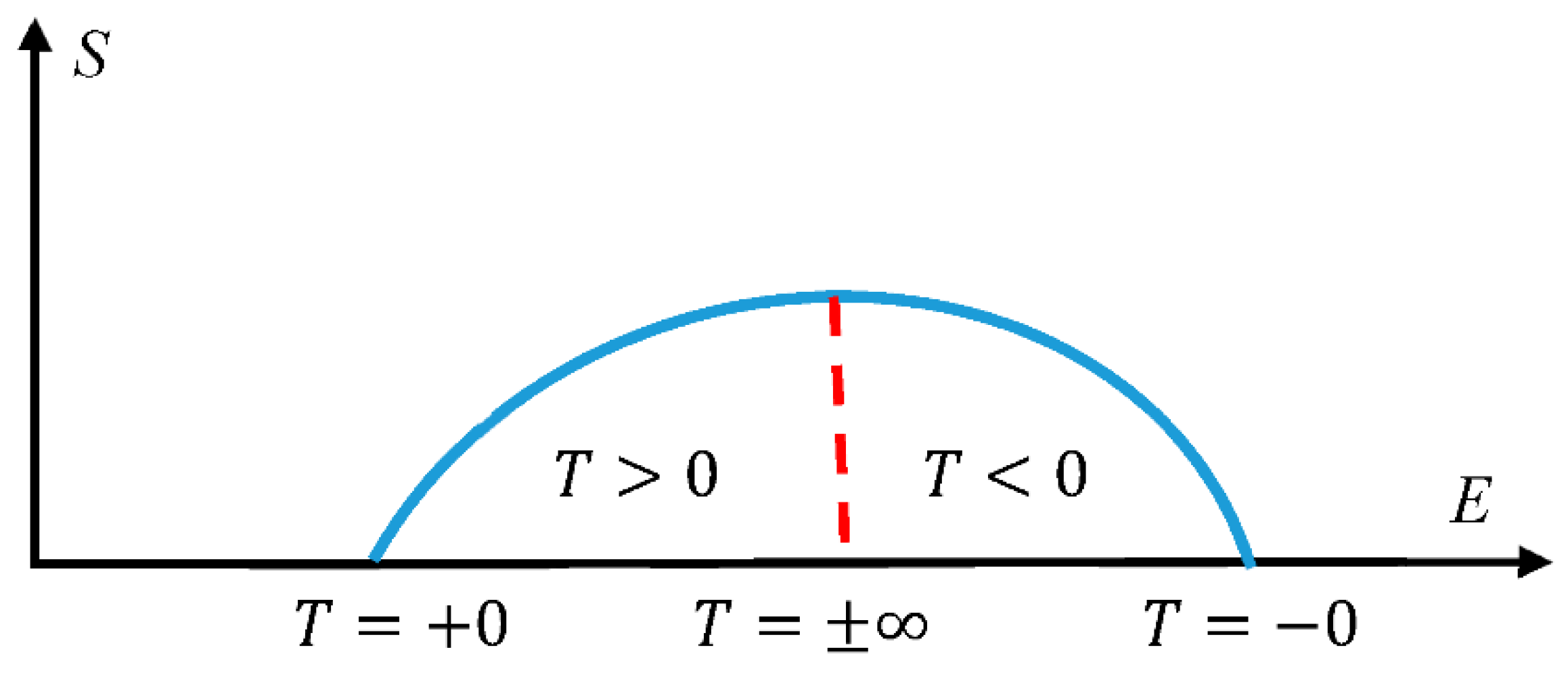
2.6. Boltzmann and Gibbs Temperatures: Is a Negative Absolute Temperature Possible?
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Carus, T.L. De Rerum Natura; Rizzoli: Milano, Italy, 1976. [Google Scholar]
- Chang, H. Inventing Temperature. Measurement and Scientific Progress; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Schroeder, D.V. Thermal Physics; Addison Wesley Longman: San Francisco, CA, USA, 2000. [Google Scholar]
- Cropper, W.H. Carnot’s function: Origins of the thermodynamic concept of temperature. Am. J. Phys. 1987, 55, 120. [Google Scholar] [CrossRef]
- Erlichson, H. Kelvin and the absolute temperature scale. Eur. J. Phys. 2001, 22, 325–328. [Google Scholar]
- Sivukhin, D. General Physics Course; Fizmatlit: Moscow, Russia, 2005; Volume 2. (In Russian) [Google Scholar]
- Bormashenko, E.; Shkorbatov, A.; Gendelman, O. The Carnot engine based on the small thermodynamic system: Its efficiency and the ergodic hypothesis. Am. J. Phys. 2007, 75, 911–915. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Quantum mechanical Carnot engine. J. Phys. A Math. Gen. 2000, 33, 4427–4436. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity, Thermodynamics and Cosmology; Oxford University Press: Oxford, UK, 1934. [Google Scholar]
- Ott, H. Lorentz-Transformation der Wärme und der Temperatur. Z. Phys. 1963, 175, 70–104. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Matsas, G.E.A. Laying the ghost of the relativistic temperature transformation. Phys. Lett. A 1996, 223, 401–403. [Google Scholar] [CrossRef]
- Landsberg, P.; Matsas, G.E.A. The impossibility of a universal relativistic temperature transformation. Phys. A Stat. Mech. Appl. 2004, 340, 92–94. [Google Scholar] [CrossRef]
- Bormashenko, E. Entropy of Relativistic Mono-Atomic Gas and Temperature Relativistic Transformation in Thermodynamics. Entropy 2007, 9, 113–117. [Google Scholar] [CrossRef]
- Reif, F. Statistical Physics, Berkley Physics Course, V. 5; McGraw Hill: New York, NY, USA, 1967. [Google Scholar]
- Lanczos, C. The Variational Principles of Mechanics; University of Toronto Press: Toronto, ON, Canada, 1962. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Course of Theoretical Physics; Elsevier: Oxford, UK, 2011; Volume 5. [Google Scholar]
- Walters, P. An Introduction to Ergodic Theory; Springer: Berlin, Germany, 1982. [Google Scholar]
- Kittel, C.H. Thermal Physics; John and Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Baierlein, R. Thermal Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bormashenko, E. Entropy, Information, and Symmetry; Ordered Is Symmetrical, II: System of Spins in the Magnetic Field. Entropy 2020, 22, 235. [Google Scholar] [CrossRef]
- Riek, R. A Derivation of a Microscopic Entropy and Time Irreversibility from the Discreteness of Time. Entropy 2014, 16, 3149–3172. [Google Scholar] [CrossRef]
- Riek, R. Entropy is a consequence of a discrete time. J. Phys. Conf. Ser. 2015, 626, 12025. [Google Scholar] [CrossRef]
- Pohl, R.W. Mechanik, Akustik and Wärmelehre; Springer: Berlin, Germany, 2013. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Verlinde, E.P. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 2011, 1–27. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Landauer, R. Information is Physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Landauer, R. Minimal Energy Requirements in Communication. Science 1996, 272, 1914–1918. [Google Scholar] [CrossRef] [PubMed]
- Norton, J.D. Eaters of the lotus: Landauer’s principle and the return of Maxwell’s demon. Stud. Hist. Philos. Sci. B 2005, 36, 375–411. [Google Scholar] [CrossRef]
- Norton, J.D. Waiting for Landauer. Stud. Hist. Philos. Sci. Part B 2011, 42, 184–198. [Google Scholar] [CrossRef]
- Herrera, L. The Mass of A Bit of Information and The Brillouin’s Principle. Fluct. Noise Lett. 2014, 13, 1450002. [Google Scholar] [CrossRef]
- Herrera, L. The Gibbs Paradox, the Landauer Principle and the Irreversibility Associated with Tilted Observers. Entropy 2017, 19, 110. [Google Scholar] [CrossRef]
- Herrera, L. Landauer Principle and General Relativity. Entropy 2020, 22, 340. [Google Scholar] [CrossRef]
- Vopson, M.M. The mass-energy-information equivalence principle. AIP Adv. 2019, 9, 95206. [Google Scholar] [CrossRef]
- Müller, J.G. Information Contained in Molecular Motion. Entropy 2019, 21, 1052. [Google Scholar] [CrossRef]
- Müller, J.G. Photon Detection as a Process of Information Gain. Entropy 2020, 22, 392. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Information Erasure. Phys. Rev. Lett. 2009, 102, 250602. [Google Scholar] [CrossRef] [PubMed]
- Parrondo, J.M.R.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Aydin, A.; Sisman, A.; Kosloff, R. Landauer’s Principle in a quantum Szilard engine without Maxwell’s Demon. Entropy 2020, 22, 294. [Google Scholar] [CrossRef]
- Wheeler, J.A. Information, physics, quantum: The search for links. In Proceedings of the III International Symposium on Foundations of Quantum Mechanics, Tokyo, Japan, 28–31 August 1989. [Google Scholar]
- Knuth, K.H. Information-Based Physics and the Influence Network. In It from Bit or Bit from It? The Frontiers Collection; Aguirre, A., Foster, B., Merali, Z., Eds.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Knuth, K.H.; Walsh, J.L. An Introduction to Influence Theory: Kinematics and Dynamics. Ann. Phys. 2018, 531, 1800091. [Google Scholar] [CrossRef]
- Caticha, A. Entropic Dynamics. Entropy 2015, 17, 6110–6128. [Google Scholar] [CrossRef]
- Bormashenko, E. Informational Reinterpretation of the Mechanics Notions and Laws. Entropy 2020, 22, 631. [Google Scholar] [CrossRef]
- Szilard, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z. Phys. 1929, 53, 840–856. (In German) [Google Scholar] [CrossRef]
- Bormashenko, E. The Landauer Principle: Re-Formulation of the Second Thermodynamics Law or a Step to Great Unification? Entropy 2019, 21, 918. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Hooft, H. Holographic Principle. In The Subnuclear Series, Basics and Highlights in Fundamental Physics; Zichichi, A., Ed.; World Scientific: Singapore, 2001; Volume 37, pp. 72–100. [Google Scholar]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Ćirković, M.M.; Perović, S. Alternative explanations of the cosmic microwave background: A historical and an epistemological perspective. Stud. Hist. Philos. Sci. Part B 2018, 62, 1–18. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Page, L.A., Jr.; Partridge, R.B. Finding the Big Bang; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Copi, C.; Schramm, D.; Turner, M. Big-bang nucleosynthesis and the baryon density of the universe. Science 1995, 267, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Schramm, D.N.; Turner, M.S. Big-bang nucleosynthesis enters the precision era. Rev. Mod. Phys. 1998, 70, 303–318. [Google Scholar] [CrossRef]
- Purcell, E.M.; Pound, R.V. A Nuclear Spin System at Negative Temperature. Phys. Rev. 1951, 81, 279–280. [Google Scholar] [CrossRef]
- Dunkel, J.; Hilbert, S. Consistent thermostatistics forbids negative absolute temperatures. Nat. Phys. 2013, 10, 67–72. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E. What Is Temperature? Modern Outlook on the Concept of Temperature. Entropy 2020, 22, 1366. https://doi.org/10.3390/e22121366
Bormashenko E. What Is Temperature? Modern Outlook on the Concept of Temperature. Entropy. 2020; 22(12):1366. https://doi.org/10.3390/e22121366
Chicago/Turabian StyleBormashenko, Edward. 2020. "What Is Temperature? Modern Outlook on the Concept of Temperature" Entropy 22, no. 12: 1366. https://doi.org/10.3390/e22121366
APA StyleBormashenko, E. (2020). What Is Temperature? Modern Outlook on the Concept of Temperature. Entropy, 22(12), 1366. https://doi.org/10.3390/e22121366