Thermodynamics of a Phase-Driven Proximity Josephson Junction
Abstract
1. Introduction
2. Thermodynamics of Hybrid Systems
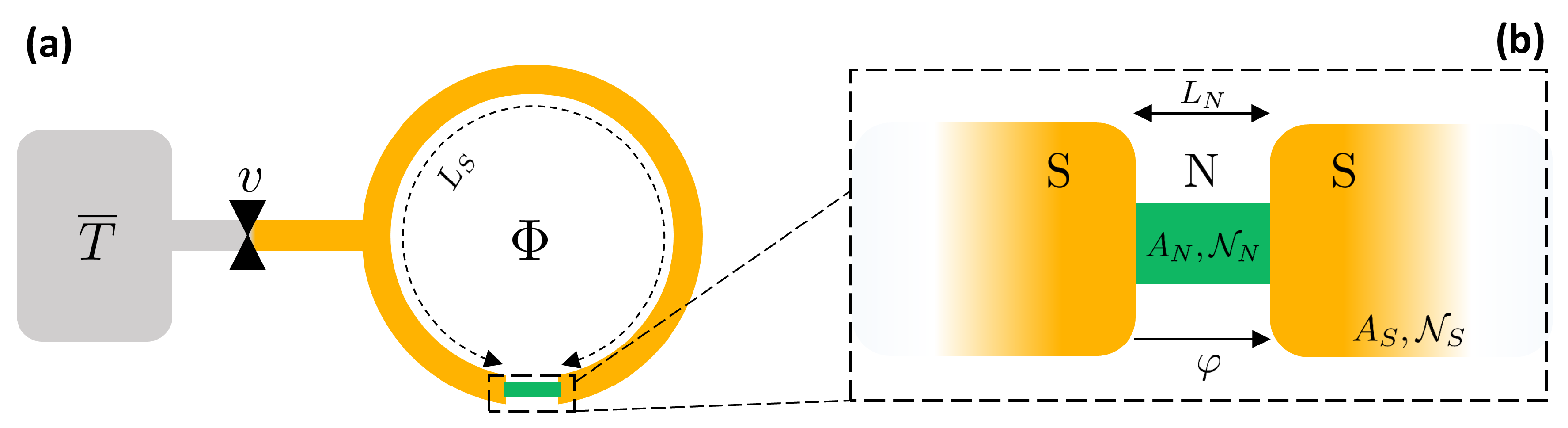
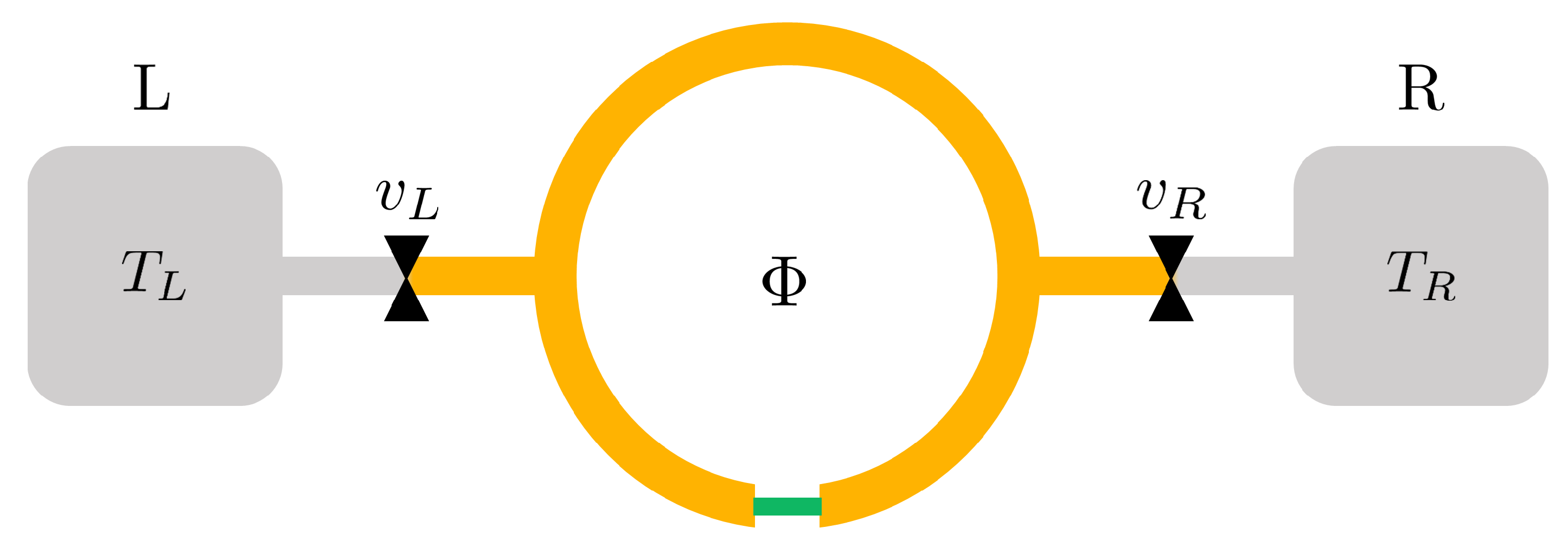
2.1. Model
2.2. Hybrid Junction as Thermodynamic System
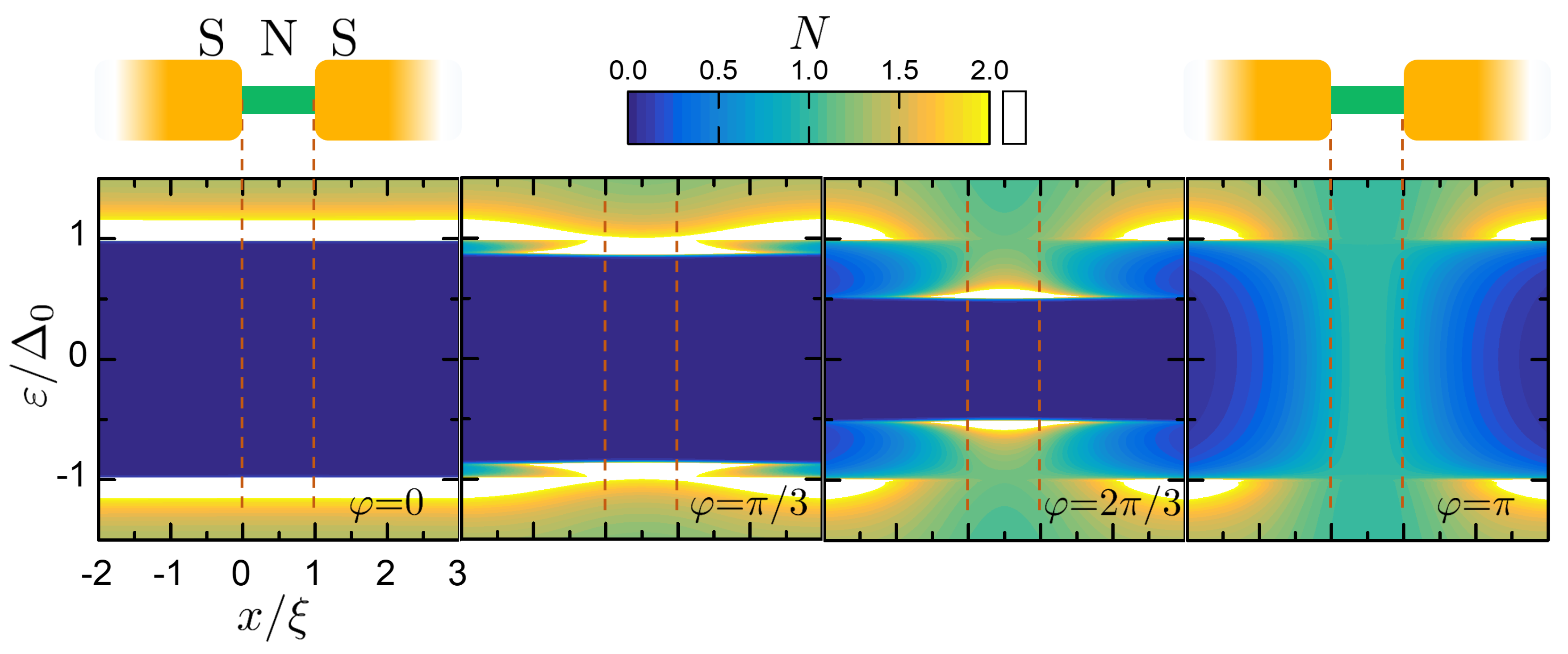
2.3. Proximity Induced Minigap
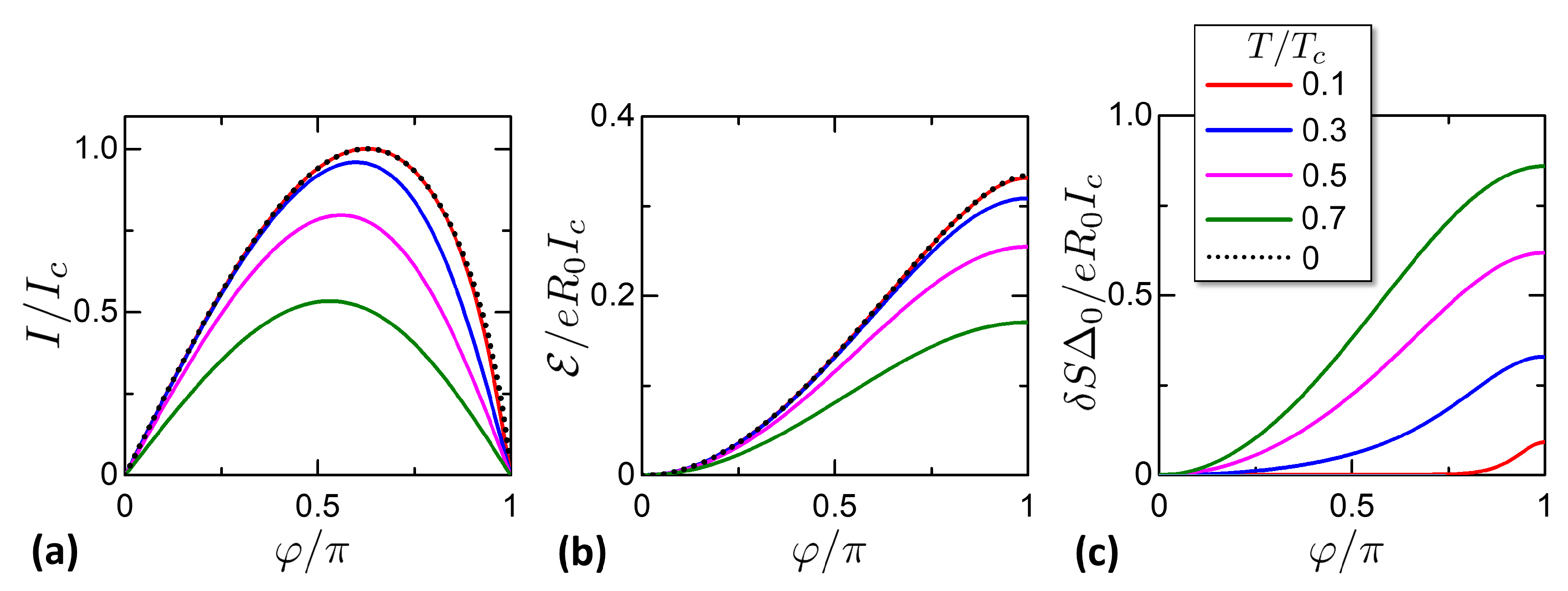
2.4. Kulik-Omel’yanchuk Theory
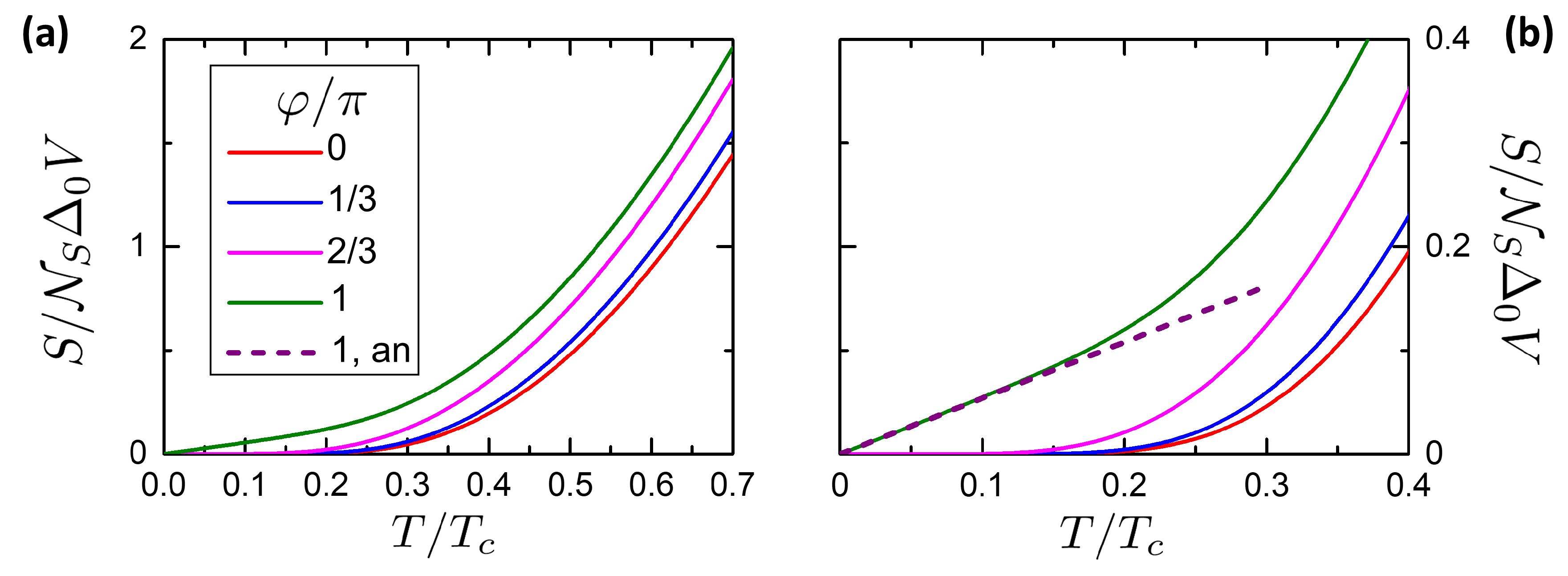
2.5. Total Entropy
3. Thermodynamic Processes
3.1. Isothermal Process
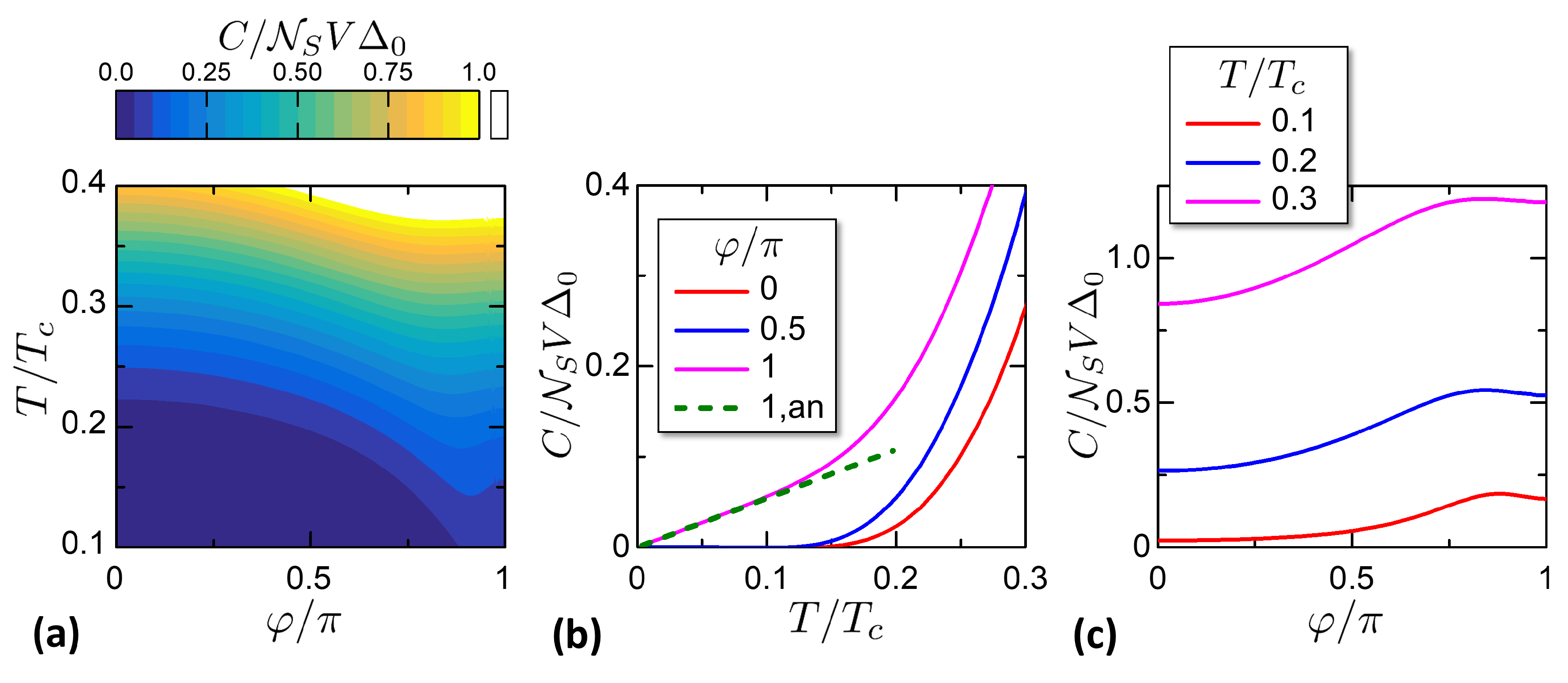
3.2. Isophasic Process and Heat Capacity
3.3. Isentropic Process
4. Thermodynamic Cycles
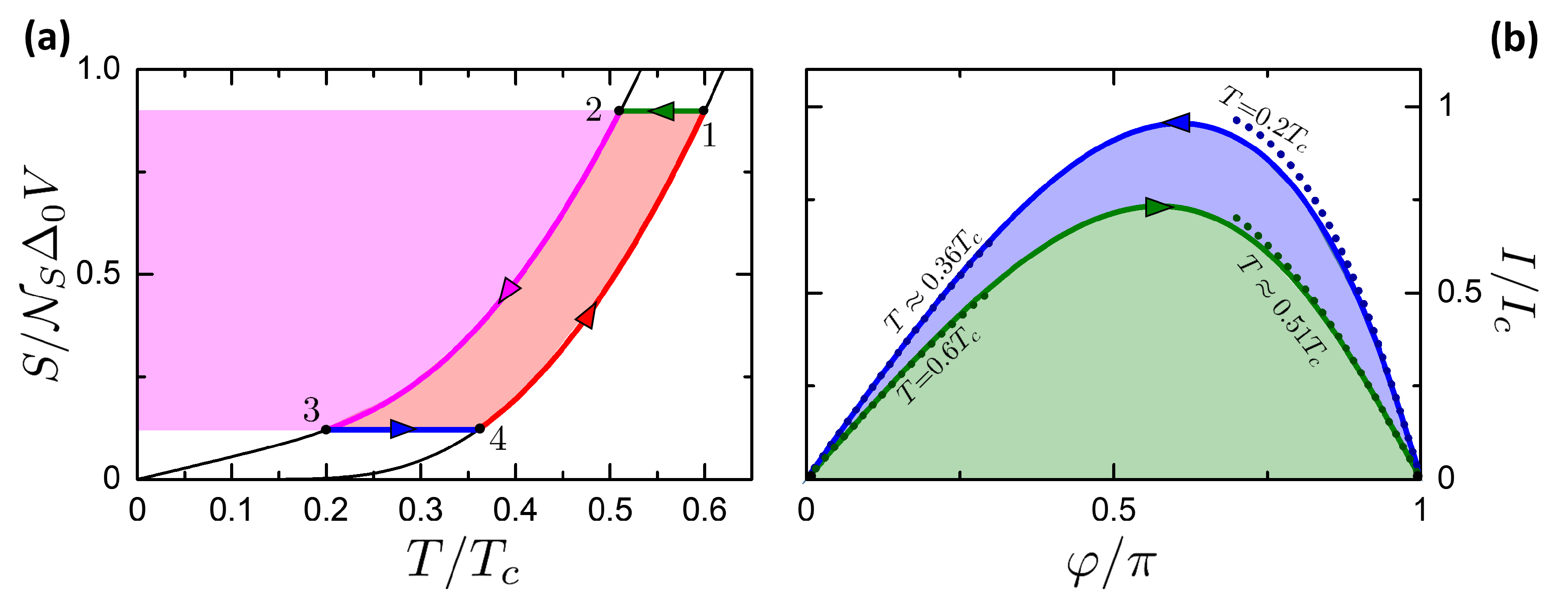
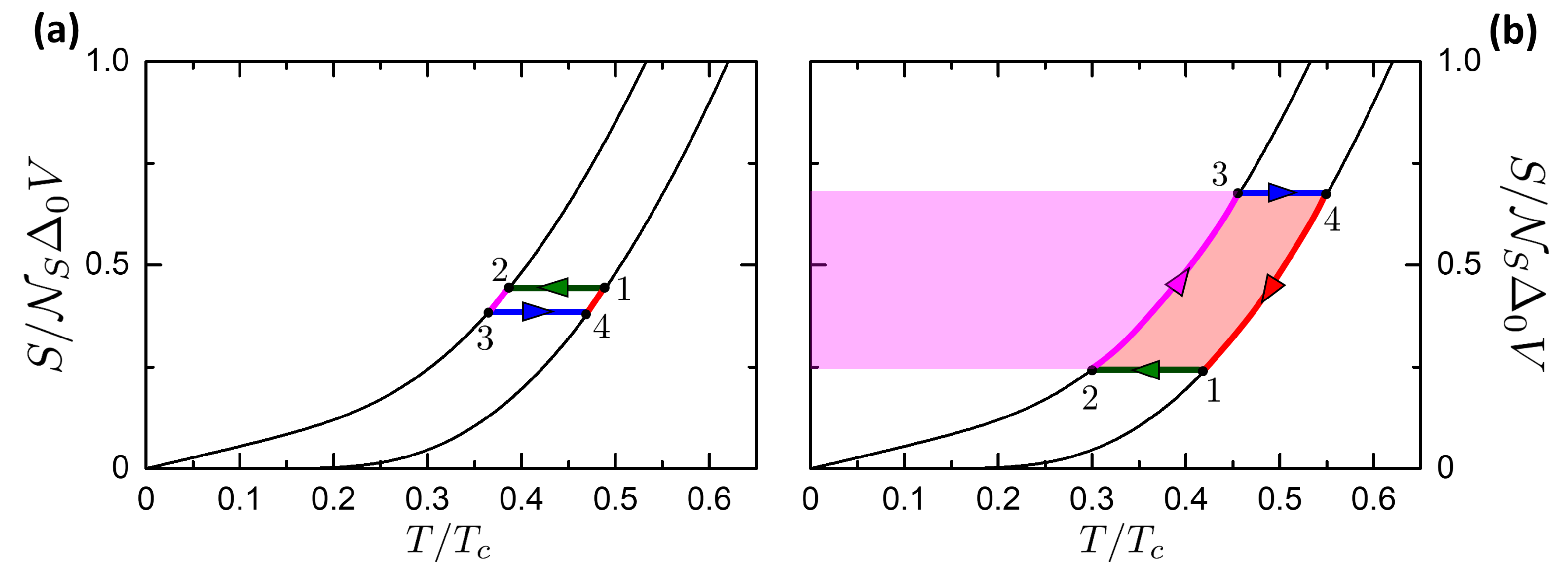
4.1. Josephson-Otto Cycle
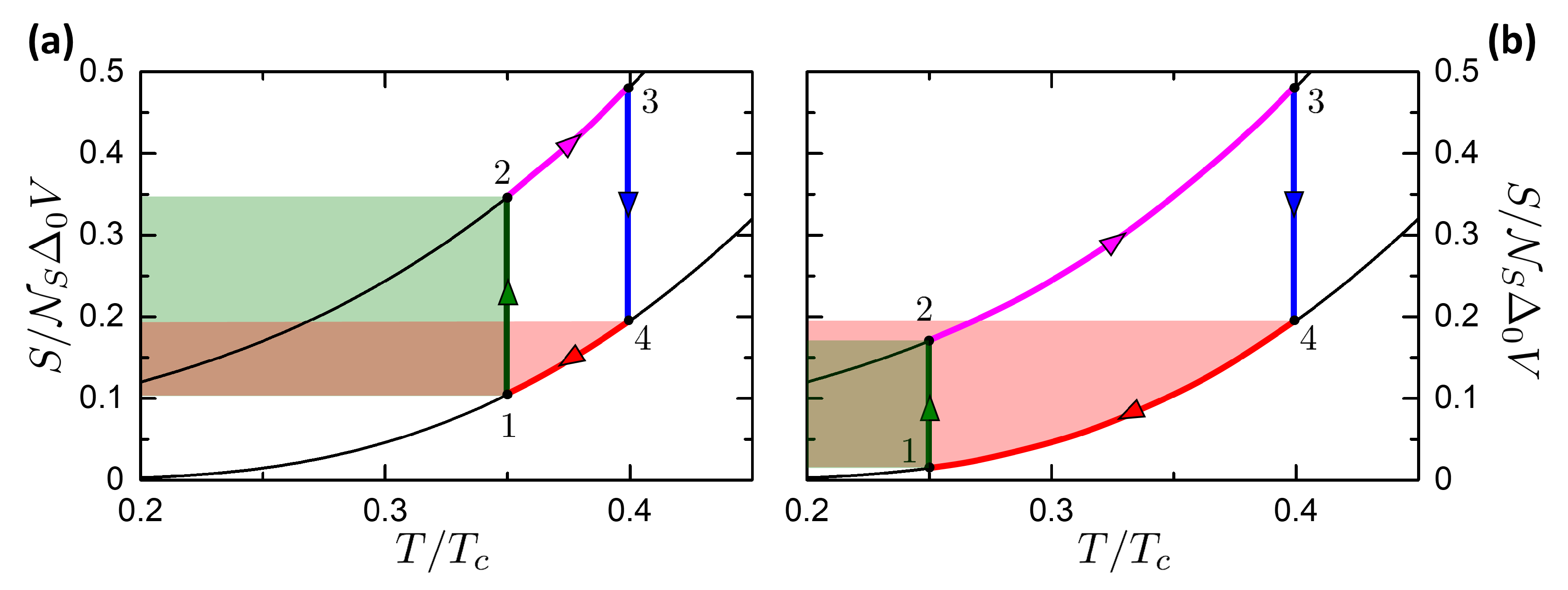
- Isophasic . By opening the thermal valve , the system goes from the state to . The system releases heat to the left reservoir (magenta area in Figure 8a). No work is performed, .
- Isentropic . All thermal valves are again closed to make the system thermally isolated. The system is driven from the state to . By construction, if then it is . In this process the system returns a work ( according to our convention), represented by the sum of the green and blue areas in Figure 8b. No heat is exchanged, .
- Isophasic . By opening the thermal valve , the system goes from the state to . The system absorbs heat from the reservoir at (magenta+pink area in Figure 8a). No work is performed, .
- Isentropic . All thermal valves are closed to make the system thermally isolated. The system is driven from the state at the ambient temperature to , where . In this process, the universe spends a work ( for of Section 3). No heat is exchanged, .
- Isophasic . By opening the thermal valve , the system goes from the state to , removing the heat from the CS (magenta area in Figure 9b). No work is performed, .
- Isentropic . All thermal valves are closed. The system is driven from the state to . Now, . In this process, the system returns a work . No heat is exchanged, .
- Isophasic . By opening the thermal valve , the system goes from the state to . The system releases heat to the reservoir at , since , which correspond to the magenta+pink area in Figure 9b. The temperature plays an analogous role of the hot heat exchanger that is present in the refrigerators. No work is performed, .
4.2. Josephson-Stirling Cycle
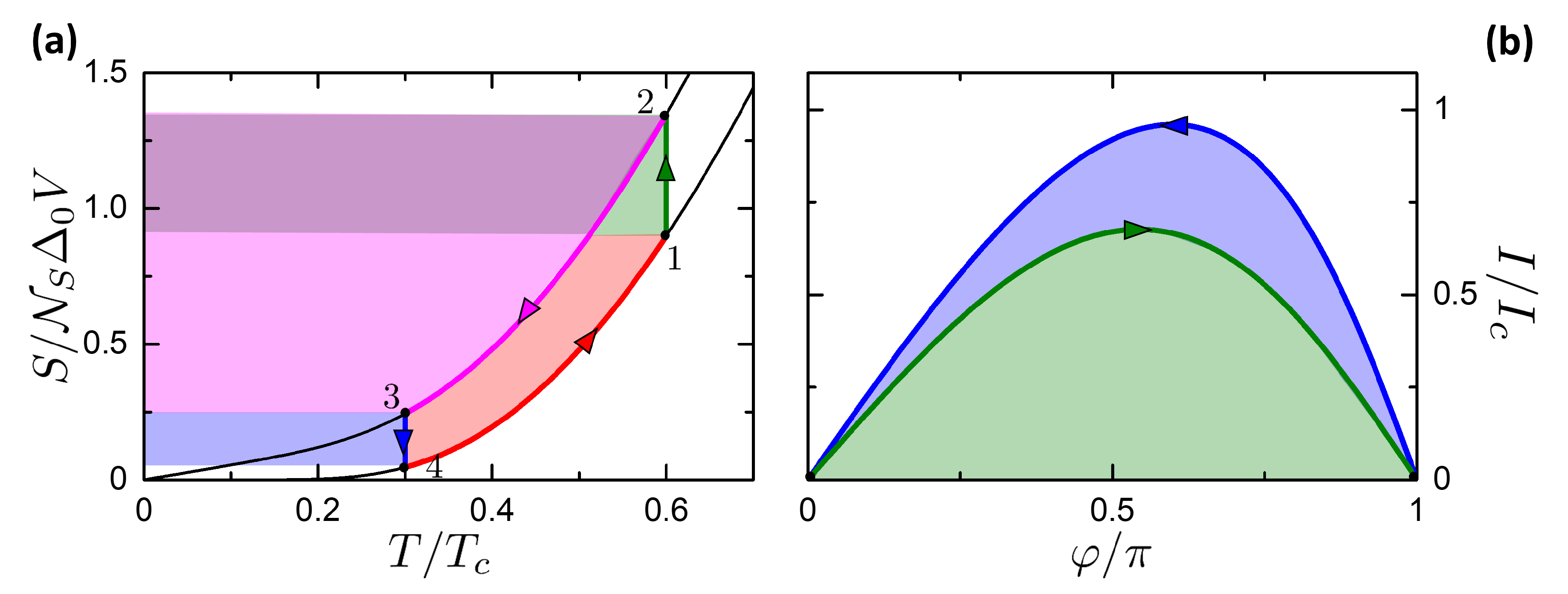
- Isothermal . The thermal valves is open and is closed, so that the system is in thermal contact with the right reservoir. The system is driven from the state to . Here a work is spent represented by the green area in Figure 12b. The heat is absorbed from the reservoir, represented by the green + dark purple area in Figure 12a.
- Isophasic . By closing and opening , the system goes from the state to . The system releases heat to the left reservoir, represented by the light purple + dark purple area. No work is performed, .
- Isothermal . The valves are kept in the same state: open and closed. The system is driven from the state to . In this process the system returns a work represented by the sum of the green and blue areas in Figure 12b. The heat is released to the left reservoir, represented by the blue area in Figure 12a.
- Isophasic . By closing and opening , the system goes from the state to . The system absorbs the heat from the reservoir at , given by the sum of the areas in blue, red and light purple in Figure 12a. No work is performed, .
5. Experimental Feasibility
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
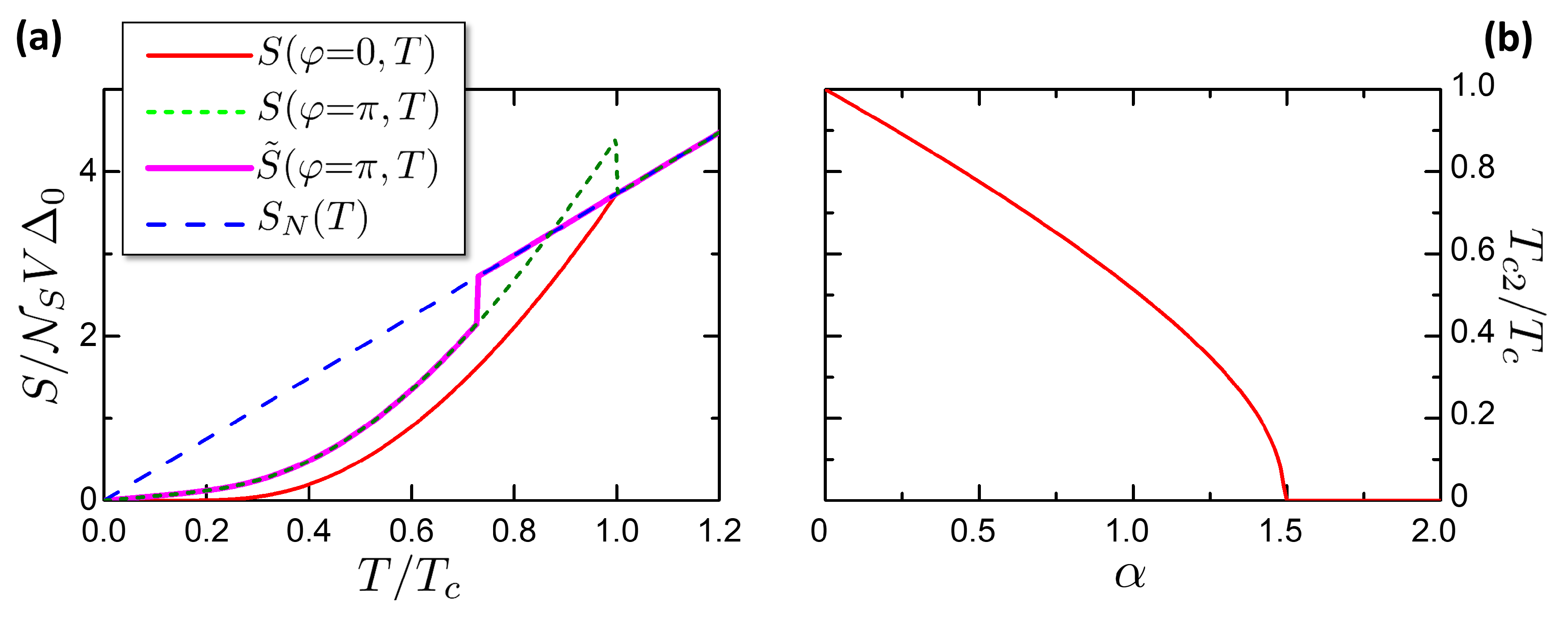
Appendix A. Thermodynamics Close to the Critical Temperature
References
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Pekola, J.P. The role of quantum information in thermodynamics—A topical review. Nat. Phys. 2015, 11, 118. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1274. [Google Scholar] [CrossRef]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Guiducci, S.; Carrega, M.; Biasiol, G.; Sorba, L.; Beltram, F.; Heun, S. Toward Quantum Hall Effect in a Josephson Junction. Phys. Status Solidi (RRL) Rapid Res. Lett. 2019, 13, 1800222. [Google Scholar] [CrossRef]
- Guiducci, S.; Carrega, M.; Taddei, F.; Biasiol, G.; Courtois, H.; Beltram, F.; Heun, S. Full electrostatic control of quantum interference in an extended trenched Josephson junction. Phys. Rev. B 2019, 99, 235419. [Google Scholar] [CrossRef]
- Giazotto, F.; Taddei, F.; Governale, M.; Castellana, C.; Fazio, R.; Beltram, F. Cooling Electrons by Magnetic-Field Tuning of Andreev Reflection. Phys. Rev. Lett. 2006, 97, 197001. [Google Scholar] [CrossRef]
- Fornieri, A.; Giazotto, F. Towards phase-coherent caloritronics in superconducting circuits. Nat. Nanotechnol. 2017, 12, 944–952. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, R. SU(2) Yang–Mills Theory: Waves, Particles, and Quantum Thermodynamics. Entropy 2016, 18, 310. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Wang, L.B.; Saira, O.P.; Pekola, J.P. Fast thermometry with a proximity Josephson junction. Appl. Phys. Lett. 2018, 112, 013105. [Google Scholar] [CrossRef]
- Zgirski, M.; Foltyn, M.; Savin, A.; Norowski, K.; Meschke, M.; Pekola, J. Nanosecond Thermometry with Josephson Junctions. Phys. Rev. Appl. 2018, 10, 044068. [Google Scholar] [CrossRef]
- Gasparinetti, S.; Viisanen, K.L.; Saira, O.P.; Faivre, T.; Arzeo, M.; Meschke, M.; Pekola, J.P. Fast Electron Thermometry for Ultrasensitive Calorimetric Detection. Phys. Rev. Appl. 2015, 3, 014007. [Google Scholar] [CrossRef]
- Giazotto, F.; Heikkilä, T.T.; Luukanen, A.; Savin, A.M.; Pekola, J.P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 2006, 78, 217–274. [Google Scholar] [CrossRef]
- Giazotto, F.; Solinas, P.; Braggio, A.; Bergeret, F.S. Ferromagnetic-Insulator-Based Superconducting Junctions as Sensitive Electron Thermometers. Phys. Rev. Appl. 2015, 4, 044016. [Google Scholar] [CrossRef]
- Govenius, J.; Lake, R.E.; Tan, K.Y.; Möttönen, M. Detection of Zeptojoule Microwave Pulses Using Electrothermal Feedback in Proximity-Induced Josephson Junctions. Phys. Rev. Lett. 2016, 117, 030802. [Google Scholar] [CrossRef]
- Lee, G.H.; Efetov, D.K.; Ranzani, L.; Walsh, E.D.; Ohki, T.A.; Taniguchi, T.; Watanabe, K.; Kim, P.; Englund, D.; Chung Fong, K. Graphene-based Josephson junction microwave bolometer. arXiv 2019, arXiv:1909.05413. [Google Scholar]
- Giazotto, F.; Heikkilä, T.T.; Pepe, G.P.; Helistö, P.; Luukanen, A.; Pekola, J.P. Ultrasensitive proximity Josephson sensor with kinetic inductance readout. Appl. Phys. Lett. 2008, 92, 162507. [Google Scholar] [CrossRef]
- Guarcello, C.; Braggio, A.; Solinas, P.; Pepe, G.P.; Giazotto, F. Josephson-Threshold Calorimeter. Phys. Rev. Appl. 2019, 11, 054074. [Google Scholar] [CrossRef]
- Vischi, F.; Carrega, M.; Braggio, A.; Paolucci, F.; Bianco, F.; Roddaro, S.; Giazotto, F. Electron cooling with graphene-insulator-superconductor tunnel junctions and applications to fast bolometry. arXiv 2019, arXiv:1906.10988. [Google Scholar]
- Solinas, P.; Giazotto, F.; Pepe, G.P. Proximity SQUID Single-Photon Detector via Temperature-to-Voltage Conversion. Phys. Rev. Appl. 2018, 10, 024015. [Google Scholar] [CrossRef]
- Virtanen, P.; Ronzani, A.; Giazotto, F. Josephson Photodetectors via Temperature-to-Phase Conversion. Phys. Rev. Appl. 2018, 9, 054027. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Mueller, T.; Avouris, P.; Ferrari, A.C.; Vitiello, M.S.; Polini, M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780–793. [Google Scholar] [CrossRef]
- Mitrofanov, O.; Viti, L.; Dardanis, E.; Giordano, M.C.; Ercolani, D.; Politano, A.; Sorba, L.; Vitiello, M.S. Near-field terahertz probes with room-temperature nanodetectors for subwavelength resolution imaging. Sci. Rep. 2017, 7, 44240. [Google Scholar] [CrossRef]
- Giordano, M.C.; Viti, L.; Mitrofanov, O.; Vitiello, M.S. Phase-sensitive terahertz imaging using room-temperature near-field nanodetectors. Optica 2018, 5, 651–657. [Google Scholar] [CrossRef]
- McKitterick, C.B.; Prober, D.E.; Vora, H.; Du, X. Ultrasensitive graphene far-infrared power detectors. J. Phys. Condens. Matter 2015, 27, 164203. [Google Scholar] [CrossRef]
- McKitterick, C.B.; Prober, D.E.; Rooks, M.J. Electron-phonon cooling in large monolayer graphene devices. Phys. Rev. B 2016, 93, 075410. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrea, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Sothmann, B.; Giazotto, F.; Hankiewicz, E.M. High-efficiency thermal switch based on topological Josephson junctions. New J. Phys. 2017, 19, 023056. [Google Scholar] [CrossRef]
- Yang, J.; Elouard, C.; Splettstoesser, J.; Sothmann, B.; Sánchez, R.; Jordan, A.N. Thermal transistor and thermometer based on Coulomb-coupled conductors. Phys. Rev. B 2019, 100, 045418. [Google Scholar] [CrossRef]
- Goffman, M.F.; Urbina, C.; Pothier, H.; Nygard, J.; Marcus, C.M.; Krogstrup, P. Conduction channels of an InAs-Al nanowire Josephson weak link. New J. Phys. 2017, 19, 092002. [Google Scholar] [CrossRef]
- Dutta, B.; Peltonen, J.T.; Antonenko, D.S.; Meschke, M.; Skvortsov, M.A.; Kubala, B.; König, J.; Winkelmann, C.B.; Courtois, H.; Pekola, J.P. Thermal Conductance of a Single-Electron Transistor. Phys. Rev. Lett. 2017, 119, 077701. [Google Scholar] [CrossRef]
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef]
- Ronzani, A.; Karimi, B.; Senior, J.; Chang, Y.C.; Peltonen, J.T.; Chen, C.; Pekola, J.P. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 2018, 14, 991–995. [Google Scholar] [CrossRef]
- Sivre, E.; Anthore, A.; Parmentier, F.D.; Cavanna, A.; Gennser, U.; Ouerghi, A.; Jin, Y.; Pierre, F. Heat Coulomb blockade of one ballistic channel. Nat. Phys. 2017, 14, 145–148. [Google Scholar] [CrossRef]
- Strambini, E.; Bergeret, F.S.; Giazotto, F. Proximity nanovalve with large phase-tunable thermal conductance. Appl. Phys. Lett. 2014, 105, 082601. [Google Scholar] [CrossRef]
- Giazotto, F.; Martínez-Pérez, M.J. The Josephson heat interferometer. Nature 2012, 492, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Bours, L.; Sothmann, B.; Carrega, M.; Strambini, E.; Braggio, A.; Hankiewicz, E.M.; Molenkamp, L.W.; Giazotto, F. Phase-Tunable Thermal Rectification in the Topological SQUIPT. Phys. Rev. Appl. 2019, 11, 044073. [Google Scholar] [CrossRef]
- Wang, L.; Li, B. Thermal Logic Gates: Computation with Phonons. Phys. Rev. Lett. 2007, 99, 177208. [Google Scholar] [CrossRef]
- Paolucci, F.; Marchegiani, G.; Strambini, E.; Giazotto, F. Phase-Tunable Thermal Logic: Computation with Heat. Phys. Rev. Appl. 2018, 10, 024003. [Google Scholar] [CrossRef]
- Hwang, S.Y.; Sothmann, B. Phase-coherent caloritronics with ordinary and topological Josephson junctions. arXiv 2019, arXiv:1905.09262. [Google Scholar]
- Bauer, A.G.; Sothmann, B. Phase-dependent heat transport in Josephson junctions with p-wave superconductors and superfluids. Phys. Rev. B 2019, 99, 214508. [Google Scholar] [CrossRef]
- Timossi, G.F.; Fornieri, A.; Paolucci, F.; Puglia, C.; Giazotto, F. Phase-Tunable Josephson Thermal Router. Nano Lett. 2018, 18, 1764–1769. [Google Scholar] [CrossRef]
- Muhonen, J.T.; Meschke, M.; Pekola, J.P. Micrometre-scale refrigerators. Rep. Prog. Phys. 2012, 75, 046501. [Google Scholar] [CrossRef]
- Leivo, M.M.; Pekola, J.P.; Averin, D.V. Efficient Peltier refrigeration by a pair of normal metal/insulator/superconductor junctions. Appl. Phys. Lett. 1996, 68, 1996–1998. [Google Scholar] [CrossRef]
- Courtois, H.; Nguyen, H.Q.; Winkelmann, C.B.; Pekola, J.P. High-performance electronic cooling with superconducting tunnel junctions. C. R. Phys. 2016, 17, 1139–1145. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Peltonen, J.T.; Meschke, M.; Pekola, J.P. Cascade Electronic Refrigerator Using Superconducting Tunnel Junctions. Phys. Rev. Appl. 2016, 6, 054011. [Google Scholar] [CrossRef]
- Solinas, P.; Bosisio, R.; Giazotto, F. Microwave quantum refrigeration based on the Josephson effect. Phys. Rev. B 2016, 93, 224521. [Google Scholar] [CrossRef]
- Koppinen, P.J.; Maasilta, I.J. Phonon Cooling of Nanomechanical Beams with Tunnel Junctions. Phys. Rev. Lett. 2009, 102, 165502. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, D.; Sánchez, R.; López, R.; Sothmann, B. Nonlinear chiral refrigerators. Phys. Rev. B 2019, 99, 245304. [Google Scholar] [CrossRef]
- Karimi, B.; Pekola, J.P. Otto refrigerator based on a superconducting qubit: Classical and quantum performance. Phys. Rev. B 2016, 94, 184503. [Google Scholar] [CrossRef]
- Marchegiani, G.; Virtanen, P.; Giazotto, F.; Campisi, M. Self-Oscillating Josephson Quantum Heat Engine. Phys. Rev. Appl. 2016, 6, 054014. [Google Scholar] [CrossRef]
- Vischi, F.; Carrega, M.; Virtanen, P.; Strambini, E.; Braggio, A.; Giazotto, F. Thermodynamic cycles in Josephson junctions. Sci. Rep. 2019, 9, 3238. [Google Scholar] [CrossRef]
- Haack, G.; Giazotto, F. Efficient and tunable Aharonov-Bohm quantum heat engine. arXiv 2019, arXiv:1905.12672. [Google Scholar]
- Manikandan, S.K.; Giazotto, F.; Jordan, A.N. Superconducting Quantum Refrigerator: Breaking and Rejoining Cooper Pairs with Magnetic Field Cycles. Phys. Rev. Appl. 2019, 11, 054034. [Google Scholar] [CrossRef]
- Carrega, M.; Sassetti, M.; Weiss, U. Optimal work-to-work conversion of a nonlinear quantum Brownian duet. Phys. Rev. A 2019, 99, 062111. [Google Scholar] [CrossRef]
- Benenti, G.; Casati, G.; Saito, K.; Whitney, R. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 2017, 694, 1–124. [Google Scholar] [CrossRef]
- Heikkilä, T.T.; Silaev, M.; Virtanen, P.; Bergeret, F.S. Thermal, electric and spin transport in superconductor/ferromagnetic-insulator structures. Prog. Surf. Sci. 2019, 94, 100540. [Google Scholar] [CrossRef]
- Marchegiani, G.; Virtanen, P.; Giazotto, F. On-chip cooling by heating with superconducting tunnel junctions. EPL (Europhys. Lett.) 2018, 124, 48005. [Google Scholar] [CrossRef]
- Sánchez, D.; López, R. Nonlinear phenomena in quantum thermoelectrics and heat. C. R. Phys. 2016, 17, 1060–1071. [Google Scholar] [CrossRef]
- Hussein, R.; Governale, M.; Kohler, S.; Belzig, W.; Giazotto, F.; Braggio, A. Nonlocal thermoelectricity in a Cooper-pair splitter. Phys. Rev. B 2019, 99, 075429. [Google Scholar] [CrossRef]
- Marchegiani, G.; Braggio, A.; Giazotto, F. Nonlinear thermoelectricity with particle-hole symmetry in transport. arXiv 2019, arXiv:1909.04590. [Google Scholar]
- Pannetier, B.; Courtois, H. Andreev Reflection and Proximity effect. J. Low Temp. Phys. 2000, 118, 599–615. [Google Scholar] [CrossRef]
- Courtois, H.; Charlat, P.; Gandit, P.; Mailly, D.; Pannetier, B. The Spectral Conductance of a Proximity Superconductor and the Reentrance Effect. J. Low Temp. Phys. 1999, 116, 187–213. [Google Scholar] [CrossRef]
- Likharev, K.K. Superconducting weak links. Rev. Mod. Phys. 1979, 51, 101–159. [Google Scholar] [CrossRef]
- de Bruyn Ouboter, R. On the thermodynamics of a superconducting ring interrupted by a weak superconducting junction. Phys. B Condens. Matter 1988, 154, 42–55. [Google Scholar] [CrossRef]
- Ouboter, R.D.B.; Wolff, E.D. On the thermodynamics of a superconducting ring interrupted by a weak superconducting junction: II (continuation). Phys. B Condens. Matter 1989, 159, 234–248. [Google Scholar] [CrossRef]
- van den Brink, A.M.; Dekker, H. Superconducting correlations and the thermodynamics of Josephson junctions. Phys. A Stat. Mech. Its Appl. 1997, 237, 471–514. [Google Scholar] [CrossRef]
- van den Brink, A.M.; Dekker, H. Josephson-junction thermodynamics and the superconducting phase transitionin a SQUID device. Phys. Rev. B 1997, 55, R8697–R8700. [Google Scholar] [CrossRef]
- Vleeming, B.; Andriesse, M.; van den Brink, A.; Dekker, H.; de Bruyn Ouboter, R. Periodic oscillations of the critical temperature versus the applied magnetic flux in a four-terminal SQUID. Phys. B Condens. Matter 1997, 239, 216–222. [Google Scholar] [CrossRef]
- Lechevet, J.; Neighbor, J.E.; Shiffman, C.A. Thermodynamics of the Proximity Effect: Specific-Heat Jumps in Lamellar Lead-Tin Eutectic Alloys. Phys. Rev. B 1972, 5, 861–864. [Google Scholar] [CrossRef]
- Manuel, P.; Veyssié, J.J. Specific-heat jump of superconducting lamellas with pair-breaking boundary conditions. Phys. Rev. B 1976, 14, 78–88. [Google Scholar] [CrossRef]
- Zaitlin, M.P. Heat capacity and density of states of a normal-metal—Superconductor bilayer. Phys. Rev. B 1982, 25, 5729–5736. [Google Scholar] [CrossRef]
- Kobes, R.L.; Whitehead, J.P. Free-energy calculations in a self-consistent model of the proximity effect. Phys. Rev. B 1988, 38, 11268–11274. [Google Scholar] [CrossRef]
- Kosztin, I.; Kos, I.C.V.; Stone, M.; Leggett, A.J. Free energy of an inhomogeneous superconductor: A wave-function approach. Phys. Rev. B 1998, 58, 9365–9384. [Google Scholar] [CrossRef]
- Eilenberger, G.; Jacobs, A.E. Bogoliubov equations, boundary conditions, and the free energy of inhomogeneous superconductors: A new method. J. Low Temp. Phys. 1975, 20, 479–521. [Google Scholar] [CrossRef]
- Kulik, I.; Omel’yanchuk, A.N. Contribution to the microscopic theory of the Josephson effect in superconducting bridges. JETP Lett. 1975, 21, 96. [Google Scholar]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef]
- Virtanen, P.; Vischi, F.; Strambini, E.; Carrega, M.; Giazotto, F. Quasiparticle entropy in superconductor/normal metal/ superconductor proximity junctions in the diffusive limit. Phys. Rev. B 2017, 96, 245311. [Google Scholar] [CrossRef]
- Hammer, J.C.; Cuevas, J.C.; Bergeret, F.S.; Belzig, W. Density of states and supercurrent in diffusive SNS junctions: Roles of nonideal interfaces and spin-flip scattering. Phys. Rev. B 2007, 76, 064514. [Google Scholar] [CrossRef]
- Cochran, J.F.; Mapother, D.E. Superconducting Transition in Aluminum. Phys. Rev. 1958, 111, 132–142. [Google Scholar] [CrossRef]
- Giaever, I.; Megerle, K. Study of Superconductors by Electron Tunneling. Phys. Rev. 1961, 122, 1101–1111. [Google Scholar] [CrossRef]
- Langenberg, D.N.; Scalapino, D.J.; Taylor, B.N. Josephson-type superconducting tunnel junctions as generators of microwave and submillimeter wave radiation. IEEE Proc. 1966, 54, 560. [Google Scholar] [CrossRef]
- D’Ambrosio, S.; Meissner, M.; Blanc, C.; Ronzani, A.; Giazotto, F. Normal metal tunnel junction-based superconducting quantum interference proximity transistor. Appl. Phys. Lett. 2015, 107, 113110. [Google Scholar] [CrossRef]
- Giazotto, F.; Peltonen, J.T.; Meschke, M.; Pekola, J.P. Superconducting quantum interference proximity transistor. Nat. Phys. 2010, 6, 254. [Google Scholar] [CrossRef]
- Ronzani, A.; Altimiras, C.; Giazotto, F. Highly Sensitive Superconducting Quantum-Interference Proximity Transistor. Phys. Rev. Appl. 2014, 2, 024005. [Google Scholar] [CrossRef]
- Taddei, F.; Giazotto, F.; Fazio, R. Properties of Mesoscopic hybrid Superconducting Systems. J. Comp. Theor. Nanosci. 2005, 2, 329. [Google Scholar] [CrossRef]
- Kulik, I.; Ellialtiogammalu, R. Quantum Mesoscopic Phenomena and Mesoscopic Devices in Microelectronics; Nato Science Series C; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Belzig, W.; Wilhelm, F.K.; Bruder, C.; Schön, G.; Zaikin, A.D. Quasiclassical Green’s function approach to mesoscopic superconductivity. Superlattices Microstruct. 1999, 25, 1251–1288. [Google Scholar] [CrossRef]
- Nazarov, Y.V. Circuit Theory of Andreev Conductance. Phys. Rev. Lett. 1994, 73, 1420–1423. [Google Scholar] [CrossRef]
- Nazarov, Y.V. Novel circuit theory of Andreev reflection. Superlattices Microstruct. 1999, 25, 1221–1231. [Google Scholar] [CrossRef]
- Heedt, S.; Traverso Ziani, N.; Crépin, F.; Prost, W.; Trellenkamp, S.; Schubert, J.; Grützmacher, D.; Trauzettel, B.; Schäpers, T. Signatures of interaction-induced helical gaps in nanowire quantum point contacts. Nat. Phys. 2017, 13, 563–1231. [Google Scholar] [CrossRef]
- Zhou, F.; Charlat, P.; Spivak, B.; Pannetier, B. Density of States in Superconductor-Normal Metal-Superconductor Junctions. J. Low. Temp. Phys. 1998, 110, 841–850. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Cuevas, J.C. The Vortex State and Josephson Critical Current of a Diffusive SNS Junction. J. Low Temp. Phys. 2008, 153, 304–324. [Google Scholar] [CrossRef]
- Vischi, F.; Carrega, M.; Strambini, E.; D’Ambrosio, S.; Bergeret, F.S.; Nazarov, Y.V.; Giazotto, F. Coherent transport properties of a three-terminal hybrid superconducting interferometer. Phys. Rev. B 2017, 95, 054504. [Google Scholar] [CrossRef]
- Heikkilä, T.T.; Särkkä, J.; Wilhelm, F.K. Supercurrent-carrying density of states in diffusive mesoscopic Josephson weak links. Phys. Rev. B 2002, 66, 184513. [Google Scholar] [CrossRef]
- Giazotto, F.; Taddei, F. Hybrid superconducting quantum magnetometer. Phys. Rev. B 2011, 84, 214502. [Google Scholar] [CrossRef]
- le Sueur, H.; Joyez, P.; Pothier, H.; Urbina, C.; Esteve, D. Phase Controlled Superconducting Proximity Effect Probed by Tunneling Spectroscopy. Phys. Rev. Lett. 2008, 100, 197002. [Google Scholar] [CrossRef] [PubMed]
- Grosso, G.; Parravicini, G. Solid State Physics; Elsevier Science: Cambridge, MA, USA, 2000. [Google Scholar]
- Rabani, H.; Taddei, F.; Bourgeois, O.; Fazio, R.; Giazotto, F. Phase-dependent electronic specific heat of mesoscopic Josephson junctions. Phys. Rev. B 2008, 78, 012503. [Google Scholar] [CrossRef]
- Rabani, H.; Taddei, F.; Giazotto, F.; Fazio, R. Influence of interface transmissivity and inelastic scattering on the electronic entropy and specific heat of diffusive superconductor-normal metal-superconductor Josephson junctions. J. Appl. Phys. 2009, 105, 093904. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Kos, I.C.V.; Stone, M. Gradient expansion for the free energy of a clean superconductor. Phys. Rev. B 1999, 59, 9545–9557. [Google Scholar] [CrossRef]
- Court, N.A.; Ferguson, A.J.; Lutchyn, R.; Clark, R.G. Quantitative study of quasiparticle traps using the single-Cooper-pair transistor. Phys. Rev. B 2008, 77, 100501. [Google Scholar] [CrossRef]
- de Gennes, P.G. Superconductivity of Metals and Alloys; Advanced Book Classics; Advanced Book Program, Perseus Books: New York, NY, USA, 1999. [Google Scholar]
- Abrikosov, A.; Gorkov, L.; Dzyaloshinski, I. Methods of Quantum Field Theory in Statistical Physics; Dover Books on Physics Series; Dover Publications: New York, NY, USA, 1975. [Google Scholar]
- Dickerson, R.H.; Mottmann, J. Not all counterclockwise thermodynamic cycles are refrigerators. Am. J. Phys. 2016, 84, 413–418. [Google Scholar] [CrossRef]
- Bizarro, J.P.S. Comment on “Not all counterclockwise thermodynamic cycles are refrigerators” [Am. J. Phys. 84, 413–418 (2016)]. Am. J. Phys. 2017, 85, 861–863. [Google Scholar] [CrossRef]
- Mungan, C.E. Coefficient of performance of Stirling refrigerators. Eur. J. Phys. 2017, 38, 055101. [Google Scholar] [CrossRef]
- Deacon, C.G.; Goulding, R.; Haridass, C.; de Young, B. Demonstration experiments with a Stirling engine. Phys. Educ. 1994, 29, 180–183. [Google Scholar] [CrossRef]
- Wheatley, J.C.; Swift, G.W.; Migliori, A. The natural heat engine. Los Alamos Sci. 1986, 14, 2. [Google Scholar]
- Kopnin, N.B.; Galperin, Y.M.; Bergli, J.; Vinokur, V.M. Nonequilibrium electrons in tunnel structures under high-voltage injection. Phys. Rev. B 2009, 80, 134502. [Google Scholar] [CrossRef]
- Barends, R.; Baselmans, J.J.A.; Yates, S.J.C.; Gao, J.R.; Hovenier, J.N.; Klapwijk, T.M. Quasiparticle Relaxation in Optically Excited High-Q Superconducting Resonators. Phys. Rev. Lett. 2008, 100, 257002. [Google Scholar] [CrossRef]
- Gousev, Y.P.; Gol’tsman, G.N.; Semenov, A.D.; Gershenzon, E.M.; Nebosis, R.S.; Heusinger, M.A.; Renk, K.F. Broadband ultrafast superconducting NbN detector for electromagnetic radiation. J. Appl. Phys. 1994, 75, 3695–3697. [Google Scholar] [CrossRef]
- Sergeev, A.; Mitin, V. Electron-phonon interaction in disordered conductors: Static and vibrating scattering potentials. Phys. Rev. B 2000, 61, 6041–6047. [Google Scholar] [CrossRef]
- Kopnin, N.B. Theory of Nonequilibrium Superconductivity; Clarendon Press: Oxford, UK, 2001. [Google Scholar]
- Timofeev, A.V.; García, C.P.; Kopnin, N.B.; Savin, A.M.; Meschke, M.; Giazotto, F.; Pekola, J.P. Recombination-Limited Energy Relaxation in a Bardeen-Cooper-Schrieffer Superconductor. Phys. Rev. Lett. 2009, 102, 017003. [Google Scholar] [CrossRef]
- Maisi, V.F.; Lotkhov, S.V.; Kemppinen, A.; Heimes, A.; Muhonen, J.T.; Pekola, J.P. Excitation of Single Quasiparticles in a Small Superconducting Al Island Connected to Normal-Metal Leads by Tunnel Junctions. Phys. Rev. Lett. 2013, 111, 147001. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vischi, F.; Carrega, M.; Braggio, A.; Virtanen, P.; Giazotto, F. Thermodynamics of a Phase-Driven Proximity Josephson Junction. Entropy 2019, 21, 1005. https://doi.org/10.3390/e21101005
Vischi F, Carrega M, Braggio A, Virtanen P, Giazotto F. Thermodynamics of a Phase-Driven Proximity Josephson Junction. Entropy. 2019; 21(10):1005. https://doi.org/10.3390/e21101005
Chicago/Turabian StyleVischi, Francesco, Matteo Carrega, Alessandro Braggio, Pauli Virtanen, and Francesco Giazotto. 2019. "Thermodynamics of a Phase-Driven Proximity Josephson Junction" Entropy 21, no. 10: 1005. https://doi.org/10.3390/e21101005
APA StyleVischi, F., Carrega, M., Braggio, A., Virtanen, P., & Giazotto, F. (2019). Thermodynamics of a Phase-Driven Proximity Josephson Junction. Entropy, 21(10), 1005. https://doi.org/10.3390/e21101005





