Abstract
This paper is devoted to change-point detection using only the ordinal structure of a time series. A statistic based on the conditional entropy of ordinal patterns characterizing the local up and down in a time series is introduced and investigated. The statistic requires only minimal a priori information on given data and shows good performance in numerical experiments. By the nature of ordinal patterns, the proposed method does not detect pure level changes but changes in the intrinsic pattern structure of a time series and so it could be interesting in combination with other methods.
1. Introduction
Most of real-world time series are non-stationary, that is, some of their properties change over time. A model for some non-stationary time series is provided by a piecewise stationary stochastic process: its properties are locally constant except for certain time-points called change-points, where some properties change abruptly [1].
Detecting change-points is a classical problem being relevant in many applications, for instance in seismology [2], economics [3], marine biology [4], and in many other science fields. There are many methods for tackling the problem [1,5,6,7,8]. However, most of the existing methods have a common drawback: they require certain a priori information about the time series. It is necessary to know either a family of stochastic processes providing a model for the time series (see for instance [9] where autoregressive (AR) processes are considered) or at least to know which characteristics (mean, standard deviation, etc.) of the time series reflect the change (see [7,10]). In real-world applications, such information is often unavailable [11].
Here, we suggest a new method for change-point detection that requires minimal a priori knowledge: we only assume that the changes affect the evolution rule linking the past of the process with its future (a formal description of the considered processes is provided by Definition 4). A natural example of such change is an alteration of the increments distribution.
Our method is based on ordinal pattern analysis, a promising approach to real-valued time series analysis [12,13,14,15,16,17,18]. In ordinal pattern analysis, one considers order relations between values of a time series instead of the values themselves. These order relations are coded by ordinal patterns; specifically, an ordinal pattern of an order describes order relations between successive points of a time series. The main step of ordinal pattern analysis is the transformation of an original time series into a sequence of ordinal patterns, which can be considered as an effective kind of discretization extracting structural features from the data. A result of this transformation is demonstrated in Figure 1 for order . Note that the distribution of ordinal patterns contains much information on the original time series making them interesting for data analysis, especially for data from nonlinear systems (see [19,20]).
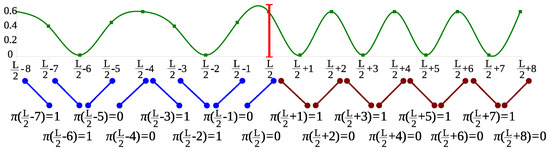
Figure 1.
A part of a piecewise stationary time series with a change-point at (marked by a vertical line) and corresponding ordinal patterns of order (below the plot).
For detecting a change-point in a time series with values in , one generally considers x as a realization of a stochastic process X and computes for x a statistic that should reach its maximum at . Here, we suggest a statistic on the basis of the conditional entropy of ordinal patterns introduced in [21]. The latter is a complexity measure similar to the celebrated permutation entropy [12] with particularly better performance (see [20,21]).
Let us provide an “obvious” example only to motivate our approach and to illustrate its idea.
Example 1.
Consider a time series , and its central part is shown in Figure 1. The time series is periodic before and after , but, at , there occurs a change (marked by a vertical line): the “oscillations” become faster. Figure 1 also presents the ordinal patterns of order at times t underlying the time series. Note that there are only two ordinal patterns of order 1: the increasing (coded by 0) and the decreasing (coded by 1). Both ordinal patterns occur with the same frequency before and after the change-point.
However, the transitions between successive ordinal patterns change at . Indeed, before the change-point , both ordinal patterns have two possible successors (for instance, the ordinal pattern is succeeded by the ordinal pattern , which in turn is succeeded by the ordinal pattern ), whereas after the change-point the ordinal patterns 0 and 1 are alternating. A measure of diversity of transitions between ordinal patterns is provided by the conditional entropy of ordinal patterns. For the sequence of ordinal patterns of order 1, the (empirical) conditional entropy for is defined as follows:
(throughout the paper, and, more general, if a term a is not defined, and denotes the number of elements of a set A).
To detect change-points, we use a test statistic for defined as follows:
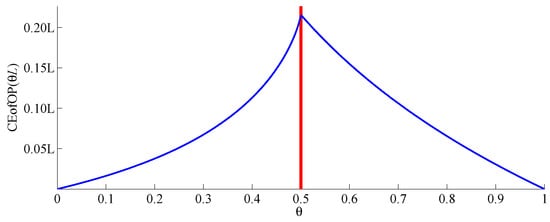
for with . According to the properties of conditional entropy (see Section 2.2 for details), attains its maximum when coincides with a change-point. Figure 2 demonstrates this for the time series from Figure 1.

Figure 2.
Statistic for the sequence of ordinal patterns of order 1 for the time series from Figure 1.
For simplicity and in view of real applications, in Example 1, we define ordinal patterns and the statistic immediately for concrete time series. However, for theoretical consideration, it is clearly necessary to define the statistic for stochastic processes. For this, we refer to Section 2.2.
To illustrate applicability of the statistic, let us discuss a real-world data example. Note that here multiple change-points are detected as described below.
Example 2.
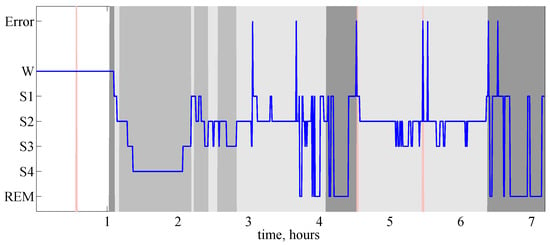
Here, we consider electroencephalogram (EEG) recording 14 from the sleep EEG dataset kindly provided by Vasil Kolev (see Section 5.3.2 in [22] for details and further results on this dataset). We employ the following procedure for an automatic discrimination between sleep stages from the EEG time series: first, we split time series into pseudo-stationary intervals by finding change-points with the CEofOP statistic (change-points are detected in each EEG channel separately), then we cluster all the obtained intervals. Figure 3 illustrates the outcome of the proposed discrimination for single EEG channel in comparison with the manual scoring by an expert; the automated identification of a sleep type (waking, REM, light sleep, deep sleep) is correct for 79.6% of 30-s epochs. Note that the borders of the segments (that is the detected change-points) in most cases correspond to the changes of sleep stage.

Figure 3.
Hypnogram (bold curve) and the results of ordinal-patterns-based discrimination of sleep EEG. Here, the y-axis represents the results of the expert classification: W stands for waking, stages S1, S2 and S3, S4 indicate light and deep sleep, respectively, REM stands for REM sleep and Error—for unclassified samples. Results of ordinal-patterns-based discrimination are represented by the background colour: white colour indicates epochs classified as waking state, light gray—as light sleep, gray—as deep sleep, dark gray—as REM, red colour indicates unclassified segments
The statistic was first introduced in [18], where we have employed it as a component of a method for sleep EEG discrimination. However, no theoretical details of the method for change-point detection were provided there. This paper aims to fill in this gap and provides a justification for the statistic. Numerical experiments given in the paper show better performance of our method than of a similar one based on the Corrected Maximum Mean Discrepancy (CMMD) statistic developed by one of the authors and collaborators [23,24]. A numerical comparison with the classical parametric Brodsky–Darkhovsky method [11] suggests good applicability of the method to nonlinear data, in particular if there is no level change. This is remarkable since our method is only based on the ordinal structure of a time series.
Matlab 2016 (MathWorks, Natick, MA, USA) scripts implementing the suggested method are available at [25].
2. Methods
This section is organized as follows. In Section 2.1, we provide a brief introduction into ordinal pattern analysis. In particular, we define the conditional entropy of ordinal patterns and discuss its properties. In Section 2.2, we introduce the statistic. In Section 2.3, we formulate an algorithm for detecting multiple change-points by means of the statistic.
2.1. Preliminaries
Central objects of the following are stochastic processes on a probability space with values in . Here, and , allowing both finite and infinite lengths of processes. We consider only univariate stochastic processes to keep notation simple, however—with the appropriate adaptations—there are no principal restrictions on the dimension of a process. is stationary if, for all with , the distributions of and coincide.
Throughout this paper, we discuss detection of change-points in a piecewise stationary stochastic process. Simply speaking, a piecewise stationary stochastic process is obtained by “gluing” several pieces of stationary stochastic processes (for a formal definition of piecewise stationarity, see, for instance, ([26], Section 3.1)).
In this section, we recall the basic facts from ordinal pattern analysis (Section 2.1.1), present the idea of ordinal-patterns-based change-point detection (Section 2.1.2), and define the conditional entropy of ordinal patterns (Section 2.1.3).
2.1.1. Ordinal Patterns
Let us recall the definition of an ordinal pattern [14,17,18].
Definition 1.
For , denote the set of permutations of by . We say that a real vector has ordinal pattern of order if
and
As one can see, there are different ordinal patterns of order d.
Definition 2.
Given a stochastic process for , the sequence with
is called the random sequence of ordinal patterns of order of the process X. Similarly, given a realization of X, the sequence of ordinal patterns of order d for x is defined as with
For simplicity, we say that is the length of the sequence ; however, in fact, it consists of elements.
Definition 3.
A stochastic process for is said to be ordinal-d-stationary if for all the probability does not depend on t for . In this case, we call
the probability of the ordinal pattern in X.
The idea of ordinal pattern analysis is to consider the sequence of ordinal patterns and the ordinal patterns distribution obtained from it instead of the original time series. Though implying the loss of nearly all the metric information, this often allows for extracting some relevant information from a time series, in particular, when it comes from a complex system. For example, ordinal pattern analysis provides estimators of the Kolmogorov–Sinai entropy [21,27,28] of dynamical systems, measures of time series complexity [12,18,29], measures of coupling between time series [16,30] and estimators of parameters of stochastic processes [13,31] (see also [15,32] for a review of applications to real-world time series). Methods of ordinal pattern analysis are invariant with respect to strictly-monotone distortions of time series [14] do not need information about range of measurements, and are computationally simple [17]. This qualifies it for application in the case that no much is known about the system behind a time series, possibly as a first exploration step.
For a discussion of the properties of ordinal patterns sequence, we refer to [13,31,33,34,35]. For the following, we need two results stated below.
Lemma 1
(Corollary 2 from [33]). Each process with associated stationary increment process is ordinal-d-stationary for each .
Probability distributions of ordinal patterns are known only for some special cases of stochastic processes [13,33,35]. In general, one estimates probabilities of ordinal patterns by their empirical probabilities. Consider a sequence of ordinal patterns. For any the frequency of occurrence of an ordinal pattern among the first ordinal patterns of the sequence is given by
Note that, in Equation (2), we do not count with in order to be consistent with the conditional entropy following below and considering two successive ordinal patterns. A natural estimator of the probability of an ordinal pattern i in the ordinal-d-stationary case is provided by its relative frequency in the sequence :
2.1.2. Stochastic Processes with Ordinal Change-Points
Sequences of ordinal patterns are invariant to certain changes in the original stochastic process X, such as shifts (adding a constant to the process) ([15], Section 3.4.3) and scaling (multiplying the process by a positive constant) [14]. However, in many cases, changes in the original process X affect also the corresponding random sequences of ordinal patterns and ordinal patterns distributions. On the one hand, this impedes application of ordinal pattern analysis to non-stationary time series. Namely, most of ordinal-patterns-based quantities require ordinal-d-stationarity of a time series [12,15,16] and may be unreliable when this condition fails. On the other hand, one often can detect change-points in the original process by detecting changes in the sequence of ordinal patterns.
Below, we consider piecewise stationary stochastic processes that are processes consisting of several stationary segments glued together. The time points where the signals are glued correspond to abrupt changes in the properties of the process and are called change-points. The first ideas of using ordinal patterns for detecting change-points were formulated in [23,24,34,36,37,38]. The advantage of the ordinal-patterns-based methods is that they require less information than most of the existing methods for change-point detection: it is assumed that the stochastic process is not from a specific family and that the change does not affect specific characteristics of the process. Instead, we consider further change-points with the following property.
Definition 4.
Let with be a piecewise stationary stochastic process with a change-point . We say that is an ordinal change-point if there exist some with and some such that and are ordinal-d-stationary but is not. A stochastic process of length less than is ordinal-d-stationary by definition.
This approach seems to be natural for many stochastic processes and real-world time series. Note that a change-point where a change in mean occurs need not be ordinal, since the mean is irrelevant for the distribution of ordinal patterns ([15], Section 3.4.3). However, there are many methods that effectively detect changes in mean; the proposed method here is intended for use in a more complex case, when there is no classical method, or it is not clear, which of them to apply.
We illustrate Definition 4 by two examples. Piecewise stationary autoregressive processes considered in Example 3 are classical and provide models for linear time series. Since many real-world time series are nonlinear, we introduce in Example 4 a process originated from nonlinear dynamical systems. These two types of processes are used throughout the paper for empirical investigation of change-point detection methods.
Example 3.
A first order piecewise stationary autoregressive process with change-points is defined as
where are the parameters of the autoregressive model and
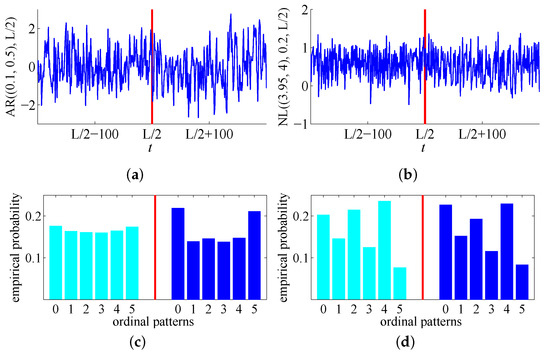
for all for , where and , with ϵ being the standard white Gaussian noise, and AR(0): = . AR processes are often used for the investigation of methods for change-points detection (see, for instance, [23,24]), since they provide models for a wide range of real-world time series. Figure 4a illustrates a realization of a ‘two piece’ AR process with a change-point at . By ([13], Proposition 5.3), the distributions of ordinal patterns of order reflect change-points for piecewise stationary AR processes. Figure 4c illustrates this for the realization from Figure 4a: empirical probability distributions of ordinal patterns of order before and after the change-point differ considerably.

Figure 4.
Upper row: parts of realizations of piecewise stationary autoregressive (AR) (a) and noisy logistic (NL) (b) processes with change-points marked by vertical lines, L = 20,000. Lower row: empirical probability distributions of ordinal patterns of order in the realizations of AR (c) and NL (d) processes are different before and after the change-point.
Example 4.
A classical example of a nonlinear system is provided by the logistic map on the unit interval:
with , for and . The behaviour of this map significantly varies for different value r; we are especially interested in with chaotic behaviour. In this case, there exists an invariant ergodic measure absolutely continuous with respect to the Lebesgue measure [39,40], therefore Equation (3) defines a stationary stochastic process :
with being a uniformly distributed random number. Note that, for almost all either the map is chaotic or hyperbolic roughly meaning that an attractive periodic orbit is dominating it. This is a deep result in one-dimensional dynamics (see [40] for details). In the hyperbolic case, after some transient behaviour, numerically, one only sees some periodic orbit, which has long periods in the interval . From the practical viewpoint, i.e., when considering short orbits, dynamics for that interval can be considered as chaotic since already small changes of r result in chaotic behaviour also in the theoretical sense.
Let us include some observational noise by adding standard white Gaussian noise ϵ to an orbit:
where is the level of noise.
Orbits of logistic maps, particularly with observational noise, are often used as a studying and illustrating tool of nonlinear time series analysis (see [41,42]). This justifies as a natural object for study a piecewise stationary noisy logistic (NL) process with change-points , defined as
where are the values of control parameter, are the levels of noise, and
with
for all for , with , and is a uniformly distributed random number.
Figure 4b shows a realization of a ‘two-piece’ NL process with a change-point at ; as one can see in Figure 4d, the empirical distributions of ordinal patterns of order before the change-point and after the change-point do not coincide. In general, the distributions of ordinal patterns of order reflect change-points for the NL processes (which can be easily checked).
The NL and AR processes have rather different ordinal patterns distributions, being the reason for using them for empirical investigation of change-point detection methods in Section 3.
2.1.3. Conditional Entropy of Ordinal Patterns
Here, we define the conditional entropy of ordinal patterns, which is a cornerstone of the suggested method for ordinal-change-point detection. Let us call a process for ordinal--stationary if for all the probability of pairs of ordinal patterns
does not depend on t for (compare with Definition 3). Obviously, ordinal--stationarity implies ordinal--stationarity.
For an ordinal--stationary stochastic process, consider the probability of an ordinal pattern to occur after an ordinal pattern . Similarly to Equation (1), it is given by:
for . If , let .
Definition 5.
The conditional entropy of ordinal patterns of order of an ordinal -stationary stochastic process X is defined by:
For brevity, we refer to as the “conditional entropy” when no confusion can arise. The conditional entropy characterizes the mean diversity of successors of a given ordinal pattern . This quantity often provides a good practical estimation of the Kolmogorov–Sinai entropy for dynamical systems; for a discussion of this and other theoretical properties of conditional entropy, we refer to [21]. Here, we only note that the Kolmogorov–Sinai entropy quantifies unpredictability of a dynamical system.
One can estimate the conditional entropy from a time series by using the empirical conditional entropy of ordinal patterns [18]. Consider a sequence of ordinal patterns of order with length . Similarly to Equation (2), the frequency of occurrence of an ordinal patterns pair is given by
for . The empirical conditional entropy of ordinal patterns for is defined by
As a direct consequence of Lemma 1, the empirical conditional entropy approaches the conditional entropy under certain assumptions. Namely, the following holds.
Corollary 1.
For the sequence of ordinal patterns of order of a realization of an ergodic stochastic process with associated stationary increment process , it holds almost surely that
2.2. A Statistic for Change-Point Detection Based on the Conditional Entropy of Ordinal Patterns
We now consider the classical problem of detecting a change-point on the basis of a realization x of a stochastic process X having at most one change-point, that is, it holds either or (compare [6]). To solve this problem, one estimates a tentative change-point as the time-point that maximizes a test statistic . Then, the value of is compared to a given threshold in order to decide whether is a change-point.
The idea of ordinal change-point detection is to find change-points in a stochastic process X by detecting changes in the sequence of ordinal patterns for a realization of X. Given at most one ordinal change-point in X, one estimates its position by using the fact that
- characterize the process before the change;
- correspond to the transitional state;
- characterize the process after the change.
Therefore, a position of a change-point can be estimated by an ordinal-patterns-based statistic that, roughly speaking, measures dissimilarity between the distributions of ordinal patterns for and for .
Then, an estimate of the change-point is given by
A method for detecting one change-point can be extended to an arbitrary number of change-points using the binary segmentation [43]: one applies a single change-point detection procedure to the realization x; if a change-point is detected, then it splits x into two segments in each of which one is looking for a change-point. This procedure is repeated iteratively for the obtained segments until all of them either do not contain change-points or are too short.
The key problem is the selection of an appropriate test statistic for detecting changes on the basis of a sequence of ordinal patterns of a realization of the process for . We suggest to use the following statistic:
for all with . The intuition behind this statistic comes from the concavity of conditional entropy (not only for ordinal patterns but in general, see Section 2.1.3 in [44]). It holds
Therefore, if the probabilities of ordinal patterns change at some point , but do not change before and after , then tends to attain its maximum at . If the probabilities do not change at all, then for L being sufficiently large, Inequality (9) tends to hold with equality. More rigorously, when segments of a stochastic process before and after the change-point have infinite length, the following result takes place.
Corollary 2.
Let be an ergodic -ordinal-stationary stochastic process on a probability space . For , let be the random sequence of ordinal patterns of order d of . Then, for any it holds
-almost sure.
Corollary 2 is a simple consequence of Theorem A1 (Appendix A.1). Another important property of the statistic is its close connexion with the classical likelihood ratio statistic (see Appendix A.2 for details).
Let us now rewrite Equation (8) in a straightforward form. Let and be the frequencies of occurrence of an ordinal pattern and of an ordinal patterns pair (given by Equations (2) and (5), respectively). By setting and , we get using Equation (6)
This statistic was first introduced and applied to the segmentation of sleep EEG time series in [18].
To demonstrate the “nonlinear” nature of the statistic, we provide Example 5 concerning transition from a time series to its surrogate. Although being in a sense tailor-made, this example shows that discerns changes that cannot be detected by conventional “linear” methods.
Remark 1.
The question whether a time series is linear or nonlinear often arises in data analysis. For instance, linearity should be verified before using such powerful methods as Fourier analysis. For this, one usually employs a procedure known as surrogate data testing [45,46,47]. It utilises the fact that a linear time series is statistically indistinguishable from any time series sharing some of its properties (for instance, second moments and amplitude spectrum). Therefore, one can generate surrogates having the certain properties of the original time series without preserving other properties, irrelevant for a linear system. If such surrogates are significantly different from the original series, then nonlinearity is assumed.
Example 5.
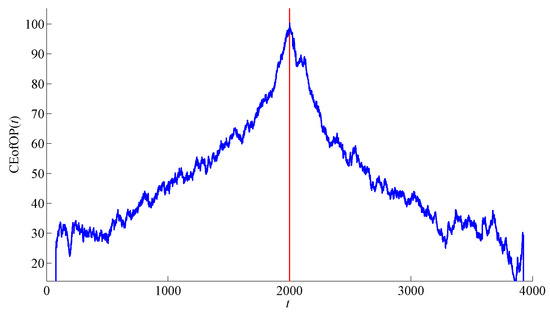
Consider a time series obtained by gluing a realisation of a noisy logistic process NL of length (without changes) with its surrogate of the same length (to generate surrogates, we use the iterative amplitude adjusted Fourier transform (AAFT) algorithm suggested by [46] and implemented by [48]). This compound time series has a change-point at , whose conventional methods may fail to detect since the surrogate has the same autocorrelation function as the original process (for instance, this is the case for the Brodsky–Darkhovsky method considered further in Section 3). However, the ordinal pattern distributions for the original time series and its surrogate generally are significantly different. Therefore, the statistic detects the change-point, which is illustrated by Figure 5.

Figure 5.
Maximum of statistic detects the change-point (indicated by the vertical line) in a time series, obtained by “gluing” a realization of a noisy logistic stochastic process with its surrogate.
Remark 2.
Although the idea that ordinal structure is a relevant indicator of time series linearity/nonlinearity is not new [12,15], to our knowledge, it was not rigorously proved that the distribution of ordinal patterns is altered by surrogates. This is clearly beyond the scope of this paper and will be discussed elsewhere as a separate study; here, it is sufficient for us to provide an empirical evidence for this.
2.3. Algorithm for Change-Point Detection via the CEofOP Statistic
Consider a sequence of ordinal patterns of order with length , corresponding to a realization of some piecewise stationary stochastic process. To detect a single change-point via the statistic, we first estimate its possible position by
where is a minimal length of a sequence of ordinal patterns that is sufficient for a reliable estimation of empirical conditional entropy.
Remark 3.
From the representation CEofOPstat, it follows that, for a reasonable computation of the CEofOP statistic, a reliable estimation of eCE before and after the assumed change-point is required. For this, the stationary parts of a process should be sufficiently long. We take , which is equal to the number of all possible pairs of ordinal patterns of order d (see [18] for details). Consequently, the length L of a time series should satisfy
Note that this does not impose serious limitations on the suggested method, since condition (12) is not too restrictive for . However, it implies using of either or , since does not provide effective change-point detection (see Example 3 and Appendix A.1), while in most applications demands too large sample sizes.
In order to check whether is an actual change-point, we test between the hypotheses:
- :
- parts and of the sequence come from the same distribution;
- :
- parts and of the sequence come from different distributions.
This test is performed by comparing to a threshold h, such that, if the value of is above the threshold, one rejects in favour of . The choice of the threshold is ambiguous: the lower h, the higher the possibility of false rejection of in favour of (false alarm, meaning that the test indicates a change of the distribution although there is no actual change) is. On the contrary, the higher h, the higher the possibility of false rejection of the is.
As it is usually done, we consider the threshold h as a function of the desired probability of false alarm. To compute , we shuffle blocks of ordinal patterns from the original sequence, in order to create new artificial sequences. Each such sequence has the same length as the original, but the segments on the left and on the right of the assumed change-point should have roughly the same distribution of ordinal patterns, even if the original sequence is not stationary. This procedure uses the ideas described in [49,50] and is similar to block bootstrapping [51,52,53,54]. The scheme of detecting at most one change-point via the statistic, including the computing of a threshold is provided in Algorithm 1.
| Algorithm 1 Detecting at most one change-point |
| Input: sequence of ordinal patterns of order d, nominal probability of false alarm Output: estimate of a change-point if change-point is detected, otherwise return 0.
|
To detect multiple change-points, we use an algorithm that consists of two steps:
- Step 1:
- preliminary estimation of boundaries of the stationary segments with a threshold computed for doubled nominal probability of false alarm (that is, with a higher risk of detecting false change-points).
- Step 2:
- verification of the boundaries and exclusion of false change-points: a change-point is searched for a merging of every two adjacent intervals.
Details of these two steps are displayed in Algorithm 2. Step 1 is the usual binary segmentation procedure as suggested in [43]. Since this procedure detects change-points sequentially, they may be estimated incorrectly. To improve localization and eliminate false change-points, we introduce Step 2 following the idea suggested in [11].
| Algorithm 2 Detecting multiple change-points |
| Input: sequence of ordinal patterns of order d, nominal probability of false alarm. Output: estimates of the number of stationary segments and of their boundaries .
|
3. Numerical Simulations and Results
In this section, we empirically investigate performance of the method for change-point detection via the statistic. We apply it to the noisy logistic processes and to autoregressive processes (see Section 2.1.2) and compare performances of change-point detection by the suggested method and by the following existing methods:
- The ordinal-patterns-based method for detecting change-points via the CMMD statistic [23,24]: A time series is split into windows of equal lengths , empirical probabilities of ordinal patterns are estimated in every window. If there is a ordinal change-point in the time series, then the empirical probabilities of ordinal patterns should be approximately constant before the change-point and after the change-point, but they change at the window with the change-point. To detect this change, the CMMD statistic was introduced. (Note that the definition of the CMMD statistic in [23] contains a mistake, which is corrected in [24]. The results of numerical experiments reported in [23] also do not comply with the actual definition of the CMMD statistic (see Section 4.2.1.1 and 4.5.1.1 in [22] for details). In the original papers [23,24], authors do not estimate change-points, but only the corresponding window numbers; for the algorithm of change-point estimation by means of the CMMD statistic, we refer to Section 4.5.1 in [22].
- Two versions of the classical Brodsky–Darkhovsky method [11]: the Brodsky–Darkhovsky method can be used for detecting changes in various characteristics of a time series , but the characteristic of interest should be selected in advance. In this paper, we consider detecting changes in mean, which is just the basic characteristic, and in correlation function which reflects relations between the future and the past of a time series and seems to be a natural choice for detecting ordinal change-points. Changes in mean are detected by the generalized version of the Kolmogorov–Smirnov statistic [11]:where the parameter regulates properties of the statistic, is basically used (see [11] for details). Changes in the correlation function are detected by the following statistic:
Remark 4.
Note that we consider the statistic , which is intended to detect changes in mean, though ordinal-patterns-based statistics do not detect these changes. This is motivated by the fact that changes in the noisy logistic processes are on the one hand changes in mean, and, on the other hand, ordinal changes in the sense of Definition 4. Therefore, they can be detected both by and by ordinal-patterns-based statistics. In general, by the nature of ordinal time series analysis, changes in mean and in the ordinal structure are in some sense complementary.
We use orders of ordinal patterns for computing the statistic ( provides worse results because of reduced sensitivity, while higher orders are applicable only to rather long time series due to condition (12)). For the CMMD statistic, we take and the window size . There are no special reasons for this choice except the fact that is sufficient for estimating probabilities of ordinal patterns of order inside the windows, since (Section 9.3 [15]). Results of the experiments remain almost the same for .
Nominal probability of false alarm has been taken for all methods (in the case of the CMMD statistic, we have used the equivalent value , see Section 4.3.2 in [22] for details).
In Section 3.1, we study how well the statistics for change-point detection estimate the position of a single change-point. Since we expect that performance of the statistics for change-point detection may strongly depend on the length of realization, we check this in Section 3.2. Finally, we investigate the performance of various statistics for detecting multiple change-points in Section 3.3.
3.1. Estimation of the Position of a Single Change-Point
Consider N = 10,000 realizations with for each of the processes listed in Table 1. A single change occurs at a random time uniformly distributed in . For all processes, length of sequences of ordinal patterns is taken, with .

Table 1.
Processes used for investigation of the change-point detection.
To measure the overall accuracy of change-point detection via some statistic S as applied to the process X, we use three quantities. Let us first determine the error of the change-point estimation provided by the statistic S for the j-th realization of a process X:
where is the actual position of the change-point and is its estimate obtained by using S. Then, the fraction of satisfactorily estimated change-points (averaged over N realizations) is defined by:
where is the maximal satisfactory error, we take . The bias and the root mean squared error (RMSE) are respectively given by
A large and a bias and close to zero are standing for a high accuracy of the estimation of a change-point. Results of the experiments are presented in Table 2 and Table 3 for NL and AR processes, respectively. For every process, the best values of performance measures are shown in bold.

Table 2.
Performance of different statistics for estimating change-point in noisy logistic (NL) processes

Table 3.
Performance of different statistics for estimating change-point in autoregressive (AR) processes.
Let us summarize: for the considered processes, the CEofOP statistic estimates change-point more accurately than the CMMD statistic. For the NL processes, the CEofOP statistic has almost the same performance as the Brodsky–Darkhovsky method; for the AR processes, performance of the classical method is better, though CEofOP has lower bias. In contrast to the ordinal-patterns-based methods, the Brodsky–Darkhovsky method is unreliable when there is a lack of a priori information about the time series. For instance, changes in NL processes only slightly influence the correlation function and does not provide a good indication of changes (cf. performance of and in Table 2). Here, note that level shifts before and after a time point do not change .
Meanwhile, changes in the AR processes do not influence the expected value (see Example 3), which does not allow for detecting them using (see Table 3). Therefore, we do not consider the statistic in further experiments.
Note that performance of the statistic is only slightly better for than for , and for even decreases, although one can expect better change-point detection for higher d. As we show in the following session, this is due to the fact that the performance of the statistic depends on the length L of the time series. In particular, = 20,480 is not sufficient for applying the statistic with .
3.2. Estimating Position of a Single Change-Point for Different Lengths of Time Series
Here, we study how the accuracy of change-point estimation for the three considered statistics depends on the length L of a time series. We take 50,000 realizations of NL, , and AR, for realization lengths L = 24 W, 28 W, …, 120 W. Again, we consider a single change at a random time . Results of the experiment are presented in Figure 6.
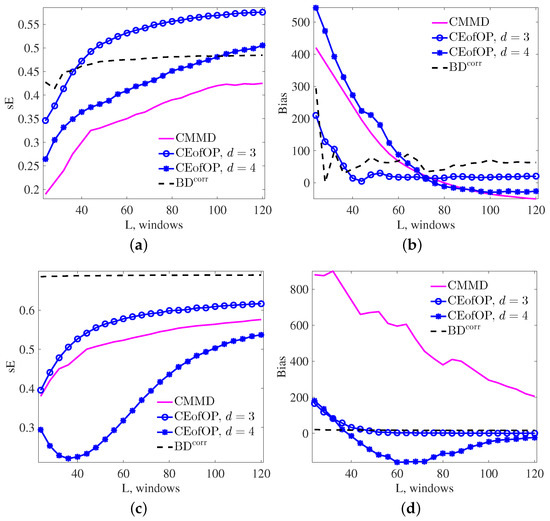
Figure 6.
Measures of change-point detection performance for NL (a,b) and AR (c,d) processes with different lengths, where L is the product of window numbers given on the x-axis with window length .
In summary, performance of the CEofOP statistic is generally better than for the CMMD statistic, but strongly depends on the length of time series. This emphasizes importance of condition (12). From the results of our experiments, we recommend choosing d, satisfying . In comparison with the classical Brodsky–Darkhovsky method, CEofOP has better performance for NL processes (see Figure 6a,b), and lower bias for AR processes (see Figure 6d).
3.3. Detecting Multiple Change-Points
Here, we investigate how well the considered statistics detect multiple change-points. Methods for change-point detection via the CEofOP and the CMMD statistics are implemented according to Section 2.3 and Section 4.5.1 in [22], respectively. We consider here CEofOP only for , since it provided the best change-point detection in previous experiments. The Brodsky–Darkhovsky method is implemented according to [11] with only one exception: to compute a threshold for it, we use the shuffling procedure (Algorithm 1), which in our case provided better results than the technique described in [11].
We consider here two processes, and , with change-points being independent and uniformly distributed in for with , , , and W. For both processes, we generate realizations with . We consider unequal lengths of stationary segments to study methods for change-point detection in more realistic conditions.
As we apply change-point detection via a statistic S to realization , we obtain estimates of the number of stationary segments and of change-points positions for . Since the number of estimated change-points may be different from the actual number of changes, we suppose that the estimate for is provided by the nearest . Therefore, the error of estimation of the k-th change-point provided by S is given by
To assess the overall accuracy of change-point detection, we compute two quantities. The fraction of satisfactory estimates of a change-point , is given by
where is the maximal satisfactory error; we take . The average number of false change-points is defined by:
Results of the experiment are presented in Table 4 and Table 5, and the best values are shown in bold.

Table 4.
Performance of change-point detection methods for the process with three change-points .

Table 5.
Performance of change-point detection methods for the process with three change-points .
In summary, since distributions of ordinal patterns for NL and AR processes have different properties, results for them differ significantly. The CEofOP statistic provides good results for the NL processes. However, for the AR processes, its performance is much worse: only the most prominent change is detected rather well. Weak results for two other change-points are caused by the fact that the CEofOP statistic is rather sensitive to the lengths of stationary segments (we have already seen this in Section 3.2), and in this case they are not very long.
4. Conclusions and Open Points
In this paper, we have introduced a method for change-point detection via the CEofOP statistic and have tested it for time series coming from two classes of models with quite different behavior, namely piecewise stationary noisy logistic and autoregressive processes.
The empirical investigations suggest that the method proposed provides better detection of ordinal change-points than the ordinal-patterns-based method introduced in [23,24]. Performance of our method for the two model classes considered is particularly comparable to that for the classical Brodsky–Darkhovsky method, but, in contrast to it, ordinal-patterns-based methods require less a priori knowledge about the time series. This can be especially useful in the case of considering nonlinear models where the autocorrelation function does not describe distributions completely. Here, the point is that with exception of the mean much of the distribution is captured by its ordinal structure. Thus (together with methods finding changes in mean), the CEofOP statistic can be used at least for a first exploration step. It is remarkable that our method behaves well with respect to the bias of the estimation, possibly qualifying it to improve localization of change-points found by other methods.
Although numerical experiments and tests to real-world data cannot replace rigorous theoretical studies, the results of the current study show the potential of the change-point detection via the CEofOP statistic. However, there are some open points listed below:
- A method for computing a threshold h for the statistic without shuffling the original time series is of interest, since this procedure is rather time consuming. One possible solution is to utilize Theorem A1 (Appendix A.1) and to precompute thresholds using the values of . However, this approach requires further investigation.
- The binary segmentation procedure [43] is not the only possible method for detecting multiple change-points. In [8,55], an alternative approach is suggested: the number of stationary segments is estimated by optimizing a contrast function, then the positions of the change-points are adjusted. Likewise, one can consider a method for multiple change-point detection based on maximizing the following generalization of statistic:where is an estimate of number of stationary segments, , and are estimates of change-points. Further investigation in this direction could be of interest.
- As we have seen in Section 3.2, CEofOP statistic requires rather large sample sizes to provide reliable change-point detection. This is due to the necessity of the empirical conditional entropy estimation (see Section 2.3). In order to reduce the required sample size, one may consider more effective estimates of the conditional entropy—for instance, the Grassberger estimate (see [56] and also Section 3.4.1 in [22]). However, elaboration of this idea is beyond the scope of this paper.
- We did not use the full power of ordinal time series analysis, which often considers ordinal patterns taken from sequences of equidistant time points of some distance . This generalization of the case with successive points allows for addressing different scales and so to extract more information on the distribution of a time series [57], also being useful for change-point detection.
- In this paper, only one-dimensional time series are considered, though there is no principal limitation for applying ordinal-patterns-based methods to multivariate data (see [28]). Discussion of using ordinal-patterns-based methods for detecting change-point in multivariate data (for instance, in multichannel EEG) is therefore of interest.
- We have considered here only the “offline” detection of changes, which is used when the acquisition of a time series is completed. Meanwhile, in many applications, it is necessary to detect change-points “online”, based on a small number of observations after the change [1]. Development of online versions of ordinal-patterns-based methods for change-point detection may be an interesting direction of a future work.
Author Contributions
A.M.U. and K.K. conceived and designed the method, performed the numerical experiments and wrote the paper.
Funding
This work was supported by the Graduate School for Computing in Medicine and Life Sciences funded by Germany’s Excellence Initiative [DFG GSC 235/1].
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Theoretical Underpinnings of the CEofOP Statistic
Appendix A.1. Asymptotic Behavior of the CEofOP Statistic
Here, we consider the values of for the case when segments of a stochastic process before and after the change-point have infinite length.
Let us first introduce some notation. Given an ordinal--stationary stochastic process X for , the distribution of pairs of ordinal patterns is denoted by , with for all . One easily sees the following: the conditional entropy of ordinal patterns is represented as , where
Here, recall that .
Theorem A1.
Let and be ergodic -ordinal-stationary stochastic processes on a probability space with probabilities of pairs of ordinal patterns of order given by and , respectively. For and , let be the random sequence of ordinal patterns of order d of
Then, for all it holds that
-almost sure, where
By definition, Equation (A1) defines a stochastic process of length with a potential ordinal change-point , i.e., the position of relative to L is principally the same for all L, and the statistics considered are stabilizing for increasing L. Equation (A1) can be particularly interpreted as a part of a stochastic process including exactly one ordinal chance point. We omit the proof of Theorem A1 since it is a simple computation.
Due to the properties of the conditional entropy, it holds that
Values of can be computed for a piecewise stationary stochastic process with known probabilities of ordinal patterns before and after the change-point. To apply Theorem A1, probabilities of pairs of ordinal patterns of order d are also needed, but they can be calculated from the probabilities of ordinal patterns of order . As one can verify, probability of any pair of ordinal patterns is equal either to the probability of a certain ordinal pattern of order or to the sum of two such probabilities.
In [13], authors compute probabilities of ordinal patterns of orders (Proposition 5.3) and (Theorem 5.5) for stationary Gaussian processes (in particular, for autoregressive processes). Below, we use these results to illustrate Theorem A1.
Consider an autoregressive process with a single change-point for . Using the results from [13], we compute distributions , of ordinal pattern pairs for orders and, on this basis, we calculate the values of for different values of and . The results are presented in Table A1 and Table A2.

Table A1.
Values of for an autoregressive process (coefficient 100 here is only for the sake of readability).
Table A1.
Values of for an autoregressive process (coefficient 100 here is only for the sake of readability).
| 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 0.99 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0 | 0.02 | 0.07 | 0.15 | 0.26 | 0.40 | 0.56 | 0.74 | 0.95 | 1.18 | 1.44 | |
| 0.10 | 0.02 | 0 | 0.02 | 0.06 | 0.14 | 0.25 | 0.37 | 0.53 | 0.71 | 0.91 | 1.13 | |
| 0.20 | 0.07 | 0.02 | 0 | 0.02 | 0.06 | 0.13 | 0.23 | 0.36 | 0.51 | 0.68 | 0.88 | |
| 0.30 | 0.15 | 0.06 | 0.02 | 0 | 0.01 | 0.06 | 0.13 | 0.22 | 0.34 | 0.49 | 0.66 | |
| 0.40 | 0.26 | 0.14 | 0.06 | 0.01 | 0 | 0.01 | 0.06 | 0.12 | 0.22 | 0.33 | 0.48 | |
| 0.50 | 0.40 | 0.25 | 0.13 | 0.06 | 0.01 | 0 | 0.01 | 0.05 | 0.12 | 0.21 | 0.33 | |
| 0.60 | 0.56 | 0.37 | 0.23 | 0.13 | 0.06 | 0.01 | 0 | 0.01 | 0.05 | 0.12 | 0.21 | |
| 0.70 | 0.74 | 0.53 | 0.36 | 0.22 | 0.12 | 0.05 | 0.01 | 0 | 0.01 | 0.05 | 0.12 | |
| 0.80 | 0.95 | 0.71 | 0.51 | 0.34 | 0.22 | 0.12 | 0.05 | 0.01 | 0 | 0.01 | 0.05 | |
| 0.90 | 1.18 | 0.91 | 0.68 | 0.49 | 0.33 | 0.21 | 0.12 | 0.05 | 0.01 | 0 | 0.01 | |
| 0.99 | 1.44 | 1.13 | 0.88 | 0.66 | 0.48 | 0.33 | 0.21 | 0.12 | 0.05 | 0.01 | 0 | |

Table A2.
Values of for an autoregressive process.
Table A2.
Values of for an autoregressive process.
| 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 0.99 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0 | 0.04 | 0.15 | 0.33 | 0.56 | 0.85 | 1.18 | 1.55 | 1.95 | 2.40 | 2.88 | |
| 0.10 | 0.04 | 0 | 0.04 | 0.14 | 0.31 | 0.53 | 0.80 | 1.12 | 1.48 | 1.89 | 2.34 | |
| 0.20 | 0.15 | 0.04 | 0 | 0.03 | 0.13 | 0.29 | 0.51 | 0.77 | 1.08 | 1.44 | 1.85 | |
| 0.30 | 0.33 | 0.14 | 0.03 | 0 | 0.03 | 0.13 | 0.28 | 0.49 | 0.75 | 1.06 | 1.43 | |
| 0.40 | 0.56 | 0.31 | 0.13 | 0.03 | 0 | 0.03 | 0.12 | 0.27 | 0.48 | 0.74 | 1.06 | |
| 0.50 | 0.85 | 0.53 | 0.29 | 0.13 | 0.03 | 0 | 0.03 | 0.12 | 0.27 | 0.48 | 0.74 | |
| 0.60 | 1.18 | 0.80 | 0.51 | 0.28 | 0.12 | 0.03 | 0 | 0.03 | 0.12 | 0.27 | 0.48 | |
| 0.70 | 1.55 | 1.12 | 0.77 | 0.49 | 0.27 | 0.12 | 0.03 | 0 | 0.03 | 0.12 | 0.28 | |
| 0.80 | 1.95 | 1.48 | 1.08 | 0.75 | 0.48 | 0.27 | 0.12 | 0.03 | 0 | 0.03 | 0.13 | |
| 0.90 | 2.40 | 1.89 | 1.44 | 1.06 | 0.74 | 0.48 | 0.27 | 0.12 | 0.03 | 0 | 0.03 | |
| 0.99 | 2.88 | 2.34 | 1.85 | 1.43 | 1.06 | 0.74 | 0.48 | 0.28 | 0.13 | 0.03 | 0 | |
According to Theorem A1, for , being a sequence of ordinal patterns of order d for a realization of , it holds almost certainly that
Figure A1 shows how fast that this convergence is. Note that the statistic for orders allows for distinguishing between change and no change in the considered processes for . For , the values of the statistic for order are already very close to its theoretical values, whereas, for , this length does not seem sufficient.

Figure A1.
Empirical values of CEofOP statistics converge to the theoretical values for autoregressive processes as L increases for (a) and (b). Here, AR, stands for the process . The provided empirical values are obtained either as 5th percentile (for ) or as 95th percentile (for ) from 1000 trials.
Appendix A.2. CEofOP Statistic for a Sequence of Ordinal Patterns Forming a Markov Chain
In this subsection, we show that there is a connection between the statistic and the classical likelihood ratio statistic. Though taking place only in a particular case, this connection reveals the nature of the statistic.
First, we set up necessary notations. Consider a sequence of ordinal patterns for that transition probabilities of ordinal patterns may change at some . The basic statistic for testing whether there is a change in the transition probabilities is the likelihood ratio statistic ([1], Section 2.2.3):
where is the likelihood of the hypothesis H given a sequence of ordinal patterns, and the hypotheses are given by
where , are transition probabilities of ordinal patterns before and after t, respectively.
Proposition A1.
Random sequence of ordinal patterns of order forms a Markov chain with at most one change-point; then, for a sequence of ordinal patterns being a realization of of length , it holds that
Proof.
First, we estimate the probabilities and the transition probabilities before (p) and after (q) the change ([58], Section 2):
Then, as one can see from ([58], Section 3.2), we have
Assume that the first ordinal pattern is fixed in order to simplify the computations. Then, and it holds that:
Since , one finally obtains:
Appendix A.3. Change-Point Detection by the CEofOP Statistic and from Permutation Entropy Values
One may ask whether special techniques of ordinal change-point detection make sense at all when one can simply compute permutation entropy [12] of a time series in sliding windows and then apply traditional methods for change-point detection to the resulting sequence of permutation entropy values. Indeed, permutation entropy that measures non-uniformity of ordinal patterns distribution is sensitive to the changes in this distribution and can be an indicator of ordinal change-points. However, we show in Figure A2, there is no straightforward way to detect change-point from permutation entropy values.
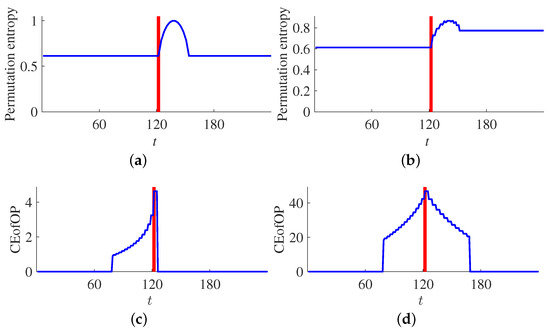
Figure A2.
Permutation entropy computed in sliding windows (a,b) and values of the CEofOP statistics (c,d) for artificial time series with sequences of ordinal patterns and , respectively, where , . Both sequences of ordinal patterns have a change-point at (indicated by red vertical line) and are given by and . Permutation entropy is computed in sliding windows of length . While peaks of the CEofOP statistics clearly indicate the change-points, there is no straightforward way to detect changes from the values of permutation entropy.
References
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Amorèse, D. Applying a change-point detection method on frequency-magnitude distributions. Bull. Seismol. Soc. Am. 2007, 97, 1742–1749. [Google Scholar] [CrossRef]
- Perron, P.M.; Bai, J. Computation and Analysis of Multiple Structural Change Models. J. Appl. Econ. 2003, 18, 1–22. [Google Scholar]
- Walker, K.; Aranis, A.; Contreras-Reyes, J. Possible Criterion to Estimate the Juvenile Reference Length of Common Sardine (Strangomera bentincki) off Central-Southern Chile. J. Mar. Sci. Eng. 2018, 6, 82. [Google Scholar] [CrossRef]
- Brodsky, B.E.; Darkhovsky, B.S. Nonparametric Methods in Change-Point Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Carlstein, E.; Muller, H.G.; Siegmund, D. Change-Point Problems; Institute of Mathematical Statistics: Hayward, CA, USA, 1994. [Google Scholar]
- Brodsky, B.E.; Darkhovsky, B.S. Non-Parametric Statistical Diagnosis. Problems and Methods; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Lavielle, M.; Teyssière, G. Adaptive Detection of Multiple Change-Points in Asset Price Volatility. In Long Memory in Economics; Teyssière, G., Kirman, A.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 129–156. [Google Scholar]
- Davis, R.A.; Lee, T.C.M.; Rodriguez-Yam, G.A. Structural break estimation for nonstationary time series models. J. Am. Stat. Assoc. 2006, 101, 223–239. [Google Scholar] [CrossRef]
- Preuss, P.; Puchstein, R.; Dette, H. Detection of multiple structural breaks in multivariate time series. J. Am. Stat. Assoc. 2015, 110, 654–668. [Google Scholar] [CrossRef]
- Brodsky, B.E.; Darkhovsky, B.S.; Kaplan, A.Y.; Shishkin, S.L. A nonparametric method for the segmentation of the EEG. Comput. Methods Progr. Biomed. 1999, 60, 93–106. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Shiha, F. Order patterns in time series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Keller, K.; Sinn, M.; Emonds, J. Time series from the ordinal viewpoint. Stoch. Dyn. 2007, 7, 247–272. [Google Scholar] [CrossRef]
- Amigó, J.M. Permutation Complexity in Dynamical Systems. Ordinal Patterns, Permutation Entropy and All That; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pompe, B.; Runge, J. Momentary information transfer as a coupling measure of time series. Phys. Rev. E 2011, 83, 051122. [Google Scholar] [CrossRef] [PubMed]
- Unakafova, V.A.; Keller, K. Efficiently measuring complexity on the basis of real-world data. Entropy 2013, 15, 4392–4415. [Google Scholar] [CrossRef]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal patterns, entropy, and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Antoniouk, A.; Keller, K.; Maksymenko, S. Kolmogorov–Sinai entropy via separation properties of order-generated σ-algebras. Discret. Contin. Dyn. Syst. A 2014, 34, 1793–1809. [Google Scholar]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation Entropy: New Ideas and Challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Unakafov, A.M.; Keller, K. Conditional entropy of ordinal patterns. Physica D 2014, 269, 94–102. [Google Scholar] [CrossRef]
- Unakafov, A.M. Ordinal-Patterns-Based Segmentation and Discrimination of Time Series with Applications to EEG Data. Ph.D. Thesis, University of Lübeck, Lübeck, Germany, 2015. [Google Scholar]
- Sinn, M.; Ghodsi, A.; Keller, K. Detecting Change-Points in Time Series by Maximum Mean Discrepancy of Ordinal Pattern Distributions. In Proceedings of the 28th Conference on Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, 14–18 August 2012; pp. 786–794. [Google Scholar]
- Sinn, M.; Keller, K.; Chen, B. Segmentation and classification of time series using ordinal pattern distributions. Eur. Phys. J. Spec. Top. 2013, 222, 587–598. [Google Scholar] [CrossRef]
- Unakafov, A.M. Change-Point Detection Using the Conditional Entropy of Ordinal Patterns. 2017. Available online: https://mathworks.com/matlabcentral/fileexchange/62944-change-point-detection-using-the-conditional-entropy-of-ordinal-patterns (accessed on 13 September 2018).
- Stoffer, D.S. Frequency Domain Techniques in the Analysis of DNA Sequences. In Handbook of Statistics: Time Series Analysis: Methods and Applications; Rao, T.S., Rao, S.S., Rao, C.R., Eds.; Elsevier: New York, NY, USA, 2012; pp. 261–296. [Google Scholar]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Keller, K. Permutations and the Kolmogorov–Sinai entropy. Discret. Contin. Dyn. Syst. 2012, 32, 891–900. [Google Scholar] [CrossRef]
- Pompe, B. The LE-statistic. Eur. Phys. J. Spec. Top. 2013, 222, 333–351. [Google Scholar] [CrossRef]
- Haruna, T.; Nakajima, K. Permutation complexity and coupling measures in hidden Markov models. Entropy 2013, 15, 3910–3930. [Google Scholar] [CrossRef]
- Sinn, M.; Keller, K. Estimation of ordinal pattern probabilities in Gaussian processes with stationary increments. Comput. Stat. Data Anal. 2011, 55, 1781–1790. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K. Permutation entropy: One concept, two approaches. Eur. Phys. J. Spec. Top. 2013, 222, 263–273. [Google Scholar] [CrossRef]
- Sinn, M.; Keller, K. Estimation of ordinal pattern probabilities in fractional Brownian motion. arXiv, 2008; arXiv:0801.1598. [Google Scholar]
- Bandt, C. Autocorrelation type functions for big and dirty data series. arXiv, 2003; arXiv:1411.3904. [Google Scholar]
- Elizalde, S.; Martinez, M. The frequency of pattern occurrence in random walks. arXiv, 2014; arXiv:1412.0692. [Google Scholar]
- Cao, Y.; Tung, W.; Gao, W.; Protopopescu, V.; Hively, L. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.J.; Wang, X.; Huang, Z.T.; Sha, Z.C. Detection of Radio Transient Signal Based on Permutation Entropy and GLRT. In Wireless Personal Communications; Wesley, Addison Longman Incorporated: Boston, MA, USA, 2015; pp. 1–11. [Google Scholar]
- Schnurr, A.; Dehling, H. Testing for structural breaks via ordinal pattern dependence. arXiv, 2015; arXiv:1501.07858. [Google Scholar]
- Thunberg, H. Periodicity versus chaos in one-dimensional dynamics. SIAM Rev. 2001, 43, 3–30. [Google Scholar] [CrossRef]
- Lyubich, M. Forty years of unimodal dynamics: On the occasion of Artur Avila winning the Brin prize. J. Mod. Dyn. 2012, 6, 183–203. [Google Scholar] [CrossRef]
- Linz, S.; Lücke, M. Effect of additive and multiplicative noise on the first bifurcations of the logistic model. Phys. Rev. A 1986, 33, 2694. [Google Scholar] [CrossRef]
- Diks, C. Nonlinear Time series analysis: Methods and Applications; World Scientific: Singapore, 1999. [Google Scholar]
- Vostrikova, L.Y. Detecting disorder in multidimensional random processes. Sov. Math. Dokl. 1981, 24, 55–59. [Google Scholar]
- Han, T.S.; Kobayashi, K. Mathematics of Information and Coding; Translated from the Japanese by J. Suzuki; American Mathematical Society: Providence, RI, USA, 2002; p. 286. [Google Scholar]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Gautama, T. Surrogate Data. MATLAB Central File Exchange. 2005. Available online: https://www.mathworks.com/matlabcentral/fileexchange/4612-surrogate-data (accessed on 13 September 2018).
- Polansky, A.M. Detecting change-points in Markov chains. Comput. Stat. Data Anal. 2007, 51, 6013–6026. [Google Scholar] [CrossRef]
- Kim, A.Y.; Marzban, C.; Percival, D.B.; Stuetzle, W. Using labeled data to evaluate change detectors in a multivariate streaming environment. Signal Process. 2009, 89, 2529–2536. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Applications; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lahiri, S.N. Resampling Methods for Dependent Data; Springer: New York, NY, USA, 2003. [Google Scholar]
- Härdle, W.; Horowitz, J.; Kreiss, J.P. Bootstrap methods for time series. Int. Stat. Rev. 2003, 71, 435–459. [Google Scholar] [CrossRef]
- Bühlmann, P. Bootstraps for time series. Stat. Sci. 2002, 17, 52–72. [Google Scholar] [CrossRef]
- Lavielle, M. Detection of multiple changes in a sequence of dependent variables. Stoch. Process. Their Appl. 1999, 83, 79–102. [Google Scholar] [CrossRef]
- Grassberger, P. Entropy estimates from insufficient samplings. arXiv, 2003; arXiv:physics/0307138. [Google Scholar]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Anderson, T.W.; Goodman, L.A. Statistical inference about Markov chains. Ann. Math. Stat. 1957, 28, 89–110. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).