Abstract
We review an argument that bipartite “PR-box” correlations, though designed to respect relativistic causality, in fact violate relativistic causality in the classical limit. As a test of this argument, we consider Greenberger–Horne–Zeilinger (GHZ) correlations as a tripartite version of PR-box correlations, and ask whether the argument extends to GHZ correlations. If it does—i.e., if it shows that GHZ correlations violate relativistic causality in the classical limit—then the argument must be incorrect (since GHZ correlations do respect relativistic causality in the classical limit.) However, we find that the argument does not extend to GHZ correlations. We also show that both PR-box correlations and GHZ correlations can be retrocausal, but the retrocausality of PR-box correlations leads to self-contradictory causal loops, while the retrocausality of GHZ correlations does not.
PACS:
03.65.Ta; 03.65.Ca; 03.30.+p; 03.65.Ud
Quantum mechanics might make more sense to us if we could derive it from simple axioms with clear physical content, instead of opaque axioms about Hilbert space. Aharonov [1,2] and, independently, Shimony [3,4] conjectured that quantum mechanics might follow from the two axioms of nonlocality and relativistic causality (no superluminal signalling). For example, quantum correlations respect relativistic causality, but they are nonlocal: they violate the Bell-CHSH [5,6,7] inequality. Could quantum mechanics be unique in reconciling these axioms, just as the special theory of relativity is unique in reconciling the axioms of relativistic causality and the equivalence of inertial frames? So-called “PR-box” [8] correlations disprove this conjecture. Like quantum correlations, they respect relativistic causality; but unlike quantum correlations, they violate the Bell-CHSH inequality maximally. Nevertheless, Ref. [9] argues that the addition of one minimal axiom of clear physical content—namely, the existence of a classical limit—suffices for ruling out PR-box correlations.
The additional axiom is minimal in the following sense: Quantum mechanics has a classical limit in which there are no uncertainty relations; there are only jointly measurable macroscopic observables. This classical limit—our direct experience—is an inherent constraint, a boundary condition, on quantum mechanics and on any generalization of quantum mechanics. Thus PR-box correlations, too, must have a classical limit. Reference [9] argues that in this classical limit, PR-box correlations (and, by extension [10,11], all stronger-than-quantum bipartite correlations) allow observers “Alice” and “Bob” to exchange superluminal signals. (A similar statement appears in Ref. [12] with “macroscopic locality” taking the place of “classical limit”. Yet Ref. [12] assumes that Alice and Bob can detect fluctuations of order in their measurements, an assumption we do not make.) The argument [9,10] relies on measurement sequences that are observable but exponentially improbable. It is therefore of interest to test the argument by applying it to a different problem. In particular, GHZ correlations [13] are a tripartite version of PR-box correlations in the sense of being all-or-nothing correlations (perfect correlations and anticorrelations). Could Alice, Bob and an additional observer, “Jim”, use GHZ correlations, in the classical limit, to exchange superluminal signals? Does the argument of Ref. [9] lead to this conclusion? If so, it is clearly an incorrect argument: quantum mechanics and its classical limit do not violate relativistic causality! The first section of this paper reviews the arguments of Ref. [9] and attempts to extend them to show how Alice, Bob and Jim could exchange superluminal signals in the classical limit; but this attempt fails. The second section compares PR-box and GHZ correlations to show how retrocausality is self-contradictory in the first case but not in the second.
1. GHZ and PR-Box Correlations in the Classical Limit
Let Alice and Bob make spacelike separated measurements on pairs of particles. For each pair (indexed by i), one member of the pair is in Alice’s laboratory, and she can choose to measure observables or (but not both) on it; the other member is in Bob’s laboratory, and Bob can choose to measure observables or (but not both) on it. All four observables , , and take values with equal probability. The definition of PR-box correlations,
implies that Alice can manipulate the correlations between the observables , of Bob’s particle by choosing whether to measure or : indeed, and are perfectly correlated if she measures (as both of them are perfectly correlated with her outcome), and perfectly anticorrelated if she measured (as is correlated with her outcome and is anticorrelated with it). Thus, even though Alice’s choice of measurement does not affect Bob’s distribution of either or , it does affect correlations between these two observables. So can Alice exploit these correlations to signal to Bob? No, she cannot, since, by assumption, and are incompatible and Bob cannot measure both. But, notably, this assumption cannot apply in the classical limit.
Following Ref. [9], we define the classical limit of PR-box correlations as follows: Macroscopic (classical) quantities are averages over arbitrarily large ensembles of microscopic observables. To see how this definition applies, let us consider an ensemble of N pairs shared by Alice and Bob and obeying Equation (1). Apparently, the N pairs are just as useless for signalling as one pair, since, for each pair, Bob is allowed to measure only or . But the classical limit as defined means that given a large enough ensemble, Bob can measure quantities which depend upon macroscopic averages such as and , obtaining some information about both of them. There is no fundamental limit on how many times Alice and Bob can repeat their measurements, hence no matter how large they choose N (so as to minimize the variances in B and ), there is no limit to the strength of the (anti-)correlations that they may observe.
Now let us imagine two possible scenarios. In one scenario, Alice measures consistently on all her N particles. In the other scenario, she measures consistently on all her N particles. What does Bob obtain from his measurements? The average value of B is . Even typical deviations of B are small, i.e., of order , so they disappear in the classical limit. Apparently the scenarios lead to the exact same conclusion: Bob cannot read Alice’s 1-bit message, encoded in her choice of what to measure.
Yet it will sometimes happen (with probability ) that B will take the value 1. If Alice and Bob repeat either scenario exponentially many times, they can produce arbitrarily many cases of . True, there will be measurement errors in Bob’s results, but in the classical limit Bob must obtain at least information about B . Now if Alice consistently measures , Bob can expect to obtain with probability close to . And he can also expect to obtain with the probability, and not with probability , because Alice’s choice has correlated with . Conversely, if Alice consistently measures , then Bob can expect to obtain with probability close to , and he can also expect to obtain with the probability, and not with probability , because Alice’s choice has anticorrelated with . Another way for Bob to get Alice’s message is to observe the variance in his measurements of : if Alice measures consistently, the distribution of (over repeated trials with N pairs at a time) is binomial, while the distribution of has zero variance, and vice versa in the other scenario. Thus Alice can send Bob a (superluminal) message in the classical limit.
It does not matter that the price of a one-bit message from Alice to Bob may be astronomical. As long as it is possible, at any price, it constitutes a violation of relativistic causality, which we cannot allow. Hence PR-box correlations violate relativistic causality in the classical limit, as claimed. (Note that we cannot obtain the classical limit by setting . Rather, we take N finite but arbitrarily large, and for any N, there is no fundamental bound on the number of times Alice and Bob can repeat their measurements in order to obtain the accuracy they need for B and , etc.)
Before proceeding to tripartite (GHZ) correlations, let us stop to consider bipartite correlations. Does the above argument imply that they, too, allow signalling in the classical limit? If so, it cannot be correct. Most similar to PR-box correlations are quantum correlations that saturate Tsirelson’s bound [14] for the Bell-CHSH inequalities. Without loss of generality, we can consider entangled pairs of spin-1/2 particles in the state . In this state, Alice and Bob always obtain perfect correlations if they measure spin along the same axes in the plane.
Quantum correlations saturate Tsirelson’s bound when , , and , where each of the four observables takes the values . (We suppress the index i.) Their correlations are
If Alice measures a, then b and are correlated with her results. If she measures , then b is correlated with her results and is anticorrelated. Can Bob thus detect what Alice measures? As in the discussion of PR-box correlations, we can compute and compare the variances of vs. . But, by definition, these observables correspond to and , respectively, i.e., to a and on Bob’s particle in the pair, which is left in the same state as Alice’s. Now if Alice measures a consistently on her particles and Bob measures , the variance in Bob’s results is maximal just because the variance in Alice’s results is maximal. (That is, she has equal probability to obtain ). Conversely, if Alice measures a consistently on her particles and Bob measures , the variance in Bob’s results is maximal simply because a measurement of after Alice measures a is equally likely to be , whatever Alice obtains. We thus find that the correlations in Equation (2) are not strong enough to induce any difference between the variances of the observables and . Indeed, they are the strongest correlations that do not induce such a difference and therefore do not permit signalling in the classical limit [10,11].
Reference [9] claims that correlations that are too strong violate relativistic causality in the classical limit, and that PR-box correlations are too strong because they provide absolute “all or nothing” correlations. But quantum mechanics, as well, provides “all or nothing” correlations. Consider a triplet of spin-half particles in a GHZ state shared by Alice, Bob and Jim in their respective laboratories. Suppose that these observers measure either or on their respective particles. Let denote Alice’s outcome from a measurement of (the x component of the spin of her particle) and let denote Alice’s outcome from a measurement of (the y component of the spin), with analogous notations for Bob and Jim. The state is an eigenstate of the following four operators, satisfying
The implication is that if all three observers measure on their particles, they will discover that . Similarly, if the appropriate measurements are carried out, they will discover that as in Equation (3). In their famous paper [13], Greenberger, Horne and Zeilinger (GHZ) used these facts to show that there is no way to assign simultaneous values consistently to all six variables , , , , and . This fact rules out any local hidden variable model for the GHZ state.
Can Alice, Bob and Jim use GHZ states to signal? For definiteness, let us assume that Jim tries to send a signal to Alice and Bob via his choice of what to measure, or . Before going to the classical limit, let’s ask whether Jim can send Alice and Bob a signal using just a few triplets. Note that if Jim measures and gets , then and must be correlated; we write . In the same notation, . In fact, if Jim measures , we find whatever he gets. On the other hand, if Jim measures , we obtain the analogous equation , whatever he gets, and no correlation between and or and . Are these correlations of any use? Alice and Bob measure all their observables to infer Jim’s choice.
But the commutation relations
imply that Alice and Bob obtain and to see if they are anticorrelated or, alternatively, can obtain and to see if they are correlated! In the first case, Jim must have measured and in the second case, he must have measured . Right?
Wrong. This scheme fails. To see why, we first note that if Alice and Bob measure both and , they will certainly find that simply because the product of operators equals , which yields when applied to . Likewise, if Alice and Bob measure both and , they will verify that , simply because the product of operators equals , which yields 1 when applied to . In fact, Alice and Bob can learn nothing about Jim’s choice from their measurements.
We are back to square one. So let us try to apply the classical-limit argument of Ref. [9]. By analogy with Ref. [9], let Alice, Bob and Jim make collective measurements on ensembles of N triplets at a time, with Jim measuring either or consistently on his particles. For large enough N, we can define a collective variable , if Jim chooses to measure , or alternatively , if he chooses to measure , where the and represent Jim’s particles in any given ensemble. (As before, we suppress the index i.) We can then define also the collective variables , , and . In some (rare) cases, one or more of these collective variables may even reach . Above we noted that, for a given triplet of particles, Alice and Bob cannot measure all their observables , , and to infer Jim’s choice. But, according to the classical-limit argument, there cannot be such complementary between and , or between and . Alice and Bob must have access to at least information about all these variables. True, their expectation values all vanish, but if Alice, Bob and Jim repeat their measurements exponentially many times, they will find fluctuations as large as . Since Equation (3) involves products, we cannot directly sum over it to get a relation between or and , , and . Even so, suppose Jim measures and obtains for every particle in his ensemble. Then for each of the other two particles in the triplet, and are correlated and and are anticorrelated. But Alice and Bob will not be able to detect this correlation unless another “miracle” occurs, in addition to the “miracle” that happened in Jim’s laboratory. For example, suppose that . It follows from Equation (3) that (up to fluctuations due to measurement errors). Then Alice and Bob could compare their results for and to uncover a striking correlation between them and conclude that Jim had measured and not .
But this conclusion can be valid only if the statistics support it. In this scenario, we have assumed rare fluctuations: and . Since the two fluctuations are independent, their combined probability is the product of their individual probabilities, namely . For this rare scenario, we don’t need to assume also that ; Equation (3) requires it. Thus, with probability , Alice and Bob will obtain . Does this result imply that Jim consistently measured on his particles? How likely is it that Alice and Bob would have obtained and if Jim had chosen to measure on all his particles, making and uncorrelated? The probability would have been , exactly the same. So, once again, Alice and Bob have no way of reading Jim’s one-bit message (his choice of what to measure). Likewise, Alice and Bob can try to signal to Jim by, say, measuring . If they get , Jim will certainly obtain . But the probability that Jim will obtain by chance is , at least as large as the probability that Alice and Bob will obtain or even the probability that Alice and Bob will obtain for all the N pairs in their ensemble.
The statistics don’t work out in the case of GHZ triplets as they do in the case of PR-box pairs. We therefore conclude that despite the similarity between Equations (1) and (3), GHZ correlations do not allow Jim to signal to Alice and Bob by choosing which observable to measure (at least via the above attempts), even if we assume a classical limit in which they can measure the ensemble averages of incompatible observables. The argument of Ref. [9] passes the test we prepared for it.
2. Retrocausality in PR-Box and GHZ Correlations
Instantaneous signalling directly violates relativity theory, opening the door to causal loops and contradictions. In particular, consider the classical limit of a PR-box ensemble, with Alice sending one bit of information to distant Bob. In an “unprimed” reference frame, Bob receives Alice’s message instantaneously (at time ); but in an appropriate “primed” reference frame, Alice’s bit could be a message into the past, e.g., Bob receives her bit (at time ) before she sends it (at time ). Applying the principle of relativity, we infer that in the primed reference frame, Bob could send a bit at time that Alice would receive instantaneously (at time ) before sending . Then if Alice’s device is set to echo whatever message she receives from Bob (so that ), and Bob’s device is set to yield the inverse of the message he receives from Alice (so that ), together they create a self-contradictory causal loop, as in Figure 1.
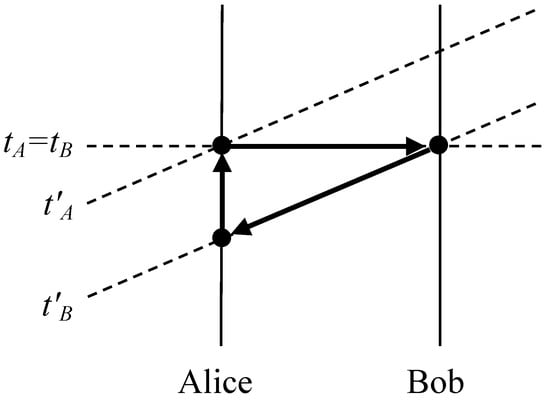
Figure 1.
The horizontal dotted line represents an equal-time surface in the unprimed frame, while the tilted dotted lines represent two equal-time surfaces in the primed frame. The arrows, each representing a cause and an effect, form a closed causal loop.
From this example it may seem obvious that PR-box correlations and GHZ correlations are distinguished, in that PR-box correlations in the classical limit can be retrocausal, and create self-contradictory causal loops, whereas GHZ correlations cannot be retrocausal. It is therefore of interest to note that this distinction is valid. GHZ correlations can be understood as retrocausal, as well! Yet the predictions implied by Equation (3) do not create causal loops. How can quantum correlations affect distant or past events without creating causal loops?
Reference [15] imagines an action called “jamming” in which Jim “the Jammer” can, by pushing a button on a device he holds, decide at any moment whether to turn an ensemble of entangled pairs of particles shared by Alice and Bob into a product state. Although jamming is action at a distance, it is consistent with relativistic causality if two conditions are met. The first condition, the condition, states that Alice and Bob cannot infer Jim’s decision from the results of their measurements. For example, if—regardless of Jim’s decision—Alice measures either a or , and obtains results with equal probability, and likewise Bob measures either b or , and obtains results with equal probability, then the unary condition is fulfilled. The condition states that if is the spacetime event of Alice’s measurements on her ensemble, is the spacetime event of Bob’s measurements on ensemble, and is the spacetime of event of Jim pushing the button on his device, then the overlap of the forward light cones of and lies entirely within the forward light cone of . (See Figure 2). As shown in Ref. [15], if jamming obeys the unary and binary conditions, then it is consistent with relativistic causality even though and may be earlier in time than . While jamming is natural in the context of quantum information theory, in Ref. [15] it provides an example of how a nonlocal equation of motion can be consistent with the no-signalling constraint.
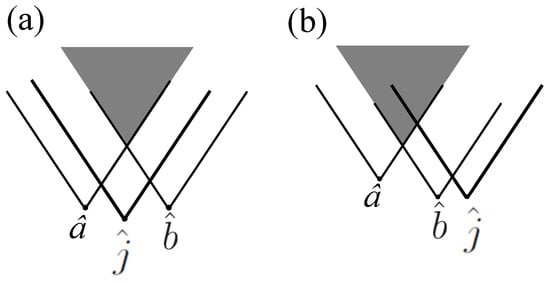
Figure 2.
The overlap of the future light cones of and either (a) lies or (b) does not lie entirely within the future light cone of .
We return now to the GHZ correlations of Equation (3) and show that they permit jamming [16]. Suppose Alice, Bob and Jim share an ensemble of particle triplets in the GHZ state. If Jim consistently measures , he disentangles Alice’s particles from Bob’s, regardless of the outcomes he gets. If he measures , Alice’s particles remain entangled with Bob’s particles, and their spins are correlated. For example, and are perfectly correlated or perfectly anticorrelated, depending on Jim’s outcome. If the information regarding Jim’s outcomes is delivered to Alice and Bob, they can bin their measurements in two ensembles corresponding to Jim’s outcomes . They will find that their results, within each ensemble, are perfectly (anti-)correlated in the case that Jim had chosen to measure , or uncorrelated in case he had measured .
This realization of jamming satisfies the unary condition because, regardless of Jim’s decision, Alice’s measurements of average to zero, and likewise for Bob’s measurements of . It fulfills the binary condition because Jim must report to Alice and Bob the results of his measurements of or for them to determine, from the results of their measurements, whether their pairs were entangled or not. Now, Alice and Bob can make their determination only in the overlap of the future light cones of and , which must lie in the future light cone of for them to receive Jim’s input. Thus jamming via GHZ triplets is consistent with relativistic causality. Nevertheless, Jim’s decision, whether to leave the pairs shared by Alice and Bob in entangled or product states, can take place even later than and , and even at a timelike separation from both measurements and . (See Figure 3). Even then, it is only in the forward light cone of that Alice and Bob can combine their data and determine whether Jim jammed their measurements.
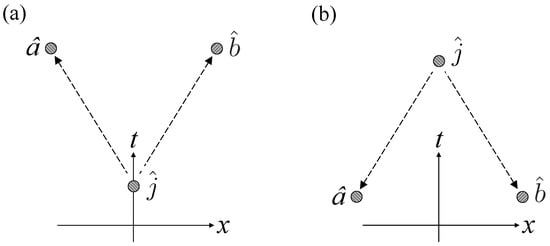
Figure 3.
Configurations in which Jim can (a) causally and (b) retrocausally put pairs of particles shared by Alice and Bob in product or entangled states, as he chooses. The dashed arrows connect cause with effect.
So what makes PR-box correlations different from GHZ correlations, such that the former violate relativistic causality (in the classical limit) while the latter do not? We might have replied, “PR-box correlations are retrocausal whereas GHZ correlations are not”. But we have just seen that this distinction fails. So let us return to our comparison, in the first section, of PR-box correlations and bipartite quantum correlations. We noted that even quantum correlations that violate the Bell-CHSH inequality maximally are not strong enough to permit signalling. Are GHZ correlations, which like PR-box correlations can be 0 or 1, strong enough? No! They are indeed stronger, but their strength dissipates over the two stages Alice and Bob require in attempting to receive Jim’s signal. Relativistic causality in the classical limit is a subtle, but effective, constraint on quantum mechanics.
We introduced this work by stating that three axioms with clear physical meaning, namely nonlocality, relativistic causality, and the existence of a classical limit, might be sufficient for deriving quantum mechanics, or at least an important part of the theory. We can consider reducing these three axioms to two simply by eliminating nonlocality as an axiom. Indeed, axioms in physical theories are, in general, constraints. The constraint of locality could be an axiom, but absence of this constraint need not be an axiom. And it seems from our work that quantum mechanics is just as nonlocal as it can be without violating relativistic causality. The retrocausality we have seen in jamming via GHZ correlations suggests that also retrocausality, like nonlocality, can appear wherever it is not forbidden by relativistic causality.
Author Contributions
Daniel Rohrlich proposed the calculations and the authors contributed equally to the writing and revisions of the paper.
Acknowledgments
We thank all the Referees for helpful comments. This publication was made possible through the support of grants from the John Templeton Foundation (Project ID 43297), from the Israel Science Foundation (grant no. 1190/13). The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of either of these supporting foundations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aharonov, Y.; University of South Carolina, Columbia, SC, USA. Unpublished Lecture Notes.
- Aharonov, Y.; Rohrlich, D. Quantum Paradoxes: Quantum Theory for the Perplexed; Wiley-VCH: Weinheim, Germany, 2005; Chapters 6, 18. [Google Scholar]
- Shimony, A. Controllable and uncontrollable nonlocality. In Foundations of Quantum Mechanics in Light of the New Technology; Kamefuchi, S., Fujikawa, K., Eds.; Japan Physical Society: Tokyo, Japan, 1983; p. 225. [Google Scholar]
- Shimony, A. Events and processes in the quantum world. In Quantum Concepts of Space and Time; Penrose, R., Isham, C., Eds.; Clarendon Press: Oxford, UK, 1986; p. 182. [Google Scholar]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Bell, J.S. The theory of local beables. Epist. Lett. 1976, 9, 11. [Google Scholar]
- Popescu, S.; Rohrlich, D. Quantum nonlocality as an axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Rohrlich, D. PR-box correlations have no classical limit. In Quantum Theory: A Two-Time Success Story [Yakir Aharonov Festschrift]; Struppa, D.C., Tollaksen, J.M., Eds.; Springer: Milan, Italy, 2013; pp. 205–211. [Google Scholar]
- Rohrlich, D. Stronger-than-quantum bipartite correlations violate relativistic causality in the classical limit. arXiv, 2014; arXiv:1408.3125. [Google Scholar]
- Gisin, N. Quantum correlations in Newtonian space and time: Faster than light communication or nonlocality. In (The Frontiers Collection) Quantum [Un]Speakables II: Half a Century of Bell’s Theorem; Bertlmann, R., Zeilinger, A., Eds.; Springer: Berlin, Germany, 2017; pp. 321–330. [Google Scholar]
- Navascués, M.; Wunderlich, H. A glance beyond the quantum model. Proc. R. Soc. A 2010, 466, 881–890. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.; Zeilinger, A. Going beyond Bell’s theorem. In Bell’s Theorem, Quantum Theory, and Conceptions of the Universe; Kafatos, M., Ed.; Kluwer Academic Pub.: Dordrecht, The Netherlands, 1989; pp. 69–72. [Google Scholar]
- Tsirelson, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93–100. [Google Scholar] [CrossRef]
- Grunhaus, J.; Popescu, S.; Rohrlich, D. Jamming nonlocal quantum correlations. Phys. Rev. A 1996, 53, 3781–3874. [Google Scholar] [CrossRef] [PubMed]
- Rohrlich, D. Three attempts at two axioms for quantum mechanics. In Probability in Physics; Ben-Menahem, Y., Hemmo, M., Eds.; Springer: Berlin, Germany, 2012; pp. 187–200. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).