The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly México M8.2 Earthquake on 7 September 2017
Abstract
1. Introduction
2. Natural Time Analysis. The Entropy Defined in Natural Time and the Associated Complexity Measures
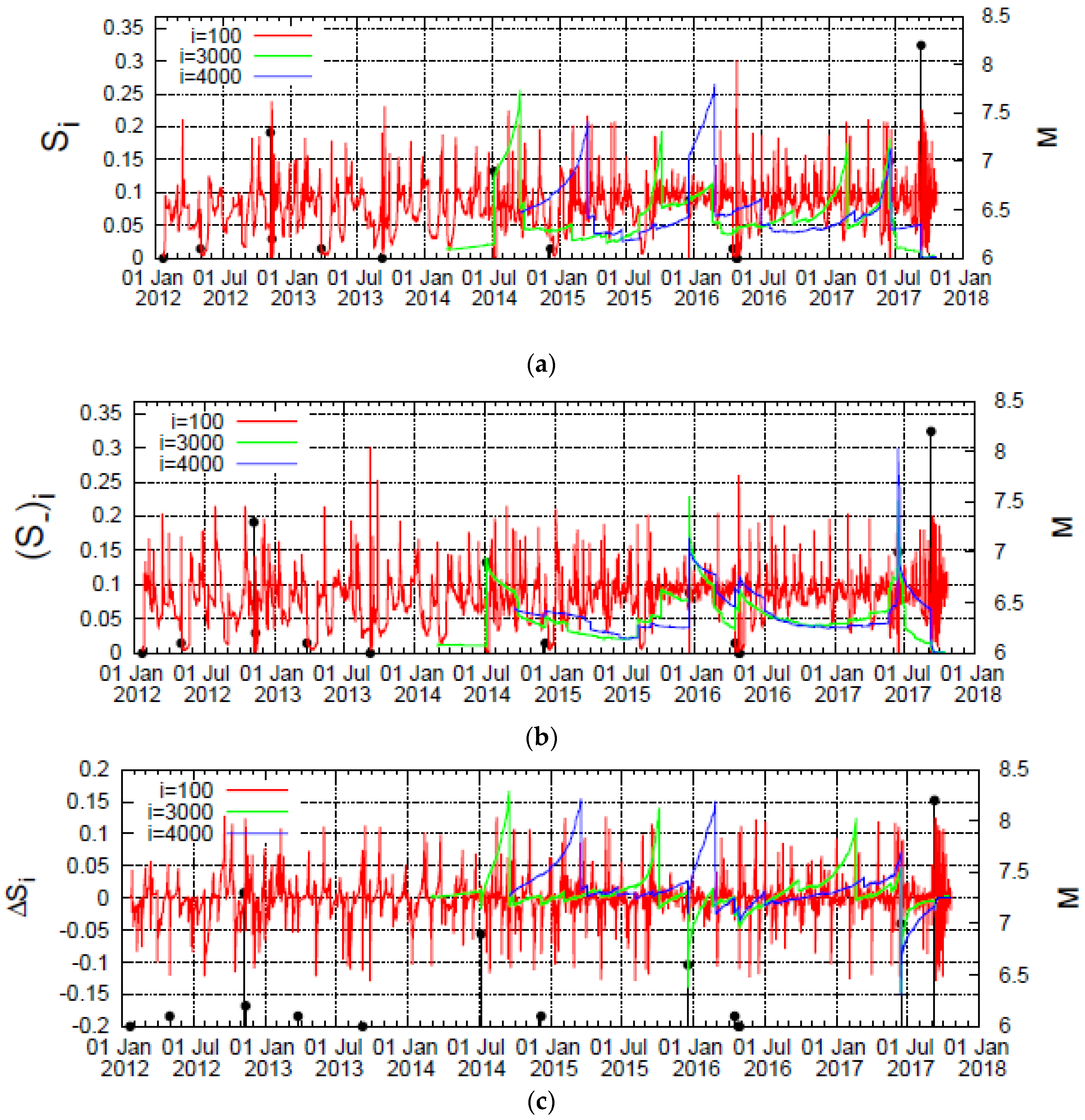
3. Data and Analysis
4. Results
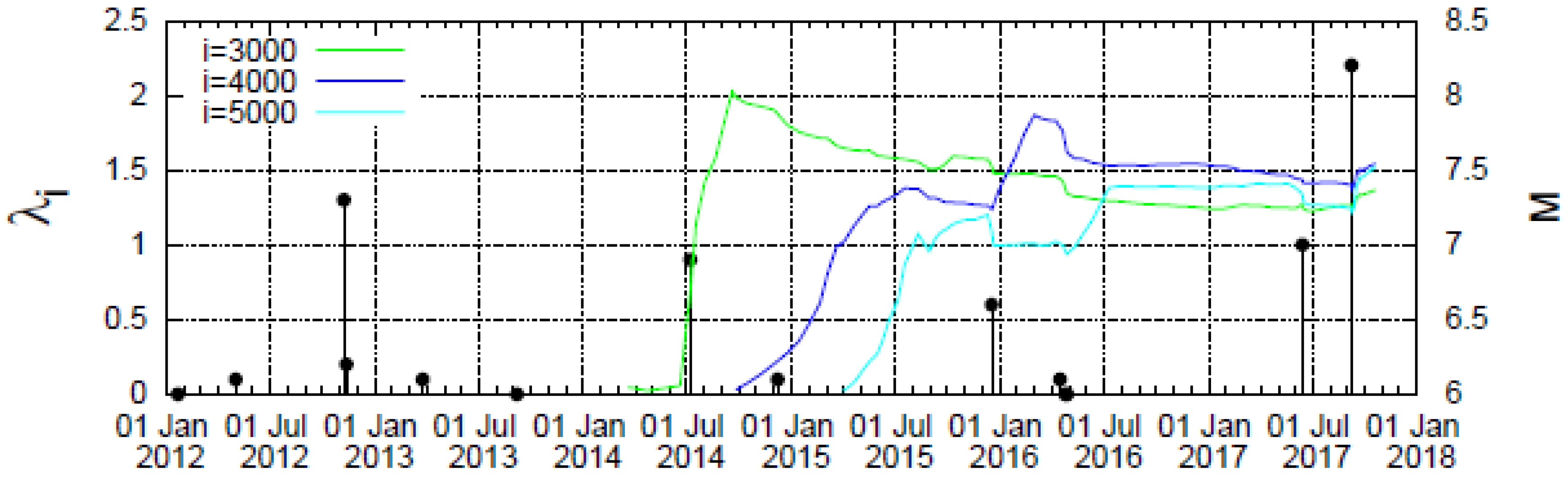
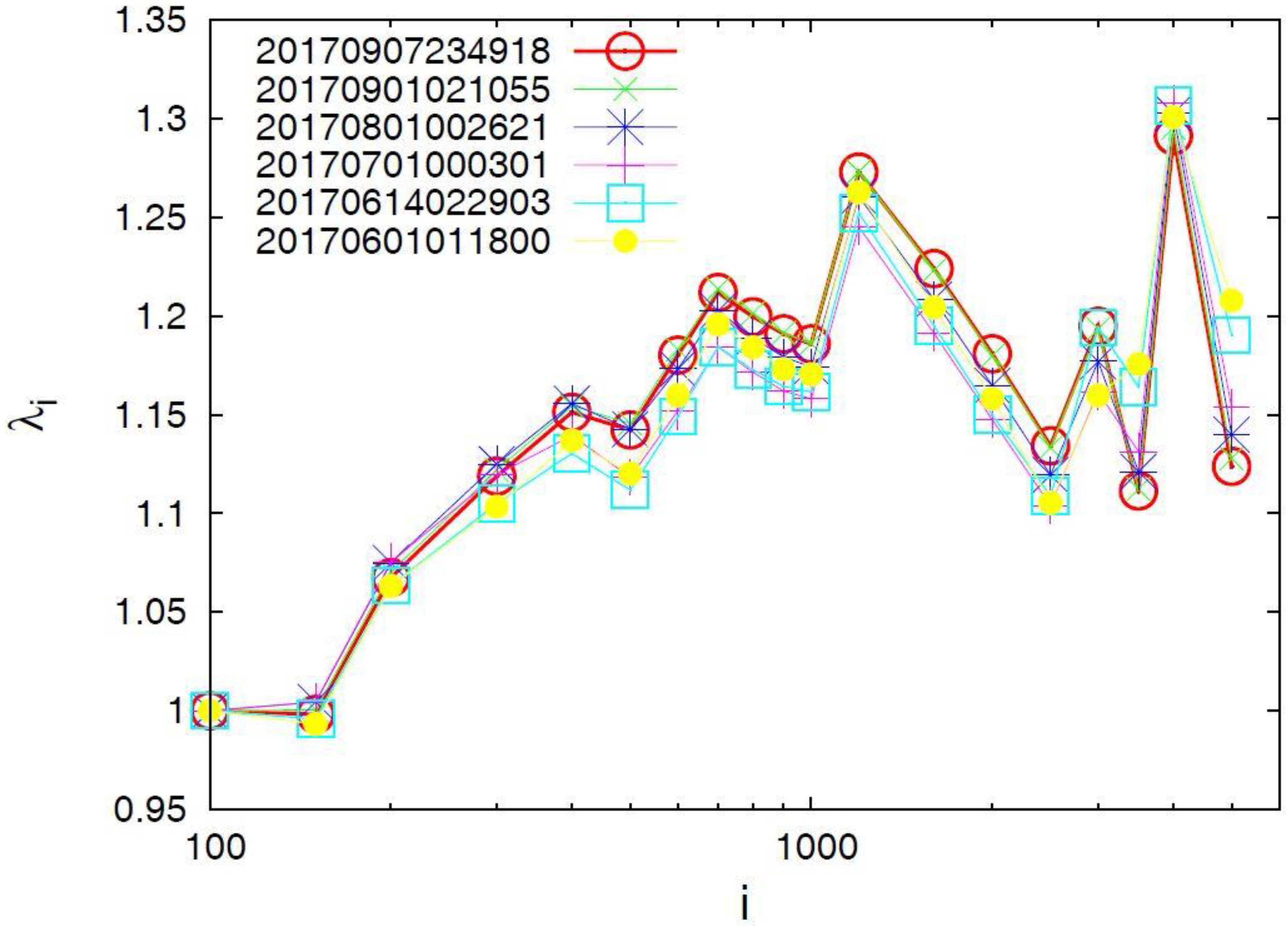
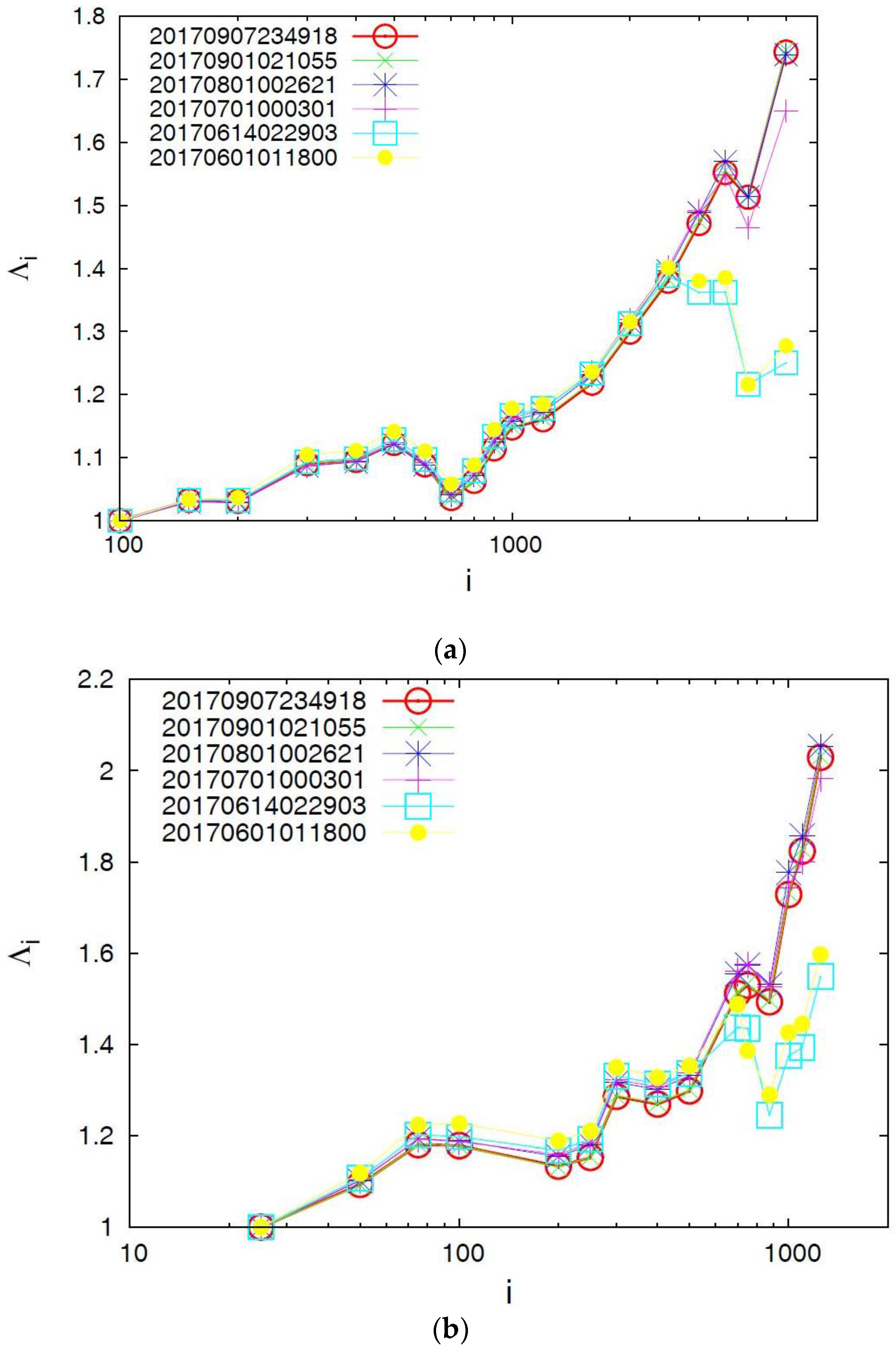
4.1. Results for the Complexity Measure λi
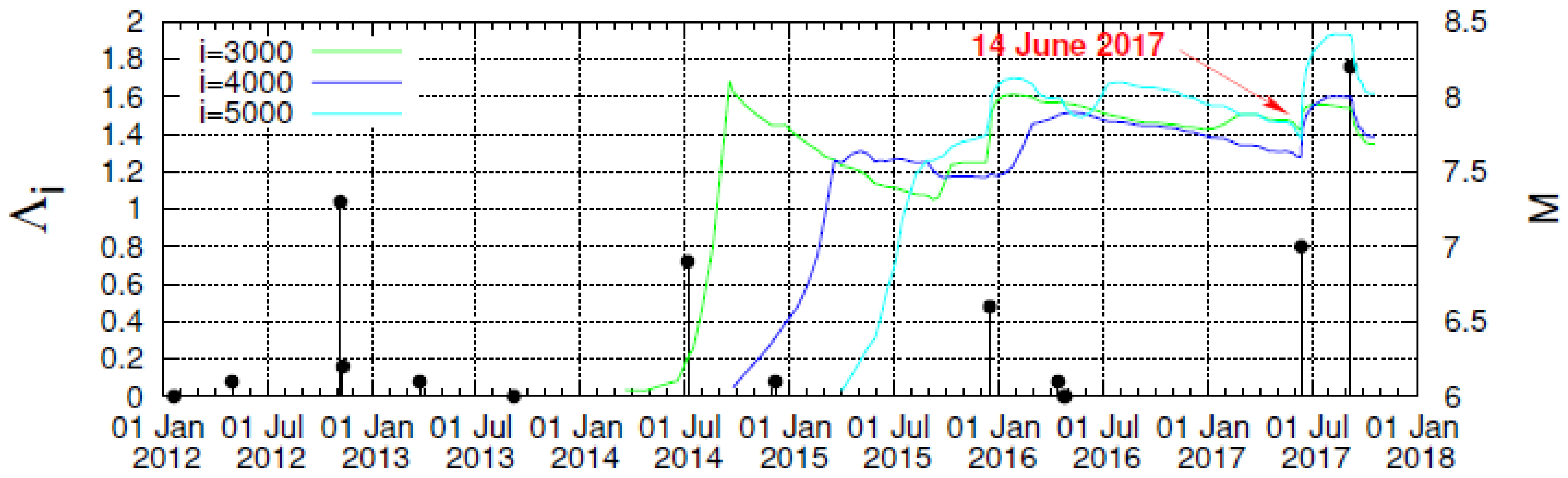
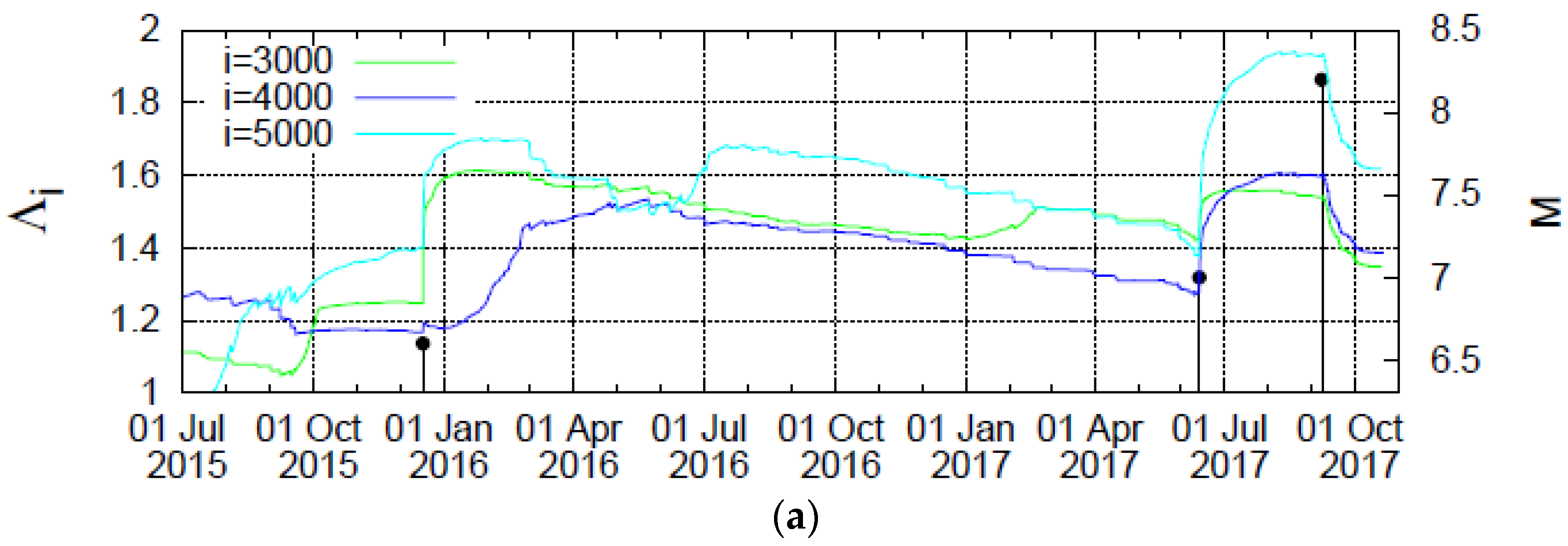
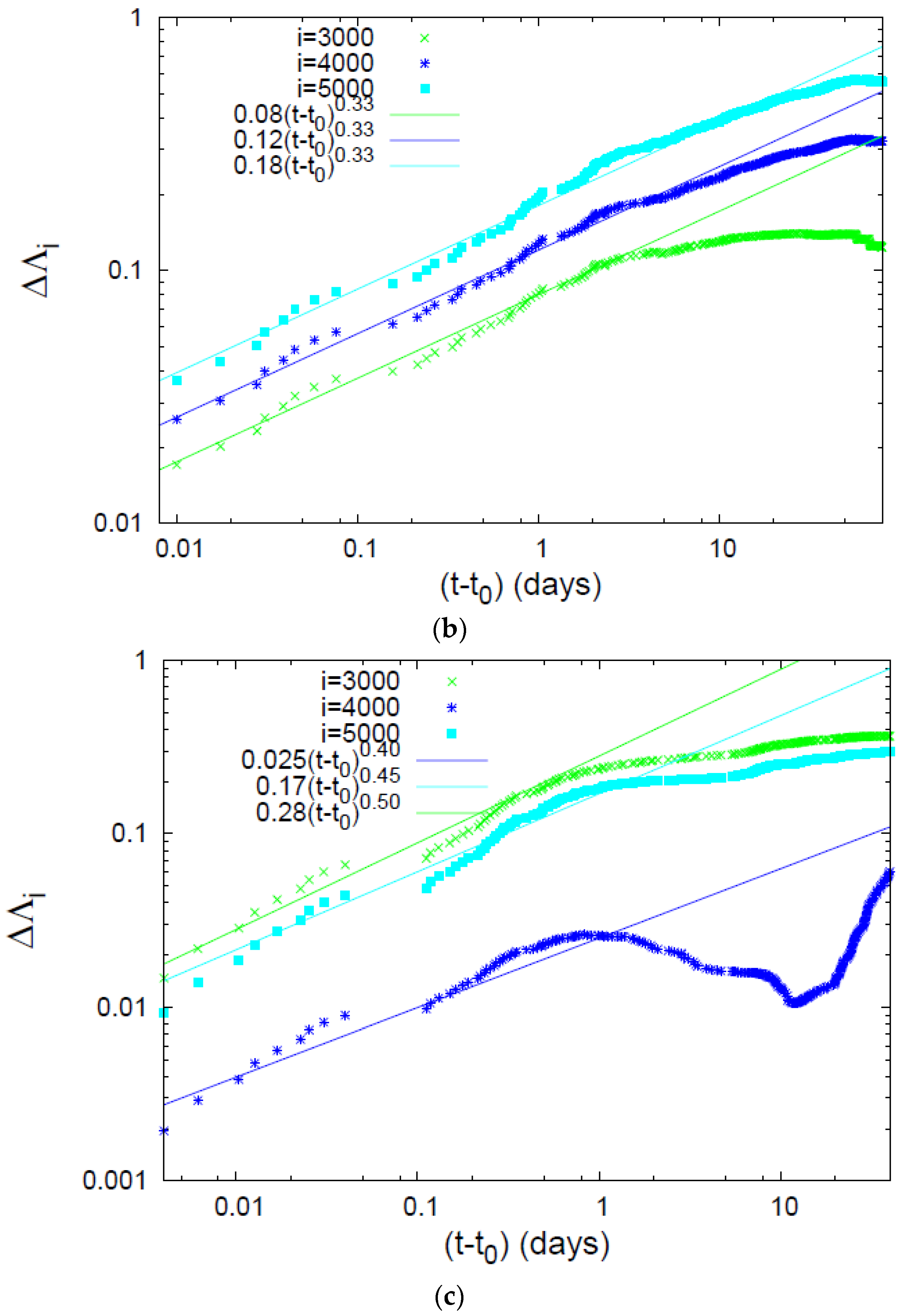
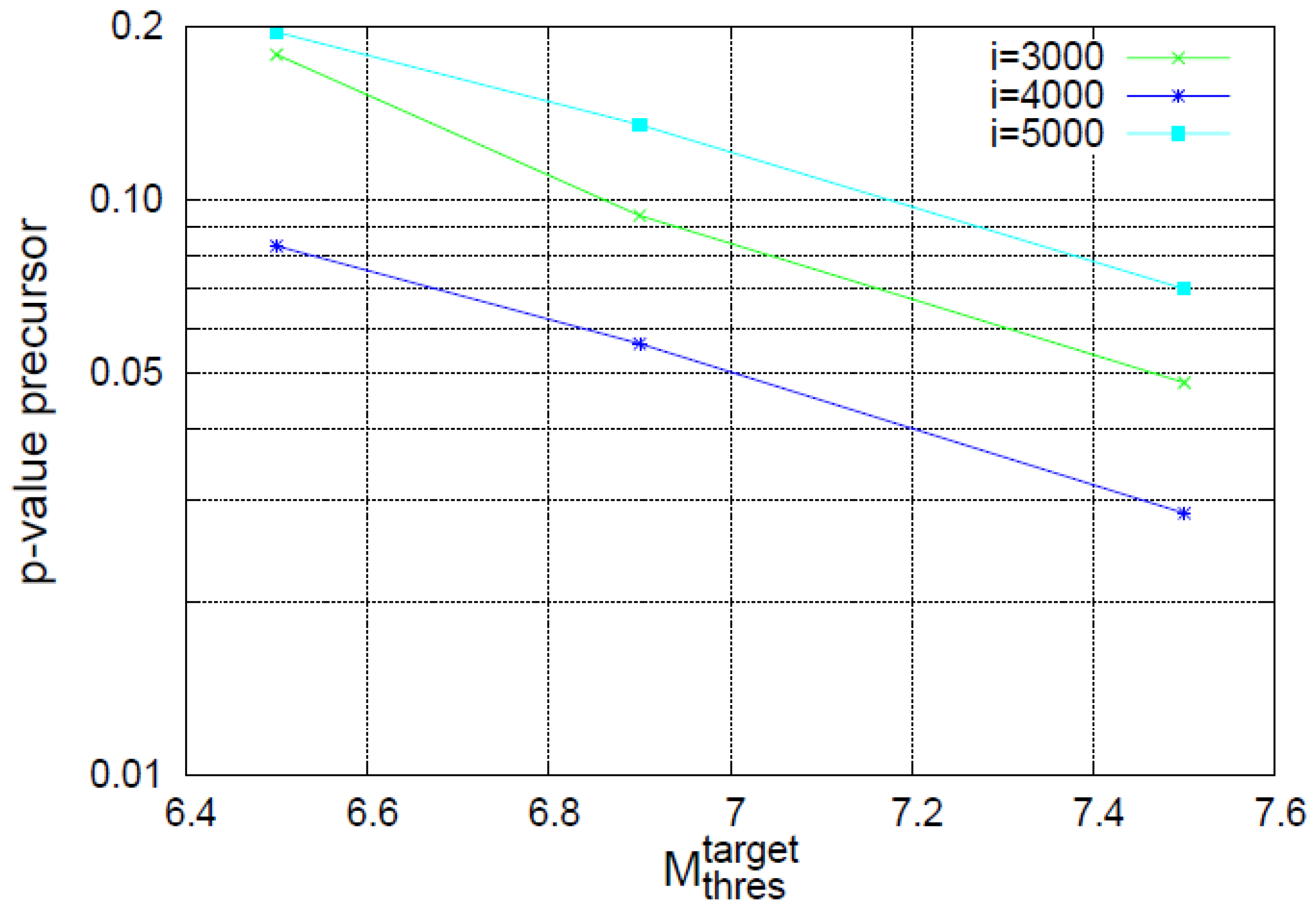
4.2. Results for the Complexity Measure Λi
5. Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Mega, E.R. Deadly Mexico earthquake had unusual cause. Nature 2017, 549. [Google Scholar] [CrossRef]
- Wade, L. Unusual quake rattles Mexico. Science 2017, 357, 1084. [Google Scholar] [CrossRef] [PubMed]
- Witze, A. Pair of deadly Mexico quakes puzzles scientists. Nature 2017, 549. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Campos, X.; Kim, Y.; Husker, A.; Davis, P.M.; Clayton, R.W.; Iglesias, A.; Pacheco, J.F.; Singh, S.K.; Manea, V.C.; Gurnis, M. Horizontal subduction and truncation of the Cocos Plate beneath central Mexico. Geophys. Res. Lett. 2008, 35, l18303. [Google Scholar] [CrossRef]
- Manea, V.; Manea, M.; Ferrari, L.; Orozco-Esquivel, T.; Valenzuela, R.; Husker, A.; Kostoglodov, V. A review of the geodynamic evolution of flat slab subduction in Mexico, Peru, and Chile. Tectonophysics 2016, 695 (Suppl. C), 27–52. [Google Scholar] [CrossRef]
- Witze, A. Deadly Mexico quakes not linked. Nature 2017, 549, 442. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Natural time analysis: On the deadly Mexico M8.2 earthquake on 7 September 2017. Phys. A 2018, 506, 625–634. [Google Scholar] [CrossRef]
- Olami, Z.; Feder, H.J.S.; Christensen, K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244–1247. [Google Scholar] [CrossRef] [PubMed]
- Ramos, O.; Altshuler, E.; Måløy, K.J. Quasiperiodic events in an earthquake model. Phys. Rev. Lett. 2006, 96, 098501. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Kantz, H. Prediction of extreme events in the OFC model on a small world network. Eur. Phys. J. 2011, 79, 7–11. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The new view of time. In Precursory Seismic Electric Signals, Earthquakes and Other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sarlis, N.; Skordas, E.; Varotsos, P. The change of the entropy in natural time under time-reversal in the Olami-Feder-Christensen earthquake model. Tectonophysics 2011, 513, 49–53. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Entropy in natural time domain. Phys. Rev. E 2004, 70, 011106. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Natural entropy fluctuations discriminate similar-looking electric signals emitted from systems of different dynamics. Phys. Rev. E 2005, 71, 011110. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S.; Uyeda, S.; Kamogawa, M. Natural time analysis of critical phenomena. Proc. Natl. Acad. Sci. USA 2011, 108, 11361–11364. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-temporal complexity aspects on the interrelation between seismic electric signals and seismicity. Pract. Athens Acad. 2001, 76, 294–321. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Some properties of the entropy in the natural time. Phys. Rev. E 2005, 71, 032102. [Google Scholar] [CrossRef] [PubMed]
- Lesche, B.J. Instabilities of Rényi entropies. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Lesche, B. Rényi entropies and observables. Phys. Rev. E 2004, 70, 017102. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Identifying sudden cardiac death risk and specifying its occurrence time by analysing electrocardiograms in natural time. Appl. Phys. Lett. 2007, 91, 064106. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 014906. [Google Scholar] [CrossRef]
- Nicholas, V.; Sarlis, S.; Christopoulos, R.G.; Bemplidaki, M.M. Change ΔS of the entropy in natural time under time reversal: Complexity measure upon change of scale. Eur. Lett. 2015, 109, 18002. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Garber, A.; Hallerberg, S.; Kantz, H. Predicting extreme avalanches in self-organized critical Sandpiles. Phys. Rev. E 2009, 80, 026124. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der Alterung von NiederschlagendurchUmlosen (Ostwald-Reifung). Z. Elektrochem. 1981, 65, 581–591. [Google Scholar]
- Bray, A.J. Theory of phase-ordering kinetics. Adv. Phys. 1994, 43, 357–459. [Google Scholar] [CrossRef]
- Siegmund, J.F.; Siegmund, N.; Donner, R.V. CoinCalc—A new R package for quantifying simultaneities of event series. Comput. Geosci. 2017, 98, 64–72. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1944, 49, 1685–1689. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Mantegna, R.N.; Simons, M.; Stanley, H.E. Statisticalproperties of DNA sequences. Phys. A 1995, 221, 180–192. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossoverphenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Posadas, A. Fragment-Asperity Interaction Model for Earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; França, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L. Maximum Likelihood Estimation of the Nonextensive Parameters of the Earthquake Cumulative 375 Magnitude Distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Nonextensive Statistical Seismology: An Overview. In Complexity of Seismic Time Series; Chelidze, T., Vallianatos, F., Telesca, L., Eds.; Elsevier: New York, NY, USA, 2018; pp. 25–59. [Google Scholar]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. A Nonextensive Statistical Physics Analysis of the 1995 Kobe, 379 Japan Earthquake. Pure Appl. Geophys. 2015, 172, 1923–1931. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Rojas, A.; Flores-Márquez, E.L.; Sarlis, N.V.; Varotsos, P.A. The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly México M8.2 Earthquake on 7 September 2017. Entropy 2018, 20, 477. https://doi.org/10.3390/e20060477
Ramírez-Rojas A, Flores-Márquez EL, Sarlis NV, Varotsos PA. The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly México M8.2 Earthquake on 7 September 2017. Entropy. 2018; 20(6):477. https://doi.org/10.3390/e20060477
Chicago/Turabian StyleRamírez-Rojas, Alejandro, Elsa Leticia Flores-Márquez, Nicholas V. Sarlis, and Panayiotis A. Varotsos. 2018. "The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly México M8.2 Earthquake on 7 September 2017" Entropy 20, no. 6: 477. https://doi.org/10.3390/e20060477
APA StyleRamírez-Rojas, A., Flores-Márquez, E. L., Sarlis, N. V., & Varotsos, P. A. (2018). The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly México M8.2 Earthquake on 7 September 2017. Entropy, 20(6), 477. https://doi.org/10.3390/e20060477





