Comparison of Compression-Based Measures with Application to the Evolution of Primate Genomes
Abstract
1. Introduction
2. Methods
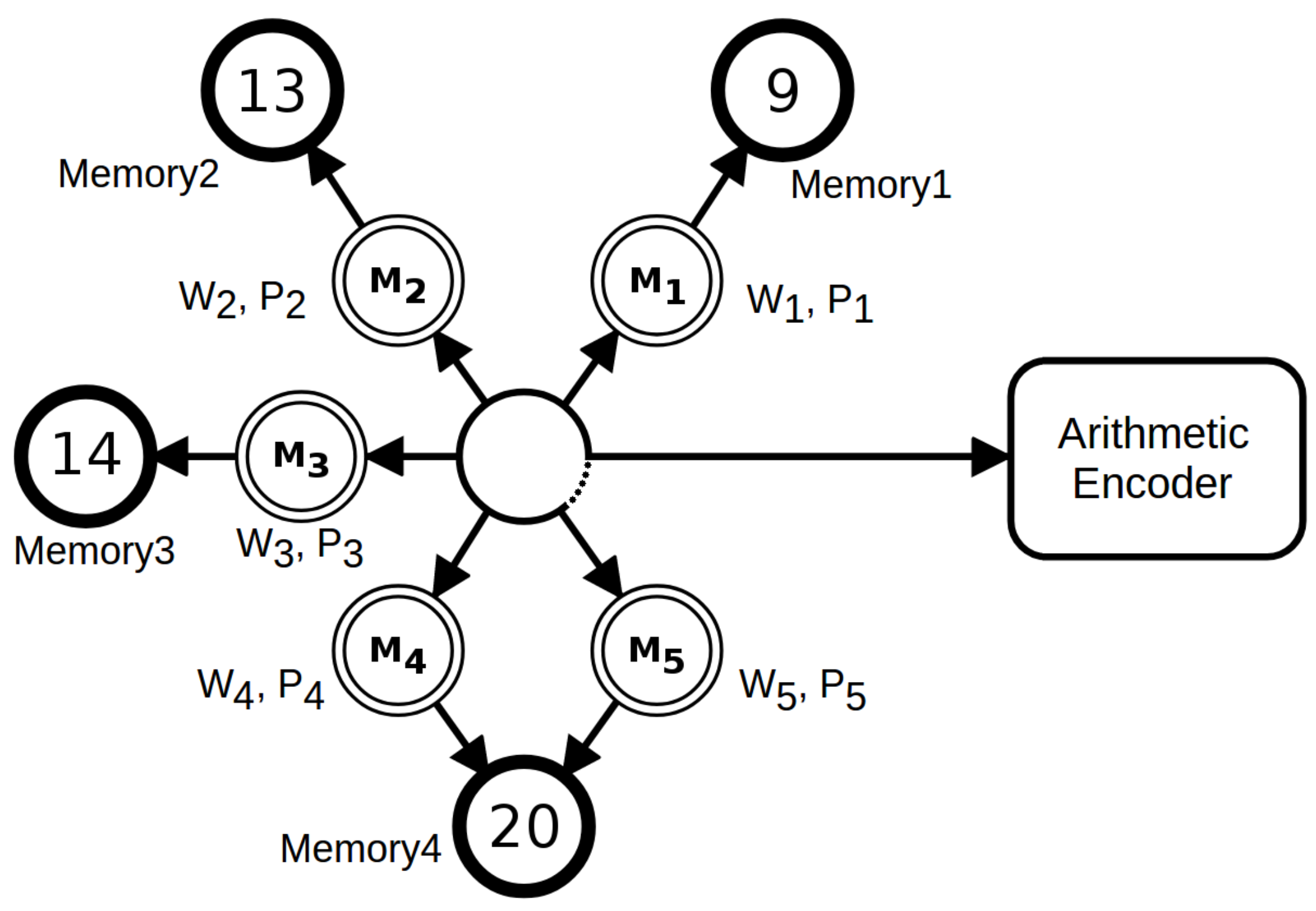
2.1. Compressor and Parameters
- → mixture of seven models with a decayment () of 0.95 and a cache-hash of 30:
- 1
- tolerant context model: depth: 17, alpha: 0.02, tolerance: 5;
- 2
- context model: depth: 17, alpha: 0.002, inverted repeats: no;
- 3
- tolerant context model: depth: 14, alpha: 0.1, tolerance: 3;
- 4
- context model: depth: 14, alpha: 0.005, inverted repeats: no;
- 5
- context model: depth: 11, alpha: 0.01, inverted repeats: no;
- 6
- context model: depth: 8, alpha: 0.1, inverted repeats: no;
- 7
- context model: depth: 5, alpha: 1, inverted repeats: no;
- and → mixture of eight models with a decayment () of 0.95 and a cache-hash of 30:
- 1
- tolerant context model: depth: 17, alpha: 0.1, tolerance: 5;
- 2
- context model: depth: 17, alpha: 0.005, inverted repeats: no;
- 3
- tolerant context model: depth: 14, alpha: 1, tolerance: 3;
- 4
- context model: depth: 14, alpha: 0.01, inverted repeats: no;
- 5
- context model: depth: 11, alpha: 0.1, inverted repeats: no;
- 6
- context model: depth: 8, alpha: 1, inverted repeats: no;
- 7
- context model: depth: 5, alpha: 1, inverted repeats: no;
- 8
- context model: depth: 3, alpha: 1, inverted repeats: no.
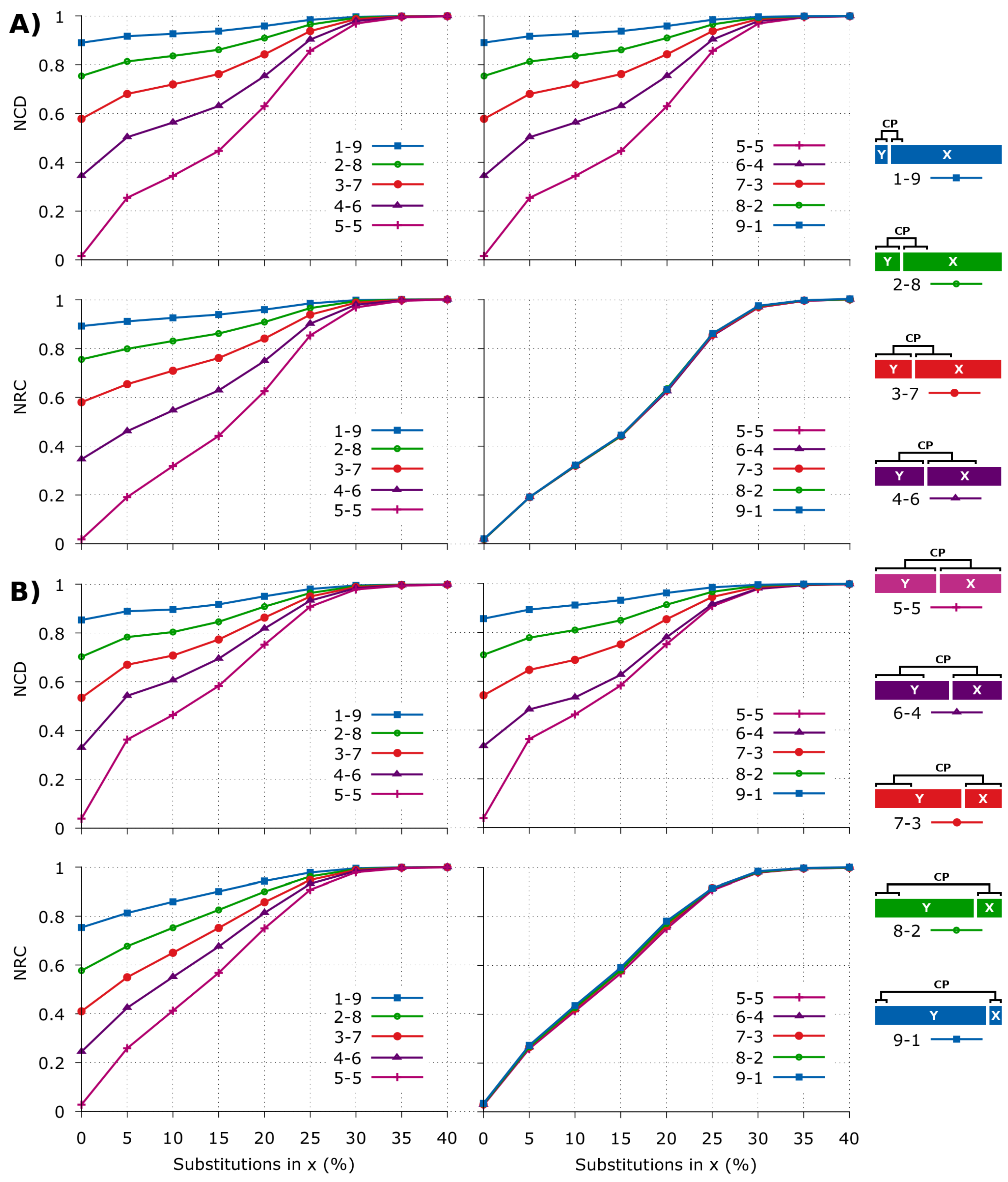
2.2. NCD versus NRC in Synthetic Data
3. Results
3.1. Dataset
3.2. Parameters
- mtDNA→ mixture of five models with a decayment () of 0.95:
- 1
- tolerant context model: depth: 13, alpha: 0.1, tolerance: 5;
- 2
- context model: depth: 13, alpha: 0.005, inverted repeats: yes;
- 3
- context model: depth: 10, alpha: 0.01, inverted repeats: yes;
- 4
- context model: depth: 6, alpha: 1, inverted repeats: no;
- 5
- context model: depth: 3, alpha: 1, inverted repeats: no;
- mRNA→ mixture of seven models with a decayment () of 0.88 and a cache-hash of 200:
- 1
- tolerant context model: depth: 20, alpha: 0.1, tolerance: 5;
- 2
- context model: depth: 20, alpha: 0.005, inverted repeats: yes;
- 3
- context model: depth: 14, alpha: 0.02, inverted repeats: yes;
- 4
- context model: depth: 13, alpha: 0.05, inverted repeats: no;
- 5
- context model: depth: 11, alpha: 0.1, inverted repeats: no;
- 6
- context model: depth: 9, alpha: 1, inverted repeats: no;
- 7
- context model: depth: 4, alpha: 1, inverted repeats: no;
- gDNA→ mixture of six models with a decayment () of 0.88 and a cache-hash of 250:
- 1
- tolerant context model: depth: 20, alpha: 0.1, tolerance: 5;
- 2
- context model: depth: 20, alpha: 0.005, inverted repeats: yes;
- 3
- context model: depth: 14, alpha: 0.02, inverted repeats: yes;
- 4
- context model: depth: 13, alpha: 0.05, inverted repeats: no;
- 5
- context model: depth: 11, alpha: 0.1, inverted repeats: no;
- 6
- context model: depth: 9, alpha: 1, inverted repeats: no.
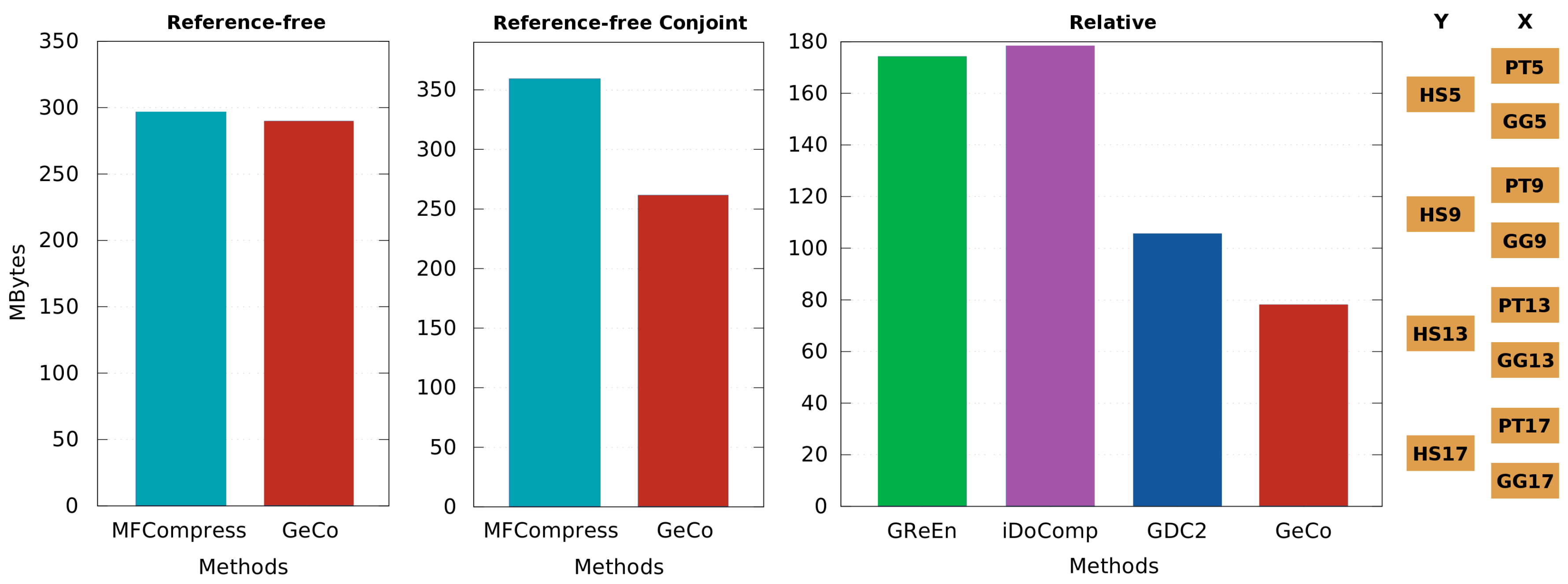
3.3. Comparison of Compressors
3.4. Expectation
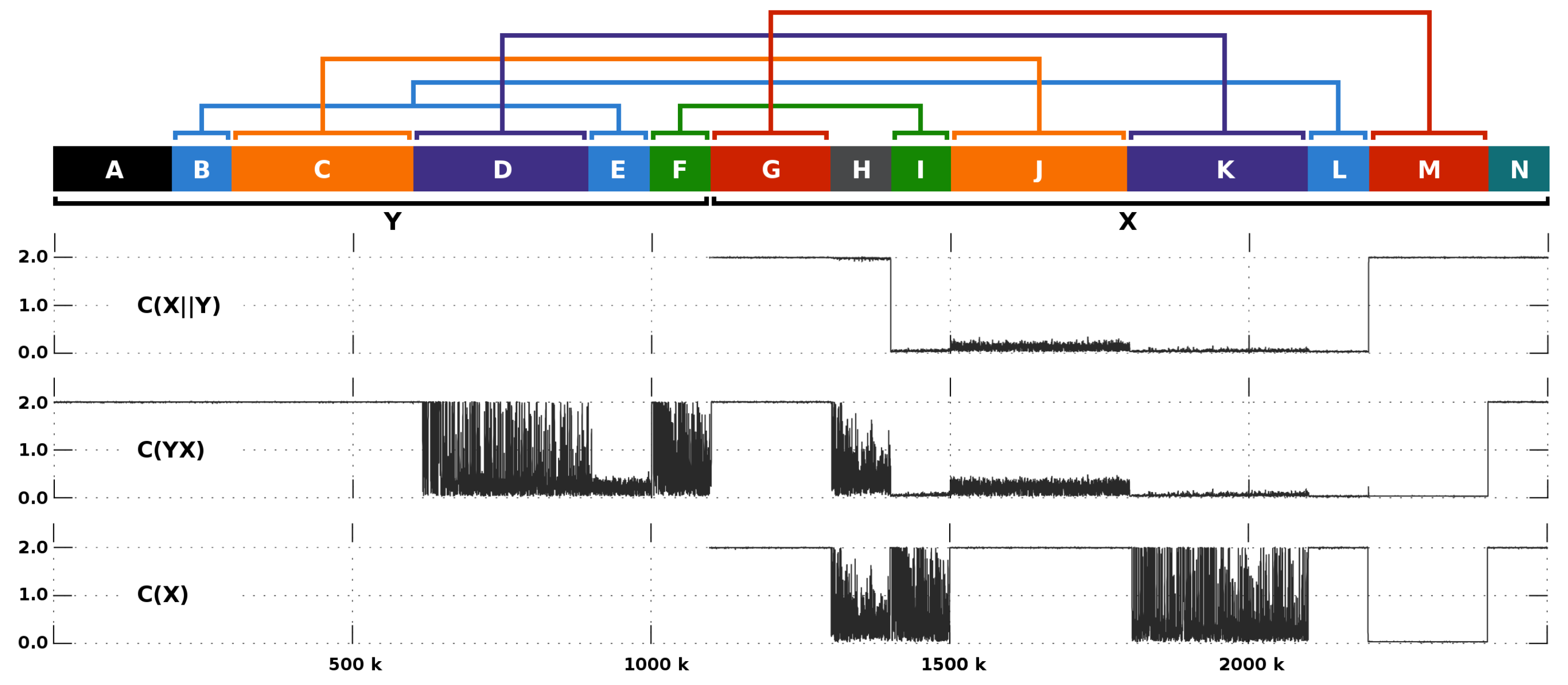
3.5. Primate Analysis
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| NC | Normalized Compression |
| NCD | Normalized Compression Distance |
| NRC | Normalized Relative Compression |
| DNA | Deoxyribonucleic acid |
| mtDNA | mitochondrial DNA |
| gDNA | nuclear DNA |
| cpDNA | chloroplast DNA |
| mRNA | messenger Ribonucleic acid |
| SNP | Single Nucleotide Polymorphism |
| GeCo | Genomic Compressor (tool) |
References
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Niven, R.K. Combinatorial entropies and statistics. Eur. Phys. J. B 2009, 70, 49–63. [Google Scholar] [CrossRef]
- Mantaci, S.; Restivo, A.; Rosone, G.; Sciortino, M. A new combinatorial approach to sequence comparison. Theory Comput. Syst. 2008, 42, 411–429. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inf. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part II. Inf. Control 1964, 7, 224–254. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. ACM 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Wallace, C.S.; Boulton, D.M. An information measure for classification. Comput. J. 1968, 11, 185–194. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Hutter, M. Algorithmic information theory: A brief non-technical guide to the field. arXiv, 2004; arXiv:cs/0703024. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications, 3rd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Levin, L.A. Laws of information conservation (nongrowth) and aspects of the foundation of probability theory. Problemy Peredachi Informatsii 1974, 10, 30–35. [Google Scholar]
- Shen, A.; Uspensky, V.A.; Vereshchagin, N. Kolmogorov Complexity and Algorithmic Randomness; American Mathematical Society: Providence, RI, USA, 2017. [Google Scholar]
- Hammer, D.; Romashchenko, A.; Shen, A.; Vereshchagin, N. Inequalities for Shannon entropy and Kolmogorov complexity. J. Comput. Syst. Sci. 2000, 60, 442–464. [Google Scholar] [CrossRef]
- Henriques, T.; Gonçalves, H.; Antunes, L.; Matias, M.; Bernardes, J.; Costa-Santos, C. Entropy and compression: Two measures of complexity. J. Eval. Clin. Pract. 2013, 19, 1101–1106. [Google Scholar] [CrossRef] [PubMed]
- Soler-Toscano, F.; Zenil, H.; Delahaye, J.P.; Gauvrit, N. Calculating Kolmogorov complexity from the output frequency distributions of small Turing machines. PLoS ONE 2014, 9, e96223. [Google Scholar] [CrossRef] [PubMed]
- Soler-Toscano, F.; Zenil, H. A computable measure of algorithmic probability by finite approximations with an application to integer sequences. Complexity 2017, 2017, 7208216. [Google Scholar] [CrossRef]
- Gauvrit, N.; Zenil, H.; Soler-Toscano, F.; Delahaye, J.P.; Brugger, P. Human behavioral complexity peaks at age 25. PLoS Comput. Biol. 2017, 13, e1005408. [Google Scholar] [CrossRef] [PubMed]
- Pratas, D.; Pinho, A.J. On the Approximation of the Kolmogorov Complexity for DNA Sequences. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Faro, Portugal, 20–23 June 2017; Springer: Berlin, Germany, 2017; pp. 259–266. [Google Scholar]
- Kettunen, K.; Sadeniemi, M.; Lindh-Knuutila, T.; Honkela, T. Analysis of EU languages through text compression. In Advances in Natural Language Processing; Springer: Berlin, Germany, 2006; pp. 99–109. [Google Scholar]
- Terwijn, S.A.; Torenvliet, L.; Vitányi, P.M.B. Nonapproximability of the normalized information distance. J. Comput. Syst. Sci. 2011, 77, 738–742. [Google Scholar] [CrossRef]
- Rybalov, A. On the strongly generic undecidability of the halting problem. Theor. Comput. Sci. 2007, 377, 268–270. [Google Scholar] [CrossRef]
- Bloem, P.; Mota, F.; de Rooij, S.; Antunes, L.; Adriaans, P. A safe approximation for Kolmogorov complexity. In Proceedings of the International Conference on Algorithmic Learning Theory, Bled, Slovenia, 8–10 October 2014; Springer: Berlin, Germany, 2014; pp. 336–350. [Google Scholar]
- Bennett, C.H.; Gács, P.; Vitányi, M.L.P.M.B.; Zurek, W.H. Information distance. IEEE Trans. Inf. Theory 1998, 44, 1407–1423. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitányi, P.M.B. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Cilibrasi, R.; Vitányi, P.M.B. Clustering by compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Ferragina, P.; Giancarlo, R.; Greco, V.; Manzini, G.; Valiente, G. Compression-based classification of biological sequences and structures via the universal similarity metric: Experimental assessment. BMC Bioinform. 2007, 8, 252. [Google Scholar] [CrossRef] [PubMed]
- El-Dirany, M.; Wang, F.; Furst, J.; Rogers, J.; Raicu, D. Compression-based distance methods as an alternative to statistical methods for constructing phylogenetic trees. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 1107–1112. [Google Scholar]
- Nikvand, N.; Wang, Z. Generic image similarity based on Kolmogorov complexity. In Proceedings of the 2010 17th IEEE International Conference on Image Processing (ICIP-2010), Hong Kong, China, 26–29 September 2010; pp. 309–312. [Google Scholar]
- Pratas, D.; Pinho, A.J. A conditional compression distance that unveils insights of the genomic evolution. In Proceedings of the Data Compression Conference (DCC-2014), Snowbird, UT, USA, 26–28 March 2014. [Google Scholar]
- Cebrián, M.; Alfonseca, M.; Ortega, A. The normalized compression distance is resistant to noise. IEEE Trans. Inform. Theory 2007, 53, 1895–1900. [Google Scholar] [CrossRef]
- Cebrián, M.; Alfonseca, M.; Ortega, A. Common pitfalls using the normalized compression distance: What to watch out for in a compressor. Commun. Inf. Syst. 2005, 5, 367–384. [Google Scholar]
- Seaward, L.; Matwin, S. Intrinsic plagiarism detection using complexity analysis. In Proceedings of the SEPLN, San Sebastian, Spain, 8–10 September 2009; pp. 56–61. [Google Scholar]
- Merivuori, T.; Roos, T. Some Observations on the Applicability of Normalized Compression Distance to Stemmatology. In Proceedings of the Second Workshop on Information Theoretic Methods in Science and Engineering, Tampere, Finland, 17–19 August 2009. [Google Scholar]
- Antão, R.; Mota, A.; Machado, J.T. Kolmogorov complexity as a data similarity metric: Application in mitochondrial DNA. Nonlinear Dyn. 2018, 4, 1–13. [Google Scholar] [CrossRef]
- Pratas, D.; Pinho, A.J.; Garcia, S.P. Computation of the Normalized Compression Distance of DNA Sequences using a Mixture of Finite-context Models. In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), Algarve, Portugal, 1–4 February 2012; pp. 308–311. [Google Scholar]
- La Rosa, M.; Rizzo, R.; Urso, A.; Gaglio, S. Comparison of genomic sequences clustering using Normalized Compression Distance and evolutionary distance. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Zagreb, Croatia, 3–5 September 2008; Springer: Berlin, Germany, 2008; pp. 740–746. [Google Scholar]
- Nykter, M.; Yli-Harja, O.; Shmulevich, I. Normalized Compression Distance for gene expression analysis. In Proceedings of the Workshop on Genomic Signal Processing and Statistics (GENSIPS), Newport, RI, USA, 22–24 May 2005. [Google Scholar]
- Nykter, M.; Price, N.D.; Aldana, M.; Ramsey, S.A.; Kauffman, S.A.; Hood, L.E.; Yli-Harja, O.; Shmulevich, I. Gene expression dynamics in the macrophage exhibit criticality. Proc. Natl. Acad. Sci. USA 2008, 105, 1897–1900. [Google Scholar] [CrossRef] [PubMed]
- Mihailović, D.T.; Mimić, G.; Nikolić-Djorić, E.; Arsenić, I. Novel measures based on the Kolmogorov complexity for use in complex system behavior studies and time series analysis. Open Phys. 2015, 13. [Google Scholar] [CrossRef]
- Tran, N. The normalized compression distance and image distinguishability. In Proceedings of the SPIE Human Vision and Electronic Imaging XII, San Jose, CA, USA, 29 January–1 February 2007; p. 64921D. [Google Scholar]
- Coltuc, D.; Datcu, M.; Coltuc, D. On the Use of Normalized Compression Distances for Image Similarity Detection. Entropy 2018, 20, 99. [Google Scholar] [CrossRef]
- Pinho, A.J.; Ferreira, P.J.S.G. Image similarity using the normalized compression distance based on finite context models. In Proceedings of the 2011 18th IEEE International Conference on Image Processing (ICIP-2011), Brussels, Belgium, 11–14 September 2011. [Google Scholar]
- Vázquez, P.P.; Marco, J. Using Normalized Compression Distance for image similarity measurement: An experimental study. Vis. Comput. 2012, 28, 1063–1084. [Google Scholar] [CrossRef]
- Nikvand, N.; Wang, Z. Image distortion analysis based on normalized perceptual information distance. Signal Image Video Process. 2013, 7, 403–410. [Google Scholar] [CrossRef]
- Telles, G.P.; Minghim, R.; Paulovich, F.V. Normalized compression distance for visual analysis of document collections. Comput. Graph. 2007, 31, 327–337. [Google Scholar] [CrossRef]
- Axelsson, S. Using Normalized Compression Distance for classifying file fragments. In Proceedings of the ARES’10 International Conference on Availability, Reliability, and Security, Krakow, Poland, 15–18 February 2010; pp. 641–646. [Google Scholar]
- Cohen, A.R.; Vitányi, P. Normalized compression distance of multisets with applications. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1602–1614. [Google Scholar] [CrossRef] [PubMed]
- Cilibrasi, R.; Vitányi, P.; Wolf, R.D. Algorithmic clustering of music based on string compression. Comput. Music J. 2004, 28, 49–67. [Google Scholar] [CrossRef]
- Alfonseca, M.; Cebrián Ramos, M.; Ortega, A. Evolving computer-generated music by means of the Normalized Compression Distance. In Proceedings of the 5th WSEAS Conference on Simulation, Modeling and Optimization (SMO ’05), Corfu Island, Greece, 17–19 August 2005. [Google Scholar]
- Foster, P.; Dixon, S.; Klapuri, A. Identifying cover songs using information-theoretic measures of similarity. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 2015, 23, 993–1005. [Google Scholar] [CrossRef]
- Klenk, S.; Thom, D.; Heidemann, G. The Normalized Compression Distance as a distance measure in entity identification. In Proceedings of the Industrial Conference on Data Mining, Miami, FL, USA, 6–9 December 2009; Springer: Berlin, Germany, 2009; pp. 325–337. [Google Scholar]
- Yoshizawa, S.; Terano, T.; Yoshikawa, A. Assessing the impact of student peer review in writing instruction by using the Normalized Compression Distance. IEEE Trans. Prof. Commun. 2012, 55, 85–96. [Google Scholar] [CrossRef]
- Bailey, M.; Oberheide, J.; Andersen, J.; Mao, Z.M.; Jahanian, F.; Nazario, J. Automated classification and analysis of internet malware. In Proceedings of the International Workshop on Recent Advances in Intrusion Detection, Gold Coast, Australia, 5–7 September 2007; Springe: Berlin, Germany, 2007; pp. 178–197. [Google Scholar]
- Borbely, R.S. On Normalized Compression Distance and large malware. J. Comput. Virol. Hacking Tech. 2016, 12, 235–242. [Google Scholar] [CrossRef]
- Threm, D.; Yu, L.; Ramaswamy, S.; Sudarsan, S.D. Using Normalized Compression Distance to measure the evolutionary stability of software systems. In Proceedings of the 2015 IEEE 26th International Symposium on Software Reliability Engineering (ISSRE), Gaithersbury, MD, USA, 2–5 November 2015; pp. 112–120. [Google Scholar]
- Henard, C.; Papadakis, M.; Harman, M.; Jia, Y.; Le Traon, Y. Comparing white-box and black-box test prioritization. In Proceedings of the 2016 IEEE/ACM 38th International Conference on Software Engineering (ICSE), Austin, TX, USA, 14–22 May 2016; pp. 523–534. [Google Scholar]
- Martins, L.G.; Nobre, R.; Cardoso, J.M.; Delbem, A.C.; Marques, E. Clustering-based selection for the exploration of compiler optimization sequences. ACM Trans. Archit. Code Optim. (TACO) 2016, 13, 8. [Google Scholar] [CrossRef]
- Rios, R.A.; Lopes, C.S.; Sikansi, F.H.; Pagliosa, P.A.; de Mello, R.F. Analyzing the Public Opinion on the Brazilian Political and Corruption Issues. In Proceedings of the 2017 Brazilian Conference on Intelligent Systems (BRACIS), Uberlandia, Brazil, 2–5 October 2017; pp. 13–18. [Google Scholar]
- Ting, C.L.; Fisher, A.N.; Bauer, T.L. Compression-Based Algorithms for Deception Detection. In Proceedings of the International Conference on Social Informatics, Oxford, UK, 13–15 September 2017; Springer: Berlin, Germany, 2017; pp. 257–276. [Google Scholar]
- Cerra, D.; Israel, M.; Datcu, M. Parameter-free clustering: Application to fawns detection. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2009), Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Cerra, D.; Datcu, M. Algorithmic relative complexity. Entropy 2011, 13, 902–914. [Google Scholar] [CrossRef]
- Pratas, D. Compression and Analysis of Genomic Data. Ph.D. Thesis, University of Aveiro, Aveiro, Portugal, 2016. [Google Scholar]
- Helmer, S.; Augsten, N.; Böhlen, M. Measuring structural similarity of semistructured data based on information-theoretic approaches. VLDB J. Int. J. Very Large Data Bases 2012, 21, 677–702. [Google Scholar] [CrossRef]
- Cerra, D.; Datcu, M. Expanding the algorithmic information theory frame for applications to Earth observation. Entropy 2013, 15, 407–415. [Google Scholar] [CrossRef]
- Cerra, D.; Datcu, M.; Reinartz, P. Authorship analysis based on data compression. Pattern Recognit. Lett. 2014, 42, 79–84. [Google Scholar] [CrossRef]
- Coutinho, D.P.; Figueiredo, M. Text Classification Using Compression-Based Dissimilarity Measures. Int. J. Pattern Recognit. Artif. Intell. 2015, 29, 1553004. [Google Scholar] [CrossRef]
- Pinho, A.J.; Pratas, D.; Ferreira, P.J.S.G. Authorship attribution using relative compression. In Proceedings of the Data Compression Conference (DCC-2016), Snowbird, UT, USA, 29 March–1 April 2016. [Google Scholar]
- Brás, S.; Ferreira, J.H.T.; Soares, S.C.; Pinho, A.J. Biometric and emotion identification: An ECG compression based method. Front. Psychol. 2018, 9, 467. [Google Scholar] [CrossRef] [PubMed]
- Pratas, D.; Silva, R.M.; Pinho, A.J.; Ferreira, P.J.S.G. An alignment-free method to find and visualise rearrangements between pairs of DNA sequences. Sci. Rep. 2015, 5, 10203. [Google Scholar] [CrossRef] [PubMed]
- Pratas, D.; Pinho, A.J.; Ferreira, P.J.S.G. Efficient compression of genomic sequences. In Proceedings of the Data Compression Conference (DCC-2016), Snowbird, UT, USA, 29 March–1 April 2016; pp. 231–240. [Google Scholar]
- Pratas, D.; Pinho, A.J.; Silva, R.M.; Rodrigues, J.M.O.S.; Hosseini, M.; Caetano, T.; Ferreira, P.J.S.G. FALCON-meta: A method to infer metagenomic composition of ancient DNA. bioRxiv 2018, 267179. [Google Scholar] [CrossRef]
- Coutinho, D.; Figueiredo, M. An information theoretic approach to text sentiment analysis. In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM), Barcelona, Spain, 15–18 February 2013; pp. 577–580. [Google Scholar]
- Pinho, A.J.; Pratas, D.; Garcia, S.P. GReEn: A tool for efficient compression of genome resequencing data. Nucleic Acids Res. 2012, 40, e27. [Google Scholar] [CrossRef] [PubMed]
- Wandelt, S.; Leser, U. FRESCO: Referential compression of highly similar sequences. IEEE/ACM Trans. Comput. Biol. Bioinform. 2013, 10, 1275–1288. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Peng, H.; Wong, L.; Li, J. High-speed and high-ratio referential genome compression. Bioinformatics 2017, 33, 3364–3372. [Google Scholar] [CrossRef] [PubMed]
- Dawy, Z.; Hagenauer, J.; Hoffmann, A. Implementing the context tree weighting method for content recognition. In Proceedings of the Data Compression Conference (DCC-2004), Snowbird, UT, USA, 23–25 March 2004. [Google Scholar]
- Darwin, C.; Bynum, W.F. The Origin of Species by Means of Natural Selection: Or, The Preservation of Favored Races in the Struggle for Life; John Murray: London, UK, 1859. [Google Scholar]
- Huxley, T.H. Evidence as to Mans Place in Nature by Thomas Henry Huxley; Williams and Norgate: London, UK, 1863. [Google Scholar]
- Delsuc, F.; Brinkmann, H.; Philippe, H. Phylogenomics and the reconstruction of the tree of life. Nat. Rev. Genet. 2005, 6, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Wolf, Y.I.; Rogozin, I.B.; Grishin, N.V.; Koonin, E.V. Genome trees and the tree of life. Trends Genet. 2002, 18, 472–479. [Google Scholar] [CrossRef]
- Tomkins, J. How genomes are sequenced and why it matters: Implications for studies in comparative genomics of humans and chimpanzees. Answ. Res. J. 2011, 4, 81–88. [Google Scholar]
- O’Rawe, J.A.; Ferson, S.; Lyon, G.J. Accounting for uncertainty in DNA sequencing data. Trends Genet. 2015, 31, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Henn, B.M.; Botigué, L.R.; Bustamante, C.D.; Clark, A.G.; Gravel, S. Estimating the mutation load in human genomes. Nat. Rev. Genet. 2015, 16, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Harris, K. Evidence for recent, population-specific evolution of the human mutation rate. Proc. Natl. Acad. Sci. USA 2015, 112, 3439–3444. [Google Scholar] [CrossRef] [PubMed]
- Jeong, C.; Di Rienzo, A. Adaptations to local environments in modern human populations. Curr. Opin. Genet. Dev. 2014, 29, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Beres, S.; Kachroo, P.; Nasser, W.; Olsen, R.; Zhu, L.; Flores, A.; de la Riva, I.; Paez-Mayorga, J.; Jimenez, F.; Cantu, C.; et al. Transcriptome remodeling contributes to epidemic disease caused by the human pathogen Streptococcus pyogenes. MBio 2016, 7, e00403-16. [Google Scholar] [CrossRef] [PubMed]
- Fumagalli, M.; Sironi, M. Human genome variability, natural selection and infectious diseases. Curr. Opin. Immunol. 2014, 30, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Rieseberg, L.H. Chromosomal rearrangements and speciation. Trends Ecol. Evol. 2001, 16, 351–358. [Google Scholar] [CrossRef]
- Roeder, G.S.; Fink, G.R. DNA rearrangements associated with a transposable element in yeast. Cell 1980, 21, 239–249. [Google Scholar] [CrossRef]
- Long, H.; Sung, W.; Kucukyildirim, S.; Williams, E.; Miller, S.F.; Guo, W.; Patterson, C.; Gregory, C.; Strauss, C.; Stone, C.; et al. Evolutionary determinants of genome-wide nucleotide composition. Nat. Ecol. Evol. 2018, 2, 237–240. [Google Scholar] [CrossRef] [PubMed]
- Golan, A. Foundations of Info-Metrics: Modeling and Inference with Imperfect Information; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Gray, M.W. The evolutionary origins of organelles. Trends Genet. 1989, 5, 294–299. [Google Scholar] [CrossRef]
- Seligmann, H. Alignment-based and alignment-free methods converge with experimental data on amino acids coded by stop codons at split between nuclear and mitochondrial genetic codes. Biosystems 2018, 167, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Kimura, M. The Neutral Theory of Molecular Evolution; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Zielezinski, A.; Vinga, S.; Almeida, J.; Karlowski, W.M. Alignment-free sequence comparison: Benefits, applications, and tools. Genome Biol. 2017, 18, 186. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Bai, X.; Lu, Y.Y.; Tang, K.; Wang, Y.; Reinert, G.; Sun, F. Alignment-Free Sequence Analysis and Applications. Annu. Rev. Biomed. Data Sci. 2018, arXiv:1803.09727v11. [Google Scholar]
- Ferreira, P.J.S.G.; Pinho, A.J. Compression-based normal similarity measures for DNA sequences. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP-2014, Florence, Italy, 4–9 May 2014; pp. 419–423. [Google Scholar]
- Pratas, D.; Hosseini, M.; Pinho, A.J. Substitutional Tolerant Markov Models for Relative Compression of DNA Sequences. In Proceedings of the 11th International Conference on Practical Applications of Computational Biology & Bioinformatics, Porto, France, 21–23 June 2017; Springer: Berlin, Germany, 2017; pp. 265–272. [Google Scholar]
- Bell, T.C.; Cleary, J.G.; Witten, I.H. Text Compression; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
- Pinho, A.J.; Pratas, D.; Ferreira, P.J.S.G. Bacteria DNA sequence compression using a mixture of finite-context models. In Proceedings of the IEEE Workshop on Statistical Signal Processing, Nice, France, 28–30 June 2011. [Google Scholar]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Pratas, D.; Pinho, A.J. Exploring deep Markov models in genomic data compression using sequence pre-analysis. In Proceedings of the 22nd European Signal Processing Conference (EUSIPCO-2014), Lisbon, Portugal, 1–5 September 2014; pp. 2395–2399. [Google Scholar]
- Pratas, D.; Pinho, A.J.; Rodrigues, J.M.O.S. XS: A FASTQ read simulator. BMC Res. Notes 2014, 7, 40. [Google Scholar] [CrossRef] [PubMed]
- Grumbach, S.; Tahi, F. Compression of DNA sequences. In Proceedings of the Data Compression Conference (DCC-93), Snowbird, UT, USA, 30 March–1 April 1993; pp. 340–350. [Google Scholar]
- Grumbach, S.; Tahi, F. A new challenge for compression algorithms: Genetic sequences. Inf. Process. Manag. 1994, 30, 875–886. [Google Scholar] [CrossRef]
- Rivals, E.; Delahaye, J.P.; Dauchet, M.; Delgrange, O. A guaranteed compression scheme for repetitive DNA sequences. In Proceedings of the Data Compression Conference (DCC-96), Snowbird, UT, USA, 31 March–3 April 1996; p. 453. [Google Scholar]
- Loewenstern, D.; Yianilos, P.N. Significantly lower entropy estimates for natural DNA sequences. In Proceedings of the Data Compression Conference (DCC-97), Snowbird, UT, USA, 25–27 March 1997; pp. 151–160. [Google Scholar]
- Matsumoto, T.; Sadakane, K.; Imai, H. Biological sequence compression algorithms. Genome Inform. 2000, 11, 43–52. [Google Scholar]
- Chen, X.; Kwong, S.; Li, M. A compression algorithm for DNA sequences. IEEE Eng. Med. Biol. Mag. 2001, 20, 61–66. [Google Scholar] [CrossRef]
- Chen, X.; Li, M.; Ma, B.; Tromp, J. DNACompress: Fast and effective DNA sequence compression. Bioinformatics 2002, 18, 1696–1698. [Google Scholar] [CrossRef] [PubMed]
- Tabus, I.; Korodi, G.; Rissanen, J. DNA sequence compression using the normalized maximum likelihood model for discrete regression. In Proceedings of the Data Compression Conference (DCC-2003), Snowbird, UT, USA, 25–27 March 2003; pp. 253–262. [Google Scholar]
- Manzini, G.; Rastero, M. A simple and fast DNA compressor. Softw. Pract. Exp. 2004, 34, 1397–1411. [Google Scholar] [CrossRef]
- Korodi, G.; Tabus, I. An efficient normalized maximum likelihood algorithm for DNA sequence compression. ACM Trans. Inform. Syst. 2005, 23, 3–34. [Google Scholar] [CrossRef]
- Behzadi, B.; Le Fessant, F. DNA compression challenge revisited. In Proceedings of the Combinatorial Pattern Matching, CPM-2005, Jeju Island, Korea, 19–22 June 2005; Springer: Jeju Island, Korea, 2005; Volume 3537, pp. 190–200. [Google Scholar]
- Korodi, G.; Tabus, I. Normalized maximum likelihood model of order-1 for the compression of DNA sequences. In Proceedings of the Data Compression Conference (DCC-2007), Snowbird, UT, USA, 27–29 March 2007; pp. 33–42. [Google Scholar]
- Cao, M.D.; Dix, T.I.; Allison, L.; Mears, C. A simple statistical algorithm for biological sequence compression. In Proceedings of the Data Compression Conference (DCC-2007), Snowbird, UT, USA, 27–29 March 2007; pp. 43–52. [Google Scholar]
- Kaipa, K.K.; Bopardikar, A.S.; Abhilash, S.; Venkataraman, P.; Lee, K.; Ahn, T.; Narayanan, R. Algorithm for dna sequence compression based on prediction of mismatch bases and repeat location. Proceedings of 2010 IEEE International Conference on the Bioinformatics and Biomedicine Workshops (BIBMW), Hong Kong, China, 18 December 2010; pp. 851–852. [Google Scholar]
- Gupta, A.; Agarwal, S. A novel approach for compressing DNA sequences using semi-statistical compressor. Int. J. Comput. Appl. 2011, 33, 245–251. [Google Scholar] [CrossRef]
- Pinho, A.J.; Ferreira, P.J.S.G.; Neves, A.J.R.; Bastos, C.A.C. On the representability of complete genomes by multiple competing finite-context (Markov) models. PLoS ONE 2011, 6, e21588. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhou, J.; Ji, Z.; Shi, Y. DNA sequence compression using adaptive particle swarm optimization-based memetic algorithm. IEEE Trans. Evol. Comput. 2011, 15, 643–658. [Google Scholar] [CrossRef]
- Mohammed, M.H.; Dutta, A.; Bose, T.; Chadaram, S.; Mande, S.S. DELIMINATE–A fast and efficient method for loss-less compression of genomic sequences. Bioinformatics 2012, 28, 2527–2529. [Google Scholar] [CrossRef] [PubMed]
- Pinho, A.J.; Pratas, D. MFCompress: A compression tool for FASTA and multi-FASTA data. Bioinformatics 2014, 30, 117–118. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wang, S.; Kim, J.; Xiong, H.; Ohno-Machado, L.; Jiang, X. DNA-COMPACT: DNA Compression Based on a Pattern-Aware Contextual Modeling Technique. PLoS ONE 2013, 8, e80377. [Google Scholar] [CrossRef] [PubMed]
- Dai, W.; Xiong, H.; Jiang, X.; Ohno-Machado, L. An Adaptive Difference Distribution-Based Coding with Hierarchical Tree Structure for DNA Sequence Compression. In Proceedings of the Data Compression Conference (DCC-2013), Snowbird, UT, USA, 20–22 March 2013; pp. 371–380. [Google Scholar]
- Guo, H.; Chen, M.; Liu, X.; Xie, M. Genome compression based on Hilbert space filling curve. In Proceedings of the 3rd International Conference on Management, Education, Information and Control (MEICI 2015), Shenyang, China, 29–31 May 2015; pp. 29–31. [Google Scholar]
- Xie, X.; Zhou, S.; Guan, J. CoGI: Towards compressing genomes as an image. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 1275–1285. [Google Scholar] [CrossRef] [PubMed]
- Benoit, G.; Lemaitre, C.; Lavenier, D.; Drezen, E.; Dayris, T.; Uricaru, R.; Rizk, G. Reference-free compression of high throughput sequencing data with a probabilistic de Bruijn graph. BMC Bioinform. 2015, 16, 288. [Google Scholar] [CrossRef] [PubMed]
- Fritz, M.H.Y.; Leinonen, R.; Cochrane, G.; Birney, E. Efficient storage of high throughput DNA sequencing data using reference-based compression. Genome Res. 2011, 21, 734–740. [Google Scholar] [CrossRef] [PubMed]
- Kozanitis, C.; Saunders, C.; Kruglyak, S.; Bafna, V.; Varghese, G. Compressing genomic sequence fragments using SlimGene. J. Comput. Biol. 2011, 18, 401–413. [Google Scholar] [CrossRef] [PubMed]
- Deorowicz, S.; Grabowski, S. Compression of DNA sequence reads in FASTQ format. Bioinformatics 2011, 27, 860–862. [Google Scholar] [CrossRef] [PubMed]
- Wandelt, S.; Leser, U. Adaptive efficient compression of genomes. Algorithms Mol. Biol. 2012, 7, 30. [Google Scholar] [CrossRef] [PubMed]
- Qiao, D.; Yip, W.K.; Lange, C. Handling the data management needs of high-throughput sequencing data: SpeedGene, a compression algorithm for the efficient storage of genetic data. BMC Bioinform. 2012, 13, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Ochoa, I.; Hernaez, M.; Weissman, T. iDoComp: A compression scheme for assembled genomes. Bioinformatics 2014, 31, 626–633. [Google Scholar] [CrossRef] [PubMed]
- Deorowicz, S.; Danek, A.; Niemiec, M. GDC 2: Compression of large collections of genomes. Sci. Rep. 2015, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Rajasekaran, S. NRGC: A novel referential genome compression algorithm. Bioinformatics 2016, 32, 3405–3412. [Google Scholar] [CrossRef] [PubMed]
- Stephens, Z.D.; Lee, S.Y.; Faghri, F.; Campbell, R.H.; Zhai, C.; Efron, M.J.; Iyer, R.; Schatz, M.C.; Sinha, S.; Robinson, G.E. Big data: Astronomical or genomical? PLoS Biol. 2015, 13, e1002195. [Google Scholar] [CrossRef] [PubMed]
- Hanus, P.; Dingel, J.; Chalkidis, G.; Hagenauer, J. Compression of whole genome alignments. IEEE Trans. Inf. Theory 2010, 56, 696–705. [Google Scholar] [CrossRef]
- Jones, D.C.; Ruzzo, W.L.; Peng, X.; Katze, M.G. Compression of next-generation sequencing reads aided by highly efficient de novo assembly. Nucleic Acids Res. 2012, 40, e171. [Google Scholar] [CrossRef] [PubMed]
- Hach, F.; Numanagić, I.; Alkan, C.; Sahinalp, S.C. SCALCE: Boosting sequence compression algorithms using locally consistent encoding. Bioinformatics 2012, 28, 3051–3057. [Google Scholar] [CrossRef] [PubMed]
- Matos, L.M.O.; Pratas, D.; Pinho, A.J. A compression model for DNA multiple sequence alignment blocks. IEEE Trans. Inf. Theory 2013, 59, 3189–3198. [Google Scholar] [CrossRef]
- Bonfield, J.K.; Mahoney, M.V. Compression of FASTQ and SAM format sequencing data. PLoS ONE 2013, 8, e59190. [Google Scholar] [CrossRef] [PubMed]
- Holley, G.; Wittler, R.; Stoye, J.; Hach, F. Dynamic alignment-free and reference-free read compression. In Proceedings of the International Conference on Research in Computational Molecular Biology, Hong Kong, China, 3–7 May 2017; Springer: Berlin, Germany, 2017; pp. 50–65. [Google Scholar]
- Cox, A.J.; Bauer, M.J.; Jakobi, T.; Rosone, G. Large-scale compression of genomic sequence databases with the Burrows-Wheeler transform. Bioinformatics 2012, 28, 1415–1419. [Google Scholar] [CrossRef] [PubMed]
- Popitsch, N.; Haeseler, A. NGC: Lossless and lossy compression of aligned high-throughput sequencing data. Nucleic Acids Res. 2013, 41, e27. [Google Scholar] [CrossRef] [PubMed]
- Wan, R.; Anh, V.N.; Asai, K. Transformations for the compression of FASTQ quality scores of next-generation sequencing data. Bioinformatics 2012, 28, 628–635. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.A.; Wen, Z.; Deng, Q.; Chu, Y.; Sun, Y.; Zhu, Z. LW-FQZip 2: A parallelized reference-based compression of FASTQ files. BMC Bioinform. 2017, 18, 179. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.; Pratas, D.; Pinho, A.J. A survey on data compression methods for biological sequences. Information 2016, 7, 56. [Google Scholar] [CrossRef]
- Prado-Martinez, J.; Sudmant, P.H.; Kidd, J.M.; Li, H.; Kelley, J.L.; Lorente-Galdos, B.; Veeramah, K.R.; Woerner, A.E.; O’Connor, T.D.; Santpere, G.; et al. Great ape genetic diversity and population history. Nature 2013, 499, 471–475. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Jun, S.R.; Leuze, M.; Ussery, D.; Nookaew, I. Viral phylogenomics using an alignment-free method: A three-step approach to determine optimal length of k-mer. Sci. Rep. 2017, 7, 40712. [Google Scholar] [CrossRef] [PubMed]
- Locke, D.; Segraves, R.; Carbone, L.; Archidiacono, N.; Albertson, D.; Pinkel, D.; Eichler, E. Large-scale variation among human and great ape genomes determined by array comparative genomic hybridization. Genome Res. 2003, 13, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Ventura, M.; Catacchio, C.R.; Alkan, C.; Marques-Bonet, T.; Sajjadian, S.; Graves, T.A.; Hormozdiari, F.; Navarro, A.; Malig, M.; Baker, C.; et al. Gorilla genome structural variation reveals evolutionary parallelisms with chimpanzee. Genome Res. 2011, 21, 1640–1649. [Google Scholar] [CrossRef] [PubMed]
- Roos, C.; Zinner, D.; Kubatko, L.S.; Schwarz, C.; Yang, M.; Meyer, D.; Nash, S.D.; Xing, J.; Batzer, M.A.; Brameier, M.; et al. Nuclear versus mitochondrial DNA: Evidence for hybridization in colobine monkeys. BMC Evol. Biol. 2011, 11, 77. [Google Scholar] [CrossRef] [PubMed]
- Alkan, C.; Kidd, J.M.; Marques-Bonet, T.; Aksay, G.; Antonacci, F.; Hormozdiari, F.; Kitzman, J.O.; Baker, C.; Malig, M.; Mutlu, O.; et al. Personalized copy number and segmental duplication maps using next-generation sequencing. Nat. Genet. 2009, 41, 1061. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Evolution by gene duplication: An update. Trends Ecol. Evol. 2003, 18, 292–298. [Google Scholar] [CrossRef]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Chevreux, B.; Pfisterer, T.; Drescher, B.; Driesel, A.J.; Müller, W.E.; Wetter, T.; Suhai, S. Using the miraEST assembler for reliable and automated mRNA transcript assembly and SNP detection in sequenced ESTs. Genome Res. 2004, 14, 1147–1159. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, K.H.; Li, W.H.; Sharp, P.M. Rates of nucleotide substitution vary greatly among plant mitochondrial, chloroplast, and nuclear DNAs. Proc. Natl. Acad. Sci. USA 1987, 84, 9054–9058. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M. Evolution of the mutation rate. Trends Genet. 2010, 26, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Farré, M.; Ruiz-Herrera, A. Role of chromosomal reorganisations in the human-chimpanzee speciation. In Encyclopedia of Life Sciences (eLS); John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Farré, M.; Micheletti, D.; Ruiz-Herrera, A. Recombination rates and genomic shuffling in human and chimpanzee—A new twist in the chromosomal speciation theory. Mol. Biol. Evol. 2013, 30, 853–864. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.; Pratas, D.; Pinho, A.J. On the role of inverted repeats in DNA sequence similarity. In Proceedings of the International Conference on Practical Applications of Computational Biology & Bioinformatics, Porto, Portugal, 21–23 June 2017; Springer: Berlin, Germany, 2017; pp. 228–236. [Google Scholar]
- Fleagle, J.G. Primate Adaptation and Evolution; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Richly, E.; Leister, D. NUMTs in sequenced eukaryotic genomes. Mol. Biol. Evol. 2004, 21, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, F.; Balacco, D.; Preste, R.; Diroma, M.; Forino, R.; Ventura, M.; Attimonelli, M. NumtS colonization in mammalian genomes. Sci. Rep. 2017, 7, 16357. [Google Scholar] [CrossRef] [PubMed]
- Damas, J.; Samuels, D.C.; Carneiro, J.; Amorim, A.; Pereira, F. Mitochondrial DNA rearrangements in health and disease—A comprehensive study. Hum. Mutat. 2014, 35, 1–14. [Google Scholar] [CrossRef] [PubMed]

| Species | mtDNA | mRNA | gDNA | |||
|---|---|---|---|---|---|---|
| Length | Reference | Length | Version | Length | Version | |
| Human | 16,569 | NC_012920.1 | 587,117,742 | GRCh38.p7 | 2,948,627,755 | GRCh38.p7 |
| Chimpanzee | 16,554 | NC_001643.1 | 351,298,530 | 3.0 | 2,845,195,942 | 3.0 |
| Gorilla | 16,412 | NC_011120.1 | 153,150,229 | 4 | 2,788,268,060 | 4 |
| Orangutan | 16,499 | NC_002083.1 | 102,315,527 | 2.0.2 | 2,722,968,486 | 2.0.2 |
| Gibbon | 16,478 | NC_021957.1 | 110,221,273 | 3.0 | 2,611,673,151 | 3.0 |
| Baboon | 16,516 | NC_020006.2 | 312,140,410 | 3.0 | 2,727,993,489 | 3.0 |
| Marmoset | 16,499 | NC_025586.1 | 172,133,747 | 3.2 | 2,618,690,967 | 3.2 |
| Total | 115,548 | - | 1,788,377,458 | - | 19,263,417,850 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pratas, D.; Silva, R.M.; Pinho, A.J. Comparison of Compression-Based Measures with Application to the Evolution of Primate Genomes. Entropy 2018, 20, 393. https://doi.org/10.3390/e20060393
Pratas D, Silva RM, Pinho AJ. Comparison of Compression-Based Measures with Application to the Evolution of Primate Genomes. Entropy. 2018; 20(6):393. https://doi.org/10.3390/e20060393
Chicago/Turabian StylePratas, Diogo, Raquel M. Silva, and Armando J. Pinho. 2018. "Comparison of Compression-Based Measures with Application to the Evolution of Primate Genomes" Entropy 20, no. 6: 393. https://doi.org/10.3390/e20060393
APA StylePratas, D., Silva, R. M., & Pinho, A. J. (2018). Comparison of Compression-Based Measures with Application to the Evolution of Primate Genomes. Entropy, 20(6), 393. https://doi.org/10.3390/e20060393






