State Entropy and Differentiation Phenomenon
Abstract
:1. Introduction
2. State Representation by Density Operator
3. Differentiation Phenomenon in Quantum Measurement Process
4. Characteristic Quantity of State Distribution
5. State Entropy
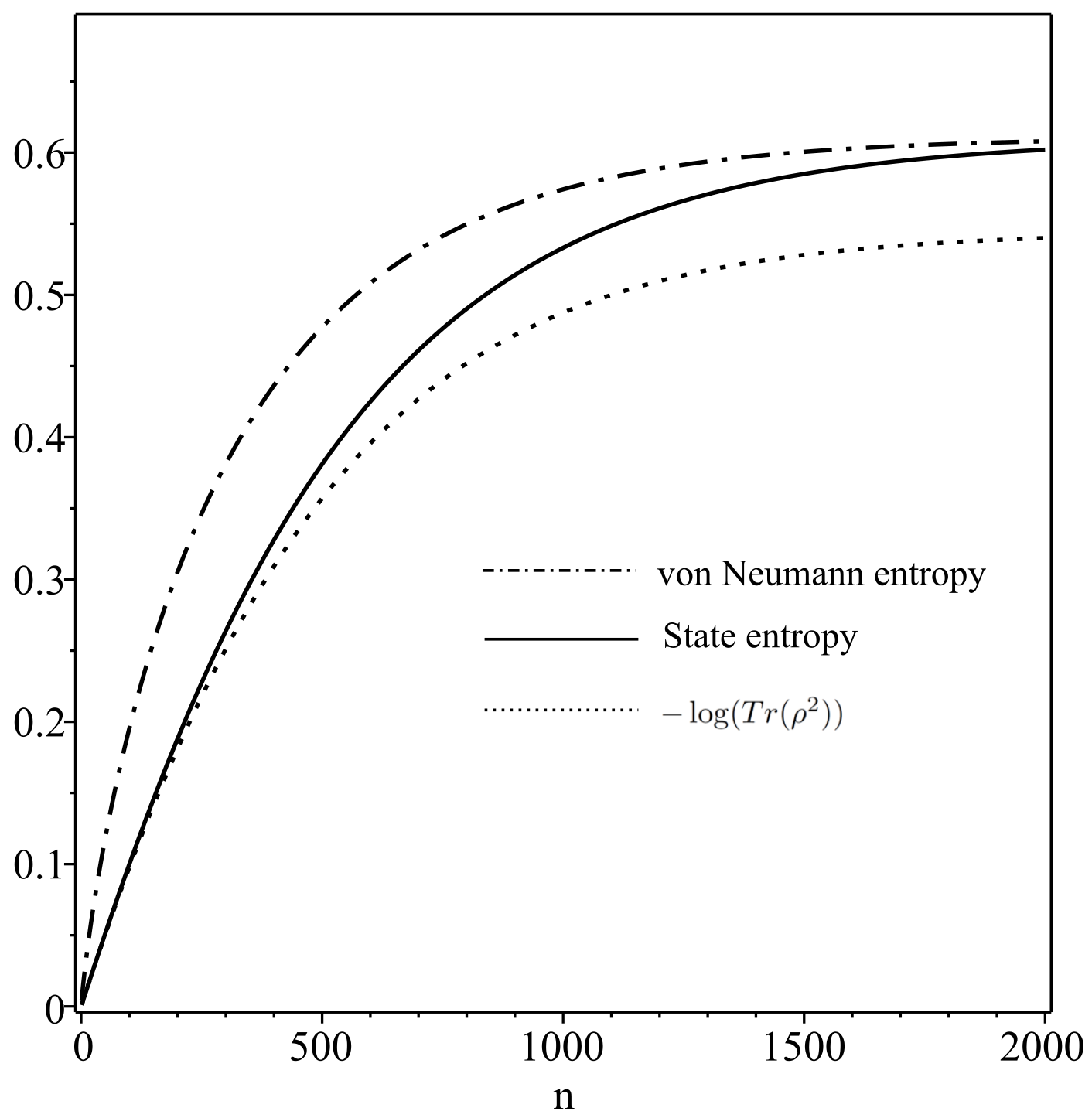
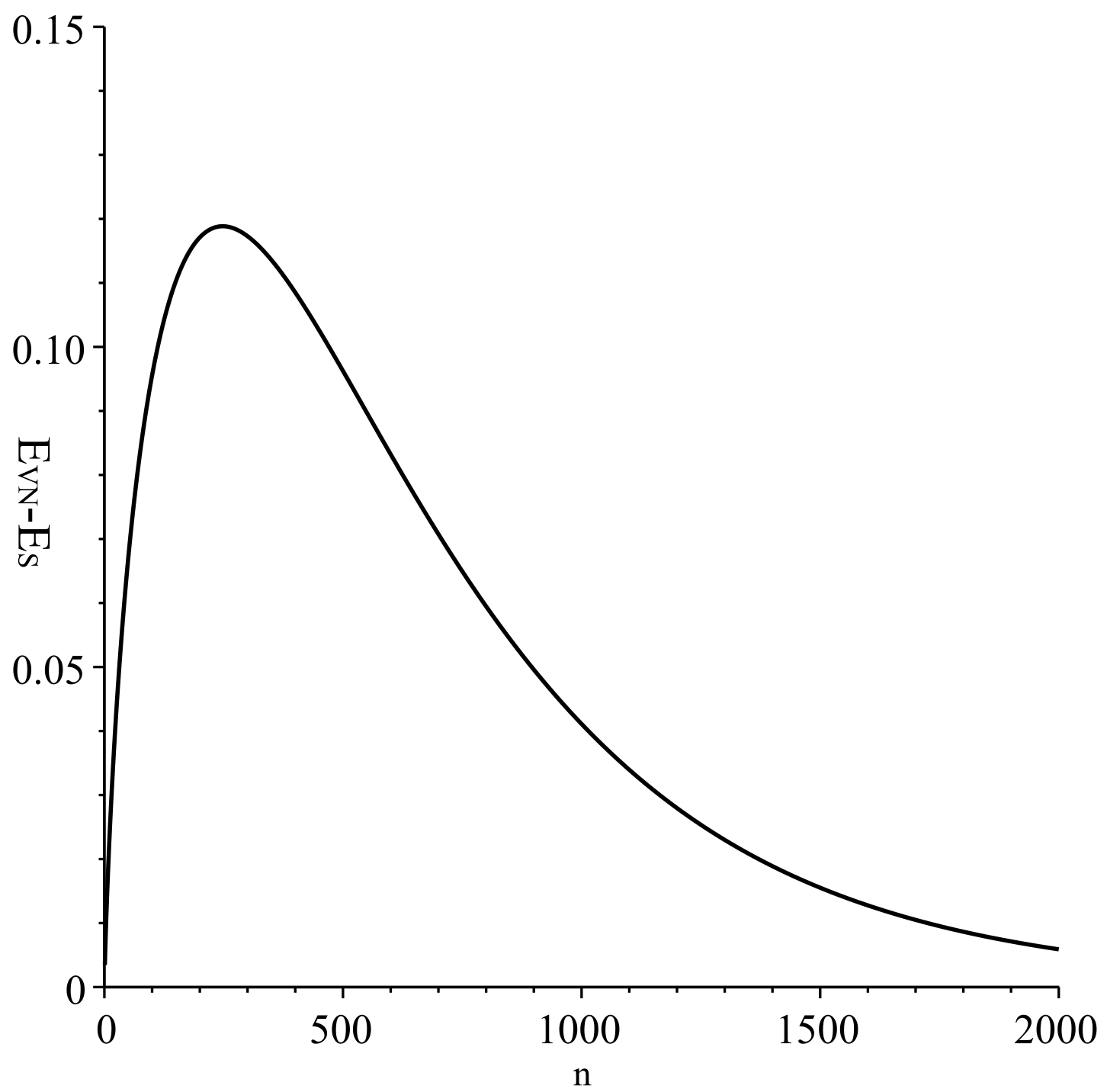
6. Model of Differentiation and Calculation of State Entropy
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. State Entropy and other Quantum Entropies
References
- Von Neumann, J. Thermodynamik quantummechanischer Gesamheiten. Gott. Nach. 1927, 1, 273–291. [Google Scholar]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Horodecki, M.; Oppenheim, J.; Winter, A. Partial quantum information. Nature 2005, 436, 673–676. [Google Scholar] [CrossRef] [PubMed]
- Umegaki, H. Conditional expectations in an operator algebra IV (entropy and information). Kodai Math. Sem. Rep. 1962, 14, 59–85. [Google Scholar] [CrossRef]
- Ohya, M. Fundamentals of Quantum Mutual Entropy and Capacity. Open Syst. Inf. Dyn. 1999, 6, 69–78. [Google Scholar] [CrossRef]
- Asano, M.; Basieva, I.; Khrennikov, A.; Yamato, I. A model of differentiation in quantum bioinformatics. Prog. Biophys. Mol. Biol. 2017, 130, 88–98. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive semigroups of N-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Khrennikov, A. Classical and quantum mechanics on information spaces with applications to cognitive, psychological, social and anomalous phenomena. Found. Phys. 1999, 29, 1065–1098. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like formalism for cognitive measurements. Biosystems 2003, 70, 211–233. [Google Scholar] [CrossRef]
- Khrennikov, A. On quantum-like probabilistic structure of mental information. Open Syst. Inf. Dyn. 2014, 11, 267–275. [Google Scholar] [CrossRef]
- Khrennikov, A. Information Dynamics in Cognitive, Psychological, Social, and Anomalous Phenomena; Ser.: Fundamental Theories of Physics; Kluwer: Dordreht, The Netherlands, 2004. [Google Scholar]
- Busemeyer, J.B.; Wang, Z.; Townsend, J.T. Quantum dynamics of human decision making. J. Math. Psychol. 2006, 50, 220–241. [Google Scholar] [CrossRef]
- Haven, E. Private information and the ‘information function’: A survey of possible uses. Theory Decis. 2008, 64, 193–228. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Sornette, D. Processing Information in Quantum Decision Theory. Entropy 2009, 11, 1073–1120. [Google Scholar] [CrossRef]
- Khrennikov, A. Ubiquitous Quantum Structure: From Psychology to Finances; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2010. [Google Scholar]
- Asano, M.; Masanori, O.; Tanaka, Y.; Khrennikov, A.; Basieva, I. Quantum-like model of brain’s functioning: Decision making from decoherence. J. Theor. Biol. 2011, 281, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Busemeyer, J.R.; Pothos, E.M.; Franco, R.; Trueblood, J. A quantum theoretical explanation for probability judgment errors. Psychol. Rev. 2011, 118, 193–218. [Google Scholar] [CrossRef] [PubMed]
- Asano, M.; Ohya, M.; Khrennikov, A. Quantum-Like Model for Decision Making Process in Two Players Game—A Non-Kolmogorovian Model. Found. Phys. 2011, 41, 538–548. [Google Scholar] [CrossRef]
- Asano, M.; Ohya, M.; Tanaka, Y.; Khrennikov, A.; Basieva, I. Dynamics of entropy in quantum-like model of decision making. AIP Conf. Proc. 2011, 63, 1327. [Google Scholar]
- Bagarello, F. Quantum Dynamics for Classical Systems: With Applications of the Number Operator; Wiley: New York, NY, USA, 2012; Volume 90, p. 015203. [Google Scholar]
- Busemeyer, J.R.; Bruza, P.D. Quantum Models of Cognition and Decision; Cambridge Press: Cambridge, UK, 2012. [Google Scholar]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y. Quantum-like dynamics of decision-making. Phys. A Stat. Mech. Appl. 2010, 391, 2083–2099. [Google Scholar] [CrossRef]
- De Barros, A.J. Quantum-like model of behavioral response computation using neural oscillators. Biosystems 2012, 110, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y. Quantum-like generalization of the Bayesian updating scheme for objective and subjective mental uncertainties. J. Math. Psychol. 2012, 56, 166–175. [Google Scholar] [CrossRef]
- De Barros, A.J.; Oas, G. Negative probabilities and counter-factual reasoning in quantum cognition. Phys. Scr. 2014, T163, 014008. [Google Scholar] [CrossRef]
- Wang, Z.; Busemeyer, J.R. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top. Cogn. Sci. 2013, 5, 689–710. [Google Scholar] [PubMed]
- Dzhafarov, E.N.; Kujala, J.V. On selective influences, marginal selectivity, and Bell/CHSH inequalities. Top. Cogn. Sci. 2014, 6, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Solloway, T.; Shiffrin, R.M.; Busemeyer, J.R. Context effects produced by question orders reveal quantum nature of human judgments. Proc. Natl. Acad. Sci. USA 2014, 111, 9431–9436. [Google Scholar] [CrossRef] [PubMed]
- Khrennikov, A. Quantum-like modeling of cognition. Front. Phys. 2015, 3, 77. [Google Scholar] [CrossRef]
- Boyer-Kassem, T.; Duchene, S.; Guerci, E. Testing quantum-like models of judgment for question order effect. Math. Soc. Sci. 2016, 80, 33–46. [Google Scholar] [CrossRef]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y. A Quantum-like Model of Selection Behavior. J. Math. Psychol. 2016. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Sornette, D. Quantum Probabilities as Behavioral Probabilities. Entropy 2017, 19, 112. [Google Scholar] [CrossRef]
- Igamberdiev, A.U.; Shklovskiy-Kordi, N.E. The quantum basis of spatiotemporality in perception and consciousnes. Prog. Biophys. Mol. Biol. 2017, 130, 15–25. [Google Scholar] [CrossRef] [PubMed]
- De Barros, J.A.; Holik, F.; Krause, D. Contextuality and indistinguishability. Entropy 2017, 19, 435. [Google Scholar] [CrossRef]
- Bagarello, F.; Di Salvo, R.; Gargano, F.; Oliveri, F. (H,ρ)-induced dynamics and the quantum game of life. Appl. Math. Mod. 2017, 43, 15–32. [Google Scholar] [CrossRef]
- Takahashi, K.S.-J.; Makoto, N. A note on the roles of quantum and mechanical models in social biophysics. Prog. Biophys. Mol. Biol. 2017, 130 Pt A, 103–105. [Google Scholar] [CrossRef] [PubMed]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y.; Yamato, I. Quantum-like model of diauxie in Escherichia coli: Operational description of precultivation effect. J. Theor. Biol. 2012, 314, 130–137. [Google Scholar] [CrossRef] [PubMed]
- Accardi, L.; Ohya, M. Compound channels, transition expectations, and liftings. Appl. Math. Optim. 1999, 39, 33–59. [Google Scholar] [CrossRef]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y.; Yamato, I. A model of epigenetic evolution based on theory of open quantum systems. Syst. Synth. Biol. 2013, 7, 161. [Google Scholar] [CrossRef] [PubMed]
- Asano, M.; Hashimoto, T.; Khrennikov, A.; Ohya, M.; Tanaka, A. Violation of contextual generalization of the Leggett-Garg inequality for recognition of ambiguous figures. Phys. Scr. 2014, 2014, T163. [Google Scholar] [CrossRef]
- Asano, M.; Basieva, I.; Khrennikov, A.; Ohya, M.; Tanaka, Y.; Yamato, I. Quantum Information Biology: From Information Interpretation of Quantum Mechanics to Applications in Molecular Biology and Cognitive Psychology. Found. Phys. 2015, 45, 1362. [Google Scholar] [CrossRef]
- Asano, M.; Khrennikov, A.; Ohya, M.; Tanaka, Y.; Yamato, I. Three-body system metaphor for the two-slit experiment and Escherichia coli lactose-glucose metabolism. Philos. Trans. R. Soc. A 2016. [Google Scholar] [CrossRef] [PubMed]
- Ohya, M.; Volovich, I. Mathematical Foundations of Quantum Information and Computation and its Applications to Nano- and Bio-Systems; Springer: Berlin, Germany, 2011. [Google Scholar]
- Asano, M.; Khrennikov, A.; Ohya, M.; Tanaka, Y.; Yamato, I. Quantum Adaptivity in Biology: From Genetics to Cognition; Springer: Berlin, Germany, 2015. [Google Scholar]
- Oaksford, M.; Chater, N. A Rational Analysis of the Selection Task as Optimal Data Selection. Psychol. Rev. 1994, 101, 608–631. [Google Scholar] [CrossRef]
- Pothos, E.M.; Chater, N. A simplicity principle in unsupervised human categorization. Cogn. Sci. 2002, 26, 303–343. [Google Scholar] [CrossRef]
- Miller, G.A. Free Recall of Redundant Strings of Letters. J. Exp. Psychol. 1958, 56, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Jamieson, R.K.; Mewhort, D.J.K. The influence of grammatical, local, and organizational redundancy on implicit learning: An analysis using information theory. J. Exp. Psychol. Learn. Mem. Cogn. 2005, 31, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 July 1960; Volume 1, p. 547. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479. [Google Scholar] [CrossRef]
- Salicrú, M.; Menéndez, M.L.; Morales, D.; Pardo, L. Asymptotic distribution of (h,ϕ)-entropies. Commun. Stat. Theory Methods 1993, 22, 2015. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Zozor, S.; Holik, F.; Portesi, M.; Lamberti, P.W. A family of generalized quantum entropies: Definition and properties. Quantum Inf. Proc. 2016, 15, 3393–3420. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asano, M.; Basieva, I.; Pothos, E.M.; Khrennikov, A. State Entropy and Differentiation Phenomenon. Entropy 2018, 20, 394. https://doi.org/10.3390/e20060394
Asano M, Basieva I, Pothos EM, Khrennikov A. State Entropy and Differentiation Phenomenon. Entropy. 2018; 20(6):394. https://doi.org/10.3390/e20060394
Chicago/Turabian StyleAsano, Masanari, Irina Basieva, Emmanuel M. Pothos, and Andrei Khrennikov. 2018. "State Entropy and Differentiation Phenomenon" Entropy 20, no. 6: 394. https://doi.org/10.3390/e20060394
APA StyleAsano, M., Basieva, I., Pothos, E. M., & Khrennikov, A. (2018). State Entropy and Differentiation Phenomenon. Entropy, 20(6), 394. https://doi.org/10.3390/e20060394






