Abstract
We first calculate the heat capacities of the nonlinear electrodynamics (NED) black hole for fixed mass and electric charge, and the electric capacitances for fixed mass and entropy. Then, we study the properties of the Ruppeiner thermodynamic geometry of the NED black hole. Lastly, some discussions on the thermal stability of the NED black hole and the implication to the flatness of its Ruppeiner thermodynamic geometry are given.
PACS:
98.80.-k; 04.62.+v
1. Introduction
The thermodynamics of black holes are established on the basis of the definitions of the entropy and temperature of black hole [1,2,3,4]. The temperature of the horizon of a black hole is proportional to its surface gravity. In Einstein gravity, the entropy of the horizon of a black hole is proportional to its horizon area (the entropy area law of a black hole). Using the brick-wall method [5], one can check the entropy area law of a black hole. However, the result from the brick-wall model depends on the choice for the membrane near the horizon. Whether the entropy of a black hole satisfies the entropy area law will depend on the adopted gravity theory.
For the thermodynamic system described by the N thermodynamic variables including the entropy, the internal energy, and so on, one can construct the corresponding thermodynamic geometry associated with the entropy, the internal energy and other thermodynamic variable [6,7,8,9]. The Ruppeiner geometry can reflect the fluctuation property of an equilibrium thermodynamic system. The curvature scalar of the Ruppeiner geometry is related to the correlation volume of a thermodynamic system, and its divergent point is the critical point of the thermodynamic phase transition. The properties of the thermodynamic geometries of the black hole have been widely studied [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. It has been found that the Ruppeiner thermodynamic geometry of the Reissner–Nordström (RN) black hole is flat [37]. On the other hand, some regular black hole solutions have been found in the gravity theory coupling to nonlinear electrodynamics (NED) [39,40,41,42]. The regular NED black hole with exponential mass function approaches to the RN black hole asymptotically [40]. The entropy of black hole depends on the action of gravity theory [43,44,45,46,47,48]. In the NED gravity theory, the entropy of a black hole is still the Bekenstein entropy [1,2,49]. So, it is expected that, like the Ruppeiner thermodynamic geometry of the RN black hole, the Ruppeiner thermodynamic geometry of the regular NED black hole with exponential mass function will be flat.
In this paper, we study the thermodynamic properties and the properties of thermodynamic geometry of the regular NED black hole. In Section 2, we calculate the heat capacity and the electric capacitance of the NED black hole. In Section 3, we study the properties of the Ruppeiner thermodynamic geometry of NED black hole. Lastly, we discuss some problems on the thermodynamic properties of the NED black hole.
2. Thermodynamic Properties of NED Black Hole
The action of Einstein gravity coupling to the nonlinear electrodynamics is [50]
where g and R are the metric determinant and Ricci curvature scalar associated with metric , is the Lagrangian of the NED source with . By defining with , then one has the Legendre transformation
where is a function of P, and . In the dual representation, the energy-momentum tensor is given as
Recently, some regular solutions in Einstein gravity coupling to the nonlinear electrodynamics have been obtained [51,52]. For the static, spherically symmetric metric
where with the mass function, the Einstein field equation yields [40]
For
the mass function takes the exponential form
where M and q are the mass and electric charge of the NED spacetime. The NED black hole possesses the two horizons with the outer (inner) horizon radius (). For the ratio with , the two horizons of NED black hole coincide, as shown in Figure 1.
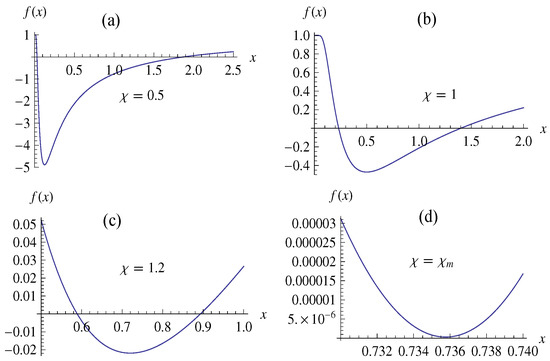
Figure 1.
The metric function with for the four cases: (a) ; (b) , (c) , (d) .
In the following, we will discuss the thermal and electric properties of the NED black hole. From
the outer horizon temperature of the NED black hole is obtained as
From , one gets the mass of NED spacetime. The mass M includes the mass of NED black hole (the mass enclosed by the outer horizon of NED black hole) and the mass outside the outer horizon of NED black hole.
which approaches as . The Misner-Sharp energy enclosed by the sphere surface of radius r in the spherically symmetric spacetime takes [53]
Putting in Equation (11) gives
where denotes the energy inside the outer horizon of the NED black hole, which is less than the mass of NED spacetime.
In the process that the outer horizon radius of the NED black hole increases , the energy correspondingly increases . In this process, the entropy of the outer horizon increases and the heat energy flowing into the black hole through the outer horizon is . According to Ref. [54], the volume enclosed by the outer horizon of the NED black hole is given as . The work done by the outer horizon of the NED black hole is , where is the radial pressure on the outer horizon. As a result, the first law of thermodynamics for the NED black hole is expressed as
The thermal stability of the NED black hole may be checked by determining the sign of its heat capacity [55]. The heat capacity of the NED black hole associated with the outer horizon is defined as [56]
where the subscript X denotes the thermodynamic process with thermodynamic quantity X fixed. The heat capacity defined by Equation (14) differs from the one given by Equation (58) in Ref. [57]. For the latter definition, the heat capacity for a fixed M is zero.
For a fixed q, the heat capacity is given as
Clearly, is non-negative and thus the NED black hole is thermally stable in the process with M fixed. At , is divergent, and for it is positive.
From the formula for the electrostatic field [40], the electric field of NED black hole is obtained as
Integrating the electric field E gives the electric potential of the NED black hole as [49]
with an integration constant. Taking , then and . Under this boundary condition, the electric potential on the outer horizon of the NED black hole is given as
For the extremal black hole, the electric potential on the horizon of the NED black hole reduces to .
The electric capacitance of the NED black hole is defined as
where is the inverse temperature of the outer horizon of the NED black hole and is defined as
For a fixed M, the electric capacitance of the NED black hole is obtained as
or
As , there is . At , is divergent and it is positive for . For a fixed , the electric capacitance of the NED black hole is
or
As , . is divergent at , and is positive for . Equations (25) and (27) show that the NED black hole with a small charge/mass ratio is electrostatically stable in the process with M fixed and the one with fixed.
The NED black hole possesses the two horizons for . The observer outside the outer horizon may detect the thermal properties of the outer horizon. We live in the spacetime with a cosmological horizon lying in the outside of us. Similarly, one can imagine that there are some observers inside the inner horizon of the NED black hole. For such a kind of observers, the inner horizon will be of equal importance as the outer horizon for us. In order to get a complete understanding for the thermal properties of the black hole with two horizons, we also need to study the thermal properties of its inner horizon.
The entropy and temperature of the inner horizon of the NED black hole are and , respectively. From , the radial pressure on the inner horizon of the NED black hole is given as . Similar to the case of the outer horizon, the first law of thermodynamics for the inner horizon of NED black hole is
where is the energy inside the inner horizon of the NED black hole and is the volume enclosed by the inner horizon of the NED black hole [54].
In terms of with , is expressed as
which is a negative temperature. The two heat capacities of the NED black hole associated with the inner horizon are
Clearly, both and are negative definite. This implies that the inner horizon of the NED black hole is thermally unstable.
Putting in Equation (20) with gives the electric potential on the inner horizon of the NED black hole as
The two electric capacities of the NED black hole associated with the inner horizon are
At , is divergent, and it is positive for . At , is divergent, and it is positive for .
3. Thermodynamic Geometry of NED Black Hole
Some thermodynamic properties of the thermodynamic system may be studied by the thermodynamic geometry method [6,7,8]. The Ruppeiner thermodynamic metric takes the following form [9]
where S is the entropy of the thermodynamic system, and () denote the other thermodynamic quantities.
For the black hole with two horizons described by the two thermodynamic quantities, the Ruppeiner metric associated with the entropy of the outer horizon takes the form
with and . According to Equation (36), the Ruppeiner metric matrix of the NED black hole is obtained as
with the determinant .
The components of Christoffel connection associated with the Ruppeiner metric (36) read
where , and . For the Ruppeiner metric (37), the components of Christoffel connection are
The Ricci tensor of the Ruppeiner thermodynamic geometry associated with the Ruppeiner metric (36) are
where
For the Ruppeiner metric (37), all the components of the Ricci tensor are zero and thus the Ricci scalar of the Ruppeiner thermodynamic geometry is zero.
Similarly, one can construct the Ruppeiner thermodynamic geometry metric associated with the inner horizon of the NED black hole as . The corresponding Christoffel connection components may be obtained from Equations (40)–(45) under the substitution . So, the Ricci tensor of the Ruppeiner thermodynamic geometry associated with the inner horizon of the NED black hole is also zero.
4. Discussions
The thermodynamic properties and the Ruppeiner thermodynamic geometry of the NED black hole have been studied. The thermodynamic systems related to the outer horizon and the inner horizon of the NED black hole satisfy the first law of thermodynamics with the internal energy . It should be mentioned that the NED black hole releases heat energy when the inner horizon entropy increases, since the inner horizon temperature is negative. Equations (17) and (18) shows that the outer horizon of the NED black hole with a big is thermally stable. Equations (30) and (31) means that the inner horizon of the NED black hole is always thermally unstable, since there are and for an arbitrary value of . For a black hole with two horizons, there are two effective thermodynamic systems. One system associated with outer horizon may be described by the thermodynamic quantities , M and q. The other associated with inner horizon may be described by , M and q. Both of the Ruppeiner thermodynamic geometries associated with the outer and inner horizons of the NED black hole are flat. This reflects that there is no interaction between the particles in the two thermodynamic systems [58]. As a result, there exists no thermodynamic phase transition of the NED black hole.
Acknowledgments
This work is partially supported by the National Natural Science Foundation of China (Grant No. 11775036).
Conflicts of Interest
The author declare no conflicts of interest.
References
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Wald, R.M. The Thermodynamics of Black Holes. Living Rev. Rel. 2001, 4, 6. [Google Scholar] [CrossRef] [PubMed]
- Hooft, G. On the quantum structure of a black hole. Nucl. Phys. 1985, B256, 727. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 1975, 63, 2479. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605, Erratum in 1996, 68, 313. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamic curvature and phase transitions in Kerr-Newman black holes. Phys. Rev. D 2008, 78, 024016. [Google Scholar] [CrossRef]
- Li, G.Q.; Mo, J.X. Phase transition and thermodynamic geometry of f(R) AdS black holes in the grand canonical ensemble. Phys. Rev. D 2016, 93, 124021. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Kamvar, N. Thermodynamic geometry of black holes in f(R) gravity. Eur. Phys. J. C 2016, 76, 476. [Google Scholar] [CrossRef]
- Sahay, A. Restricted thermodynamic fluctuations and the Ruppeiner geometry of black holes. Phys. Rev. D 2017, 95, 064002. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A.; Panahiyan, S.; Panah, B.E. Phase transition and thermodynamic geometry of Einstein–Maxwell-dilaton black holes. Phys. Rev. D 2015, 92, 064028. [Google Scholar] [CrossRef]
- Zhang, J.L.; Cai, R.G.; Yu, H.W. Phase transition and thermodynamical geometry of Reissner-Nordström-AdS black holes in extended phase space. Phys. Rev. D 2015, 91, 044028. [Google Scholar] [CrossRef]
- Mansoori, S.A.H.; Mirza, B.; Fazel, M. Hessian matrix, specific heats, Nambu brackets, and thermodynamic geometry. J. High Energy Phys. 2015, 4, 115. [Google Scholar] [CrossRef]
- Zhang, J.L.; Cai, R.G.; Yu, H.W. Phase transition and thermodynamical geometry for Schwarzschild AdS black hole in AdS5 × S5 spacetime. J. High Energy Phys. 2015, 2, 143. [Google Scholar] [CrossRef]
- Suresh, J.; Tharanath, R.; Varghese, N.; Kuriakose, V.C. The thermodynamics and thermodynamic geometry of the Park black hole. Eur. Phys. J. C 2014, 74, 2819. [Google Scholar] [CrossRef]
- Han, Y.W.; Chen, G.; Lan, M.J. Legendre transformations and the thermodynamic geometry of 5D black holes. Chin. Phys. C 2013, 37, 035101. [Google Scholar] [CrossRef][Green Version]
- Wei, S.W.; Liu, Y.X. Critical phenomena and thermodynamic geometry of charged Gauss–Bonnet AdS black holes. Phys. Rev. D 2013, 87, 044014. [Google Scholar] [CrossRef]
- Lala, A.; Roychowdhury, D. Ehrenfest’s scheme and thermodynamic geometry in Born-Infeld AdS black holes. Phys. Rev. D 2012, 86, 084027. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. Thermodynamic geometry and topological Einstein–Yang–Mills black holes. Entropy 2012, 14, 1045–1078. [Google Scholar] [CrossRef]
- Biswas, R.; Chakraborty, S. Black hole thermodynamics in Horava Lifshitz gravity and the related geometry. Astrophys. Space Sci. 2011, 332, 193–199. [Google Scholar] [CrossRef]
- Niu, C.; Tian, Y.; Wu, X.N. Critical phenomena and thermodynamic geometry of Reissner-Nordström-anti-de Sitter black holes. Phys. Rev. D 2012, 85, 024017. [Google Scholar] [CrossRef]
- Akbar, M.; Quevedo, H.; Saifullah, K.; Sanchez, A.; Taj, S. Thermodynamic geometry of charged rotating BTZ black holes. Phys. Rev. D 2011, 83, 084031. [Google Scholar] [CrossRef]
- Sahay, A.; Sarkar, T.; Sengupta, G. On the phase structure and thermodynamic geometry of R-charged black holes. J. High Energy Phys. 2010, 2010, 125. [Google Scholar] [CrossRef]
- Banerjee, R.; Ghosh, S.; Roychowdhury, D. New type of phase transition in Reissner Nordström–AdS black hole and its thermodynamic geometry. Phys. Lett. B 2011, 696, 156–162. [Google Scholar] [CrossRef]
- Banerjee, R.; Modak, S.K.; Samanta, S. Second order phase transition and thermodynamic geometry in Kerr–AdS black holes. Phys. Rev. D 2011, 84, 064024. [Google Scholar] [CrossRef]
- Sahay, A.; Sarkar, T.; Sengupta, G. On the thermodynamic geometry and critical phenomena of AdS black holes. J. High Energy Phys. 2010, 2010, 82. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X.; Wang, Y.Q.; Guo, H. Thermodynamic geometry of black hole in the deformed Hořava–Lifshitz gravity. Europhys. Lett. 2012, 99, 20004. [Google Scholar] [CrossRef]
- Biswas, R.; Chakraborty, S. Black holes in the Einstein–Gauss–Bonnet theory and the geometry of their thermodynamics—II. Astrophys. Space Sci. 2010, 326, 39. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. On the microscopic perspective of black branes thermodynamic geometry. Entropy 2010, 12, 2097–2143. [Google Scholar] [CrossRef]
- Sarkar, T.; Sengupta, G.; Tiwari, B.N. Thermodynamic geometry and extremal black holes in string theory. J. High Energy Phys. 2008, 810, 76. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.W.; Park, Y.J. Ruppeiner geometry and 2D dilaton gravity in the thermodynamics of black holes. Phys. Lett. B 2008, 663, 342–350. [Google Scholar] [CrossRef][Green Version]
- Quevedo, H.; Vazquez, A. The geometry of thermodynamics. AIP Conf. Proc. 2008, 977, 165–172. [Google Scholar]
- Sarkar, T.; Sengupta, G.; Tiwari, B.N. On the thermodynamic geometry of BTZ black holes. J. High Energy Phys. 2006, 611, 15. [Google Scholar] [CrossRef]
- Shen, J.Y.; Cai, R.G.; Wang, B.; Su, R.K. Thermodynamic geometry and critical behavior of black holes. Int. J. Mod. Phys. A 2007, 22, 11–27. [Google Scholar] [CrossRef]
- Åman, J.; Bengtsson, I.; Pidokrajt, N. Geometry of black hole thermodynamics. Gen. Rel. Grav. 2003, 35, 1733–1743. [Google Scholar] [CrossRef]
- Hendi, S.H.; Li, G.Q.; Mo, J.X.; Panahiyan, S.; Panah, B.E. New perspective for black hole thermodynamics in Gauss–Bonnet-Born-Infeld massive gravity. Eur. Phys. J. C 2016, 76, 571. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Four-parametric regular black hole solution. Gen. Rel. Grav. 2005, 37, 635–641. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Wang, P. Horizon entropy in modified gravity. Phys. Rev. D 2005, 72, 024030. [Google Scholar] [CrossRef]
- Vollick, D.N. Noether charge and black hole entropy in modified theories of gravity. Phys. Rev. D 2007, 76, 124001. [Google Scholar] [CrossRef]
- Hendi, S.H.; Panah, B.E.; Panahiyan, S. Thermodynamical structure of AdS black holes in massive gravity with stringy gauge-gravity corrections. Class. Quant. Gravit. 2016, 33, 235007. [Google Scholar] [CrossRef]
- Briscese, F.; Elizalde, E. Black hole entropy in modified-gravity models. Phys. Rev. D 2008, 77, 044009. [Google Scholar] [CrossRef]
- Saini, A.; Stojkovic, D. Nonlocal (but also nonsingular) physics at the last stages of gravitational collapse. Phys. Rev. D 2014, 89, 044003. [Google Scholar] [CrossRef]
- Myung, Y.S. Entropy of a black hole in infinite-derivative gravity. Phys. Rev. D 2017, 95, 106003. [Google Scholar] [CrossRef]
- Culetu, H. On a regular charged black hole with a nonlinear electric source. Int. J. Theor. Phys. 2015, 54, 2855–2863. [Google Scholar] [CrossRef]
- Salazar, H.; García, A.; Plebański, J. Duality rotations and type D solutions to Einstein equations with nonlinear electromagnetic sources. J. Math. Phys. 1987, 28, 2171–2181. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Regular multihorizon black holes in modified gravity with nonlinear electrodynamics. Phys. Rev. D 2017, 96, 104008. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Wang, X. Construction of regular black holes in general relativity. Phys. Rev. D 2016, 94, 124027. [Google Scholar] [CrossRef]
- Misner, C.M.; Sharp, D.H. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, B571. [Google Scholar] [CrossRef]
- Parikh, M.K. Volume of black holes. Phys. Rev. D 2006, 73, 124201. [Google Scholar] [CrossRef]
- Cai, R.G.; Hu, Y.P.; Pan, Q.Y.; Zhang, Y.L. Thermodynamics of black holes in massive gravity. Phys. Rev. D 2015, 91, 024032. [Google Scholar] [CrossRef]
- Wei, Y.H.; Cui, X.; Zhao, J.X. Thermodynamic Properties and Thermodynamic Geometries of Black p-Branes. Commun. Theor. Phys. 2016, 65, 28. [Google Scholar]
- Myung, Y.S.; Kim, Y.W.; Park, Y.J. Thermodynamics of regular black hole. Gen. Rel. Grav. 2009, 41, 1051–1067. [Google Scholar] [CrossRef]
- Ruppeiner, G. Some Early Ideas on the Metric Geometry of Thermodynamics. J. Low Temp. Phys. 2016, 185, 246–261. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).