1. Introduction
Computer simulations are widely used in learning tasks, where a single simulation is an instance of the system [
1,
2]. A simple approach to the learning task is to randomly sample input variables and run the simulations for each input to obtain the features of the systems. Similar approaches are utilized in Monte Carlo techniques [
3]. However, even a single simulation can be computationally costly due to its high complexity, and so, obtaining a trustworthy result via sufficient simulations becomes intractable. Mathematical methods and statistical theorems are introduced to generate surrogate models to replace the simulations, especially when dealing with complex systems with many parameters [
4,
5]. Although the main drawback of surrogate models is that only approximations can be obtained, they are computationally efficient whilst maintaining the essential information of the systems, hence analyzing the properties of the system. Attempting to construct surrogate models with an acceptable number of simulations necessitates the development of robust techniques to determine their reliability and validity [
6,
7,
8]. Plenty of researchers are working on improving sampling strategies to decrease the number of simulations, which makes the task more significant [
9]. With an increasing number of surrogate models being developed, there needs to be a comprehensive understanding of the uncertainties introduced by those models. The main purpose of uncertainty quantification (UQ) is to establish a relationship between input and output, i.e., the propagation of input uncertainties, and then to quantify the difference between surrogate models and original simulations. UQ can provide a measure of the surrogate model’s accuracy and an indication of how to update the model at the same time [
10,
11,
12].
Denote f as a function (or simulator) of the original system, then given experimental design , the output is produced, where caption notation is used because the input and output are usually vectors (or matrices) in simulations. From a statistical perspective, the input uncertainties are introduced by their randomness, so we represent the input with a random variable , whose prior probability density function (PDF) is , such as the multivariate Gaussian distribution; as for the output uncertainties, a common technique is to integrate the system uncertainty and the approximation error as a noise term . In fact, the output is also a random variable determined by and . Now, suppose a surrogate is constructed to approximate , then UQ is used to identify the distribution and statistical features (for example, Kullback–Leibler divergence) of , which are essential to the validation and verification of surrogates. Basically, there are two preconditions that need to be satisfied: firstly, the surrogate models are well defined, i.e., any is a measurable function with respect to (w.r.t) corresponding probability space ; secondly, techniques are needed that learn from the prior information to obtain the best guess of the true function.
There is a number of studies proposing different surrogates for specific applications in the literature, such as multivariate adaptive regression splines (MARS) [
13], support vector regression (SVR) [
14], artificial neural network (ANN) [
15] for reliability and sensitivity analyses and kriging [
16] for structural reliability analysis. We mainly focus on two popular methods that have been extensively studied recently. One popular method that is extensively studied in the literature is the polynomial chaos expansion (PCE), also known as a spectral approach [
17]. PCE aims to represent an arbitrary random variable of interest as a spectral expansion function of other random variables with prior PDF. Xiu et al. [
18,
19,
20] have generalized the PCE in terms of the Askey scheme of polynomials, so the surrogates can be expressed by a series of orthogonal polynomials w.r.t the distributions of the input variables. These polynomials can be extended as a basis of a polynomial space. In general, methods used to solve PCE problems are categorized as two types: intrusive and non-intrusive. The main idea behind the intrusive methods is the substitution of the input
and output
with the truncated PCE and calculating the coefficients with the help of Galerkin projection [
21]. However, the explicit formation of
f is required to compose the Galerkin system, and a specific algorithm or program is needed to solve a particular problem. It is for these reasons that the intrusive models are not widely used; non-intrusive methods have been developed to avoid these limitations [
21,
22]. There are two main aspects of the non-intrusive methods: one is the choice of sampling strategies, for example Monte Carlo techniques; the other one is computational approaches. These two aspects are not independent of each other: for example, if
, then the Gaussian quadrature method is introduced to solve the numerical integration and
is the set of corresponding quadrature points. Another one of the more common methods in constructing surrogate models is the Gaussian process (GP), which is actually a Bayesian approach. Instead of attempting to identify a specific real model of the system, the GP method provides a posterior distribution over the model in order to make robust predictions about the system. As described in the highly influential works [
23,
24,
25,
26], the GP can be treated as a distribution over functions with properties controlled by a kernel. For the two prerequisites discussed in the previous paragraph, the GP generates a surrogate model that lies in a space spanned by kernels; meanwhile, Bayesian linear regression or classification methods are introduced to utilize the prior information.
Both the PCE and GP methods build surrogates, but there are some differences between them. The PCE method builds surrogates of a random variable as a function of another prior random variable rather than the distribution density function itself. The PCE surrogates are based on the orthogonal polynomial basis corresponding to the , so it is simple to obtain the mean and standard deviation of . In contrast, the GP utilizes the covariance information so that it performs better in capturing the local features. Although both the PCE and GP approaches are feasible methods to compute the mean and standard deviation of , the PCE performs more efficiently than the GP method.
As mentioned above, both the PCE and GP methods have their own trade-offs to consider when building surrogates, and there exists a connection to be explored. According to Paul Constantine’s work [
27], ordinary kriging (i.e., GP in geostatistics) interpolation can be viewed as a transformed version of the least squares (LS) problem, and the PCE can be viewed as the least squares with selected basis and weights. However, the GP reverts to interpolation when the noise term is zero. When taking the noise term into consideration, the Gaussian process with the kernel (i.e., covariance matrix)
can be viewed as a ridge regression problem [
28] with a regularization term. Furthermore, different numerical methods can affect the precision of the PCE method, as well. For example, Xiu [
20] analyzed the aliasing error w.r.t the projection method and interpolation method. Thus, the inherent connection of the two models cannot be simply summarized as an LS solution, and how to output a model with high precision remains an interesting question.
There are connections between the PCE and GP methods that have been explored by R. Schobi, etc. They introduced a new meta-modeling method naming PC-kriging [
29] (polynomial-chaos-based kriging) to solve the problems like rare event estimation [
30], structural reliability analysis [
31], quantile estimation [
32], etc. In their papers, the PCE models can be viewed as a special form of GP where a Dirac function is introduced as the kernel. They also proposed the idea that the PCE models have better performance in capturing the global features and that the GP models approximate the local characteristics. We would like to describe the PC-kriging method as a GP model with a PCE-form trend function along with a noise term. The global features are dominated by the PCE trend, and local structures (residuals) are approximated by the ordinary GP process. The PC-kriging model thus introduces the coefficients as parameters to be optimized, and the solution can be derived by Bayesian linear regression with the basis consisting of the PCE polynomials. They also use the LARSalgorithms to calibrate the model and to select a sparse design. They construct a rigid framework to optimize the parameters, validate and calibrate the model and evaluate the model accuracy.
Unlike the PC-kriging, which takes the PCE as a trend, this paper focuses on the construction of the kernel in the GP to solve the regression problems, through which we can combine the two methods into a unified framework, unifying positive aspects from both and in so doing refining the surrogates. In other words, we wish to find the connection between the GP and the PCE by analyzing the attribution of their solutions, and we want to propose a new approach to achieve high-precision predictions. The main idea of this paper is described as follows. Firstly, the PCE surrogate is embedded in a Hilbert space whose bases are the orthonormal polynomials themselves, then a suitable inner product and a Mercer kernel [
33] are defined to build a reproducing kernel Hilbert space (RKHS) [
33]. Secondly, on the other hand, the kernel of the GP can be de-composited as the product of eigenfunctions, and we can define an inner product to generate a RKHS, as well. We have explicitly elaborated the two procedures respectively and proven that the two RKHS are isometrically isomorphic. Hence, a connection between these two approaches has been established via RKHS. Furthermore, we can obtain a solution of the PCE model by solving a GP model with the Mercer kernel w.r.t the PCE polynomial basis. We name this approach Gaussian processes on polynomial chaos basis (GPCB). In order to illustrate the capability of the GPCB method, we use the Kullback–Leibler divergence [
34] to explicitly compare the PDFs of the posterior prediction of the GPCB and PCE method. Provided that the true function can be approximated by a finite number of PCE bases, it can be concluded that the GPCB can converge to the optimal subset of the RKHS wherein the true function lies.
The experimental design from the PCE model, i.e., the full tensor product of quadratures in each dimension, is used in the GPCB. We have overcome two concerns about the PCE and GP, respectively. Firstly, the PCE is based on a truncated polynomial basis, while the GPCB keeps all polynomials, which can be regarded as maintaining information in every feature. Secondly, the GP’s behavior depends on the experimental design; however, it often achieves the optimal result in local small datasets. The quadrature points derived from the PCE model are distributed evenly in the input space, and those points have high numerical precision w.r.t the polynomial basis; hence, they can work well with the GPCB. However, we must admit that the GPCB is still a GP approach, so when the dimension of input variables grows, the computational burden is on the table. In order to cope with the high dimensional problems, sampling strategies to lower the number of experimental designs are put on the table. The AK-MCSmethod [
35] is a useful tool that adaptively selects new experimental designs; however, the experimental design tends to validate the selected surrogate model. We propose a new method that is model-free and that makes full use of the quadrature points. We randomly choose a sparse subset from the quadrature points to form a new experimental design while maintaining the accuracy. Several classical sampling strategies like MC, Halton and LHS are introduced to compare their capabilities. Our sample scheme has superior performance under the conditions in this paper. The GPCB is a novel method to build surrogate models, and it can be used for various physical problems such as reliability analysis and risk assessment.
This paper is divided into two parts. In Part 1, we discuss the mathematical rigor of the method: a brief summary of PCE and GP is presented in
Section 2; the reproducing kernel Hilbert space (RKHS) is introduced to connect these two methods in
Section 3; the GPCB method is proposed based on the discussion in
Section 4; meanwhile, a theoretical Kullback–Leibler divergence between the GPCB and PCE method is demonstrated. In Part 2, an explicit Mehler kernel is presented with the Hermite polynomial basis in the last part of
Section 4; several tests of the GPCB with some benchmark functions are presented in
Section 5, along with the random constructive sampling method for high dimensional problems.
4. Gaussian Process on Polynomial Chaos Basis
and
are isomorphic as discussed in previous
Section 3, so it is natural to come up with the idea that GP can be conducted with
as the Mercer Kernel generated by polynomial basis in the PCE, and the new model is called Gaussian process on polynomial chaos basis (GPCB). In fact, the GPCB generates a PCE-like model, but with a different philosophy. Note that the posterior distribution of the predictions regarding experimental design
can be calculated analytically, so we are able to compute the KL divergence as well, which are presented as follows.
4.1. Comparison of the PCE and GPCB with the Kullback–Leibler Divergence
The true distribution of the system is always implicit in practice. Without loss of generality, the underlying true system is assumed to be
if
such that it can be approximated by the polynomials to any degree of accuracy [
20].
Firstly, we presume that
, i.e.,
in Equation (
4) is an unbiased estimator of
. Hence, the PCE approximation can be considered as a precise approximate of the true function. We compare the performance of the GPCB and the PCE method by comparing their difference in the posterior distribution of the prediction. It is known that given experimental design
and kernel function
, the distribution of the prediction of the GPCB reads:
where conditions
are dropped in
for simplicity and
. Similarly, the prediction of the PCE with the projection method is
, which is derived from the estimation
. Here,
,
,
is a diagonal matrix. The corresponding prediction variance is
. Dropping the conditions in
as well, the previous results indicate:
We can evaluate the discrepancy between
and
, hence comparing their performance. The KL divergence can be calculated analytically:
where
are simplified notations for the corresponding parts in Equation (
16). In fact,
b is the point-wise ratio between the posterior variances of the predictions, and
a represents the difference between the posterior mean of the prediction. We discuss the properties of
starting from a special case to the general conditions hereafter.
Let
k be a truncated kernel with the
M basis of PCE, i.e.,
. Actually, it can be seen as the assignment of
with the value of zero, which can be achieved by optimizing the value
with a specific procedure.
b can be simplified as:
where
is a diagonal matrix and
is the eigenvalue decomposition. Let
be the maximum eigenvalue and
be the minimal one; the above interval holds because
K is a positive definite matrix. Note that
b is an invariant with fixed
. On the other hand, the distribution of
a is as follows:
Here,
denotes the mean value of the observations, i.e., the true response. It is necessary to state that the randomness of
a is brought by the random variable
in observation
Y. In fact, we have the expectation of
as follows:
Presume that the observation Y is normalized, as well as ; hence, can be estimated as . The main difference is affected by the kernel (or ) and the term . More specifically, The GPCB can achieve a smaller variance than the PCE method in a point-wise manner because , and the differences between the predictions of the two methods is of the order of . Furthermore, if is sufficient small, i.e., , we have , thus . If , i.e., we investigate the noise-free models, then and , which enforces and , respectively. This means that and are identical distributions, i.e., .
We can conclude that the expected value of is bounded by a certain constant, which mainly depends on the and . In other words, since is given in the prior, and the are optimized; hence, the is constrained, which means that the GPCB is as stable as the PCE method. Nonetheless, if has reached a desired prediction precision, then with the kernel constructed with the same basis can have a desirable precision, as well as smaller variance.
Secondly, we consider that
, where the
of the PCE method is not an unbiased estimate of
any longer. Let
denote the PCE approximation with the
basis; under the circumstance,
is achieved by tuning the value of
via a certain learning method; hence,
is also bounded by a constant according to Equation (
19), i.e., the GPCB can converge to the precise PCE prediction
, as well. However, the KL divergence
is given as:
We denote as the basis that belongs to the model , but . It is shown that the biased PCE has smaller variance, however with a bias whose mean value depends on . We notice that represents the high-order polynomials; hence, the bias can be considerably large for general cases, and so is the . We can conclude that even though the biased PCE has smaller variance, the relatively large bias can lead to a false prediction.
In fact, if the underlying system is smooth enough to be modeled by a polynomial approximation, then we can adaptively increase the number of polynomial bases (and the experimental designs if necessary) to reach a precise approximation. However, on the other hand, we can directly use the GPCB method, which is a one-step Bayesian approximation, that converges to the hypothetical true system
. Roughly speaking, the GPCB finds
automatically by tuning the parameters
instead of adaptively changing the value of
P in the PCE method. It indeed provides more convenience for computation. The key problem is the evaluation of
. Specifically, we introduce the Mehler kernel [
37], which is an analytic expression of the Mercer kernel constructed by Hermite polynomials, and discuss the learning procedure of
.
4.2. Construction of the Kernel with Hermite Polynomials
Recall that we have
in PCE as an orthonormal basis, then we regard them as eigenfunctions of a kernel
. Since
follows the standard Gaussian distribution, then
, where
is the
i-th variable of
and
is the Hermite polynomial of degree
l:
Here, we denote the real
l-th multi-index of the
l-th polynomial in Equation (
2) as
,
and
, then according to the previous analysis, we can get
. We have Mehler kernel
[
37] with orthonormal Hermite polynomials as eigenfunctions:
where the eigenvalue is
for parameter
,
is the symbol representing the row gradient operator, i.e.,
, and
is defined similarly. Specifically, in the one-dimensional case:
where the eigenvalue
. The truncated kernel
, and its attribution can be investigated by varying
and
M.
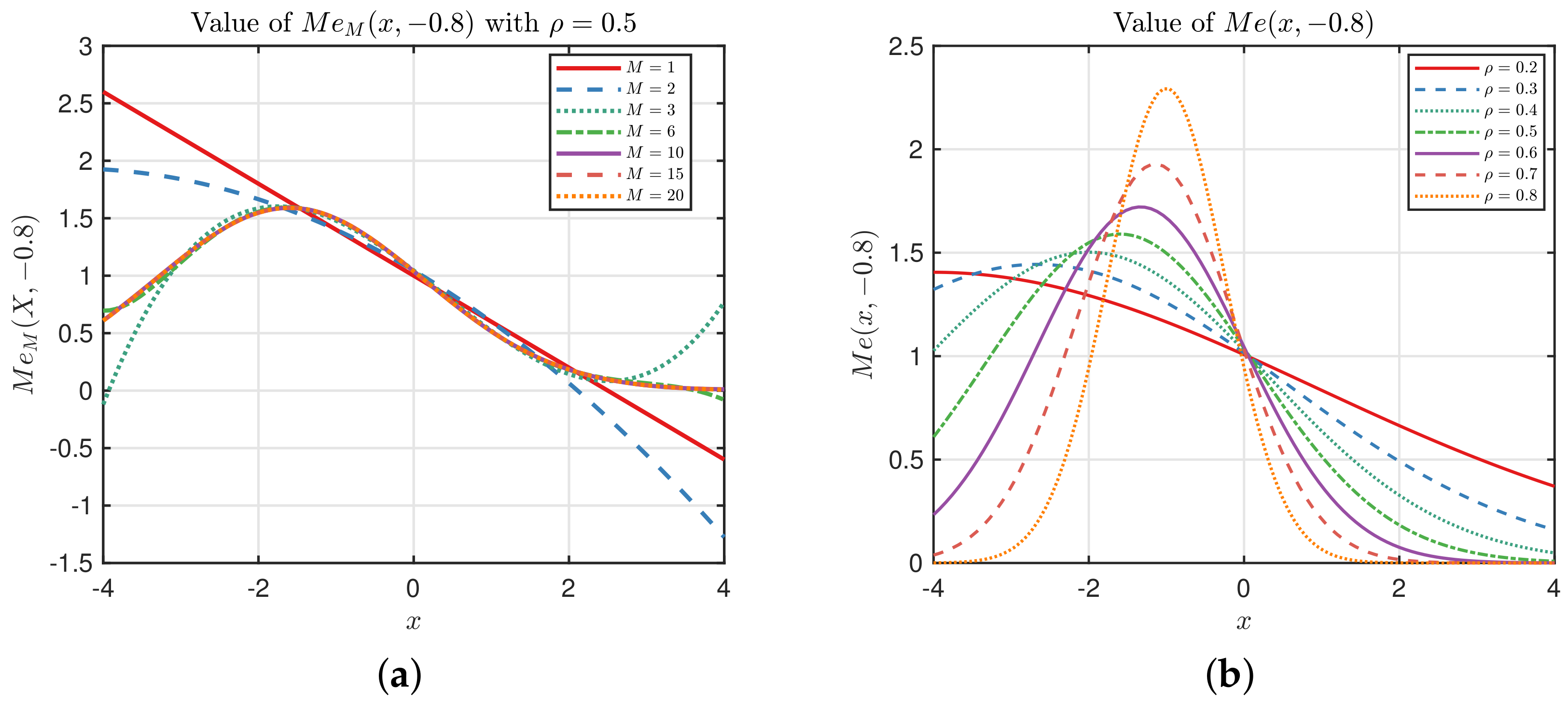
Figure 2a illustrates the truncated kernel
, which shows that
tends to converge to
as
M grows.
Figure 2b shows the values of
with different
. It presents to us that the influence of eigenvalue
is greater on the Mehler kernel.
4.3. Learning the Hyper-Parameter of
It is clear that
has a great impact on the kernel values, hence affecting the convergence of the
. We start with a simple example, where
is the true underlying function, and the noise term is ignored in the observation. Considering the Taylor expansion of
,
can be approximated by the PCE with sufficiently large
M. In fact, we can calculate the projection
to seek the value of
M. When
,
. On the other hand, as discussed in
Section 4.1, the GPCB can find
M automatically by tuning the hyper-parameter
. Let the experimental design
be the zeros of
of Equation (
21), i.e., quadrature points corresponding to degree 10; we compare the performance of the GPCB with
equal to
, respectively. The results are displayed in
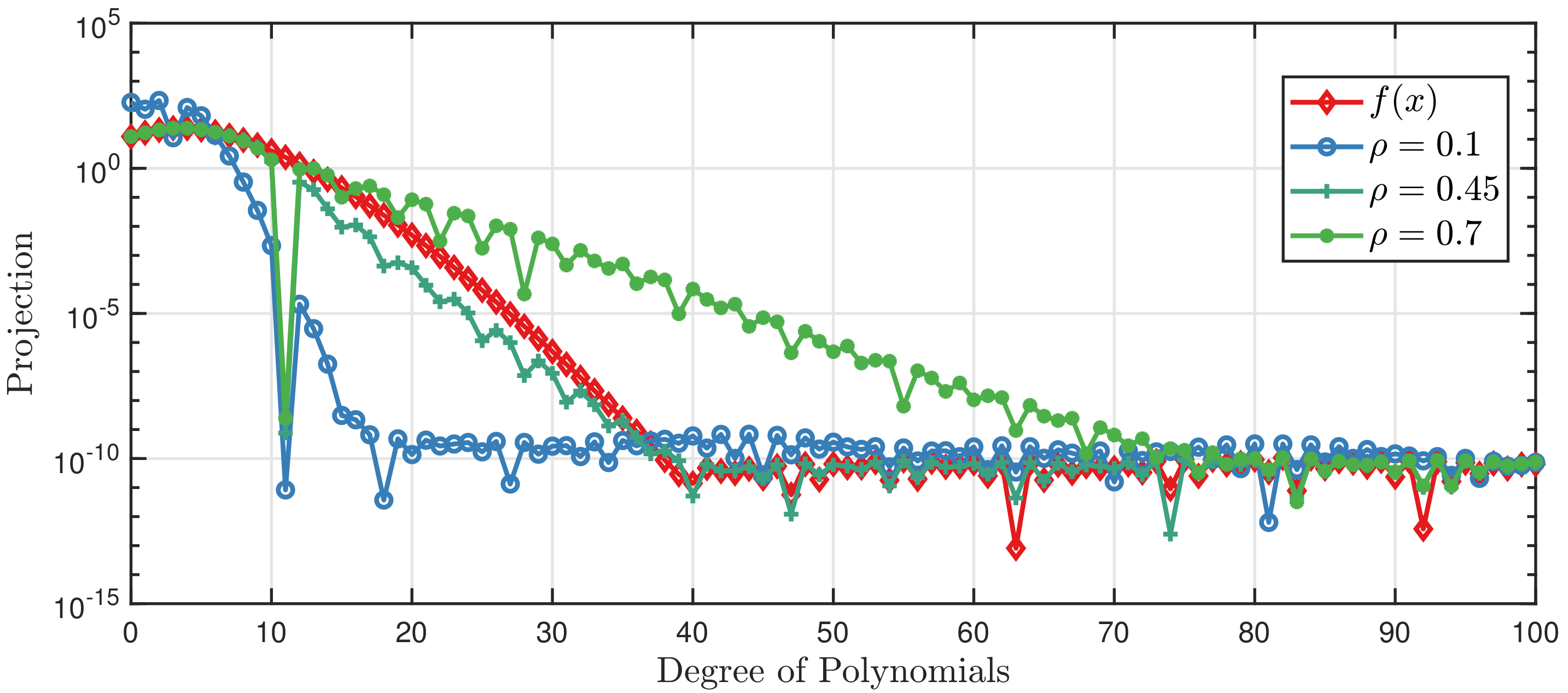
Figure 3. Note that the projection value is the absolute value of the true value in the figure for better illustration. It shows that we are able to approximate
with polynomials up to degree 40. If
for the Mehler kernel, the GPCB almost converges to exact
, whereas
leads to a fast convergence rate and
results in a slow convergence rate.
Figure 3 shows that the
has a crucial impact on the performance of the GPCB method, so a tractable method to optimize
is needed. A natural criterion is the KL divergence, which can be minimized by finding the optimal hyper-parameters
. We discussed the KL divergence of the GPCB and the PCE surrogates under the assumption that the PCE surrogate model can approximate the true system to any degree of accuracy. However, the distribution of the real system is usually unknown, which makes the calculation of KL divergence intractable. In fact, it can be easily deduced that the minimization of KL divergence is equivalent to minimizing the negative log marginal likelihood
, which (actually is
) reads:
It is important to optimize
and
to obtain a suitable kernel to get an accurate approximation. Classical methods like gradient-based techniques can be used to search for the optimal
; however, it may perform poorly because it is locally optimized. As we can see in Equation (
23), it is indicated that
should take a value between zero and one, so we can propose a global method to solve our optimization problem. The algorithm for generating a GPCB approximation is given in Algorithm 1:
![Entropy 20 00191 i001 Entropy 20 00191 i001]()
5. Numerical Investigation
In this section, we investigate the GPCB method for various benchmark functions. Firstly, we investigate the same example in
Figure 3; however, the noise term is considered, i.e.,
is the observation, where
. Three methods, i.e., GP with the RBF kernel, PCE and GPCB, are implemented. It is necessary to note that the Monte Carlo (MC) sampling strategy is used in the normal GP approaches, and Gaussian quadrature points are introduced in the GPCB approach. The main reason is that the quadrature points are too sparse for the widely-used kernels to capture the local features. For example, in this case,
in PCE, then the maximum quadrature point is
, which is beyond
. In the first set of experiments, let
in PCE, which means 11 sample points are used in the experiments; furthermore, 10,000 samples are introduced as test dataset to output the ECDF (empirical cumulative distribution function) and RMSE (root-mean-squared error). The GP algorithm is implemented by the gpml toolbox [
38] written in MATLAB with four different kernels, i.e., linear, quadratic, Gaussian and Matérn-3/2 kernels. The comparisons of the results are displayed in
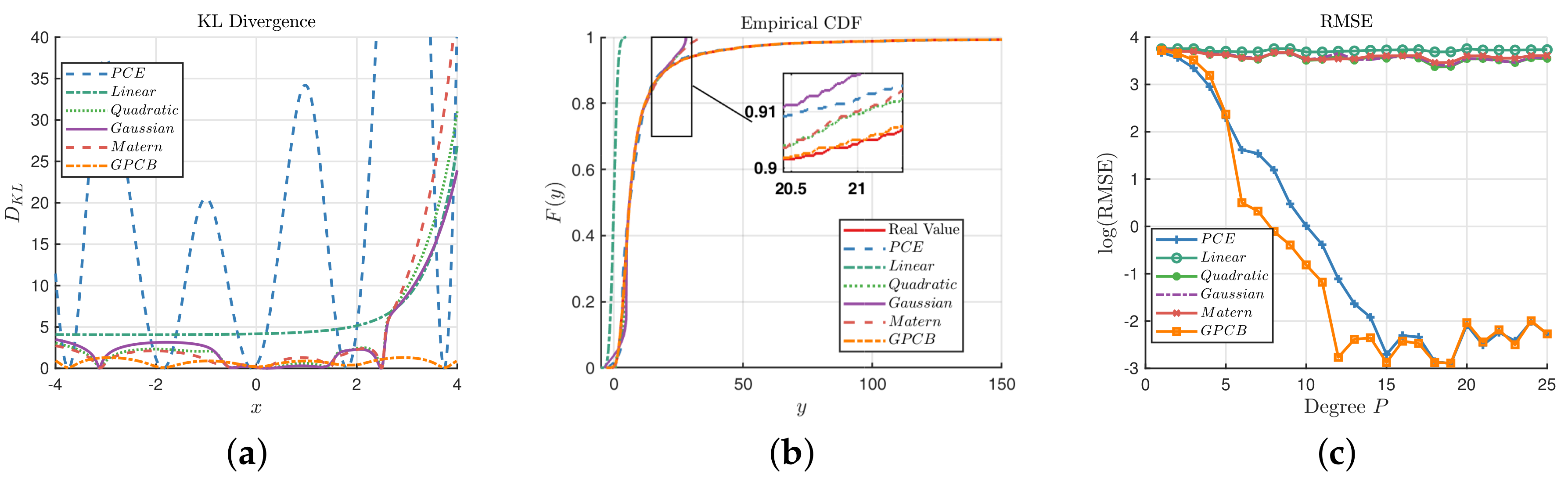
Figure 4.
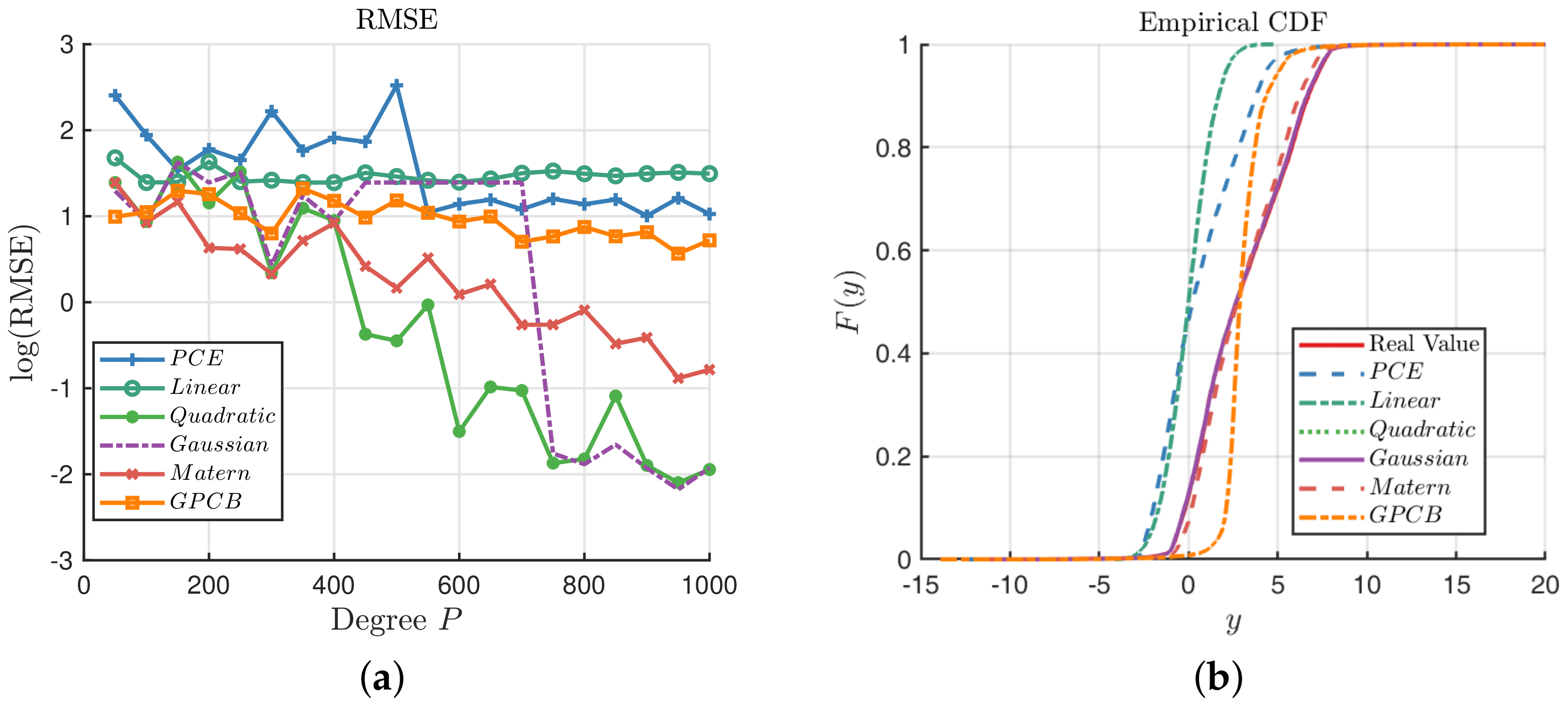
Figure 4a illustrates the point-wise KL divergence between the true value of
and the predictions on the interval
based on Equation (
16). It is clear that the distribution of GPCB prediction is statistically closest to the true response, although the GP methods with quadratic, Gaussian and Matérn-3/2 kernels outperform the GPCB at some points.
Figure 4b compares the ECDF of
y based on the test dataset. It shows that both the PCE and GPCB have a similar ECDF with the true value. Upon closer inspection, which is shown in the magnified subregion, it is obvious that the ECDF of the GPCB is almost exactly the same as the real ECDF, which shows that GPCB has actually captured the feature of
with high precision. At the same time, the RMSEs of the PCE, linear kernel, quadratic kernel, Gaussian kernel, Matérn-3/2 kernel and GPCB are
, respectively. We have implemented another experiment, which uses the degree
P (i.e., the number of experimental design) as the second set of experiments, which are illustrated in
Figure 4c.
Figure 4c shows that GPCB generally outperforms the ordinary GP with the RBF kernel, which indicates that GPCB performs better with a few (or sparse) training points. It is notable that the PCE and GPCB perform with almost the same precision when the degree is greater than 16. It echoes the idea that PCE and GPCB are statistical equivalent, as we present in
Section 4.1.
Similar experiments are conducted with a two-dimensional function, which is expressed as
. Let
,
be the real model where
is an independent noise term with a normal distribution
. Unlike the first test function, this test example is a limit state function. Let the maximum degree for each dimension
be seven for the PCE method, which makes 64 training points in total. Another dataset of 10,000 independent samples is introduced as the test set to calculate the ECDF and RMSE, as well. Similarly, we have the point-wise KL divergence in the region
as shown in
Figure 5a. It is clear that the GPCB is globally closer to the true distribution than other methods. The GP with quadratic, Gaussian and Matérn-3/2 kernels can approximate the center part well, while the PCE does not seem to perform as well.
Figure 5b shows that the six methods except the linear kernel are able to reconstruct the distribution of the prediction, and upon closer observation, we find that the ECDF of the GPCB and Matérn-3/2 kernel are the best approximations among the six methods. We also consider another set of experiments focusing on the number of experimental designs, which equals
for the 2D function. The RMSEs of the three methods with respect to different
are displayed in
Figure 5c. It also shows that the PCE and GPCB generally outperform the normal GP approaches, and the GPCB has the best performance.
To summarize, the GPCB generates a surrogate of infinite series, while the PCE can only generate a surrogate with up to polynomials, and they tend to behave with similar precision when P is large enough. A set of sparse quadrature points sampled in the PCE, which are derived from the Gaussian quadrature rule, is a good design for the GPCB. The GPCB with those training points generally performs better than the normal GP methods and PCE. However, the size of such a training set grows dramatically with the dimension ( in total), so it is not practical in real-life applications. We aim to present a strategy of sampling from those quadrature points, namely candidate points in the next section, and analyze the performance of our algorithm on the selected points.
5.1. A Random Constructive Design in High Dimensional Problems
As the dimension of a system grows, so do the number of design points of PCE due to a tensor product of quadrature points in each dimension. It is possible that PCE could deal with thousands of points of training data with acceptable computational time; however, it becomes expensive for GP approaches, including our GPCB approach. Monte Carlo sampling techniques can substitute quadrature design; however, these are not always stable. Other sampling strategies like Halton sampling and Latin hypercube sampling [
39] are widely used.
In this work, we want to utilize the high accuracy of quadrature points and also want to reduce the massive number of points. Let , and is the maximum degree in each dimension, so quadrature points are needed in each dimension, which makes the total number of tensor products of quadrature points be . We seek to find a subset of the candidate design . Furthermore, we wish to obtain a subset having a good coverage rate in the space. Therefore, we proposed the random definite design in our paper. Note that the LHS design can be extended to a larger interval and can produce points at midpoints (endpoints), so we use the LHS design to sample N indices from the interval. More specifically, we presume that the points in are equally important, so we arrange those points with a certain order to get their indices. Then, we sample from the indices with the LHS design, and each index is related to a certain quadrature point. It can be easily implemented by the MATLAB built-in function lhsdesign. The corresponding N points are what we need.
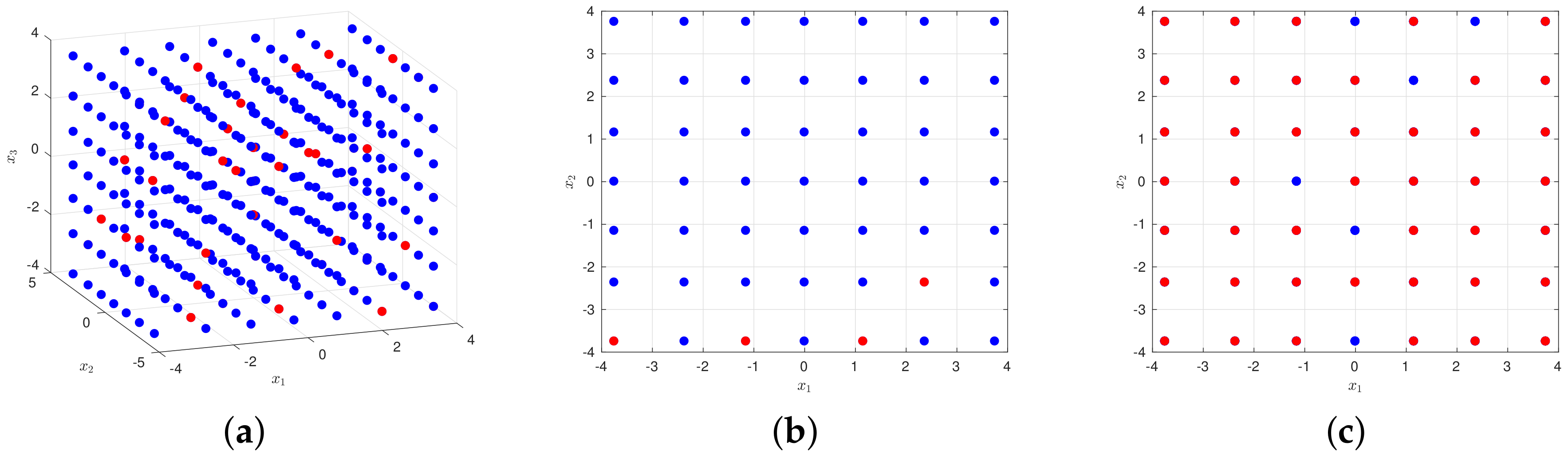
Take a three-dimensional input space as an example, where
. Set
, then
. The candidate design and its subset of 50 points
are illustrated in
Figure 6. We can see from the figure that our sampling is sparse in the whole set of candidate points, and it behaves uniformly in dimension one as illustrated in
Figure 6b, with similar conclusions in the other two dimensions. When projecting our sampling from dimension three to get
Figure 6c, we can see that the selected points almost cover every point of
, which means it has all features in dimensions one and two, i.e., quadrature point values of the two dimensions. It shows that such a method can generate a sparse subset meanwhile guaranteeing the coverage rate in the whole candidate design. We name it the random constructive design.
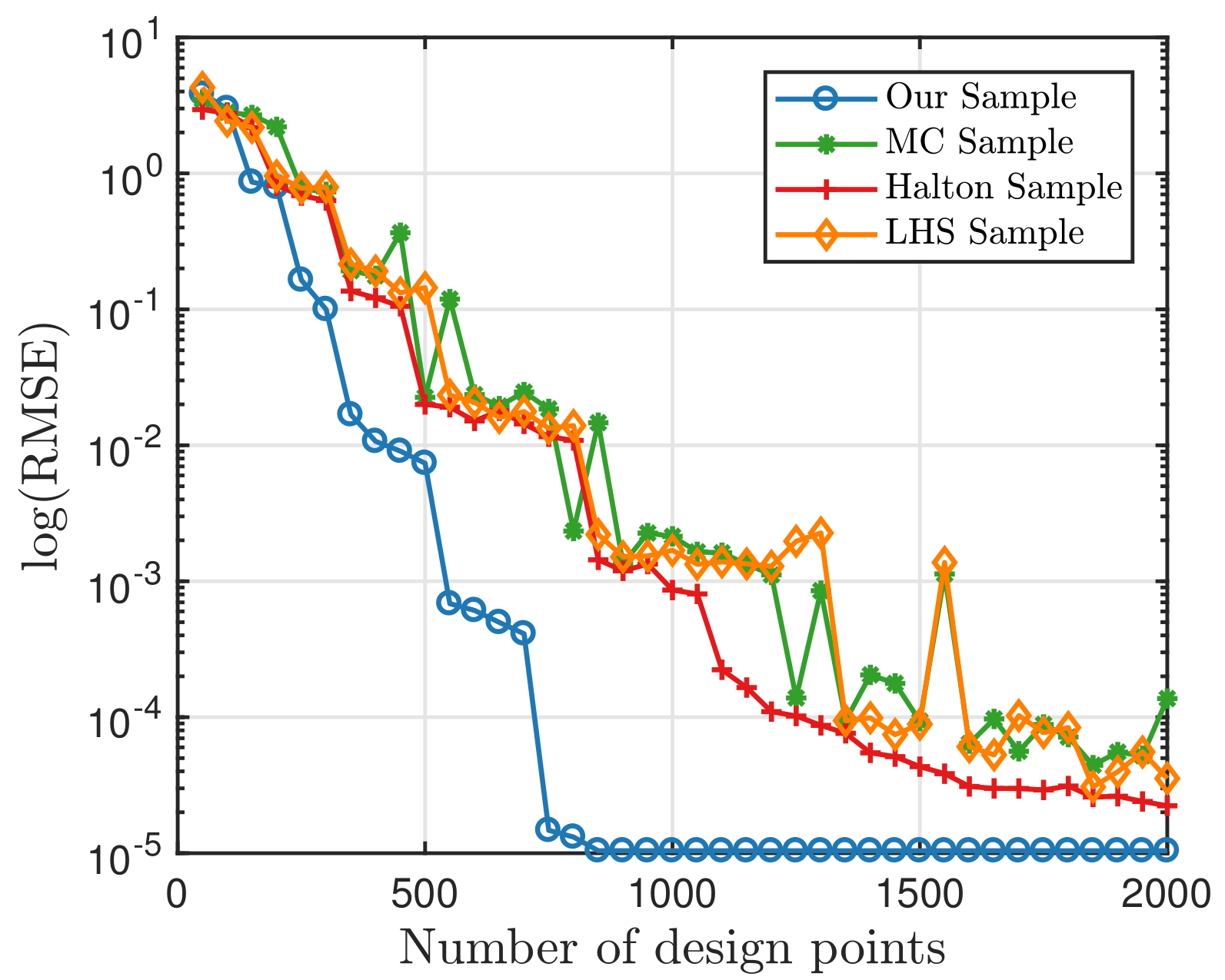
Now, we want to find out whether these samples retain their capability of accuracy. Firstly, we use the PCE method to test those samples. We will look into the benchmark Ishigami function [
40]:
, where four different sampling strategies are compared here. Set
, and the candidate design
has a size of 4096. The error term
is eliminated in this simulation for the accuracy test. The RMSE are computed on 10,000 independently-sampled data, and the results are presented below in
Figure 7. It can be seen that our sample always performs better than other samples. When the number of samples surpasses 900, the RMSE becomes
, which equals the RMSE with the whole candidate points. Therefore, we only select
of
and get the same precision. Furthermore, if we set our precision to be
, only 400 points are needed. This shows that the quadrature points have high precision in numerical calculation. In other words, the points in the candidate set are good points.
Then, the random constructive design is used with the PCE, GP and GPCB methods for the Ishigami function, with the noise term added in the observations. We take the RMSE as a criterion to compare their performance, and the results are illustrated in
Figure 8.
Figure 8a shows that the GPCB is always better than the PCE method, and they tend to behave the same. However, as the number of sampling points grows, the GP with the quadratic kernel, Gaussian kernel and Matérn-3/2 kernel generally outperform the other methods. We can see that the Ishigami function is a bounded function; therefore, it is likely to fill the whole observation space as the number of samples increases, hence improving the accuracy of the GP method. We plot the ECDF with respect to the three methods when
in
Figure 8b. It is clear that the GP with the quadratic kernel, Gaussian kernel and Matérn-3/2 kernel can almost recover the true distribution of the response, which is beyond the capability of the PCE and GPCB.
A six-dimensional problem is being tested with the G-function [
41], which is not like the Ishigami function and is unbounded in the domain
:
The experiment is performed with the same approaches, and the results are shown below in
Figure 9.
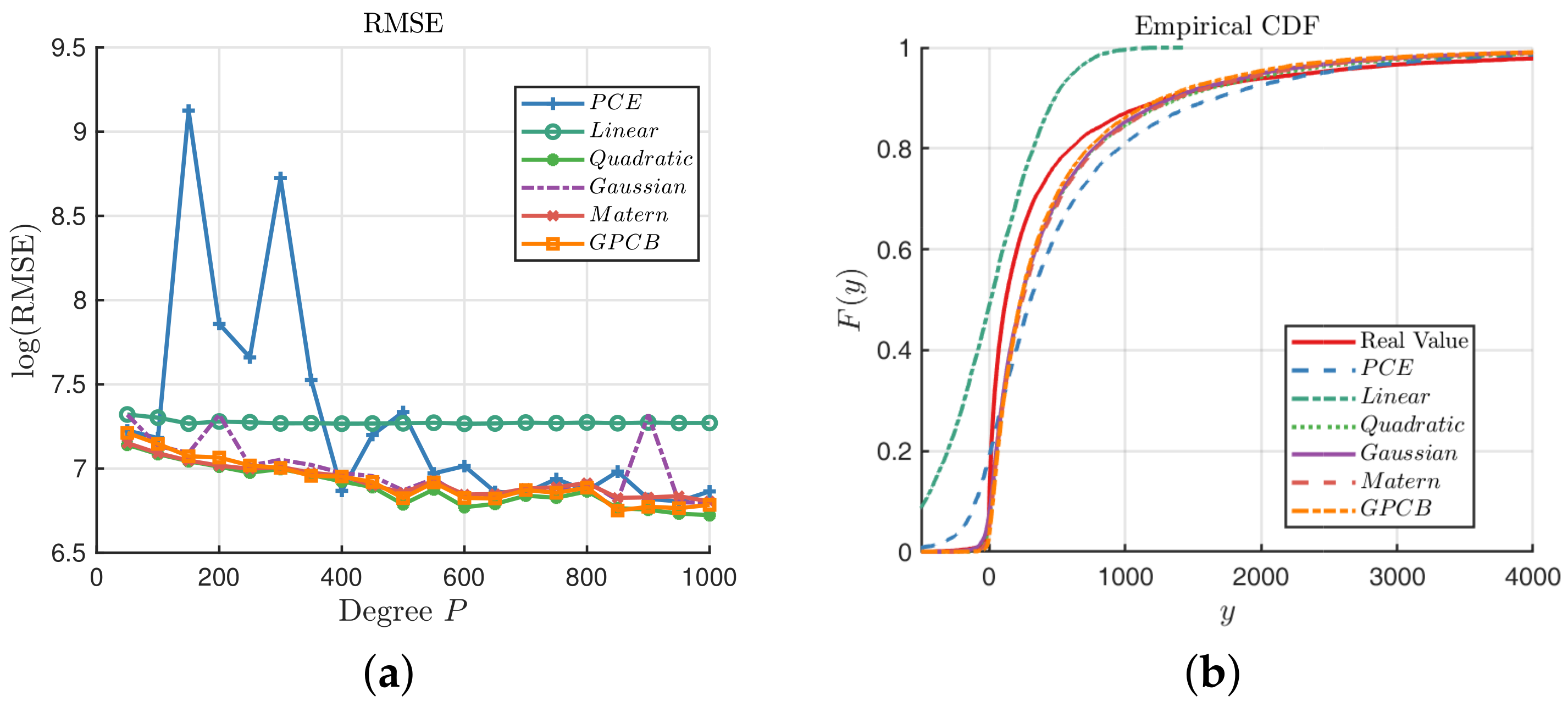
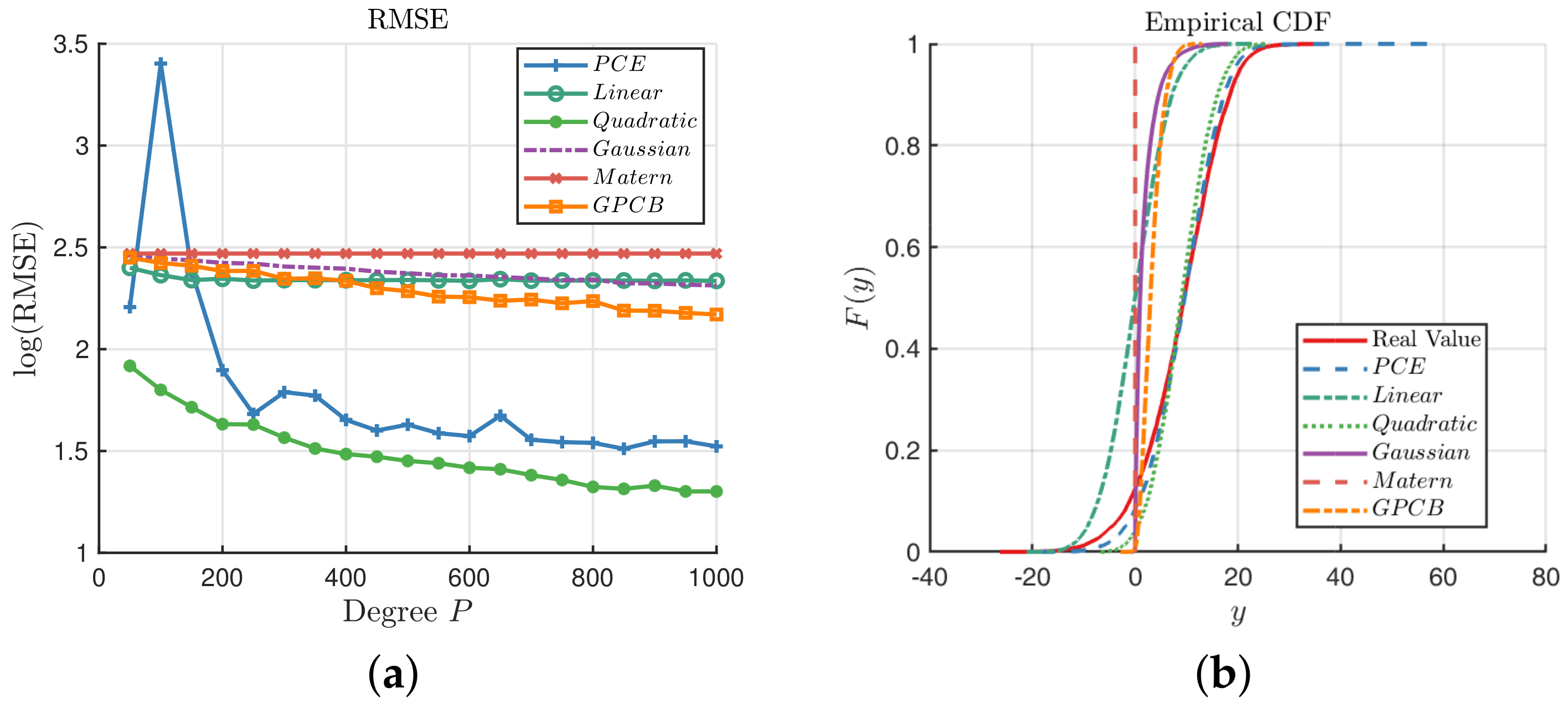
Figure 9a shows that the GPCB outperforms the PCE and GP with the Gaussian Kernel, and it has similar precision with the quadratic and Matérn-3/2 kernels. We notice that the GPCB is more stable than the PCE method, which behaves badly especially when
.
Figure 9b shows that none of these three methods can reconstruct the probability of
y very well; however, we can note that the GPCB is still comparatively the closest.
Finally, we are going to present a more complicated model with 15 dimensional functions with the following form:
The distribution of
is the product of 15 independent distributions, i.e.,
. This function is introduced by the work of O’Hagan, where
are defined in [
42]. We can see that this function is dominated by the linear and quadratic term, so it may be well approximated by the low-order PCE model. Let
in the PCE model; we can see from
Figure 10a that the GP with the quadratic kernel performs best among the six methods, while the PCE performs better than the GPCB and other GP methods. On the other hand, the GPCB is always generally better than the GP method except with the quadratic kernel for this function. When
, the PCE can generate
y, which follows the real distribution according to the ECDF in
Figure 10b.