Abstract
As the complementary concept of intuitionistic fuzzy entropy, the knowledge measure of Atanassov’s intuitionistic fuzzy sets (AIFSs) has attracted more attention and is still an open topic. The amount of knowledge is important to evaluate intuitionistic fuzzy information. An entropy-based knowledge measure for AIFSs is defined in this paper to quantify the knowledge amount conveyed by AIFSs. An intuitive analysis on the properties of the knowledge amount in AIFSs is put forward to facilitate the introduction of axiomatic definition of the knowledge measure. Then we propose a new knowledge measure based on the entropy-based divergence measure with respect for the difference between the membership degree, the non-membership degree, and the hesitancy degree. The properties of the new knowledge measure are investigated in a mathematical viewpoint. Several examples are applied to illustrate the performance of the new knowledge measure. Comparison with several existing entropy and knowledge measures indicates that the proposed knowledge has a greater ability in discriminating different AIFSs and it is robust in quantifying the knowledge amount of different AIFSs. Lastly, the new knowledge measure is applied to the problem of multiple attribute decision making (MADM) in an intuitionistic fuzzy environment. Two models are presented to determine attribute weights in the cases that information on attribute weights is partially known and completely unknown. After obtaining attribute weights, we develop a new method to solve intuitionistic fuzzy MADM problems. An example is employed to show the effectiveness of the new MADM method.
1. Introduction
The concept of the fuzzy set [1] was developed by Zadeh to model and process uncertain information in a much better way. By assigning the membership degree between 0 and 1 to elements with respect to a set, the fuzzy set can describe the state between “belong to” and “not belong to.” Therefore, many kinds of uncertainties that cannot be depicted by classical sets can be well-described by fuzzy sets. Since its inception, fuzzy set theory has been applied in many areas such as automatic control, pattern recognition, decision making, and more [2,3,4,5,6]. To enhance its ability and agility in handling with uncertainty, many researchers have been dedicated to extend the concept of the fuzzy set. Atanassov’s intuitionistic fuzzy set (AIFS) [7], as an extension of the fuzzy set, was defined by introducing a hesitancy degree to quantify the gap between 1 and the sum of membership degree and non-membership degree. The introduction of the hesitancy degree can depict the uncertainty on membership and non-membership grades, which bring capability of dealing with uncertainty in practical applications. Due to its advantage in coping with uncertainty, the AIFS theory has attracted attention from researchers [8,9]. Current research on the AIFS theory mainly focuses on its mathematical characteristics [10,11,12], its application in decision-making [13,14,15,16], and its relation with other uncertainty theories [17,18], etc.
The concept of entropy was first introduced in thermodynamics. The entropy proposed by Boltzmann is a classical entropy, which is also known as Boltzmann entropy [19]. However, there is no effective method for calculating Boltzmann entropy until Shannon developed an alternative way [20]. Recently, some methods for computing Boltzmann entropy have been developed based on specific applications [19,21,22,23]. The entropy of a fuzzy set was first proposed by Zadeh [1] to depict the fuzziness. Following Zadeh’s work, De Luca and Termini [24] proposed a probabilistic entropy measure for fuzzy sets. They also put forward some axiomatic properties for the fuzzy entropy measure, according to which fuzzy entropy can be defined. Yager [25] proposed an entropy measure for fuzzy sets based on the distance between a fuzzy set and its complementation. Yager’s concept was extended by Higashi and Klir [26] to a more general kind of fuzzy complementation. Because of its importance in depicting a fuzzy set, the entropy measure of fuzzy sets has been developing to an active topic in fuzzy set theory.
Similarly, the entropy measure of AIFSs has also attracted researchers. Burillo and Bustince [27] first presented the entropy measure for AIFSs to quantify the intuitionism of AIFSs. Then, Szmidt and Kacprzyk [28] developed the axioms proposed by Burillo and Bustince [27] and introduced a new entropy measure for AIFSs based on the ratio between the nearer distance and the further distance. Hung and Yang [29] presented axiomatic definitions for entropy of AIFSs from a probabilistic point of view. It was pointed by Vlachos and Sergiadis [30] that entropy of an AIFS should capture both fuzziness and intuitionism of AIFS. Based on such a perspective, Vlachos and Sergiadis [30] defined an entropy measure based on the concept of discrimination information and cross entropy between AIFSs. Szmidt et al. [31,32] also insisted that we cannot measure the uncertainty hidden in AIFSs merely by using the entropy measure.
Knowledge measure is usually regarded as the dual measure of entropy. In fact, if an entropy cannot capture all uncertainty in AIFSs, it is not reasonable to treat knowledge and entropy as a dual measure. We hold the perspective that the uncertainty of an AIFS includes both fuzziness and intuitionism. Therefore, the entropy of an AIFS is the combination of fuzzy entropy and intuitionistic entropy. In such a case, the entropy of an AIFS can be called as intuitionistic fuzzy entropy, which captures all kinds of uncertainty in an AIFS. This kind of intuitionistic fuzzy entropy is also an uncertain measure of AIFS. Thus, the knowledge measure can be regarded as the dual measure of intuitionistic fuzzy entropy or uncertainty. Many attempts were made [32] to cope with the knowledge measure of AIFSs by combining entropy measure and the hesitancy margin. Nguyen [33] presented a knowledge measure for AIFSs based on the distance between an AIFS and the most uncertain one. Guo [34] also proposed an axiomatic definition for the knowledge measure of AIFSs and developed a new knowledge measure following his axioms. However, we find that Nguyen’s knowledge measure and Guo’s knowledge measure may bring unreasonable results due to the distance measure it used. Therefore, it is desirable to develop a new knowledge measure for AIFSs.
To provide a more effective and reasonable knowledge measure for AIFSs, we will cope with the definition of knowledge measure of AIFSs. In this paper, we will define a new knowledge measure based on the two factors affecting knowledge amount. Our aim is to provide a new technique to measure the knowledge amount conveyed by AIFSs. Based on the intuitive analysis on the properties of knowledge amount, we present a new axiomatic definition of the knowledge measure, which differs from existing axiomatic definitions in the desired monotonicity. Afterward, a new knowledge measure is put forward together with its properties and related proofs. Comparison with other measures is made to illustrate the performance of the new knowledge measure. To validate the applicability of the new knowledge measure, we apply it in the application of multiple attribute decision making (MADM) problems in an intuitionistic fuzzy environment. A new method for solving MADM problems under the intuitionistic fuzzy condition is developed based on the new knowledge measure. An illustrative example is presented to show the effectiveness and rationality of the provided method for solving intuitionistic fuzzy MADM problems. The main contribution of this paper lies in the introduction of the effective knowledge measure, which is proved to be robust in distinguishing the knowledge amount conveyed by different AIFSs.
The rest of this paper is arranged according to the following. A brief introduction on AIFSs is proposed in the second section. A new knowledge measure for AIFSs is introduced in the third section, following the proposition axiomatic definition of knowledge measure. The properties of the new knowledge measure are also investigated in Section 3. Numerical examples and comparative analysis are presented in the fourth section to validate the performance of the new knowledge measure. The new knowledge measure is applied to MADM problems in an intuitionistic fuzzy environment in the fifth section where two models for determining attribute weights and a method for solving MADM problems are developed. In Section 5, we also use an example on the MADM problem to verify the effectiveness of the proposed method for solving MADM problems under an intuitionistic fuzzy condition. Some conclusions are presented in the last section.
2. Atanassov’s Intuitionistic Fuzzy Sets
The concept of the fuzzy set was introduced by Zadeh in 1965. It was defined based on the following.
Definition 1 [1].
Letbe the universe of discourse, then a fuzzy setdefined incan be expressed as follows:
whereis the degree of membership for x with respect to A.
Definition 2 [7].
An intuitionistic fuzzy setindefined by Atanassov can be written as:
whereis named as the membership degree andis named as the non-membership degree. The sum of them is less than 1, i.e.,
The hesitancy degree of the elementto the setcan be written as:
It is obvious that,.
When,, the AIFS degenerates into an ordinary fuzzy set.
For clarity, the coupleis usually written as, which is also called an intuitionistic fuzzy value (IFV).
Definition 3 [7].
For two AIFSs A and B defined in X, the following relations can be defined:
- (R1)
- ;
- (R2)
- ;
- (R3)
- , where is the complement of .
Definition 4 [7].
For two IFVs,,, the partial order between them is defined as:.
For a linear order of IFVs, Chen and Tan [35] defined the score function of IFV asto rank multiple IFVs. Then Hong and Choi [36] defined an accuracy functionto measure the accuracy of an IFV. Based on score and accuracy functions, Xu and Yager [37] developed a linear order relation for IFVs. Given two IFVsand, we have the following relations:;;.
3. A New Knowledge Measure for AIFSs
Let be the discourse universe. For an AIFS A defined in X, the measure used to quantify its knowledge amount should have some intuitive properties. Rationally, the knowledge measure must be a nonnegative function. The knowledge amount of an AIFS and that of its complement should be equal to each other. When an AIFS degrade into a classical fuzzy set, its knowledge amount increases with the difference between the membership degree and the non-membership degree. Moreover, for an AIFS in which the difference between membership and non-membership grades are fixed, the knowledge amount behaves dually to the hesitancy degree. Since a crisp set provided the maximum knowledge, the knowledge amount reaches its maximum if the AIFS reduces into a crisp set. On the contrary, for each indicates full ignorance, so the knowledge amount reaches its minimum value 0 in such a case. Moreover, in the condition of , the greater hesitant degree implies the less uncertainty amount.
Having these intuitive properties in mind, we can propose the following axiomatic definition for the knowledge measure of AIFSs.
Definition 5.
For an AIFS A defined in, its knowledge measure is a mappingsatisfying the following properties:
- (KP1)
- if and only if A is a crisp set.
- (KP2)
- if and only if,.
- (KP3)
- is increasing withand decreasing with,.
- (KP4)
- .
We note that in References [33,34], the third property of entropy for AIFS is stated as: if is less fuzzy than , i.e., for , , or for , . We can see that this property indicates that the knowledge amount behaves dually to the fuzziness of an AIFS, which does not consider the impact of the hesitancy degree. The condition and indicate . Therefore, . Similarly, given and , we have , . Therefore, we can say the knowledge measure is decreasing with fuzziness. It may be arbitrary to give the property that if is less fuzzy than . Hence, when the hesitancy degree is fixed, we also can say if is less fuzzy than , which is consistent with our proposed property. Moreover, the cases of and indicate that , but cannot infer or . Generally, it has been known that the fuzziness of an AIFS including classical fuzzy sets is related to the difference between membership and non-membership grades. Thus, it is not comprehensive to equate the concept of fuzziness to the relation of inclusion.
The above analysis indicates that the amount of knowledge for AIFSs is decreasing with fuzziness, but there is no determinative relation between them if the hesitancy degree is ignored. The third property in Reference [34] is a strict constraint for defining the knowledge measure. Similarly, this kind of properties for intuitionistic fuzzy entropy and uncertainty measures [28,33,38] are also incomplete and stricter because of the absence of the hesitancy degree and the equivalence between fuzziness and the inclusion relation of AIFSs.
It is known that several divergence measures have been proposed based on Shannon entropy. Kullback–Leibler divergence (K–L divergence) [39] is one of the most popular divergence measures developed from Shannon entropy [20]
Let X be a discrete random variable. P1 and P2 are two probability distributions for X. The K–L divergence between P1 and P2 is defined by the equation below [35].
where pij is the probability of occurrence of the value X = xj for each of the probability distribution Pi, I = 1, 2. To construct a symmetric divergence measure, the divergence measure between P1 and P2 can be defined by the formula below.
In applications, to avoid the undefined case of zero denominator, the symmetric divergence measure can be modified by the equation below.
Then, we can construct a knowledge measure for an AIFS A defined in by measuring the divergence between A and the most uncertain AIFS . Based on the previously mentioned axiomatic definition for the knowledge measure of AIFSs and the modified divergence measure in Reference (7), the knowledge measure can be expressed by the following equation.
where , .
Then, we will prove that the proposed knowledge measure KS(A) satisfies all properties in Definition 5.
Theorem 1.
For an AIFS A defined in, thenif and only if A is a crisp set.
Proof.
(1) For a crisp subset of X, we have , and , . Then we can get . For AIFS A defined in , we can get and . Then, it follows that , and .
Considering the function with , we have:
, .
This indicates that f(x,y) is strictly increasing with x and strictly decreasing with y. Hence, f(x,y) has a single maximum point (1,0) where , and .
Therefore, each part of , i.e., and , is less than . By , we can infer that and for all , which indicates that , and for all .
Therefore, A is a crisp set.
Therefore, we have if and only if A is a crisp set. □
Theorem 2.
For an AIFS A defined in, thenif and only iffor each.
Proof.
The condition indicates that . Therefore, we have , . Then can be yielded.
For , given , , and , we can get and . indicates that and for all . Therefore, we have for each .
Then, we can get that if and only if for each . □
Theorem 3.
For an AIFS A defined in,is increasing withand decreasing with,.
Proof.
In the proof of Theorem 1, it has been pointed out that the function with is strictly increasing with x and strictly decreasing with y.
Therefore, the summation of all is increasing with and decreasing with .
Then, it follows that is increasing with and decreasing with , . □
Theorem 4.
For an AIFS, A defined in,.
Proof.
This is straightforward by the definition of and . □
Theorem 1–4 illustrates that the proposed mapping satisfies all properties in the axiomatic definition of the knowledge measure. Therefore, is a knowledge measure of AIFSs.
To provide a visual perception on the proposed knowledge measure, we consider an AIFS A defined in X = {x}. Based on the geometric interpretation of AIFSs proposed by Szmidt and Kacprzyk [28], the values of the knowledge amount are projected to the hyper plane in the unit intuitionistic fuzzy cube, as shown in Figure 1. The change of knowledge amount according to the distribution of membership and non-membership grades can be reflected by this figure. We note that, in the condition of , the knowledge amount is decreasing with the hesitancy degree. For a fixed hesitancy degree, the knowledge amount is increasing the difference between the membership degree and the non-membership degree. This is consistent with the proposed axiomatic properties of the knowledge measure.
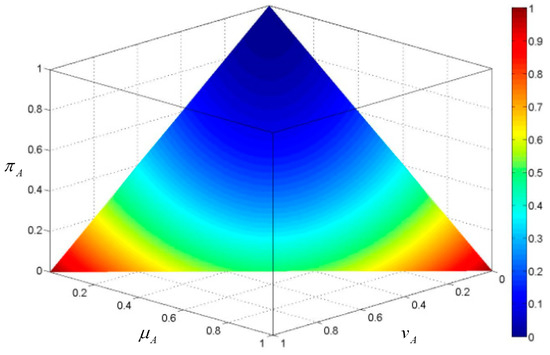
Figure 1.
The value of the knowledge measure KS (A).
4. Numerical Examples
In this section, the performance of the proposed knowledge measure KS will be validated based on two numerical examples. To illustrate the effectiveness and performance of the proposed Biparametric uncertainty measure for AIFSs, some existing intuitionistic fuzzy entropy measures will be adopted for comparison. Therefore, we first recall some widely used entropy measures for AIFSs.
The entropy measure proposed by Zeng and Li [40] is shown below.
The entropy measure proposed by Burillo and Bustince [27] is shown below.
The entropy measure proposed by Szmidt and Kacprzyk [28] is based on the equation below.
The entropy measure proposed by Vlachos and Sergiadis [30] is shown below.
The entropy measure proposed by Hung and Yang [29] is illustrated below.
The knowledge measure proposed by Szmidt, Kacprzyk, and Bujnowski [32] is shown in the equation below.
Nguyen’s knowledge measure [33] equals the following.
Guo’s knowledge measure [34] is based on the equation below.
Example 1.
Four AIFSs defined in X = {x} are given as: A1 = <x,0.5,0.5>, A2 = <x,0.25,0.25>, A3 = <x,0.25,0.5>, A4 = <x, 0.2,0.3>.
According to the eight existing measures and our proposed uncertainty measure, we can calculate the uncertainty degree and amount of knowledge. The comparative results are shown in Table 1.

Table 1.
Comparison results of example 1. (counter-intuitive results are in bold type).
From Table 1, we can see that the entropy measure EZL, ESK, and EVS cannot discriminate the uncertainty of A1 and A2. Since the entropy measure EBB is defined based on the hesitancy degree of AIFSs, it assigns zero uncertainty to A1, which is unreasonable. Moreover, the uncertainty grades of A2 and A4 cannot be distinguished by EBB because their hesitancy degrees are identical. It is also shown that uncertainty grades of A2 and A4 calculated by the entropy measure E2HC are equal to each other.
It is also shown that the knowledge measures KSKB, KN, KG, together with our proposed measure KS can discriminate these four AIFSs well from the perspective of the amount of knowledge. For the ranking order of the knowledge amount, we see that the measures KSKB and KG yield the results K(A3) > K(A1) > K(A4) > K(A2). When the knowledge measure KN is applied, we can obtain that K(A1) > K(A3) > K(A2) > K(A4). Our proposed measure KS leads to the order K(A1) > K(A3) > K(A4) > K(A2). Comparing AIFSs A1 and A3, we can see that the difference between the membership and non-membership degree of A1 is less than that of A3. However, A3 has more of a hesitancy degree than A1. According to the monotonicity of the knowledge measure proposed in Definition 5, the knowledge amount of A1 and A3 cannot be determined. But for A2 and A4, it is shown that A2 has less Δ, i.e., the difference between its membership and non-membership grades, and more hesitancy degree π than A4. Therefore, A4 should convey a higher amount of knowledge than A2. In such a case, the knowledge measure KN is less reasonable than the other three knowledge measures.
This example indicates that our proposed knowledge measure is effective in measuring the knowledge amount. It is competent to reflect the intuitive relation between different AIFSs.
Example 2.
Nine AIFSs defined in X = {x} are considered. These AIFSs are given as: A1 = <x,0.7,0.2>, A2 = <x,0.5,0.3>, A3 = <x,0.5,0>, A4 = <x,0.5,0.5>, A5 = <x,0.5,0.4>, A6 = <x,0.6,0.2>, A7 = <x,0.4,0.4>, A8 = <x,1,0>, and A9 = <x,0,0>.
Based on five widely used entropy measures EZL, EBB, ESK, EVS, and E2HC, three knowledge measures KSKB, KN, and KG, and our proposed measures KS, we can calculate the uncertainty of these nine AIFSs. The results are shown in Table 2.

Table 2.
Comparison results of example 2 (counter-intuitive results are in bold type).
We note that the AIFS A9 = <x,0,0> is the most uncertain one with the least amount of knowledge. Therefore, its uncertainty measure should be 1 and the knowledge amount is 0. It can be seen that only E2HC cannot produce reasonable results for AIFS A9 = <x,0,0>. For AIFS A8 = <x,1,0>, it is the most certain one conveying the maximum knowledge amount. Hence, its uncertainty degree is 0 and the knowledge amount is 1 since the results were produced by all measures in Table 2. Moreover, we can see that all entropy measures may bring counter-intuitive results, which have been highlighted in a bold type in Table 2. These unreasonable results show that these entropy measures are not competent to distinguishing different AIFSs. The knowledge measure KSKB assigned the same knowledge amount to AIFSs A3 = <x,0.5,0> and A4 = <x,0.5,0.5>, which indicates the poorer discriminant ability of KSKB. By the proposed axiomatic definition, we cannot rank the knowledge amount of A3 and A4 since and is greater that and , respectively. Comparing A1 and A3, we find that and . Therefore, A1 has a greater knowledge amount than A3, which can be yielded by all knowledge measures. For AIFSs A1 and A5, they have the same hesitancy degree. The greater difference between the membership and non-membership grades of A1 brings more knowledge amount than A5, as shown by the results of all knowledge measures. We can also rank the knowledge amount of AIFSs A2, A6, and A7 in the same way. We note that AIFSs A4, A7, and A9 have the same , so the less hesitancy degree indicates a greater knowledge amount. Thus, the knowledge conveyed by A4, A7, and A9 should be ranked as K(A4) > K(A7) > K(A9). It is shown that all knowledge measures can provide this ranking order. This example tells us that our proposed knowledge measure is effective to distinguish the knowledge amount of different AIFSs.
Example 3.
We consider an AIFS A defined in X = {6,7,8,9,10}. The AIFS A is defined as:
.
De et al. [41] have defined an exponent operations for AIFS defined in . Given a non-negative real number m, is defined as:
Based on the operations in Equation (17), we have:
.
.
.
.
Considering the characterization analysis on linguistic variables, we can regard the AIFS A as ‘‘LARGE’’ in X. Correspondingly, AIFSs A0.5, A2, A3 and A4 can be regarded as “More or less LARGE”, “Very LARGE”, “Quite very LARGE”, and “Very very LARGE”, respectively.
Intuitively, from A0.5 to A4, the uncertainty hidden in them becomes less and the knowledge amount conveyed by them increases. So the following relations hold:
To make a comparison, entropy measures EZL, EBB, EVS, E2HC, and knowledge measures KSKB, KN, and KG are employed to facilitate analysis. In Table 3, we present the results obtained based on different measures to facilitate comparative analysis.

Table 3.
Comparative results of all AIFSs with respect to B (counter-intuitive results are in bold type).
We can note that the AIFS A will be assigned more entropy than the AIFS A0.5 when entropy measures EZL, EBB, and ESK are applied. The ranking orders obtained based on these measures are listed below.
.
.
.
It is shown that these ranked orders do not satisfy intuitive analysis in Equation (18), while other entropy measures can induce desirable results. In this example, E2HC and EVS perform well. This illustrates that these entropy measures are not robust enough to distinguish the uncertainty of AIFSs with linguistic information.
Moreover, the results produced by knowledge measures KSKB, KN, and KG are also not reasonable, which are shown as the equations below.
,
,
.
However, our proposed knowledge measure KS indicates that:
.
Therefore, the knowledge measures KSVB, KN, and KG are not suitable for differentiating the knowledge amount conveyed by AIFSs. The effectiveness of our proposed knowledge measure KI is indicated by this example once again.
From the above examples, we can conclude that entropy measures EZL, EBB, ESK, EVS, and E2HC perform poor because of their lack of robustness and discriminability. Our proposed knowledge measure performs much better than knowledge measures KSVB, KN, and KG.
5. Application in Solving Intuitionistic Fuzzy MADM
In this section, the proposed knowledge measure will be applied in solving multiple attribute decision making (MADM) problems. The MADM problems to be considered can be described below.
All alternatives consist of a set denoted as . The set of all considered attributes is expressed as . The weight vector of attributes is with . Due to the limitation of the decision-maker’s knowledge and expertise, an intuitionistic fuzzy form expresses the evaluation information provided under each attribute. The intuitionistic fuzzy decision matrix given by the decision maker is expressed as:
where the evaluation result of alternative Gi with respect to the attribute Aj, provided by the decision-maker in the form of an intuitionistic fuzzy value.
When solving MADM problems, the weights of attributes are important. If the attribute weights are completely known, this MADM problem can be solved by aggregating all intuitionistic fuzzy information under different attributes and comparing the final intuitionistic fuzzy values. However, in a practical application, the attribute weights are usually partially known or completely unknown [42]. Therefore, the attribute weights must be determined before solving the MADM problems. The attribute weights can be empirically assigned by experts. However, this method is subjective and the partial information on the attribute weights may not be used sufficiently. Therefore, we can propose a new model to determine the attribute weights based on the proposed knowledge measure. Generally, we hope the evaluation results of all alternatives under one attribute are distinguished enough to facilitate our decision making. Therefore, we can set the total knowledge amount as the objective function of optimization. By maximizing the sum of the knowledge amount under all attributes, we can construct the following models.
where H is the set of all incomplete information about attribute weights and is the knowledge amount calculated by our proposed knowledge measure, i.e., .
When the attribute weights are completely unknown, the attribute under which the total knowledge is greater should be assigned more weight. Therefore, we can calculate attribute weights by using the following equation.
When the attribute weights are obtained, the intuitionistic fuzzy MADM problems can be solved by aggregating the intuitionistic fuzzy information under all attributes. Many weighted aggregation operators have been proposed for integrating intuitionistic fuzzy information. In this section, we will use the well-known intuitionistic fuzzy weighted averaging (IFWA) operator [43] to solve the MADM problems under an intuitionistic fuzzy environment. The intuitionistic fuzzy information of alternative Gi can be aggregated to an intuitionistic fuzzy value zi, which is expressed as:
Then the score function S(zi) and accuracy function H(zi) of zi () can be calculated as:
Lastly, all alternatives can be ranked into an order according to the linear order relation between IFVs based on score function and accuracy function.
Next, an example will be applied to demonstrate the performance of our proposed method for solving MADM problems in an intuitionistic fuzzy condition.
Example 4.
A capital company will invest a sum of money to a project. Considering the complexity of economic development, they choose five companies as candidates. Five companies to be considered are shown as:
- G1: A cell phone company.
- G2: A food company.
- G3: An automobile sales company.
- G4: A computer company.
- G5: a TV company.
The investment company evaluates these five companies from four attributes, which are:
- A1: The investment risk.
- A2: The capital gain.
- A3: The social and political impact.
- A4: The environmental impact.
The evaluated results with intuitionistic fuzzy information are shown as:
Case 1.
The information on the attribute weights is incomplete. The partial information on attribute weights is listed in set H, .
The total knowledge amount under each attribute can be calculated by the equations below.
; ;
; .
The optimal model to determine the attribute weights can be constructed as:
Then the weighting vector of the attribute can be obtained as:
Using the IFWA operator, we can aggregate the intuitionistic fuzzy information for each alternative with respect to all attributes. Then we have:
Z1 = <0.3738, 0.5218>, Z2 = <0.6203, 0.2962>, Z3 = <0.5568, 0.3327>,
Z4 = <0.4787, 0.3323>, Z5 = <0.5776, 0.1990>.
Calculating the score values of these integrated intuitionistic fuzzy information, we can get:
S(Z1) = −0.1480, S(Z2) = 0.3241, S(Z3) = 0.2240, S(Z4) = 0.1464, S(Z5) = 0.3787.
According to these scores and the linear order relation between IFVs, all alternatives can be ranked as the following order: .
Using the method proposed in Reference [44] based on and , we can solve this MADM problem in such a case. The weighting vector can be obtained as: . The ranking order of all alternatives is , which is identical to the ranking order obtained by our proposed method. This indicates that the proposed method for solving MADM is reasonable and effective.
Case 2.
There is no information for the attribute weights. Based on the proposed knowledge measure, we can calculate the total knowledge amount of all intuitionistic fuzzy information under one attribute. They are listed as:
; ;
; .
The attribute weights can be obtained by Equation (19),
; ; ; .
Therefore, the weighting vector is .
Applying the weighting factors and IFWA operator, we can aggregate the evaluation results of an alternative across all attributes. The integrated result for each alternative is:
Z1 = <0.4259,0.4697>, Z2 = <0.6459,0.2806>, Z3 = <0.5561,0.3493>,
Z4 = <0.5616,0.2740>, Z5 = <0.5660,0.2064>.
The scores of the intuitionistic fuzzy evaluation information of all alternatives can be obtained as:
S(Z1) = −0.0438, S(Z2) = 0.3562, S(Z3) = 0.2069, S(Z4) = 0.2876, S(Z5) = 0.3596.
All alternatives can be ranked into the following order: .
For comparative analysis, we can also solve this decision-making problem based on Xia and Xu’s method based on and [44]. The yielded weighting vector is . The ranked order of five alternatives is . We can see that both of our proposed method based on KS and the method in Reference [44] can take G5 as the best choice for investment. Even though the order between G3 and G4 obtained by our method is different from that obtained by Xia and Xu’ method, this difference has no effect on choosing the best company to invest. Actually, the solution of an MADM problem only concerns the best alternative. The order of other alternatives is beyond the ultimate goal of an MADM problem.
This example demonstrates that the proposed methods for solving MADM problems are competent to getting reasonable results. Compared with Xia and Xu’s method, our proposed optimal model is easier, which will reduce the computation burden. Moreover, our defined knowledge measure is more concise than the cross entropy and entropy measure defied in Reference [44]. Thus, the priority of the new knowledge measure is also verified.
6. Conclusions
In this paper, the definition of knowledge measure for AIFSs is addressed. The axiomatic definition of the knowledge measure is first proposed based on intuitive analysis on the knowledge amount. Then we proposed a new knowledge measure for AIFSs. The properties of the new knowledge measure are investigated from a mathematical viewpoint. Numerical examples are applied to illustrate the performance of the new knowledge measure. Comparative analysis on the experimental results indicates that the proposed knowledge measure is effective in discriminating the knowledge amount of different AIFSs. Unlike other existing measures that may lead to unreasonable results, the proposed new knowledge measure is robust in quantifying the knowledge amount of different kinds of AIFSs. Based on the new knowledge measure, we proposed two methods for determining attribute weights in intuitionistic fuzzy MADM problems in the cases that the information on attribute weights is partially known and completely unknown, respectively. Following the determination of attribute weights, we develop a new method to solve the MADM problem. To verify the effectiveness and rationality of the proposed models and the MADM method, we take an MADM problem as an example to make a comparison. The results show that the proposed method is effective enough to obtain reasonable results. Moreover, the proposed method has advantages in reducing computation burden and implementation.
We must point out that the proposed knowledge measure is not the only effective knowledge measure for AIFSs. It is also not the most effective one. In the future, further investigation on the definition of a more effective knowledge measure should be carried out. Moreover, a deeper relation between the knowledge amount and entropy is not investigated in this paper. Although we claim that the membership and non-membership grades influence the knowledge amount, the mechanism behind such an influence is not mined. These are also areas to focus on in future research.
Author Contributions
Conceptualization, G.W. and Y.S. Methodology, J.Z. and Y.S. Validation, Y.S. and G.W. Writing—Original Draft Preparation, J.Z. Writing—Review and Editing, Y.S. Funding Acquisition, Y.S.
Funding
The National Natural Science Foundation of China, grant numbers 61703426, 61876189, 61806219, 61273275, and 61503407; the China Postdoctoral Science Foundation, grant number 2018M633680, funded this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Bogiatzis, A.C.; Papadopoulos, B.K. Producing fuzzy inclusion and entropy measures and their application on global image thresholding. Evol. Syst. 2018, 9, 331–353. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M.; Yager, R.R. An overview of fuzzy research with bibliometric indicators. Appl. Soft Comput. 2015, 27, 420–433. [Google Scholar] [CrossRef]
- Blanco-Mesa, F.; Merigó, J.M.; Gil-Lafuente, A.M. Fuzzy decision making: A bibliometric-based review. J. Intell. Fuzzy Syst. 2017, 32, 2033–2050. [Google Scholar] [CrossRef]
- Pozna, C.; Minculete, N.; Precup, R.E.; Kóczy, L.T.; Ballagi, Á. Signatures: Definitions, operators and applications to fuzzy modeling. Fuzzy Sets Syst. 2012, 201, 86–104. [Google Scholar] [CrossRef]
- Jankowski, J.; Kazienko, P.; Watróbski, J.; Lewandowska, A.; Ziemba, P.; Zioło, M. Fuzzy multi-objective modeling of effectiveness and user experience in online advertising. Exp. Syst. Appl. 2016, 65, 315–331. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yu, D.; Liao, H.C. Visualization and quantitative research on intuitionistic fuzzy studies. J. Intell. Fuzzy Syst. 2016, 30, 3653–3663. [Google Scholar] [CrossRef]
- Yu, D.; Shi, S. Researching the development of Atanassov intuitionistic fuzzy set: Using a citation network analysis. Appl. Soft Comput. 2015, 32, 189–198. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, C.H. A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition. Inf. Sci. 2015, 291, 96–114. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xue, A. A novel similarity measure on intuitionistic fuzzy sets with its applications. Appl. Intell. 2015, 42, 252–261. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Quan, W.; Huang, W. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2017, 1–14. [Google Scholar] [CrossRef]
- Li, D.F.; Wang, Y.C.; Liu, S.; Shan, F. Fractional programming methodology for multi-attribute group decision-making using IFS. Appl. Soft Comput. 2009, 9, 219–225. [Google Scholar] [CrossRef]
- Yager, R.R. An intuitionistic view of the Dempster–Shafer belief structure. Soft Comput. 2014, 18, 2091–2099. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y. Uncertainty measure in evidence theory with its applications. Appl. Intell. 2018, 48, 1672–1688. [Google Scholar] [CrossRef]
- Fan, C.; Song, Y.; Fu, Q.; Lei, L.; Wang, X. New operators for aggregating intuitionistic fuzzy information with their application in decision making. IEEE Access. 2018, 6, 27214–27238. [Google Scholar] [CrossRef]
- Fan, C.; Song, Y.; Lei, L.; Wang, X.; Bai, S. Evidence reasoning for temporal uncertain information based on relative reliability evaluation. Exp. Syst. Appl. 2018, 113, 264–276. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence and intuitionistic fuzzy sets. Appl. Intell. 2018, 48, 3950–3962. [Google Scholar] [CrossRef]
- Gao, P.C.; Zhang, H.; Li, Z.L. An efficient analytical method for computing the Boltzmann entropy of a landscape gradient. Trans. GIS 2018, 22, 1046–1063. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cushman, S.A. Calculating the configurational entropy of a landscape mosaic. Landsc. Ecol. 2016, 31, 481–489. [Google Scholar] [CrossRef]
- Cushman, S.A. Calculation of configurational entropy in complex landscapes. Entropy 2018, 20, 298. [Google Scholar] [CrossRef]
- Gao, P.C.; Zhang, H.; Li, Z.L. A hierarchy-based solution to calculate the configurational entropy of landscape gradients. Landsc. Ecol. 2017, 32, 1133–1146. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control. 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Yager, R.R. On the measure of fuzziness and negation, part 1: Membership in the unit interval. Int. J. Gen. Syst. 1979, 5, 221–229. [Google Scholar] [CrossRef]
- Higashi, M.; Klir, G. On measures of fuzziness and fuzzy complements. Int. J. Gen. Syst. 1982, 8, 169–180. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy Sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. Fuzzy entropy on intuitionistic fuzzy sets. Int. J. Intell. Syst. 2006, 21, 443–451. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic fuzzy information-applications to pattern recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J.; Bujnowski, P. On some measures of information and knowledge for intuitionistic fuzzy sets. Notes IFS 2010, 16, 1–11. [Google Scholar]
- Szmidt, E.; Kacprzyk, J.; Bujnowski, P. How to measure the amount of knowledge conveyed by Atanassov’s intuitionistic fuzzy sets. Inf. Sci. 2014, 257, 276–285. [Google Scholar] [CrossRef]
- Nguyen, H. A new knowledge-based measure for intuitionistic fuzzy sets and its application in multiple attribute group decision making. Expert. Syst. Appl. 2015, 42, 8766–8774. [Google Scholar] [CrossRef]
- Guo, K. Knowledge measure for Atanassov’s intuitionistic fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 24, 1072–1078. [Google Scholar] [CrossRef]
- Chen, S.M.; Tan, J.M. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Guo, K.; Song, Q. On the entropy for Atanassov’s intuitionistic fuzzy sets: An interpretation from the perspective of amount of knowledge. Appl. Soft Comput. 2014, 24, 328–340. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Zeng, W.Y.; Li, H.X. Relationship between similarity measure and entropy of interval-valued fuzzy sets. Fuzzy Sets Syst. 2006, 157, 1477–1484. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. Some operations on intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 477–484. [Google Scholar] [CrossRef]
- Wei, G.W. Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting. Knowl.-Based Syst. 2008, 21, 833–836. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xia, M.; Xu, Z. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion. 2012, 13, 31–47. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).