Heat Transfer Performance of a Novel Multi-Baffle-Type Heat Sink
Abstract
1. Introduction
2. Problem Description
2.1. Geometric Configurations and Computational Domain
2.2. Mathematical Model
- (1)
- The volume force and the effect of surface tension are all neglected.
- (2)
- No radiation and gravity is assumed.
- (3)
- The thermo-physical properties of water are considered as constant and incompressible.
- (4)
- Axial conduction and viscous dissipation are not considered.
- (1)
- The coolant used is water and the multi-baffle-type heat sink (MBHS) is fabricated using aluminum.
- (2)
- A uniform heat flux of q = 58000 W/m2 is applied to the bottom of heat sinks, and other surfaces are considered to be adiabatic.
- (3)
- The inlet velocity u1 (Table 2) and is assumed to remain constant. The inlet temperature Tin = 293 K.
- (4)
- The outflow condition in the software is set at the outlet.
2.3. Parameter Definition
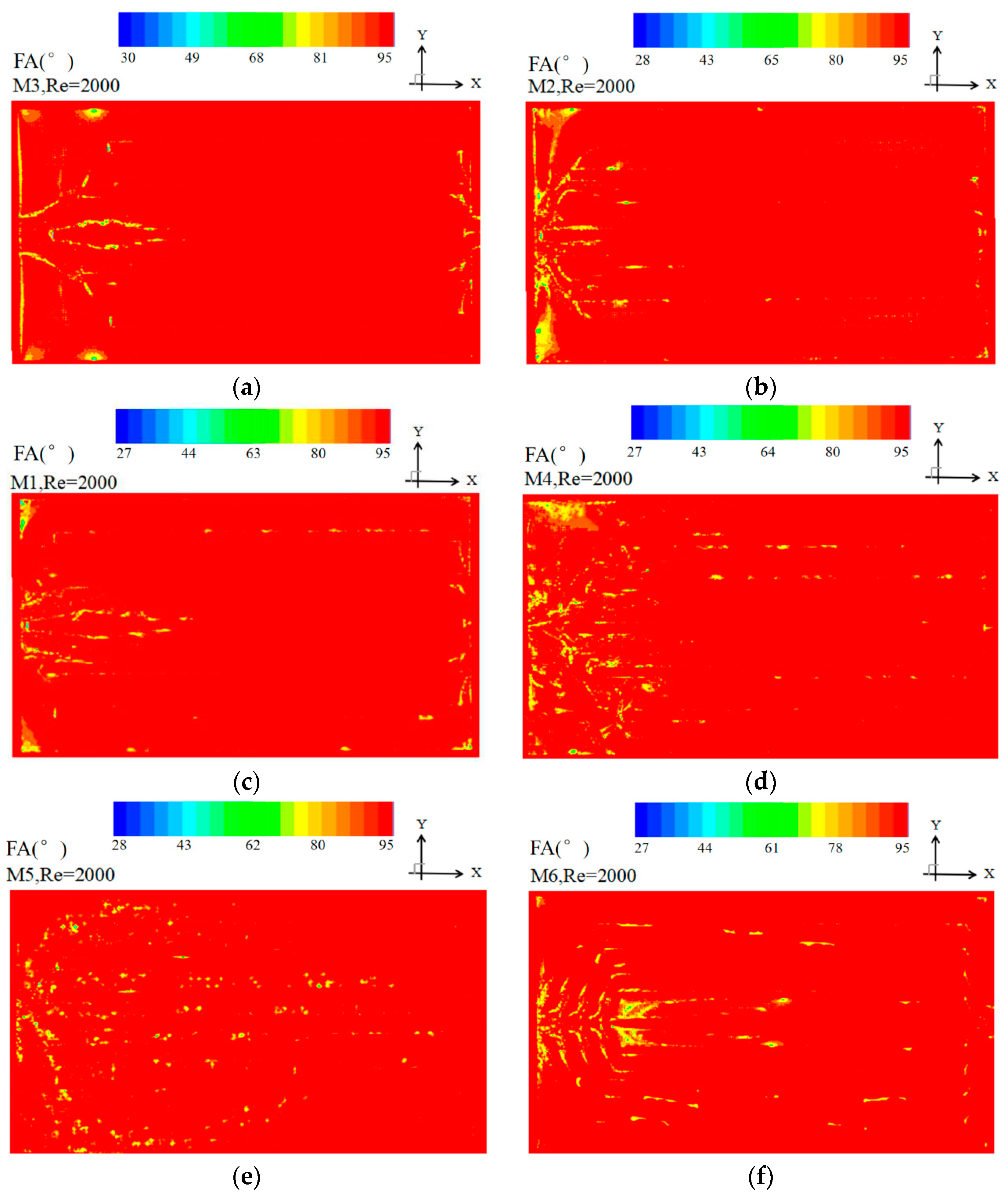
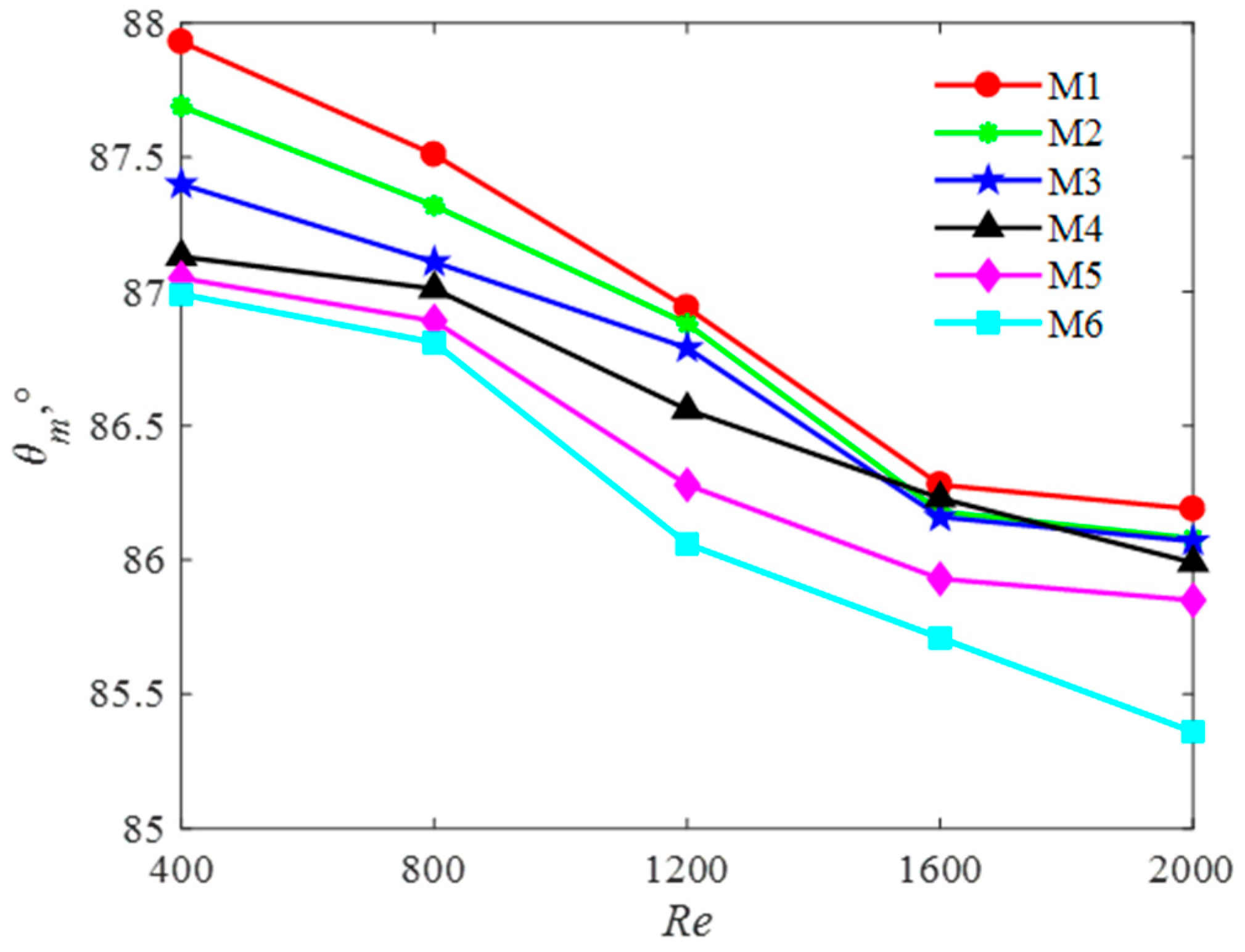
2.4. Field Synergy Principle
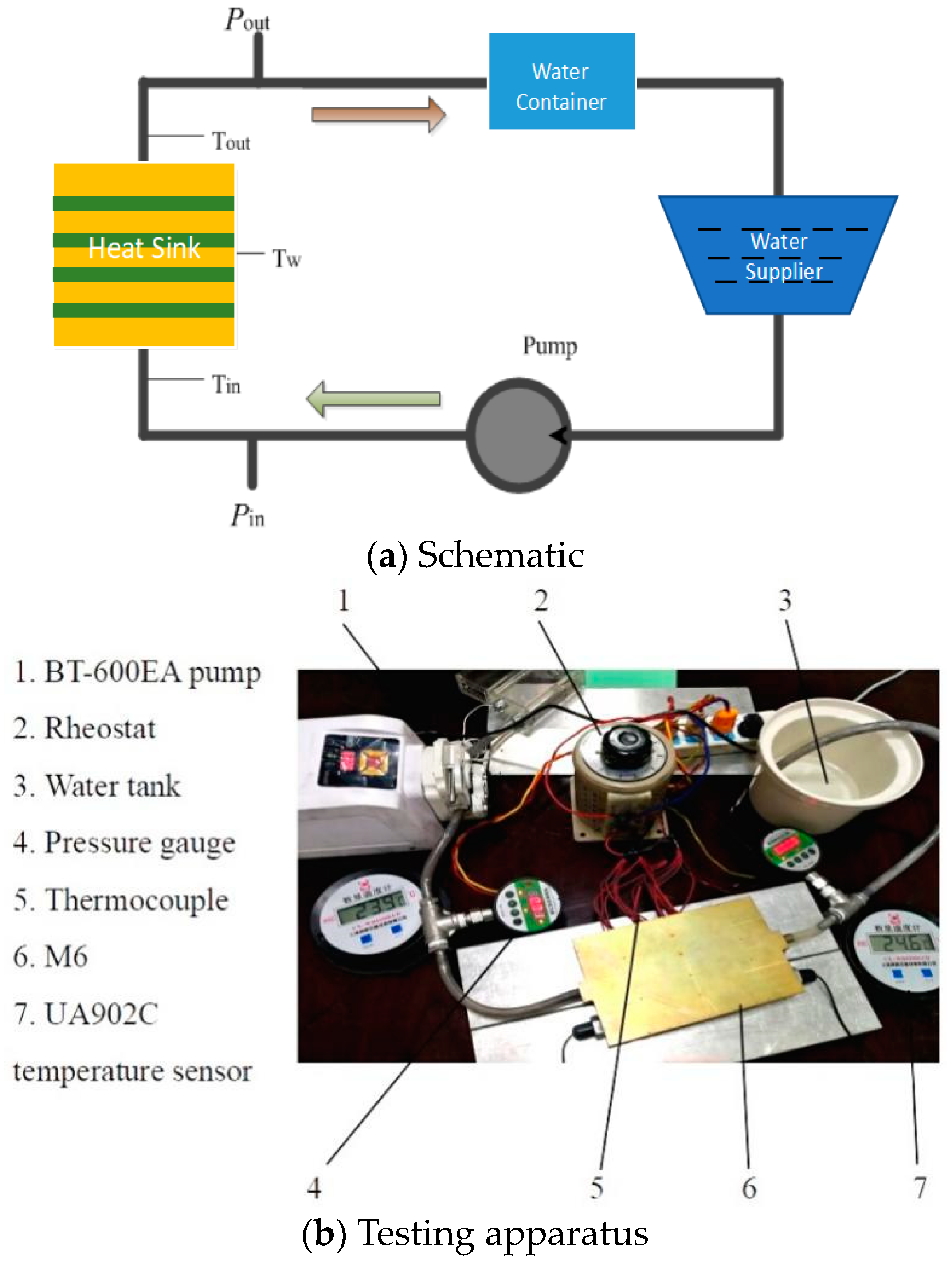
3. Experiment Apparatus and Procedure
4. Experimental Results
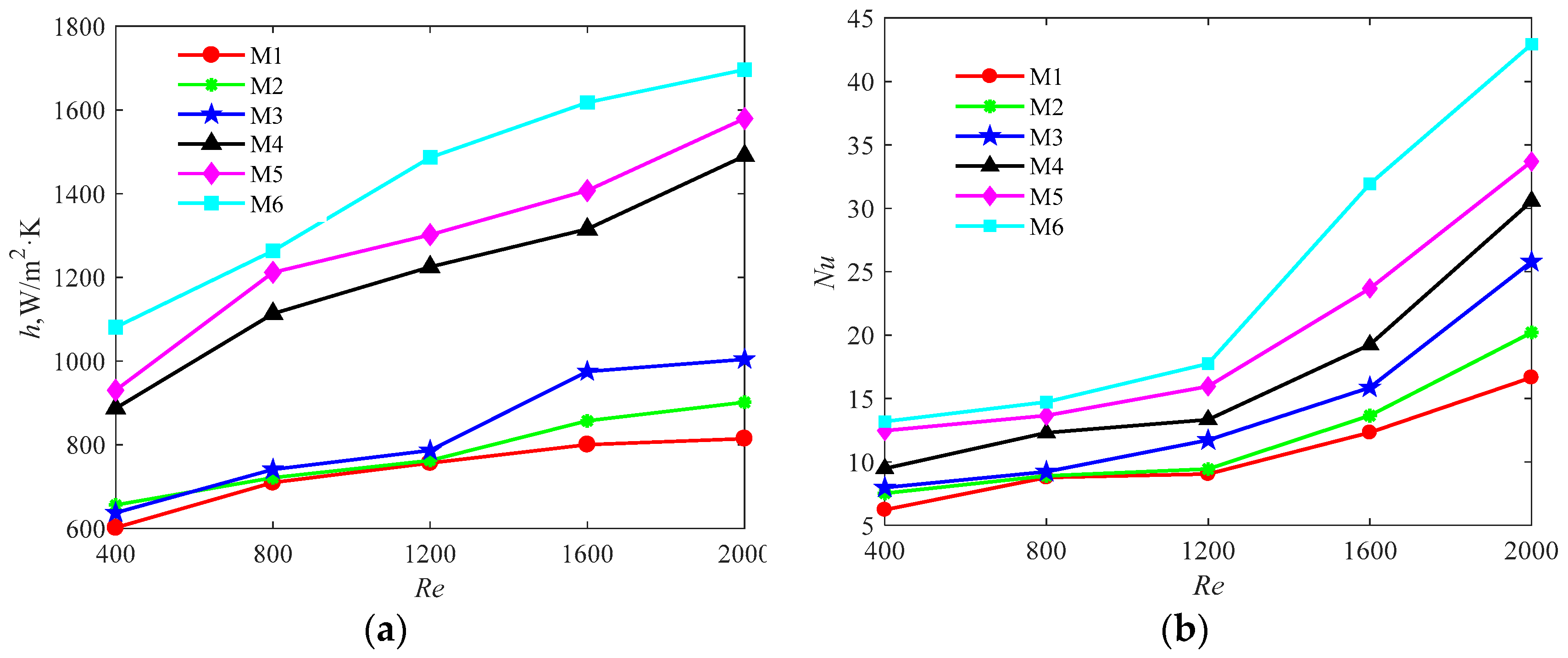
4.1. Convective Heat Transfer Coefficient and Nusselt Number
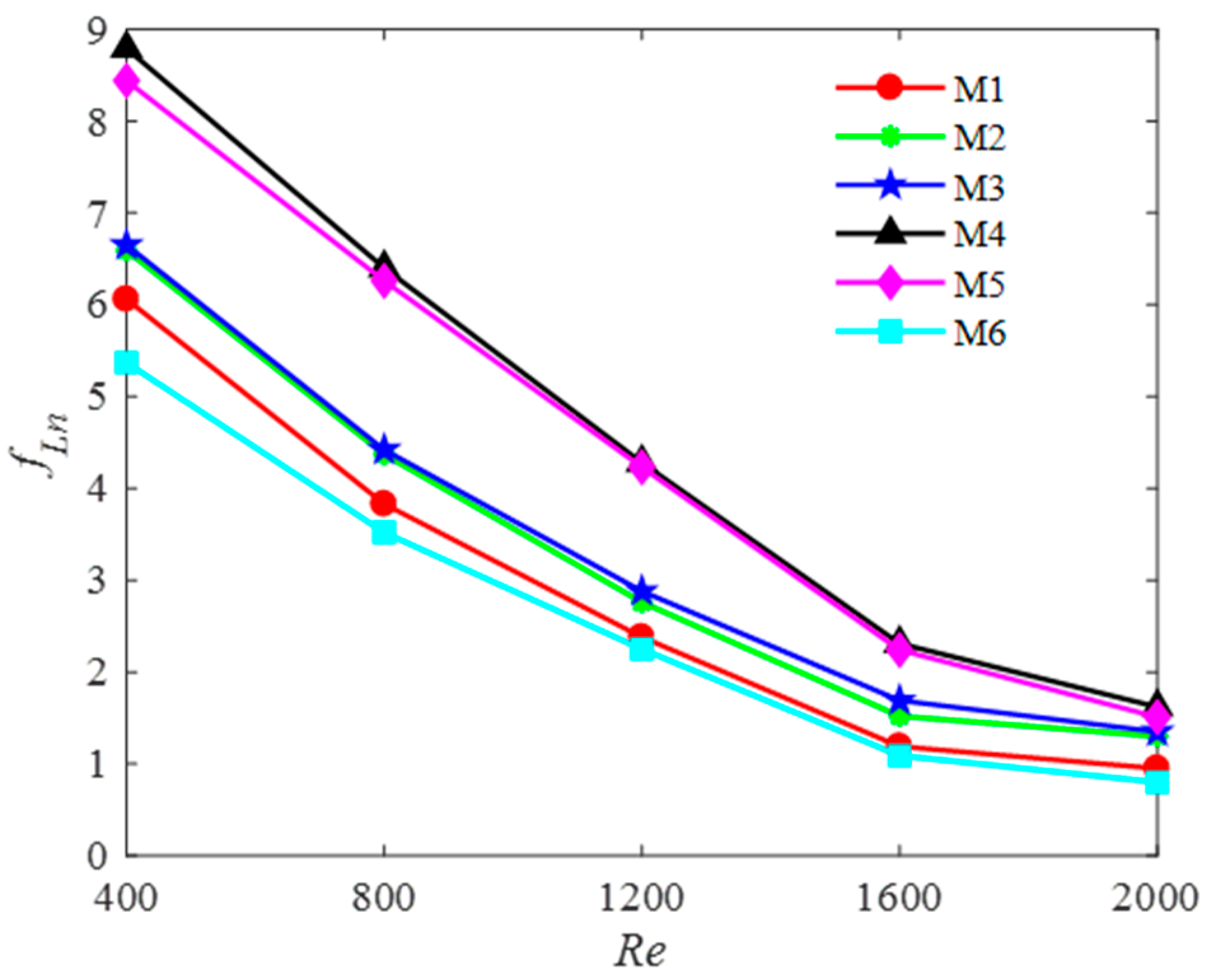
4.2. Pressure Drop and Friction Factor
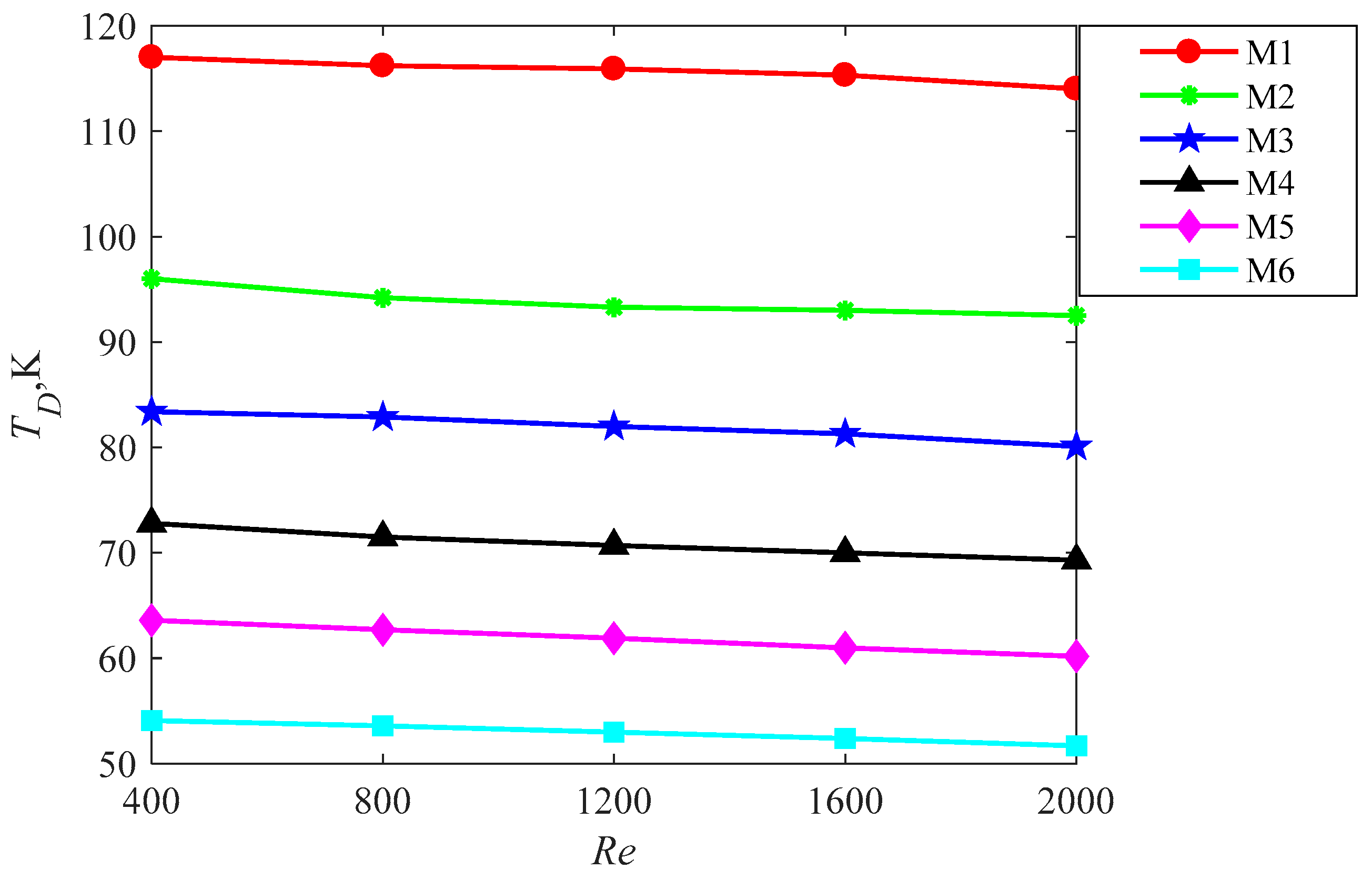
5. Results and Discussion
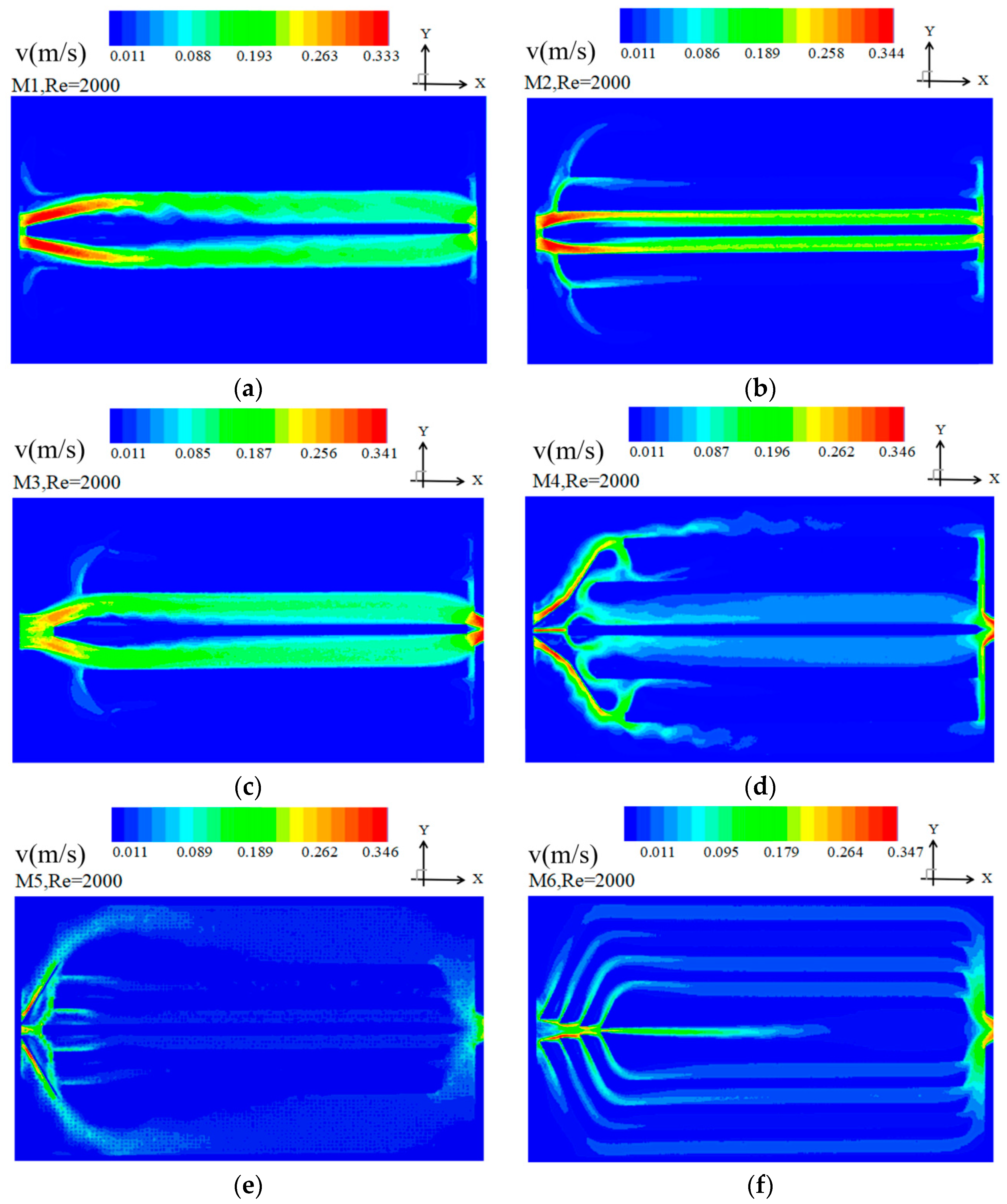
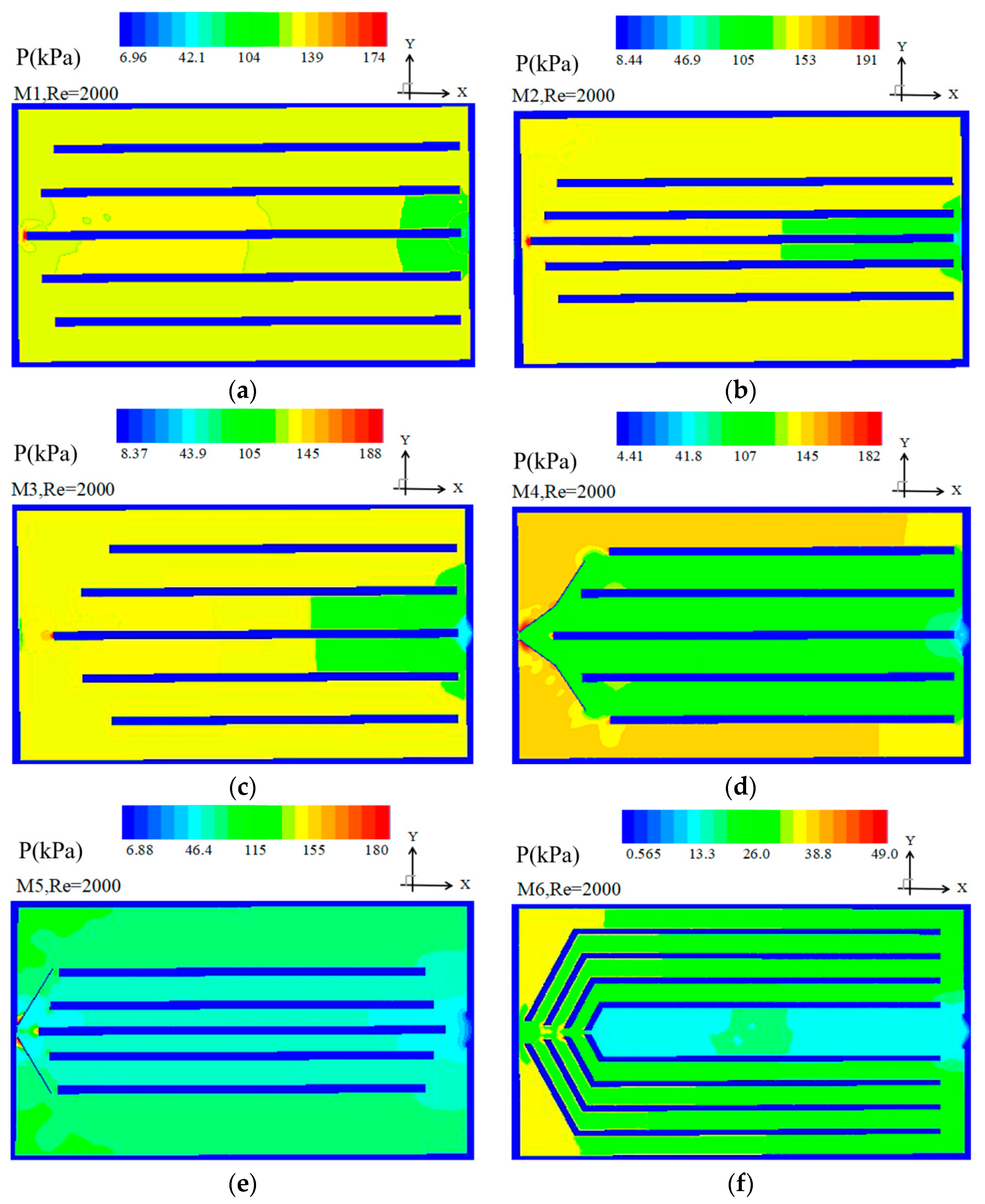
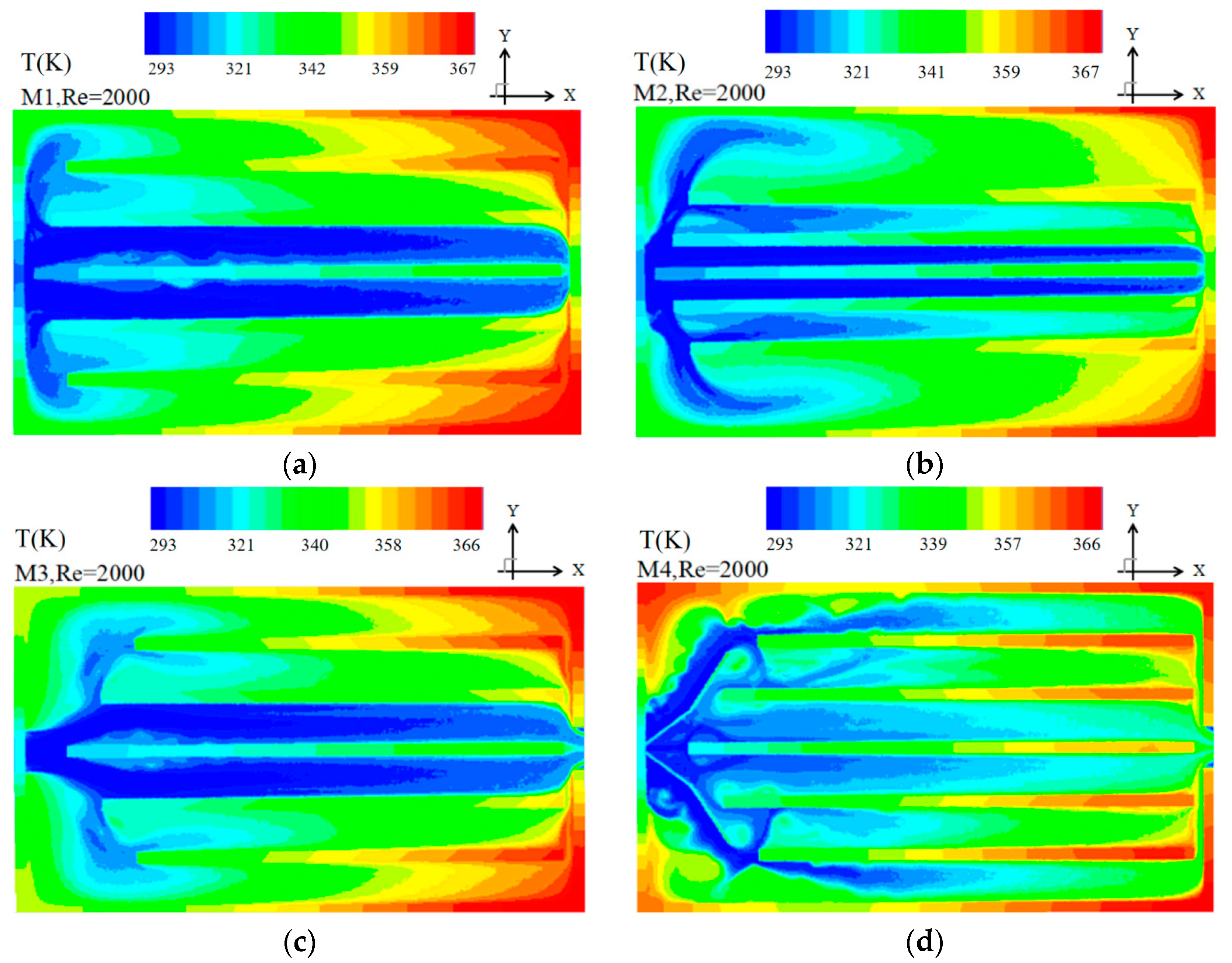
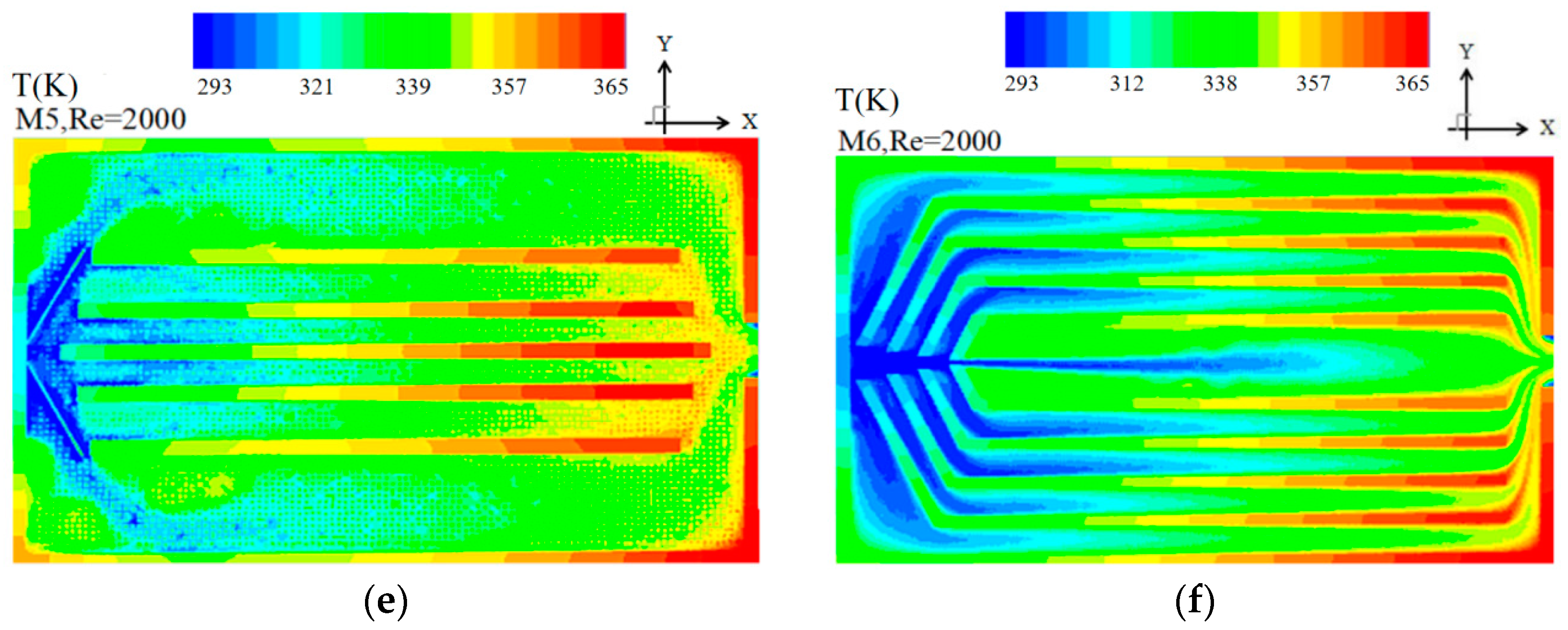
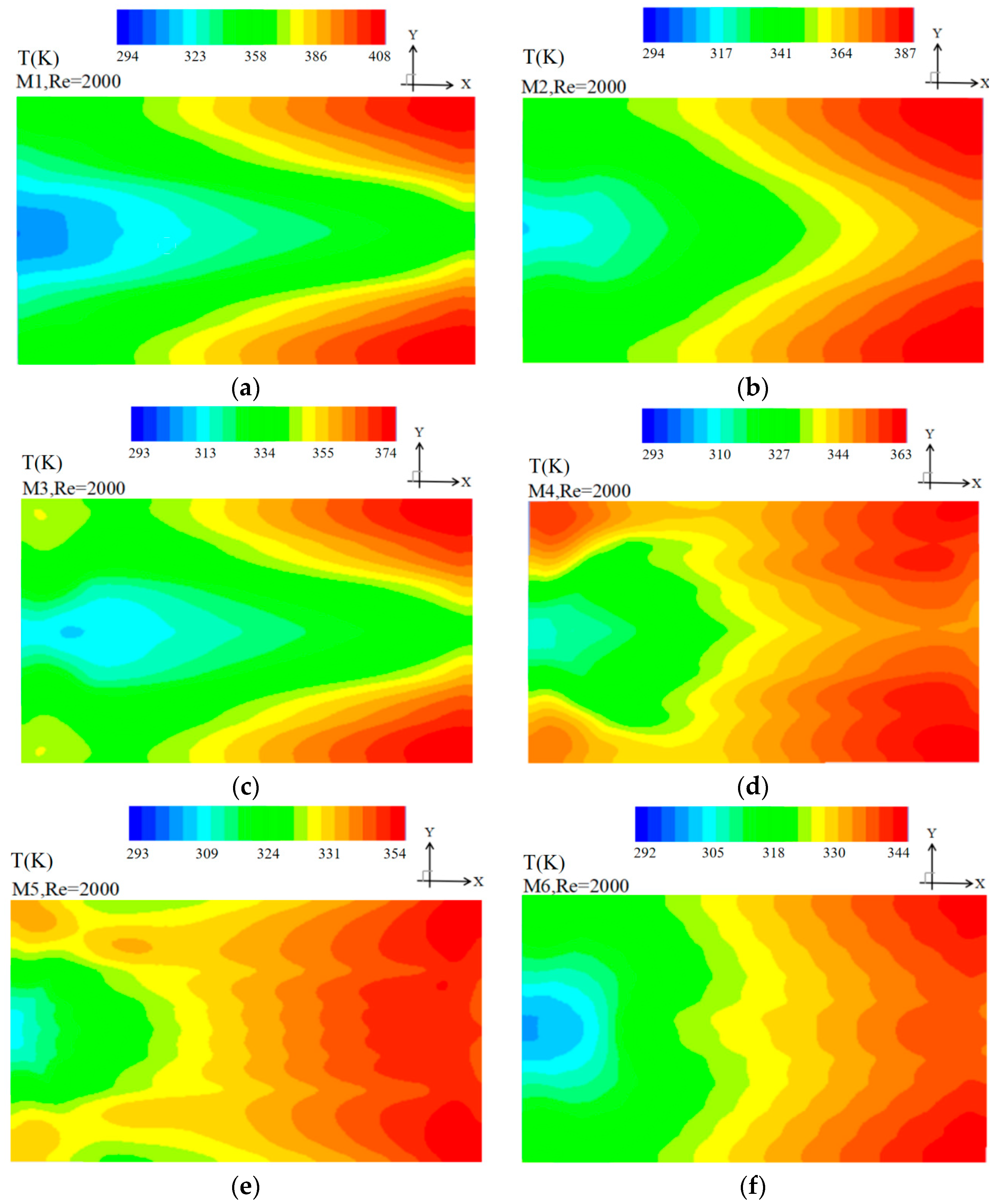
5.1. Simulation Results
5.1.1. Grid Independency
5.1.2. Simulation procedure
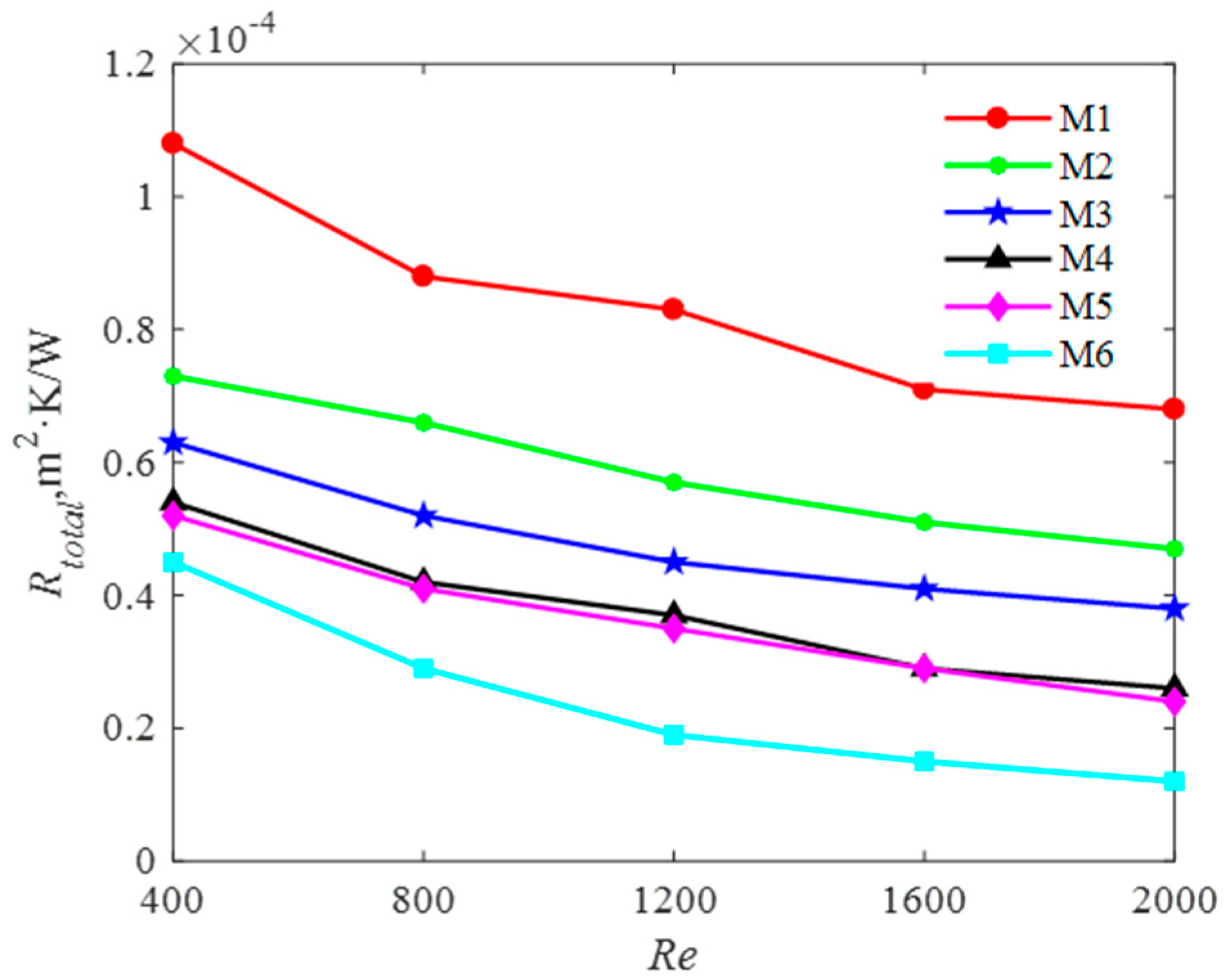
5.2. Model Comparison
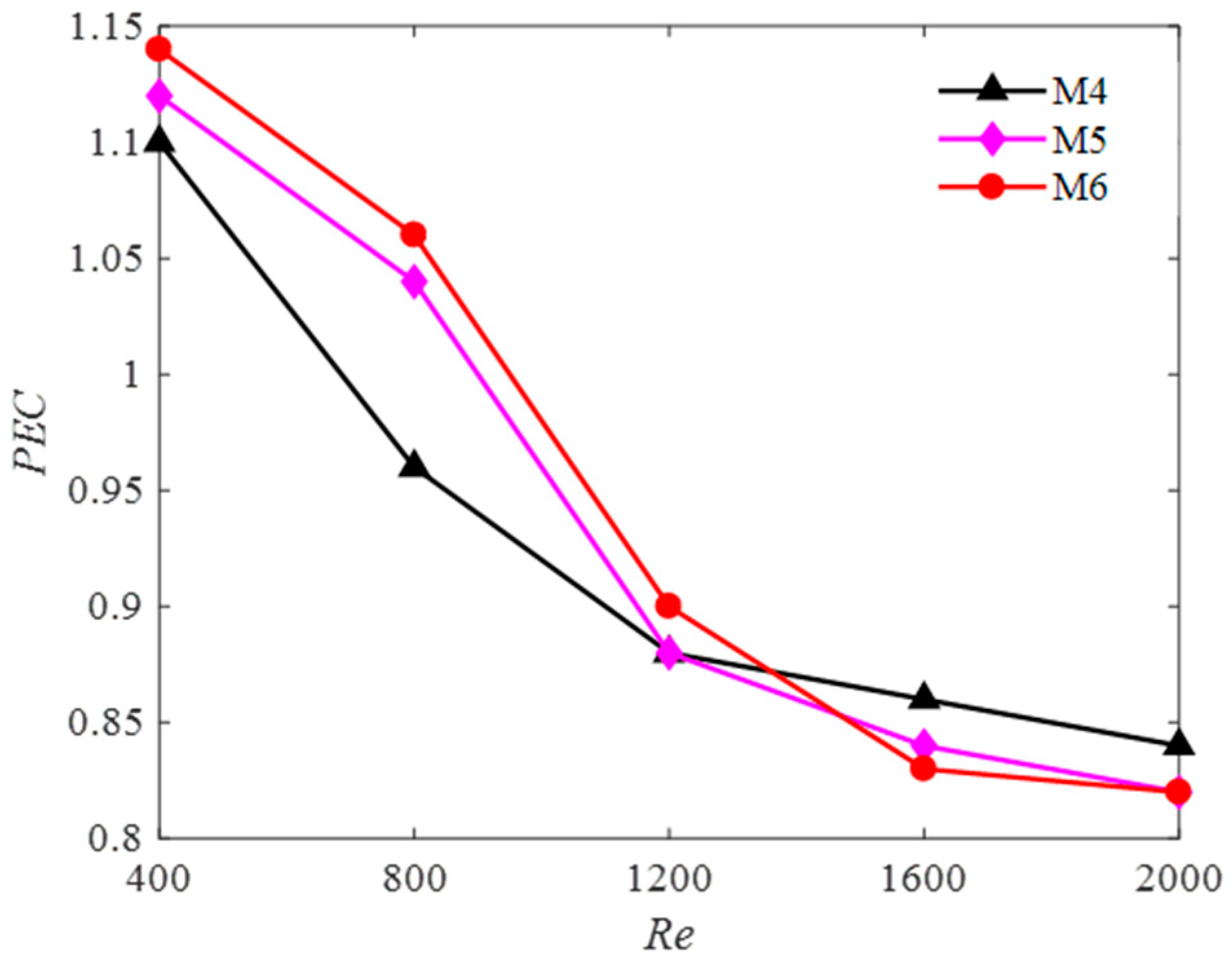
5.3. Model Selection and Limits
6. Conclusions
- (1)
- As compared with the five models M1–M5, the velocity field of M6 is more uniformly distributed without the aid of external electronic devices.
- (2)
- M6 takes the advantage of dispersing heat from the high-temperature zone in a well-proportioned way.
- (3)
- The heat-transfer and flow performance of the heat sink can be effectively improved by employing optimally shaped baffles.
- (4)
- The average synergistic field angle decreases with the increase of the multi-baffle.
- (5)
- The heat-transfer coefficients and pressure drop of the experimental and simulation results are consistent with each other, which verifies the correctness of the numerical method and results.
- (6)
- Among six models, M6 possesses the lowest total thermal resistance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Ac | cross sectional area, m2 | Tb,avg | average channel base temperature, K |
| DM | degree of maldistribution | temperature gradient | |
| Dh | hydraulic diameter, m | ΔT | average temperature difference, K |
| f | friction factor | Tm | average fluid temperature, K |
| f0 | friction factor of a plain channel | Tin | inlet temperature, K |
| H | total height of cooling plate, mm | Tout | outlet temperature, K |
| H1 | height of the counter sink, mm | Th | average temperature of heating surface, K |
| hconv | convective heat transfer coefficient, W/m2 K | TD | temperature difference between the maximum and minimum temperature of heating surface, K |
| ks | thermal conductivity of Al, W/m K | u1 | axial velocity, m/s |
| Kf | thermal conductivity of fluid, W/m K | um | mean axial velocity, m/s |
| L | length of heat sink, mm | velocity vector | |
| Li | length of flow channel, mm | Wi | width of flow channel, mm |
| L0i | length of baffle, mm | xi | rectangular coordinates |
| MFR | mass flow ratio coefficient | Greek symbols | |
| Nu | Nusselt number | kinematic viscosity, kg/ms | |
| Nu0 | Nusselt number of a plain channel | density, kg/m3 | |
| p | wetting perimeter, m | average field synergy angle, ° | |
| ΔP | pressure drop of heat sink, Pa | baffles intersection angle, ° | |
| Pout | outlet pressure, Pa | head loss coefficient | |
| Pin | inlet pressure, Pa | Subscripts | |
| q | heat flux, W/m2 | ave | average |
| qm | mass flow rate of liquid, kg/s | i | index in x-direction |
| Re | Reynolds number | j | index in y-direction |
| Rtotal | total thermal resistance, m2·K/W | n | flow channel number |
| s | average absolute deviation | w | heating surface |
| T | temperature, K | x,y,z | three coordinates shown in Figure 1, mm |
References
- Al-Neama, A.F.; Khatir, Z.; Kapur, N.; Summers, J.; Thompson, H.M. An experimental and numerical investigation of chevron fin structures in serpentine minichannel heat sinks. Int. J. Heat Mass Transf. 2018, 120, 1213–1228. [Google Scholar] [CrossRef]
- Vinodhan, V.L.; Rajan, K.S. Computational analysis of new microchannel heat sink configurations. Energy Convers. Manag. 2014, 86, 595–604. [Google Scholar] [CrossRef]
- Ma, D.D.; Xia, G.D.; Wang, J.; Yang, Y.C.; Jia, Y.T.; Zong, L.X. An experimental study on hydrothermal performance of microchannel heat sinks with 4-ports and offset zigzag channels. Energy Convers. Manag. 2017, 152, 157–165. [Google Scholar] [CrossRef]
- Guo, X.F.; Fan, Y.L.; Luo, L.G. Multi-channel heat exchanger-reactor using arborescent distributors: A characterization study of fluid distribution, heat exchange performance and exothermic reaction. Energy 2014, 69, 728–741. [Google Scholar] [CrossRef]
- Guo, X.; Fan, Y.; Luo, L. Mixing performance assessment of a multi-channel mini heat exchanger reactor with arborescent distributor and collector. Chem. Eng. J. 2013, 227, 16–27. [Google Scholar] [CrossRef]
- Mu, Y.T.; Chen, L.; He, Y.L.; Tao, W.Q. Numerical study on temperature uniformity in a novel mini-channel heat sink with different flow field configurations. Int. J. Heat Mass Transf. 2015, 85, 147–157. [Google Scholar] [CrossRef]
- Wang, C.C.; Yang, K.S.; Tsai, J.S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part II: Modified inlet header. Appl. Therm. Eng. 2011, 31, 3235–3242. [Google Scholar] [CrossRef]
- Afshari, E.; Dehkordi, M.M.; Rajabian, H. An investigation of the PEM fuel cells performance with partially restricted cathode flow channels and metal foam as a flow distributor. Energy 2017, 118, 705–715. [Google Scholar] [CrossRef]
- Afshari, E.; Rad, M.Z.; Shariati, Z. A study on using metal foam as coolant fluid distributor in the polymer electrolyte membrane fuel cell. Int. J. Hydrog. Energy 2016, 41, 1902–1912. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.W.; Lew, J.V. CFD study on flow distribution uniformity in fuel distributors having multiple structural bifurcations of flow channels. Int. J. Hydrog. Energy 2010, 35, 9186–9198. [Google Scholar] [CrossRef]
- Wang, J.Y. Pressure drop and flow distribution in parallel-channel configurations of fuel cells: U-type arrangement. Int. J. Hydrog. Energy 2008, 33, 6339–6350. [Google Scholar] [CrossRef]
- Wang, X.D.; Huan, Y.X.; Cheng, C.H.; Jang, J.Y.; Lee, D.J.; Yan, W.M.; Su, A. An inverse geometry design problem for optimization of single serpentine flow field of PEM fuel cell. Int. J. Hydrog. Energy 2010, 35, 4247–4257. [Google Scholar] [CrossRef]
- Luo, L.; Tondeur, D.; Gall, H.; Corbel, S. Constructal approach and multi-scale components. Appl. Therm. Eng. 2007, 27, 1708–1714. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, X.; Luo, L.; Yuan, W. Experimental investigation of the flow distribution of a 2-dimensional constructal distributor. Exp. Therm. Fluid Sci. 2008, 33, 77–83. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.W.; Wang, K. The flow downstream of a bifurcation of a flow channel for uniform flow distribution via cascade flow channel bifurcations. Appl. Therm. Eng. 2015, 81, 114–127. [Google Scholar] [CrossRef]
- Brenk, A.; Pluszka, P.; Malecha, Z. Numerical study of flow maldistribution in multi-plate heat exchangers based on robust 2D model. Energies 2018, 11, 3121. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.W. Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels. Int. J. Heat Fluid Flow 2013, 40, 165–179. [Google Scholar] [CrossRef]
- Cao, J.; Kraut, M.; Dittmeyer, R.; Zhang, L.; Xu, H. Numerical analysis on the effect of bifurcation angle and inlet velocity on the distribution uniformity performance of consecutive bifurcating fluid flow distributors. Int. Commun. Heat Mass Transf. 2018, 93, 60–65. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Efficacy of a novel liquid block working with a nanofluid containing graphene nanoplatelets decorated with silver nanoparticles compared with conventional CPU coolers. Appl. Therm. Eng. 2017, 127, 1233–1245. [Google Scholar] [CrossRef]
- Jiao, A.; Zhang, R.; Jeong, S. Experimental investigation of header configuration on flow mal-distribution in plate-fin heat exchanger. Appl. Therm. Eng. 2003, 23, 1235–1246. [Google Scholar] [CrossRef]
- Kim, S.; Choi, E.; Cho, Y.I. The effect of header shapes on the flow distribution in a manifold for electronic packaging applications. Int. Commun. Heat Mass Transf. 1995, 22, 329–341. [Google Scholar] [CrossRef]
- Li, W.Y. Study of flow distribution and its improvement on the header of plate-fin heat exchanger. Cryogenics 2004, 44, 823–831. [Google Scholar]
- JTong, C.K.; Sparrow, E.M.; Abraham, J.P. Geometric strategies for attainment of identical outflows through all of the exit ports of a distribution manifold in a manifold system. Appl. Therm. Eng. 2009, 29, 3552–3560. [Google Scholar]
- Shi, J.Y.; Qu, X.H.; Qi, Z.G.; Chen, J.P. Effect of inlet manifold structure on the performance of the heater core in the automobile air-conditioning systems. Appl. Therm. Eng. 2010, 30, 1016–1021. [Google Scholar] [CrossRef]
- Zhang, Z.; Mehendale, S.; Tian, J.J.; Li, Y.Z. Fluid flow distribution and heat transfer in plate-fin heat exchangers. Heat Transf. Eng. 2015, 36, 806–819. [Google Scholar] [CrossRef]
- Pistoresi, C.; Fan, Y.L.; Luo, L.G. Numerical study on the improvement of flow distribution uniformity among parallel mini-channels. Chem. Eng. Process 2015, 95, 63–71. [Google Scholar] [CrossRef]
- Kumaran, R.M.; Kumaraguruparan, G.; Sornakumar, T. Experimental and numerical studies of header design and inlet/outlet configurations on flow mal-distribution in parallel micro-channels. Appl. Therm. Eng. 2013, 58, 205–216. [Google Scholar] [CrossRef]
- Wang, C.C.; Yang, K.S.; Tsai, J.S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part I: Typical inlet header. Appl. Therm. Eng. 2011, 31, 3226–3234. [Google Scholar] [CrossRef]
- Zhang, Z.; Mehendale, S.; Tian, J.; Li, Y. Experimental investigation of distributor configuration on flow maldistribution in plate-fin heat exchangers. Appl. Therm. Eng. 2015, 85, 111–123. [Google Scholar] [CrossRef]
- Liu, X.Q.; Yu, J.L. Numerical study on performances of mini-channel heat sinks with non-uniform inlets. Appl. Therm. Eng. 2016, 93, 856–864. [Google Scholar] [CrossRef]
- Ahmed, A.Y.; Waaly, A.; Paul, M.C.; Dobson, P. Liquid cooling of non-uniform heat flux of a chip circuit by subchannels. Appl. Therm. Eng. 2017, 115, 558–574. [Google Scholar]
- Wen, J.; Li, Y.; Zhou, A.; Zhang, K. An experimental and numerical investigation of flow patterns in the entrance of plate-fin heat exchanger. Int. J. Heat Mass Transf. 2006, 49, 1667–1678. [Google Scholar] [CrossRef]
- Ismail, L.S.; Ranganayakulu, C.; Shah, R.K. Numerical study of flow patterns of compact plate-fin heat exchangers and generation of design data for offset and wavy fins. Int. J. Heat Mass Transf. 2009, 52, 3972–3983. [Google Scholar] [CrossRef]
- Dabiri, S.; Hashemi, M.; Rahimi, M.; Bahiraei, M.; Khodabandeh, E. Design of an innovative distributor to improve flow uniformity using cylindrical obstacles in header of a fuel cell. Energy 2018, 152, 719–731. [Google Scholar] [CrossRef]
- Luo, L.; Wei, M.; Fan, Y.; Flamant, G. Heuristic shape optimization of baffled fluid distributor for uniform flow distribution. Chem. Eng. Sci. 2015, 123, 542–556. [Google Scholar] [CrossRef]
- Lei, C.; Guo, D.X.; Hua, S.W. Laminar flow and heat transfer characteristics of interrupted microchannel heat sink with ribs in the transverse microchambers. Int. J. Them Sci. 2016, 110, 1–11. [Google Scholar]
- Lei, C.; Wang, L. Thermal-hydraulic performance of interrupted microchannel heat sinks with different rib geometries in transverse microchambers. Int. J. Them Sci. 2018, 127, 201–212. [Google Scholar]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Schultz, R.; Cole, R. Uncertainty Analysis in Boiling Nucleation; AIChE Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1979. [Google Scholar]
- Chai, L.; Xia, G.; Zhou, M.; Li, J.; Qi, J. Optimum thermal design of interrupted microchannel heat sink with rectangular ribs in the transverse microchambers. Appl. Them. Eng. 2013, 51, 880–889. [Google Scholar] [CrossRef]
- Webb, R.L. Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design. Int. J. Heat Mass Transf. 1981, 24, 715–726. [Google Scholar] [CrossRef]
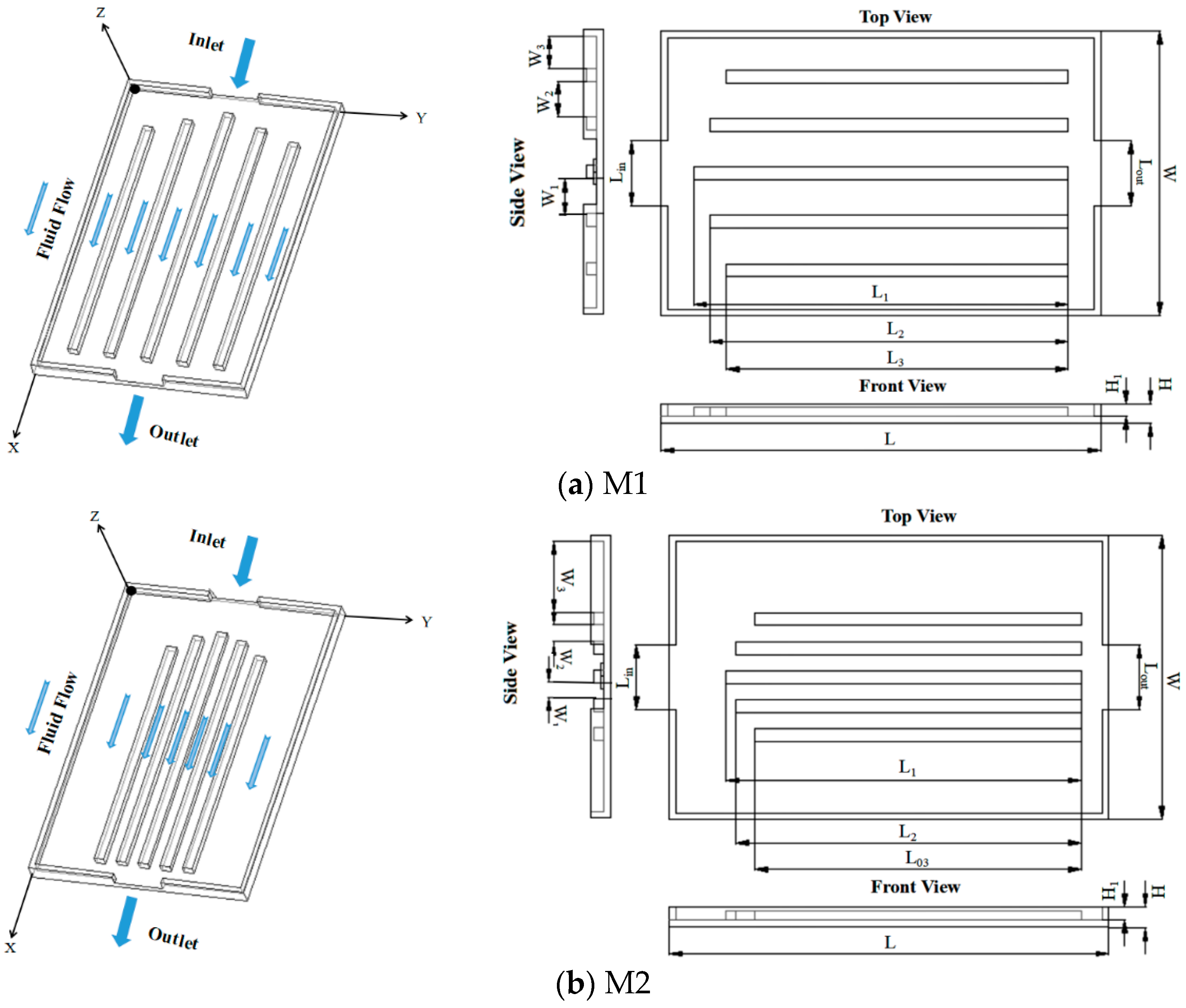



| Model | L/W/H (mm) H1/Lin/Lout | Ln (mm) (n = 1, 2, 3, 4) | Wn (mm) (n = 1, 2, 3, 4, 5) | L0n (mm) (n = 1, 2, 3, 4) | α/β (°) |
|---|---|---|---|---|---|
| M1 | 214/139/5 | 198/191/185 | 17.8/17.8/17.8 | -- | -- |
| 3/18/18 | |||||
| M2 | 214/139/5 | 198/191/185 | 9/13/31.4 | -- | -- |
| 3/18/18 | |||||
| M3 | 214/139/5 | 186/173/160 | 17.8/17.8/17.8 | -- | -- |
| 3/18/18 | |||||
| M4 | 214/139/5 | 186/173/160 | 17.8/17.8/17.8 | 22/28 | 80° 120° |
| 3/18/18 | |||||
| M5 | 214/139/5 | 186/173/168 | 9/13/31.4 | 34 | 120° |
| 3/18/18 | |||||
| M6 | 214/139/5 | 170/166 162/158 | 15.5/13.6 12.6/11.7 | 16/30 42/54 | 115° 30° |
| 3/18/18 |
| u1 (m/s) | 0.06 | 0.12 | 0.18 | 0.24 | 0.3 |
|---|---|---|---|---|---|
| Re | 400 | 800 | 1200 | 1600 | 2000 |
| Parameter | Absolute Uncertainty | Relative Uncertainty |
|---|---|---|
| Slot width (l1) | ±0.01 mm | |
| Slot depth (w1) | ±0.01 mm | |
| Temperature | ±1 K | |
| Pressure | ±2% | |
| Liquid flow rate | ±1% | |
| Power | ±2% | |
| Heat loss of the heat unit | 4.1% | |
| Heat transfer coefficient | 8.3% | |
| Average velocity | 3.9% | |
| Friction coefficient | 9.5% |
| V (m/s) | ΔTexp (K) | ΔTsim (K) | ΔT Error | ΔPexp (Pa) | ΔPsim (Pa) | ΔP Error | hexp (W/m2·K) | hsim (W/m2·K) | h Error | Nuexp | Nusim | Nu Error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.06 | 118.2 | 115.4 | 2.4% | 5220 | 5110 | 1.3% | 725.42 | 681.15 | 6.1% | 13.3 | 12.9 | 3.0% |
| 0.12 | 83.5 | 78.0 | 6.6% | 7700 | 7450 | 3.6% | 1349.62 | 1263.31 | 6.4% | 14.8 | 14.1 | 4.7% |
| 0.18 | 53.8 | 49.5 | 8.0% | 11300 | 11260 | 0.5% | 1612.04 | 1601.53 | 0.7% | 15.9 | 15.5 | 2.5% |
| 0.24 | 46.5 | 43.1 | 7.3% | 17900 | 17300 | 3.4% | 1706.87 | 1623.32 | 4.9% | 29.4 | 28.8 | 2.0% |
| 0.3 | 33.7 | 31.8 | 5.6% | 29650 | 28800 | 2.9% | 1758.59 | 1674.85 | 6.3% | 38.2 | 37.5 | 1.8% |
| Grid Number | ΔP (KPa) | Relative Error | ΔT (K) | Relative Error |
|---|---|---|---|---|
| 1496772 | 29.63 | 0.0082% | 372.33 | 0.0072% |
| 2423946 | 29.63 | 0.0064% | 372.35 | 0.0072% |
| 3422575 | 29.64 | ------- | 372.37 | ------- |
| 4496728 | 29.65 | 0.0023% | 372.37 | ------- |
| 5393368 | 29.66 | 0.0023% | 372.35 | 0.0037% |
| Factor | θ° | ΔT (K) | h (W/m2·K) | Nu | ΔP (kPa) | f |
|---|---|---|---|---|---|---|
| M6 | 85.33 | 51.7 | 1758.59 | 42.6 | 29.6 | 0.82 |
| Improvements | min | min | max | max | max | min |
| Model | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| DM | 0.591 | 0.669 | 0.763 | 0.767 | 0.882 | 0.915 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Liu, H.-l.; Shao, X.-d. Heat Transfer Performance of a Novel Multi-Baffle-Type Heat Sink. Entropy 2018, 20, 979. https://doi.org/10.3390/e20120979
Cao X, Liu H-l, Shao X-d. Heat Transfer Performance of a Novel Multi-Baffle-Type Heat Sink. Entropy. 2018; 20(12):979. https://doi.org/10.3390/e20120979
Chicago/Turabian StyleCao, Xin, Huan-ling Liu, and Xiao-dong Shao. 2018. "Heat Transfer Performance of a Novel Multi-Baffle-Type Heat Sink" Entropy 20, no. 12: 979. https://doi.org/10.3390/e20120979
APA StyleCao, X., Liu, H.-l., & Shao, X.-d. (2018). Heat Transfer Performance of a Novel Multi-Baffle-Type Heat Sink. Entropy, 20(12), 979. https://doi.org/10.3390/e20120979





