Abstract
The present study characterizes the flow of three-dimensional viscoelastic magnetohydrodynamic (MHD) nanofluids flow with entropy generation analysis past an exponentially permeable stretched surface with simultaneous impacts of chemical reaction and heat generation/absorption. The analysis was conducted with additional effects nonlinear thermal radiation and convective heat and mass boundary conditions. Apposite transformations were considered to transform the presented mathematical model to a system of differential equations. Analytical solutions of the proposed model were developed via a well-known homotopy analysis scheme. The numerically calculated values of the dimensionless drag coefficient, local Nusselt number, and mass transfer Nusselt number are presented, with physical insights. The graphs depicting the consequences of numerous parameters on involved distributions with requisite deliberations were also a part of this model. It is seen that the Bejan number is an increasing function of the thermal radiation parameter.
1. Introduction
Rapid growth in the usage of nanofluids in varied engineering arenas such as cancer therapy, finer coolants in nuclear reactors and computers, numerous electronic devices in military sectors [1], oil and water [2,3], rapid spry cooling, the food industry, vehicles and transformers, polymer extrusion, safe surgeries, quenching in foundries, and glass blowing [4] have encouraged scientists and researchers to scrutinize the numerous aspects of nanofluid flow past different geometries. Nanofluids are an amalgamation of nanoparticles of size < 100 nm (i.e., metals, nitrides, carbides, and nanotubes (single or multiwalled)) and orthodox fluids such as water, toluene, engine, kerosene oil, ethylene and triethylene glycol. Nanofluids are considered to be the best coolants in all engineering applications. It was Choi [5] who experimentally revealed that nanofluids possess enhanced thermal conductivity. Afterward, Buongiorno [6] framed a model pointing out that the heat transfer process is triggered in the case of nanofluids due to thermophoretic diffusion and the Brownian motion of nanoparticles. Later, Khan and Pop [7] discussed nanofluid flow past a stretched surface. Makinde and Aziz supported this model through convective boundary conditions over a stretched surface [8]. The impact of radiative nanoparticle flow with Lorentz force past a spongy semi annulus region was investigated by Sheikholeslami et al. [9]. Li et al. [10] examined the effect of adding nanoparticles in the process of solidification of Nano-enhanced phase change material (NEPCM) in the presence of thermal radiation. The flow of water-based nanofluid containing carbon nanotubes past a permeable medium with the effects of Darcy–Forchheimer was deliberated by Muhammad et al. [11]. Lu et al. [12] pondered on the flow of micropolar nanofluids in the presence of magnetohydrodynamic (MHD), homogeneous-heterogeneous reactions, mixed convection, and thermal radiation past a nonlinear stretched surface, numerically. The combined impacts of Arrhenius activation energy with heat and mass stratification on micropolar nanofluid flow in the presence of binary chemical reactions was studied by Ramzan et al. [13]. Lu et al. [14] did a tremendous study considering the three-layer vertical nanofluid model following a Buongiorno scheme. Li et al. [15], using Finite Element method (FEM), calculated the influence of the transportation of nanoparticles in a permeable enclosure due to electric force. Recently, some studies have discussed the applications of nanofluids in varied fields such as electrokinetic transport [16], heat transfer [17], and mass transfer [18].
The inevitable and dynamic applications of MHD nanofluids (e.g., wound treatment, gastric medications, targeted drug release, sterilized devices, magnetic resonance imagining (MRI), asthma treatment, and removal of tumors with hyperthermia) have attracted the attention of scientists and researchers in studying the related field of nanofluids. Sheikholeslami [19] deliberated the flow of copper oxide-water nanofluids in a spongy channel due to magnetic field effects using the Lattice Boltzmann method (LBM) method. In a recent article, Lu et al. [20] envisaged the model of MHD Carreau nanofluid flow over a radially stretching surface with allied impacts of nonlinear thermal radiation with newly established zero mass flux boundary conditions. They solved the proposed model numerically by engaging the MATLAB bvp4c function. The simultaneous influences of thermal radiation and Cattaneo–Christov heat flux (instead of conventional Fourier’s law of heat conduction) on the MHD nanofluid flow between two parallel plates were examined by Dogonchi and Ganji [21]. They found an analytical solution to the suggested problem by using the Duan–Rach approach (DRA), which facilitates finding undetermined coefficients without the help of numerical techniques. Sheikholeslami [22] deliberated the MHD non-Darcy nanofluid flow in a permeable cubic enclosure using the LBM (lattice Boltzmann method) and highlighted that the Nusselt number is an escalating function of permeability and buoyancy forces. Keeping in mind the applications of nanofluid flow in the attendance of magnetohydrodynamics, some featured recent explorations [23,24,25,26,27] have been added to the literature review.
The study of heat and mass transfer of nanofluid flows with chemical reactions past stretched surfaces has numerous significant applications in core industries such as chemical and metallurgical engineering. Examples include polymer production and food processing. Furthermore, heat and mass transfer models with chemical reaction effects are vital in several processes and have gained attention in recent years. Fascinating applications pertaining to chemical reactions embrace the distribution of temperature and moisture over agricultural fields and groves of fruit trees, the energy transfer of drying and evaporation at the surface of a water body, and the energy transfer of a wet cooling tower.
Entropy is pronounced the nonavailability of the system’s thermal energy for translation into mechanical work. The second law of thermodynamics asserts that throughout the process of conversion of energy into some beneficial work, there is forfeiture of energy that lowers the performance of energy conservation gadgets. Basically, entropy generation is directly proportionate to a loss of energy. Subsequently, entropy generation in a system results in the reduction of the quantity of energy present (exergy). Thus, the efficiency of the thermal system may be enhanced by slashing the entropy generation. In this regard, it is necessary to have the idea of energy generation’s distribution throughout a thermodynamic process with the intention of reduction in entropy generation. The idea of entropy generation was first floated by Bejan [28], who examined the reason for energy generation in a convective heat transfer model. The analysis of entropy generation in viscous fluid flow with an impact of suction and injection past a flat surface was conducted by Reveillere and Baytas [29]. The flow of MHD nanofluid past a spongy narrow vertical channel under the influences of nonlinear thermal radiation, entropy generation, and convective boundary conditions was considered by Lopez et al. [30]. Sheikholeslami [31] deliberated the analysis of exergy and entropy under the influence of Lorentz force past a permeable medium using a new numerical scheme, Control volume finite element method (CVFEM). Some useful recent explorations may be found in References [32,33,34,35,36].
The significance of non-Newtonian fluids cannot be denied due to their involvement in varied engineering and industrial applications such as petroleum production, the thinning of copper wires, and plastic manufacturing [37]. To exhibit such models, Naiver–Stokes equations are not enough since a single constitutive relation does not portray the core requirements of non-Newtonian fluids. That is why several discrete models have been proposed in the literature. Among these, viscoelastic fluid is the differential-type non-Newtonian fluid model that is simplest on its own and exhibits the characteristics of normal stress and shear rate viscosity. Hayat et al. [38] examined the flow of 3D viscoelastic nanofluid over an exponential stretched surface with mixed convection. The 3D viscoelastic nanofluid flow with nonlinear thermal radiation near a stagnation point was discussed by Farooq et al. [39]. Ramzan et al. [40,41,42] deliberated the flow of 3D viscoelastic nanofluid flow with the impacts of Newtonian heating, chemical reaction and MHD, and Soret–Dufour effects. The 3D flow of viscoelastic flow with temperature-dependent thermal conductivity was deliberated by Alsaedi et al. [43]. Some recent attempts considering viscoelastic fluids can be seen in References [44,45].
The literature review above indicates that few studies have been made on three-dimensional viscoelastic nanofluid flows associated with entropy generation and nonlinear thermal radiation past an exponential stretched surface. Therefore, we present our study on such an investigation by solving the proposed model analytically with three dimensionless distributions (Section 2) and examining the effects of different parameters (Section 5).
2. Mathematical Modeling
We considered the flow of MHD viscoelastic nanofluid past a permeable exponentially stretched surface with entropy generation. The analysis was performed in the attendance of nonlinear thermal radiation, chemical reaction, and heat generation and absorption with convective heat and mass boundary conditions. The magnetic field was applied parallel to the z axis. The Hall and electric field effects were overlooked. The induced magnetic field was also ignored due to our assumption of a small Reynolds number. The permeable surface was stretched in both the x and y directions with respective velocities and , as shown in Figure 1.
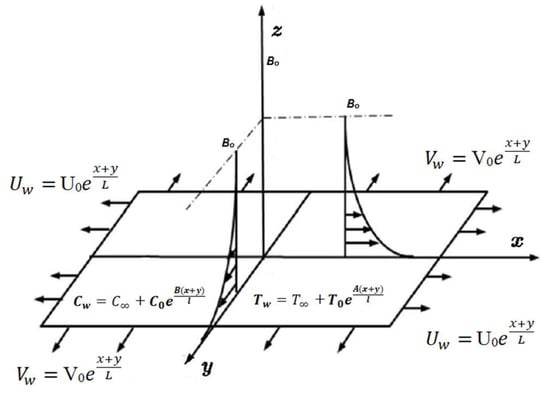
Figure 1.
Geometry of the problem.
The mathematical model, under assumptions, is represented by the following equations [46]:
subjected to the boundary conditions
The surface stretching velocities, temperature, and concentration of the wall were given by
The transformations are presented as given below:
Equation (1) was satisfied automatically, whereas Equations (2)–(5) took the form
subject to the transformed boundary conditions
The parameters given in Equations (9)–(12) are defined as follows:
Skin Friction Coefficient and Local Nusselt and Sherwood Numbers
The equations of the skin friction coefficients along the x and y directions were given by
The equations of the skin friction coefficients in dimensionless form were given by
and the rates of heat and mass transfers in dimensionless forms were appended
3. Convergence Analysis
The convergence of the series solutions was adjusted and regulated with the aid of auxiliary parameters , and . For tolerable ranges, -curves were drawn and are given in Figure 2. These admissible ranges were , and , which were and These values were corroborated by the numerical values given in Table 1.
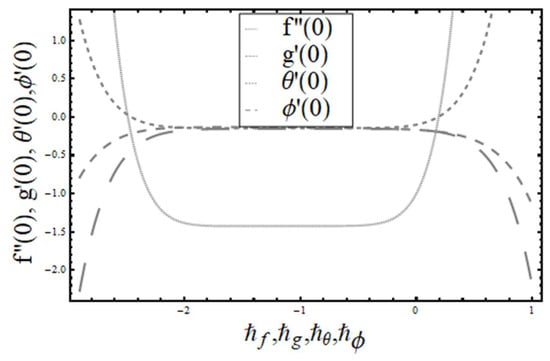
Figure 2.
The ħ curves for .

Table 1.
Series solution convergence for varied orders of approximations when = 0.1, Nb = 0.5, Nt = 0.3, K = 0.2, M = 0.3, Le = 1, Pr = 1.2, Rd = 0.2, A = B = 0.1.
3.1. Homotopic Solutions
The homotopy analysis method necessitated the initial guesstimates (, , ) with auxiliary linear operators (, ) in the form [43]
These auxiliary linear operators possessed the ensuing features
where , are arbitrary constants.
3.2. Deformation Problems at Zeroth Order
Here,
where , and characterize the nonzero convergence control parameters and specifies the embedding parameter, whereas the nonlinear operators , and are specified by
For and , we get
The subsequent expressions were attained via Taylor’s series expansion:
The convergence of control parameters , and were selected in such a way that the series (36)–(39) converged at . Then
3.3. The m-th Order Problem
The equations of the m-th order are
The general solutions for Equations (48)–(51) in terms of special solutions are given by
4. Entropy Analysis
The equation of entropy generation [47,48,49] was given by
where a, b, c and d represent the thermal irreversibility or entropy generation due to heat transfer, the concentration irreversibility or entropy generation due to mass transfer, the entropy generation due to viscous effects in the fluid, and the entropy generation due to magnetic effects of the fluid, respectively. Then
and
is the characteristic entropy generation rate. Using the transformations in Equation (6), Equation (21) takes the form
where
An important Bejan number defined by the ratio of entropy generation due to thermal effect and total entropy generated by thermal, concentration, and fluid frictions forces was as follows [50]:
In dimensionless form, it became
The value of the irreversibility parameter must lie between . if then there is no entropy generated due to heat transfer. When , then the entropy generation due to fluid friction is dominant over the entropy generation due to heat transfer. On the other hand, if , then reverse relation is obvious for the entropy generation due to heat and total entropy generation.
The averaged entropy generation number could be evaluated using the following integral formula:
where is the length of the boundary layer region.
5. Results and Discussion
This section is dedicated to having a deep insight into changes of sundry parameters on involved profiles. The ranges of all parameters were selected via Turkyilmazoglu [51]. Figure 3 was drawn to show the impact of viscoelastic parameter on both velocities. Both velocity distributions were declining functions of . Augmented values of the meant the development of tensile stress, which ultimately lowered both velocity components. The impression of magnetic parameter on both velocity components is depicted in Figure 4. A diminishing behavior was witnessed for both velocity components. A strong Lorentz force was perceived due to the magnetic field, hindering the movement of the fluid flow. Thus, the reduction in velocity components was noticed. Figure 5 is outlined to grasp the impact of chemical reaction parameter and Prandtl number on the concentration field. It was visualized that the rate of mass transfer was on the decline with augmented values of Thus, the respected boundary layer was also enhanced. Smaller values of thermal diffusivity augmented the and thereby lowered the concentration distributions. The outcome of temperature exponent and Prandtl number on temperature profile can be visualized in Figure 6. The Prandtl number is the quotient of momentum to thermal diffusivity. Smaller numbers for thermal diffusivity meant higher values of , thus lowering the temperature. A similar effect was noted in the case of . Figure 7 was illustrated to depict the influence of thermophoretic parameter and Brownian motion parameter on temperature field. It was comprehended that temperature was an increasing function of both parameters. This is because smaller particles were pushed toward the colder surface from the hotter one. Another reason for this phenomenon is that enhanced random movement of the fluid’s particles also became the main source of heightening the temperature of the fluid. To understand the influence of Brownian motion parameter and thermophoresis parameter on the concentration distribution, Figure 8 was plotted. Higher values of both parameters augmented the concentration profile. Smaller particles were pulled toward the colder region due to increased values of the thermophoretic parameter, thus lowering the concentration of the fluid. Figure 9 was drawn to grasp the impact of radiation parameter and heat absorption parameter on the temperature field. In the experiment, the temperature rose with higher values of . This is because growing values of Rd meant more emission of heat that ultimately raised the temperature of the fluid. Also, the higher estimates of produced more heat that also resulted in an increase in the fluid’s temperature. The variation of magnetic parameter M for the entropy generation is presented in Figure 10. Initially, due to drag forces produced by the magnetic field, the energy was produced, which increased the entropy of the fluid. However, as it moved away from the plate, the influence of these forces reduced gradually and eventually lessened the effect of entropy as well. The effect of viscoelastic parameter on entropy generation and the Bejan number is displayed in Figure 11 and Figure 12, respectively. Both the figures clearly indicate that the enhancement of values of enhanced entropy generation as well as the Bejan number near the surface due to an increase in viscous effects. However, the opposite trend was noticed in both cases while moving away from the surface. In Figure 13, a relationship between the thermal radiation parameter and dimensionless Bejan number is portrayed. An increment in thermal radiation parameter enhanced the internal heat generation in the moving fluid, which caused the Bejan number to escalate. Figure 14, Figure 15, Figure 16 and Figure 17 were illustrated to show the impacts of dimensionless temperature difference Ω, Reynolds number Re, thermal radiation parameter Rd, and Brinkman number Br on the variation of local entropy generation number Ns, respectively. From Figure 14, it is revealed that as the temperature difference increased, a decrease in the entropy generation parameter was noticed. Larger values of Ω did not affect the viscous part of the entropy generation. However, only the thermal entropy generation segment was responsible for higher temperature gradients in the transverse direction. In Figure 15, Figure 16 and Figure 17, Ns was an increasing function of these three: Re, Rd, and Br. Figure 18 and Figure 19 were drawn to depict the influence of M, K, Pr, and Rd on average entropy Ns(avg). From these figures, it was gathered that Ns(avg) was an escalating function of all four parameters. This meant irreversibility mounted as the group parameters grew.
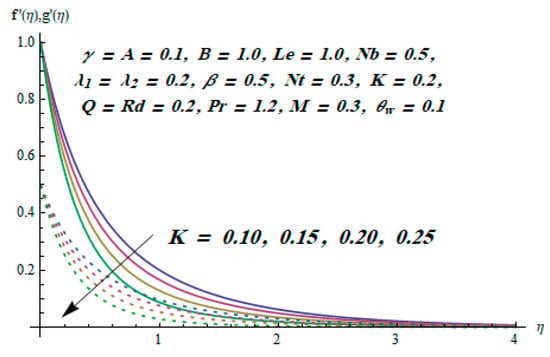
Figure 3.
Effect of K on .
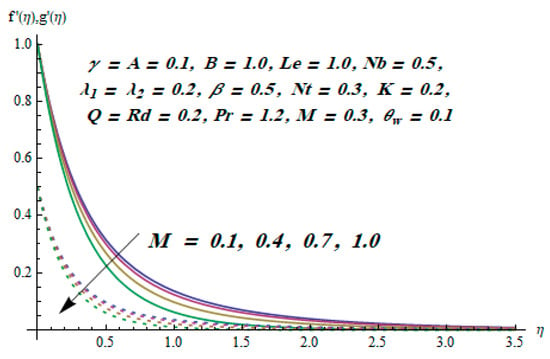
Figure 4.
Effect of M on and .
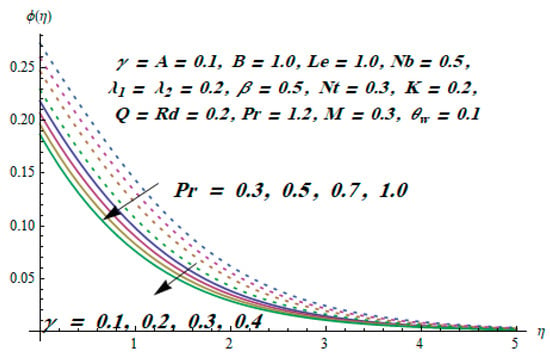
Figure 5.
Effect of Pr and γ on .
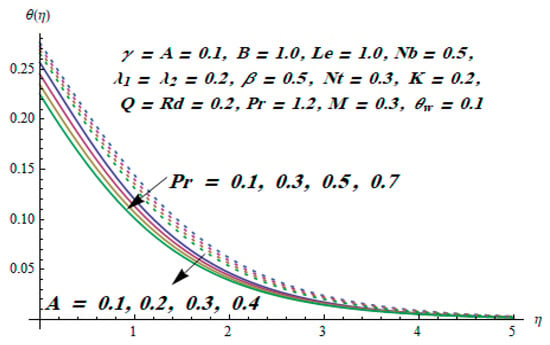
Figure 6.
Effect of Pr and A on .
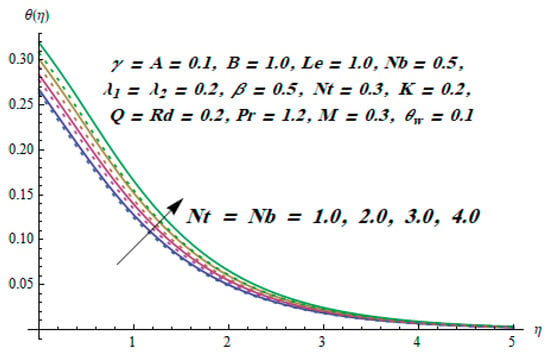
Figure 7.
Effect of on .
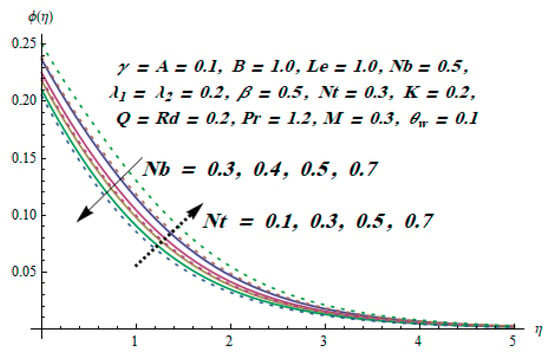
Figure 8.
Effect of Nt and Nb on .
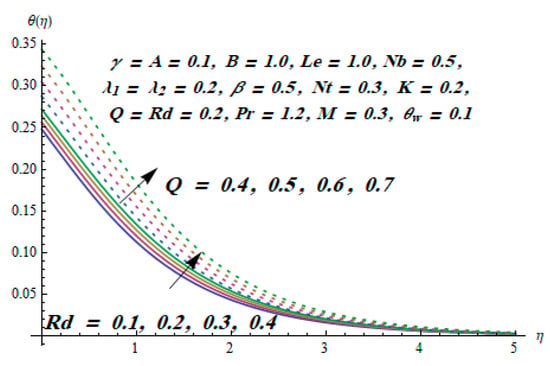
Figure 9.
Effect of Rd and Q on .
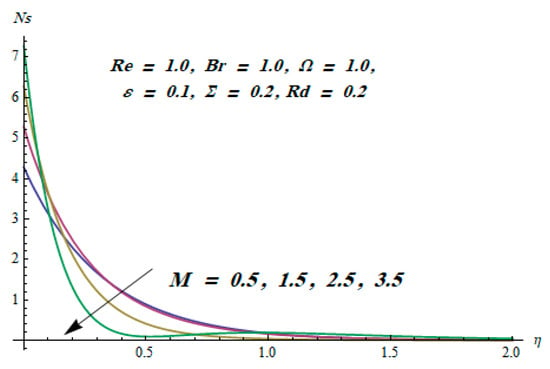
Figure 10.
Effect of M on .
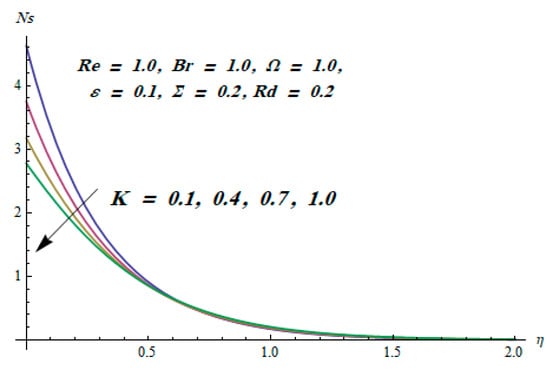
Figure 11.
Effect of K on .
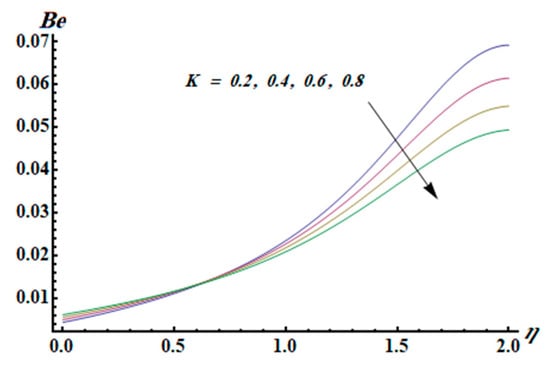
Figure 12.
Effect of K on .
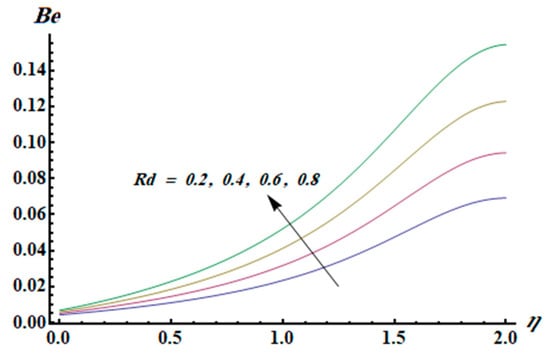
Figure 13.
Effect of Rd on .
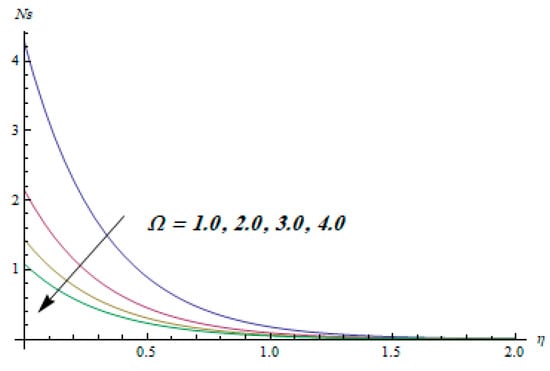
Figure 14.
Effect of Ω on .
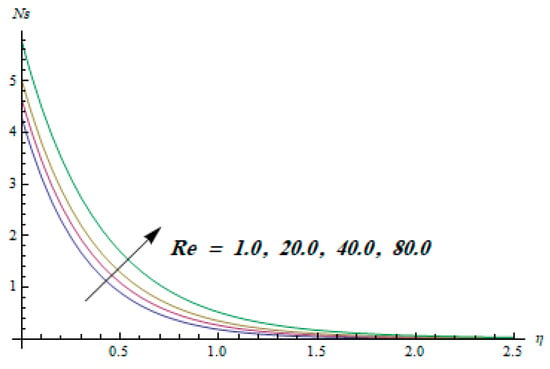
Figure 15.
Effect of Re on .
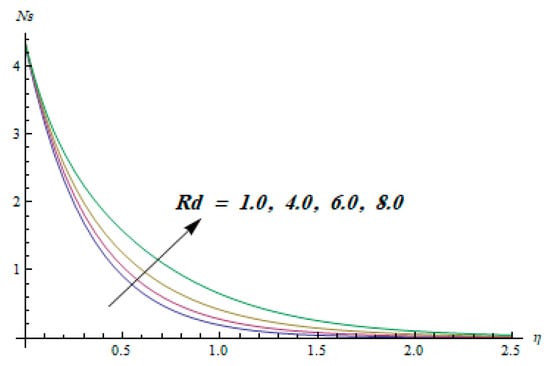
Figure 16.
Effect of Rd on .
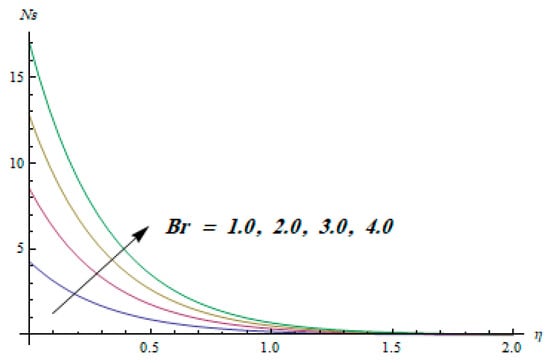
Figure 17.
Effect of Br on .
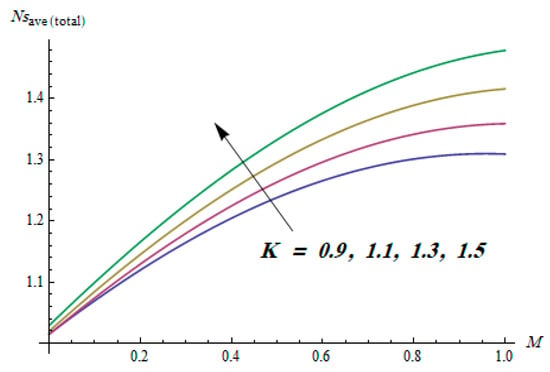
Figure 18.
Effect of M and K on average entropy generation.
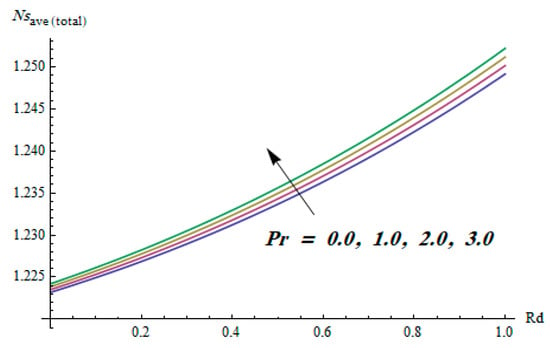
Figure 19.
Effect of Pr and Rd on average entropy generation.
Table 2 was initiated for the rate of heat and mass transfers versus varied involved parameters. It was noticed that the Nusselt number was a growing function of and was a declining function of Similarly, the Sherwood number decreased for the values of and increased for the values of Table 3 depicts the values of both skin friction coefficients along and directions. It was gathered that both coefficients were growing functions of and Table 4 was erected to check the reliability of the presented solution by comparing it to Liu et al. [52] in the limiting case. An excellent concurrence was obtained, confirming the reliability of the presented results.

Table 2.
Values of local Nusselt and Sherwood numbers for involved parameters.

Table 3.
Values of skin friction coefficients for involved parameters.

Table 4.
Comparison of present values to Liu et al. [52] in the limiting case when (also, values of the convective boundary were neglected).
6. Concluding Remarks
Entropy generation of 3D viscoelastic nanofluid fluid flow past an exponential stretched surface with nonlinear thermal radiation, chemical reaction, and magnetohydrodynamics was discussed analytically with the homotopy analysis method. The whole analysis was completed with the effect of heat generation and absorption supported by convective heat and mass boundary conditions. The main findings of the analysis are:
- The velocity components were declining functions of the viscoelastic parameter.
- The temperature field improved with an increase in radiation parameter.
- Thermophoresis and Brownian motion parameters had an opposite effect on concentration distribution.
- With growing values of the magnetic parameter, both velocity components declined.
- The Bejan number is an increasing function of the thermal radiation parameter.
- Entropy generation decreased for escalating values of the temperature difference parameter.
Author Contributions
Data curation, U.F.; Formal analysis, M.Z.; Funding acquisition, M.S.; Investigation, A.S.; Methodology, M.S.; Project administration, M.R.; Software, J.D.C.; Supervision, M.R.; Validation, D.L.; Visualization, M.B.
Funding
This research was funded by National Natural Science Foundation China (Nos. 11571140 and 11671077), Faculty of Science, Jiangsu University, Zhenjiang, China.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Nomenclature
| a, b, c, d, e | Dimensional constants |
| η | Similarity variable |
| A | Temperature exponent |
| B | Concentration exponent |
| Be | Bejan number |
| β0 | Magnetic field strength |
| C | Concentration of fluid |
| Cf | Skin friction |
| cp | Specific heat |
| Cw | Concentration on wall |
| C∞ | Ambient concentration |
| C0 | Reference concentration |
| Br | Brinkman number |
| DB | Brownian diffusion coefficient |
| DT | Thermophoretic diffusion coefficient |
| f, g | Dimensionless velocities |
| Effective heat capacity of nanoparticles | |
| k | Thermal conductivity |
| K | Viscoelastic parameter |
| ko | Elastic parameter |
| K* | Mean absorption coefficient |
| α | Effective heat capacity of fluid |
| Le | Lewis number |
| Nb | Brownian motion parameter |
| Nt | Thermophoresis parameter |
| Nux | Nusselt number |
| M | Magnetic parameter |
| Pr | Prandtl number |
| Q | Heat absorption |
| Rd | Thermal radiation parameter |
| Re | Reynolds number |
| SG | Volumetric entropy generation |
| Nux | Local Nusselt number |
| NS | Entropy generation rate |
| Cfx, Cfy | Skin friction coefficients |
| Shx | Sherwood number |
| T | Temperature of fluid |
| Tw | Wall temperature |
| Constants | |
| T∞ | Ambient temperature |
| Ue | Stretching velocity |
| Uw | Linear stretching velocity |
| (u, v, w) | Velocity components |
| (x, y, z) | Coordinate axes |
| M | Hartmann number |
| Kinematic viscosity | |
| λ1 | Relaxation time |
| Λ2 | Ratio of relaxation to retardation time |
| ρ | Density of fluid |
| σ | Electrical conductivity |
| σ* | Stefan–Boltzmann constant |
| μ | Dynamic viscosity |
| τ | Ratio of nanoparticle |
| τw | Skin friction coefficient |
| Ω | Dimensionless temperature difference |
| ε | Dimensionless nanoparticle volume difference |
| Σ | Nanoparticle mass transfer parameter |
| θ | Dimensionless temperature |
| ϕ | Dimensionless concentration |
| α1 | Normal stress moduli |
| Kc | Chemical reaction coefficient |
| Reference length |
References
- Saidur, R.; Leong, K.Y.; Mohammad, H. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W.; Long, G.; Chen, H.; Kang, H.; Ren, W. A fractal model for water flow through unsaturated porous rocks. Fractals 2018, 26, 1840015. [Google Scholar] [CrossRef]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Estman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Li, Z. Investigation of Lorentz forces and radiation impacts on nanofluid treatment in a porous semi annulus via Darcy law. J. Mol. Liquids 2018, 272, 8–14. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Kandasamy, R.; Al-Mdallal, Q.M. Influence of adding nanoparticles on solidification in a heat storage system considering radiation effect. J. Mol. Liquids 2018, 273, 589–605. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.-C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ahmad, S.; Chung, J.D.; Farooq, U. A numerical treatment of MHD radiative flow of Micropolar nanofluid with homogeneous-heterogeneous reactions past a nonlinear stretched surface. Sci. Rep. 2018, 8, 12431. [Google Scholar] [CrossRef]
- Ramzan, M.; Ullah, N.; Chung, J.D.; Lu, D.; Farooq, U. Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 2017, 7, 12901. [Google Scholar] [CrossRef]
- Lu, D.C.; Farooq, U.; Hayat, T.; Rashidi, M.M.; Ramzan, M. Computational analysis of three-layer fluid model including a nanomaterial layer. Int. J. Heat Mass Transf. 2018, 122, 222–228. [Google Scholar] [CrossRef]
- Li, Z.; Ramzan, M.; Shafee, A.; Saleem, S.; Al-Mdallal, Q.M.; Chamkha, A.J. Numerical approach for nanofluid transportation due to electric force in a porous enclosure. Microsyst. Technol. 2018, 1–14. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, Y.; Zhou, Z.; Qu, J.; Zhou, L.; Wang, J.; Zhang, F. Convection Heat Transfer Performance of Fractal Tube Bank under cross flow. Fractals 2018. [Google Scholar] [CrossRef]
- Xiao, B.; Chen, H.; Xiao, S.; Cai, J. Research on relative permeability of nanofibers with capillary pressure effect by means of fractal-monte carlo technique. J. Nanosci. Nanotechnol. 2017, 17, 6811–6817. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation for CuO-H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method. J. Mol. Liquids 2018, 249, 739–746. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; ul Huda, N.; Chung, J.D.; Farooq, U. Nonlinear radiation effect on MHD Carreau nanofluid flow over a radially stretching surface with zero mass flux at the surface. Sci. Rep. 2018, 8, 3709. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ganji, D.D. Impact of Cattaneo–Christov heat flux on MHD nanofluid flow and heat transfer between parallel plates considering thermal radiation effect. J. Taiwan Inst. Chem. Eng. 2017, 80, 52–63. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Lattice Boltzmann method simulation for MHD non-Darcy nanofluid free convection. Phys. B Condens. Matter 2017, 516, 55–71. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Mann, A.B. On MHD radiative Jeffery nanofluid flow with convective heat and mass boundary conditions. Neural Comput. Appl. 2017, 30, 2739–2748. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Lu, D.C.; Farooq, U. Impact of generalized Fourier’s and Fick’s laws on MHD 3D second grade nanofluid flow with variable thermal conductivity and convective heat and mass conditions. Phys. Fluids 2017, 29, 093102. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. MHD stagnation point Cattaneo–Christov heat flux in Williamson fluid flow with homogeneous–heterogeneous reactions and convective boundary condition—A numerical approach. J. Mol. Liquids 2017, 225, 856–862. [Google Scholar] [CrossRef]
- Ramzan, M.; Chung, J.D.; Ullah, N. Partial slip effect in the flow of MHD micropolar nanofluid flow due to a rotating disk—A numerical approach. Res. Phys. 2017, 7, 3557–3566. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of thermal and solutal stratification on Jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption. Int. J. Mech. Sci. 2017, 131, 317–324. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Reveillere, A.; Baytas, A.C. Minimum entropy generation for laminar boundary layer flow over a permeable plate. Int. J. Exergy 2010, 7, 164–177. [Google Scholar] [CrossRef]
- López, A.; Ibáñez, G.; Pantoja, J.; Moreira, J.; Lastres, O. Entropy generation analysis of MHD nanofluid flow in a porous vertical microchannel with nonlinear thermal radiation, slip flow and convective-radiative boundary conditions. Int. J. Heat Mass Transf. 2017, 107, 982–994. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2018, 344, 319–333. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Entropy generation due to natural convection of a nanofluid in a partially open triangular cavity. Adv. Powder Technol. 2017, 28, 244–255. [Google Scholar] [CrossRef]
- Sheremet, M.; Pop, I.; Öztop, H.F.; Abu-Hamdeh, N. Natural convection of nanofluid inside a wavy cavity with a non-uniform heating: Entropy generation analysis. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 958–980. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Grosan, T.; Pop, I. Natural convection and entropy generation in a square cavity with variable temperature side walls filled with a nanofluid: Buongiorno’s mathematical model. Entropy 2017, 19, 337. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Sheikholeslami, M.; Zeeshan, A. Entropy analysis on electro-kinetically modulated peristaltic propulsion of magnetized nanofluid flow through a microchannel. Entropy 2017, 19, 481. [Google Scholar] [CrossRef]
- Farooq, U.; Afridi, M.; Qasim, M.; Lu, D. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Model and comparative study for flow of viscoelastic nanofluids with Cattaneo-Christov double diffusion. PLoS ONE 2017, 12, e0168824. [Google Scholar] [CrossRef]
- Hayat, T.; Ashraf, B.; Shehzad, S.A.; Alsaedi, A.; Bayomi, N. Three-dimensional mixed convection flow of viscoelastic nanofluid over an exponentially stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 333–357. [Google Scholar] [CrossRef]
- Farooq, M.; Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A.; Khan, M.I. MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. J. Mol. Liquids 2016, 221, 1097–1103. [Google Scholar] [CrossRef]
- Ramzan, M.; Yousaf, F. Boundary layer flow of three-dimensional viscoelastic nanofluid past a bi-directional stretching sheet with Newtonian heating. AIP Adv. 2015, 5, 057132. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M. Three-dimensional flow of an elastico-viscous nanofluid with chemical reaction and magnetic field effects. J. Mol. Liquids 2016, 215, 212–220. [Google Scholar] [CrossRef]
- Ramzan, M.; Inam, S.; Shehzad, S.A. Three dimensional boundary layer flow of a viscoelastic nanofluid with Soret and Dufour effects. Alex. Eng. J. 2016, 55, 311–319. [Google Scholar] [CrossRef]
- Alsaedi, A.; Hayat, T.; Muhammad, T.; Shehzad, S.A. MHD three-dimensional flow of viscoelastic fluid over an exponentially stretching surface with variable thermal conductivity. Comput. Math. Math. Phy. 2016, 56, 1665–1678. [Google Scholar] [CrossRef]
- Mustafa, M.; Ahmad, R.; Hayat, T.; Alsaedi, A. Rotating flow of viscoelastic fluid with nonlinear thermal radiation: A numerical study. Neural Comput. Appl. 2018, 29, 493–499. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Shehzad, S.A.; Alsaedi, A. Cattaneo-Christov double-diffusion theory for three-dimensional flow of viscoelastic nanofluid with the effect of heat generation/absorption. Res. Phys. 2018, 8, 489–495. [Google Scholar] [CrossRef]
- Hayat, T.; Shah, F.; Hussain, Z.; Alsaedi, A. Outcomes of double stratification in Darcy–Forchheimer MHD flow of viscoelastic nanofluid. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 145. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Shafeeurrahman, M. Entropy Generation Due to MHD Mixed Convection of Nanofluid Between Two Concentric Cylinders with Radiation and Joule Heating Effects. J. Nanofluids 2017, 6, 1227–1237. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Saffarian, M.R.; Pourrajab, R.; Ghalambaz, M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 2013, 27, 927–937. [Google Scholar] [CrossRef]
- Abelman, S.; Zaib, A. Entropy generation of nanofluid flow over a convectively heated stretching sheet with stagnation point flow having nimonic 80a nanoparticles: Buongiorno model. In Proceedings of the 13th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Portoroz, Slovenia, 17–19 July 2017. [Google Scholar]
- Shit, G.C.; Haldar, R.; Mandal, S. Entropy generation on MHD flow and convective heat transfer in a porous medium of exponentially stretching surface saturated by nanofluids. Adv. Powder Technol. 2017, 28, 1519–1530. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Determination of the correct range of physical parameters in the approximate analytical solutions of nonlinear equations using the Adomian decomposition method. Mediterr. J. Math. 2016, 13, 4019–4037. [Google Scholar] [CrossRef]
- Liu, I.-C.; Wang, H.-H.; Peng, Y.-F. Flow and heat transfer for three-dimensional flow over an exponentially stretching surface. Chem. Eng. Commun. 2013, 200, 253–268. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).