1. Introduction
Paleoclimate records, such as ice and sediment cores, provide us with long and detailed accounts of Earth’s ancient climate system. Collection of these data sets can be very expensive, and the extraction of proxy data from them is often time consuming, as well as susceptible to both human and machine error. Ensuring the accuracy of these data is as challenging as it is important. Most of these cores are only fully measured one time, and most are unique in the time period and region that they “observe”, making comparisons and statistical tests impossible. Moreover, these records may be subject to many different effects—known, unknown, and conjectured—between deposition and collection. These challenges make it very difficult to understand how much information is actually present in these records, how to extract it in a meaningful way, and how best to use it while not overusing it.
An important first step in that direction would be to identify where the information in a proxy record appears to be missing, disturbed, or otherwise unusual. This knowledge could be used to flag segments of these data sets that warrant further study, either to isolate and repair any problems or, more excitingly, to identify hidden climate signals. Anomaly detection is a particularly thorny problem in paleorecords, though. Collecting an ice core from polar regions can cost tens of millions of $US. Given the need for broad geographic sampling in a resource-constrained environment, replicate cores from nearby areas have been rare. This has restricted anomaly detection methods in paleoscience to the most simple approaches: e.g., discarding observations that lie beyond five standard deviations from the mean. Laboratory technology is another issue. Until recently, for instance, water isotopes in ice cores could only be measured at multi-centimeter resolution, a spacing that would lump years or even decades worth of climate information into each data point. The absence of ground truth is a final challenge, particularly since the paleoclimate evidence in a core can be obfuscated by natural processes: material in a sediment core may be swept away by an ocean current, for instance, and ice can be deformed by the flow of the ice sheet. These kinds of effects can not only destroy data, but also alter it in ways that can create spurious signals that appear to carry scientific meaning but are in fact meaningless to the climate record.
Thanks to new projects and advances in laboratory techniques, the resolution challenge is quickly becoming a thing of the past [
1]. In addition to the recently measured West Antarctic Ice Sheet (WAIS) Divide ice core, many additional high-resolution records are becoming available, such as the South Pole Ice Core (SPC) [
2] and the Eastern Greenland Ice Core Project (EGRIP) [
3]. Replicate data is on the horizon as well, which may solve some of the statistical challenges. The SPC project, for instance, will involve dual analysis (i.e., two replicate sticks of ice) from three separate subsections of the ice core. However, replicate analyses of deep ice cores beyond a few hundred meters of ice will not occur any time soon, let alone multiple cores from a single location (see Endnote [
4]—which refers to References [
5,
6]). Thus, a rigorous statistics-based treatment of this problem is still a distant prospect for deep ice cores. In the meantime, information-theoretic methods—which can work effectively with a
single time-series data set—can be very useful. In previous work, we showed that estimates of the Shannon entropy rate can extract new scientific knowledge from individual ice-core records [
7,
8]. There were hints in those results that this family of techniques could be more generally useful in anomaly detection. This paper is a deeper exploration of that matter.
To this end, we used permutation entropy techniques to study the water-isotope records in the WAIS Divide ice core. The resolution of these data, which were measured using state-of-the-art laboratory technology [
1,
9], is an order of magnitude higher than that of traditionally measured deep ice core paleoclimate records (e.g., [
10]) and also representative of new data sets that are becoming available. We identified abrupt changes in the complexity of these isotope records using sliding-window calculations of the permutation entropy [
11] (PE) and a weighted variant of that method known as weighted permutation entropy (WPE) that is intended to balance noise levels and the scale of trends in the data [
12]. Via close examination of both the data and the laboratory records, we mapped the majority of these abrupt changes to regions of missing data and instrument error. Guided by that mapping, we remeasured and reanalyzed one of these segments of the core, where the PE and WPE results suggested an increased noise level, and the laboratory records indicated that the processing had been performed by an older version of the analysis pipeline. The PE and the WPE of this newly measured data—produced using state-of-the-art equipment—are much lower and consistent with the values in neighboring regions of the core. This not only validates our conjecture that permutation entropy techniques can be used to identify anomalies but also suggests a general approach for improving paleoclimate data sets in a targeted, cost-effective way.
Permutation entropy is a complexity measure: it reports the amount of new information that appears, on average, at each point in a sequence. In the context of a time series, this translates to a measure of how information propagates forward temporally. This has implications for predictability [
13,
14], among other things; indeed, these measures have been shown to converge to the Kolmogorov–Sinai entropy under suitable conditions [
15,
16], as described in
Section 2.2. The goal here is not to measure the complexity of paleoclimate data in any formal way, however. Our intent, and the underlying conjecture behind our approach, are more practical: abrupt changes in a quantity like permutation entropy suggest that something changed, either in the system or the data. The following section describes the data and methods that we used to demonstrate the efficacy of that approach.
3. Results
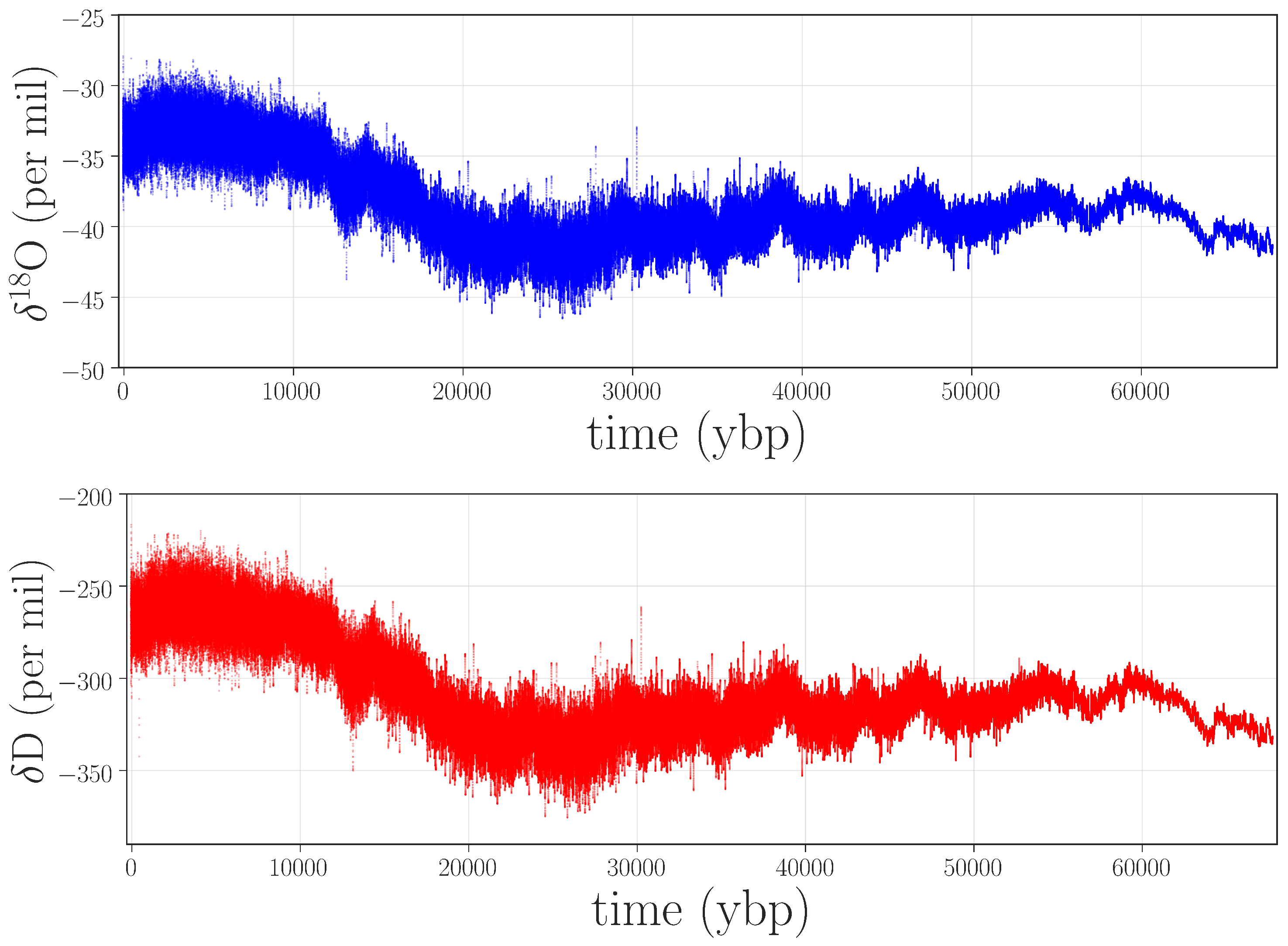
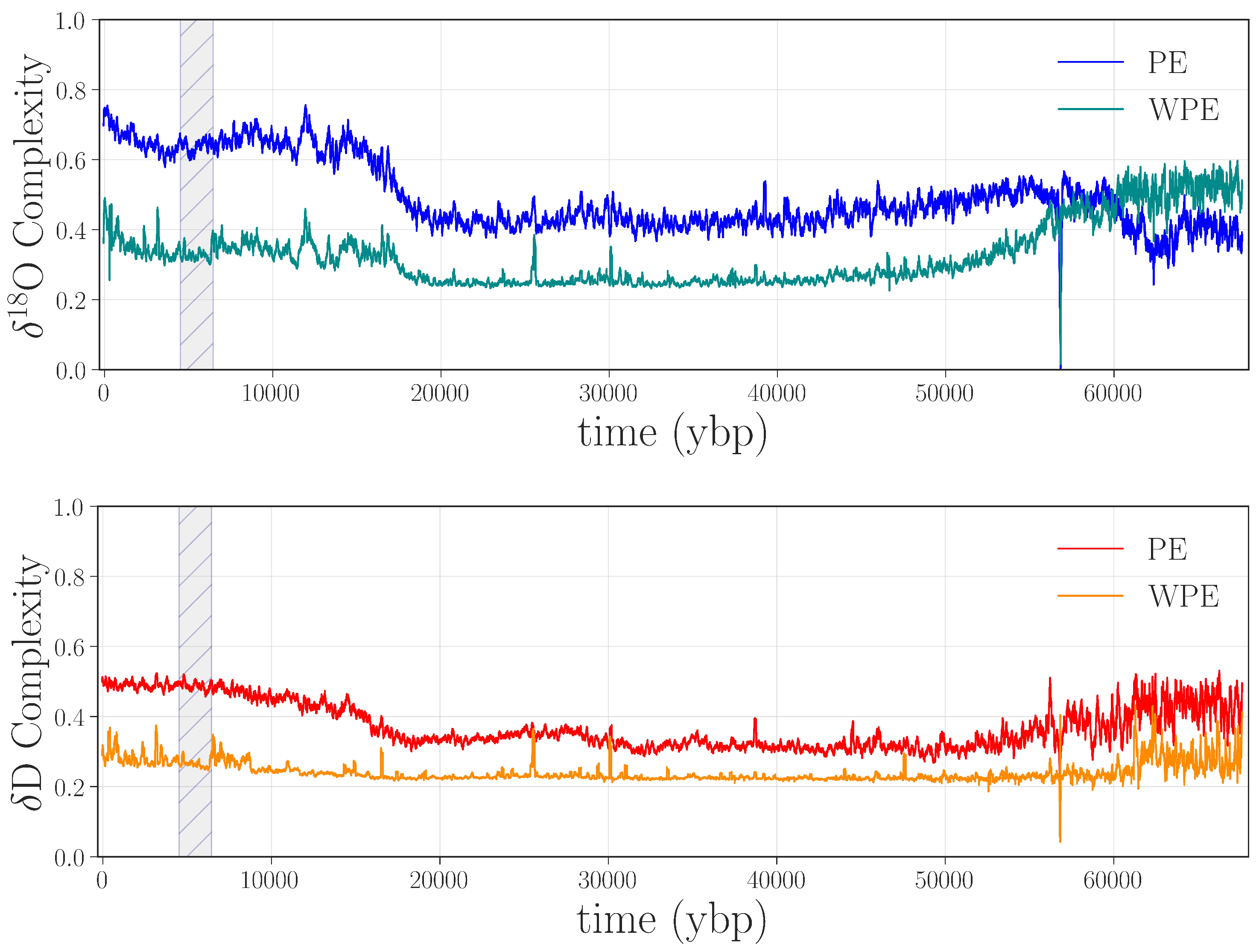
Figure 2 shows the weighted and unweighted permutation entropies of the
O and
D data from
Figure 1.
Figure 2.
Permutation entropies of the
O and
D data from
Figure 1, calculated in rolling 2400-point windows (i.e.,
) with a word length
and a delay
.
Top panel: weighted (WPE) and unweighted (PE) permutation entropy of
O in cyan and blue, respectively.
Bottom panel: WPE and PE of
D in orange and red, respectively.
Figure 2.
Permutation entropies of the
O and
D data from
Figure 1, calculated in rolling 2400-point windows (i.e.,
) with a word length
and a delay
.
Top panel: weighted (WPE) and unweighted (PE) permutation entropy of
O in cyan and blue, respectively.
Bottom panel: WPE and PE of
D in orange and red, respectively.
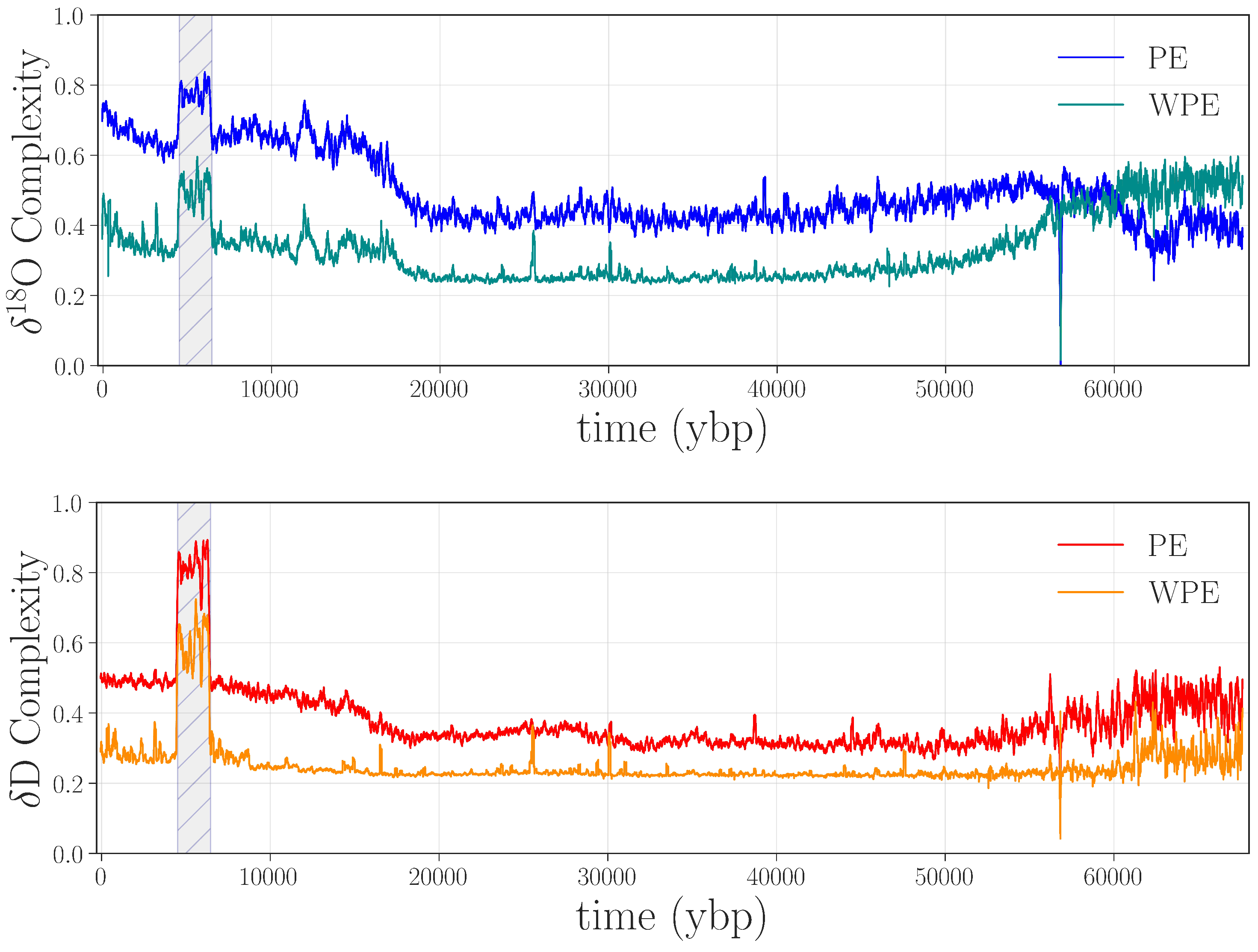
There are a number of interesting features in these four curves, many of which have scientific implications, as discussed in [
7,
8]. Here, we focus on apparent anomalies in the complexity of these climate signals: i.e., discontinuities or abrupt changes in the curves. The most obvious such feature is the large jump in all four traces between ≈4.5 and 6.5 kybp, shown shaded in gray in
Figure 2. This sharp increase in the complexity of both signals indicates that something is fundamentally different about this segment of the record, compared with the surrounding regions: in particular, that the values of both
D and
O depend less on their previous values during this period than in surrounding regions—i.e., that a large amount of new information is produced at each time step by the system that generated the data. There are two potential culprits for such an increase: data issues or a pair of radical, rapid climate shifts at either end of this time period. Since no such shifts are known or hypothesized by the climate-science community, we conjectured that this jump was due to processing-related issues in the data.
Recall that PE and WPE are designed to bring out different aspects of the information in the data. In view of this, the fact that
both calculations pick up on this particular feature is meaningful: it suggests that the underlying issue is not just noise—which would be at least partially washed out by the weighting term, causing the jumps in WPE to be smaller than those in PE. Rather, there may be other causes at work here. Going back to the laboratory records and the original papers, we found that an older, less precise, instrument was used to analyze this section of ice, and that this region of the core received the poorest possible quality score [
19,
40]. This part of the core is from the aforementioned brittle zone, which shatters when removed from the ice sheet. This not only makes the timeline difficult to establish, as mentioned in
Section 2.1, but can also affect the
D and
O values, as the drilling fluid can penetrate the ice and contaminate the measurements [
19]. This could easily disturb the amplitude-encoded information in the core. Unfortunately, permutation entropy techniques cannot tell us what the underlying causes of this anomaly are; that requires expert analysis and laboratory records. Even so, their ability to flag problems and help experts form scientific hypotheses about their causes is a major advantage of these information-theoretic techniques.
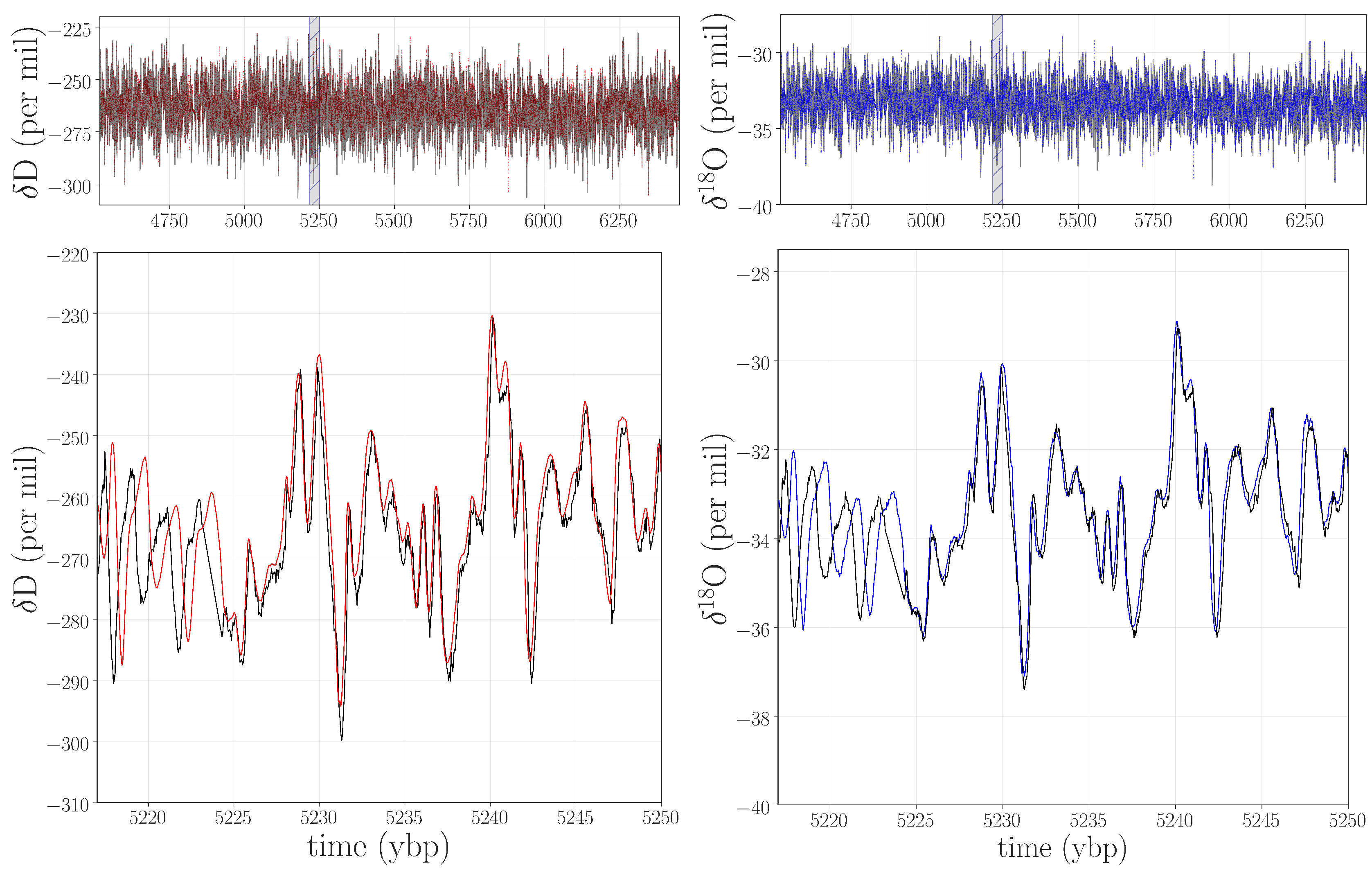
As a case in point, we tested our hypotheses about the gray-shaded jump in
Figure 2 by remeasuring the 331 m segment of the WAIS Divide ice core that corresponds to this time period. After obtaining the archived ice from the National Science Foundation Ice Core Facility (NSF-ICF), we remeasured the isotope data with state-of-the-art equipment, repeating the depth-to-age conversion and temporal regularization processes described in
Section 2. Plots of these new traces appear in
Figure 3, with the old values shown in black.
Figure 3.
Top panels: the remeasured
D (red) and
O (blue) data points in the range of ≈4.5–6.5 kybp, with the original records shown in gray. Bottom panels: a closeup of a small segment of those traces, marked with a gray box in the top panels. Note that the vertical scales here are different than in
Figure 1.
Figure 3.
Top panels: the remeasured
D (red) and
O (blue) data points in the range of ≈4.5–6.5 kybp, with the original records shown in gray. Bottom panels: a closeup of a small segment of those traces, marked with a gray box in the top panels. Note that the vertical scales here are different than in
Figure 1.
Visual examination of these traces makes two things apparent: lower levels of high-frequency noise in the new signals and small phase offsets between the old and new data. The lower noise levels were, of course, the point of the resampling. The minor phase disparities are a consequence of updates in the laboratory pipeline and the difficulties posed by this particular section of the core. In the years since the creation of the first generation of this system—which was used to measure the original data—there have been a number of updates and improvements. As a result, there are subtle differences (on the order of a few centimeters) in the depth registration between the remeasured and the original data. This is a particular challenge in the brittle zone, since the broken or shattered ice pieces are difficult to piece back together and can settle along fractures, reducing the length of the ice stick by a few centimeters. This can even cause complete data loss in short segments. Remeasuring this ice using state-of-the-art technology has allowed us to improve the data in several important ways, such as by reducing the overall noise levels, improving the depth registration, and even filling in missing parts of the original record that we obtained upon remeasuring the archived ice.
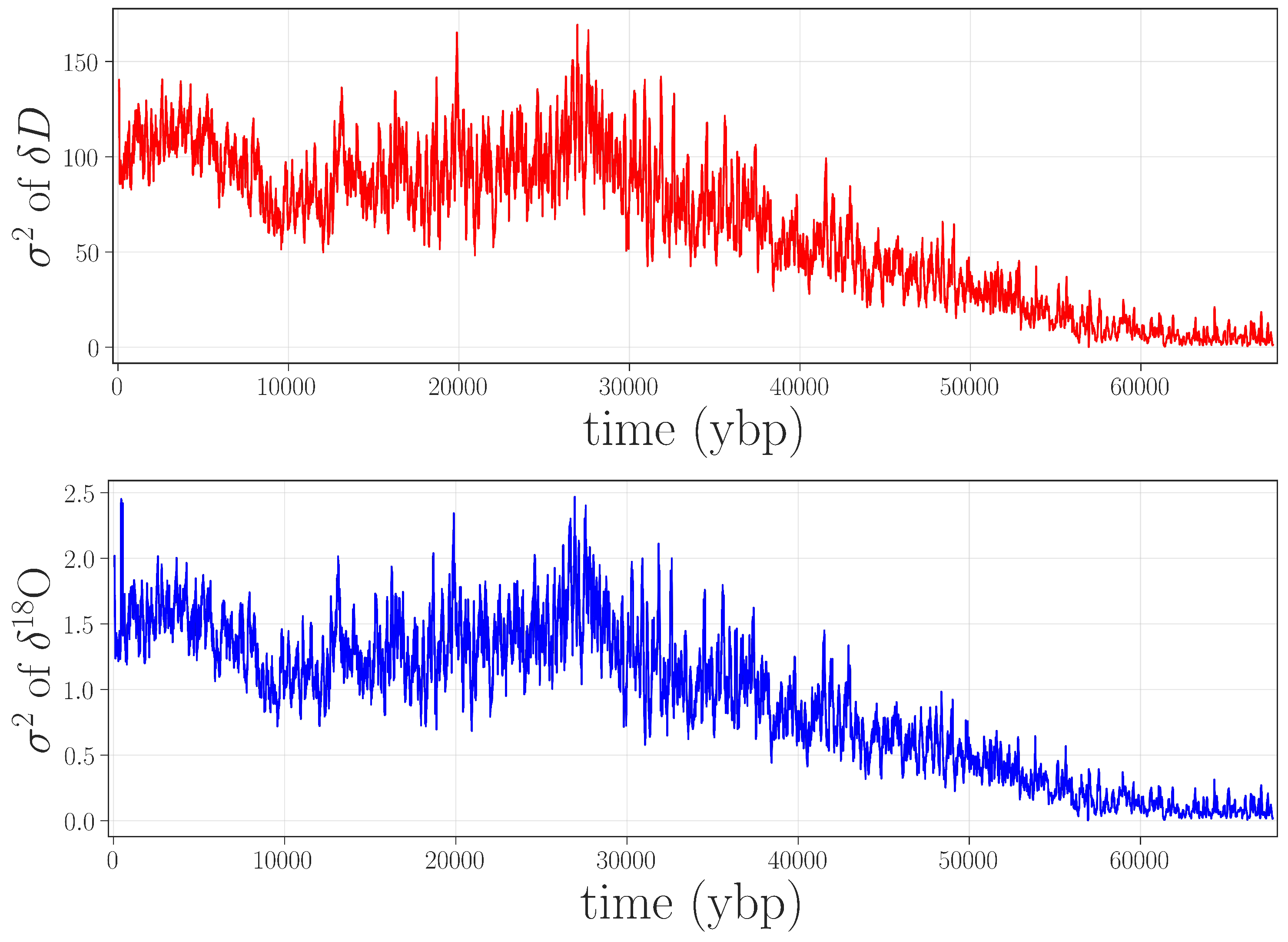
Given the kind of issues that were present in the data, such as increased small-scale variance, it is worth considering whether simpler approaches—less computationally complex than permutation entropy, and with fewer free parameters—would be equally effective in flagging the gray-shaded jump in
Figure 2. Because of the inherent data challenges (unknown processes at work on the data, lack of replicates, laboratory issues, etc.), this community has been traditionally limited to fairly rudimentary approaches to anomaly detection: e.g., discarding observations that lie beyond five standard deviations from the mean. Accordingly, we performed a rolling-variance calculation on the same isotope records using a 2400-point window. These results, shown in
Figure 4, do not bring out the ≈4.5–6.5 kybp feature, nor do they identify the other anomalies that are described later in this paper.
Figure 4.
A simple anomaly detection algorithm. Here,
is estimated on a rolling 2400-point overlapping window for
D (
top) and
O (
bottom). Neither the feature in the gray-shaded box in
Figure 2 nor the other anomalies described later in this paper are brought out by this calculation.
Figure 4.
A simple anomaly detection algorithm. Here,
is estimated on a rolling 2400-point overlapping window for
D (
top) and
O (
bottom). Neither the feature in the gray-shaded box in
Figure 2 nor the other anomalies described later in this paper are brought out by this calculation.
Of course, there are surely other anomaly detection methods that could be useful for identifying anomalies in paleoclimate records. However, permutation entropy methods identify these problems quite clearly, are relatively simple and fast to compute and, while they have several parameters to tune, the results are quite robust to these choices.
The last step in validating that the jump in the curves in
Figure 2 indicated an anomaly was to replace the data points between 4.5 and 6.5 kybp in the
D and
O records of
Figure 1 with the remeasured values from
Figure 3 and repeat the PE and WPE calculations. The results are quite striking, as shown in
Figure 5: the large square waves are completely absent from the PE and WPE traces of the repaired data set.
Figure 5.
PE and WPE of O (top panel) and D (bottom panel) using remeasured data from 1037–1368 m (≈4.5–6.5 kybp).
Figure 5.
PE and WPE of O (top panel) and D (bottom panel) using remeasured data from 1037–1368 m (≈4.5–6.5 kybp).
This experiment—the longest high-resolution remeasurement and reanalysis of an ice core that has been performed to date—not only confirms our conjecture that this anomaly was due to instrument error but also allowed us to improve an important section of the data using a targeted, highly focused effort.
The repaired segment of water-isotope data (≈4.5–6.5 kybp) captures a climate signal from the Holocene era, and thus may contain useful information about the onset of climactic shifts during the beginnings of human civilization. In view of this, recognizing and repairing issues with these data is particularly meaningful. Again, permutation entropy calculations alone cannot tell us the underlying mechanism for abrupt changes. However, their ability to identify a region of the core that should be revisited—because of issues that would only have been apparent with a laborious, fine-grained traditional analysis of the data—is a major advantage. This result highlights the main point that we wish to make in this paper: PE and WPE are useful methods for identifying anomalies in time-series data from paleoclimate records. This is particularly useful in contexts where the data are difficult and/or expensive to collect and analyze. In these situations, a tightly focused new study, specifically targeting the offending area using permutation entropy, can maximize the benefit with minimal effort.
Another obvious feature in
Figure 5 is the downward spike at around 58 kybp in all four curves. Alerted by this anomaly in WPE and PE, we returned to the laboratory records and found that 1.107 m (110.1 years) of ice was unavailable from the record in this region, and so a span of ≈2387 points in the
D and
O traces were filled in by interpolation. This series of points—a linear ramp with positive slope—translated to a long series of “1234” permutations. This causes a drop in the PE curves as the calculation window passes across this expanse of completely predictable values. Indeed, for calculations with
and
, there is a brief period where 99.45% of the “data” in that window has the same permutation, which causes WPE to fall precipitously, then spike back up as the window starts to move back onto non-interpolated data.
The large jump from ≈4.5 to 6.5 kybp and the spike at 58 kybp are only a few of the abrupt changes in the permutation entropy traces. The other spikes and dips in those curves, we believe, are also associated with anomalies in the data. Some of these features appear in both PE and WPE; others appear in PE but not WPE (e.g., at 38.7 kybp in
D) or vice versa (e.g., 25.6, 30.1, and 47.5 kybp for
D and
O). This brings out the differential nature of these two techniques and the power of the combined analysis: each can, independently, detect types of anomalies that the other misses. In the remainder of this section, we dissect a representative subset of the anomalies in
Figure 5 to illustrate this claim, beginning with the case in which WPE, but not PE, suggests data issues. Manual re-examination of the data in the regions around 25.6, 30.1, and 47.5 kybp revealed that the
D and
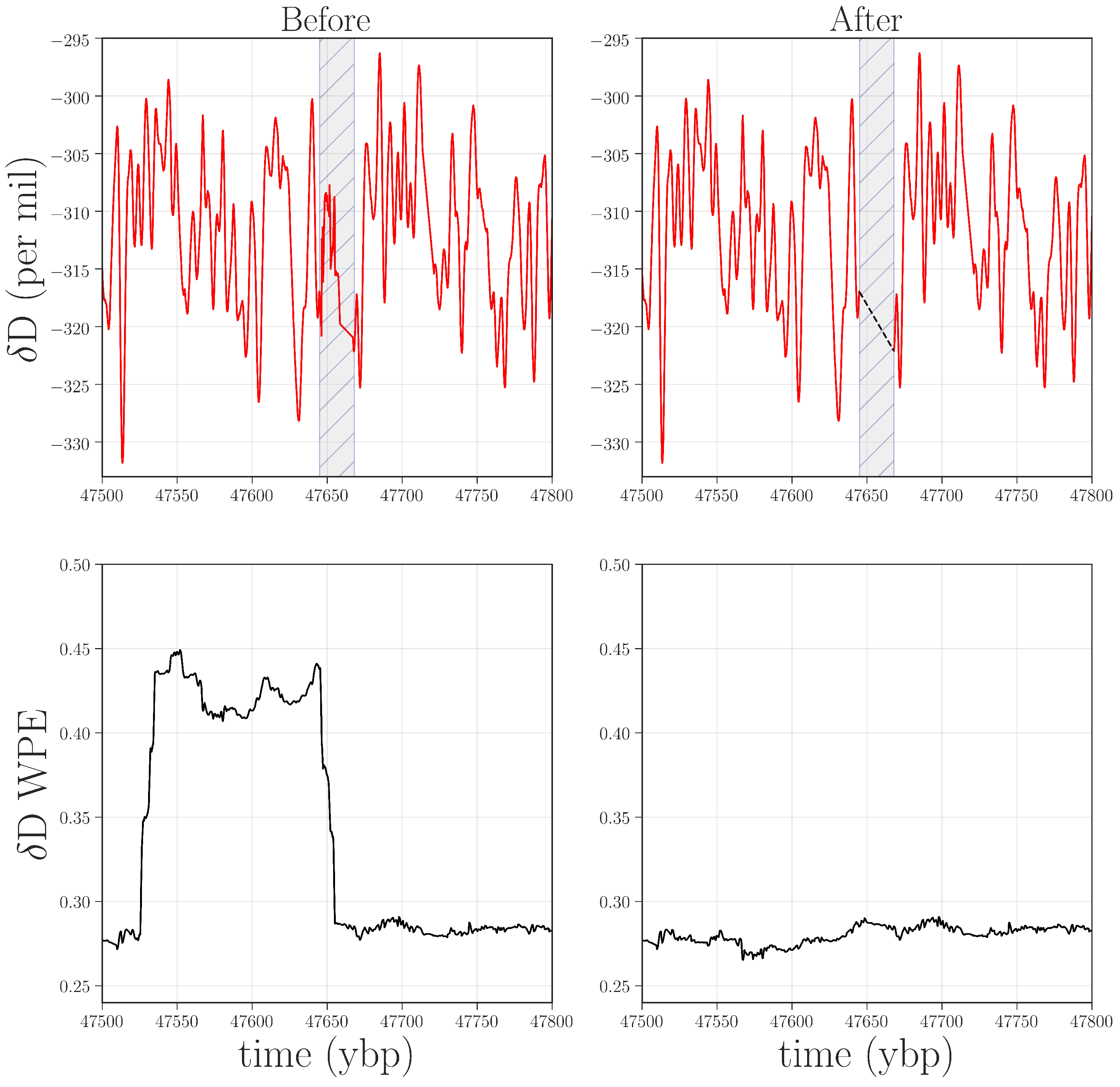
O signal in these regions had been compromised in very small segments of the record (<1 m of ice). The top left panel of
Figure 6 shows the region around 47.5 kybp. The signal is visibly different in the small shaded region, combining sharp corners and high-frequency oscillations—unlike the comparatively smooth signal in the regions before and after this segment. WPE is much better at picking up this kind of anomaly because there has been a drastic shift in the information that is encoded in the
amplitude of the signal. PE, in contrast, does not flag this segment because the distribution of permutations in this region is similar to that of original signal. However, the variance of each delay vector is quite different than in the surrounding signal: an effect to which PE is blind, but that WPE is designed to emphasize.
Figure 6.
Top row: D data from 47.5 to 47.8 kybp before and after removal of and interpolation over (black dashed line) a range of faulty values (shaded in gray). Bottom row: WPE calculated from the corresponding traces. The width of the square wave in the lower left plot is the size of the WPE calculation window (2400 points at 1/20th year per point) plus the width of the anomaly. The horizontal shift between the earliest faulty value and the rise in WPE is due to the windowed nature of the WPE calculation.
Figure 6.
Top row: D data from 47.5 to 47.8 kybp before and after removal of and interpolation over (black dashed line) a range of faulty values (shaded in gray). Bottom row: WPE calculated from the corresponding traces. The width of the square wave in the lower left plot is the size of the WPE calculation window (2400 points at 1/20th year per point) plus the width of the anomaly. The horizontal shift between the earliest faulty value and the rise in WPE is due to the windowed nature of the WPE calculation.
There are many potential mechanisms that could be causing this distortion in the amplitude: extreme events, for instance, such as large volcanic eruptions, or the same kinds of data and data-processing issues that are discussed above. Returning again to the laboratory records, we discovered that the CRDS-CFA system had malfunctioned while analyzing this region. We could, as before, confirm that this was the cause of the anomaly by remeasuring this region of the core. If the outliers disappeared as a result, that would resolve some significant data issues with only a minimal, targeted amount of effort and expense. If they did
not disappear, then the permutation entropy calculations would have identified a region where the record warranted further investigation by paleoclimate experts. To date, we have not carried out this experiment, but plan to request archived ice from the NSF-ICF for remeasurement and reanalysis. Access to this limited and irreplaceable resource is, justifiably so, highly guarded—particularly in regard to the deeper ice. In lieu of that experiment, we reprocessed the data from the region surrounding
–
kybp in the
D record by removing the offending data points and interpolating across the interval. As shown in the bottom-right panel of
Figure 6, this removes the small square wave from the WPE trace. Without being able to remeasure this ice, of course, we cannot narrow down the cause of this anomaly. Even so, the WPE results are useful in that they allow us to do some targeted reprocessing of the data in order to mitigate the effects.
Spikes in PE that are
not associated with equally strong spikes in WPE are indications of effects that are dominated by small-scale noise.
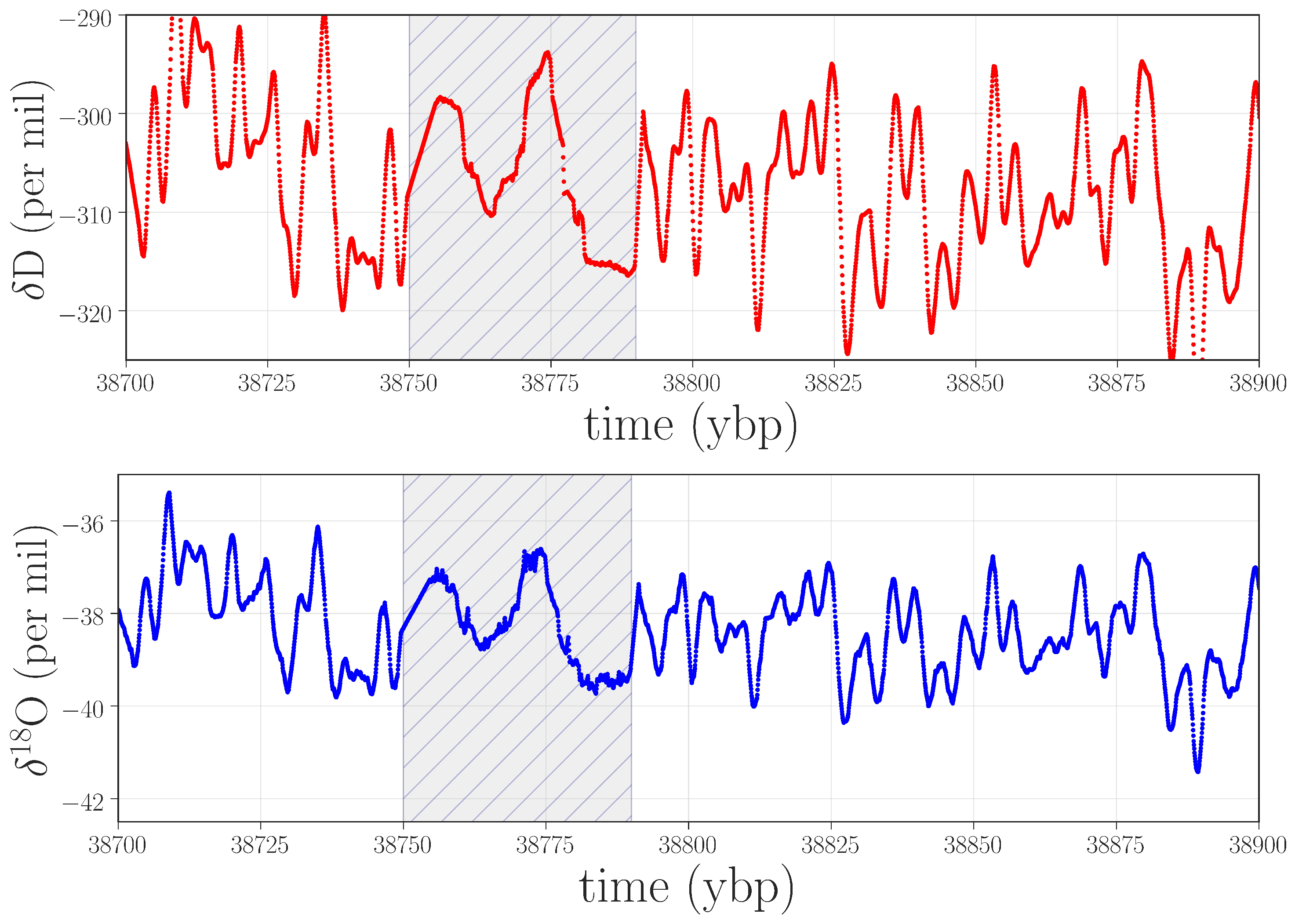
Figure 7 shows an example of the isotope record in one of these regions.
Figure 7.
Isotope data near 38.7 kybp that produced a spike in PE but not in WPE. According to the lab records, the graphical user interface froze during the analysis of this segment of the ice, compromising the results.
Figure 7.
Isotope data near 38.7 kybp that produced a spike in PE but not in WPE. According to the lab records, the graphical user interface froze during the analysis of this segment of the ice, compromising the results.
In contrast to the situation in
Figure 6, which is dominated by high-frequency oscillations, this anomaly takes the form of a strong low-frequency component with a small band of superimposed noise. The weighting strategy in WPE causes it to ignore these features, but PE picks up on them very clearly (see Endnote [
41]). To diagnose the cause of this anomaly, we again returned to the lab records, finding that the graphical user interface froze while analyzing this particular ice stick, and that the data-processing routines involved in distance registration and isotope content were compromised.
Finally, there is a single spike (near 16.6 kybp in the WPE of D) where visual inspection of the raw data by expert paleoscientists does not suggest any issues, nor are there any recorded problems in the laboratory records. This is not part of any sections of the core that are known to be problematic, like the brittle zone, and most likely warrants further investigation.
4. Discussion
This manuscript illustrates the potential of information theory as a forensic tool for paleoclimate data, identifying regions with anomalous amounts of complexity so that they can be investigated further. As a proof-of-concept demonstration of this claim, we used permutation entropy techniques to isolate issues in water-isotope data from the WAIS Divide core, then remeasured and reanalyzed one of the associated regions using state-of-the-art laboratory equipment. The results of this experiment—the longest segment of replicate ice-core analysis in history—verified that the issue flagged by these information-theoretic techniques in that region were caused by outdated laboratory techniques, as we had conjectured. We also showed that permutation entropy techniques identified several other smaller anomalies throughout the record, which we showed were caused by various minor mishaps in the data processing pipeline. Finally, unlike other anomaly detection studies that use either PE or WPE, we showed that using these two techniques together, rather than in isolation, enables the detection of a much richer landscape of possible anomalies.
This reanalysis approach is already providing valuable insights that reach well beyond the scope of this work. Compared with the prohibitive cost and time commitment of collecting a new core, remeasuring ice from an archived core can be comparatively easy and inexpensive if the region requiring reanalysis can be precisely and clearly defined. This forms the basis for what we believe will be an effective general targeted reinvestigation methodology that can be applied not only to the water-isotope record from the WAIS Divide ice core but also to other high-resolution paleoclimate records. Indeed, several such records are being finalized at the time of this publication, which makes this a perfect time to start developing, applying, and evaluating sophisticated anomaly detection methods for these important data sets. Excitingly, as a result of the study reported in this manuscript, PE-based techniques are now being added to the quality control phase of the analysis pipeline for at least one of these new high-resolution records.
The information in paleoclimate records contains valuable clues and insights about the Earth’s past climate, and perhaps about its future. While these records hold a lot of promise, it is crucial—especially in an era of rampant climate-change denial—to be careful when extracting the useful and meaningful information from these records while simultaneously identifying regions that are problematic. For a multitude of reasons, distinguishing useful information from a lack thereof can be a particularly challenging task in paleodata. This is especially true in parts of these records that are hard to analyze, such as the brittle zone of the WDC. Our work has identified a number of intervals in this core where the data require a closer look, including several that contain information corresponding to the time period of the dawn of human civilization.