Optimized Adaptive Local Iterative Filtering Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis
Abstract
1. Introduction
2. The Theory of the Proposed Method
2.1. The Theory of Adaptive Local Iterative Filtering
| Algorithm 1 Adaptive local iterative filtering algorithm |
| ALIF Algorithm IMF = ALIF(f) |
| IMF = { } While the number of extrema of do While the stopping criterion is not satisfied do Compute the filter length for End while End while |
- (1)
- and for
- (2)
- (1)
- , for any
- (2)
- , for any
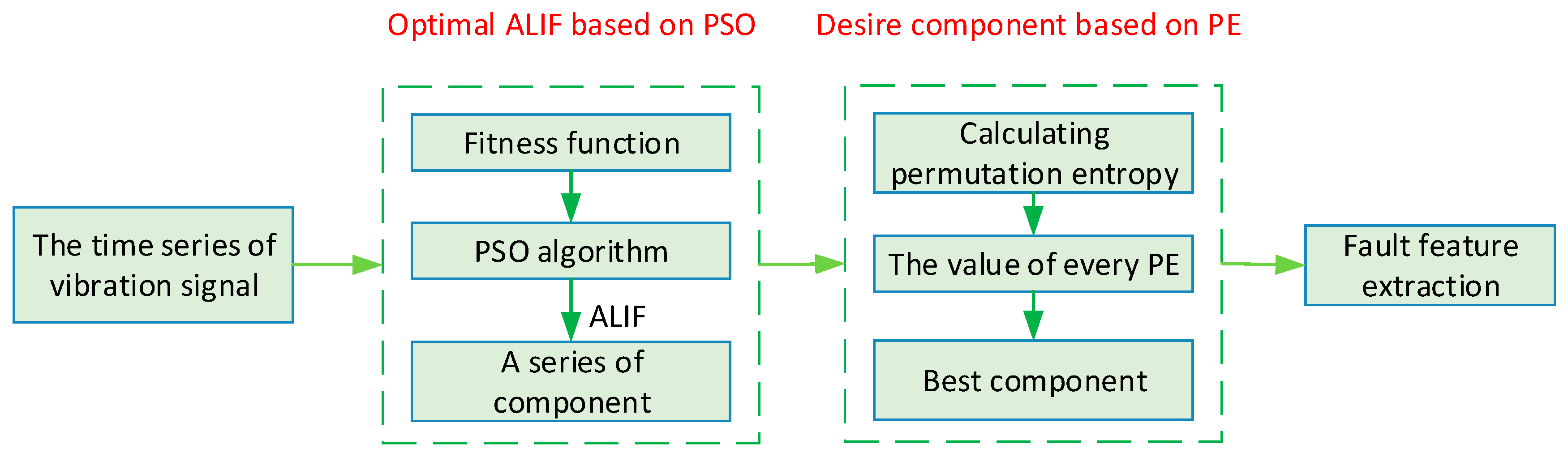
2.2. Adaptive Local Iterative Filtering Based on Particle Swarm Optimization
2.3. The Desired Component Selection Base on PE
3. Numerical Simulation Analysis
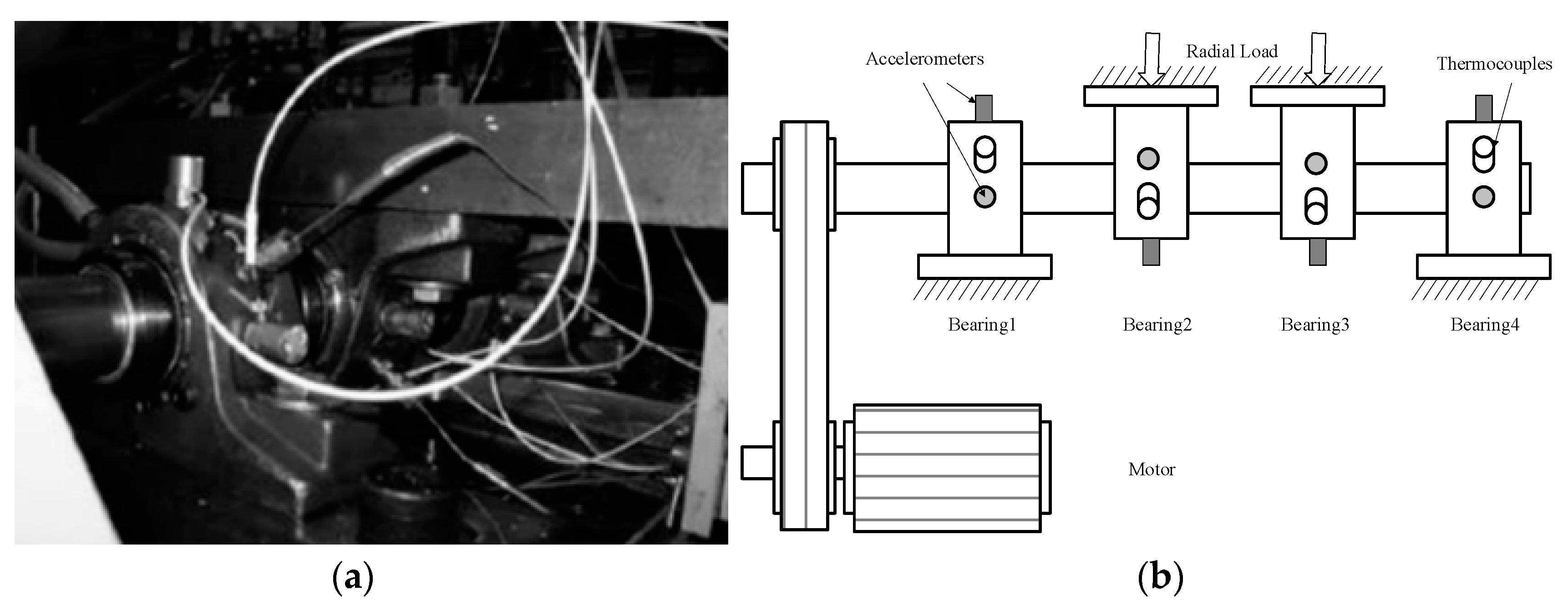
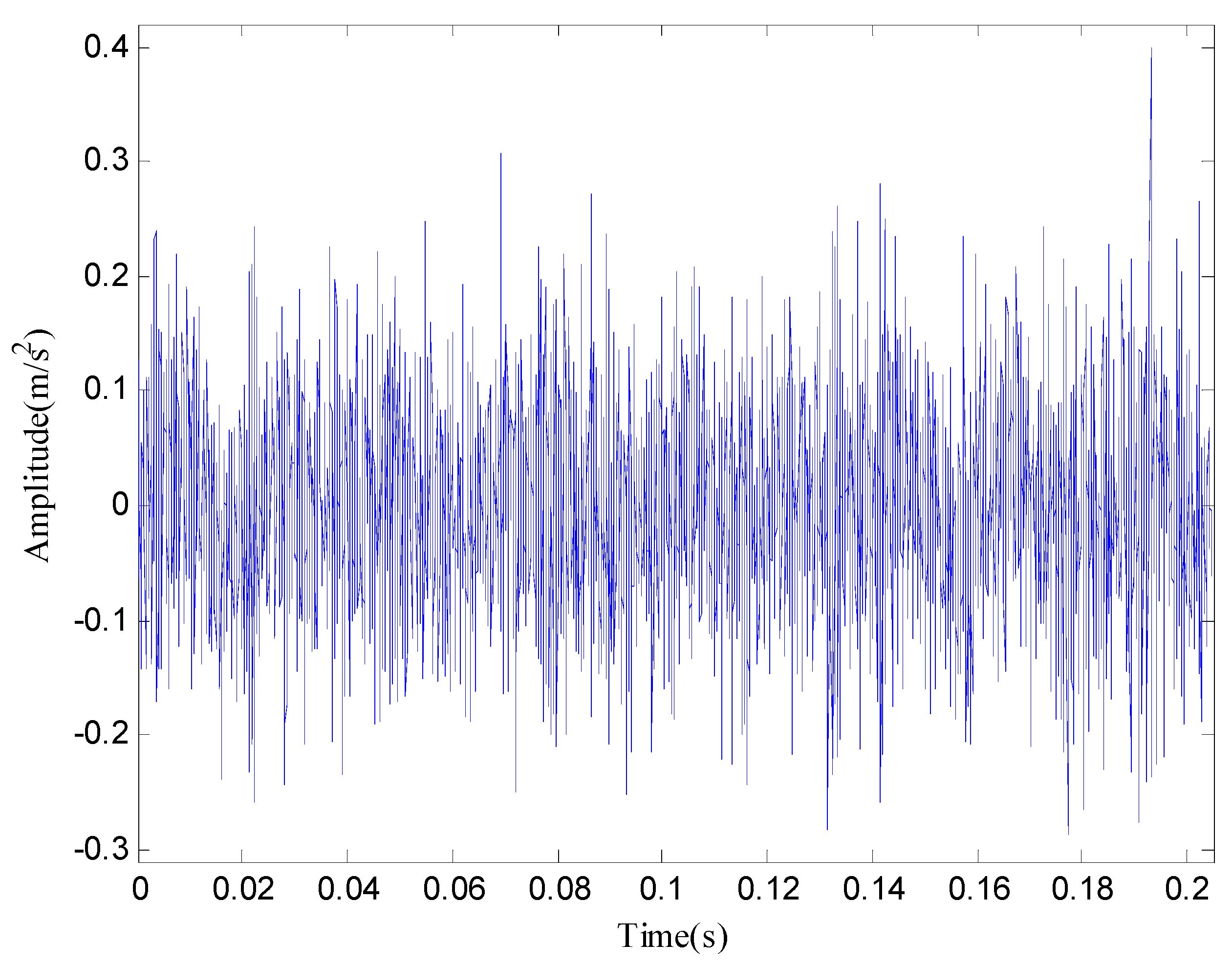
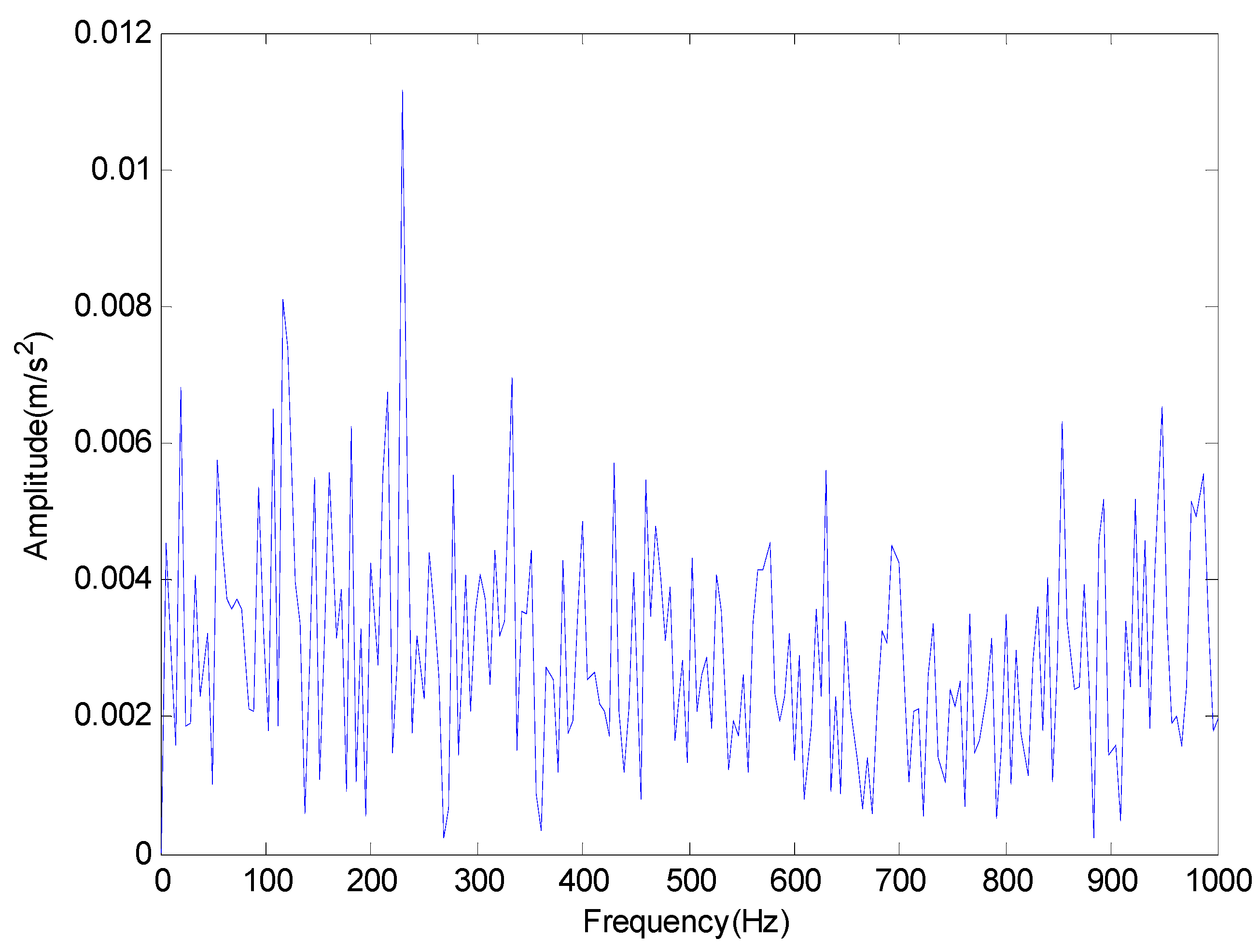
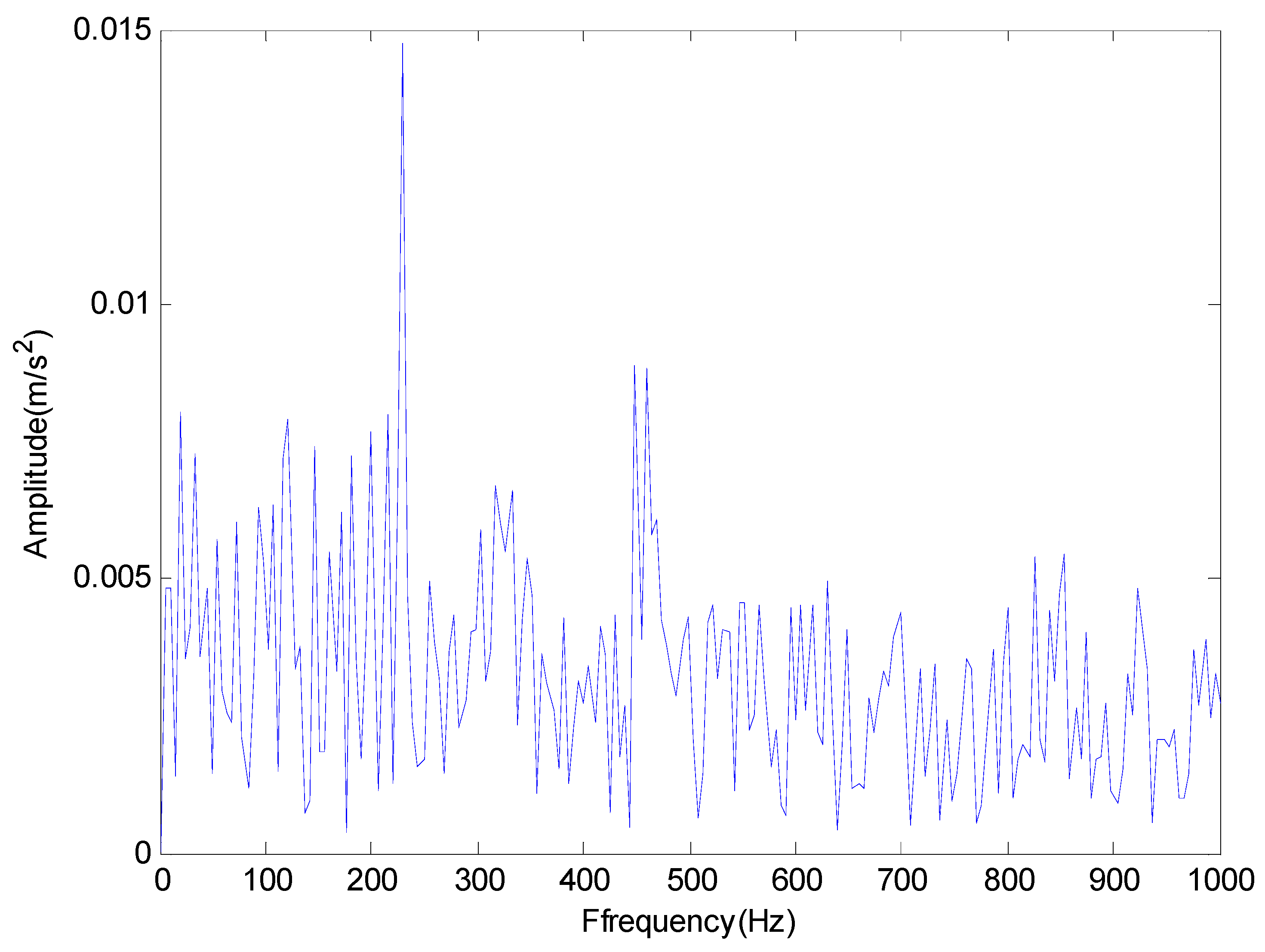
4. Experimental Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Fei, S. Fault Diagnosis of Bearing by Utilizing LWT-SPSR-SVD-Based RVM with Binary Gravitational Search Algorithm. Shock Vib. 2018, 2018, 8385021. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Dou, L. Compound Fault Diagnosis of Bearings Using an Improved Spectral Kurtosis by MCDK. Math. Probl. Eng. 2018, 2018, 6513045. [Google Scholar] [CrossRef]
- Dybała, J.; Zimroz, R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Li, H.; Yang, R.; Wang, C.; He, C.; Sciubba, E. Investigation on Planetary Bearing Weak Fault Diagnosis Based on a Fault Model and Improved Wavelet Ridge. Energies 2018, 11, 1286. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z. Multi-dimensional variational mode decomposition for bearing-crack detection in wind turbines with large driving-speed variations. Renew. Energy 2018, 116, 55–73. [Google Scholar] [CrossRef]
- Tang, H.; Chen, J.; Dong, G. Dynamic linear models-based time series decomposition and its application on bearing fault diagnosis. J. Vib. Control 2015, 21, 975–988. [Google Scholar] [CrossRef]
- Pang, B.; Tang, G.; Tian, T.; Zhou, C. Rolling Bearing Fault Diagnosis Based on an Improved HTT Transform. Sensors 2018, 18, 1203. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Hamadache, M.; Lee, D.; Mucchi, E.; Dalpiaz, G. Vibration-Based Bearing Fault Detection and Diagnosis via Image Recognition Technique Under Constant and Variable Speed Conditions. Appl. Sci. 2018, 8, 1392. [Google Scholar] [CrossRef]
- Berredjem, T.; Benidir, M. Bearing faults diagnosis using fuzzy expert system relying on an Improved Range Overlaps and Similarity method. Expert Syst. Appl. 2018, 108, 134–142. [Google Scholar] [CrossRef]
- Xu, K.; Wang, G.; Xing, Z. A Feature Extraction Method of Rolling Bearing Fault Signal Based on the Singular Spectrum Analysis and Linear Autoregressive Model. In International Conference on Electrical and Information Technologies for Rail Transportation; Springer: Singapore, 2017; pp. 291–300. [Google Scholar]
- Qian, Y.; Yan, R.; Gao, R.X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Ma, Z.; Ruan, W.; Chen, M.; Li, X. An Improved Time-Frequency Analysis Method for Instantaneous Frequency Estimation of Rolling Bearing. Shock Vib. 2018, 2018, 8710190. [Google Scholar] [CrossRef]
- Sharma, G.K.; Kumar, A.; Rao, C.B.; Jayakumar, T.; Raj, B. Short time Fourier transform analysis for understanding frequency dependent attenuation in austenitic stainless steel. NDT E Int. 2013, 53, 1–7. [Google Scholar]
- Satpathi, K.; Yeap, Y.M.; Ukil, A.; Geddada, N. Short-time fourier transform based transient analysis of vsc interfaced point-to-point dc system. IEEE Trans. Ind. Electron. 2018, 65, 4080–4091. [Google Scholar] [CrossRef]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- He, S.; Liu, Y.; Chen, J.; Zi, Y. Wavelet transform based on inner product in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2016, 70, 1–35. [Google Scholar]
- Lau EC, C.; Ngan, H.W. Detection of motor bearing outer raceway defect by wavelet packet transformed motor current signature analysis. IEEE Trans. Instrum. Meas. 2010, 59, 2683–2690. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; Huang, T.; You, G. Multisensor signal denoising based on matching synchrosqueezing wavelet transform for mechanical fault condition assessment. Meas. Sci. Technol. 2018, 29, 045104. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond.-A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Alickovic, E.; Kevric, J.; Subasi, A. Performance evaluation of empirical mode decomposition, discrete wavelet transform, and wavelet packed decomposition for automated epileptic seizure detection and prediction. Biomed. Signal Process. Control 2018, 39, 94–102. [Google Scholar] [CrossRef]
- Piersanti, M.; Materassi, M.; Cicone, A.; Spogli, L.; Zhou, H.; Ezquer, R.G. Adaptive Local Iterative Filtering: A promising technique for the analysis of nonstationary signals. J. Geophys. Res. 2018, 123, 1031–1046. [Google Scholar] [CrossRef]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmonic Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef]
- Du, K.L.; Swamy, M.N.S. Particle swarm optimization. In Search and Optimization by Metaheuristics; Birkhäuser: Cham, Switzerland, 2016. [Google Scholar]
- Ghamisi, P.; Benediktsson, J.A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 309–313. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A social learning particle swarm optimization algorithm for scalable optimization. Inf. Sci. 2015, 291, 43–60. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Zhang, Y.; Philips, P.; Yang, J.; Yuan, T.F. Identification of green, oolong and black teas in China via wavelet packet entropy and fuzzy support vector machine. Entropy 2015, 17, 6663–6682. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Li, J.; Yan, J.; Liu, X.; Ouyang, G. Using permutation entropy to measure the changes in EEG signals during absence seizures. Entropy 2014, 16, 3049–3061. [Google Scholar] [CrossRef]
- Shi, Z.; Song, W.; Taheri, S. Improved LMD, permutation entropy and optimized K-means to fault diagnosis for roller bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Dwyer, R. Detection of non-Gaussian signals by frequency domain kurtosis estimation. In Proceedings of the IEEE International Conference on ICASSP’83 Acoustics, Speech, and Signal Processing, Boston, MA, USA, 14–16 April 1983; Volume 8, pp. 607–610. [Google Scholar]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Shan, H.; Lin, J. Early fault diagnosis of bearings using an improved spectral kurtosis by maximum correlated kurtosis deconvolution. Sensors 2015, 15, 29363–29377. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
- Barszcz, T.; Jabłoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement—Parts 1 and 2”. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- Bandt, C. Permutation entropy and order patterns in long time series. In Time Series Analysis and Forecasting; Springer: Cham, Switzerland, 2016; pp. 61–73. [Google Scholar]
- Cicone, A. Nonstationary signal decomposition for dummies. arXiv, 2017; arXiv:1710.04844. [Google Scholar]
- Cicone, A.; Zhou, H. Multidimensional iterative Filtering method for the decomposition of high-dimensional non-stationary signals. Numer. Math. Theory Methods Appl. 2017, 10, 278–298. [Google Scholar] [CrossRef]
- Cicone, A.; Zhou, H. Numerical Analysis for Iterative Filtering with New Efficient Implementations Based on FFT. arXiv, 2018; arXiv:1802.01359. [Google Scholar]
- Lin, L.; Wang, Y.; Zhou, H. Iterative Filtering as an alternative algorithm for empirical mode decomposition. Adv. Adapt. Data Anal. 2009, 1, 543–560. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.K.; Moodie, C.A.S. Application of the largest Lyapunov exponent algorithm for feature extraction in low speed slew bearing condition monitoring. Mech. Syst. Signal Process. 2015, 50, 116–138. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis for cyclostationary machine signals, application to ball bearing diagnostics. Mech. Syst. Syst. Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Antoni, J.; Bonnardot, F.; Raad, A.; Badaoui, M.E. Cyclostationary modelling of rotating machine vibration signals. Mech. Syst. Signal Process. 2004, 18, 1285–1314. [Google Scholar] [CrossRef]
- Muruganatham, B.; Sanjith, M.A.; Krishnakumar, B.; Murty, S.S. Roller element bearing fault diagnosis using singular spectrum analysis. Mech. Syst. Signal Process. 2013, 35, 150–166. [Google Scholar] [CrossRef]
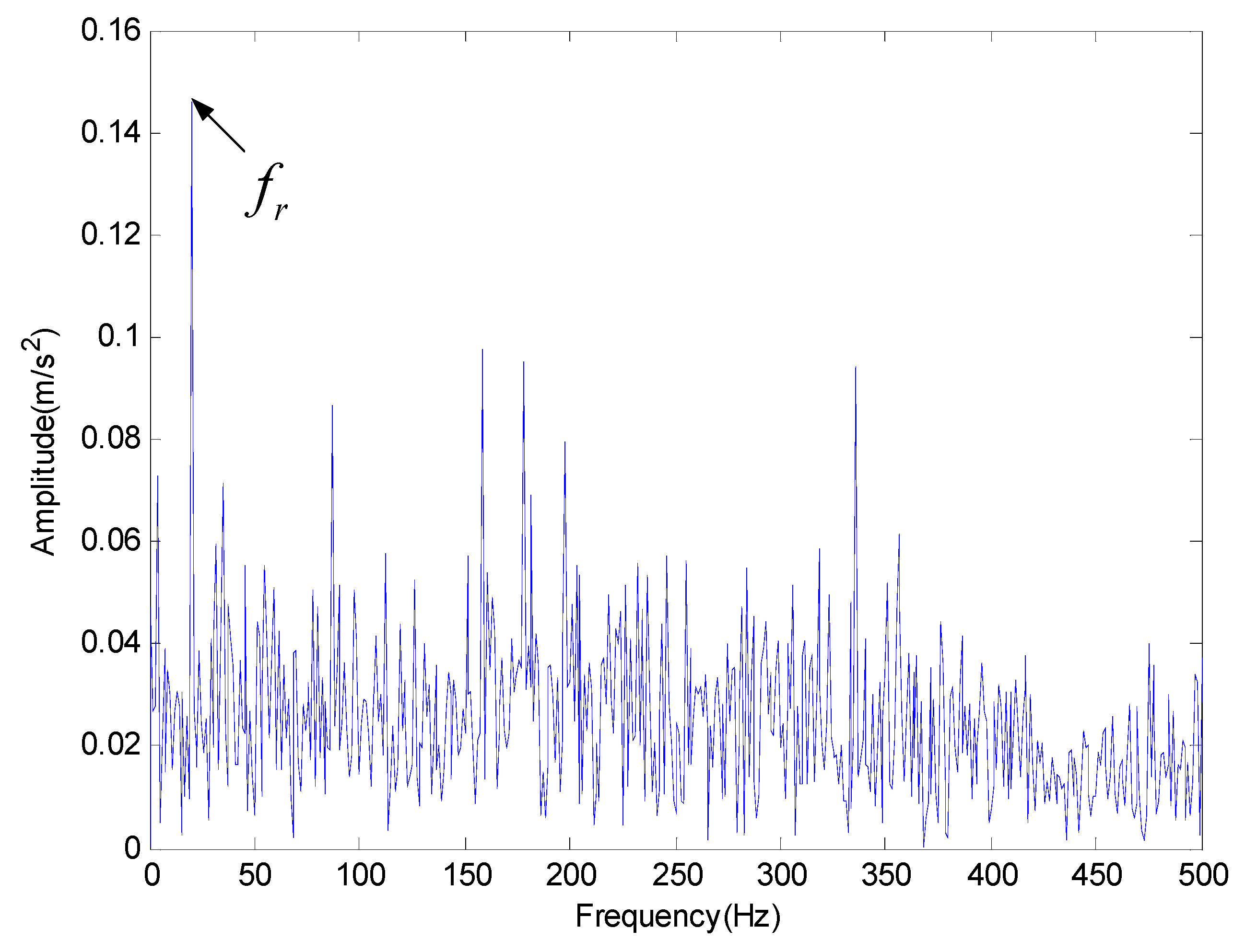
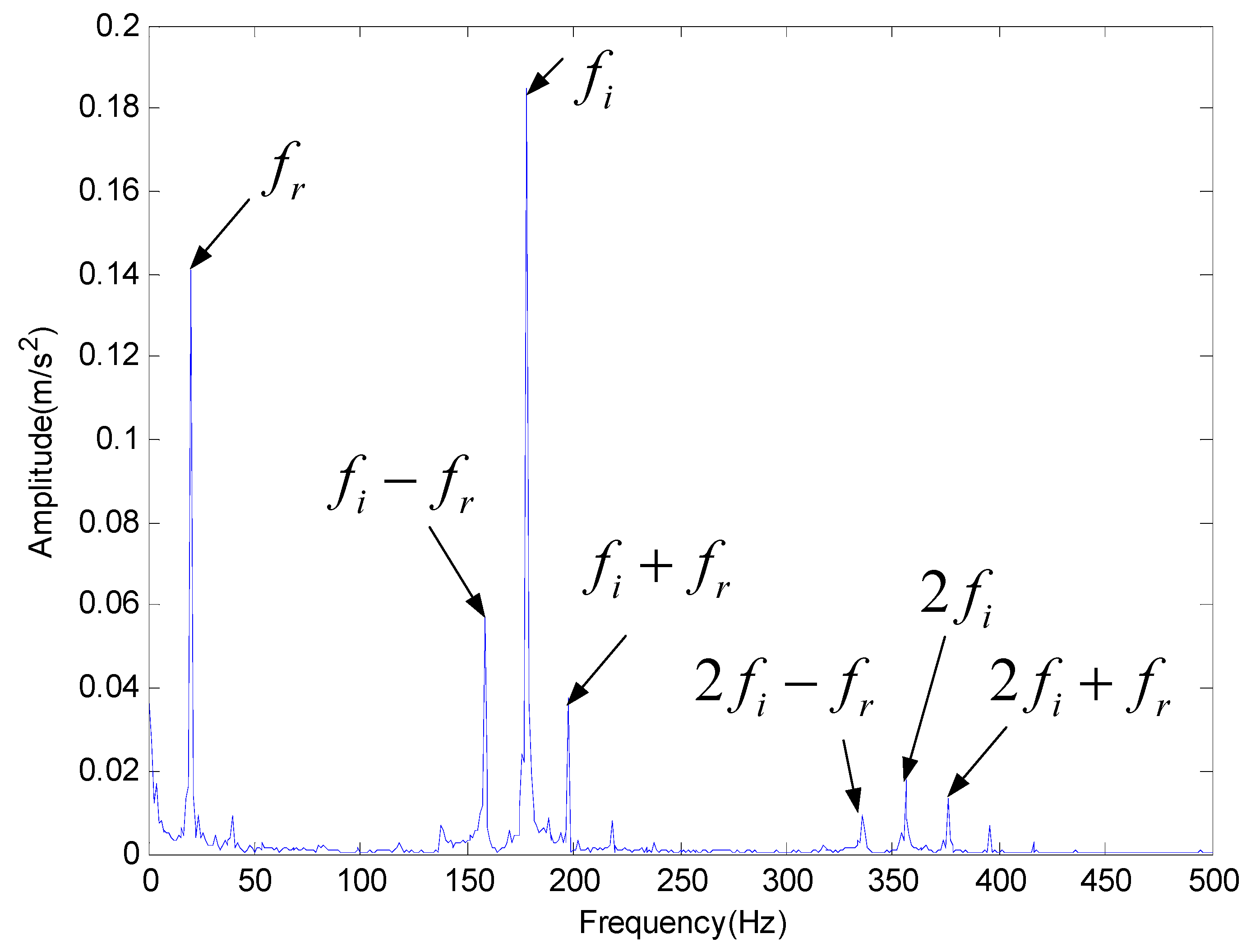
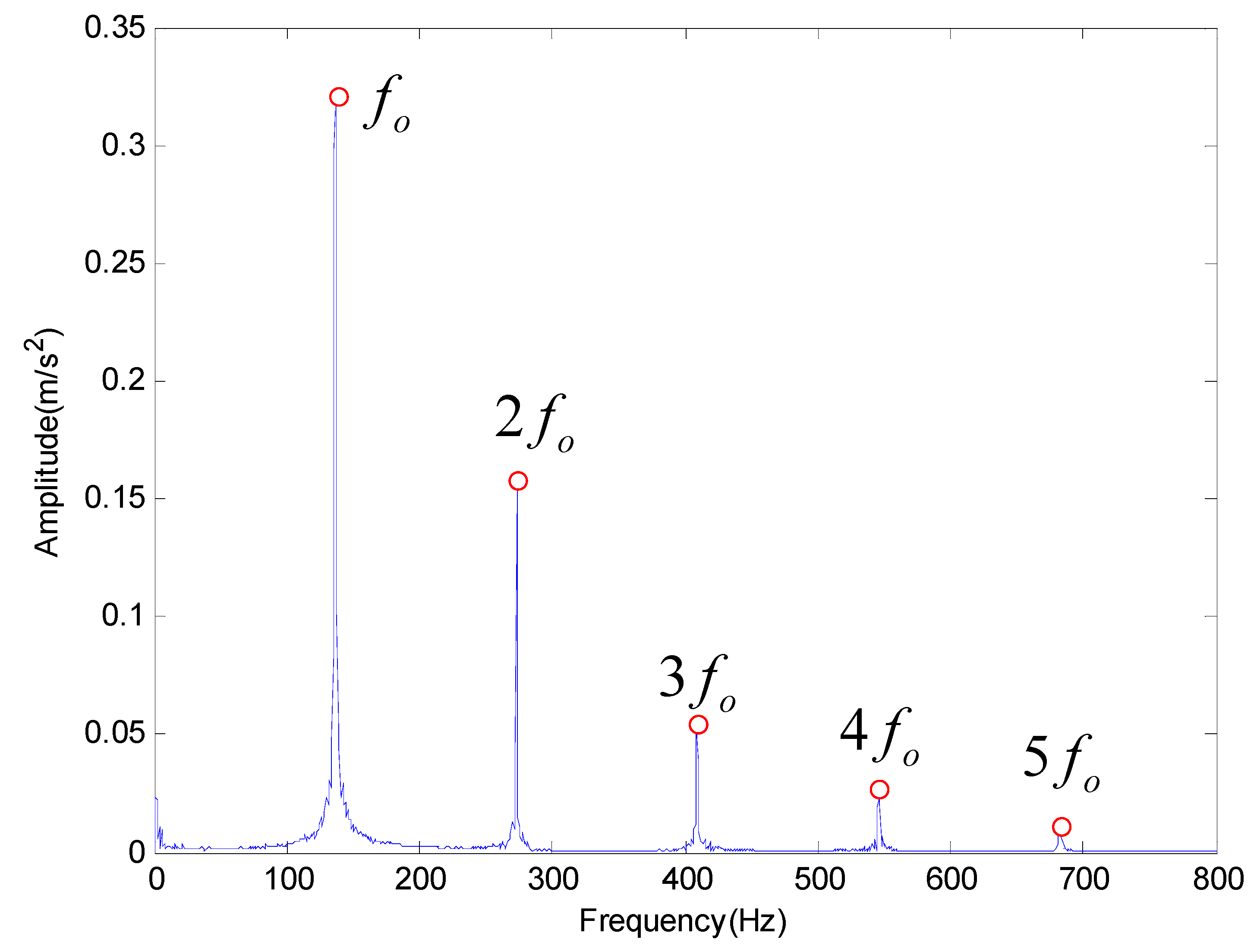
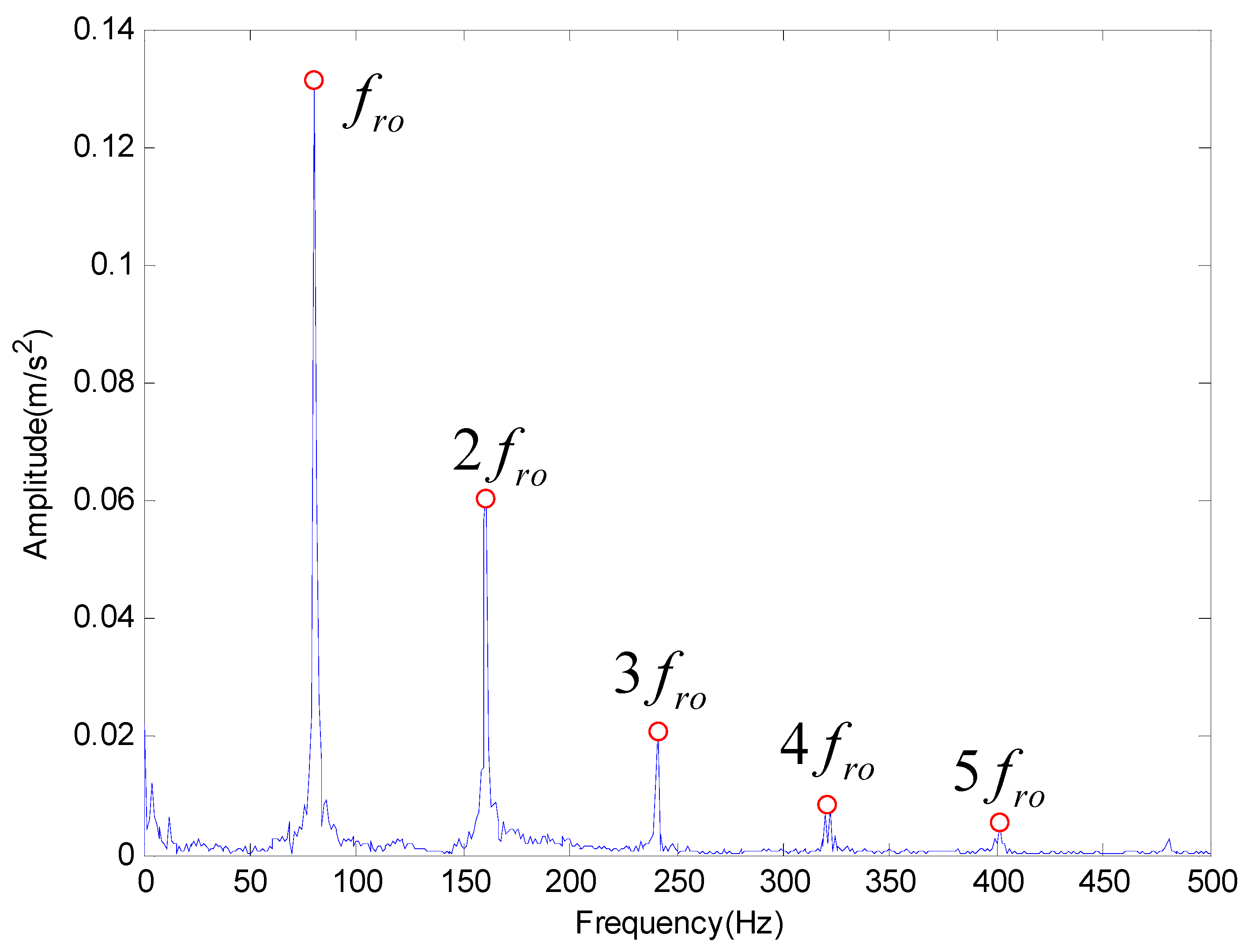
| Inner Race Frequency (Hz) | Outer Race Frequency (Hz) | Rolling Element Frequency (Hz) |
|---|---|---|
| 180 | 135 | 80 |
| (Hz) | (Hz) | (Hz) | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 20 | 20 | 2048 | 800 | 0.01 | 1 | 0 | 0 |
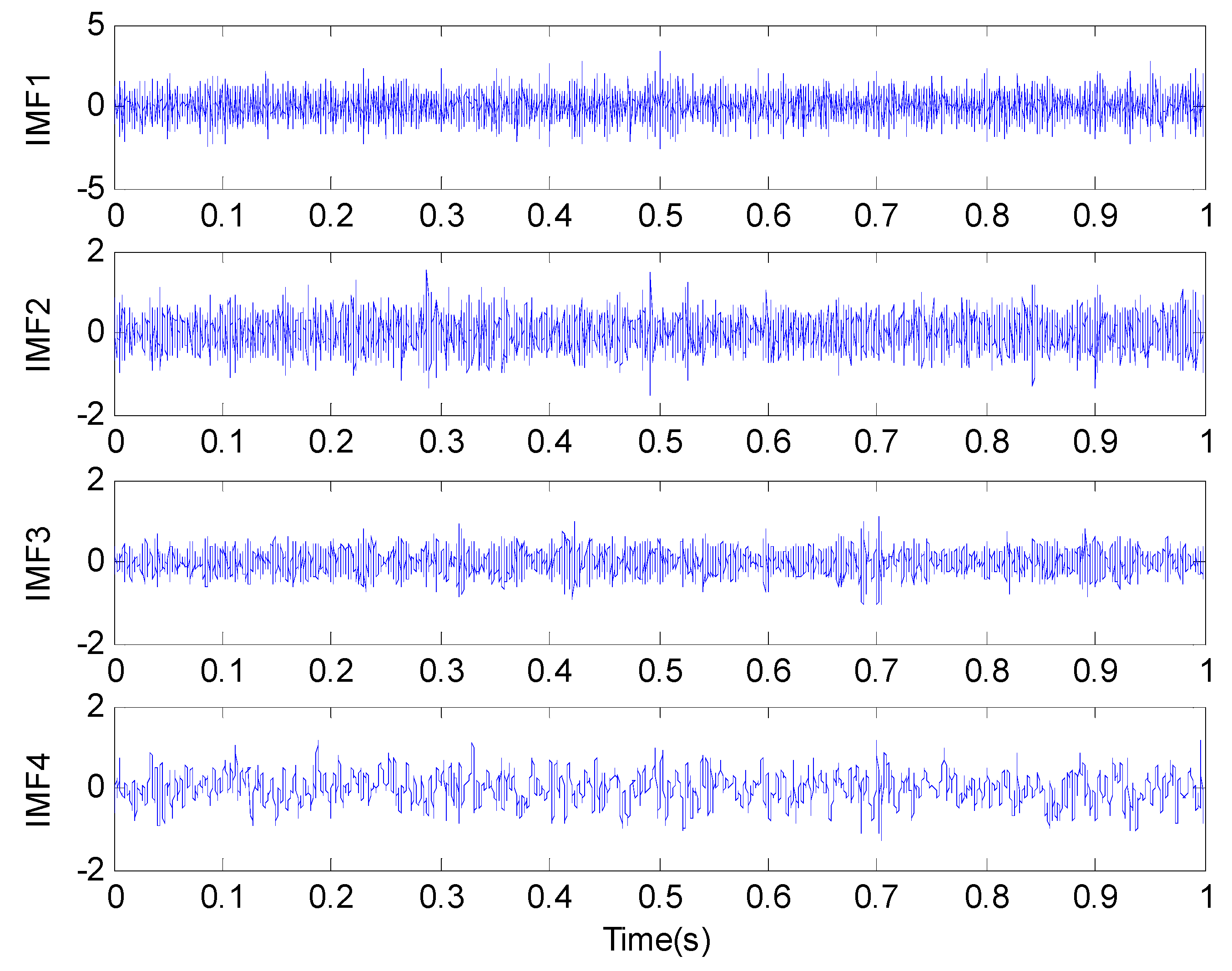
| IMF Order | 1 | 2 | 3 | 4 |
| PE Value | 0.8887 | 0.7072 | 0.5184 | 0.3754 |
| Bearing Type | Outside Diameter d2/mm | Ball Diameter/mm | Ball Number n | Contact Angle α |
|---|---|---|---|---|
| ZA2115 | 71.5 | 8.4 | 16 | 15.17 |
| Group | Sample Channels | Fault Description |
|---|---|---|
| Group 1 | 8 | Inner race defect that occurred in bearing 3 and roller element defect occurred in bearing 4. |
| Group 2 | 4 | Outer race failure that occurred in bearing 1. |
| Group 3 | 4 | Outer race failure that occurred in bearing 3. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Zhang, Y.; Yi, C. Optimized Adaptive Local Iterative Filtering Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2018, 20, 920. https://doi.org/10.3390/e20120920
Lv Y, Zhang Y, Yi C. Optimized Adaptive Local Iterative Filtering Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy. 2018; 20(12):920. https://doi.org/10.3390/e20120920
Chicago/Turabian StyleLv, Yong, Yi Zhang, and Cancan Yi. 2018. "Optimized Adaptive Local Iterative Filtering Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis" Entropy 20, no. 12: 920. https://doi.org/10.3390/e20120920
APA StyleLv, Y., Zhang, Y., & Yi, C. (2018). Optimized Adaptive Local Iterative Filtering Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy, 20(12), 920. https://doi.org/10.3390/e20120920






