Abstract
In this work we study the distributed representations learnt by generative neural network models. In particular, we investigate the properties of redundant and synergistic information that groups of hidden neurons contain about the target variable. To this end, we use an emerging branch of information theory called partial information decomposition (PID) and track the informational properties of the neurons through training. We find two differentiated phases during the training process: a first short phase in which the neurons learn redundant information about the target, and a second phase in which neurons start specialising and each of them learns unique information about the target. We also find that in smaller networks individual neurons learn more specific information about certain features of the input, suggesting that learning pressure can encourage disentangled representations.
1. Introduction
Neural networks are famously known for their excellent performance, yet are infamously known for their thin theoretical grounding. While common deep learning “tricks” that are empirically proven successful tend to be later discovered to have a theoretical justification (e.g., the Bayesian interpretation of dropout [1,2]), deep learning research still operates “in the dark” and is guided almost exclusively by empirical performance.
One common topic in learning theory is the study of data representations, and in the case of deep learning it is the hierarchy of such representations that is often hailed as the key to neural networks’ success [3]. More specifically, disentangled representations have received increased attention recently [4,5,6], and are particularly interesting given their reusability and their potential for transfer learning [7,8]. A representation can be said to be disentangled if it has factorisable or compositional structure, and has consistent semantics associated to different generating factors of the underlying data generation process.
In this article we explore the evolution of learnt representations in the hidden layer of a restricted Boltzmann machine as it is being trained. Are groups of neurons correlated or independent? To what extent do neurons learn the same information or specialise during training? If they do so, when? To answer these questions, we need to know how multiple sources of information (the neurons) contribute to the correct prediction of a target variable—which is known as a multivariate information problem.
To this end, the partial information decomposition (PID) framework by Williams and Beer [9], which seeks a rigorous mathematical generalisation of mutual information to the multivariate setting, provides an excellent foundation for this study [9]. In PID, the information that multiple sources contain about a target is decomposed into unique non-negative information atoms, the distribution of which gives insight into the interactions between the sources.
1.1. Why Information Theory?
Information theory was developed to optimise communication through noisy channels, and it quickly found other areas of application in mathematical and computer sciences. Nevertheless, it is not commonly linked to machine learning, and it is not part of the standard deep learning engineer’s toolkit or training. So why, then, is information theory the right tool to study neural networks?
To answer that question, we must first consider some of the outstanding theoretical problems in deep learning: what kind of stimuli do certain neurons encode; how do different layers compress certain features of an input image; or how can we transfer learnt information from one dataset to another?
These problems (encodings, compression, transfer) are precisely among the problems information theory was made to solve. Casting these questions within the established framework of information theory gives us a solid language to reason about these systems and a comprehensive set of quantitative methods to study them.
We can also motivate this choice from a different perspective: in the same way as neuroscientists have been using information theory to study computation in biological brains, here we try to understand an artificially developed neural code [10]. Although the code used by artificial neural networks is most likely much simpler than the one used by biological brains, deep learning researchers can benefit from the neuroscientists’ set of tools.
1.2. Related Work
When it comes to representations, the conventional way of obtaining insights about a network has typically been through visualisation. Famously, Le et al. [11] trained a neural network on web-scraped images and reported finding neural receptive fields consisting mostly of human faces, human bodies and cat faces [11]. Later, Zeiler and Fergus [12] devised a technique to visualise the features learnt by neurons in hidden layers, and provided good qualitative evidence to support the long-standing claim that deeper layers learn increasingly abstract features of the input [12].
While visualisation is a great exploration tool, it provides only qualitative insights and is therefore unable to make strong statements about the learning dynamics. Furthermore, as later work showed, the specific values of weights are highly sensitive to the details of the optimisation algorithm used, and therefore cannot be used to make definite judgements about the network’s behaviour [13,14].
More recently, there is a small line of emerging work investigating the behaviour of neural networks from an information-theoretic perspective [15,16,17,18,19,20], with some work going as far back as [21]. The most relevant of these is the work by Schwartz-Ziv and Tishby [16], who show that feed-forward deep neural networks undergo a dynamic transition between drift- and diffusion-like regimes during training.
The main contribution of this article is to show how PID can be used for the analysis of learning algorithms, and its application to neural generative models. The results of our PID analysis show two distinct learning phases during the optimisation of the network, and a decrease in the specialisation of single neurons in bigger networks.
2. Methods
2.1. Restricted Boltzmann Machines
We deal with the problem of multiclass classification, in which we have a dataset of tuples, where y is a discrete label (also called the target variable) and is a vector of predictor variables. The goal is to learn an approximation to the joint distribution of the predictors and the labels, . We will use a class of neural generative models known as Boltzmann machines.
Boltzmann machines (BMs) are energy-based probabilistic graphical models, the origin of which goes as far back as Paul Smolensky’s Harmonium [22]. Of particular interest are the so-called restricted Boltzmann machines (RBMs). These are called restricted because all the nodes in the model are separated in two layers, and intra-layer connections are prohibited. These typically receive the names of visible and hidden layers.
In this article we follow [23] and perform classification with a discriminative RBM (DRBM). To do this, we introduce the vector of target classes y as part of the visible layer, such that the DRBM represents the joint distribution over the hidden, visible, and target class variables. The distribution parametrized by the DRBM is:
where is the DRBM energy function, given by
where for the C different classes. For comparison, the energy function for a standard RBM is the same but with the last two terms removed. Figure 1 shows a schematic diagram of a DRBM and the variables involved.
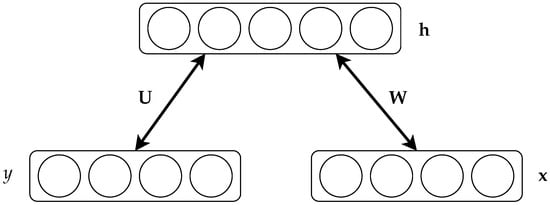
Figure 1.
Graphical representation of the discriminative restricted Boltzmann machine (DRBM) and its components. Vectors and correspond to the training input and label, respectively, is the activation of the hidden neurons, and and are the weight matrices to be learned. (Adapted from [23]).
Now that the model is specified, we calculate the predictive posterior density given DRBM parameters . At this point, the restricted connectivity of RBMs comes into play—this connectivity induces conditional independence between all neurons in one layer given the other layer. This resulting intra-layer conditional independence allows us to factorise and to write the following conditional distributions [24]:
where is the standard sigmoid function. With these equations at hand, we can classify a new input vector by sampling from the predictive posterior , or we can sample from the joint distribution via Gibbs sampling.
Finally, the network needs to be trained to find the right parameters that approximate the distribution of the data. We use a standard maximum likelihood objective function,
Gradients of this objective cannot be obtained in closed form, and we must resort to contrastive sampling techniques. In particular, we use the constrastive divergence (CD) algorithm [24] to estimate the gradient, and we apply fixed-step size stochastic gradient updates to all parameters in the network. The technical details of CD and other contrastive sampling estimators are outside the scope of this paper, and the interested reader is referred to the original publications for more information [24,25].
2.2. Information Theory
In this section we introduce a few relevant tools from information theory (IT) that we will use to analyse the networks trained as explained in the previous section. For a broader introduction to IT and more rigorous mathematical detail, we refer the reader to [26].
We focus on systems of discrete variables with a finite number of states. Throughout the paper we will deal with the scenario in which we have one target variable and a number of source variables. We refer to the target variable as Y (matching the nomenclature in Section 2.1), to the source variables as , and let Z denote generically any nonempty subset of the set of all sources. Summations always run over all possible states of the variables considered.
Mutual information (MI) is a fundamental quantity in IT that quantifies how much information is shared between two variables Z and Y, and is given by
MI can be thought of as a generalised (non-linear) correlation, which is higher the more a given value of Z constrains possible values of Y. Note that this is an average measure—it quantifies the information about Y gained when observing Z on average. In a similar fashion, specific information [27] quantifies the information contained in Z associated with a particular outcome y of Y, and is given by
Specific information quantifies to what extent the observation of Z makes outcome y more likely than otherwise expected based on the prior . Conveniently, MI can easily be written in terms of specific information as
2.2.1. Non-Negative Decomposition of Multivariate Information
In this section we discuss the main principles of the PID framework proposed by Williams and Beer [9]. Technical details will not be covered, and the interested reader is referred to the original paper [9].
The goal of PID is to decompose the joint mutual information that two or more sources have about the target, , into interpretable non-negative terms. For simplicity, we present the two-variable case here, although the framework applies to an arbitrary number of sources. In the two-variable PID (or PI-2), there are three types of contributions to the total information of about Y which form the basic atoms of multivariate information:
- Unique information U one of the sources provides and the other does not.
- Redundant information R both sources provide.
- Synergistic information S the sources provide jointly, which is not known when either of them is considered separately.
There is a very intuitive analogy between this decomposition and set theory—in fact, the decomposition for any number of variables can be shown to have a formal lattice structure if R is mapped to the set intersection operation. This mapping corresponds to the intuitive notion that R should quantify the overlapping information of and . Consequently, these quantities can be represented in a Venn diagram called the PI diagram, shown in Figure 2.
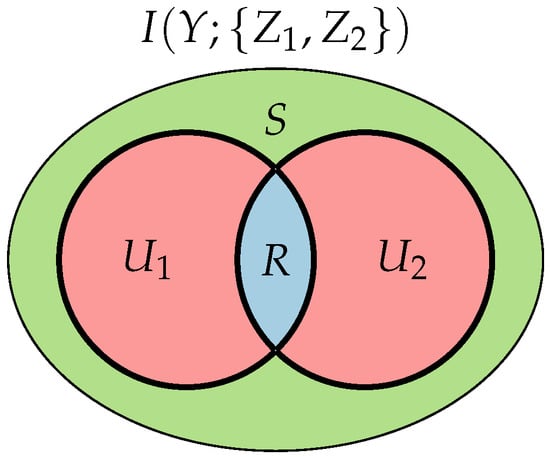
Figure 2.
Partial information (PI) diagram for two source variables and a target. The outer ellipse corresponds to the mutual information (MI) between both sources and the target, , and both inner circles (highlighted in black) to the MI between each source and the target, . Coloured areas represent the PI terms described in the text.
Mathematically, the relation between MI and S, R, and U (which we refer to jointly as PI terms) can be written as follows:
This is an underdetermined system of three equations with four unknowns, which means the PI decomposition in itself does not provide a method to calculate the PI terms. To do that, we need to specify one of the four variables in the system, typically by providing an expression to calculate either R or S. There are a number of proposals in the literature [28,29,30,31], but at the time of writing there is no consensus on any one candidate.
In this study we follow the original proposal by Williams and Beer [9] and use as a measure of redundancy, defined as
where is the specific information in Equation (6). (In fact, in their original article DeWeese and Meister [27] propose two quantities to measure “the information gained from one symbol”: specific information and specific surprise. Confusingly, Williams and Beer’s specific information is actually DeWeese and Meister’s specific surprise.) Despite the known flaws of , we chose it for its tractability and inclusion-exclusion properties. With this definition of redundancy and the standard MI expression in Equation (5), we can go back to system (7) and calculate the rest of the terms.
While all the terms in PI-2 can be readily calculated with the procedure above, with more sources, the number of terms explodes very quickly—to the point that the computation of all PI terms is intractable even for very small networks. Conveniently, with , we can compute the overall redundancy, synergy, and unique information terms for arbitrarily many sources—restricted only by the computational cost and amount of data necessary to construct large joint probability tables. We write here the overall redundancy, synergy, and unique information equations for completeness, but the interested reader is referred to [32] for a full derivation:
where is defined exactly the same as , except substituting max for min [32].
3. Results
Instead of generating a synthetic dataset, we used the MNIST dataset of hand-written digits. We used a stochastic binarised version of MNIST—every time an image was fed as input to the network, the value of each pixel was sampled from a binomial distribution with a probability equal to the normalised intensity of that pixel. Then, we used Equations (3) to sample the state of the network, and repeated this process to build the probability distributions of interest.
For training, the gradients were estimated with contrastive divergence [24] and the weights were optimised with vanilla stochastic gradient descent with fixed learning rate (0.01). We did not make strong efforts to optimise the hyperparameters used during training.
To produce the results below, we trained an ensemble of 100 RBMs and took snapshots of these networks during training. Each RBM in the ensemble was initialised and trained separately using a different random number generator seed. All information-theoretic measures are reported in bits and debiased with random permutation tests. To debias the estimation of any measure on a given set of data, we generated many surrogate data sets by randomly permuting the original data, calculating the mean of the measure across all surrogates, and subtracting this from the original estimation on the unshuffled data [33].
3.1. Classification Error and Mutual Information
First, we trained a small RBM with 20 hidden neurons and inspected its learning curve during training. In Figure 3, we show the classification error and the mutual information between the predicted labels and the real labels Y during training, averaged for the ensemble of 100 RBMs.
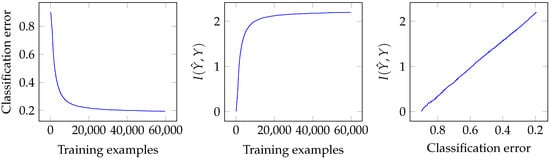
Figure 3.
Classification error and mutual information between real and predicted labels, , calculated through training. Note: X-axis in the rightmost plot is reversed for illustration pusposes, so that training time goes from left to right.
As expected, classification error decreased and MI increased during training, the relationship between the two being an almost perfect line. This gives us an intuitive correspondence between a relatively abstract measure like bits and a more easily interpretable measure like error rate. We note that a perfect classifier with 0 error rate would have 3.32 .
As should be apparent to any occasional reader of the machine learning literature, the classification error presented in Figure 3 is worse than the authors reported originally in [23], and significantly worse than the state of the art on this dataset. The main reason for this is that we are restricting our network to a very small size to obtain a better resolution of the phenomena of interest.
3.2. Phases of Learning
In this section we investigate the evolution of the network through training, and show three complementary pieces of evidence for the existence of two separate learning phases. We describe the main results illustrated in Figure 4 and Figure 5.
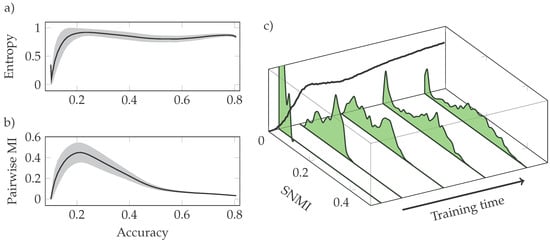
Figure 4.
Single-neuron entropy and mutual information follow non-trivial patterns during training. (a) Entropy quickly rises up to close to its maximum value of 1 bit. (b) Inter-neuron correlation as measured by pairwise MI peaks midway through training. (c) Histograms of single-neuron MI (SNMI) split midway through training, implying that some neurons actually lose information. Average SNMI is shown in black projected on the frame box.
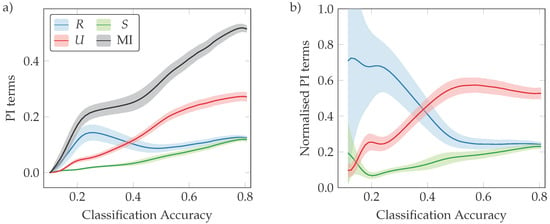
Figure 5.
PI terms (a) and PI terms normalised by joint mutual information (b). Mutual information (MI) in black, redundancy (R) in blue, synergy (S) in green, and unique information (U) in red. MI increases consistently during training, but the PI terms reveal a transition between a redundancy-dominated phase and a unique-information-dominated phase.
First, in Figure 4a, we show the evolution of the average entropy of single neurons in the hidden layer, where the average is taken over all neurons in the same network. Entropy increases rapidly at the start of training until it settles around the 0.8 to 0.9 bit range, relatively close to its maximum possible value of 1 bit. This means that throughout most of the training (including the final state), most of the informational capacity of the neurons was being actively used—if this were not the case, in a network with low entropy in which most neurons do not change their states much, the encoding capability of the network would be heavily reduced.
As a measure of inter-neuron correlation, we calculated the average pairwise mutual information (PWMI) between hidden neurons , defined as
PWMI is shown in Figure 4b, and is the first sign of the transition mentioned above—it increases rapidly at the start, it reaches a peak at an intermediate point during training, and then decays back to near zero.
Next, we calculate the average MI between a single hidden neuron and the target, , which we refer to as single-neuron mutual information (SNMI), and show the results in Figure 4c. As expected, at first neurons barely have any information about the target, and early in training we see a quick uniform increase in SNMI.
Remarkably, at the transition point there is a split in the SNMI histogram, with around half of the neurons reverting back to low values of SNMI and the other half continuing to increase. At the whole network level, we do not find any sign of this split, as shown by the monotonically decreasing error rate in Figure 3. This is a seemingly counterintuitive finding—some neurons actually get worse at predicting the target as the network learns. We currently do not have a solid explanation for this phenomenon, although we believe it could be due to the effects of local minima or to the neurons relying more on synergistic interactions at the cost of SNMI, as suggested by the results below.
After exploring the behaviour of individual neurons, we now turn to PID and study the interactions between them when predicting the target. Since a full PID analysis of the whole network is intractable, we follow a procedure inspired by [34] to estimate the PI terms of the learnt representation: we sample pairs of neurons, calculate the PI terms for each of them, apply random permutation correction to each pair separately, and finally compute averages over all pairs. We present results obtained with following Section 2.2.1, but qualitatively identical results are obtained if the more modern measures in [28,35] are used.
We calculate synergy S, redundancy R, and total unique information , as well as their normalised versions calculated by dividing S, R, or U by the joint mutual information . Results are depicted in Figure 5, and error intervals shown correspond to two standard deviations across pairs.
Here we see again a transition between two phases of learning. Although synergy and joint MI increase steadily at all times, there is a clear distinction between a first phase dominated by redundancy and a second one dominated by unique information. It is at this point that neurons specialise, suggesting that this is when disentangled representations emerge.
These three phenomena (peak in PWMI, split SNMI histogram, and redundant-unique information transition) do not happen at the same time. In the figures shown, the peak in PWMI marks the onset of the decline of redundancy, and the split in SNMI happens between then and the point when redundancy is overtaken by unique information. However, this is a consistent pattern we have observed in networks of multiple sizes, and in bigger networks these three events tend to come closer in time (results not shown).
We note that there is a relation between PWMI and R and between SNMI and U. As indicated in Equation (7), SNMI is an upper bound on that neuron’s unique information; and usually, higher PWMI comes with higher redundancy between the neurons. However, although they follow similar shapes, these magnitudes do not quantify the same thing. Take the OR logical gate as an example—if we feed it a uniform distribution of all possible inputs (00, 01, 10, 11), both input bits will be perfectly uncorrelated, yet their redundancy (according to ) will be nonzero.
These findings are in line with those of Schwartz-Ziv and Tishby [16], who observe a similar transition in a feed-forward neural network classifier. One of the pieces of evidence for Schwartz-Ziv and Tishby’s [16] claim is in the change of gradient signal dynamics from a drift to a diffusion regime. We did not analyse gradient dynamics as part of this study, but investigating the relationship between informational and dynamical accounts of learning is certainly a promising topic.
3.3. Neural Interactions
In this last set of experiments, we examine the representations learnt jointly by larger groups of neurons. Due to computational constraints, we run the analyses only on fully trained networks instead of at multiple points during training. We train networks of different sizes, ranging from 20 to 500 hidden neurons (using the same algorithm, but allowing each network to train for more epochs until convergence), and consider larger groups of neurons for the PID analysis. We use a procedure similar to the one used in the previous section, but this time sampling tuples of K neurons, and calculating their overall synergy following Equation (9). We refer to this as the PI-K synergy. Results are shown in Figure 6.
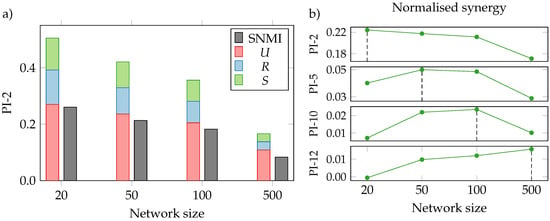
Figure 6.
Partial information decomposition (PID) analysis of larger groups of neurons in networks of different sizes. (a) Single-neuron MI is consistently smaller in bigger networks, indicating that, although the network as a whole is a better classifier, each individual neuron has a less-efficient encoding; (b) Normalised PI-K synergy, with network size increasing from left to right and K from top to bottom. Network with maximum synergy for each PI-K highlighted with a vertical dashed line. The PI group size with the highest synergy becomes larger in larger networks, indicating that in bigger networks one needs to consider larger groups to capture strong cooperative interactions.
The first result in Figure 6a is that SNMI decreases consistently with network size. This represents reduced efficiency in the neurons’ compression—despite the overall accuracy of the network being significantly higher for bigger networks (∼20% error rate for a network with 20 hidden neurons vs. ∼5% for a network with 500), each individual neuron contains less information about the target. This suggests that the representation is more distributed in bigger networks, as emphasised below.
What is somewhat counterintuitive is that normalised unique information actually grows in bigger networks, which is apparently in contradiction with more distributed representations. However, these two are perfectly compatible—bigger networks have more and less correlated neurons, and despite U growing relative to S and R, it still decreases significantly in absolute terms. Note that the U term plotted in Figure 6 is the sum of the unique information of both neurons in the pair; naturally, for one neuron , Equation (7).
Interestingly, Figure 6b shows that the network size that achieves maximum normalised synergy shifts to the right as we inspect larger groups of neurons. For bigger networks, bigger groups carry more synergistic information, meaning that representations also become more distributed. There is a consistent pattern that in bigger networks we need to explore increasingly high neural groups to see any meaningful PI values, which means that perhaps part of the success of bigger networks is that they make better use of higher-order correlations between hidden neurons. This can be seen as a signature of bigger networks achieving richer and more complex representations [36].
3.4. Limitations
The main limitation of the vanilla PID formulation is that the number of PI terms scales very rapidly with bigger group sizes—the number of terms in the PI decomposition of a system with n sources is the -st Dedekind number, which is 7579 terms for a five-variable system and has not been computed yet for systems of more than eight variables. For this reason, we have restricted our analyses mostly to pairs of neurons, although in practice we expect larger groups of neurons to have strong effects on the prediction. Potentially some approximation to the whole PID or a reasonable grouping of PI terms could help scale this type of analysis to larger systems.
On a separate topic, some of the phenomena of interest we have described in this article (two phases of learning, peak in correlation between the neurons) happen very early on during training, in practice. In a real-world ML setting, most of the time is spent in the last phase where error decreases very slowly; and so far, we have not seen any unusual behaviour in that region. Future work should focus on this second phase and try to characterise it in more detail, with the aim of improving performance or speeding convergence.
4. Conclusions
In this article we have used information theory—in particular the partial information decomposition framework—to explore the latent representations learned by a restricted Boltzmann machine. We have found that the learning process of neural generative models has two distinct phases: a first phase dominated by redundant information about the target, and another phase in which neurons specialise and each of them learns unique information about the target and synergy. This is in line with the findings of Schwartz-Ziv and Tishby [16] in feed-forward networks, and we believe further research should explore the differences between generative and discriminative models in this regard.
Additionally, we found that representations learned by bigger networks are more distributed, yet significantly less efficient at the single-neuron level. This suggests that the learning pressure of having fewer neurons encourages those neurons to specialise more, and therefore yields more disentangled representations. The interesting challenge is to find a principled way of encouraging networks towards disentangled representations while preserving performance.
An interesting piece of follow-up work would be to investigate whether these findings generalise to other deep generative models—most notably, variational autoencoders [37]. We believe that further theoretical study of these learning systems is necessary to help us understand, interpret, and improve them.
Acknowledgments
The authors would like to thank Raúl Vicente for insightful discussions, and Pietro Marchesi for valuable feedback in the early stages of this project.
Author Contributions
Tycho M.S. Tax and Pedro A.M. Mediano designed the experiments; Tycho M.S. Tax performed the experiments; Tycho M.S. Tax and Pedro A.M. Mediano analysed the results; and Pedro A.M. Mediano, Tycho M.S. Tax and Murray Shanahan wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. arXiv 2015, arXiv:1206.5538. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. arXiv 2012, arXiv:1206.5538. [Google Scholar] [CrossRef] [PubMed]
- Higgins, I.; Matthey, L.; Glorot, X.; Pal, A.; Uria, B.; Blundell, C.; Mohamed, S.; Lerchner, A. Early Visual Concept Learning with Unsupervised Deep Learning. arXiv 2016, arXiv:1606.05579. [Google Scholar]
- Mathieu, M.; Zhao, J.; Sprechmann, P.; Ramesh, A.; LeCun, Y. Disentangling Factors of Variation in Deep Representations Using Adversarial Training. arXiv 2016, arXiv:1611.03383. [Google Scholar]
- Siddharth, N.; Paige, B.; Van de Meent, J.W.; Desmaison, A.; Wood, F.; Goodman, N.D.; Kohli, P.; Torr, P.H.S. Learning Disentangled Representations with Semi-Supervised Deep Generative Models. arXiv 2017, arXiv:1706.00400. [Google Scholar]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building Machines That Learn and Think Like People. arXiv 2016, arXiv:1604.00289. [Google Scholar] [CrossRef] [PubMed]
- Garnelo, M.; Arulkumaran, K.; Shanahan, M. Towards Deep Symbolic Reinforcement Learning. arXiv 2016, arXiv:1609.05518. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Rieke, F.; Bialek, W.; Warland, D.; de Ruyter van Steveninck, R. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1997; p. 395. [Google Scholar]
- Le, Q.V.; Ranzato, M.; Monga, R.; Devin, M.; Chen, K.; Corrado, G.S.; Dean, J.; Ng, A.Y. Building High-Level Features Using Large Scale Unsupervised Learning. arXiv 2011, arXiv:1112.6209. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin, Germany, 2014; pp. 818–833. [Google Scholar]
- Choromanska, A.; Henaff, M.; Mathieu, M.; Arous, G.B.; LeCun, Y. The Loss Surfaces of Multilayer Networks. arXiv 2014, arXiv:1412.0233. [Google Scholar]
- Kawaguchi, K. Deep Learning Without Poor Local Minima. arXiv 2016, arXiv:1605.07110. [Google Scholar]
- Sørngård, B. Information Theory for Analyzing Neural Networks. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Schwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Achille, A.; Soatto, S. On the Emergence of Invariance and Disentangling in Deep Representations. arXiv 2017, arXiv:1706.01350. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar]
- Berglund, M.; Raiko, T.; Cho, K. Measuring the Usefulness of Hidden Units in Boltzmann Machines with Mutual Information. Neural Netw. 2015, 64, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Frean, M.; Leary, L.; Lewis, J.; Ma, K.W.D.; McWilliams, B. The Shattered Gradients Problem: If Resnets are the Answer, Then What is the Question? arXiv 2017, arXiv:1702.08591. [Google Scholar]
- Hinton, G.E.; van Camp, D. Keeping the Neural Networks Simple by Minimizing the Description Length of the Weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory (COLT), Santa Cruz, CA, USA, 26–28 July 1993; ACM: New York, NY, USA, 1993; pp. 5–13. [Google Scholar]
- Smolensky, P. Information Processing in Dynamical Systems: Foundations of Harmony Theory; Technical Report, DTIC Document; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Larochelle, H.; Bengio, Y. Classification Using Discriminative Restricted Boltzmann Machines. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 536–543. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, T. Training Restricted Boltzmann Machines Using Approximations to the Likelihood Gradient. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM Press: New York, NY, USA, 2008; pp. 1064–1071. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- DeWeese, M.R.; Meister, M. How to Measure the Information Gained from one Symbol. Netw. Comput. Neural Syst. 1999, 12, 325–340. [Google Scholar] [CrossRef]
- Ince, R.A.A. Measuring Multivariate Redundant Information with Pointwise Common Change in Surprisal. Entropy 2017, 19. [Google Scholar] [CrossRef]
- Griffith, V.; Ho, T. Quantifying Redundant Information in Predicting a Target Random Variable. Entropy 2015, 17, 4644–4653. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate Measure of Redundant Information. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer: Berlin, Germany, 2013; pp. 251–269. [Google Scholar]
- Williams, P.L. Information Dynamics: Its Theory and Application to EmbodiedCognitive Systems. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 2011. [Google Scholar]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, Redundancy, and Multivariate Information Measures: An Experimentalist’s Perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Montúfar, G.; Ay, N.; Ghazi-Zahedi, K. Geometry and Expressive Power of Conditional Restricted Boltzmann Machines. J. Mach. Learn. Res. 2015, 16, 2405–2436. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).