Abstract
There are numerous examples that show how the exploitation of the body’s physical properties can lift the burden of the brain. Examples include grasping, swimming, locomotion, and motion detection. The term Morphological Computation was originally coined to describe processes in the body that would otherwise have to be conducted by the brain. In this paper, we argue for a synergistic perspective, and by that we mean that Morphological Computation is a process which requires a close interaction of body and brain. Based on a model of the sensorimotor loop, we study a new measure of synergistic information and show that it is more reliable in cases in which there is no synergistic information, compared to previous results. Furthermore, we discuss an algorithm that allows the calculation of the measure in non-trivial (non-binary) systems.
1. Introduction
There are numerous examples that show how the exploitation of the body’s physical properties can lift the burden of the brain. Examples range from grasping [1,2,3], swimming [4,5,6], locomotion [7,8,9,10], to motion detection [11]. Probably the most prominent example in this field is the Passive Dynamic Walker [9], which is a purely mechanical system that mimics human walking. It has carefully chosen length and weight proportions of the leg segments, as well as carefully designed feet. If placed on a slope, it will show a natural, appealing walking behaviour, which is a strong indication that human walking does not have to be fully controlled, but that part of it can result from physical interactions of the legs (weight, friction, etc.) with their environment (slope, gravity, etc.). Another impressive example is human grasping which exploits at least two different physical interactions. First, as a result of the skin’s softness and friction, even fragile objects can be hold securely with some variation of grip posture and grip pressure. This means that the brain does not have to carefully control the position of the fingers, the tightness of the grasp, and, in particular, does not have to precisely estimate the shape of the object. This leads to a significant reduction of the computational burden for the brain in grasping. The second effect that is used is the friction in the hand’s tendon network, which has been shown to perform logic computation and affect torque production capabilities [2].
The term Morphological Computation [12] was originally coined to describe processes in the body that would otherwise have to be conducted by the brain [13]. One of the main questions that arises, and is so far unsolved, regards the distinction between the Passive Dynamic Walker and a ball rolling downhill. Both cases are purely mechanical systems, but one would assign morphological computation to the Passive Walker, whereas one would generally have difficulties in stating that the ball is performing computation or reducing the computational complexity for a brain. There are three possible solutions to this problem. Their relation to synergy will be addressed below. First, as argued in [14,15], the Passive Walker itself is not performing computation, but it shows that morphological computation can be present in human walking. Second, the definition of physical computation [16] offers a possibility to distinguish between pure physics and physical computation. Physical computation requires four ingredients. First, a function that encodes the data of the user into an initial state of the system, second, a physical process that transforms the initial state into some target state, third, a decoding function that transforms the target state back into something that the user can process, and, finally, a theory about how the system works. The implications of this theory of physical computation, in particular with respect to morphological computation, are discussed in [17]. With respect to the ball and the Passive Walker, the theory of [16] would lead to the conclusion that both are computing if there is a user that translates their states, e.g., to measure the slope. This is in accordance with the initial definition given by [12] and is also used as a basis for [18,19], which are discussed below. The third possibility can be summarised in the following way (cited from [20]): “nonneural body parts could be described as parts of a computational system, but they do not realise computation autonomously, only in connection with some kind of […] central control system.” If we now compare the three different approaches, they don’t seem to be entirely different. All three cases argue that morphological computation requires the interaction of a brain with the body. In the context of this work, this is understood as a synergistic perspective on morphological computation. This will be explained in more detail, after related work on formalising morphological computation is presented next.
Pfeifer and Iida [21] state that “One problem with the concept of morphological computation is that while intuitively plausible, it has defied serious quantification efforts.” Since then, there are basically two different streams of formalising morphological computation, which can be divided into a dynamical systems approach and an information theoretic approach. The two approaches do not stand in opposition but should rather be seen as complimentary [22]. The first approach [18,19] models processes in the body in the context of reservoir computing [23,24]. This means that the body is understood as a type of physical reservoir computer and the controller or brain harnesses the body dynamics to produce a behaviour. Examples are the spine-driven robot [7], which uses the spine dynamics as part of its controller and the dynamics of an octopus arm that can be used for computation [25]. Within this first approach, there are also several works that discuss the importance of a tight body–brain–environment coupling, of which the following are just a few examples [13,26,27,28,29,30,31]. Although very intuitive and compelling, this approach does not allow to quantify how the body reduces the computational burden of the brain. This is the motivation for the second, information theoretic approach [15]. The guiding idea is to model the sensorimotor loop as a causal graph [32] (details will follow below) and, based on that, ask how much internal processes (with respect to the agent’s perspective) contributed to an observed behaviour, as opposed to body–environment interactions. The information theoretic measures have been successfully applied to quantify morphological computation in muscle models [14] and soft robotics [1] and relations have been drawn to unique and synergistic information [33] based on the work by [34]. Unfortunately, at that time, the synergistic information could only be calculated for simple binary models of the sensorimotor loop, which prohibited a further investigation in non-trivial systems or even real data. This is where this work is targeted at. Based on the complexity measure by Ay [35] and Perrone and Ay [36], we investigate synergistic information in binary and non-binary models of the sensorimotor loop and compare the results to our previous work in [33].
This work is organised in the following way. Section two discusses in detail the relation between synergistic information and morphological computation, based on previous work and the causal model of the sensorimotor loop. The third section presents the parametrised model of the sensorimotor loop, which is used to analyse and compare the new measure with previous work. The fourth section presents numerical results which are discussed in the final section.
2. A Synergistic Perspective on Morphological Computation
The introduction gave a motivation to understand morphological computation as a process that occurs as the result of some type of control that exploits physical properties of the body. This is one way to distinguish morphological computation from purely physical processes and can be understood as a synergistic coupling of brain and body that is required for morphological computation. This section will give a formal motivation to quantifying morphological computation as synergistic information, which is based on our previous work [15,33]. For a derivation of an information theoretic quantification, it is helpful to have a causal model of the sensorimotor loop [32], which is presented first.
2.1. Causal Model of the Sensorimotor Loop
We assume that there is a canonical way to separate a cognitive system into four parts, namely brain, sensors, actuators, and body. We are fully aware that the system–environment separation is a very difficult and yet unsolved question for biological systems (see e.g., [37] for a discussion). This holds even more in the case of the distinction between the body and brain. Yet, in order to derive a quantification, we have to assume that there is such a distinction.
In our conceptual model of the sensorimotor loop, which is derived from [22], the brain or controller sends signals to the actuators that influence the environment (see Figure 1). We prefer the notion of the system’s Umwelt [31,38,39], which is the part of the system’s environment that can be affected by the system and itself affects the system. The state of the actuators and the Umwelt are not directly accessible to the cognitive system, but the loop is closed as information about both the Umwelt and the actuators are provided to the controller by the system’s sensors. In addition to this general concept, which is widely used in the embodied artificial intelligence community (see e.g., [22]), we introduce the notion of world to the sensorimotor loop, that is, the system’s morphology and the system’s Umwelt. This differentiation between body and world is analogous to the agent–environment distinction made in the context of reinforcement learning [40], where the environment is defined as everything that cannot be changed arbitrarily by the agent.
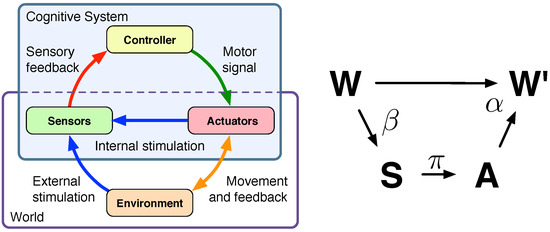
Figure 1.
Sensorimotor Loop. Left-hand side: schematics of the sensorimotor loop (redrawn from [22]), Right-hand side: causal diagram of a reactive system.
Revisiting the list of examples given in the introduction (e.g., locomotion, grasping), it is seen that most behaviours that are interesting in the context of morphological computation can be modelled sufficiently as reactive behaviours. Hence, for the remainder of this work, we will omit the controller and assume that the sensors are directly connected to the actuators. For a discussion of the causal diagram for non-reactive systems, the reader is referred to [32]. Quantifications of morphological computation for non-reactive systems are discussed in [15].
The causal diagram of the sensorimotor loop is shown on the right-hand side of Figure 1. The random variables A, S, W, and refer to actuator signals, sensor signals, and the current and next world state. Directed edges reflect causal dependencies between the random variables. The random variables S and A are not to be mistaken with the sensors and actuators. The variable S is the output of the sensors, which is available to the controller or brain, and the action A is the input that the actuators take. Consider an artificial robotic system as an example. Then the sensor state S could be the pixel matrix delivered by a camera sensor and the action A could be a numerical value that is taken by a motor controller and converted in currents to drive a motor.
Throughout this work, we use capital letters (X, Y, …) to denote random variables, non-capital letters (x, y, …) to denote a specific value that a random variable can take, and calligraphic letters (, , …) to denote the alphabet for the random variables. This means that is the specific value that the random variable X can take a time , and it is from the set . Greek letters refer to generative kernels, i.e., kernels that describe an actual underlying mechanism or a causal relation between two random variables. In the causal graphs throughout this paper, these kernels are represented by direct connections between corresponding nodes. This notation is used to distinguish generative kernels from others, such as the conditional probability of a given that w was previously seen, denoted by , which can be calculated or sampled but that does not reflect a direct causal relation between the two random variables A and W (see Figure 1).
We abbreviate the random variables for better comprehension in the remainder of this work, as all measures consider random variables of consecutive time indices. Therefore, we use the following notation. Random variables without any time index refer to time index t and hyphened variables to time index . The two variables W and refer to and , respectively.
2.2. Quantifying Morphological Computation as Synergistic Information
We can now restate the two original concepts of quantifying morphological computation [15] (see Figure 2) and also discuss their relationship to synergistic information [33] as defined by [34]. This will build the foundation for the comparison with quantifying synergistic information based on the measure proposed by [35].

Figure 2.
Visualisation of the two concepts and . Left-hand side: causal diagram for a reactive system. Centre: causal diagram assuming no effect of the action A on the next world state . Right-hand side: causal diagram assuming no effect of the previous world state W on the next world state .
The basis for both original concepts and is the world dynamics kernel , which describes how the next world states depends on the current world state W and the current action A (see Figure 1, right-hand side, and Figure 2, left-hand side, respectively). For the first concept , let us assume that there is no dependence of the next world state on the current action A. In this case, the world dynamics kernel reduces to (which is given by , see also Figure 2, centre). As a result, we would state that we have maximal morphological computation, as the system’s behaviour is not controlled by the brain at all. An example of such a system is the Passive Dynamic Walker that was discussed in the introduction of this work. We can measure how much the observed behaviour differs from this assumption with the Kullback-Leibler divergence. This leads to the following formalisation:
Unfortunately, Equation (1) is zero for maximal morphological computation, which is why we initially chose to normalise and invert it, leading to the following definition:
The second concept, starts with the opposite assumption, namely, that the current world state W does not have any influence on the next world state (see Figure 2, right-hand side). In this case, the world dynamics kernel reduces to (which is given by , see also Figure 2) and analogously to the following definition for :
The relation of the measures to transfer entropy [41,42] and the information bottleneck [43] are discussed in [15]. In the context of this work, we focus on their relation to synergistic information as defined by [34] and [35,36].
Next, we briefly restate the information decomposition by [34,44] that was used in the context of morphological computation in [33].
2.3. Synergistic Information Based on the Decomposition of the Multivariate Mutual Information
Consider three random variables and Z. Suppose that a system wants to predict the value of the random variable X, but it can only access the information in Y or Z. The question is, how is the information that Y and Z carry about X distributed over Y and Z? In general, there may be redundant or shared information (information contained in both Y and Z), but there may also be unique information (information contained in either Y or Z). Finally, there is also the possibility of synergistic or complementary information, i.e., information that is only available when Y and Z are taken together. The classical example for synergy is the XOR function: if Y and Z are binary random variables and if , then neither Y nor Z contain any information about X (in fact, X is independent of Y and X is independent of Z), but when Y and Z are taken together, they completely determine X.
The total information that contains about X can be quantified by the mutual information . However, there is no canonical way to separate these four kinds of informations. Different variations have been proposed (see e.g., [34,36,44,45,46,47]), but a final definition has yet to be found.
Mathematically, one would like to have four functions, namely shared information (), unique information of Y (), unique information of Z (), and finally synergistic information (also named complementary information in [34], ) that satisfy
It follows from the defining equations [34] and the chain rule of mutual information that an information decomposition always satisfies
Several candidates have been proposed for , , and so far (see e.g., [45,46]). A new candidate will be presented below (see Section 4.2). In this section, we will describe the decomposition of [34] that is defined in the following way.
Let be the set of all possible joint distributions of X, Y, and Z. Fix an element (the “true” joint distribution of X, Y, and Z).
Define
as the set of all joint distributions that have the same marginal distributions on the pairs and . Then
where denotes the co-information as defined in [48]. Here, a subscript Q in an information quantity means that the quantity is computed with respect to Q as the joint distribution.
In [34], the formulas for , , and are derived from considerations about decision problems in which the objective is to predict the outcome of X. In the context of morphological computation, we want to apply the information decomposition in the following way. We will set , , and . In the context of the sensorimotor loop, W and A not only have information about but they actually control . However, from an abstract point of view, the situation is similar: in the sensorimotor loop, we also expect to find aspects of redundant, unique, and complementary influence of W and A on . Formally, since everything is defined probabilistically, we can still use the same functions , , and . We believe that the arguments behind the definition of , , and remain valid in the setting of the sensorimotor loop where we need it.
The reason for investigating the unique and synergistic information is indicated in Equation (8), which we will rewrite here in terms of the sensorimotor loop in the following way:
Equation (14) shows that can be decomposed into unique and synergistic information. This also shows the advantage of the information decomposition approach as defined by [34]. Synergistic and unique information can be computed from the other, if the conditional mutual information is known. The conditional mutual information can be easily derived from observation, given that there are enough samples with respect to the dimensionality of and A. We are not only interested in mathematically rigorous definitions but also in applicability to real data. This is where the decomposition by [34] currently has a disadvantage. There is no algorithm known to us to compute synergistic and unique information for non-trivial systems, i.e., non-binary systems. For the binary model of the sensorimotor loop (see below), we used an approximation in our previous work [33] that was already described in the original paper [34]. We will compare our previous results with a new measure that can be computed also for non-trivial systems as below. However, there is a more important problem with the definitions given by [34]. They do not incorporate the probability distributions over the inputs, in this case, the random variables W and A, which means that the synergistic measure can falsely detect correlations in the input as synergistic information (this will be shown in the results section and discussed at the end of this work).
Applicability to non-trivial systems and potential false positives are the two reasons why we introduce a measure for synergistic information based on [35,36] in the remainder of this section.
2.4. Synergistic Information as the Difference between the Whole and the Sum of Its Parts
The basic idea of the complexity measure defined by [35] is summarised in the paper in the following way: “The whole is more than the sum of its elementary parts.” The underlying information theoretic idea is best explained along the schematics shown in Figure 3.
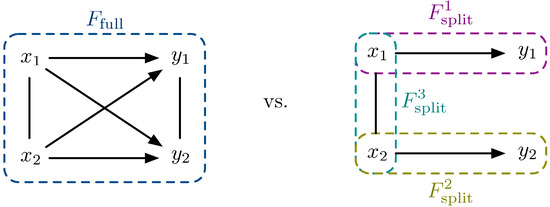
Figure 3.
Quantifying complexity. Left-hand side: full model of two input and two output variables. Right-hand side: split model, as proposed by [35].
The left-hand side of Figure 3 shows the “whole”, while the right-hand side shows “the elementary parts” of a stochastic system with two input variables, and , and two output variables, and . We refer to the graphical model on the left-hand side of Figure 3 as the full model, whereas the model on the right-hand side will be referred to as the split model. The full model assumes that every output node is connected to every input node. The split model assumes every input node only affects one output node. The undirected connection between the input nodes indicates that the input distribution is taken into account in both models. Both models are defined by their feature sets F. In the example given above, the feature set for the full model is given by and the feature set for the split model is given by . Note that we have explicitly included the feature corresponding to the input distribution . The divergence between the full and split models is defined as a measure for complexity in [35]. Variations of this measure have been proposed in [49,50] and compared in [51].
As discussed earlier in this work, we are primarily interested in the relation of the three random variables W, A, and , which represent the current world state, the current action, and the next world state, respectively. Hence, we translate the quantification for complexity [35] that was originally formulated for four random variables (see Figure 3) to three random variables (see Figure 4). The resulting quantification is also known as synergistic information and was first discussed in [36].
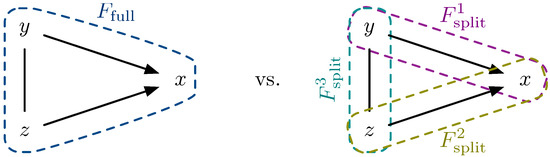
Figure 4.
Quantifying synergy. Left-hand side: full model of two input and two output variables. Right-hand side: split model, as proposed by [36].
Given three random variables X, Y, and Z (see Figure 4), the synergistic information is defined as the averaged Kullback-Leibler divergence
where the full and split models are defined by the feature sets depicted in Figure 4.
In their work, the authors showed that the main difference between the synergistic measure defined by [34] and the synergistic measure defined by [36] is that the former does not take the input distribution into account. This is shown by the following Equation (cited from [36]):
The difference between the measure proposed by [34,36] is seen in line 3 of Equation (17) (compare with Equation (9)). Another difference is that the measure by [34] can so far not be calculated for non-trivial systems, e.g., with the iterative scaling algorithm discussed in the next section.
Applying the measure by [36] to the sensorimotor loop and in the context of morphological computation, we are asking how much the observation of our embodied agent’s behaviour differs from the assumption that there is no synergistic term. In other words, we are measuring the averaged Kullback-Leibler divergence
where the feature set of the full model is defined as and the feature set of the split model is defined as (see Figure 4, where , , and ).
2.5. Maximum Entropy Estimation with the Iterative Scaling Algorithm
There is a standard method to calculate the maximum entropy estimation of a probability distribution based on features, known as iterative scaling, which is well-established in this field and goes back to the work of Darroch and Ratcliff [52] and Csiszár [53]. The algorithm can be summarised in the following form (for joint distributions). Let be the target distribution (in our case , see Section 3.1), V be the set of random variables (in the context of this work ), and F be the feature set (e.g., ). For the sake of simplicity in presentation, we use the following abbreviations: , is either , , or (depending on the index i) and is either , , or depending on the selected feature. The target distribution (that is approximated with the maximum entropy method) is denoted by . As an example, the target distribution for the first feature is given by . Iterative scaling is then defined in the following way:
In words, we initialise the joint distribution to be the uniform distribution. In each iteration, we pick one feature from the set of features. We then multiply the marginal distribution of this feature in the target distribution () with the conditional distribution of the remaining variables conditioned on the chosen feature (). In the notion above, refers to the iterative selection of features based on the current iteration step n, modulo the number of defined features. This algorithm is proved to converge [52,53] and is used in the numerical simulations below (source code is available at [54]). Next, we discuss the parametrised model of the sensorimotor loop which is used in this work to evaluate and compare the different measures.
3. Parametrised Model of the Sensorimotor Loop
The previous section discussed five different measures, namely , , , and . The first four were evaluated in previous publications [14,15] based on a binary model of the sensorimotor loop. was also evaluated on data from hopping models [14] and in the context of soft robotics [1]. This is why we concentrate on and in the context of this work. A new proposal for the unique information will follow below (see Section 4.2).
In our previous work [33], we used an approximation to calculate the synergistic information and were only able to apply it to binary systems. As stated earlier, we are interested in applying synergistic information to real-world applications, hence, this section has two goals. The first goal is to compare how the previous results to the new measure. The second goal is to investigate how the new measure perform on non-binary systems in a fully controlled setting, i.e., model setting. This is a necessary step, before applying the measures to real data, as we need to understand if the results comply with the intuitive understanding of morphological computation.
The next section introduces the binary and non-binary model of the sensorimotor loop. The binary model is used to compare the results of our new measure with our previous results on [33].
3.1. Binary Model of the Sensorimotor Loop
The causal diagram of the sensorimotor loop (see Figure 1) implies that we need to define four different maps, namely the world dynamics kernel , the policy , the sensor map , and finally, the input distribution . Note that in this section we operate on binary random variables, i.e., . The binary model of the sensorimotor loop is then defined by the following set of equations (see also [1,15]):
In the context of this work, we will only vary the parameters , , and , which means that we will change the causal dependence of (parameter ), the causal dependence of (parameter ), and finally, the causal dependence of (parameter ). The other parameters are set such that they result in a uniform distribution of the corresponding kernels, i.e., .
Next, we will first present the modification that allows us to model the non-binary sensorimotor loop, before the results are discussed in the next section (see Section 4).
3.1.1. Non-Binary Model of the Sensorimotor Loop
A generalisation from the binary model to a non-binary model requires to modify the function that operates on the state values. In case of a binary alphabet , the function was simply given by the product. We explain the approach to generalise this function used in this work based on the policy . For the non-binary model, the policy is now given by:
There are various ways in which the function can be chosen. Our choice of the function is derived from the requirement to have a single parameter that allows us to smoothly transition from an independence to a strong dependence (we will briefly discuss a different method at the end of this paragraph). Therefore, we chose to normalise the values and such that they are mapped onto the interval . This allows us to use define similar to the binary case (see Equation (23)) as the product of both mapped random variables, i.e.,
As this example indicates, we chose the same number of bins for all random variables .
It must be noted here that this choice of is a projection of the full space of couplings to a subspace. In particular, there will be cases in which the effects of , , and cannot be fully separated. One such example is the case in which , , and are large and , w, and a are all equal to N. The reason is that the bases spanning the space given by our choice of are not orthogonal (as in the case of Equation (21) to Equation (24)). Walsh bases are one possible way to define the function(s) f such that they are orthogonal with respect to the inner product given by the uniform distribution.
This concludes the description of the parametrised binary and non-binary model of the sensorimotor loop. The next section presents the numerical results obtained with these two models.
4. Numerical Simulations
In this section, we plot the numerical results for two measures, and . is plotted to compare our previous results [33] with the results obtained from with the iterative scaling algorithm. The entire source code used in this work is available at [54].
4.1. Results for the Binary Sensorimotor Loop
This section begins with revisiting the point made earlier about the difference between and with respect to including the input distribution as part of the feature set. Figure 5 shows two experiments with the binary model of the sensorimotor loop. Both plots show the results for and , i.e., without the synergistic term (see Equation (21)). The first plot (left-hand side), shows the result for . Along the diagonal , we see a region in which the synergistic information is non-zero. This is counter-intuitive as the higher-order interaction term is set to zero (, see Equation (21)) and the bases in the binary model of the sensorimotor loop are orthogonal. Hence, high values of and should not result in non-zero values for the synergistic information in these cases. The second plot shows the results for with the feature set . The plot shows that this measure results in zero synergistic information for and any choice of , which is what we expect.
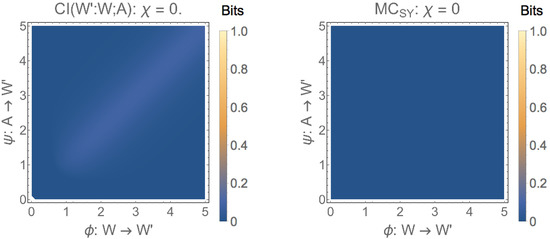
Figure 5.
(left-hand side) and (right-hand side) without synergistic information present in the model, i.e., . The comparison of the plots reveal that has regions with non-zero values, although no synergistic information is present. By that we mean that the higher order interaction term is set to zero (see Equation (21)). No false positives are found for in this case.
The difference between these two approaches becomes more evident if we increase the synergistic coupling factor . Figure 6 shows the two measures for varying values of . We see that for increasing values of , the amount of detected synergistic information increases for both measures, however in different ways. shows increasing regions with high values along the diagonal, whereas shows areas in which the synergistic information is close to zero for values of . The latter is surprising because, in the binary case, the three basis are orthogonal and hence the synergistic information should be distinguishable from the pair-wise interactions, also for high values of and . This issue will be addressed again in the discussion. The plots for the non-binary case, in particular for 4 and 8 bins, are shown below (see Figure 7). Note, that was omitted for those cases, as it was not computable for non-trivial systems at this time.
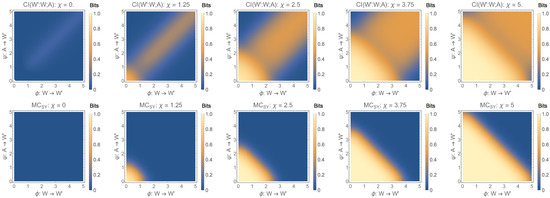
Figure 6.
(top) and (bottom) for with .
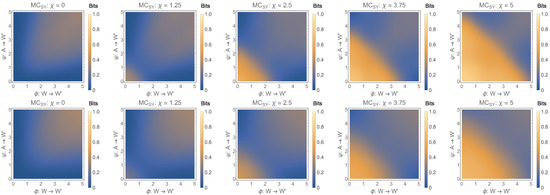
Figure 7.
with (top) and (bottom).
4.2. New Measure for Unique Information
Equation (14) shows that the conditional mutual information is given by the sum of the unique information and the synergistic information . Given that is a new measure for synergy (first introduced in [36]), we can now also give a new definition for the unique information in terms of and , denoted by , because it captures the part of that results from uncontrolled physical interactions:
Note, that is not equivalent to the definition of given above, because . Figure 8 shows , , and for 2, 4, and 8 bins and varying values of the synergistic parameter .
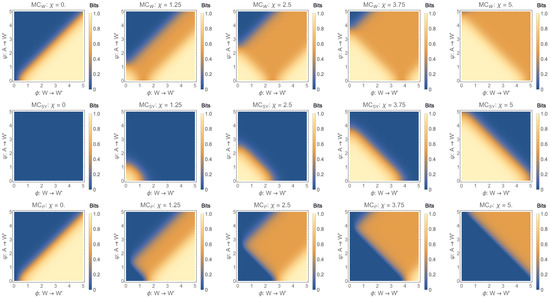
Figure 8.
From left to right . From top to bottom: , , , for binary system, i.e., . Note that each plot in the upper row () is the sum the corresponding plot in the second row () and the final row ().
5. Discussion
This work is a continuation of our previous work on the quantification of morphological computation. Initially, we proposed two measures and that are based on calculating the conditional mutual information in the sensorimotor loop [15]. In a later work, we investigated the relation of the conditional mutual information to unique and synergistic information [54], while primarily focussing on unique information at that time. In this work, we investigated synergistic information and compared a measure based on [35] with the synergistic information that was independently discovered in [34,44]. The main difference between the two measures is that the previously utilised measure does not take the input distribution into account. We have shown in this work that omitting the input distribution can lead to positive synergistic information in cases in which it should be zero. Furthermore, we showed that the new measure can be calculated for non-trivial systems with the iterative scaling method.
Although the new measure has significantly better properties (no false positives), it does show false negative results. This means that the measure is close to zero for high values of , i.e., for a high synergistic term in our parametrised model, if two other couplings (parameter ) and (parameter ) are large. It seems that in the case in which or are large, it is increasingly difficult to detect synergistic information. At this point it is not quite clear if this is a general problem or something that is specific to the measure . This is the work of currently ongoing investigations.
Acknowledgments
This work was partly funded by the German Priority Program DFG-SPP 1527 “Autonomous Learning.” This publication was also made possible through the support of a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of the John Templeton Foundation.
Author Contributions
K.G.-Z. and N.A. proposed and discussed the research. K.G.-Z. carried out most of the research and took the main responsibility for writing the article. C.L. wrote the Iterative Scaling code and contributed to the writing of the paper. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghazi-Zahedi, K.; Deimel, R.; Montúfar, G.; Wall, V.; Brock, O. Morphological Computation: The Good, the Bad, and the Ugly. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Valero-Cuevas, F.J.; Yi, J.W.; Brown, D.; McNamara, R.V.; Paul, C.; Lipson, H. The tendon network of the fingers performs anatomical computation at a macroscopic scale. IEEE Trans. Biomed. Eng. 2007, 54, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.R.; Lipson, H.; Jaeger, H.M. Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef]
- Beal, D.N.; Hover, F.S.; Triantafyllou, M.S.; Liao, J.C.; Lauder, G.V. Passive propulsion in vortex wakes. J. Fluid Mech. 2006, 549, 385–402. [Google Scholar] [CrossRef]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish Exploiting Vortices Decrease Muscle Activity. Science 2003, 302, 1566–1569. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, M.; Iida, F.; Pfeifer, R. “Cheap” underwater locomotion: Roles of morphological properties and behavioral diversity. In Proceedings of the 9th International Conference on Climbing and Walking Robots, Brussels, Belgium, 12–14 September 2006. [Google Scholar]
- Zhao, Q.; Nakajima, K.; Sumioka, H.; Hauser, H.; Pfeifer, R. Spine dynamics as a computational resource in spine-driven quadruped locomotion. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1445–1451. [Google Scholar]
- Iida, F.; Pfeifer, R. “Cheap” rapid locomotion of a quadruped robot: Self-stabilization of bounding gait. In Proceedings of the International Conference on Intelligent Autonomous Systems, Tokyo, Japan, 7–9 March 2004; pp. 642–649. [Google Scholar]
- McGeer, T. Passive walking with knees. In Proceedings of the International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 1640–1645. [Google Scholar]
- Rieffel, J.A.; Valero-Cuevas, F.J.; Lipson, H. Morphological communication: Exploiting coupled dynamics in a complex mechanical structure to achieve locomotion. J. R. Soc. Interface 2010, 7, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Franceschini, N.; Pichon, J.M.; Blanes, C.; Brady, J. From insect vision to robot vision. Philos. Trans. R. Soc. B 1992, 337, 283–294. [Google Scholar] [CrossRef]
- Paul, C. Morphological computation: A basis for the analysis of morphology and control requirements. Robot. Auton. Syst. 2006, 54, 619–630. [Google Scholar] [CrossRef]
- Pfeifer, R.; Bongard, J.C. How the Body Shapes the Way We Think: A New View of Intelligence; The MIT Press (Bradford Books): Cambridge, MA, USA, 2006. [Google Scholar]
- Ghazi-Zahedi, K.; Haeufle, D.F.; Montufar, G.F.; Schmitt, S.; Ay, N. Evaluating Morphological Computation in Muscle and DC-motor Driven Models of Hopping Movements. Front. Robot. AI 2016, 3. [Google Scholar] [CrossRef]
- Zahedi, K.; Ay, N. Quantifying Morphological Computation. Entropy 2013, 15, 1887–1915. [Google Scholar] [CrossRef]
- Horsman, C.; Stepney, S.; Wagner, R.C.; Kendon, V. When does a physical system compute? Proc. R. Soc. A 2014, 470. [Google Scholar] [CrossRef] [PubMed]
- Müller, V.C.; Hoffmann, M. What is Morphological Computation? On How the Body Contributes to Cognition and Control. Artif. Life 2017, 23, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Füchslin, R.M.; Dzyakanchuk, A.; Flumini, D.; Hauser, H.; Hunt, K.J.; Luchsinger, R.H.; Reller, B.; Scheidegger, S.; Walker, R. Morphological Computation and Morphological Control: Steps toward a Formal Theory and Applications. Artif. Life 2012, 19, 9–34. [Google Scholar] [CrossRef] [PubMed]
- Hauser, H.; Ijspeert, A.; Füchslin, R.M.; Pfeifer, R.; Maass, W. Towards a theoretical foundation for morphological computation with compliant bodies. Biol. Cybern. 2011, 105, 355–370. [Google Scholar] [CrossRef] [PubMed]
- Nowakowski, P.R. Bodily Processing: The Role of Morphological Computation. Entropy 2017, 19, 295. [Google Scholar] [CrossRef]
- Pfeifer, R.; Iida, F. Morphological computation: Connecting body, brain and environment. Jap. Sci. Mon. 2005, 58, 48–54. [Google Scholar]
- Pfeifer, R.; Lungarella, M.; Iida, F. Self-Organization, Embodiment, and Biologically Inspired Robotics. Science 2007, 318, 1088–1093. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Maass, W.; Natschläger, T.; Markram, H. Real-Time Computing Without Stable States: A New Framework for Neural Computation Based on Perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K.; Hauser, H.; Kang, R.; Guglielmino, E.; Caldwell, D.G.; Pfeifer, R. Computing with a muscular-hydrostat system. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1504–1511. [Google Scholar]
- Hauser, H.; Corucci, F. Morphosis—Taking Morphological Computation to the Next Level. In Soft Robotics: Trends, Applications and Challenges: Proceedings of the Soft Robotics Week, April 25-30, 2016, Livorno, Italy; Laschi, C., Rossiter, J., Iida, F., Cianchetti, M., Margheri, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 117–122. [Google Scholar]
- Nurzaman, S.G.; Yu, X.; Kim, Y.; Iida, F. Guided Self-Organization in a Dynamic Embodied System Based on Attractor Selection Mechanism. Entropy 2014, 16, 2592–2610. [Google Scholar] [CrossRef]
- Nurzaman, S.G.; Yu, X.; Kim, Y.; Iida, F. Goal-directed multimodal locomotion through coupling between mechanical and attractor selection dynamics. Bioinspir. Biomim. 2015, 10, 025004. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, R.; Iida, F.; Gòmez, G. Morphological computation for adaptive behavior and cognition. Int. Congr. Ser. 2006, 1291, 22–29. [Google Scholar] [CrossRef]
- Pfeifer, R.; Gómez, G. Morphological Computation—Connecting Brain, Body, and Environment; Springer: Berlin/Heidelberg, Germany, 2009; pp. 66–83. [Google Scholar]
- Clark, A. Being There: Putting Brain, Body, and World Together Again; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Ay, N.; Zahedi, K. On the causal structure of the sensorimotor loop. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin, Germany, 2014; Volume 9. [Google Scholar]
- Ghazi-Zahedi, K.; Rauh, J. Quantifying Morphological Computation based on an Information Decomposition of the Sensorimotor Loop. In Proceedings of the 13th European Conference on Artificial Life (ECAL 2015), York, UK, 20–24 July 2015; pp. 70–77. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- Perrone, P.; Ay, N. Hierarchical Quantification of Synergy in Channels. Front. Robot. AI 2016, 2, 35. [Google Scholar] [CrossRef]
- Von Foerster, H. On Self-Organizing Systems and Their Environments. In Understanding Understanding; Springer: New York, NY, USA, 2003; pp. 1–19. [Google Scholar]
- Von Uexkuell, J. A Stroll Through the Worlds of Animals and Men. In Instinctive Behavior; Schiller, C.H., Ed.; International Universities Press: New York, NY, USA, 1957; pp. 5–80. [Google Scholar]
- Ay, N.; Löhr, W. The Umwelt of an embodied agent—A measure-theoretic definition. Theory Biosci. 2015, 134, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, CA, USA, 1998. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Transfer Entropy; Springer: Berlin, Germany, 2016. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 29 September–1 October 1999; pp. 368–377. [Google Scholar]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:10042515. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.K.P.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection Information Based on Common Randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Bell, A.J. The co-information lattice. In Proceedings of the Fifth International Workshop on Independent Component Analysis and Blind Signal Separation: ICA 2003, Nara, Japan, 1–4 April 2003. [Google Scholar]
- Amari, S.I. Information Geometry and Its Applications; Springer: Berlin, Germany, 2016. [Google Scholar]
- Oizumi, M.; Tsuchiya, N.; Amari, S.I. Unified framework for information integration based on information geometry. Proc. Natl. Acad. Sci. USA 2016, 113, 14817–14822. [Google Scholar] [CrossRef] [PubMed]
- Kanwal, M.S.; Grochow, J.A.; Ay, N. Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines. Entropy 2017, 19, 16. [Google Scholar] [CrossRef]
- Darroch, J.N.; Ratcliff, D. Generalized Iterative Scaling for Log-Linear Models. Ann. Math. Stat. 1972, 43, 1470–1480. [Google Scholar] [CrossRef]
- Csiszár, I. I-Divergence Geometry of Probability Distributions and Minimization Problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Ghazi-Zahedi, K. Entropy++ GitHub Repository. Available online: http://github.com/kzahedi/entropy (accessed on 25 August 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).