Comparative Analysis of Jüttner’s Calculation of the Energy of a Relativistic Ideal Gas and Implications for Accelerator Physics and Cosmology

Abstract

Jüttner used the conventional theory of relativistic statistical mechanics to calculate the energy of a relativistic ideal gas in 1911. An alternative derivation of the energy of a relativistic ideal gas was published by Horwitz, Schieve and Piron in 1981 within the context of parametrized relativistic statistical mechanics. The resulting energy in the ultrarelativistic regime differs from Jüttner’s result. We review the derivations of energy and identify physical regimes for testing the validity of the two theories in accelerator physics and cosmology.

1. Introduction

The mass-energy density of the stress-energy tensor becomes theory dependent when the temperature of an ideal gas is sufficiently high. Jüttner [1,2,3] used the conventional theory of relativistic statistical mechanics (RSM) to calculate the energy of a relativistic ideal gas. Horwitz, Schieve and Piron [4] showed that the energy of an ideal gas in the ultrarelativistic (UR) regime of parametrized relativistic statistical mechanics (PRSM) is different from the energy calculated by Jüttner [1]. The energy difference is due to the difference in partition functions used by the two theories and may have measurable consequences.

Fanchi [5,6] proposed a test using the energy difference by combining an expression for the energy calculated by Horwitz et al. [4] with a cosmological model that is consistent with the parametrized theory. The test showed that the calculation of the Friedmann scale factor depends on the choice of energy in the ultrarelativistic (UR) regime, but the test was not definitive because of uncertainties associated with important cosmological factors. The uncertainties of the values of the cosmological factors have been reduced since 1988. Furthermore, the capabilities of accelerator facilities have increased significantly and provided another venue for testing the choice of energy in the UR regime.

The purpose of this paper is to review the energy derivations and show that the energy difference between PRSM and RSM may have measurable consequences. We begin the comparative analysis by showing that the calculation of energy for a relativistic ideal gas depends on the theory used by comparing Jüttner’s [1] calculation with the Horwitz et al. [4] calculation. We then discuss the implications in accelerator physics and cosmology.

2. Jüttner Energy Calculation

We begin by summarizing Jüttner’s [1] calculation of energy for a relativistic ideal gas using the approach presented by Pauli [2] and Greiner et al. [3]. The canonical variables of N identical, non-interacting relativistic particles are $\left\{q_1,\dots ,q_N,p_1,\dots ,p_N\right\}$ where $q_i,p_i$ are the canonical coordinates and canonical momenta of particle $i$. The total energy $E$ of each particle is

$$E=m_0{c}^2{\left[1+\frac{1}{m_0^2{c}^2}\left(p_x^2+p_y^2+p_z^2\right)\right]}^{\frac{1}{2}}$$

(1)

where $m_0{c}^2$ is rest mass energy. The Hamiltonian is a function of the 2-N canonical variables. In our case, the Hamiltonian $H$ is the sum of kinetic energies

$$H=\sum _{i=1}^N{m}_0{c}^2\left\{{\left[1+\frac{1}{m_0^2{c}^2}\left(p_{xi}^2+p_{yi}^2+p_{zi}^2\right)\right]}^{\frac{1}{2}}-1\right\}$$

(2)

Rest mass energy $m_0{c}^2$ has been subtracted from the total energy $E$ of each particle.

The partition function $Z\left(T,V,1\right)$ of a single particle is

$$Z\left(T,V,1\right)=\frac{1}{h_J^3}\int \int exp\left(-\frac{E-m_0{c}^2}{k_{B}T}\right)d^3{q}_i{d}^3{p}_i$$

(3)

where $k_B$ is Boltzmann’s constant $\left(1.38\times {10}^{-23}J/{}^{\circ }K\right)$, $T$ is absolute temperature, and $h_J$ is a constant with dimension length times momentum so that $Z\left(T,V,1\right)$ is dimensionless. Integrating over the canonical coordinates gives the volume $V=\int d^{3}q$ of the gas so that

$$Z\left(T,V,1\right)=\frac{1}{h_J^3}exp\left(\frac{m_0{c}^2}{k_{B}T}\right)\left[V\int exp\left(-\frac{E}{k_{B}T}\right)d^{3}p\right]$$

(4)

The total partition function for the N identical, non-interacting relativistic particles is

$$Z=\frac{Z{\left(T,V,1\right)}^N}{N!}$$

(5)

where $N!$ accounts for the degeneracy of states associated with $N$ identical particles. Given the total partition function, we can calculate thermodynamic properties. The Helmholtz free energy is

$$F=-k_{B}TlnZ=-\frac{lnZ}{\beta },\beta =k_{B}T$$

(6)

Entropy $S$ and internal energy $E$ are calculated from $F$ as

$$S=-{\left[\frac{\partial F}{\partial T}\right]}_{N,V}$$

(7)

and

$$E=F+TS$$

(8)

Jüttner [1] showed that

$$E_J=\frac{N}{\beta }\left[1-i\sigma \frac{{H^{\prime }}_2^{(1)}(i\sigma )}{H_2^{(1)}(i\sigma )}\right]$$

(9)

where

$$\beta =k_{B}Tand\sigma =\frac{m_0{c}^2}{k_{B}T}$$

(10)

for the system of N identical, non-interacting relativistic particles. The function $H_n^{\left(i\right)}$ is the n-th order Hankel function of the i-th kind [7,8], and the prime in ${H^{\prime }}_2^{\left(1\right)}$ denotes differentiation with respect to the argument of the Hankel function. A more modern discussion of Jüttner’s calculation is given by Pauli [2] (pages 139–141).

3. Parametrized Statistical Mechanics

An alternative to Jüttner’s calculation of energy for a relativistic ideal gas was published by Horwitz et al. [4] (see also [9,10]). An understanding of the Horwitz et al. [4] calculation depends on a familiarity with parametrized statistical mechanics.

The concepts of statistical mechanics may be applied to an N-body system of particles if $N$ is sufficiently large to be statistically significant. Furthermore, it is sufficient for our purposes to assume that the number of particles $N$ is conserved. This means that annihilation and creation processes do not play a significant role in the present analysis. Parametrized Hamilton’s equations for this N-body system are

$$\frac{d{q}_i^{\mu }}{ds}=\frac{\partial K}{\partial p_{i\mu }},\frac{d{p}_i^{\mu }}{ds}=-\frac{\partial K}{\partial q_{i\mu }}.$$

(11)

where we assume $\hslash =c=1$ and $K$ is the parametrized Hamiltonian. In general, a parametrized Hamiltonian $K=K_0+K_I$ depends on a non-interaction term $K_0$ plus an interaction term $K_I$. The term $K_0$ for $N$ free particles with mass $\left\{M_i,i=1,\dots ,N\right\}$ may be written as

$$K_0={\displaystyle \sum _{i=1}^N\frac{p_{i\mathsf{\mu }}{p}_i^{\mathsf{\mu }}}{2M_i}}.$$

(12)

Substituting Equation (12) into Equation (11) gives Hamilton’s equations for the free particle system:

$$\frac{d{q}_i^{\mu }}{ds}=\frac{p_i^{\mu }}{M_i},\frac{d{p}_i^{\mu }}{ds}=0.$$

(13)

Integrating the equations of motion gives

$$q_i^{\mathsf{\mu }}=\left(q_0\right){}_i^{\mathsf{\mu }}+\frac{p_i^{\mathsf{\mu }}}{M_i}s$$

(14)

where $\left\{q_0\right\}$ denotes the set of initial space-time positions. Calibrating our clocks so that ${\left(q_0\right)}_i^0=0$ lets us calculate the relationship between the temporal coordinate ($q^{\mu }$ with $\mu =0$) and the parameter $s$ as

$$q_i^0\frac{M_i}{p_i^0}=s=t\frac{M_i}{{\mathsf{\omega }}_i}$$

(15)

where we have replaced $q_i^0$ and $p_i^0$ with the coordinate time t and energy ${\omega }_i$ respectively. We have assumed that all of the particle clocks are calibrated and run at the same rate, thus all temporal coordinates $\left\{q_i^0\right\}$ are replaced with a single coordinate time $s$.

For particle mass and energy fixed, as they are for the system under study, the differential of Equation (15) is

$$ds=\frac{M_i}{{\mathsf{\omega }}_i}dt.$$

(16)

Using Equation (16) in Equation (13) for the spatial components gives the expected result

$$\frac{d{\overrightarrow{q}}_i}{dt}=\frac{{\overrightarrow{p}}_i}{{\mathsf{\omega }}_i}.$$

(17)

3.1. Relativistic Ideal Gas

According to statistical mechanics, the state of a classical mechanical system is characterized by its trajectory in phase space. An ensemble is the collection of all states of the microscopic (or particle) system which is consistent with the constraints imposed on the macroscopic system. The primary assumption of statistical mechanics is that the observed value of a property should correspond to its ensemble average. A Gibbs ensemble is a set of independent, classical relativistic systems. Using these ideas, we derive the macroscopic thermodynamic relation governing the behavior of a relativistic ideal gas.

The forces between particles in an ideal gas should be sufficiently weak that the relation

$$p_i^{\mathsf{\mu }}{p}_{i\mathsf{\mu }}\approx M_i^2$$

(18)

holds for each particle. Particle rest masses do not change under this assumption. If we further assume that the system of N-particles is an isolated system, then it may be viewed from a statistical mechanical perspective as a microcanonical ensemble and should obey an ideal gas law, as we now show.

3.2. Microcanonical Ensemble

A microcanonical ensemble is characterized by specifying two microscopic constraints, such as fixed total energy and size. We take the phase space for the microcanonical ensemble of PRCM to be

$$\mathrm{\Gamma }\left(\mathsf{\kappa },\mathsf{\omega }\right)={\displaystyle \int \mathsf{\delta }\left(K-\mathsf{\kappa }\right)\mathsf{\delta }\left({\displaystyle \sum _{i=1}^N{p}_i^0-\mathsf{\omega }}\right)d{\mathsf{\mu }}_{p}d{\mathsf{\mu }}_q}$$

(19)

where the measures are defined as

$$d{\mu }_p=d^4{p}_1\dots d^4{p}_N,d{\mu }_q=d^4{q}_1\dots d^4{q}_N$$

(20)

Both $K$ and ${\displaystyle {\sum }_i{p}_i^0}$ are constants of the motion, i.e., their derivatives with respect to $s$ vanish.

Given a phase space integral, we define entropy in the usual way as

$$S\left(\mathsf{\kappa },\mathsf{\omega }\right)=k_B\ell n\mathrm{\Gamma }\left(\mathsf{\kappa },\mathsf{\omega }\right)$$

(21)

where $k_B$ is Boltzmann’s constant. The constraint

$${\displaystyle \sum _{i=1}^N{p}_i^0}=\mathsf{\omega }$$

(22)

with $\omega$, a constant is needed so that temperature $T$ can have the usual definition

$$\frac{1}{T}\equiv \frac{\partial S\left(\kappa ,\omega \right)}{\partial \omega }.$$

(23)

Elements of the microcanonical ensemble are uniformly distributed around

$$m_i\equiv {[{\left(p_i^0\right)}^2-{\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(24)

where $m_i\approx M_i$ by Equation (18). The space-time four-volume is limited to a finite volume of space $V$ over a finite duration $Y$. Recalling that $K\approx K_0$ since $K_0>>K_I$ for an ideal gas, we neglect the interaction potential $K_I$ and evaluate the phase space integral over the space-time coordinates to get

$$\mathrm{\Gamma }\left(\mathsf{\kappa },\mathsf{\omega }\right)\approx V^{N}f\left(\mathsf{\kappa },\mathsf{\omega }\right)$$

(25)

where

$$f\left(\mathsf{\kappa },\mathsf{\omega }\right)\equiv {\mathrm{Y}}^N{\displaystyle \int \mathsf{\delta }\left(K_0-\mathsf{\kappa }\right)\mathsf{\delta }\left({\displaystyle \sum _{i=1}^N{p}_i^0-\mathsf{\omega }}\right)}d{\mathsf{\mu }}_p.$$

(26)

3.3. Ideal Gas Law

The macroscopic thermodynamic quantities entropy and temperature are calculated from Equations (21) and (23). The results are

$$S=k_B\ell n{V}^N+k_B\ell nf\left(\mathsf{\kappa },\mathsf{\omega }\right)$$

(27)

and

$$\frac{1}{T}=\frac{k_B}{f(\kappa ,\omega )}\frac{\partial f(\kappa ,\omega )}{\partial \omega }.$$

(28)

The energy derivative in Equation (28) is obtained by taking the implicit derivative of entropy $S$ with respect to volume $V$ for $S$ constant. Taking the derivative gives

$${\frac{\partial S}{\partial V}|}_S=0=\frac{N{k}_B}{V}+\frac{k_B}{f(\kappa ,\omega )}{\left[\frac{\partial f(\kappa ,\omega )}{\partial \omega }\frac{\partial \omega }{\partial V}\right]}_S$$

(29)

Defining pressure $P$ in the usual way as

$$P\equiv -{\frac{\partial \omega }{\partial V}|}_S$$

(30)

lets us rewrite Equation (29) in the form

$$0=\frac{N{k}_B}{V}-\frac{P}{T}$$

(31)

or

$$PV=N{k}_{B}T.$$

(32)

Equation (32) is the expected result that the ideal gas law applies to an isolated, weakly interacting relativistic gas.

4. Horwitz et al., Calculation of the Energy of an Ideal Gas

The system studied above was an isolated system and was represented as a microcanonical ensemble with two macroscopic constraints. The energy of a relativistic ideal gas is obtained by working with a canonical ensemble.

4.1. Canonical Ensemble

In this case, we are physically allowing one system to be in communication with another system. We continue to work with $N$ particles, but the $N$ particles are partitioned into two subsystems. We let the experimental subsystem with $N_e$ particles exchange heat in the form of kinetic energy with the much larger “heat reservoir” subsystem containing $N_r=N-N_e>>N_e$ particles. Assuming the interactions between particles are dominated by short-range forces, we can decompose the Hamiltonian into

$$K\approx K_e+K_r.$$

(33)

The equilibrium configuration of all particles is uniform in phase space, so the constraints of the experimental subsystem must be the same as the reservoir of $N_r$ particles. The phase space integral for the microcanonical ensemble becomes

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(\omega ,M\right)=& {\displaystyle \int \delta \left(K_e-{\kappa }_e\right)\delta \left(K_r-{\kappa }_r\right)\delta \left({\omega }_r+{\omega }_e-\omega \right)}\hfill \\ & \times d^4{p}_1\dots d^4{p}_{N_e}{d}^4{q}_1\dots d^4{q}_{N_e}\hfill \\ & \times d^4{p}_{N_e+1}\dots d^4{p}_N{d}^4{q}_{N_e+1}\dots d^4{q}_N\hfill \end{array}$$

(34)

where

$${\mathsf{\omega }}_e={\displaystyle \sum _{i=1}^{N_e}{\mathsf{\omega }}_i},{\mathsf{\omega }}_r={\displaystyle \sum _{i=N_e+1}^{N=N_e+N_r}{\mathsf{\omega }}_i}.$$

(35)

Writing

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_r\left(\omega -{\omega }_e,{\kappa }_r\right)=& {\displaystyle \int \delta \left(K_r-{\kappa }_r\right)\delta \left({\omega }_r-\left(\omega -{\omega }_e\right)\right)}\hfill \\ & \times d^4{p}_{N_e+1}\dots d^4{p}_N{d}^4{q}_{N_e+1}\dots d^4{q}_N\hfill \end{array}$$

(36)

for the phase space integral of the experimental subsystem lets us simplify Equation (34). The result is

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(\omega ,\kappa \right)=& {\displaystyle \int \delta \left(K_e-{\kappa }_e\right){\mathrm{\Gamma }}_r\left(\omega -{\omega }_e,{\kappa }_r\right)}\hfill \\ & \times d^4{p}_1\dots d^4{p}_{N_e}{d}^4{q}_1\dots d^4{q}_{N_e}\hfill \end{array}$$

(37)

Introducing an integral over the Dirac delta function $\delta \left({\omega }_e-{\omega }^{\prime }\right)$ gives

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(\omega ,\kappa \right)=& {\displaystyle \int {\displaystyle \int \delta \left(K_e-{\kappa }_e\right)\delta \left({\omega }_e-{\omega }^{\prime }\right){\mathrm{\Gamma }}_r\left(\omega -{\omega }^{\prime },{\kappa }_r\right)}}\hfill \\ & \times d^4{p}_1\dots d^4{p}_{N_e}{d}^4{q}_1\dots d^4{q}_{N_e}d{\omega }^{\prime }\hfill \end{array}$$

(38)

or

$$\mathrm{\Gamma }\left(\mathsf{\omega },\mathsf{\kappa }\right)={\displaystyle \int {\mathrm{\Gamma }}_e\left({\mathsf{\omega }}^{\prime },{\mathsf{\kappa }}_e\right){\mathrm{\Gamma }}_r\left(\mathsf{\omega }-{\mathsf{\omega }}^{\prime },{\mathsf{\kappa }}_r\right)d{\mathsf{\omega }}^{\prime }}$$

(39)

where

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_e\left({\omega }^{\prime },{\kappa }_e\right)=& {\displaystyle \int \delta \left(K_e-{\kappa }_e\right)\delta \left({\omega }_e-{\omega }^{\prime }\right)}\hfill \\ & \times d^4{p}_1\dots d^4{p}_{N_e}{d}^4{q}_1\dots d^4{q}_{N_e}.\hfill \end{array}$$

(40)

Following the usual statistical arguments, we assume the existence of an energy $\omega *$ that dominates the integral over ${\omega }^{\prime }$ in a bimodal distribution such that

$$S=k_B\ell n\mathrm{\Gamma }\left(\omega ,\kappa \right)\approx k_B\ell n{\mathrm{\Gamma }}_e\left({\omega }^{*},{\kappa }_e\right)+k_B\ell n{\mathrm{\Gamma }}_r\left(\omega -{\omega }^{*},{\kappa }_r\right).$$

(41)

Equation (41) implies the additivity of entropy

$$S=S_e+S_r,$$

(42)

and the existence of a maximum $\omega *$ implies the equality of temperature for each subsystem:

$$\frac{1}{T}=\frac{\partial S_e}{\partial {\mathsf{\omega }}^{\prime }}|{}_{{\mathsf{\omega }}^{\prime }={\mathsf{\omega }}^{*}}=\frac{\partial S_r}{\partial {\mathsf{\omega }}^{\prime }}|{}_{{\mathsf{\omega }}^{\prime }=\mathsf{\omega }-{\mathsf{\omega }}^{*}}.$$

(43)

Expressing entropy in terms of the phase space integral lets us write

$$\frac{\partial \ell n{\mathrm{\Gamma }}_r}{\partial {\mathsf{\omega }}^{\prime }}|{}_{{\mathsf{\omega }}^{\prime }=\mathsf{\omega }-{\mathsf{\omega }}^{*}}=\frac{1}{k_{B}T}\equiv \mathsf{\beta }.$$

(44)

If temperature changes slowly with respect to ${\omega }^{\prime }$ in the region near ${\omega }^{\prime }=\omega -{\omega }^{*}$, we have

$${\mathrm{\Gamma }}_r\left(\mathsf{\omega }-{\mathsf{\omega }}_e,{\mathsf{\kappa }}_r\right)\approx e^{\mathsf{\beta }{\mathsf{\omega }}^{\prime }}=e^{\mathsf{\beta }\mathsf{\omega }}{e}^{-\mathsf{\beta }{\mathsf{\omega }}_e}.$$

(45)

Substituting Equation (45) into Equation (37) gives

$$\mathrm{\Gamma }\left(\mathsf{\omega },\mathsf{\kappa }\right)=e^{\mathsf{\beta }\mathsf{\omega }}{\displaystyle \int \mathsf{\delta }\left(K_e-{\mathsf{\kappa }}_e\right)e^{-\mathsf{\beta }{\mathsf{\omega }}_e}\cdot d^4{p}_1\dots d^4{p}_{N_e}{d}^4{q}_1\dots d^4{q}_{N_e}}.$$

(46)

4.2. Energy Calculation

Let us consider a gas of non-interacting, identical particles. The normalized distribution for the canonical ensemble is proportional to the integrand of Equation (46) with the proportionality constant determined by probability conservation. The resulting distribution of non-interacting identical particles is

$$D(p,q)=\mathsf{\delta }(K-\mathsf{\kappa })\frac{e^{-\mathsf{\beta }\mathsf{\omega }}}{Q_N(V^{(4)},T,\mathsf{\kappa })}$$

(47)

where we have dropped the subscript $e$, $V^{(4)}$ is the space-time four-volume, and the partition function $Q_N$ is

$$Q_N\left(V^{\left(4\right)},T,\kappa \right)\equiv {\displaystyle \int \delta \left(K-\kappa \right)e^{-\beta \omega }\frac{d{\mu }_{p}d{\mu }_q}{h_H^{4N}N!}}.$$

(48)

The measures in Equation (48) are given by (20), and $N!$ accounts for the degeneracy of states associated with $N$ identical particles. Following Horwitz [10] (page 181), we have inserted a constant $h_H^{4N}$ in the denominator of Equation (48). The constant $h_H$ has dimension momentum times length and makes the partition function $Q_N$ dimensionless. Equation (48) is the starting point for our calculation of the energy of the relativistic ideal gas.

The partition function may be simplified by recognizing that $M_i=M_0$ where $M_0$ is the particle rest mass for our system of identical particles. The resulting partition function is

$$\begin{array}{cc}\hfill Q_N\left(V^{\left(4\right)},T,\kappa \right)=& \frac{1}{h_H^{4N}N!}{\displaystyle \int \delta \left[{\displaystyle \sum _{i=1}^N\left(\frac{p_{0i}^2}{2M_0}-\frac{{\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i}{2M_0}\right)-\kappa }\right]}\hfill \\ & \times e^{-\beta {\displaystyle \sum _{i=1}^N{\omega }_i}}d{\mu }_{p}d{\mu }_q.\hfill \end{array}$$

(49)

Integrating over the space-time coordinates gives

$$\begin{array}{cc}\hfill Q_N\left(V^{\left(4\right)},T,\kappa \right)=& \frac{{\left(V^{\left(4\right)}\right)}^N}{h_H^{4N}N!}{\displaystyle \int \frac{m_{1}d{m}_1}{{\left({\overrightarrow{p}}_1\cdot {\overrightarrow{p}}_1+m_1^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\dots \frac{m_{N}d{m}_N}{{\left({\overrightarrow{p}}_N\cdot {\overrightarrow{p}}_N+m_N^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}\hfill \\ & \times 2M_0\delta \left({\displaystyle \sum _{i=1}^N{m}_i^2-N{M}_0^2}\right)e^{-\beta {\displaystyle \sum _{i=1}^N{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+m_i^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}{d}^3{p}_1\dots d^3{p}_N.\hfill \end{array}$$

(50)

where the relations

$$p^0={\left(\overrightarrow{p}\cdot \overrightarrow{p}+m^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},d{p}^0=\frac{mdm}{{\left(\overrightarrow{p}\cdot \overrightarrow{p}+m^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$$

(51)

and

$$\kappa =\frac{N{M}_0}{2}$$

(52)

have been used. To compare the parametrized expression with the result based on the conventional paradigm, we must restrict the range of masses close to $M_0$. The results of this restriction are the replacements

$$\frac{m_i}{{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+m_i^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\approx \frac{M_0}{{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$$

(53)

and

$$e^{-\mathsf{\beta }{\displaystyle \sum _{i=1}^N{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+m_i^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}\approx e^{-\mathsf{\beta }{\displaystyle \sum _{i=1}^N{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}$$

(54)

Substituting Equations (53) and (54) into (50) gives

$$\begin{array}{cc}\hfill Q_N\left(V^{\left(4\right)},T,\kappa \right)=& \frac{{\left(V^{\left(4\right)}\right)}^N}{h_H^{4N}N!}2M_0{\left(M_0\right)}^N\hfill \\ & \times {\displaystyle \int d{m}_1\dots d{m}_N\delta \left({\displaystyle \sum _{i=1}^N{m}_i^2-N{M}_0^2}\right){\left(I_{\beta }\right)}_i}\hfill \end{array}$$

(55)

where

$${\left(I_{\mathsf{\beta }}\right)}_i\equiv {\displaystyle \prod _{i=1}^N\left[{\displaystyle \int d^3{p}_i\frac{e^{-\mathsf{\beta }{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}{{\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}\right]}.$$

(56)

A comparison of the momentum integral in Equation (4) with the momentum integral in Equation (56) shows that the Horwitz et al. [4] analysis modifies the integrand by the denominator ${\left({\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. The momentum integrals differ primarily when ${\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_i$ is large.

The Jüttner distribution is a distribution of speeds of particles in an ideal gas of classical relativistic particles. It is also known as the Maxwell–Jüttner distribution because it is the relativistic analog of Maxwell’s distribution. A distribution of particle momenta such as the Jüttner distribution is needed for applications that include the theoretical description of relativistic many-particle systems, the interpretation of high-energy experiments, and understanding of astrophysical and cosmological phenomena. Chacon-Acosta et al. [11] presented references for several applications, including heavy-ion collisions and the thermal history of the universe.

Ghodrat and Montakhab [12] viewed the momentum-dependent denominator as a momentum-dependent reference density in what they called a modified Jüttner distribution. They pointed out that they had “no rigorous theoretical analysis or experimental evidence to favor one reference density or measure to the other” (page 011110-2). Chacon-Acosta et al. [11] also questioned the validity of the Horwitz et al. [4,13] analysis that led to a modified Jüttner distribution. They referenced criticisms of the modified Jüttner distribution by Debbasch [14].

Referring to the parametrized statistical mechanical framework presented by Schieve [15], Debbasch [14] argued in Section 4.2 that “The real and apparently only reason to develop the approach presented in [15] is a historical one, namely the desire to treat relativistic interactions in the framework of action-at-a-distance theories. These theories are today widely considered unrealistic; indeed, not only does the theoretical framework used in [15] allow the (non-quantum) particles to wander off their mass-shells, but action-at-a-distance theories do not seem to permit a theoretical treatment of the particle creation/annihilation phenomenon, which is naturally an experimental fact.”

Debbasch’s critique and subsequent conclusions showed a limited knowledge of parametrized theories. A more general introduction to parametrized relativistic quantum theory is provided by Fanchi [5,6], Pavšič [16], and Horwitz [10]. Parametrized relativistic quantum field theory was introduced by Fanchi [5,17], and discussed more fully by Pavšič [16] (Chapter 1), including canonical quantization and creation/annihilation operators. More recent references and a discussion of branes and quantized fields are discussed by Pavšič [18]. Horwitz [10] (Chapter 3) discussed the construction of Fock space, quantum field theory, and creation/annihilation operators. Action-at-a-distance, nonlocality and superluminal motion are discussed by Fanchi [5,6] and Pavšič [16,19]. The relativistic ideal gas in the ultrarelativistic regime is a regime where different results by Jüttner [1] and Horwtiz et al. [4] can be tested, as we discuss further in Section 4.

The energy of the ensemble is calculated as the average

$$\begin{array}{cc}\hfill ⟨\omega ⟩& =\frac{1}{h_H^{4N}N!}{\displaystyle \int \omega D\left(p,q\right)d{\mu }_{p}d{\mu }_q}\hfill \\ & =\frac{\frac{1}{h_H^{4N}N!}{\displaystyle \int \omega \delta (K-\kappa )e^{-\beta \omega }d{\mu }_{p}d{\mu }_q}}{Q_N(V^{(4)},T,\kappa )}.\hfill \end{array}$$

(57)

Equation (57) may be rewritten as

$$⟨\omega ⟩=\frac{{\displaystyle \int \delta \left(K-\kappa \right)\left[-\frac{\partial e^{-\beta \omega }}{\partial \beta }\right]\frac{d{\mu }_{p}d{\mu }_q}{h_H^{4N}N!}}}{Q_N(V^{(4)},T,\kappa )}.$$

(58)

Factoring out the derivative with respect to $\beta$ gives

$$\begin{array}{cc}\hfill ⟨\omega ⟩& =-\frac{1}{Q_N(V^{(4)},T,\kappa )}\frac{\partial }{\partial \beta }{\displaystyle \int \delta \left(K-\kappa \right)e^{-\beta \omega }\frac{d{\mu }_{p}d{\mu }_q}{h_H^{4N}N!}}\hfill \\ & =-\frac{1}{Q_N(V^{(4)},T,\kappa )}\frac{\partial }{\partial \beta }{Q}_N\left(V^{\left(4\right)},T,\kappa \right)\hfill \end{array}$$

(59)

or

$$⟨\omega ⟩\equiv {\omega }_H=-\frac{\partial \ell n{Q}_N\left(V^{\left(4\right)},T,\kappa \right)}{\partial \omega }$$

(60)

where we have written $⟨\omega ⟩$ as ${\omega }_H$. Evaluating the integral $I_{\beta }$ in Equation (56) yields

$$\begin{array}{cc}\hfill I_{\beta }& ={\displaystyle \int d^{3}p\frac{e^{-\beta \left(\overrightarrow{p}\cdot \overrightarrow{p}+M_0^2\right){}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}{{\left(\overrightarrow{p}\cdot \overrightarrow{p}+M_0^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}=-2{\pi }^2\frac{M_0}{\beta }{H}_1^{\left(1\right)}\left(i\sigma \right),\hfill \\ \hfill \sigma & \equiv M_0\beta \hfill \end{array}$$

(61)

where the function $H_n^{\left(i\right)}$ is the n-th order Hankel function of the i-th kind [7,8]. Substituting Equation (61) into Equation (55) and carrying out the derivative in Equation (60) gives

$${\mathsf{\omega }}_H=\frac{N}{\mathsf{\beta }}\left[2-i\mathsf{\sigma }\frac{H_0^{(1)}(i\mathsf{\sigma })}{H_1^{(1)}(i\mathsf{\sigma })}\right].$$

(62)

5. Energy Comparison

In the previous section, we fixed both the number of free particles and the mass of each particle. These restrictions are equivalent to specifying a system that is stationary, that is, independent of the relativistic scalar evolution parameter. The restrictions are needed to make possible a comparison of Equation (62) with Jüttner’s [1] result:

$${\mathsf{\omega }}_J=\frac{N}{\mathsf{\beta }}\left[1-i\mathsf{\sigma }\frac{{H^{\prime }}_2^{(1)}(i\mathsf{\sigma })}{H_2^{(1)}(i\mathsf{\sigma })}\right].$$

(63)

Equation (63) is equivalent to Equation (9) with units of $\hslash =1$ to be consistent with Equation (62). Differences between Equations (62) and (63) reflect differences between the parametrized theory [4,7,8] and the conventional paradigm. A more direct comparison can be made by manipulating the Hankel functions in Equation (63) to arrive at the equivalent form

$${\mathsf{\omega }}_J=\frac{N}{\mathsf{\beta }}\left[3-i\mathsf{\sigma }\frac{H_1^{(1)}(i\mathsf{\sigma })}{H_2^{(1)}(i\mathsf{\sigma })}\right].$$

(64)

Equations (62) and (64) agree in the non-relativistic limit $\left(\sigma \to \infty \right)$:

$${\left({\mathsf{\omega }}_H\right)}_{NR}={\left({\mathsf{\omega }}_J\right)}_{NR}=N{M}_0+\frac{1}{2}N{k}_{B}T.$$

(65)

At the opposite extreme—the ultrarelativistic limit $\left(\sigma \to 0\right)$—the expressions have different values:

$${\left({\mathsf{\omega }}_H\right)}_{UR}=2N{k}_{B}T$$

(66)

and

$${\left({\mathsf{\omega }}_J\right)}_{UR}=3N{k}_{B}T.$$

(67)

The ratio is

$${\left(\frac{{\omega }_J}{{\omega }_H}\right)}_{UR}=\frac{3}{2}.$$

(68)

Calculation of the energies begins by first transforming the Hankel functions to confluent hypergeometric functions [16]:

$${\omega }_H=\frac{N}{\beta }\left[2+\frac{1}{2}\frac{U\left(0.5,1,Z\right)}{U\left(1.5,3,Z\right)}\right],Z=2\sigma$$

(69)

and

$${\mathsf{\omega }}_J=\frac{N}{\mathsf{\beta }}\left[3+\frac{1}{2}\frac{U\left(1.5,3,Z\right)}{U\left(2.5,5,Z\right)}\right],Z=2\mathsf{\sigma }$$

(70)

where $U\left(a,b,Z\right)$ is a confluent hypergeometric function.

In SI units, $\sigma =\frac{M_0{c}^2}{k_{B}T}$ so that $Z=2\sigma =\frac{2M_0{c}^2}{k_{B}T}$ and $T=\frac{M_0{c}^2}{k_B\sigma }$. For a proton, we have $M_0=1.673\times {10}^{-27}kg,$ $c=3.00\times {10}^8 m/s,$ and $k_B=1.381\times {10}^{-23}J\cdot {}^{\circ }{K}^{-1}$ which gives $T=1.09\times {10}^{13}\left[{}^{\circ }K\right]$ at $\sigma =1$. In general, $Z=2\sigma$ and $T=\frac{2M_0{c}^2}{k_{B}Z}=\frac{2.18\times {10}^{13}}{Z}[{}^{\circ }K]$. For hydrogen-like masses, $M_0=1.673\times {10}^{-27}kg$, so that

$${\sigma }_{Hydrogen}\approx \left(1.1\times {10}^{13}K\right)/T.$$

(71)

We determine the temperature at which the difference between calculated energies becomes significant by evaluating the energies as a function of temperature or, equivalently, $\sigma$.

Integral representations of $U\left(1.5,3,Z\right)$ and $U\left(2.5,5,Z\right)$ were numerically evaluated using both four-point and six-point Gauss–Laguerre quadratures [20]. The difference between each of the four-point and six-point quadrature values was less than one percent, which is sufficient accuracy for our purposes. A Gauss–Laguerre quadrature does not yield asymptotically correct values for the remaining function $U\left(0.5,1,Z\right)$. It is evaluated using Lebedev’s [21] series expansion for $Z<1$, and by asymptotic approximation for $Z>10$. Intermediate values are interpolated by nonlinear regression. Results of the calculations are shown in Figure 1, Figure 2 and Figure 3. The functions are smooth on a log-log plot.

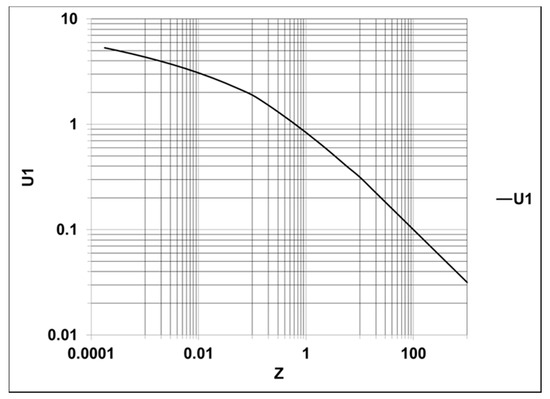
Figure 1. Function U(0.5,1,Z) versus dimensionless Z.

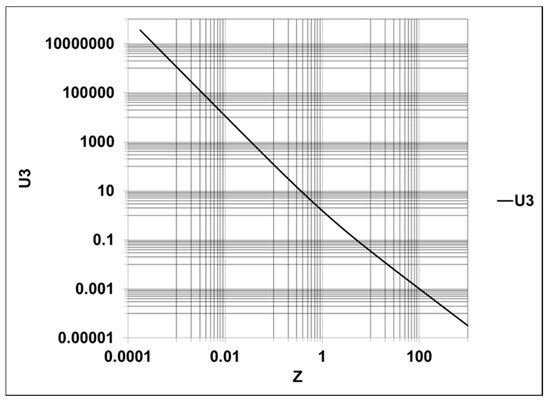
Figure 2. Function U(1.5,3,Z) versus dimensionless Z.

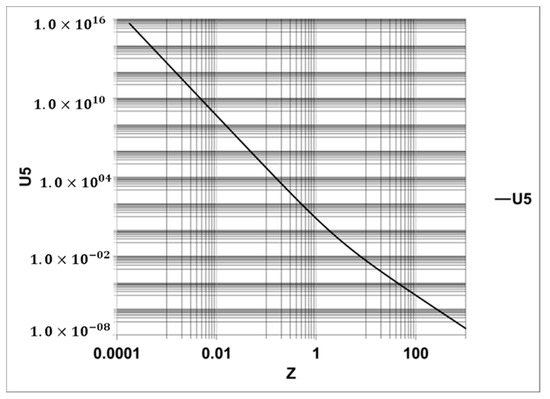
Figure 3. Function U(2.5,5,Z) versus dimensionless Z.

A physically more interesting plot is the semilogarithmic graph of ${\omega }_J/{\omega }_H$ versus $Z$ shown in Figure 4. The ratio ${\omega }_J/{\omega }_H$ as a function of $Z$ is

$$\frac{{\omega }_J}{{\omega }_H}=\left[3+\frac{1}{2}\frac{U\left(1.5,3,Z\right)}{U\left(2.5,5,Z\right)}\right]/\left[2+\frac{1}{2}\frac{U\left(0.5,1,Z\right)}{U\left(1.5,3,Z\right)}\right],Z=2\sigma$$

(72)

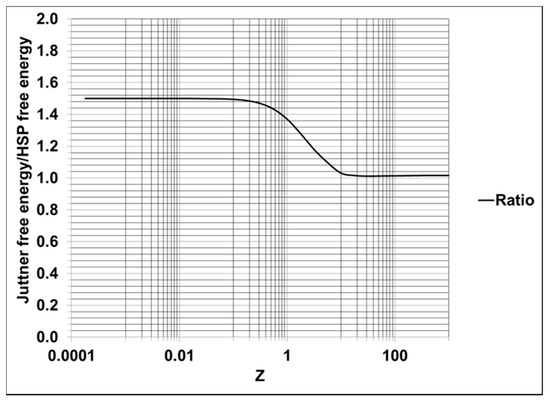
Figure 4. Ratio $E_J/E_H$ versus dimensionless Z.

According to Figure 4, the energies are equivalent for values of $Z$ greater than 10. The UR regime is reached for values of $Z$ less than 0.1.

The relatively narrow region in Figure 4 from $Z=0.1$ to $Z=10$ is the region of transition from non-relativistic to ultrarelativistic behavior. For hydrogen-like masses, the transition region occurs for temperatures ranging from $T=1.1\times {10}^{14}K$ to $T=1.1\times {10}^{12}K$, and the UR limit is reached at $T=1.1\times {10}^{14}K$. For comparison, the central temperature of the Sun is approximately $1.5\times {10}^{7}K$, which is several orders of magnitude less than the temperature associated with the beginning of the transition region.

6. Discussion and Conclusions

Energy differences can affect the energy density of the stress-energy tensor used in stellar models (e.g., the Tolman–Oppenheimer–Volkoff equation), relativistic gas dynamics, and cosmology. Of these, only cosmology was considered a viable testing ground in 1988 [22]. Today, relativistic gas dynamics has also become a viable testing ground because of advances in accelerator physics.

The transition to the UR regime in Figure 4 begins at $T=1.1\times {10}^{14}K$ which corresponds to an energy of approximately $95 MeV$, and the UR regime is reached at $T=1.1\times {10}^{14}K$ which corresponds to an energy of approximately $9.5 GeV$. Modern accelerators can operate at temperatures in the UR regime. For example, the Large Hadron Collider at CERN consists of two high energy particle beams that circulate in rings at speeds close to the speed of light. The maximum beam energy is expected to be 7 TeV in 2024 according to Patrignani et al. [23], and the design value of the total collision energy is 14 TeV [24]. The maximum beam energy of 7 TeV corresponds to temperature $T\approx 8\times {10}^{16}K$, which is in the UR regime.

Greiner et al. [3] pointed out that the collision of high energy beams of nucleons with a target can result in a gas of nucleons that approximately behaves like an ideal gas of non-interacting classical particles. It has also been observed by the ALICE Collaboration [25] that nuclear matter can transition to a quark-gluon plasma at sufficiently high temperature and energy density. The energy that is being achieved by modern accelerators is making it possible to study the behavior of matter during the earliest, and hottest, moments of the big bang. Parametrized electrodynamics [26,27] may need to be extended to study matter in a plasma state.

The difference in energy between Equations (69) and (70) could have observable consequences in cosmological models during epochs when temperatures are high enough to be in the UR regime. Fanchi [22] studied the energy difference in cosmology by using a model based on the Robertson–Walker metric and solving the resulting Friedmann equation for the age of the universe. The energy difference made its appearance through the density parameter in the model. The model was not considered a definitive test because of uncertainties associated with important cosmological parameters such as the Hubble parameter, which varied from 50 to 100 km/s/Mpc at the time. Today, some cosmological parameters are better understood but the model is considered too simple to account for the different epochs in the Standard Big-Bang model.

The Big-Bang Cosmology review article by Olive and Peacock in Patrignani et al. [28] pointed out that the Standard Big-Bang model includes the assumption that the universe was hottest and densest at the moment of the Big-Bang. The temperature and density began to decline thereafter. The early hot and dense universe was thought to be dominated by a gas of radiation or relativistic particles. The most likely periods to provide opportunities for testing the difference in energy between Equations (69) and (70) are the early universe from the Big-Bang through the quark epoch because this period is thought to exist in the UR regime. An especially fertile area for seeking a test of the energy difference is the quark-gluon plasma because it is the state of matter that has application to the quark epoch in cosmology and links to the capabilities of high energy particle accelerators.