Abstract
The information-theoretical concept transfer entropy is an ideal measure for detecting conditional independence, or Granger causality in a time series setting. The recent literature indeed witnesses an increased interest in applications of entropy-based tests in this direction. However, those tests are typically based on nonparametric entropy estimates for which the development of formal asymptotic theory turns out to be challenging. In this paper, we provide numerical comparisons for simulation-based tests to gain some insights into the statistical behavior of nonparametric transfer entropy-based tests. In particular, surrogate algorithms and smoothed bootstrap procedures are described and compared. We conclude this paper with a financial application to the detection of spillover effects in the global equity market.
MSC:
62G09; 62G10; 91B84
1. Introduction
Entropy, introduced by Shannon [1,2], is an information theoretical concept with several appealing properties, and therefore wide applications in information theory, thermodynamics and time series analysis. Based on this classical measure, transfer entropy (TE) has become a popular information theoretical measure for quantifying the flow of information. This concept, which was coined by Schreiber [3], was applied to distinguish a possible asymmetric information exchange between the variables of a bivariate system. When based on appropriate non-parametric density estimates, the TE is a flexible non-parametric measure for conditional dependence, coupling structure, or Granger causality in a general sense.
The notion of Granger causality was developed by the pioneering work of Granger [4] to capture causal interactions in a linear system. In a more general model-free world, the Granger causal effect can be interpreted as the impact of incorporating the history of another variable on the conditional distribution of a future variable in addition to its own history. Recently, various nonparametric measures have been developed to capture such difference between conditional distributions in a more complex, and typically nonlinear system. There is a growing list of such methods, based on, among others, correlation integrals [5], kernel density estimation [6], Hellinger distances [7], copula functions [8] and empirical likelihood [9].
In contrast with the above-mentioned methods, TE-based causality tests do not attempt to capture the difference between two conditional distributions explicitly. Instead, with the information theoretical interpretation, the TE offers a natural way to measure directional information transfer and Granger causality. We refer to [10,11] for detailed reviews of the relation between Granger causality and directed information theory. However, the direct application of entropy and its variants, though attractive, turns out to be difficult, if not impossible altogether, due to the lack of asymptotic distribution theory for the test statistics. For example, Granger and Lin normalize the entropy to detect serial dependence with critical values obtained from simulations [12]. Hong and White provide the asymptotic distribution for the Granger–Lin statistic with a specific kernel function [13]. Barnett and Bossomaier derive a distribution for the TE at the cost of the model-free property [14].
On the other hand, to obviate the asymptotic problem, several resampling methods on TE have been developed for providing empirical distributions of the test statistics. Two popular techniques are bootstrapping and surrogate data. Bootstrapping is a random resampling technique proposed by Efron [15] to estimate the properties of an estimator by measuring those properties from approximating distributions. The “surrogate” approach developed by Theiler et al. [16] is another randomization method initially employing Fourier transforms to provide a benchmark in detecting nonlinearity in a time series setting. It is worth mentioning that the two methods are different with respect to the statistical properties of the resampled data. For the surrogate method the null hypothesis is maintained, while the bootstrap method does not seek to impose the null hypothesis on the bootstrapped samples. We refer to [17,18] for detailed applications of the two methods.
However, not all resampling methods are suitable for entropy-based dependence measures. As Hong and White [13] put it, a standard bootstrap fails to deliver a consistent entropy-based statistic because it does not preserve the statistical properties of a degenerate U-statistic [13]. Similarly, with respect to traditional surrogates based on phase randomization of the Fourier transform, Hinich et al. [19] criticize the particularly restrictive assumption of linear Gaussian process, and Faes et al. [20] point out that it cannot preserve the whole statistical structure of the original time series.
As far as we are aware, there are several applications of both methods in entropy-based tests, for example, Su and White [7] propose a smoothed local bootstrap for entropy-based test for serial dependence, Papana et al. [21] apply stationary bootstrap in partial TE estimation, Quiroga et al. [22] use time-shifted surrogates to test the significance of the asymmetry of directional measures of coupling, and Marschinski and Kantz [23] introduce the effective TE, which relies on random shuffling surrogate in estimation. Kugiumtzis [24] and Papana et al. [21] provide some comparisons between bootstrap and surrogate methods for entropy-based tests.
In this paper, we adopt TE as a test statistic for measuring conditional independence (Granger non-causality). Being aware of the fact that the analytical null distribution may not always be accurate or available in an analytically closed form, we resort to resampling techniques for constructing the empirical null distribution. The techniques under consideration include smoothed local bootstrap, stationary bootstrap and time-shifted surrogates, all of which are shown in literature to be applicable to entropy-based test statistics. Using different dependence structures, the size and power performance of all methods are examined in simulations.
The remainder of this paper is organized as follows. Section 2 first provides the TE-based testing framework and a short introduction to kernel density estimation; then bandwidth selection rules are discussed. After presenting the resampling methods, including the smoothed local bootstrap and time-shifted surrogates for different dependence structure settings. Section 3 examines the empirical performance of different resampling methods, presenting the size and power of the tests. Section 4 considers a financial application with the TE-based nonparametric test and Section 5 summarizes.
2. Methodology
2.1. Transfer Entropy and Its Estimator
Information theory is a branch of applied mathematical theory of probability and statistics. The central problem of classical information theory is to measure transmission of information over a noisy channel. Entropy, also referred to as Shannon entropy, is one key measure in the field of information theory brought by [1,2]. Entropy measures the uncertainty and randomness associated with a random variable. Supposing that S is a random vector with density , its Shannon entropy is defined as
There is a long history of applying information theoretical measures in time series analysis. For example, Robinson [25] applies the Kullback–Leibler information criterion [26] to construct a one-sided test for serial independence. Since then, nonparametric tests using entropy measures for dependence between two time series are becoming prevalent. Granger and Lin [12] normalize the entropy measure to identify the lags in a nonlinear bivariate time series model. Granger et al. [27] study dependence with a transformed metric entropy, which turns out to be a proper measure of distance. Hong and White [13] provide a new entropy-based test for serial dependence, and the test statistic follows a standard normal distribution asymptotically.
Although those heuristic approaches work for entropy-based measures of dependence, these methodologies do not carry over directly to measures of conditional dependence, i.e., Granger causality. The term TE was coined by Schreiber [3], although it appeared in the literature earlier under different names, is a suitable measure to serve this purpose. The TE quantifies the amount of information contained in one series at k steps ahead from the state of another series, given the current and past state of itself. Suppose we have two series and , for brevity put , and , further we define a three-variate vector as , where ; and is used when there is no danger of confusion. Within this bivariate setting, W is a three dimensional continuous vector. In this paper, we limit ourselves to for simplicity, but the method can be generalized into multiple steps easily. The quantity is a nonlinear measure for the amount of information explained in Z (future Y) by X, accounting for the information on Z already contained in Y. Although TE defined in [3] applies to discrete variables, it is easily generalized to continuous variables. Conditional on Y, is defined as
Using conditional mutual information , the TE can be equivalently formulated in terms of four Shannon entropy terms as
In order to construct a test for Granger causality based on the TE, one first needs to show quantitatively that the TE is a proper basis for detecting whether the null hypothesis is satisfied. The following theorem, as a direct application of the Kullback–Leibler criterion, lays the quantitative foundation for testing based on the TE.
Theorem 1.
with equality if and only if .
Proof.
The proof of Theorem 1 is given in [28]. ☐
It is not difficult to verify that the condition for coincides with the null hypothesis of Granger non-causality defined in Equation (4), also referred to as conditional independence or no coupling. Mathematically speaking, the null hypothesis of Granger non-causality, : is not a Granger cause of , can be phrased as
for in the support of W. A nonparametric test for Granger non-causality seeks to find statistical evidence of violation of Equation (4). There are many nonparametric measures available for this purpose, some of which are mentioned above. Equation (4) provides the basis for a model-free test without imposing any parametric assumptions about the data generating process or underlying distributions for and . We only assume two things here. First, is a strictly stationary bivariate process. Second, the process has finite memory, i.e., variable lags , . The second (finite Markov order) assumption is needed in this nonparametric setting to make conditioning on past information feasible by conditioning on a finite number of past observations. Moreover, strict stationarity and the mixing properties implied by the finite Markov order assumption ensure that the transfer entropy can be estimated consistently through kernel density estimation of the underlying densities.
As far as we are aware, the direct use of TE to test Granger non-causality in nonparametric setting is difficult, if not impossible at all, due to the lack of asymptotic theory for the test statistic. As Granger and Lin [12] put it, very few asymptotic distribution results for entropy-based estimators are available. Although over the years several break-throughs have been made with application of entropy to testing serial independence, the limiting distribution of TE statistic is still unknown. One may wish to use simulation techniques to overcome the lack of asymptotic distributions. However, as noted by Su and White [7], there are estimation biases of the TE statistics for non-parametric dependence measures under the smoothed bootstrap procedure. Even for the parametric test statistic used by Barnett and Bossomaier [14], the authors noticed that the TE-based estimator is generally biased.
2.2. Density Estimation and Bandwidth Selection
The non-negativity property in Theorem 1 makes a desirable measure for constructing a one-sided test of conditional independence; any positive divergence from zero is a sign of conditional dependence of Y on X. To estimate TE there are several different approaches, such as histogram-based estimators [29], correlation sums [30] and nearest neighbor estimators [31]. However, the optimal rule for the number of neighbor points is unclear, and as Kraskov et al. [31] comment, a small value of neighbor points may lead to large statistical errors. A more natural method, kernel density estimators, the properties of which have been well studied, is applied in this paper. With the plug-in kernel estimates of densities, we may replace the expectation in Equation (2) by a sample average to get an estimate for .
A local density estimator of a -variate random vector W at is given by
where is a kernel function and h is the bandwidth. We take to be a product kernel function defined as , where is element in W. Using a standard univariate Gaussian kernel, , is the standard multivariate Gaussian kernel as described by Wand and Jones [32] and Silverman [33]. Using Equation (5) as the plug-in density estimator, and replacing the expectation by the sample mean, we obtain the estimator for the TE given by
If we estimate the Shannon entropy in Equation (1) based on a sample of size n from the -dimensional random vector W, by the sample average of the plug-in density estimates, we obtain
then Equation (6a) can be equivalently expressed in terms of four entropy estimators, that is,
To construct a statistical test, we develop the asymptotic properties of defined in Equations (6a) and (6c) through two steps. In the first step, given the density estimates the consistency of entropy estimates is achieved and then the linear combination of four entropy estimates would converge in probability to the true value. The following two theorems ensure the consistency of .
Theorem 2.
Given the kernel density estimate for , where W is a -dimensional random vector with length n, let be the plug-in estimate for the Shannon entropy as defined in Equation (6b). Then .
Proof.
The proof of Theorem 2 is given in [12] using results from [34]. ☐
The basic idea of the proof is to take the Taylor series expansion of around the true value and use the fact that , given an appropriate bandwidth sequence, converges to pointwise to obtain consistency. In the next step, the consistency of is provided by the continuous mapping theorem.
Theorem 3.
Given , with defined as in Equation (6c), .
Proof.
The proof is straightforward if one applies the Continuous Mapping Theorem. See Theorem 2.3 in [35]. ☐
Before we move to the next section, it is worth having a careful look at the issue of bandwidth selection. The bandwidth h for kernel estimation determines how smooth the density estimation is; a smaller bandwidth reveals more structure of the data, whereas a larger bandwidth delivers a smoother density estimate. Bandwidth selection is essentially a trade-off between the bias and variance in density estimation. A very small value of h could eliminate estimation bias, with a large variance. On the other hand, a large bandwidth reduces estimation variance at the expense of incorporating more bias. See Chapter 3 in [32] and [36] for details.
However, the bandwidth selection for the TE statistic is more involved. To the best of our knowledge, there is a blank in the field of optimal bandwidth selection in kernel-based TE estimator. As He et al. [37] show, when estimating the entropy estimator, two types of errors would be generated, one is from entropy estimation and the other from density estimation, and the optimal bandwidth for density estimation may not coincide with the optimal one for entropy estimation. Thus, rather than the rule-of-thumb bandwidth in [33], which aims at optimal density estimation, the bandwidth in our study should provide an accurate estimator for in the minimal mean squared error (MSE) sense, say. In [28] we develop such a bandwidth rule for a TE-based estimator. In that paper, rather than directly developing asymptotic properties for TE, we study the properties of the first order Taylor expansion of TE under the null hypothesis. The suggested bandwidth is shown to be MSE optimal and allows us to obtain asymptotic normality for the test statistic. In principal, the convergence rate of the TE estimator should be the same as the leading term of its Taylor approximation. We therefore propose to use the same rate also here, giving
where C is an unknown parameter. This bandwidth would deliver a consistent test since the variance of local estimate of will dominate the MSE. In [28] we suggest to use based on simulations, while Diks and Panchenko suggest to set for autoregressive conditional heteroskedasticity (ARCH) processes [6]. Our simulations here also may possibly prefer a larger value of C because the squared bias is of higher order and hence less concern for the TE-based statistic. A larger bandwidth could better control the estimation variance and deliver a more powerful test. As a robustness check, we adopt as well as suggested by our other simulation study [28]. To match the Gaussian kernel, we standardize the data before estimate Equation (6a)–(6c) such that the transformed time series have mean zero zero and unit variance; very similar results are obtained by matching the mean absolute deviation instead of the variance of the standard Gaussian kernel for TE estimation.
2.3. Resampling Methods
To develop simulation-based tests for the null hypothesis, given in Equation (4), of no Granger causality from X to Y, or equivalently, for conditional independence, we consider three resampling techniques, i.e., (1) time shifted surrogates developed by Quiroga et al. [22], (2) the smoothed bootstrap of Su and White [7] and (3) the stationary bootstrap introduced by Politis and Romano [38]. The first technique is widely applied in coupling measures, as for example by Kugiumtzis [39] and Papana et al. [40], while the latter two have already been used for detecting conditional independence for decades. It worth mentioning that the surrogates and bootstrap methods treat the null quite differently. Surrogate data are supposed to preserve the dependence structure imposed by while bootstrap data are not restricted to . It is possible to bootstrap the dataset without imposing the conditional independence structure of {X, Y, Z} implied by the null hypothesis; see, for instance, [41] for more details. To avoid resampling errors and to make different methods more comparable, we limit ourselves to methods that impose the null hypothesis on the resampled data. The following three different resampling methods are implemented with different sampling details.
- Time-Shifted Surrogates
- (TS.a) The first resampling method only deals with the driving variable X. Suppose we have observations {}, the time-shifted surrogates are generated by cyclically time-shifting the components of the time series. Specifically, an integer d is randomly generated within the interval , and then the first d values of {} would be moved to the end of the series, to deliver the surrogate sample . Compared with the traditional surrogates based on phase randomization of the Fourier transform, the time-shifted surrogates can preserve the whole statistical structure in X. The couplings between X and Y are destroyed, although the null hypothesis of X not causing Y is imposed.
- (TS.b) The second scheme resamples both the driving variable X and the response variable Y separately. Similar to (TS.a), is created given another random integer c from the range . In contrast with the standard time-shifted surrogates described in (TS.a), in this setting we add more noise to the coupling between X and Y.
- Smoothed Local BootstrapThe smoothed bootstrap selects samples from a smoothed distribution instead of drawing observations from the empirical distribution directly. See [42] for a discussion of the smoothed bootstrap procedure. Based on rather mild assumptions, Neumann and Paparoditis [43] show that there is no need to reproduce the whole dependence structure of the stochastic process to get an asymptotically correct nonparametric dependence estimator. Hence a smoothed bootstrap from the estimated conditional density is able to deliver a consistent statistic. Specifically, we consider two versions of the smoothed bootstrap that are different in dependence structure to some extent.
- (SMB.a) In the first setting, is resampled without replacement from the smoothed local bootstrap. Given the sample , the bootstrap sample is generated by adding a smoothing noise term such that , where is the bandwidth used in bootstrap procedure, represents a sequence of i.i.d. random variables. Without random replacement from the original time series, this procedure does not disturb the original dynamics of at all. After is resampled, both and are drawn from the smoothed conditional densities and as described in [44].
- (SMB.b) Secondly, we implement the smoothed local bootstrap as in [7]. The only difference between this setting and (SMB.a) is that the bootstrap sample is drawn with replacement from the smoothed kernel density.
- Stationary BootstrapPolitis and Romano [38] propose the stationary bootstrap to maintain serial dependence within the bootstrap time series. This method replicates the time dependence of original data by resampling blocks of the data with randomly varying block length. The lengths of the bootstrap blocks follows a geometric distribution. Given a fixed probability p, the length of block i is decided as for , and the starting points of block i are randomly and uniformly drawn from the original n observations. To restore the dependence structure exactly under the null, we combine the stationary bootstrap with the smoothed local bootstrap for our simulations.
- (STB) In short, firstly is picked randomly from the original n observations of , denoted as where . With probability p, is picked at random from the data set; and with probability , , so that would be the next observation to in original series . Proceeding in this way, can be generated. If and , the “circular boundary condition” would kick in, so that . After is generated, both and are randomly drawn from the smoothed conditional densities and as in (SMB.b).
The resampling procedure works as the follows: once the TE statistic for the original data is estimated according to Equation (6a)–(6c), we start to generate the resampled data set, which is denoted by with , where B is the number of simulations. Using the simulated sample, for each j we compute the TE statistic , in exactly the same way as was computed. The p-value for the one-sided test is calculated as
where the constant 1 is added to avoid p-values equal to zero.
A final remark concerns the difference between this paper and [21]; there both time-shifted surrogate and the stationary bootstrap are implemented for an entropy-based causality test. However, our paper provides additional insights into several aspects. Firstly, the smoothed bootstrap, being shown in the literature to work for nonparametric kernel estimators under general dependence structure, is applied in our paper. Secondly, they treat the bootstrap and surrogate sample in a similar way, but as we noted above, the bootstrap method is not designed to impose the null hypothesis but designed to keep the dependence structure present in the original data. The stationary bootstrap procedure in [21] might be incompatible with the null hypothesis of conditional independence since it destroys the dependence completely. Because they restore independence between X and Y rather than conditional independence between and during resampling, the distribution of the estimated statistics from the resampled data may not necessary correspond to that of the statistic under the null of only conditional independence. Thirdly, we provide rigorous size and power result in our simulations, which is missing in their paper.
3. Simulation Study
In this section, we investigate the performance of the five resampling methods in detecting conditional dependence for several data generating processes. In Equations (9)–(16), we use a single parameter a to control the strength of the conditional dependence. The size assessment is obtained based on testing Granger non-causality from to , and for the power we use the same process but we test for Granger non-causality from to . We set to represent moderate dependence in the size performance investigation and to evaluate the power of the tests. Further, Equation (17) represents a stationary autoregressive process with regime switching, and Equation (18) is included to investigate the power performance in the presence of two-way causal linkages, where the two control parameters are and .
In each experiment, we run 500 simulations for sample sizes . The surrogate and the bootstrap sample size is set to . For fair comparisons between (TS.a) and (TS.b), as well as between (SMB.a) and (SMB.b), we fix the seeds of the random number generator in the resampling functions to eliminate the potential effect of randomness. Besides, we use the empirical standard deviation of as the bootstrapping bandwidth and in the bandwidth equation Equation (7) for the kernel density estimation.
The processes under consideration include a linear vector autoregressive process (VAR) in Equation (9), a nonlinear VAR process in Equation (10), a bivariate ARCH process in Equation (11), a bilinear process in Equation (12), a bivariate AR(2)-GARCH process in Equation (13) where “GARCH” stands for “generalized ARCH”, a bivariate autoregressive-moving average (ARMA)-GARCH process in Equation (14), a bivariate AR(1)-EGARCH process in Equation (15) where “EGARCH” represents “exponential GARCH”, a vector error correction (VECM) process in Equation (16), a threshold AR(1) process in Equation (17), and a two-way VAR process in Equation (18).
It is worth mentioning that the data generating processes in Equations (9)–(12), (17) and (18) are stationary and of finite memory as we assumed earlier. However, it is also important to be aware of the behavior of the proposed non-parametric test for robustness consideration when the two assumptions are not satisfied. The finite memory assumption is violated in Equations (13)–(15) since the GARCH process, being equivalent to an infinite ARCH process, strictly speaking is of infinite Markov order; and the stationarity assumption does not hold in Equation (16) where and are cointegrated of order one. Since for the VECM process the two time series and are not stationary, we can not directly apply our nonparametric test. In this case, we perform the Engle–Granger approach [45] first to eliminate the influence of the co-integration, and then perform the nonparametric test on the collected stationary residuals from the linear regression of and on a constant and the co-integration term. The procedure is similar to that in [46].
- Linear vector autoregressive process (VAR).
- Nonlinear VAR. This process is considered in [47] to show the failure of linear Granger causality test.
- Bivariate ARCH process.
- Bilinear process considered in [48].
- Bivariate AR(2)-GARCH process.
- Bivariate ARMA-GARCH process.
- Bivariate AR(1)-EGARCH process.
- VECM process. Note that in this situation both and are not stationary.
- Threshold AR(1) process.
- Two-way VAR process.
The empirical rejection rates are summarized in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10. The top panels in each table summarize the empirical rejection rates obtained for the 5% and 10% nominal significance levels for processes (9)–(18) under the null hypothesis, and the bottom panels report the corresponding empirical power under the alternatives. Generally speaking, the size and power are quite satisfactory for almost all combinations of the constant C, sample size n and nominal significance level. The performance differences for the various resampling schemes are not substantial.

Table 1.
Observed size and power of the TE-based test for the linear VAR process in Equation (9).

Table 2.
Observed size and power of the TE-based test for the nonlinear VAR process in Equation (10).

Table 3.
Observed size and power of the TE-based test for the bivariate ARCH process in Equation (11).

Table 4.
Observed size and power of the TE-based test for the bilinear process in Equation (12).

Table 5.
Observed size and power of the TE-based test for the AR(2)-GARCH process in Equation (13).

Table 6.
Observed size and power of the TE-based test for the ARMA-GARCH process in Equation (14).

Table 7.
Observed size and power of the TE-based test for the AR(1)-EGARCH process in Equation (15).

Table 8.
Observed size and power of the TE-based test for the VECM process in Equation (16).

Table 9.
Observed size and power of the TE-based test for the threshold AR(1) process in Equation (17).

Table 10.
Observed Power of the TE-based test for the two-Way VAR process in Equation (18).
With respect to the size performance, most of the time we see that the realized rejection rates stay in line with the nominal size. Besides, the bootstrap methods outperform the time-shifted surrogate methods in that their empirical size is slightly closer to the nominal size. Lastly, the size of the tests is not very sensitive to the choice of the constant C apart from the cases for the models given in Equations (13)–(15), where the data generating process has infinite memory.
From the point of view of power, (TS.a) and (SMB.a) seem to outperform their counterparts, yet, the differences are subtle. Along the dimension of the sample size, clearly we see that the empirical power increases in the sample size in most cases. Furthermore, the results are very robust with respect to choices for the constant C in the kernel density estimation bandwidth. For the VAR and nonlinear processes given by Equations (9), (10) and (12) a smaller C seems to give more powerful tests while a larger C is more beneficial for detecting conditional dependence structure in the (G)ARCH processes of Equations 11 and (13)–(15).
Finally, Table 10 presents the empirical power for the two-way VAR process, where the two variables and are inter-tangled with each other. Due to the setting and in Equation (18), it is obvious that is a stronger Granger cause for than the other way around. As a consequence, the reported rejection rates in Table 10 are overall higher when testing than .
To visualize the simulation results, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 report the empirical size and power against the nominal size. Since the performance of the five difference resampling methods is quite similar, we only show the results for (SMB.a) for simplicity. In each figure, the left (right) panels show the realized size (power), and we choose () for the top (bottom) two panels. We can see from the figures that the empirical performance of the TE test are overall satisfactory, apart for those (G)ARCH processes where a small C may lead to conservative testing size for large sample sizes (see Figure 3a, Figure 5a, Figure 6a and Figure 7a). The under-rejection problem is caused by the inappropriate choice , which makes the bandwidth for kernel estimation too small. The influence of an inappropriately small bandwidth can also be seen in Figure 5b and Figure 6b, where the test has limited power for the alternative.
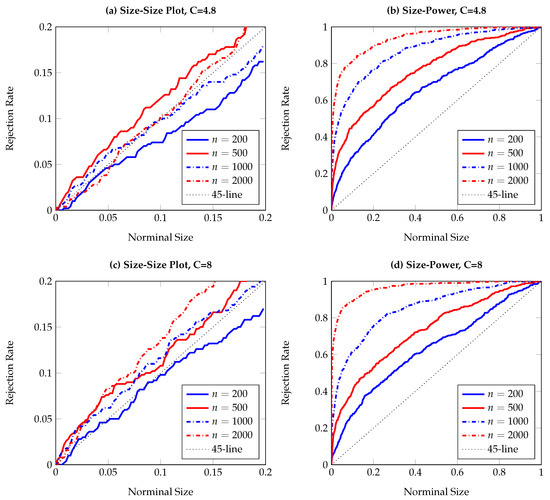
Figure 1.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The data generating process (DGP) is the bivariate VAR process in Equation (9), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
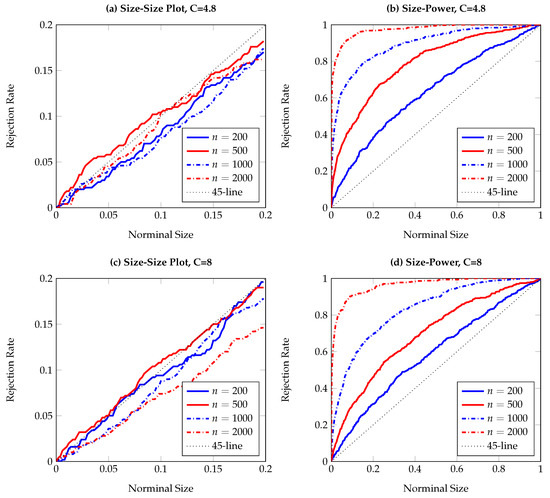
Figure 2.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate non-linear VAR process in Equation (10), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
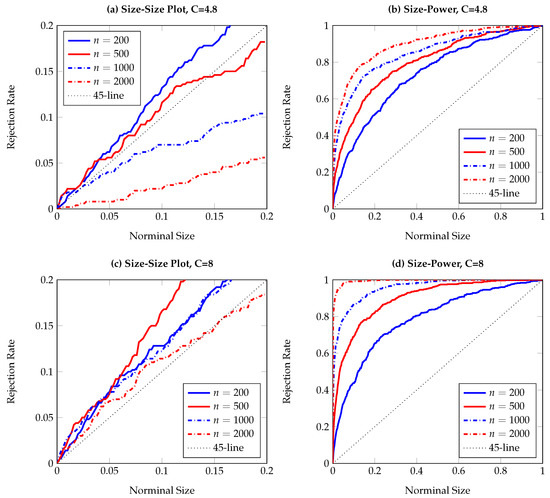
Figure 3.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate ARCH process in Equation (11), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
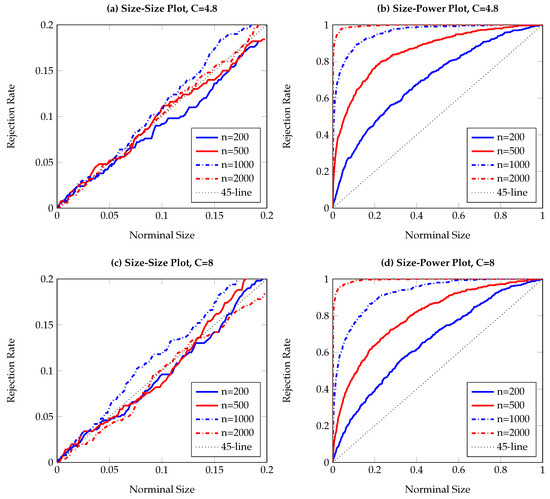
Figure 4.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bilinear process in Equation (12), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
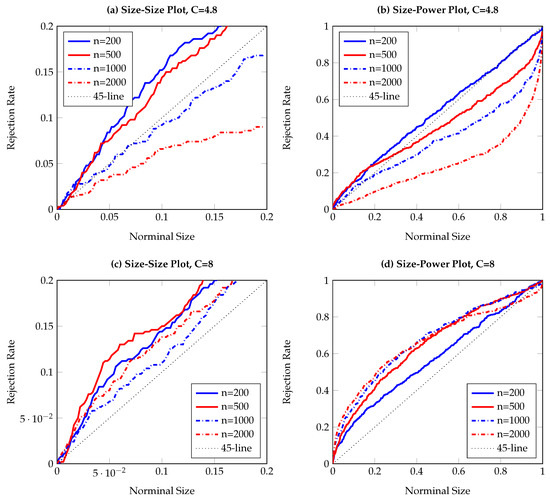
Figure 5.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate AR2-GARCH process in Equation (13), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
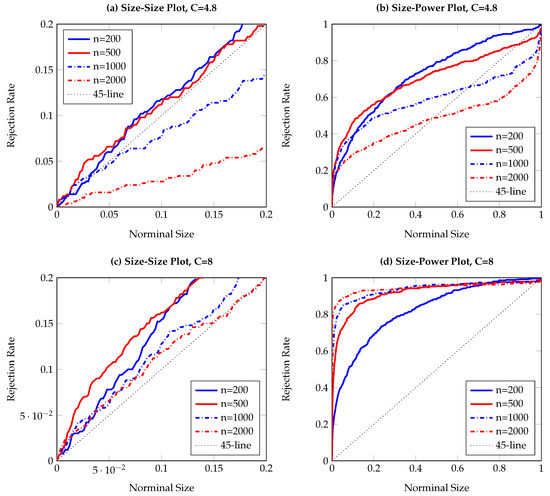
Figure 6.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate ARMA-GARCH process in Equation (14), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
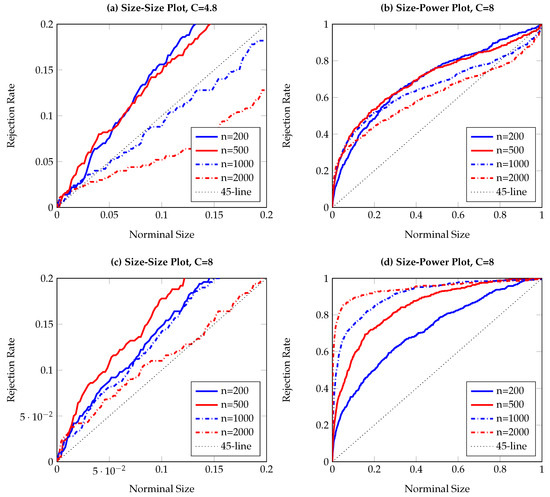
Figure 7.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate AR1-EGARCH process in Equation (15), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
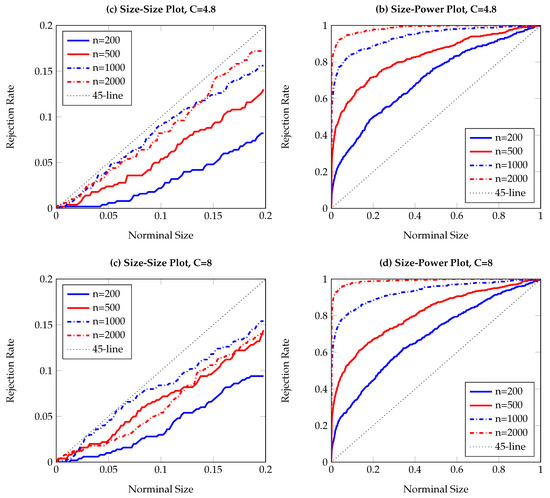
Figure 8.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the VECM process in Equation (16), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
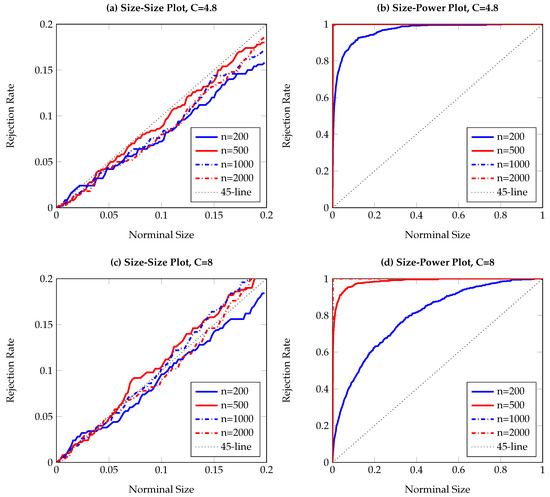
Figure 9.
Size-size and size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the bivariate threshold AR(1) process in Equation (17), with Y affecting X. The left (right) column shows observed rejection rates under the null (alternative) hypothesis. The sample size varies from to .
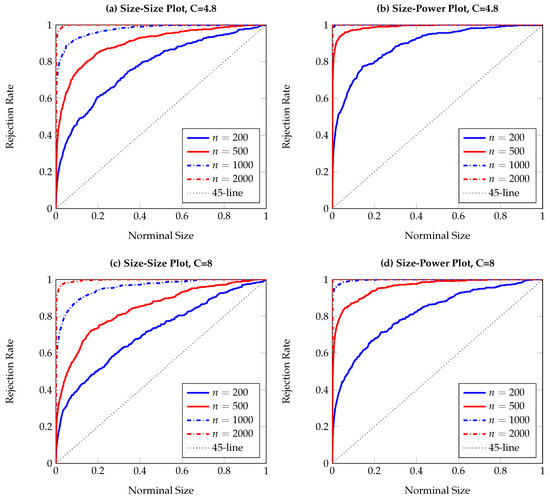
Figure 10.
Size-power plots of Granger non-causality tests, based on 500 replications and smoothed local bootstrap (a). The DGP is the two-way VAR process in Equation (18), with X affecting Y and Y affecting X. The left (right) column shows observed rejection rates for testing X (Y) causing Y (X). The sample size varies from to .
4. Application
In this section, we apply the TE-based nonparametric test on detecting financial market interdependence, in terms of both return and volatility. Diebold and Yilmaz [49] performed a variance decomposition of the covariance matrix of the error terms from a reduced-form VAR model to investigate the spillover effect in the global equity market. More recently, Gamba-Santamaria et al. [50] extended the framework and considered the time-varying feature in global volatility spillovers. Their research, although providing simple and intuitive methods for measuring directional linkages between global stock markets, may suffer from the limitation of the linear parametric modeling, as discussed above. We revisit the topic of spillovers in the global equity market by the nonparametric method.
For our analysis, we use daily nominal stock market indexes from January 1992 to March 2017, obtained from Datastream, for six developed countries including the US (DJIA), Japan (Nikkei 225), Hong Kong (Hangseng), the UK (FTSE 100), Germany (DAX 30) and France (CAC 40). The target series are weekly return and volatility for each index. The weekly returns are calculated in terms of diffferenced log prices multiplied by 100, from Friday to Friday. Where the price for Friday is not available due to a public holiday, we use the Thursday price instead.
The weekly volatility series are generated following [49] by making use of the weekly high, low, opening and closing prices, obtained from the underlying daily high, low, opening and closing data. The volatility for week t is estimated as
where is the Monday-Friday high, is the Monday–Friday low, is the Monday-Friday open and is the Monday-Friday close (in natural logarithms multiplied by 100). Futher, after deleting the volatility estimates for the New Year week in 2002, 2008 and 2013 due to the lack of observations for Nikkei 225 index, we have 1313 observations in total for weekly returns volatilities. The descriptive statistics, Ljung Box (LB) test statistics and Augmented Dickey Fuller (ADF) test statistics for both series are summarized in Table 11. From the ADF test results, it is clear that all time series are stationary for further analysis (we also performed the Johansen cointegration test pair-wisely on the price levels and no cointegration was found for the six market indexes.).

Table 11.
Descriptive statistics for global stock market return and volatility.
We firstly provide a full-sample analysis of global stock market return and volatility spillovers over the period from January 1992 to March 2017, summarized in Table 12 and Table 13. The two tables report the pairwise test statistics for conditional independence between index X and index Y, given the constant C in the bandwidth for kernel estimation is or 8 and 999 resampling time series. In other words, we test for the absence of the one-week-ahead directional linkage from index X to Y by using the five resampling methods described in Section 2. For example, the first line in the top panel in Table 12 reports the one-week-ahead influence of DJIA returns upon other indexes by using the first time-shifted surrogates method (TS.a). Given , DJIA return is shown to be a strong Granger cause for Nikkei, FTSE and CAC at the 1% level, and for DAX at the 5% level.

Table 12.
Detection of Conditional Dependence in Global Stock Returns.

Table 13.
Detection of Conditional Dependence in Global Stock Volatilities.
Based on Table 12 and Table 13, we may draw several conclusions. Firstly, the US index and German index are the most important return transmitters and Hong Kong is the largest source for volatility spillover, judged by the numbers of significant linkages. Note that this finding is similar as the result in [49], where the total return (volatility) spillovers from US (Hong Kong) to others are found to be much higher than from any other country. Figure 11 provides a graphical illustration of the global spillover network based on the result of (SMB.a) from Table 12 and Table 13. Apart from the main transmitters, we can clearly see that Nikkei and CAC are the main receivers in the global return spillover network, while DAX is the main receiver of global volatility transmission.
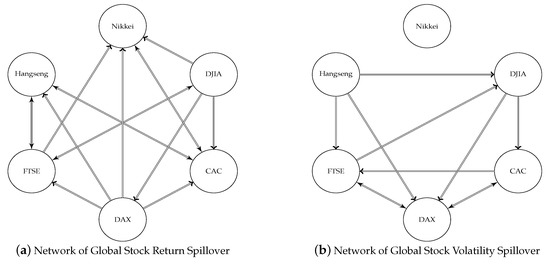
Figure 11.
Graphical representation of pairwise causalities on global stock returns and volatilities. All “→” in the graph indicate a significant directional causality at the 5% level.
Secondly, the result obtained is very robust, no matter which re-sampling method is applied. Although the differences between the five resampling methods are small, (TS.a) is seen to be slightly more powerful than (TS.b) in Table 12. The three different bootstrap methods are very consistent almost all the time, similarly to what we observed in Section 3.
However, the summary results in Table 12 and Table 13 are static in the sense that they do not take into account possible time-variation. The statistics are measurements for averaged-out directional linkages over the whole period from 1992 to 2017. The conditional dependence structure of the time series, at any point in time, can be very different. Hence, the full-sample analysis is very likely to oversee the cyclical dynamics between each pair of stock indices. To investigate the dynamics in the global stock market, we now move from the full-sample analysis to a rolling-window study. Considering a 200-week rolling window starting from the beginning of the sample and admitting a 5-week forward step for the iterative evaluation of the conditional dependence, we can assess the variation of the spillover in the global equity market over time.
Taking the return series of the DJIA as an illustration, we iteratively exploit the local smoothed bootstrap method for detecting Granger causality from and to the DJIA return in Figure 12 (all volatility series are extremely skewed, see Table 11. In a small sample analysis, the test statistics turn out to be sensitive to the clustering outliers, which typically occur during the market turmoil. As a result, the volatility dynamics are more radical and less informative than that of returns). The red line represents the p-values for the TE-based test on DJIA weekly return as the information transmitter while the blue line shows the p-values associated with testing on DJIA as a receiver of information spillover on a weekly basis from others. The plots displays an event-dependent pattern, particularly for the recent financial crisis; from early 2009 until the end of 2012, all pairwise tests show the presence of a strong bi-directional linkage. Besides, the DJIA is strongly leading the Nikkei, Hangseng and CAC during the first decade of this century.
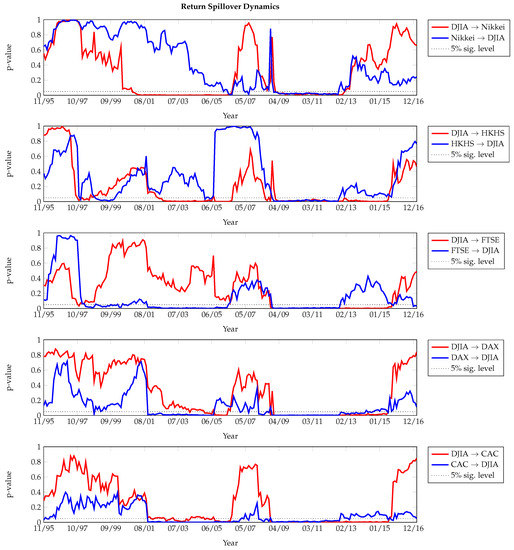
Figure 12.
Time-varying p-values for the TE-based Granger causality test in Return series. The causal linkages from DJIA to other markets, as well as the linkages from other markets to DJIA are tested.
Further, we see that the influence from other indices to the DJIA are different, typically responding to economics events. For example, the blue line in the second panel of Figure 12 plunges below the 5% level twice before the recent financial crisis, meaning that the Hong Kong Hangseng index causes fluctuations in the DJIA during those two periods; first in the late 90’s and again by the end of 2004. The timing of the first fall matches the 1997 Asian currency crisis and the latter one was in fact caused by China’s austerity policy in October 2004.
Finally, the dynamic plots provide additional insights into the sample period that the full sample analysis may omit. The DAX and CAC are found to be less relevant for future fluctuations in the weekly return of the DJIA, according to Table 12 and Figure 11. However, one can clearly see that since 2001, the p-values for DAX→DJIA and CAC→DJIA are consistently below 5% for most of the time, suggesting an increase of the integration of global financial markets.
5. Conclusions
This paper provides guidelines for the practical application of TE in detecting conditional dependence, i.e., Granger causality in a more general sense, between two time series. Although there already is a tremendous literature that tried to apply the TE in this context, the asymptotics of the statistic and the performance of the resampling-based measures are still not understood well. We have considered tests based on five different resampling methods, all of which were shown in the literature to be suitable for entropy-related tests, and investigated the size and power of the associated tests numerically. Two time-shifted surrogates and three smoothed bootstrap methods are tested on simulated data from several processes. The simulation results in this controlled environment suggest that all five measures achieve reasonable rejection rates under the null as well as the alternative hypotheses. Our results are very robust with respect to the density estimation method, including the procedure used for standardizing the location and scale of the data and the choice of the bandwidth parameter, as long as the convergence rate of the kernel estimator of TE is consistent with its first order Taylor expansion.
In the empirical application, we have shown how the proposed resampling techniques can be used on real world data for detecting conditional dependence in the data set. We use global equity data to carry out the detection in pairwise causalities in the return and volatility series among the world leading stock indexes. Our work can be viewed as a nonparametric extension of the spillover measures considered by Diebold and Yilmaz [49]. In accordance with them, we found evidence that the DJIA and the DAX are the most important return transmitters and Hong Kong is the largest source for volatility spillover. Furthermore, the rolling window-based test for Granger causality in pairwise return series demonstrated that the causal linkages in the global equity market are time-varying rather than static. The overall dependence is more tight during the most recent financial crisis, and the fluctuations of the p-values are shown to be event dependent.
As for future work, there are several directions for potential extensions. On the theoretical side, it would be practically meaningful to consider causal linkage detection beyond the single period lag and to deal with the infinite order issue in a nonparametric setting. Further nonparametric techniques need to be developed to play a similar role as the information criterion does for order selection of an estimation model in the parametric world. On the empirical side, it will be interesting to further exploit entropy-based statistics in testing conditional dependence when there exists a so-called common factor, i.e., looking at multivariate systems with more than two variables. One potential candidate for this type of test in the partial TE has been coined by Vakorin et al. [51], but its statistical properties still need to be thoroughly studied yet.
Acknowledgments
We thank the editor and two anonymous referees for their help and constructive comments. We would also like to thank seminar participants at the University of Amsterdam and the Tinbergen Institute. The authors also wish to extend particular gratitude to Simon Broda and Chen Zhou for their comments on an earlier version of this paper. We also acknowledge SURFsara for providing the computational environment of the LISA cluster.
Author Contributions
Both authors contributed equally to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423; 623–656. [Google Scholar] [CrossRef]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Hiemstra, C.; Jones, J.D. Testing for linear and nonlinear Granger causality in the stock price-volume relation. J. Financ. 1994, 49, 1639–1664. [Google Scholar] [CrossRef]
- Diks, C.; Panchenko, V. A new statistic and practical guidelines for nonparametric Granger causality testing. J. Econ. Dyn. Control 2006, 30, 1647–1669. [Google Scholar] [CrossRef]
- Su, L.; White, H. A nonparametric Hellinger metric test for conditional independence. Econom. Theory 2008, 24, 829–864. [Google Scholar] [CrossRef]
- Bouezmarni, T.; Rombouts, J.V.; Taamouti, A. Nonparametric copula-based test for conditional independence with applications to Granger causality. J. Bus. Econ. Stat. 2012, 30, 275–287. [Google Scholar] [CrossRef]
- Su, L.; White, H. Testing conditional independence via empirical likelihood. J. Econom. 2014, 182, 27–44. [Google Scholar] [CrossRef]
- Hlaváčková-Schindler, K.; Paluš, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Amblard, P.O.; Michel, O.J. The relation between Granger causality and directed information theory: A review. Entropy 2012, 15, 113–143. [Google Scholar] [CrossRef]
- Granger, C.; Lin, J.L. Using the mutual information coefficient to identify lags in nonlinear models. J. Time Ser. Anal. 1994, 15, 371–384. [Google Scholar] [CrossRef]
- Hong, Y.; White, H. Asymptotic distribution theory for nonparametric entropy measures of serial dependence. Econometrica 2005, 73, 837–901. [Google Scholar] [CrossRef]
- Barnett, L.; Bossomaier, T. Transfer entropy as a log-likelihood ratio. Phys. Rev. Lett. 2012, 109, 138105. [Google Scholar] [CrossRef] [PubMed]
- Efron, B. Computers and the theory of statistics: Thinking the unthinkable. SIAM Rev. 1979, 21, 460–480. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phy. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Horowitz, J.L. The Bootstrap. Handb. Econ. 2001, 5, 3159–3228. [Google Scholar]
- Hinich, M.J.; Mendes, E.M.; Stone, L. Detecting nonlinearity in time series: Surrogate and bootstrap approaches. Stud. Nonlinear Dyn. Econom. 2005, 9. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Nollo, G. Mutual nonlinear prediction as a tool to evaluate coupling strength and directionality in bivariate time series: Comparison among different strategies based on k nearest neighbors. Phys. Rev. E 2008, 78, 026201. [Google Scholar] [CrossRef] [PubMed]
- Papana, A.; Kyrtsou, K.; Kugiumtzis, D.; Diks, C. Assessment of resampling methods for causality testing: A note on the US inflation behavior. PLoS ONE 2017, 12, e0180852. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, R.Q.; Kraskov, A.; Kreuz, T.; Grassberger, P. Performance of different synchronization measures in real data: A case study on electroencephalographic signals. Phys. Rev. E 2002, 65, 041903. [Google Scholar] [CrossRef] [PubMed]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B Condens. Matter Complex Syst. 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Evaluation of surrogate and bootstrap tests for nonlinearity in time series. Stud. Nonlinear Dyn. Econom. 2008. [Google Scholar] [CrossRef]
- Robinson, P.M. Consistent nonparametric entropy-based testing. Rev. Econ. Stud. 1991, 58, 437–453. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Granger, C.; Maasoumi, E.; Racine, J. A dependence metric for possibly nonlinear processes. J. Time Ser. Anal. 2004, 25, 649–669. [Google Scholar] [CrossRef]
- Diks, C.; Fang, H. Detecting Granger Causality with a Nonparametric Information-Based Statistic; CeNDEF Working Paper No. 17-03; University of Amsterdam: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Moddemeijer, R. On estimation of entropy and mutual information of continuous distributions. Signal Process. 1989, 16, 233–248. [Google Scholar] [CrossRef]
- Diks, C.; Manzan, S. Tests for serial independence and linearity based on correlation integrals. Stud. Nonlinear Dyn. Econom. 2002, 6, 1–20. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; CRC Press: Boca Raton, FL, USA, 1994; Volume 60. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Joe, H. Estimation of entropy and other functionals of a multivariate density. Ann. Inst. Stat. Math. 1989, 41, 683–697. [Google Scholar] [CrossRef]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Jones, M.C.; Marron, J.S.; Sheather, S.J. A brief survey of bandwidth selection for density estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- He, Y.L.; Liu, J.N.; Wang, X.Z.; Hu, Y.X. Optimal bandwidth selection for re-substitution entropy estimation. Appl. Math. Comput. 2012, 219, 3425–3460. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. The stationary bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Direct-coupling information measure from nonuniform embedding. Phys. Rev. E 2013, 87, 062918. [Google Scholar] [CrossRef] [PubMed]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Simulation study of direct causality measures in multivariate time series. Entropy 2013, 15, 2635–2661. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Shao, J.; Tu, D. The Jackknife and Bootstrap; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Neumann, M.H.; Paparoditis, E. On bootstrapping L2-type statistics in density testing. Stat. Probab. Lett. 2000, 50, 137–147. [Google Scholar] [CrossRef]
- Paparoditis, E.; Politis, D.N. The local bootstrap for kernel estimators under general dependence conditions. Ann. Inst. Stat. Math. 2000, 52, 139–159. [Google Scholar] [CrossRef]
- Engle, R.; Granger, C. Co-integration and error correction: Representation, estimation, and testing. Econometrica 1987, 2, 251–276. [Google Scholar] [CrossRef]
- Bekiros, S.; Diks, C. The nonlinear dynamic relationship of exchange rates: Parametric and nonparametric causality testing. J. Macroecon. 2008, 30, 1641–1650. [Google Scholar] [CrossRef]
- Baek, E.G.; Brock, W.A. A General Test for Nonlinear Granger Causality: Bivariate Model; Working Paper; Iowa State University and University of Wisconsin: Madison, EI, USA, 1992. [Google Scholar]
- Davidson, J. Establishing conditions for the functional central limit theorem in nonlinear and semiparametric time series processes. J. Econom. 2002, 2, 243–269. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Gamba-Santamaria, S.; Gomez-Gonzalez, J.E.; Hurtado-Guarin, J.L.; Melo-Velandia, L.F. Volatility Spillovers Among Global Stock Markets: Measuring Total and Directional Effects; Technical Report No. 983; Banco de la Republica de Colombia: Bogotá, Colombia, 2017. [Google Scholar]
- Vakorin, V.A.; Krakovska, O.A.; McIntosh, A.R. Confounding effects of indirect connections on causality estimation. J. Neurosci. Methods 2009, 184, 152–160. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).