Abstract
There are currently around 78 nuclear power plants (NPPs) in the world based on Boiling Water Reactors (BWRs). The current parameter to assess BWR instability issues is the linear Decay Ratio (DR). However, it is well known that BWRs are complex non-linear dynamical systems that may even exhibit chaotic dynamics that normally preclude the use of the DR when the BWR is working at a specific operating point during instability. In this work a novel methodology based on an adaptive Shannon Entropy estimator and on Noise Assisted Empirical Mode Decomposition variants is presented. This methodology was developed for real-time implementation of a stability monitor. This methodology was applied to a set of signals stemming from several NPPs reactors (Ringhals-Sweden, Forsmark-Sweden and Laguna Verde-Mexico) under commercial operating conditions, that experienced instabilities events, each one of a different nature.
1. Introduction
Currently, there are 78 nuclear boiling water reactors (BWRs) in use around the world for the generation of electricity. BWRs contribute significantly to the production of global electric power and to date are the simplest energy system to transform fission energy into electrical energy, due to the direct cycle to turbine with dry saturated steam. However, there are still fundamental aspects in its operation related to the interaction of thermohydraulic processes (heat transfer in fuel and refrigerant) with the neutron kinetics process. Such interaction may, under certain operating conditions, cause BWR to malfunction and affect its stability. The problem of the stability of the BWR has been the subject of important scientific and technological work during more than four decades dedicated to its study.
Instability events are rare and may occur during BWR start up or during transients that may change the operation region of the reactor. Figure 1 shows the example of a typical power-flow map diagram of a nuclear power plant (NPP), which shows the regions where the reactor should not be operated (red box) for reasons of stability, those ones where the BWR can be operated only under supervision (brown box) and finally, the diagram shows the regions of stable reactor operation (regions where the core flow is high). Currently, there is a tendency to design higher power reactors. In addition, refinement of fuel elements has encouraged the introduction of increasingly efficient fuels that allow the plant to operate at increasingly high power levels. Such a power increase induces a higher reactivity feedback and a decrease in response time, resulting in a lower BWR stability range when the plant operates at a low mass flow and at high nominal power. Another current trend is to increase the size of the core, which causes a weaker special coupling in the neutron field which increases the susceptibility of the reactor to experiencing unstable oscillations. In summary, all current tendencies related to reactor design enhance the regions where the reactor should not be operated (reactor operation at low flow and high power).
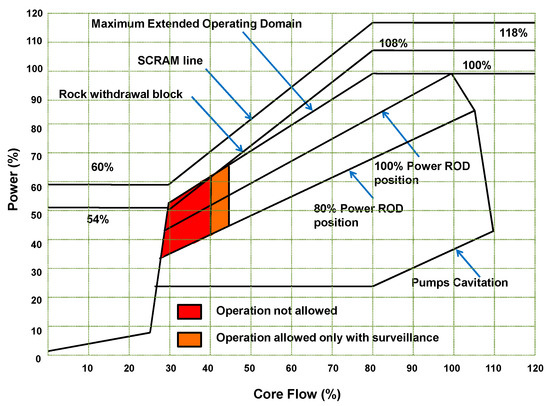
Figure 1.
Typical Power-flow map of a NPP.
Events of instability have already occurred in the past in commercial BWRs, such as the Laguna Verde Nuclear Power Plant [1,2]. Some cases of instability occurred inadvertently, while others were intentionally provoked for experimental purposes [3]. Periodic oscillations in the neutron flux were observed during these instability events via the electronic instrumentation of the reactor. After the first events of instability occurred, the corresponding authorities (regulatory commissions) requested the development of research projects to study the mechanisms involved in reactor stability in order to:
- Study the stability margins of the plant under normal operating conditions and in unusual conditions.
- Predict reactor transients in an event of instability.
- Develop measures to prevent and mitigate the consequences of an event of instability.
In BWR instability events, two kinds of instabilities are found: in-phase (global or core-wide) oscillations, and out-of-phase (regional) oscillations. In-phase oscillation, i.e., where neutron flux oscillations are in-phase at all the fuel bundles in the core, are caused by the lag introduced into the thermal-hydraulic system by the finite speed of propagation of density perturbation [4]. At high-core void fractions and low flow conditions, the feedback becomes so strong that it induces oscillations at a frequency of about 0.5 Hz. When this feedback increases, the oscillation becomes more pronounced, and oscillatory instability is reached. The term out-of-phase oscillation is applied to those instabilities in which different reactor core zones show a considerable phase shift (180°) in neutron flux oscillation, i.e., where neutron flux from one half of the core oscillates out-of-phase with respect to that one of the other half. It has been shown that stability depends on several variables such as control rod patterns, void fraction, burnup, inlet mass flow, among others.
Currently, the most common parameter to evaluate BWR stability is known as the decay ratio (DR), which is calculated from the impulse response function that stems from an autoregressive (AR) modeling of BWR signals. The decay ratio is a simple straightforward index to scale a margin to the stability boundary and this property is the main output of most stability monitoring systems [5]. The use of the DR as a feasible BWR stability measure has been widely accepted, nonetheless, it has been observed that a BWR working at an operating point with a small DR can be close to instability [6]. Also, the DR often jumps discontinuously from the well stable to the far-unstable region [7]. The BWR stability is of primary interest from the point of view of BWR operation, due to the fact, that the stability margin may be strongly reduced during plant maneuvering and transients [8]. According to these issues, the DR might not be a reliable monitoring index after all, under certain operating conditions. Besides, in regular operating conditions, the need for stationary signals might be a handicap for DR estimation. Thus, it is relevant to explore new alternative methodologies and indexes adapted to accommodate for non-stationary and non-linear BWR signal behavior.
In [9] a short time Fourier transform based technique was explored to study the time dependence of the natural frequency when the BWR signal is non-stationary. Later, the wavelet theory was applied to explore new alternatives for transient instability analysis [10,11]. However, in general BWR signals are non-stationary and non-linear, thus Fourier-based or wavelet-based approaches might lead to a biased stability analysis. Several methods for non-linear BWR stability analysis have been applied before [12,13], to study BWR signals containing stationary and non-stationary segments. In this work, the Shannon Entropy (SE) was applied, to infer whether it can be used as a novel stability parameter for BWRs. The SE is a concept that was developed by Claude E. Shannon [14] to study a discrete source through the information content of this source. The SE is a statistical index that quantifies the complexity of a signal. In this case, the BWR stability issue is assessed quantifying the complexity of BWR signals through this proposed parameter SE. A low SE value is linked to a predictable BWR event (stable scenario) whereas a high SE indicates an unpredictable BWR event (an unstable scenario).
To properly estimate the SE from BWR signals, two noise assisted empirical mode decomposition (EMD) methods were explored: the improved complete ensemble empirical mode decomposition with assisted noise (iCEEMDAN) and the noise assisted multivariate empirical mode decomposition (NA-MEMD). Both techniques were proposed in [15,16] respectively. Henceforth, for simplicity, we will refer to any of these two methods as noise assisted empirical mode decomposition method (NA-EMDm). The NA-EMDm is an algorithm that decomposes non-stationary signals that stem from non-linear systems. The method also alleviates the mode mixing phenomenon of the default EMD method, that was first proposed in [17] by Huang et al. The NA-EMDm produces a local and fully data-driven separation of a signal in fast and slow oscillations. At the end of the procedure, the original signal can be expressed as a sum of amplitude and frequency modulated (AM-FM) functions called intrinsic mode functions (IMFs), also known as modes, plus a final monotonic trend. The combination of NA-EMDm and the Hilbert transform is known as the Hilbert–Huang transform (HHT). The method we propose is based on the HHT and it estimates a parameter associated to BWR stability, in this case the previously mentioned SE. The NA-EMDm decomposes the studied BWR signal (signals in the NA-MEMD case) into IMFs. One or more of these extracted modes can be associated to the instability problem in BWRs. Through HHT it is possible to get the instantaneous frequency (IF) associated to each IMF. By tracking this IF and the SE of the IMF linked to instability, the estimation of the SE-based stability indicator is accomplished. The methodology here proposed is a continuation of a previous work [18] developed by the authors, in which a SE/iCEEMDAN technique was tested with artificial signals generated with the aid of a simple but powerful Reduced Order Model (ROM) that fits the BWR non-linear dynamic behavior. The work presented in [18] is now expanded in here to assess the stability of real BWR signals through iCEEMDAN and NA-MEMD.
The combination of EMD variants plus entropy measures has been applied before in various scientific disciplines, for instance, in [19] a methodology for the classification of electroencephalogram (EEG) signals was developed using entropy measures. The EEG signals were first decomposed through default EMD into IMFs. Later, the Shannon entropy, the Renyi entropy, the approximate entropy, the sample entropy, among other entropy measures, were computed from the extracted IMFs to study the complex electrical activities of the brain. In [20] a study was developed to analyze EEG signals to compare them with existing bi-spectral indexes (BIS), which are indicators that are often used to assess the depth of anesthesia. The MEMD was utilized to filter EEG data, later the combination of two MEMD components (IMF 2 + IMF 3) were used to express raw EEG data. Then, the sample entropy algorithm was used in the study to calculate the complexity of the patients EEG data. Furthermore, linear regression and artificial neural network methods were used to model the sample entropy using the BIS index. In [21] the original CEEMDAN was used to develop a new method for filtering time series originating from non-linear impact (signals used to study the impact events in mechanical systems for health monitoring analysis) systems. Then, the complexity of the extracted IMFs was quantified by fuzzy entropy. In [22] multiscale entropy measures were computed over different scales of IMFs extracted by EMD to study the regularity of a time series related to brain dynamics, their methodology was also extended to study multi-channel multi-trial neural data through the MEMD approach. The list of applications of methods combining a NA-EMDm plus a measure of entropy go onward, to the degree that this combination is now becoming an entropic analysis strategy to provide an information based-interpretation of data [23]. However, Shannon entropy measure was never used before [18] as a stability indicator for a BWR.
This paper is organized as follows: in Section 2 a brief introduction about BWRs and their instrumentation inside the core are presented. A full review of the two chosen NA-EMDm algorithms to understand the basic background of the decomposition methods employed, are detailed in Section 3. The SE estimator, employed as BWR stability indicator, is introduced in Section 4. In Section 5, the methodology to estimate the instantaneous frequency and the proposed SE parameter is detailed. The validation of the methodology presented in this paper is performed doing experiments with real signals taken from the Forsmark and Ringhals stability benchmarks and from a Laguna Verde instability event and presented in Section 6. Also in this same section, the SE results are compared with current DR estimations, computed via techniques based on default EMD [24,25]. Our major findings regarding our novel methodology are talked through in Section 7.
2. BWRs Background
2.1. Description of a BWR
The BWR configuration and the flow paths are illustrated in Figure 2 [26]. The reactor water recirculation system, whose objective is to circulate the required coolant flow through the reactor core, consists of two external loops to the reactor vessel. Each loop contains a pump with a directly coupled motor, a flow control valve, and two shut-off valves. The jet pump located within the reactor vessel provides a continuous internal circulation path for a major portion of the core coolant flow. The recirculation pumps take the suction from the downward flow in the annulus between the core shroud and the vessel wall. The core flow is taken from the vessel through two recirculation nozzles. Into this site, the flow is pumped to a higher pressure, distributed through a manifold to which a number of riser pipes are connected, and returned to the vessel inlet nozzles.
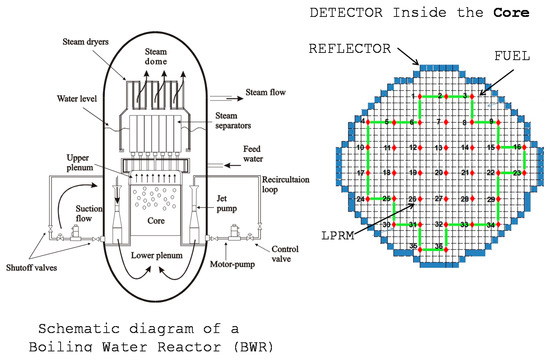
Figure 2.
Schematic diagram of a BWR and an example of a distribution of 36 LPRM (red dots) detectors located at a radial position within the core.
This flow is discharged from jet pump nozzles into the initial stage of the jet pumps throat where, due to a momentum exchange process, induces the surrounding water in the downcomer region to be drawn into the jet pumps throats. Here, these two flows are mixed and then diffused in the diffuser, to be finally discharged into the lower core plenum. The coolant water passes along the individual fuel rods inside the fuel channel where it boils and becomes a two-phase steam/water mixture. In the core, the two-phase fluid generates upward flows through the axial steam separators while the steam continues through the dryers and flows directly out through the steam lines into the turbine-generator. The condensate flow is then returned through the feedwater heaters by the condensate-feedwater pumps into the vessel. The water, which is separated from the steam in the steam separators, flows downward in the periphery of the reactor vessel and mixes with the incoming main feed flow from the turbine. This downward flow enters to the jet pumps and the remainder exits from the vessel as recirculation flow.
2.2. Instrumentation Inside the Core of a BWR
It is possible to detect BWR oscillations linked to instability via a series of detectors known as local power range monitors (LPRMs). These detectors are located radially and axially within the core vessel, as depicted in Figure 2. Their task is to monitor the local neutron flux of the reactor at a certain locality. Within the core, there is a particular detector which averages a series of LPRMs, the latter is known as average power range monitor (APRM). The APRM detectors control the emergency shutdown of a BWR (i.e., SCRAM) through a reactor protection system (RPS) mechanism that triggers when the detected APRM oscillation exceeds the security threshold. The in-phase (global or core-wide) oscillations can be observed in the APRM detectors and via the RPS and it is possible to SCRAM the reactor if a strong in-phase oscillation is observed (or the operator can also shutdown the reactor if necessary). However, the out-of-phase (regional) oscillations cannot be observed in the APRM detectors, because one out-of-phase oscillation with perfect symmetry (a phase shift of 180° between the reactor core zones that participate in the averaging operation via their respective LPRMs) will cancel the LPRMs averaging, disabling in this way the APRM monitors. Therefore, the out-of-phase oscillations must be studied at a local LPRM level. Events related to diverging power oscillations have happened before in various BWRs facilities in the past. Such events encouraged researchers to develop correction techniques to suppress these events. Nonetheless, in spite of the existence of these corrective methods, unstable events continued to occur. Thus, as an answer to these BWR unstable events, several works were developed to study the physical phenomena behind these events. The detection and suppression mechanisms dedicated to mitigate these unstable oscillations need to identify the type of oscillation through LPRM signal monitoring. The development of methods to detect unstable event is of vital importance in terms of reactor security. The main goal of these methods is to provide a stability indicator (estimated via the study of BWR signals) which grants the operator enough time to act accordingly and in such a way that his actions do not involve a SCRAM straight away. The estimated stability indicator must provide as much information as possible regarding BWR unstable dynamics with enough reliability, precision and predictive capability to bestow the operator the time needed to act.
The current BWR stability indicator is the decay rate or Decay Ratio (DR) and the frequency of the unstable oscillation (it is known that the frequency associated to unstable oscillations, due to density waves, fluctuates around 0.5 Hz). For DR validity, it is compulsory to assume that the BWR behaves as a stationary second order linear system (i.e., a harmonic oscillator). Thus, an accurate prediction for the onset of BWR instability with methods that take into account the non-stationarity and non-linearity of the signal, is the next step in the research for the operation safety in BWRs.
In the next sections the proposed non-linear methods to make an early detection (and tracking) of the density wave are introduced. Likewise, we describe the methodologies dedicated to estimate the Shannon Entropy, a measure that fulfills the role of a novel non-linear BWR stability indicator.
3. Empirical Mode Decomposition (EMD) Algorithms
3.1. The Default EMD Method
Before introducing the noise assisted variants of the empirical mode decomposition (EMD). Let us recall the basics of the default EMD method, which was first proposed by Huang et al. [17]. The standard EMD permits the decomposition of a non-stationary signal that stems from a non-linear source, into various intrinsic mode functions (IMFs) or simply modes. To be considered an IMF, a signal of interest must fulfill two criteria:
- (I)
- The number of extrema (maxima and minima) and the number of zero-crossings must be equal or differ at most by one.
- (II)
- The local mean, defined as the mean of the upper and lower envelopes, must be zero.
Method 1.
The default EMD method can be described by the next steps, but first, let x be the signal of interest to decompose into IMFs:
- Step 1.
- Set and find all extrema of .
- Step 2.
- Interpolate between minima (maxima) of to obtain the lower (upper) envelope .
- Step 3.
- Compute the mean envelope .
- Step 4.
- Compute the IMF candidate .
- Step 5.
- Is an IMF?
- Yes. Save , compute the residue , do , and treat as input data in step 2.
- No. Treat as input data in step 2.
- Step 6.
- Continue until the final residue satisfies some predefined stopping criterion.
The refinement process (steps 2–5) needed to extract every mode, requires a certain number of iterations named as siftings. The extracted modes , decompose x and are in theory, nearly orthogonal to each other. However, one of the major drawbacks of the EMD is the frequent appearance of a problem that is known as mode mixing, which is defined as a single intrinsic mode function (IMF) either consisting of signals of widely disparate scales, or a signal of a similar scale residing in different IMF components. Such issue might spoil the meaning of individual IMFs and thus, thwart any default EMD signal analysis methodology. For further details about the impact of the mode mixing problem in BWR signals, please refer to [25].
To alleviate the mode mixing inconvenience, an interesting property of the EMD is exploited: such property appears when the signal to decompose is a white Gaussian noise. When this white Gaussian noise is decomposed, the EMD behaves as an adaptive dyadic filter bank, as it is shown in Figure 3, in which, 5000 independent time series (of white Gaussian noise) of 512 points each have been generated, and the average power spectrum density (PSD) of the first seven IMFs are plotted as a function of the normalized frequency.
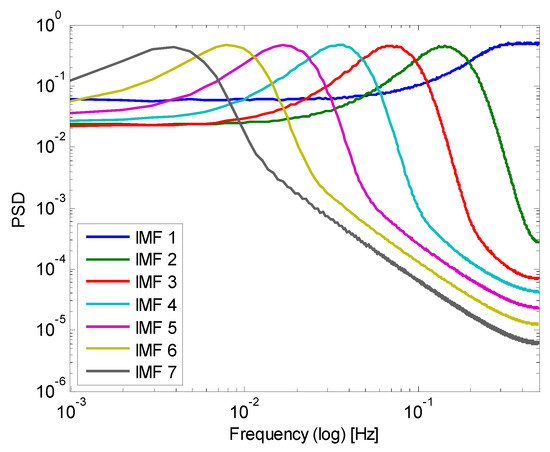
Figure 3.
EMD equivalent filter bank for a white Gaussian noise for the first 7 IMFs.
Thus, the methods that are discussed in the following sections to mitigate the mode mixing issue, add an ensemble of realizations of white noise to the signal of interest (hence, the name noise assisted method is used to define improved variations of EMD), to repair and exploit this dyadic filter bank property of the EMD, to improve IMF acquisition of the signal of interest x.
3.2. The Improved Complete Ensemble Empirical Mode Decomposition Method with Assisted Noise (iCEEMDAN)
The iCEEMDAN [15] is a recent noise-assisted (NA) variation of EMD that compensates for mode mixing. This method also addresses the most relevant disadvantages of previous NA variants of EMD, of techniques such as the EEMD [27] and the original CEEMDAN [28] method. Such handicaps are: the presence of residual noise in the modes and the existence of spurious modes (and both of them are addressed by iCEEMDAN).
Method 2.
Let x be the signal to decompose into IMFs through iCEEMDAN. Before proceeding, let us define the next three operators:
- (i)
- Let be the operator which produces the local mean (the mean envelope of the upper and lower envelopes of the studied signal interpolated by cubic splines) of the signal it is applied to.
- (ii)
- Let be the action of averaging throughout an ensemble of realizations of default EMD.
- (iii)
- Let be the operator that produces the k-th mode obtained by default EMD.
Let be a realization of white Gaussian noise with zero mean and unit variance. With this in mind, the iCEEMDAN method is described as follows:
- Step 1.
- Calculate by default EMD the local means of I realizations to obtain the first residue:
- Step 2.
- At the first stage (k = 1) calculate the first mode:
- Step 3.
- Estimate the second residue as the average of local means of the realizations and define the second mode:
- Step 4.
- For calculate the k-th residue:
- Step 5.
- Compute the k-th mode:
- Step 6.
- Go to Step 4 for next k.
Constants are chosen to obtain the desired signal to noise ratio (SNR) between the added noise and the residue to which the noise is added, nonetheless, in this work, we fixed the same SNR for all the stages of this procedure (). Studies about this parameter can be found in [29]. Although this NA-EMDm is quite useful to mitigate the mode mixing issue, there is a backlash, for it creates other problems: such as the proper choosing of parameters I which is the number of realizations of the ensemble and the standard deviation of the assisted noise added to the original signal for decomposition and thus, further works must be developed to properly estimate these two parameters (such endeavor leaves the scope of this work until further studies in the EMD literature are developed to infer the iCEEMDAN properties). Once such parameters are well established, then the BWR stability analysis might be at last fully adaptive and data driven. For all of our computations, the aforementioned parameters are fixed at: I = 100 and .
3.3. The Noise Assisted Multivariate Empirical Mode Decomposition (NA-MEMD)
The multivariate empirical mode decomposition (MEMD) is a technique that was proposed in [30] to make the classic empirical mode decomposition (EMD) suitable for processing of multichannel signals. To shed further light in the performance of this MEMD method, its behavior was analyzed in the presence of white Gaussian noise in [16] and it was found that, similarly to EMD. MEMD also in essence acts as a dyadic filter bank on each channel of the multivariate input signal, such MEMD property is illustrated in Figure 4 and its algorithm is given below. Nonetheless, unlike EMD, the MEMD better aligns the corresponding IMFs (i.e., modes) from different channels across the same frequency range which is crucial for real world applications and from such studies, the NA-MEMD method was developed to help resolve the mode mixing problem in the existing EMD algorithms.
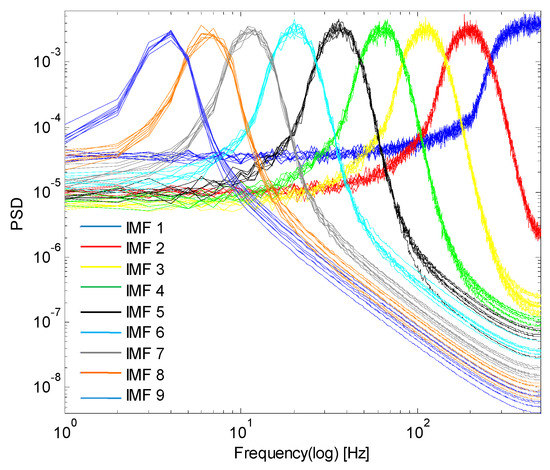
Figure 4.
Averaged spectra of IMFs (1–9) obtained for 50 realizations of eight-channel white Gaussian noise via MEMD.
The NA-MEMD method which makes use of the quasi-dyadic filter bank properties of MEMD on white noise (see Figure 4), it is capable of significantly reducing the mode mixing problem for classes of signals where the quasi-dyadic filter bank structure proves useful. Embarking upon the quasi-dyadic filter bank structure of standard EMD for broadband noise, many EMD variants were proposed, in which multiple realizations of white noise were added to the input signal before being decomposed via EMD. This helps to establish a uniformly distributed reference scale which, in turn, results in corresponding IMFs exhibiting a quasi-dyadic filter bank structure.
Following the latter idea, to explore the benefits of the quasi-dyadic filter bank structure of the default MEMD [30] on white noise, in [16] a total of m extra independent channels containing white noise are added in the MEMD decomposition of the multivariate signal of interest to exploit such interesting benefits of this filter bank property. The extracted IMFs (or modes) corresponding to the m channels of white noise are then discarded yielding a set of IMFs associated with only the original input signal. Since the added noise channels occupy a broad range in the frequency spectrum, MEMD aligns its IMFs based on the quasi-dyadic filter bank, with each component carrying a frequency sub band of the original signal. In doing so, IMFs corresponding to the original input signal also align themselves according to the structure of the quasi-dyadic filter bank. This, in turn, helps to mitigate the mode mixing problem within the extracted IMFs. The details of the NA-MEMD method are as follows, but first let us introduce the steps of the classic MEMD method:
Method 3.
Multivariate Extension of EMD for a multivariate signal :
Consider a sequence of N dimensional vectors representing a multivariate signal with N components, and denoting a set of direction vectors along the direction given by angles on a (l − 1) sphere. Then the extraction of the first IMF from the given MEMD steps is summarized in next steps:
- Step 1.
- Generate the point set based on the Hammersley sequence for sampling on an (l − 1) sphere [31].
- Step 2.
- Calculate a projection, denoted by , of the input multivariate signal along the direction vector , for all k (the whole set of direction vectors), giving as the set of projections.
- Step 3.
- Find the time instants corresponding to the maxima of the set of projected signals .
- Step 4.
- Interpolate , for all values of k, to obtain multivariate envelope curves .
- Step 5.
- For a set of K direction vectors, calculate the mean of the envelope curves as
- Step 6.
- Extract the detail using . If the detail fulfills the stoppage criterion [30] for a multivariate IMF, apply the above procedure to , otherwise apply it to .
Once the first IMF (or mode) is extracted, it is subtracted from the input signal and the same process (steps from Method 3) is applied to the resulting signal yielding the second IMF and so on, the process is repeated until all the IMFs are extracted and only a residue is left; in the multivariate case, the residue corresponds to a signal whose projections do not contain enough extrema to form a meaningful multivariate envelope. The sifting process for a multivariate IMF can be stopped when all the projected signals fulfill any of the stoppage criteria adopted in the default EMD [17].
Now, that the steps of the MEMD method have been given, the NA-MEMD is computed as follows:
Method 4.
The noise assisted multivariate empirical mode decomposition (NA-MEMD):
- Step 1.
- Create an uncorrelated Gaussian white noise time-series (m-channel) of the same length as that of the input.
- Step 2.
- Add the noise channels (m-channels) created in step 1 to the input multivariate (N-channels) signal, obtaining an (N + m)-channel signal.
- Step 3.
- Process the resulting (N + m)-channel multivariate signal using the MEMD algorithm (listed above), to obtain multivariate IMFs.
- Step 4.
- From the resulting (N + m)-variate IMFs, discard the m channels corresponding to the noise, giving a set of N-channel IMFs corresponding to the original signal.
However, it should be mentioned that the NA methods (both the iCEEMDAN and NA-MEMD) for mitigating the mode mixing problem are expected to be most useful for signals in which the dyadic filter bank decomposition is relevant. This is the case for the studied BWR signals.
4. The Shannon Entropy as Stability Indicator
In order to capture the complex dynamics of a BWR system, the Shannon Entropy (SE) [14] is studied. In statistical mechanics and information theory, entropy is a functional that quantifies the information content of a statistical ensemble or equivalently, the uncertainty of a random variable. Its application in various scientific disciplines is countless. Nonetheless, the most important example of such a functional is the Shannon Entropy (also known as average information), the concept was developed by Claude E. Shannon in 1948 [14]. Now, consider a discrete random variable x, which can take a finite number of M of possible values with corresponding probabilities , its entropy is defined as:
In general, the probability distribution for a given stochastic process is not known, and, in most situations, only small data sets from which to infer the entropy are available. For instance, it could be of interest to figure out the Shannon Entropy of a given BWR signal (or of one of its extracted through a NA-EMDm). In such circumstances, one could estimate the probability of each element i to occur, , by making some assumption on the probability distribution, as for example:
- (i)
- Parametrizing it.
- (ii)
- Dropping the most unlikely values.
- (iii)
- Assuming some a priori shape for the probability distribution.
Nevertheless, the easiest and most straightforward path to estimate them is by counting how often the value appears in the available data set. Denoting this number by and dividing by the total size N of available data set, we can obtain a relative frequency estimator given by:
Which naively approximates the probability associated to the value . With this simple estimator in mind, the easiest way to compute the SE of the data set can be done by simply replacing the probabilities by in the entropy functional, giving an estimate of the Shannon Entropy:
The quantity is an example of an entropy estimator, in a very similar sense as is an estimator of . In particular, the minimum is reached for a constant random variable, i.e., a variable with a determined outcome, which reflects in a fully localized probability distribution and for . At the opposite, is maximal, equal to , for a uniform distribution (). The SE is a quantity that increases with the number of possible states: for an unbiased coin, while for an unbiased dice . To estimate Equation (3), a histogram is required to infer the probabilities of the data set. In this work, the number of bins M of such histogram was calculated with an optimal estimator proposed in [32], which for reasons of space, this method will not be introduced in this work, but the idea behind this optimal M estimator dwells within the Bayesian probability theory.
Shannon initially proposed this functional to quantify the information loss in transmitting a given message in a communication channel [14]. A noticeable aspect of Shannon approach is to ignore semantics and focus on the physical and statistical constraints limiting the transmission of a message, regardless of its meaning. The source generating the inputs is characterized by the probability distribution . Shannon entropy thus appears as the average missing information. That is, the average information required to specify the outcome x when the receiver knows the distribution . It equivalently measures the amount of uncertainty represented by a probability distribution. In the context of communication theory, it amounts to the minimal number of bits that should be transmitted to specify x.
Based on these facts and considering that the estimator in (3) is the easiest way to estimate SE, it is the estimator used in our proposed methodologies to study the BWR stability. The SE, estimated by our naive estimator, quantifies the uncertainty of the artificial studied signals. Through this approach, the instability problem of a chaotic dynamical system such as a BWR is studied. The SE is our tool to study reactor instability and as such, the SE might serve as an alternative option to the conventional DR indicator. Our goal is to detect through SE the beginning of an incipient stability event (via a stability monitor), prior any further development of that unstable event. And to obtain from this indicator (based on SE) as much information as possible regarding the dynamics of the BWR system.
5. Methodology Based on Shannon Entropy
In this section, two stability methodologies are introduced, labeled as methodology 1 and methodology 2, based on iCEEMDAN and NA-MEMD respectively, to study individual BWR unstable events and multivariate ones. Both proposals are given by the next steps.
5.1. Methodology 1: Stability Monitor Based on the iCEEMDAN and the SE
- Step 1.
- The considered signal (APRM or LPRM) obtained from the BWR is segmented in windows of 15 s of duration.
- Step 2.
- Each segmented signal (APRM or LPRM) is studied (decomposed) using the iCEEMDAN method for a number of realizations of the ensemble I = 100 and standard deviation of the assisted noise , described above, obtaining in this way the corresponding IMFs. It is worth mentioning that the APRM or LPRM signals are not being processed before. For instance, to remove the signal trend, due that this information is contained in the residue of the decomposition.
- Step 3.
- The Hilbert transform of each IMF is computed in order to get the instantaneous frequencies contained in each IMF (this step is also known as Hilbert Huang transform, HHT, [17]).
- Step 4.
- When tracking these frequencies, it is possible to get the mode linked to instability processes. In this regard, only the IMF associated to BWR instability is considered for further processing.
- Step 5.
- The SE of the tracked IMF (mode of interest linked to BWR instability) is computed considering the estimator given in Equation (3), using the probability estimator given in Equation (2). The optimal number of bins M for the histogram, is calculated with a technique based on the Bayesian probability theory [32], within the interval (Several rules of thumb exist for determining the number of bins, such as the belief that between 5–20 bins is usually adequate [32]).
- Step 6.
- The mean and variance of the SE are calculated and averaged along all the studied segments of 15 s.
- Step 7.
- In order to range the SE between 0 and 1, the following normalization process is applied:
A reminder, a high SE estimate indicates high unpredictability of the mode linked to BWR instability (thus indicating an unstable state of operation) whereas a low SE value indicates a predictable event (thus, SE in this case, points towards a stable BWR scenario).
5.2. Methodology 2: Stability Monitor Based on the NA-MEMD and the SE
- Step 1.
- The considered multivariate signal (an array of N independent LPRM signals) obtained from the BWR are segmented in small windows of 15 s.
- Step 2.
- These segments (of 15 s each of time span) are decomposed in parallel through NA-MEMD in N independent channels. Also, m independent channels of white Gaussian noise are added (to mitigate the mode mixing problem) for decomposition (m = 3 for all of our computer simulations).
- Step 3.
- After decomposition, discard the m channels corresponding to the noise, giving a set of N-channel IMFs corresponding to the original signal segments.
- Step 4.
- The Hilbert transform of each IMF is computed in order to get the instantaneous frequencies contained in each N -channel IMFs frequencies (i.e., the HHT).
- Step 5.
- When tracking these frequencies, it is possible to get the IMFs (or modes) linked to instability processes. In this regard, only the IMFs associated to BWR instability are considered for further processing. Exploiting the NA-MEMD properties, the chosen IMFs of interest are all located at the same level of decomposition.
- Step 6.
- The SE of the tracked IMFs (modes of interest linked to BWR instability) are computed via Equation (3). The optimal number of bins M for the histogram, is calculated with the method given in [32] in a local way, within the interval 5 ≤ M ≤ 20. There are thus, N different values of SE (each SE value is linked to one LPRM in particular).
- Step 7.
- The mean and variance of the SE values are calculated and averaged along all the studied multivariate segments of 15 s.
- Step 8.
- In order to range the SE estimates between 0 and 1, the normalization procedure given in Equation (4) is again applied.
6. Results: Methodologies Performances and Discussions
The BWR signals stem from the Forsmark [3], Ringhals [33] stability Benchmarks and the Laguna Verde instability event [1,2]. The Ringhals plant stability benchmark test data has been widely applied to BWR stability studies because they cover various stability conditions, e.g., dominant fundamental mode related with in-phase instabilities, dominant first harmonic mode related with out-of-phase instabilities, and an overlapping of the two modes. The stability tests were performed (and controlled) in the Swedish BWR Ringhals Unit 1 from cycle 14 through cycle 17. The Forsmark benchmark is based on data from several measurements performed (and controlled) in the Swedish BWR reactor Forsmark 1 and 2, in the period 1989 to 1997. The Laguna Verde instability event was recorded during an unstable event that occurred in 1995 and is considered in the literature as a prototype of an in-phase instability.
6.1. Stability Analysis of the Chosen Real Cases Through the Methodology 1
This particular Methodology 1 is applied to the next three following cases:
- (I)
- Case 4 of the Forsmark stability benchmark. This event is considered a challenging case to be analyzed by the complexity of the phenomenon. For reasons of space, only this challenging case is presented in a detailed way. The studied Case 4 contains a mixture between a global oscillation mode and a regional (half core) oscillation. This event corresponds to a situation where the neutronic power reactor suffers abnormal and apparently unstable oscillations. The C4_APRM and C4_LPRM_x signals correspond to average power range monitor (APRM) and local power range monitor (LPRM) registers respectively, during the instability event. The entire case 4 was studied (a total of 23 signals, 22 LPRMs plus an APRM). However, only the analysis of one signal (C4_APRM_1) is detailed in this work and the others results (22 LPRMs) are summarized in a table.
- (II)
- Case 9 cycle 14 of the Ringhals stability benchmark. Data given comes from measurements in the Swedish BWR reactor Ringhals 1. This case consists of a total of 36 LPRMs. Again, the whole Case 9 (36 LPRMs) was studied, however only the analysis of one signal (LRPM 1) is detailed in this work and the others results of LPRMs are summarized in a table.
- (III)
- An APRM signal that stems from the Laguna Verde BWR that was recorded during an unstable event that occurred in 1995. On 24 January 1995 a power instability event occurred in Laguna Verde Unit 1, which is a BWR-5 and is operated since 1990 at a rated power of 1931 MWt. The instability event happened during a Cycle 4 power ascension without fuel damage. When the thermal power reached 37% of the rated power, the recirculation pumps were running at low speed driving 37.8% of the total core flow. The flow control valves were set to their minimum, closed position in order to operate the recirculation pumps at a high speed. The drop in drive flow resulted in a core flow reduction of 32% and, a power reduction also of 32%. Two control rods were also partially withdrawn during valve closure. The new low flow operating conditions resulted in growing power oscillations. This prototype of in-phase instability has been widely studied [1,2,34,35,36,37].
6.1.1. APRM Signal from the Forsmark Benchmark
The studied signal in this subsection is the APRM 1 of the Forsmark stability benchmark, Case 4. This signal of interest is shown in Figure 5.
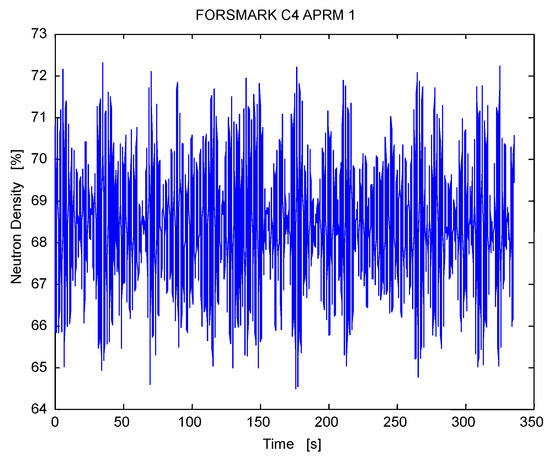
Figure 5.
APRM 1 signal from the Forsmark stability benchmark Case 4.
The Methodology 1 based on the iCEEMDAN and the SE is applied to signal shown in Figure 5. Such methodology splits the signal of interest in segments of 15 s, later the segment is decomposed through iCEEMDAN into IMFs, the HHT is calculated to obtain the instantaneous frequencies (IFs) of the IMFs. The IF of interest linked to instability is tracked (the energy of this mode connected to BWR instability is highly concentrated around 0.5 Hz in the Fourier domain, according to previous BWR stability observations). Later, the IMF linked to the IF of interest is selected for SE calculation. Figure 6, shows the analysis of one studied segment that was decomposed through iCEEMDAN into K IMFs and the IMF 3 is selected for further processing (because the IF (IF 3) of this IMF (IMF 3) is linked to BWR instability, this key IF is shown in Figure 7).
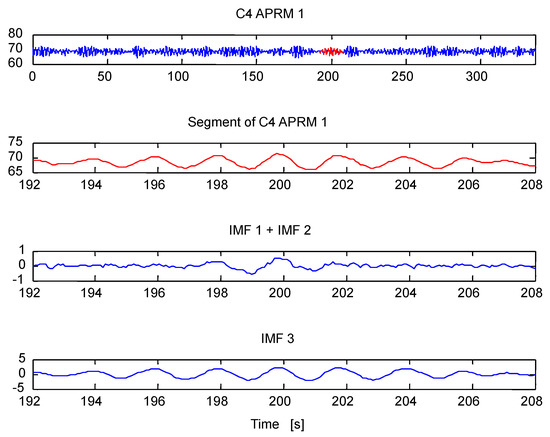
Figure 6.
iCEEMDAN decomposition of one of the segments of the APRM 1 signal, Case 4.
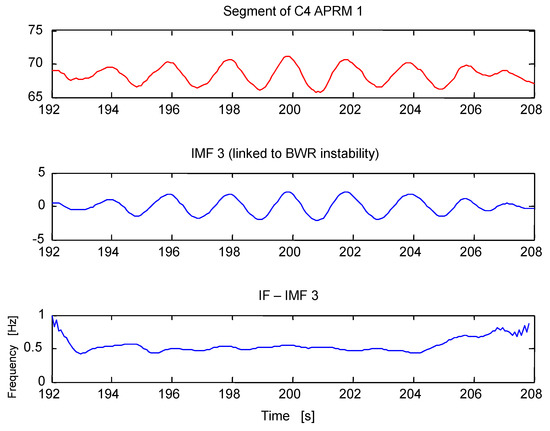
Figure 7.
Instantaneous frequency (IF 3) linked to BWR instability. The time series of IF 3 oscillates around 0.5 Hz (the region of interest for BWR instability events).
Figure 8 shows a power spectral density (PSD) estimation of the extracted IMFs of the studied segment, to visualize the spectrum of the IMF 3 linked to instability and to observe the iCEEMDAN capabilities to compensate for mode mixing, which translates into less overlap of contiguous IMFs spectrums. Figure 9 shows the plot of the estimated SE of all of the studied segments of the signal of interest. Also, in this same figure, a DR estimate of the segments is shown to illustrate the performance of the SE over the DR to analyze the stability of the studied signal. The DR was estimated in the same way as in [25]. We have established empirical stability thresholds based on our numerical experiments for the SE (Although more experiments are needed in this direction to accurately confirm this finding, but such studies leave the scope of this work). This stability threshold value is located around 0.8 (a stable segment has a SE < 0.8 whereas an unstable one has a SE > 0.8). Now, regarding the DR, a stable segment has a DR < 1. For this signal, the DR estimate indicates the beginning of an unstable event (an incipient one) whereas the SE throughout the whole time span of the signal, points to the existence of a fully developed instability event from the very beginning of the simulation. Figure 10 shows the estimated number of bins M for the extracted IMF for the studied case which remained very close to 5 bins and jumping beyond 5 in some segments.
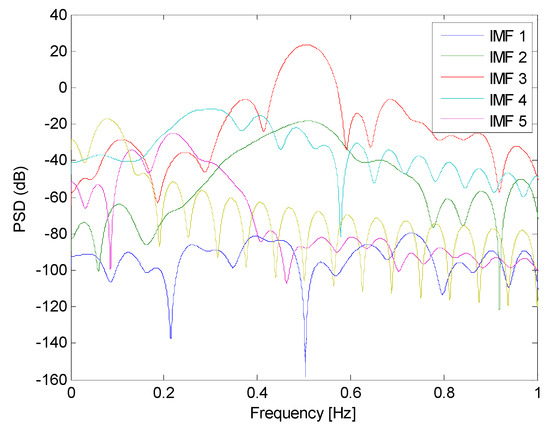
Figure 8.
PSD estimate of the extracted IMFs of the studied segment through the iCEEMDAN method.
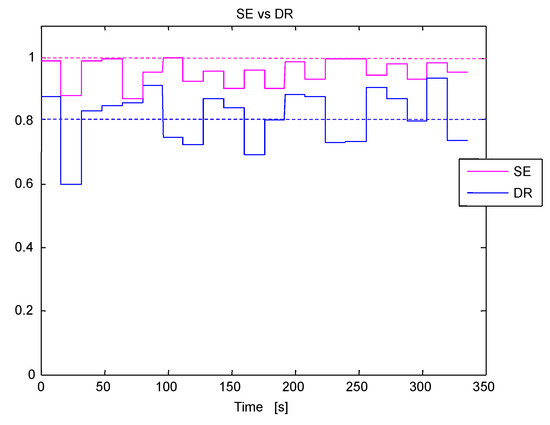
Figure 9.
Estimated Shannon Entropy (SE) and Decay Ratio (DR) along time for the APRM 1 signal. The purple dotted line located at 0.8 is the SE threshold (segments whose SE is above this line are unstable) whereas the blue dotted line at 1 is the DR threshold (segments whose DR is above this line are unstable).
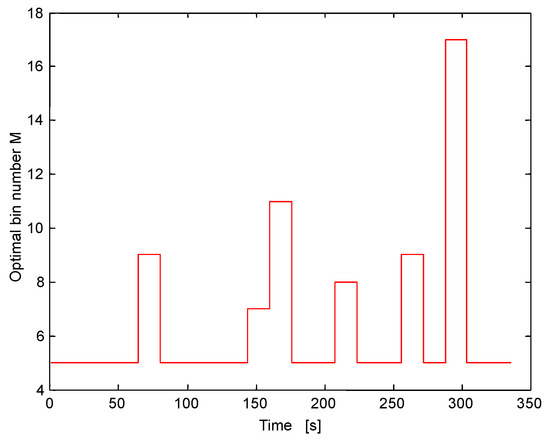
Figure 10.
Estimated optimal number of bins M computed with [32] in the interval 5 ≤ M ≤ 20.
Ultimately, the estimated SE, DR and oscillation frequency (f0) for the rest of the LPRMs of the studied Case 4 are shown in Table 1 (only average (Mean) and their standard deviations (Std) values along all the studied segments are shown in Table 1). The estimated averaged values for the DR are in perfect agreement with those estimated by the different methodologies presented in the benchmark [3]. The DR estimates indicate the beginning of an incipient instability event whereas the SE estimates indicate a fully developed instability event in the BWR. Thus, it is naive to assume that we can infer the dynamics of a complex system such as a BWR through an estimate of a linear parameter such as the DR alone. In spite of the contradictions of what these two parameters (SE and DR) are indicating, they nevertheless pinpoint to an instability event in the BWR core. Although the SE does this from the very beginning of the stability analysis.

Table 1.
Average and standard deviations values for the SE, the DR and the oscillation frequency (f0) linked to instability of the Forsmark stability benchmark, Case 4, studied through Methodology 1 based on the iCEEMDAN.
6.1.2. LPRM Signal from Ringhals Benchmark
The studied signal in this subsection stems from the Ringhals stability benchmark Case 9 cycle 14. This studied signal is shown in Figure 11.
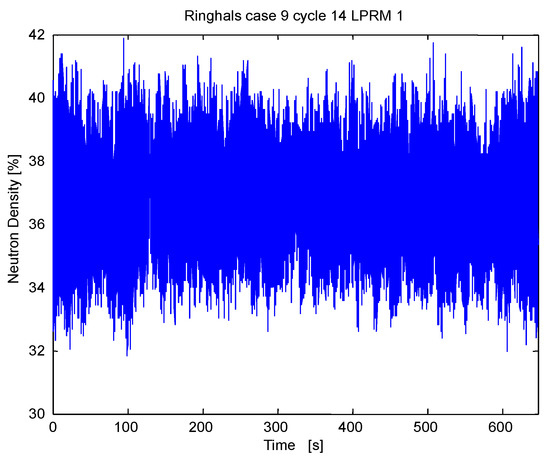
Figure 11.
LPRM 1 from the Ringhals stability benchmark, Case 9, Cycle 14.
The Methodology 1, based on the iCEEMDAN and the SE, is applied to signal shown in Figure 11. This stability methodology splits the signal of interest in short segments of 15 s, later the studied segment is decomposed through iCEEMDAN into IMFs (or modes), the Hilbert–Huang Transform (HHT) [17] is calculated to obtain the instantaneous frequencies (IFs) of the extracted IMFs. The IF of interest linked to instability (the energy of this IF of interest oscillates around 0.5 Hz) is tracked. Later, the IMF associated to this IF is selected for SE calculation. Figure 12, shows the analysis of one studied segment that was decomposed through iCEEMDAN into n IMFs and the IMF 3 is selected for further processing (because the IF (IF 3) of this IMF (IMF 3) is linked to BWR instability, this key IF is shown in Figure 13).
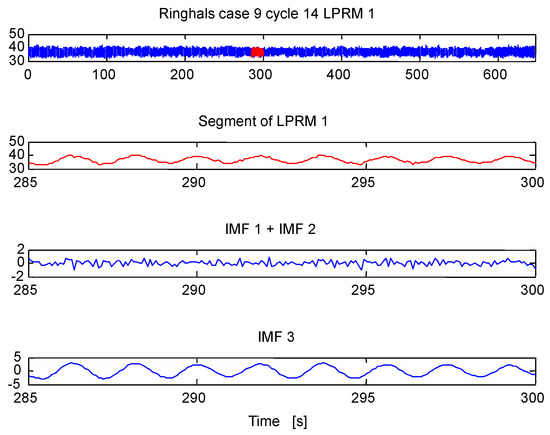
Figure 12.
iCEEMDAN decomposition of one of the segments of the signal LPRM 1, Case 9.
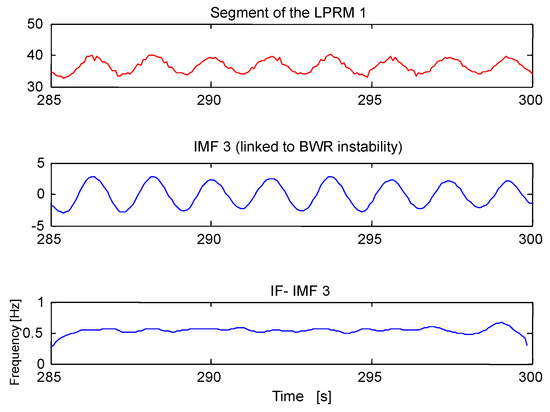
Figure 13.
Instantaneous frequency (IF 3) linked to BWR instability. The time series of IF 3 oscillates around 0.5 Hz (the region of interest for BWR instability events).
Figure 14 shows a power spectral density (PSD) estimation of the extracted IMFs of the studied segment, to visualize the spectrum of the IMF 3 linked to instability and to observe again the iCEEMDAN capabilities to compensate for mode mixing, which translates into less overlap of contiguous IMFs spectrums.
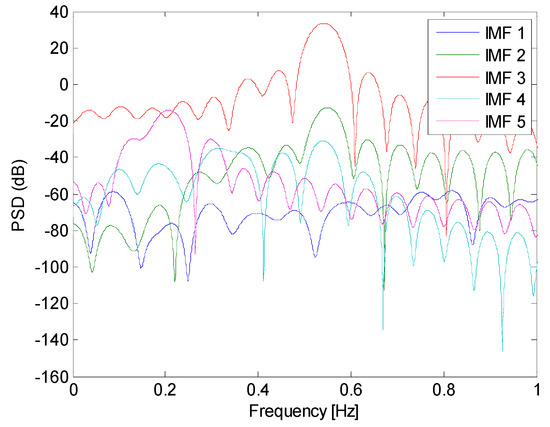
Figure 14.
PSD estimate of the extracted IMFs of the studied segment through the iCEEMDAN method.
Figure 15 shows the plot of the estimated SE of all of the studied segments of the signal of interest. As before, in this figure, a DR estimate of the segments is also shown to illustrate the performance of the SE over the DR to analyze the stability of the studied signal. The instability thresholds for the DR and for the SE are the same as before. For this signal, again the SE indicates a fully developed unstable BWR behavior whereas the DR is pointing to an early development of an instability event (a quasi-instable event), because the average DR is high (not exactly one, but approaching it). Again, the high SE estimates of the studied segments of this LRPM 1 signal are clearly indicating an out of the ordinary BWR behavior. The estimated number of bins M remained throughout most the simulation constant at 7 bins. The proposed stability monitor, given in Methodology 1, proves again to be suitable to detect unstable or not ordinary BWR behavior prior further growth of such unforeseen unstable events, that may in the worst case scenarios, trigger increasing power oscillations beyond the nominal BWR constraints. Thus, it is necessary to be able to detect any incipient unstable events as fast as possible.
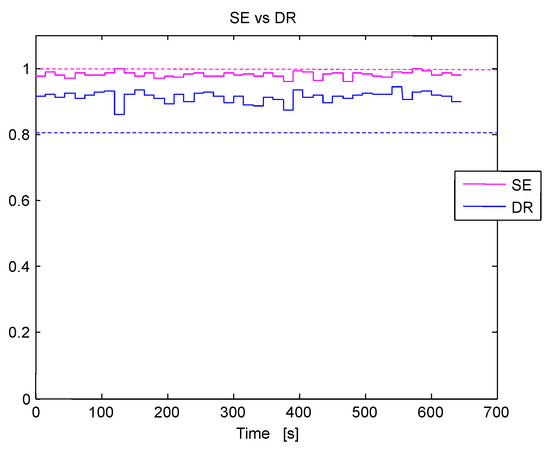
Figure 15.
Estimated Shannon Entropy (SE) and Decay Ratio (DR) estimate along time for the LRPM 1 signal, Case 9 from Ringhals stability benchmark. The purple dotted line located at 0.8 is the SE threshold (segments whose SE is above this line are unstable) whereas the blue dotted line at 1 is the DR threshold (segments whose DR is above this line are unstable).
Finally, the estimated SE, DR and oscillation frequency for the rest of the LPRMs of the studied Cycle 14 Case 9 are shown in Table 2 (only average values and standard deviations along all the studied segments are shown in Table 2). The entire case consists of a total of 72 LPRMs distributed on two different floors or levels (2 and 4) within the BWR core. In Table 2, only the analysis of the floor number 2 is studied. This floor consists of 36 LPRM detectors marked by odd numbers.

Table 2.
Average and standard deviations values for the SE, the DR and the oscillation frequency (f0) linked to instability of the Ringhals stability benchmark Case 9 Cycle 14 studied through the Methodology 1 based on the iCEEMDAN.
The estimated DR results of this studied case and shown in Table 2, were in most LPRMs high and apparently this case exhibits and out-of-phase oscillation [33] which will be scoped in more detail once Methodology 2 based on NA-MEMD is used to perform a multivariate analysis of this particular case. Overall the high SE estimated values, clearly indicate a fully developed unstable behavior of this case. Thus, the studied BWR floor 2 is unstable. The high DR estimates (but still not above the 1, which is the stability threshold that must be exceeded by the DR to trigger BWR peril alarms) although high and depicting that there is something unusual going on in the BWR core. But, the estimates are not high enough to trigger BWR protection alarms to warn the operators whereas the SE estimates would have trigger these BWR protection mechanisms.
6.1.3. APRM Laguna Verde
The studied signal in this subsection stems from an instability event that happened in Laguna Verde, in the year 1995. This signal is shown in Figure 16 and was obtained via the Integral Information Process System (IIPS). The channel A of the APRM trace shows no unstable behavior at 03:28:00 h. The value closure was initiated at 03:28:20 h. A small core flow reduction was noticeable 40 s later, and the APRM-A trace depicts signs of instability although the variations in the magnitude of the signal remained within the noise level. As the valve continued to close, the APRM-A trace shows clear unstable behavior starting at 03:30:30 h. The valve reached the minimum position at 03:31:30 h. The valve reached the minimum position at 03:31:30 h, and the oscillations continued without any significant increase in their growth rate. The operator attempted to stabilize the power level by increasing the core flow opening the vales at 03:33:20 h. As a result of increasing the core flow, the oscillation started to decay at 03:34:40 h. At 03:35:20 h the oscillation reached 3% of amplitude, when the reactor was manually scrammed (see the red boxes in Figure 16).
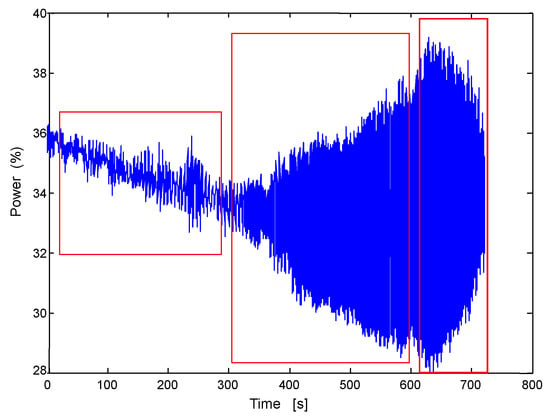
Figure 16.
Laguna Verde (LV) APRM signal of an unstable event that occurred in 1995.
As before, Figure 17 shows the decomposition of one of the segments of the signal shown in Figure 14, decomposed according to methodology number 1 based on iCEEMDAN.
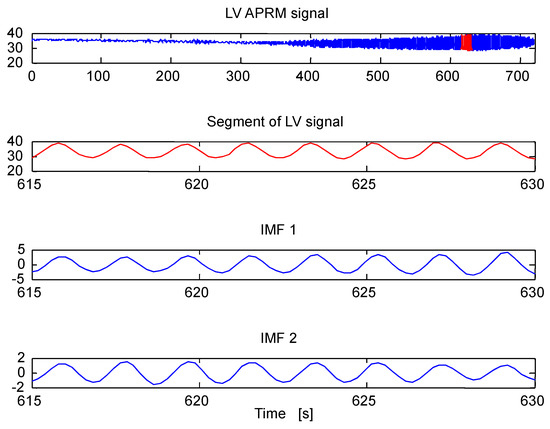
Figure 17.
iCEEMDAN decomposition of one of the segments of the APRM signal of LV instability event. Only the first 2 extracted IMFs are shown in this plot.
The IMF linked to BWR instability in this case is the IMF 1, see its instantaneous frequency IF (IF 1) oscillating around 0.5 Hz. This IF 1 is shown in Figure 18 and also the power spectral density (PSDs) estimates of all the extracted IMFs are shown in Figure 19. Observe that the PSD of IMF 2 is slightly mixed with the PSD estimate of IMF 1, but the spectral energetic content of IMF 2 is negligible in comparison with that of IMF 1.
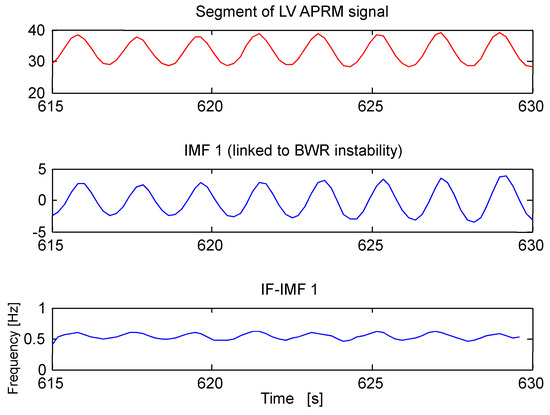
Figure 18.
Instantaneous frequency (IF 1) linked to BWR instability. The time series of IF 1 oscillates in a quasi-sinusoidal manner around 0.5 Hz (the region of interest for BWR instability events).
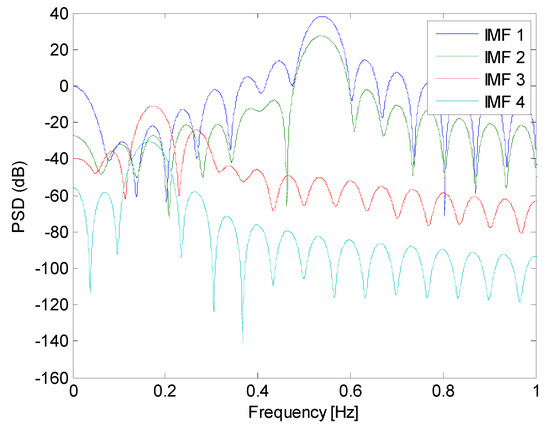
Figure 19.
PSD estimate of the extracted IMFs of the studied segment through the iCEEMDAN method.
Figure 20 shows the SE and DR estimates along all the studied segments of the APRM signal of interest. Prior the first 300 s of the signal, the DR oscillates between stability and instability. But, it is cumbersome to infer the dominant DR value due to its strong discontinuous jumps between stability and instability. However, after the 300 s mark, the DR is high and greater that its threshold value (DR = 1) and remains as such (and oscillating around 1.1) throughout the rest of the simulation. Thus, the DR indicates unstable BWR behavior but only after the 300 s mark.
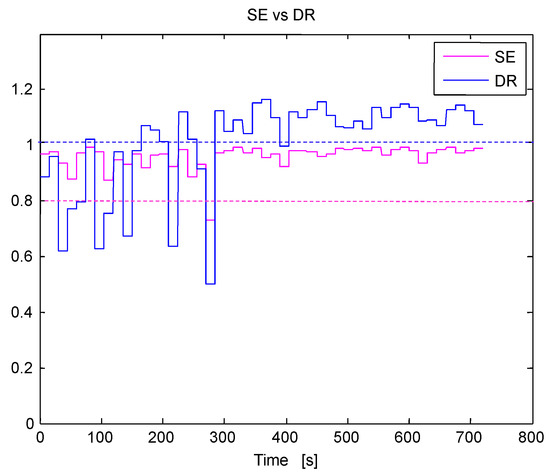
Figure 20.
Estimated Shannon Entropy (SE) and Decay Ratio (DR) estimate along time for the APRM signal. The purple dotted line located at 0.8 is the SE threshold (segments whose SE is above this line are unstable) whereas the blue dotted line at 1 is the DR threshold (segments whose DR is above this line are unstable).
The SE estimate is highly more consistent than the DR prior the 300 s mark, because the SE clearly indicates unstable behavior (whereas the DR is unable to differentiate between the two) and after the 300 s mark, the SE slightly oscillates around 1 (and not in a dramatic way as the DR does). Nevertheless, the SE always indicates unstable BWR behavior, long before the DR is able to detect it. Thus, the SE is capable of indicating unstable behavior prior any further growth in power of the unstable oscillation within the core whereas the DR is only able to detect instability (without bias) once the unstable oscillation is fully sustained and powerful enough to damage the core. The optimal number of bins for this case remained most of the simulation constant at 10 and it was again calculated with the technique described in [32]. Finally, Table 3 shows the mean SE, DR and instantaneous frequency averaged along all the segments of the signal of interest depicted previously in Figure 14.

Table 3.
Average and standard deviations values for the SE, the DR and the oscillation frequency (f0) linked to instability of the Laguna Verde APRM signal studied through the Methodology 1 based on the iCEEMDAN.
6.2. Stability Analysis of the Chosen Real Cases Through the Methodology 2
The stability methodology 2 is applied with the next following cases of nuclear power plants (NPP):
- (I)
- Multidimensional analysis of the already mentioned Case 4 of the Forsmark stability benchmark.
- (II)
- Multidimensional analysis of the also mentioned Case 9 Cycle 14 of the Ringhals stability benchmark.
Regarding Laguna Verde instability event, the methodology 2 can also be applied. However, the signals from 96 LPRMs monitoring the core are not available for this specific instability phenomenon.
6.2.1. LPRMs Signals from Forsmark Benchmark
Now, the Case 4 of the Forsmark stability benchmark is going to be studied with the stability Methodology 2 based on the NA-MEMD in a multivariate way with m = 3 independent channels of noise to mitigate mode mixing. In here, the ensemble of LPRM signals is considered in the NA-MEMD and a local estimation of SE and of the DR (calculated according to [38]) are computed based on the IMFs associated to the instability event (the oscillatory IMF around 0.5 Hz). Figure 21 shows the IMFs linked to BWR instability.
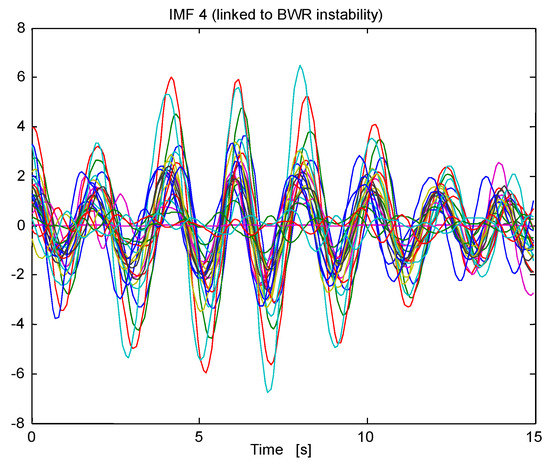
Figure 21.
NA-MEMD applied to a short time segment of the Case 4 of the Forsmark stability benchmark.
Exploiting the time alignment property of the NA-MEMD, these IMFs of interest are located at the same level of decompositions, in this case the IMFs of interest are located at the fourth level of the NA-MEMD decomposition (IMFs number 4). We highlight that in Figure 21, the IMFs of interest linked to instability are in-phase among them. The instantaneous frequencies (IFs number 4) around the region of interest (0.5 Hz) of these IMFs of interest are shown in Figure 22. Later, Figure 23 shows the estimated SE locally for each IMF of interest (IMFs number 4). However, for simplicity, only a sample of 4 IMFs are shown in this plot, the selected IMFs are LPRM 1, LPRM 7, LPRM 11 and LPRM 21. Also, the DR (depicted in Figure 24 and estimated in the same way as before) is estimated locally for each IMF but again, only four IMFs (the aforementioned four LPRM signals) are shown in such figure. In the multivariate scenario, overall the BWR is unstable because of the high SE estimates along time, in spite of the four segments that had an SE below the stability threshold (SE < 0.8). Thus, again from the very beginning of the simulation, the SE is able to detect an unusual BWR unstable behavior. The DR in the multivariate case prior the 150 s mark is apparently stable and after this 150 s mark, it fluctuates around 0.75, the DR estimate is high but not high enough to trigger the BWR warning mechanisms and thus the DR indicates quasi-instability.
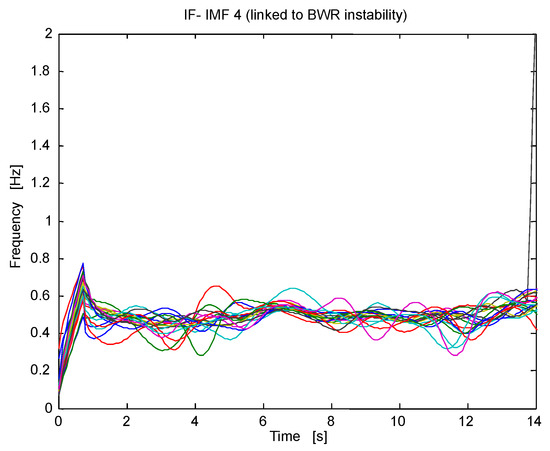
Figure 22.
Multivariate instantaneous frequency IF (IF 4) linked to BWR instability oscillating around the region of interest (0.5 Hz).
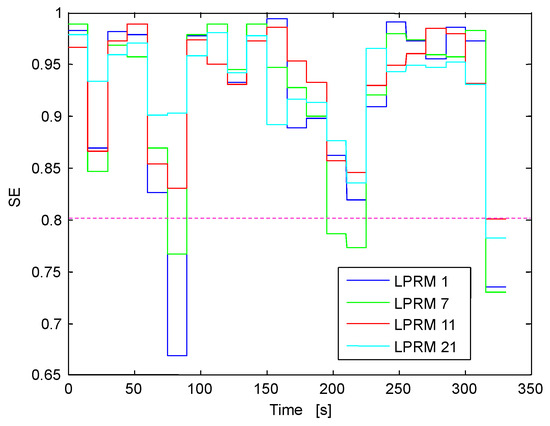
Figure 23.
Local SE estimate along time for the selected four LPRM sample. The threshold SE bar is located at the same locus as before.
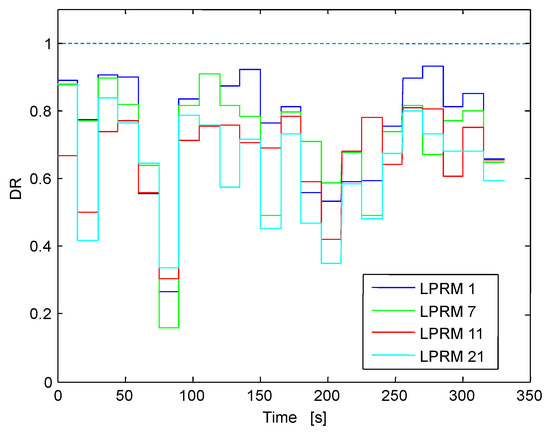
Figure 24.
Local DR estimate along time for the selected 4 LPRM sample. The threshold DR bar is located at the same locus as before.
Finally, Table 4 shows the SE, DR and f0 (all of them calculated locally) of the entire studied Case 4 of the Forsmark stability benchmark, the APRM was ignored for this analysis. The estimated parameters are similar to those that stem from the univariate analysis performed through the Methodology 1 in Table 1 of this case (the estimates in Table 4 are similar to those depicted in Table 1 and within the 10% difference).

Table 4.
Average and standard deviation values for the SE, the DR and the oscillation frequency (f0) linked to instability of the Forsmark benchmark stability Case 4 studied via stability methodology 2 based on NA-MEMD.
6.2.2. LPRMs from Ringhals Benchmark
Now, the Case 9 Cycle 14 of the Ringhals stability benchmark is studied through the Methodology 2 based on NA-MEMD. Figure 25 shows the NA-MEMD decomposition (with three independent channels of noise to compensate for mode mixing) of one of the signal segments, the IMF (IMF 4) linked to instability is shown in this figure and the type of observed oscillation is known as out-of-phase oscillation [33]. These type of oscillations can only be observed locally at the LPRM level because at the APRM level (an APRM signal is an average of n LPRMs) the averaging might cancel data, if the signals that participate in the average have ideal phase differences of 180 degrees among them. Figure 26 shows the instantaneous frequencies IFs (IF 4) of the IMFs (IMF at the 4 level of NA-MEMD decomposition) associated to BWR instability, all of the IFs oscillate around 0.5 Hz in a quasi- sinusoid way. Figure 27 shows the SE estimates along time of a sample of four LPRMs that were selected at random, the selected LPRMs were: LPRM 1, LPRM 10, LPRM 20 and LPRM 29. The SE estimates along time were high (beyond the SE stability threshold located at SE = 0.8) throughout the time span of the simulation for the four chosen LPRMs, thus the BWR is clearly unstable.
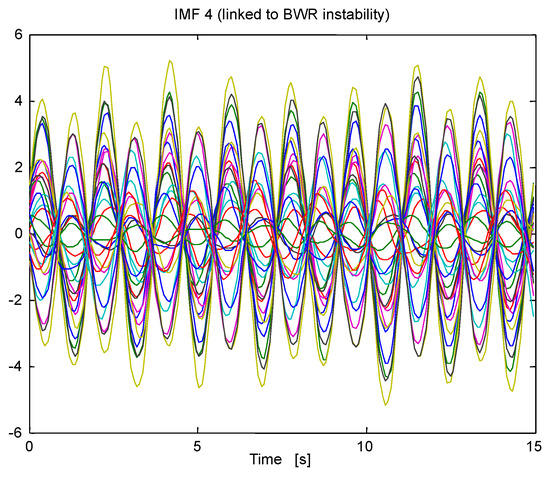
Figure 25.
NA-MEMD applied to a short time segment of the Case 9 Cycle 14 of the Ringhals stability benchmark.
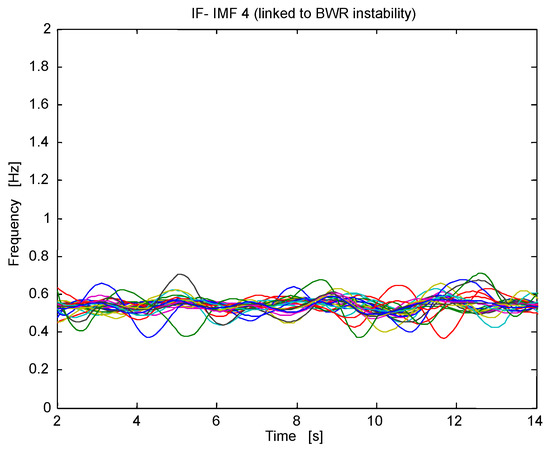
Figure 26.
Multivariate instantaneous frequency IF (IF 4) linked to BWR instability oscillating around the region of interest (0.5 Hz).
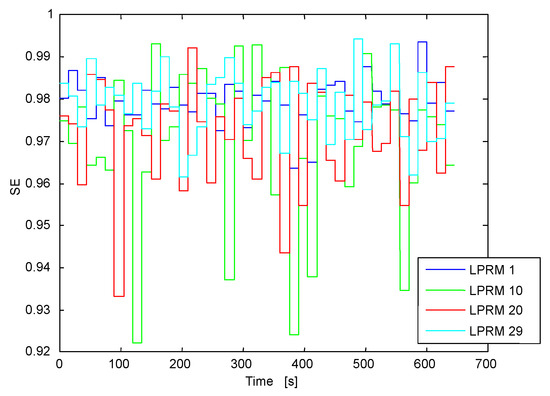
Figure 27.
Local SE estimate along time for the selected 4 LPRM sample. All of the SE estimates exceed the stability threshold (located at SE = 0.8).
Figure 28 shows the DR estimates along time for the chosen LPRMs, the DR estimates were high, clearly indicating the beginning of an unstable event, but they did not exceed the stability threshold to trigger the BWR protection mechanisms. Finally Table 5 shows the SE, DR and oscillation frequency of the entire Ringhals Case 9. Again, the computer parameters in Table 5 are similar (less than 10% of difference) with the estimates shown previously in Table 2 when this case was analyzed (in a univariate way) through Methodology 1.
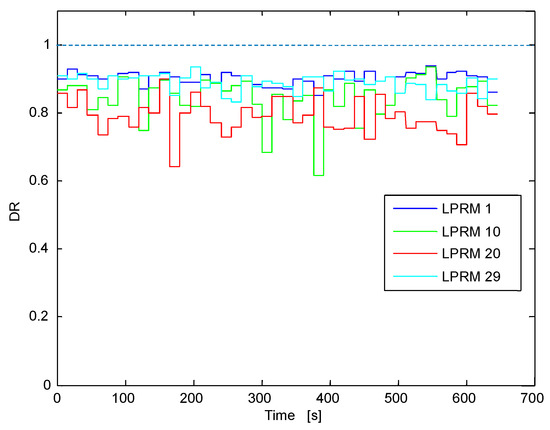
Figure 28.
Local DR estimate along time for the selected 4 LPRM sample. The threshold DR bar is located at the same locus as before.

Table 5.
Average and standard deviations values for the SE, the DR and the oscillation frequency (f0) linked to instability of the Ringhals benchmark stability Case 9 Cycle 14 studied via Methodology 2 based on NA-MEMD.
We highlight the NA-MEMD capabilities to compensate for mode mixing with only one realization of the algorithm whereas the iCEEMDAN required a total of I = 100 (the size of the ensemble) realizations of the default EMD algorithm to compensate for it. Thus, the NA-MEMD excels in computation time and the SE and DR estimates Methodology 2 provides were slightly the same as those given by stability methodology 1.
6.3. Discussion and Remarks
Some important final remarks can be put forth regarding our proposal and recent study about BWR stability:
The common mechanism for BWR instability is the density wave oscillations (DWO) effect [39]. A decrease in coolant flow increases the void fraction for a given reactor power. A high wave propagation velocity of voids (wave void) is then formed and accompanied by a high wave propagation velocity of pressure (wave pressure). Since an increase in pressure drop decreases the flow due to increased resistance to flow, a feedback loop results between inlet flow and pressure drop, which may lead to oscillations in time. In addition, as the void fraction is increased as described above, the associated decrease in moderator density induces a negative reactivity feedback. This causes the power to decrease, which reduces the void fraction and fuel temperature and allows the power to build up again. As a result, self-sustained power oscillations may appear, depending on the operation conditions.
According to [40] the in-phase instabilities are driven by the interaction between the DWO mechanism and its coupling via the void reactivity feedback with the core neutron population. On the other hand, an in-phase instability implies growing neutron oscillations that are dominated by the fundamental neutronic mode. Regarding to the first azimuthal neutronic mode may also be unstable and growing, but its contribution to the total neutron population is relatively insignificant [41].
The mechanism of density wave oscillations for two-phase flow has recently received great attention, remaining as an important issue of scientific and technological interest (e.g., [40,42,43,44,45,46,47,48]. However, the core stability is due to fluctuations in coolant flow and power generation process coupled via nuclear feedback where the non-linear nature has been a challenge for the development of stability monitors. Therefore the methodology presented in this work constitutes a significant and novel advance towards the development of stability monitors able to predict linear and nonlinear effects, as well as the transition between them.
Experiments on natural circulation BWR stability show that changing the fuel rods diameter affect to the stability performance of the system [48]. These authors clearly observed that at least two oscillatory modes exists in the system, one of them is the so-called reactor mode related to density waves travelling through the core, which is amplified by increasing the void reactivity feedback coefficient. Therefore, the methods based on SE presented in this work, are applicable to existing and advanced reactors of type BWR, and any two-phase flow system as well as characterization of stability limits [47]. A recent work showed that the stability of a BWR reactor was applied to assessment of optimum Fuel Reload Patterns for a BWR [49].
Methodology 1 developed in this work is limited to the cases of neutron signal analysis of an APRM or LPRM where the instability in-phase can be detected like in a NPP as Laguna Verde which characteristic is its size (smaller compare to Forsmark and Ringhals) and where this kind of instability phenomena is expected. Regarding Methodology 2, it can be applied to both phase in-phase and out-of-phase instabilities. Given that the stability phenomena in BWR is a complex phenomenon in a heterogeneous two-phase flow system, where void propagation waves (propagation of the gas phase in the liquid phase) and pressure propagation waves (both in gas phase and liquid phase) generate the DWO mechanics, then is preferable to implement an oscillation detector based on methodology 2.
7. Conclusions
In this work two non-linear stability monitor methodologies based on noise assisted empirical mode decomposition methods (NA-EMDm) were proposed to analyze unstable BWR signals that stemmed from the Ringhals, Forsmark stability benchmarks and the Laguna Verde instability event, with the goal in mind of estimating the Shannon Entropy of those signals to measure their uncertainty and thus assess BWR stability through such novel measure. The SE estimates were also compared with Decay Ratio results computed via previous methods based on EMD variants. The proposed stability methodologies are rooted in noise assisted empirical mode decomposition algorithms, which are techniques that decompose non-stationary signals that stem from non-linear sources in an adaptive (data-driven) way to grant a physically meaningful decomposition of data, the data (the LRPM or APRM signals are split first in segments of 15 s) is decomposed into intrinsic mode functions (or simply modes), via the Hilbert transform it is possible to compute the instantaneous frequencies of the extracted modes to track the mode linked to BWR instability (whose IF is strongly concentrated around 0.5 Hz, the region of interest for BWR unstable events). Later, once the IMF (IMFs in the multidimensional case) of interest has been detected, the SE of this particular IMF is computed to assess the BWR stability of that particular 15 s signal segment that was analyzed via any of our stability methodologies. The major findings of our BWR stability studies are resumed in the following:
(a) Regarding Methodology 1 based on the iCEEMDAN (univariate signal analysis).
• Case 4 of the Forsmark stability benchmark.
The estimated averaged values for the DR are in perfect agreement with those estimated by the different methodologies presented in [3]. The DR estimates indicate the beginning of an incipient instability event whereas the SE estimates indicate a fully developed instability event in the BWR core.
• Case 9 Cycle 14 of the Ringhals stability benchmark.
The high SE estimated values, clearly indicate again a fully developed unstable behavior of this case. Thus, the studied BWR floor 2 is unstable. The high DR estimates (but still not above the locus DR = 1) although high and depicting that there is something unusual going on in the BWR core but not high enough to trigger BWR protection mechanisms.
• The Laguna Verde instability event.
Prior to the first 300 s of the signal, the DR oscillates between stability and instability, but it is hard to infer the dominant DR value due to its strong discontinuous jumps between stability and instability. However, after the 300 s mark, the DR is high and greater that its threshold value (DR = 1) and remains as such (and oscillating around 1.1) throughout the rest of the simulation. Thus, the DR indicates unstable BWR behavior, but only after the 300 s mark. The SE estimate is much more consistent than the DR prior to the 300 s mark, because the SE clearly indicates unstable behavior (whereas the DR is unable to differentiate between the two) and after the 300 s mark, the SE oscillates slightly around 1 (and not in a dramatic way as the DR does). Nevertheless, the SE always indicates unstable BWR behavior, long before the DR is able to detect it. Thus, the SE is capable of indicating unstable behavior prior any further growth in power of the unstable oscillation within the core whereas the DR is only able to detect instability (without bias) once the unstable oscillation is fully sustained and powerful enough to damage the core.
(b) Regarding Methodology 2 based on the NA-MEMD (multivariate signal analysis).
• Multivariate analysis of the Forsmark stability benchmark (based on a sample of 4 LPRMs).
Overall the BWR is unstable because of the high SE estimates along time, in spite of four segments that had an SE below the stability threshold (SE < 0.8). Thus, again from the very beginning of the simulation, the SE is able to detect an unusual BWR unstable behavior. The DR in the multivariate case prior the 150 s mark is apparently stable and after this 150 s mark, it fluctuates around 0.75, the DR estimate is high but not high enough to be a nuisance for BWR operation.
• Multivariate analysis of the Forsmark stability benchmark (based on a sample of 4 LPRMs):
The SE estimates along time were high (beyond the SE stability threshold located at SE = 0.8) throughout the time span of the simulation for the four chosen LPRMs, thus the BWR is clearly unstable whereas, the DR estimates were high, clearly indicating the beginning of an unstable event, but they did not exceed the stability threshold to trigger the BWR protection mechanisms.
According to our simulations it is naive to assume one can infer information associated to BWR dynamics through one linear parameter alone such as the DR, because in most of our simulations, the DR only rises above its stability threshold (DR above 1) once the unstable oscillation has become powerful enough to damage the core (according to the stability analysis of the LV signal). Thus, it is necessary to propose another non-linear stability indicator (to replace the DR or to accompany it) to assess BWR stability, and the SE might be a suitable candidate to fulfill that role via our simple SE estimator or another more elaborate one that will be studied in future works.
To select which stability methodology (between 1 and 2) is the most adequate to analyze BWR signals, is still not known and further stability cases must be studied in detail to decide which type of analysis works better; whether a univariate one or a mutlivariate one. Nevertheless, the SE (and DR) estimates extracted through these decomposition methods were similar (within the 10% of difference). These noise assisted techniques have one cumbersome inconvenient and a difficult one to overcome. For instance, how to properly select the iCEEMDAN parameters I (the size of the ensemble of realizations of the EMD that this noise assisted method requires) and (the standard deviation of the added assisted noise)? Nobody knows that answer yet in the EMD literature, thus further studies are required to infer these two parameters. A similar question arises with the NA-MEMD: how many independent channels of noise are required in the decomposition scheme to mitigate the mode-mixing problem? Again, this is another question that has not been addressed in the specialized literature. However, once these questions are answered, then, our stability methodologies might be fully adaptive to be implemented in a real stability monitor and well adapted to decompose non-stationary non-linear data.
Acknowledgments
The source of funding for this publication was provided by the Mexican National Council of Science and Technology (CONACyT-México). Doctoral Scholarship number: 594513, unique CONACyT curriculum vitae (CVU): 382288. Valid between 01/01/2016 and 31/12/2019. This same scholarship grants the necessary funding to publish in open access.
Author Contributions
Alfonso Prieto-Guerrero and Gilberto Espinosa-Paredes conceived and designed the proposed stability methodologies in previous published works, and the original idea on the application of the Shannon Entropy in a stability monitor. These proposals were based on the empirical Mode Decomposition and in the Multivariate Empirical Mode Decomposition, Omar Alejandro Olvera-Guerrero improved these proposals considering the mode-mixing compensation of data, Omar Alejandro Olvera-Guerrero performed the experiments of this work, Gilberto Espinosa-Paredes, Alfonso Prieto-Guerrero and Omar Alejandro Olvera-Guerrero developed the methodology presented in this work and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gonzalez, V.M.; Amador, R.; Castillo, R. Análisis del Evento de Oscilaciones de Potencia en la CNLV: Informe Preliminar; CNSNS-TR-13, REVISION 0; Comisión Nacional de Seguridad Nuclear y Salvaguardias: Mexico City, Mexico, 1995. [Google Scholar]
- Farawila, Y.M.; Pruitt, D.W.; Smith, P.E.; Sanchez, L.; Fuentes, L.P. Analysis of the Laguna Verde instability event. In Proceedings of the National Heat Transfer Conference, Houston, TX, USA, 3–6 August 1996; Volume 9, pp. 198–202. [Google Scholar]
- Verdú, G.; Ginestar, D.; Muñoz-Cobo, J.L.; Navarro-Esbrí, J.; Palomo, M.J.; Lansaker, P.; Conde, J.M.; Recio, M.; Sartori, E. Forsmark 1&2 Stability Benchmark. Time Series Analysis Methods for Oscillations during BWR Operation; Final Report, NEA/NSC/DOC(2001)2; Nuclear Science: New York, NY, USA, 2001. [Google Scholar]
- Lahey, R.T.; Podoswski, M.Z. On the analysis of various instabilities in two-phase flow. Multiph. Sci. Technol. 1989, 4, 183–371. [Google Scholar] [CrossRef]
- Van der Hagen, T.H.; Zboray, R.; de Kruijf, W.J. Questioning the use of the decay ratio in BWR stability monitoring. Ann. Nucl. Energy 2000, 27, 727–732. [Google Scholar] [CrossRef]
- Pazsit, I. Determination of reactor stability in case of dual oscillations. Ann. Nucl. Energy 1995, 22, 377–387. [Google Scholar] [CrossRef]
- Gialdi, E.; Grifoni, S.; Parmeggiani, C.; Tricoli, C. Core stability in operating BWR: Operational experience. Prog. Nucl. Energy 1985, 15, 447–459. [Google Scholar] [CrossRef]
- Navarro-Esbri, J.; Ginestar, D.; Verdu, G. Time dependence of linear stability parameters of a BWR. Prog. Nucl. Energy 2003, 43, 187–194. [Google Scholar] [CrossRef]
- Espinosa-Paredes, G.; Prieto-Guerrero, A.; Nuñez-Carrera, A.; Amador-Garcia, R. Wavelet-based method for instability analysis in boiling water reactors. Nucl. Technol. 2005, 151, 250–260. [Google Scholar]
- Espinosa-Paredes, G.; Núñez-Carrera, A.; Prieto-Guerrero, A.; Ceceñas, M. Wavelet approach for analysis of neutronic power using data of ringhals stability benchmark. Nucl. Eng. Des. 2007, 237, 1009–1015. [Google Scholar] [CrossRef]
- Sunde, C.; Pazsit, I. Wavelet techniques for the determination of the decay ratio in boiling water reactors. Kerntechnik 2007, 72, 7–19. [Google Scholar] [CrossRef]
- Castillo, R.; Alonso, G.; Palacios, J.C. Determination of limit cycles using both the slope of correlation integral and dominant Lyapunov methods. Nucl. Technol. 2004, 145, 139–149. [Google Scholar]
- Gavilán-Moreno, C.J.; Espinosa-Paredes, G. Using Largest Lyapunov Exponent to Confirm the Intrinsic Stability of Boiling Water Reactors. Nucl. Eng. Technol. 2016, 48, 434–447. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble emd: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Ur Rehman, N.; Mandic, D.P. Filter bank property of multivariate empirical mode decomposition. IEEE Trans. Signal Process. 2011, 59, 2421–2426. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis; The Royal Society: London, UK, 1998; pp. 903–995. [Google Scholar]
- Olvera-Guerrero, O.A.; Prieto-Guerrero, A.; Espinosa-Paredes, G. Non-linear Boiling Water Reactor Stability with Shannon Entropy. Ann. Nucl. Energy 2017, 108, 1–9. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Huang, J.R.; Fan, S.Z.; Abbod, M.F.; Jen, K.K.; Wu, J.F.; Shieh, J.S. Application of multivariate empirical mode decomposition and sample entropy in EEG signals via artificial neural networks for interpreting depth of anesthesia. Entropy 2013, 15, 3325–3339. [Google Scholar] [CrossRef]
- Zhan, L.; Li, C. A comparative study of empirical mode decomposition-based filtering for impact signal. Entropy 2016, 19, 13. [Google Scholar] [CrossRef]
- Hu, M.; Liang, H. Intrinsic mode entropy based on multivariate empirical mode decomposition and its application to neural data analysis. Cogn. Neurodyn. 2011, 5, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.Y.; Lee, H.C. Entropic interpretation of empirical mode decomposition and its applications in signal processing. Adv. Adapt. Data Anal. 2010, 2, 429–449. [Google Scholar] [CrossRef]
- Prieto-Guerrero, A.; Espinosa-Paredes, G. Decay ratio estimation in boiling water reactors based on the empirical mode decomposition and the Hilbert–Huang transform. Prog. Nucl. Energy 2014, 71, 122–133. [Google Scholar] [CrossRef]
- Olvera-Guerrero, O.A.; Prieto-Guerrero, A.; Espinosa-Paredes, G. Decay Ratio estimation in BWRs based on the improved complete ensemble empirical mode decomposition with adaptive noise. Ann. Nucl. Energy 2017, 102, 280–296. [Google Scholar] [CrossRef]
- BWR/6. BWR/6 General Description of a Boiling Water Reactor, Nuclear Energy Division, General Electric Company; GE Nuclear Energy: Wilmington, NC, USA, 1975. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E.; Flandrin, P. Noise-assisted EMD methods in action. Adv. Adapt. Data Anal. 2012, 4, 1250025. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate Empirical Mode Decomposition. Proc. R. Soc. A 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Knuth, K.H. Optimal data-based binning for histograms. arXiv, 2006; arXiv:physics/0605197v1. [Google Scholar]
- Lefvert, T. OECD/NEA Ringhals 1 Stability Benchmark; Nuclear Energy Agency: Boulogne-Billancourt, France, 1996. [Google Scholar]
- Blazquez, J.; Ruiz, J. The Laguna Verde BWR/5 instability Event. Prog. Nucl. Energy 2003, 43, 195–200. [Google Scholar] [CrossRef]
- Nuñez-Carrera, A.; Espinosa-Paredes, G. Time-Scale BWR stability analysis using wavelet-based method. Prog. Nucl. Energy 2006, 48, 540–549. [Google Scholar] [CrossRef]
- Prieto-Guerrero, A.; Espinosa-Paredes, G. Decay Ratio Estimation of BWR Signals based on Wavelet Ridges. Nucl. Sci. Eng. 2008, 160, 302–317. [Google Scholar] [CrossRef]
- Moreno, C.G. Boiling water reactor instability analysis using attractor characteristics. Ann. Nucl. Energy 2016, 88, 41–48. [Google Scholar] [CrossRef]
- Prieto-Guerrero, A.; Espinosa-Paredes, G.; Laguna-Sánchez, G.A. Stability monitor for boiling water reactors based on the multivariate empirical mode decomposition. Ann. Nucl. Energy 2015, 85, 453–460. [Google Scholar] [CrossRef]
- March-Leuba, J.; Blakeman, E.D. A mechanism for out-of-phase power instabilities in Boiling Water Reactors. Nucl. Sci. Eng. 1991, 107, 173–179. [Google Scholar]
- Muñoz-Cobo, J.L.; Escrivá, A.; Domingo, M.D. In-phase instabilities in BWR with sub-cooled boiling, direct heating, and spacers effects. Ann. Nucl. Energy 2016, 87, 671–686. [Google Scholar] [CrossRef]
- Dokhane, A.; Hennig, D.; Chawla, R. Interpretation of in-phase and out-of-phase BWR oscillations using an extended reduced order model and semi-analytical bifurcation analysis. Ann. Nucl. Energy 2007, 34, 271–287. [Google Scholar] [CrossRef]
- Demeshko, M.; Dokhane, A.; Washio, T.; Ferroukhi, H.; Kawahara, Y.; Aguirre, C. Application of Continuous and Structural ARMA modeling for noise analysis of a BWR coupled core and plant instability event. Ann. Nucl. Energy 2015, 75, 645–657. [Google Scholar] [CrossRef]
- Paul, S.; Singh, S. A density variant drift flux model for density wave oscillations. Int. J. Heat Mass Transf. 2014, 69, 151–163. [Google Scholar] [CrossRef]
- Paul, S.; Singh, S. On nonlinear dynamics of density wave oscillations in a channel with non-uniform axial heating. Int. J. Therm. Sci. 2017, 116, 172–198. [Google Scholar] [CrossRef]
- Vinai, P.; Demazière, C.; Dykin, V. Modelling of a self-sustained density wave oscillation and its neutronic response in a three-dimensional heterogeneous system. Ann. Nucl. Energy 2014, 67, 41–48. [Google Scholar] [CrossRef]
- Paruya, S.; Goswami, N.; Pushpavanam, S.; Pillai, D.S.; Bidyarani, O. Periodically-forced density wave oscillations in boiling flow at low forcing frequencies: Nonlinear dynamics and control issues. Chem. Eng. Sci. 2016, 140, 123–133. [Google Scholar] [CrossRef]
- Pandey, V.; Singh, S. Characterization of stability limits of Ledinegg instability and density wave oscillations for two-phase flow in natural circulation loops. Chem. Eng. Sci. 2017, 168, 204–224. [Google Scholar] [CrossRef]
- Marcel, C.P.; Rohde, M.; Van Der Hagen, T.H.J.J. An experimental parametric study on natural circulation BWRs stability. Nucl. Eng. Des. 2017, 318, 135–146. [Google Scholar] [CrossRef]
- Castillo-Durán, R.; Ortiz-Servin, J.J.; Castillo, A.; Montes-Tadeo, J.L.; Perusquía-del-Cueto, R. A stability assessment of optimum Fuel Reload Patterns for a BWR. Ann. Nucl. Energy 2016, 94, 841–847. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).