Abstract
Aiming at the issue of extracting the incipient single-fault and multi-fault of rotating machinery from the nonlinear and non-stationary vibration signals with a strong background noise, a new fault diagnosis method based on improved autoregressive-Minimum entropy deconvolution (improved AR-MED) and variational mode decomposition (VMD) is proposed. Due to the complexity of rotating machinery systems, the periodic transient impulses of single-fault and multiple-faults always emerge in the acquired vibration signals. The improved autoregressive minimum entropy deconvolution (AR-MED) technique can effectively deconvolve the influence of the background noise, which aims to enhance the peak value of the multiple transient impulses. Nevertheless, the envelope spectrum of simulation and experimental in this work shows that there are many interference components exist on both left and right of fault characteristic frequencies when the background noise is strong. To overcome this shortcoming, the VMD is thus applied to adaptively decompose the filtered output vibration signal into a number of quasi-orthogonal intrinsic modes so as to better detect the single- and multiple-faults via those sub-band signals. The experimental and engineering application results demonstrate that the proposed method dramatically sharpens the fault characteristic frequencies (FCFs) from the impacts of bearing outer race and gearbox faults compared to the traditional methods, which show a significant improvement in early incipient faults of rotating machinery.
1. Introduction
Rolling bearings and gearboxes are widely used in rotating mechanical drive systems in manufacturing. Rotating machinery always endure heavy loads under complicated and adverse operating conditions, and as mechanical systems become increasingly complex and coupled, some slight faults such as pitting, spalling and breakage fault,, may lead to a grave danger or industrial catastrophe [1,2,3]. Therefore, the high-efficiency and accurate fault diagnosis and condition-based maintenance technique are important in both reducing operating and maintenance costs and improving plant safety.
Recently, the vibration signal processing techniques for fault characteristic extraction have attracted considerable attention and also have been proved to be effective in fault monitoring of roller bearings and gearboxes [4,5]. In general, when a defect occurs in the rotating machinery, periodical impulses will emerge in the acquired vibration signals, however, the periodical impulses are usually submerged in strong vibration responses from other mechanical components and background noise, especially during the initial fault occurrence. From another aspect, due to the complexity of rotating machinery systems, multiple faults most likely co-exist in the mixed vibration signal. Therefore, two challenges are encountered in rotating machinery fault diagnosis and feature extraction.
The first challenge is to reduce the noise interference and improve the signal to noise ratio (SNR) in the fault vibration signals. To address this issue, several methods have been proposed and are widely used in mechanical vibration analysis. Kang et al. introduced a wavelet soft-thresholding filter-based denoising method to eliminate the high-level noise from the acoustic emission (AE) time domain signals [6]. Cattani proposed a harmonic wavelet filtering technique (HWFT) that can easily enhance weak defect signals, and it can easily separate the periodic components of the signal from a mixed fault signal (even if at a certain scale approximation) [7,8]. Abbasion et al. studied the condition of an electric motor with two rolling bearings (one next to the output shaft and the other next to the fan) with one normal state and three faulty states each [9]. However, wavelet or harmonic wavelet de-noising is essentially a band-pass filter based applied on a Fourier transform with a time-variable window and is not self-adaptive in nature due to the fact different mother wavelets should be predefined for sub-bands. To address this challenge, empirical mode decomposition (EMD) and ensemble EMD (EEMD) were proposed and have shown their superiority over the wavelet and other traditional methods in many fault diagnosis applications, such as bearing fault diagnosis [10,11], gear fault diagnosis [12,13] and rotor fault diagnosis [14,15]. However, the EMD and EEMD still have some shortcomings, such as end effects and mixing problems [16,17] that still must be solved. Local mean decomposition (LMD) as a novel self-adaptive de-noising method can decompose the multi-component signals into several single-componet AM-FM signals [18]. The LMD has also been employed to extract the fault characteristic frequencies for condition monitoring of rotating machinery [19,20], unfortunately, in the actual engineering signals, a lot of extra and useless frequency components were generated along with the periodical impulse signals. On the whole, noise suppression may simultaneously attenuate target signal intensity if the target signal frequencies are involved in the noise bandwidth [21].
The second challenge is how to accurately extract the multiple fault features under complex and variable operation condition. It should be noted that different kind of faults in a mechanical system may excite the same or different resonance frequency bands, and until now, most studies upon the diagnosis of multiple-fault on rotating machinery focused on multi-faults classification or recognition, for example, Kaltungo et al. used the composite spectrum (CS) data fusion technique and composite higher order spectra (CHOS) approache to separate four different faults condition such as shaft crack, shaft misalignment, shaft rub and shaft crack and its healthy condition of rotor-related system [22,23,24] and few works have been reported on the detection of multiple-faults.
Hence, based on the above analysis, to address the first challenge, given that the impulses which are disturbed by high frequency noise and the traditional de-noising methods may simultaneously attenuate target signal intensity, in this paper, a new methodology based on improved autoregressive minimum entropy deconvolution (improved AR-MED) was proposed. Unlike the traditional de-noising methods, the AR-based linear prediction filter can firstly isolate the structure resonance signals from the measured signals, meanwhile, the impulses which are contained in the residual of the AR model, and then the residual component is enhanced by using the improved MED technique, which effectively minimizes the noise and therefore results in clear detection results, even under high frequency background noise condition. Nevertheless, the envelope spectrum of simulation and experimental in this work shows that there are many interference components exist on both left and right of fault characteristic frequencies when the background noise is strong.
To eliminate background noise effectively and address the challenge of multiple-fault feature extraction, the variational mode decomposition method [25] was proposed. The VMD can decompose a multi-component signal into a discrete number of band-limited functions (BLIMF modes), where their center frequencies can be estimated along with the decomposition online. Inspired by the VMD technique, this research utilizes VMD to detect the multiple signatures caused by gearbox multiple-faults. To this end, this paper proposes a novel hybrid method based on improved AR-MED and variational mode decomposition for single and multiple weak faults diagnosis of rotating machinery. Results of experimental and engineering application indicate that the periodic transient impulses can be detected more accurately and effectively in cases where previous approaches failed, which shows a significant improvement in early incipient fault detection of rotating machinery.
The remainder of the paper is organized as follows: in Section 2, the proposed improved AR-MED method is given. Section 3 gives some fundamental definitions, computation algorithm of VMD method and an example discussion. Section 4 validates the effectiveness of the proposed approach by simulated fault diagnosis of rotating machinery. The experimental validation and engineering application validation are presented in Section 5. Finally, Section 6 concludes this paper.
2. Improved Autoregressive Minimum Entropy Deconvolution (Improved-AR-MED)
When a pitting corrosion or spalling defect on one bearing surface strikes another contact surface, a series of successive impulses and structure resonance sequences will be generated during consecutive operation, regardless of the localized failure on the inner race, outer race or rolling elements. Generally, the fault vibration signal Sig(n) collected from the mechanical equipment can be described as a convolution between the response function of the systems transmission path h(n) and the combined structure resonance signals d(n) (deterministic signals) for the system dynamics, a fault impulse function x(n) and the background noise e(n) (illustrated in Equation (1)):
where symbol * represents convolution. The objective of many residual signal methods, including the autoregressive (AR) model-based method, is to remove the deterministic parts from the original vibration signal.
2.1. Preprocessing: AR Model-Based Method
For a stationary random sequence xn {n = 1, 2,…, N}, the p-th order AR(p) model is defined as follows [26]:
where, is the AR model coefficients and is a residual error. The calculation process of residual signal obtained from the AR model-based is as follows:
- Step 1:
- AR model order p. The optimal order of AR model can be calculated by the Akaike information criterion (AIC) [27].
- Step 2:
- AR model coefficients estimation . The AR coefficients are often determined by Yule–Walker Equations [28,29].
- Step 3:
- Residual error . Perform step1 ahead prediction on the potentially faulty vibration data and calculate the residual prediction error.
As a consequence, by subtracting the predicted parts from the original vibration signal, the residual signal can be obtained including the impulses and stationary background noise. Therefore, the fault impulses parts will be left in the residual of the AR model-based equation.
2.2. Improved AR Minimum Entropy Deconvolution
Minimum entropy deconvolution (MED) was originally proposed by Wiggins in [30] and has shown its effectiveness to enhance the impulse characteristic from a mixture vibration fault signal. The fundamental purpose of the MED is to find an inverse filter that counteracts the influence of transmission path and to search an optimum set of filter coefficients that recover the output signal which is closer to the original impulses with the maximum value of kurtosis.
Figure 1 illustrates the basic deconvolution process performed by the AR-MED filtering. This process eliminates the structure resonance signal (deterministic signal). The residual obtained from AR model-based can be used as input signal to the MED deconvolution process. The AR-MED deconvolution filter g(n) generates output signals which represents the fault impulses as close as possible to the original input x(n).
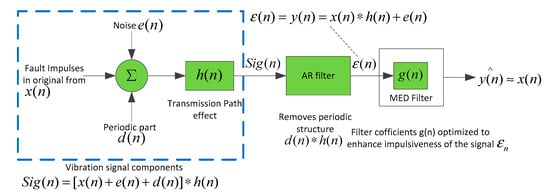
Figure 1.
AR-MED filtering deconvolution process [30,31].
Assume x(n) is fault periodic impulse signal, e(n) is background noise and h(n) is systems transmission path, thus residual signal y(n) (note: y(n) equal to residual error ) extracted from the AR model-based can be expressed as:
The objective of the MED deconvolution is to find an optimal inverse filter g(n) to recover the periodic impulse signal, that is:
where K represents the length of the inverse filter g(n).
By taking the partial derivative with respect to l for Equation (4), we have:
During the process of periodic impulse recovery x(n), the objective of inverse filter g(n) is to recover the main characteristics information and to maximize the kurtosis of x(n). The kurtosis is taken as the normalized 4-th order moment given by:
Optimum filter settings occur when the derivative of the Equation (6) is zero such as:
According to Equation (5), by using and thus the Equation (7) can be rewritten as:
Equation (8) can be written in matrix form:
The vector f is obtained from the cross correlation of input and output signal and of the inverse filter g(n), A is the Toeplitz autocorrelation matrix of the with dimension (L × L) and g is the optimum filter coefficient. Here, f (l) can be expressed as:
where, .
Finally, the inverse filter g can be obtained as:
The iterative steps of the MED are tabulated in below:
- (1)
- Assume initial filter as a centered impulse, i.e., .
- (2)
- Solve .
- (3)
- Solve .
- (4)
- Solve for new filter coefficients, i.e., .
- (5)
- Compute the error criterion, , if Err ≤ tolerance, the iteration process is finished, or Err > tolerance, then and repeat the process from step 2.
However, there are a series of limitations (such as optimal solution problem) with existing AR-MED in rotating machinery fault diagnosis, the topmost being that the AR-MED approach only deconvolves a single impulse or a finite sequence of impulses, while in the rotating machinery fault diagnosis, the purpose is to solve a transient impulse sequence to be better suited for fault detection. In the next section, an improved algorithm (namely, multiple impulses AR-MED approach) aims at overcoming the defect of a single impulse or a finite sequence of impulses problem of traditional AR-MED is given.
Definition.
Multiple points D-Norm, see reference [32]:
where and .
The multiple impulses D-Norm (MID) maximization problem can be expressed as:
where parameter t is a constant vector that represents the location of multiple impulses. For example, if , it means that the location of output impulses at t = 2, t = 6 and t = 8 will be deconvolved. Since g is the maximum of , if and only if, g is an extremal point of , the equivalent of Equation (13) can be established.
Hence, the maxima and minima are found by differentiating with respect to the filter g and equating to 0, thus we have:
where .
It follows that and , therefore, the Equation (13) can be written as:
Let , for all , and converting the Equation (15) to matrix form, then:
where . Equivalently, .
According to Equation (4), i.e., , Equation (16) can be expressed as:
If g is a solution of Equation (17), then any multiple is also a solution, namely, , we have:
Therefore multiples of are non-trivial solutions for g, we have the solution as follows:
Finally, for all , the array of possible solutions g, namely, , which can be calculated as . Furthermore, the array of outputs can be obtained, i.e., , where .
In the improved AR minimum entropy deconvolution method, the multiple transient impulses can be represented by the output solution .
3. Variational Mode Decomposition (VMD) and Example Discussion
3.1. Review of VMD
The purpose of the variational mode decomposition (VMD) is to decompose a multi-component original signal into k discrete number of band-limited Intrinsic Mode Functions (IMFs) such that each IMF is considered to compact around their respective center frequencies and its bandwidth can be estimated using the H1 Gaussian smoothness of the demodulated signal [25]. Unlike EMD and LMD methods, the number of IMF components to be involved in the decomposition is chosen prior to the decomposition processing. Here, the IMF component uk(t) can be expressed as follows:
where, is the instantaneous amplitude, the phase is a non-decreasing function and the is instantaneous phase, i.e., . In addition, contrary to the EMD and LMD methods, the IMF component generated by VMD is starting from the coarsest level, that is to say, the low IMFs represents fast oscillations (i.e., high frequency modes), and high order IMFs represents slow oscillations (i.e., low frequency modes).
The bandwidth of each IMF component uk(t) can be evaluated with following steps:
- Step 1:
- For each IMF component uk(t), the real signal is converted to the analytic signal by means of the Hilbert transform to obtain a unilateral frequency spectrum as follows:
- Step 2:
- For each IMF component uk(t), the frequency spectrum of uk(t) is translated to baseband by using modulation property to the respective estimated center frequencies. That is:
- Step 3:
- The bandwidth of each IMF component uk(t) is estimated through the H1 Gaussian smoothness of the demodulated signal, i.e., the squared L2-norm of the gradient. So the resulting is written as a constrained variational problem as follows:where, f is the original signal, represents the K-th IMF model with centre frequency , is the Dirac function, k is the number of IMF models, t is time script and symbol * denotes convolution, respectively.
To address the variational problem above, a quadratic penalty and Lagrangian multipliers are introduced, thus the augmented Lagrangian L is given by:
Then, Equation (24) can be solved by the alternate direction method of multipliers method (ADMM), the detailed ADMM algorithms of which are given in [33,34,35]. Finally, all the IMF models obtained from this solution are written as:
The iterative steps of the VMD are as follows:
- (1)
- Initialization, , , , n;
- (2)
- Execute a loop, n = n + 1;
- (3)
- For all , update is as follows:
- (4)
- Update is as follows:
- (5)
- Update is as follows:
- (6)
- Iterate steps (2) to (5) until the residual satisfies a given stopping criterion. That is:
In the end, the k IMF modes are obtained by the inverse Fast Fourier transform (IFFT) of the signal , i.e., .
3.2. Example Discussion
In order to compare the decomposition performance of the EEMD, LMD and VMD methods, the IMFs, PFs and Hilbert spectrum plots are discussed. Here, a multi-component AM-FM signal x(t) is given as follows:
where sampling point N = 1000, t = 1/1000:1/1000:1, sampling frequency Fs = 1024 Hz.
Note that the number of modes k is adaptively obtained and unchangeable in EEMD and LMD methods, however, the number of IMFs is required to predetermine for VMD method, thus the number of IMFs k in VMD was set to be 3 for the further decomposition. The time domain signal waveforms of x(t), x1(t), x2(t) and x3(t) are shown in Figure 2. Examples of IMFs and Product functions (PF) modes obtained respectively by the EEMD, LMD and VMD are illustrated in Figure 3a,c,e. The Hilbert spectrum plots of the mono-components derived from the three decomposition methods are shown in Figure 3b,d,f, respectively. It can be found from Figure 3a–d that the IMFs and PFs derived from EEMD and LMD method are all anamorphic with serve scale-mixing problem. While in the decomposition of VMD method (see Figure 3e,f), it can be clearly found that three IMFs components, i.e., IMF1(t), IMF2(t) and IMF3(t) are corresponding to the x1(t), x2(t) and x3(t) of the original AM-FM signal x(t), respectively. Moreover, the three horizontal lines (instantaneous frequency are 4 Hz, 14 HZ and 30 Hz) in Figure 3f has a narrower bandwidth than that of the EEMD and LMD methods. Therefore, the comparison results illustrate that the IMF components can be accurately extracted from the mixed signal by using the VMD method, which is much closer approximation to the real components of x(t).
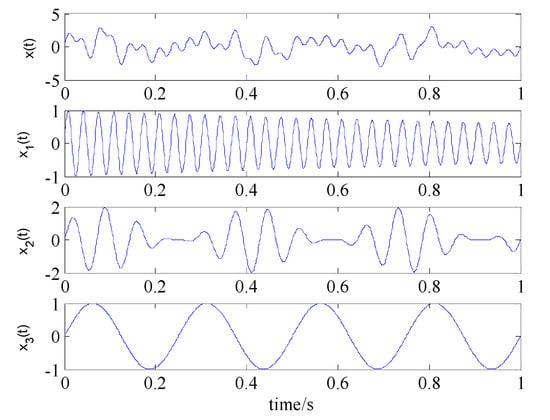
Figure 2.
The time domain waveform of the multi-component AM-FM signal x(t).
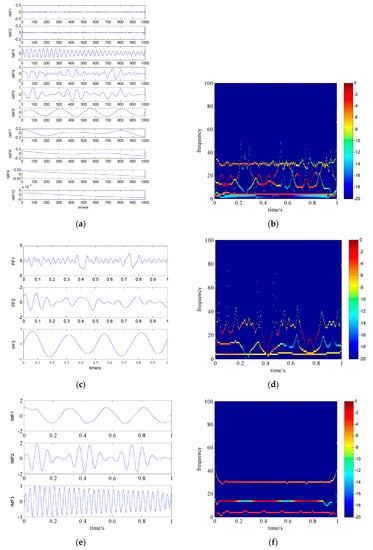
Figure 3.
Decomposition results and time-frequency distribution of the multivariate signal with noise using EEMD, LMD and VMD methods. (a) IMF components of x(t) decomposed by using EEMD; (b) Hilbert spectrum distribution of the EEMD results; (c) PF components of x(t) decomposed by using LMD; (d) Hilbert spectrum distribution of the LMD results; (e) IMF components of x(t) decomposed by using VMD; (f) Hilbert spectrum distribution of the VMD results.
4. Simulation Analysis for Weak Fault Extraction of Rotating Machinery
In order to verify the effectiveness of the above algorithms, in this section, a bearing simulation fault signal can be described by the following mathematical model:
in which A0 = 1 denotes the amplitude of modulating signal, a = 0.1 is a damping coefficient, sampling point N = 8192, t = 1/2000:1/2000:0.4096, sampling frequency Fs = 20,000 Hz, the frequencies of the above signal are as follows: f1 = 20, f2 = 35, and f3 = 2000 represents the natural frequency of excited structure. Moreover, a stationary white noise x3(t) was added to obtain the simulated signals with SNR = −6dB.
Figure 4a depicts a periodic impulse signal and Figure 4b depicts the raw simulation fault signal. It is clear to see that the periodic impulse would be easily lost or submerged within the heavy background noise. Figure 4c depicts the envelope spectrum of the raw simulation fault signal. It should be noted that the fault characteristic frequency f = 100 Hz, which convolves the resonance frequency band that cannot be detected.
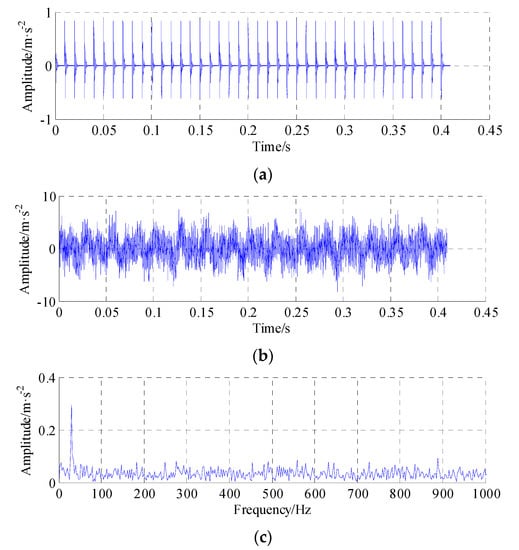
Figure 4.
Simulated signal and its envelope spectrum. (a) Periodic impulse signal; (b) Raw fault signal with heavy noise; (c) Envelope spectrum of the raw fault signal.
Hence, in order to simplify the appearance of a signal and obtain the periodic impulses from the noisy mixed signal, the AR-MED filter method was introduced directly. Figure 5a shows the AR-MED filtered signal waveform and Figure 5b illustrates the envelope spectrum of AR-MED filtered signal, respectively. It can be seen in Figure 5b that the fault characteristic frequency is also lost in the background noise. This phenomenon can be explained as follows:
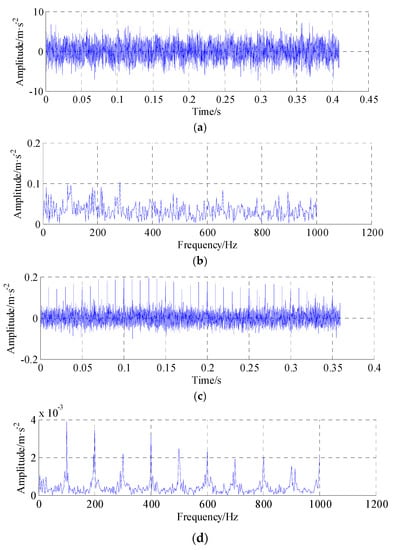
Figure 5.
Filtered signal and its envelope spectrum with AR-MED and improved AR-MED method. (a) Filtered signal with AR-MED method; (b) Envelope spectrum of AR-MED filtered signal; (c) Filtered signal with improved AR-MED method; (d) Envelope spectrum of improved AR-MED filtered signal.
- (1)
- AR-MED is optimizing the norm Kurtosis which prefers a solution of a single impulse or deterministic impulse. For the bearing fault signals, a series of periodic impulses features maybe not suit for this approach.
- (2)
- There are still a heavy noise remained in the output signal that generated by AR-MED filter, which means the impulsive convolved in the suppressed resonance frequency bands cannot be detected by AR-MED.
Figure 5c,d respectively illustrate the filtered signal waveform and its envelope spectrum with improved AR minimum entropy deconvolution method (here, the length of filter-size L = 1000). Comparing the filtering result and envelope spectrum obtained from improved AR minimum entropy deconvolution, it can be observed that multiple strong peaks were deconvolved and the fault characteristic frequency and its harmonics can be clearly observed. However, under highly noisy background the spectrum magnitude in Figure 5d is weak, and there are many interference components exist on both left and right of fault characteristic frequencies.
Consequently, the VMD approach was employed to decompose the filtered signal generated by improved AR-MED method. Since the VMD requires a predetermined number of sub-signals K, for instance, if the number of IMFs is M, then the parameter M used to determine the number of decomposition result, therefore, the resulting central frequency corresponding to different parameter K from 2 to 7 are tabulated in Table 1. As shown in Table 1, it can be seen that the K varying from 2 to 6 meets the condition that all center frequencies are better separated by the uniform distribution, while K = 7 shows that the central frequency 1699 Hz is very close to the 2100 Hz, and the natural frequency of excited structure (2000 Hz from Equation (31)) disappeared, thus the best result is given by VMD with K = 6.

Table 1.
Central frequency corresponding to different K values.
The decomposed results using VMD and their magnitude spectrum have been shown in Figure 6a,b. It is observed that all the signatures are successfully identified and clearly shown in 1st to 6-th IMF model. Here, according to the criterion of maximum kurtosis, i.e., the maximum kurtosis criterion component contains the main fault information of the mixed signal. The kurtosis is calculated to select the best fault sub-band for the envelope analysis, and the kurtosis of each IMF mode is as follows: KIMF1 = 2.2802, KIMF2 = 6.7916, KIMF3 = 3.2967, KIMF4 = 3.0748, KIMF5 = 3.0472 and KIMF6 = 3.1231. Hence, the IMF2 component was elected to extract the fault characteristic frequency.
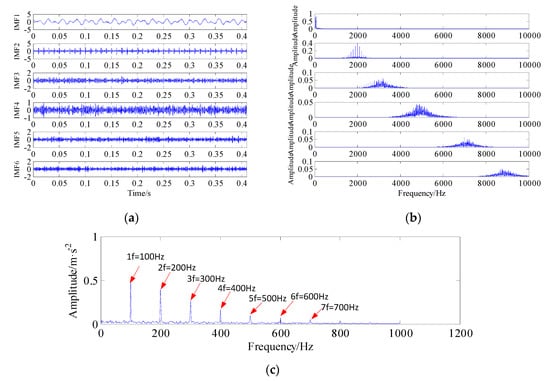
Figure 6.
Decompose results using the VMD and spectrum analysis. (a) IMF components of improved AR-MED de-noised signal decomposed by VMD; (b) The amplitude spectrum of each IMF component; (c) Envelope spectrum of IMF2.
Figure 6c shows the envelop spectrum of IMF2 component. It was observed that the fault characteristic frequency f = 100 Hz and its harmonics (i.e., 2f, 3f, 4f, 5f, 6f and 7f) are extracted by using VMD method. Meanwhile, the amplitudes of spectral peak increase dramatically, thus making the extraction of fault frequencies easy and accurate. In summary, the experimental results fully illustrate that the proposed approach was able not only to detect the fault frequencies in a weak fault signal but also to remove noise well.
5. Experimental and Engineering Application Verification
5.1. Case 1—Bearing Fault Experimental Setup
The bearing fault vibration signal was generated by the Intelligent Maintenance Systems (IMS) and University of Cincinnati (Cincinnatti, OH, USA) [36]. Four ZA-2115 double row bearings (Rexnord, Milwaukee, WI, USA) were installed on the shaft as shown in Figure 7. The rotation speed is kept constant at 2000 rpm and driven by an AC motor and coupled by rub belts. Vibration data was collected every 10 min by a NI 6062E-DAQ-Card (National Instruments, Austin, TX, USA), the sampling rate set at 20 kHz and the data length is 20,480 points. This accelerated life test was carried out successively for eight days (from 10:32:39 on 12 February 2004 to 06:22:39 on 19 February 2004, from normal to severe faults, i.e., 9840 min) until the magnetic plug exceeds a certain level and causes an electrical switch to close. The geometric parameters and ball pass frequency outer (BPFO) race of the tested bearing are presented in Table 2.
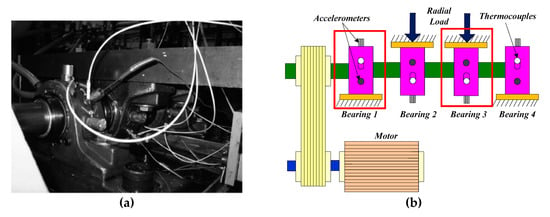
Figure 7.
Bearing test rig; (a) Ball bearing fault test rig; (b) The schematic diagram of accelerated life test.

Table 2.
Geometric parameters and expected characteristic frequencies of the tested bearing.
5.2. Case 1—Results and Discussion of Bearing Single Fault
This accelerated life test was carried for 8 days, the equivalent vibration intensity (EVI) entire life-cycle curve and kurtosis entire life-cycle curve of rolling bearings 1 are respectively shown in Figure 8a,b. The detailed algorithm of EVI is given in our previous work [37]. Figure 8b reveals that the evolution of kurtosis can be divided into three stages, i.e., normal operation, incipient fault and severe fault stage. It also can be seen in Figure 8b that the failure scope of bearing 1 is from the 6470th minute (incipient failure point) to the 9840th minute (severe damage point). During the first five days of operation, no underlying trend was observed. After the test had been carried out for 6490 min (at the end of the 5th day), the EVI and kurtosis of the vibration measurements increased significantly in the serious damage stage.
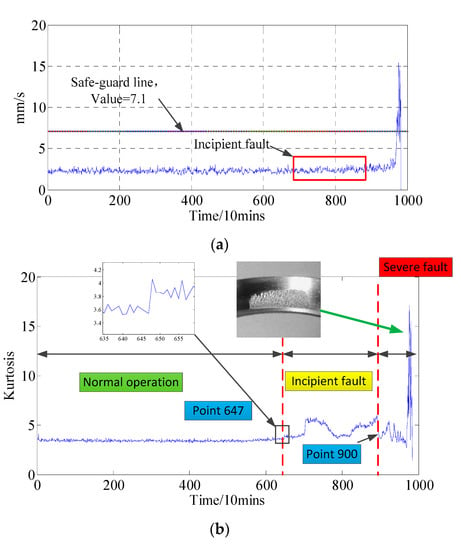
Figure 8.
Time feature (a) equivalent vibration intensity and (b) kurtosis of bearing 1 for the whole life cycle.
It also can be seen in Figure 8a,b that the range of failure probability is from incipient failure time to severe failure time, namely 6210th minute–8700th minute. Considering the early weak fault maybe submersed in heavy background noise, four sets of data (3rd day, 4th day, 5th day and 6th day, with the corresponding operation times being 2980, 4420, 5860 and 7300 min, respectively) from the experimental system were analyzed.
A summary of the vibration acceleration signals of the 3rd day discussed in this paper is given in Figure 9. The signal in the top row Figure 9a represents the raw signal without any processing. It is seen that no impacts can be located and the kurtosis value is 3.5192 (it is approximately a normal distribution), it is easy to conclude that the bearing is running stably. In the second row Figure 9b, the improved AR-MED filtered signal is presented. It can be seen that the amplitude is decreased substantially by the improved AR-MED method. The third row Figure 9c shows the IMF components of improved AR-MED denoised signal decomposed by using the VMD method, which can be help distinguish the periodic impulse signals from the mixed noisy signals. As result, the ball pass frequency outer (BPFO) signal is completely contaminated by the heavy background noise which can be confirmed from the envelope spectrum as presented in Figure 9d, here, the kurtosis value of the second IMF model is the largest. A similar analysis result can be implemented in Figure 10, where the ball pass frequency outer (BPFO) also cannot be found in the corresponding envelope spectrum.
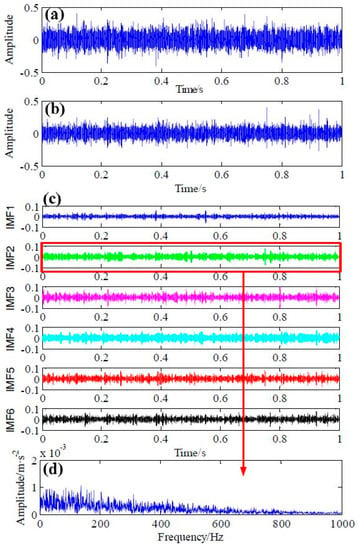
Figure 9.
Results using the proposed method of method the 3rd day’s data (2980 min); (a) The original bearing vibration signal; (b) The improved AR-MED filtered signal; (c) The IMF components of improved AR-MED filtered signal generated by VMD method; (d) The envelope spectrum of IMF2.
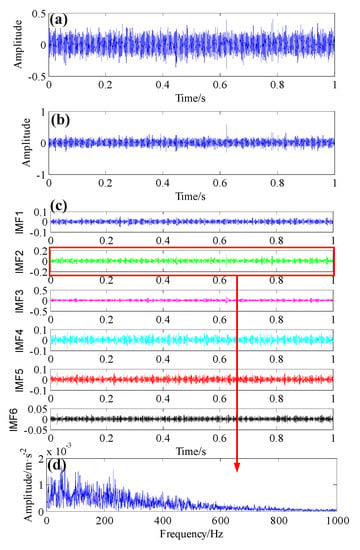
Figure 10.
Results using the proposed results of the 4th day’s data (4420 min); (a) The original bearing vibration signal; (b) The improved AR-MED filtered signal; (c) The IMF components of improved AR-MED filtered signal generated by VMD method; (d) The envelope spectrum of IMF2.
Figure 11a–d, respectively depict the raw time domain signal of the 4th day (5860 min) along with its improved AR-MED filtered signal, the IMF components and the corresponding envelope spectrum. In this case, the envelop spectrum shown in Figure 11d indicates that the characteristic frequency at 230.7 Hz and its harmonic (230.7 × 2 Hz) are extracted (it is roughly equal to the BPFO frequency), which means that there is a fault in the outer race, whereas the low-frequency noise frequencies located around it are still significant.
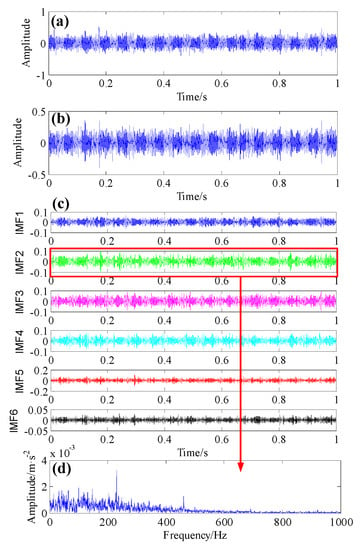
Figure 11.
Results using the proposed method method on the 5th day’s data (5860 min); (a) The original bearing vibration signal; (b) The improved AR-MED filtered signal; (c) The IMF components of improved AR-MED filtered signal generated by VMD method; (d) The envelope spectrum of IMF2.
Figure 12d depicts the corresponding envelope spectrum with peaks at 230.7 Hz and its harmonics (2f0, 3f0), which shows that the BPFO peak is highlighted while the noise interference can be ignored. By comparing Figure 11d and Figure 12d, as the failure progresses, the amplitudes of the BPFO peaks increase, thus making the feature monitoring easier and more accurate.
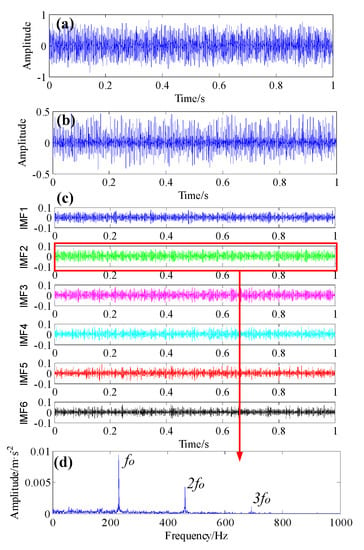
Figure 12.
Results using the proposed method on the 6th day’s data (7300 min); (a) The original bearing vibration signal; (b) The improved AR-MED filtered signal; (c) The IMF components of improved AR-MED filtered signal generated by VMD method; (d) The envelope spectrum of IMF2.
Moreover, disassembling the roller bearing and checking the running performance, the engineers found that an outer race with localized wear defect was discovered in test bearing 1 as shown in Figure 13. Indeed, it should be noted that 5860th minute is earlier than the incipient fault time 6490th minute observed in the kurtosis curves (see Figure 8b), on this occasion, the impulse features are buried in the strong background noise and are difficult to identify by the traditional kurtosis curve.

Figure 13.
Photo of outer race defect in bearing 1 after the test.
Furthermore, in order to confirm the advantages of our proposed method, the same vibration signal of 4th day (5860 min) is processed via the common wavelet and LMD methods. Figure 14a and Figure 15a show the wavelet sub-band and PF components, in which the raw vibration signals were divided into eight components, respectively. As illustrated in Figure 14a and Figure 15a, where the high-frequency models represent fast oscillations and the low-frequency models represent low oscillations in Wavelet and LMD. Generally, the useful fault information was contained in high-frequency models, based on the criterion of maximum kurtosis, the sub-band component a7 and component PF2 were applied for fault feature extraction, respectively.
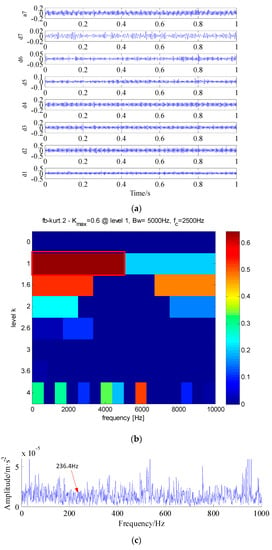
Figure 14.
Results using Wavelet method. (a) Sub-band components of original signal decomposed by using Wavelet; (b) Kurtogram of a7 sub-band component; (c) Fourier transform magnitude of the squared envelope.
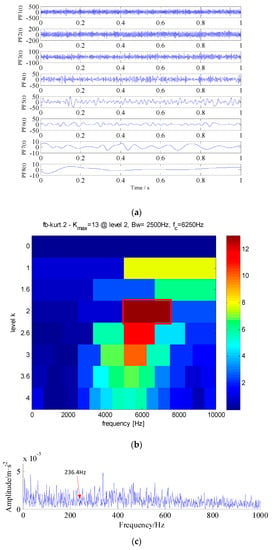
Figure 15.
Results using LMD method. (a) PF components of original signal decomposed by using LMD; (b) Kurtogram of PF2 component; (c) Fourier transform magnitude of the squared envelope.
The kurtogram of the a7 sub-band component is displayed in Figure 14b, and the kurtogram of the PF2 component is displayed in Figure 15b, from which the optimal demodulation frequency band, namely (0 Hz–4896 Hz) and (5104 Hz–7396 Hz) can be detected. Thus a band-pass filter is designed to extract the potential features from the a7 sub-band component and PF2 component. Lastly, the envelope spectrum is applied to the filtered signal, the corresponding envelop spectrums are illustrated in Figure 14c and Figure 15c, respectively.
As can be seen, the fault characteristic frequency 236.4 Hz cannot be detected by the wavelet and LMD methods in the envelope spectrum and it is also hard to distinguish the fault location from the incipient fault signal. On the whole, the proposed technique presents good performance in enhancing weak periodic signals corrupted by heavy background noise, thus re-confirming the effectiveness and efficiency in terms of the weak fault characteristic extraction.
5.3. Case 2—Gearbox Fault Experimental Setup
The gearbox fault vibration signals were collected by Qian-Peng Diagnosis Engineering Co., Ltd. (Zhenjiang, China). The rotation speed of drive gear shaft was kept constant at 1470 rpm. Vibration data was collected in the driving end by an accelerometer ADA16-8/2 (LPCI, Zhenjiang, China), the sampling frequency is 5120 Hz and the data length is 53,248 points. This multiple-fault in the gearbox couples a localized pitting in the bull gear and a localized wear fault in the pinion gear. Gear material is S45C steel, the module of bull and pinion gear is 2, the tooth number of pinion gear and bull gear is Z1 = 55 and Z2 = 75, respectively, i.e., gear number ratio is Z1:Z2 = 11:15, the pressure angle is 20° and face width of teeth is 20 mm. The overall instrument configuration and the real equipment layout figure of the gearbox test rig are shown in Figure 16a,b, respectively. The pitting fault frequency fpitting of the bull gear is fpitting = 17.96 Hz and the wear fault frequency of pinion gear is fwear = 33.41 Hz.
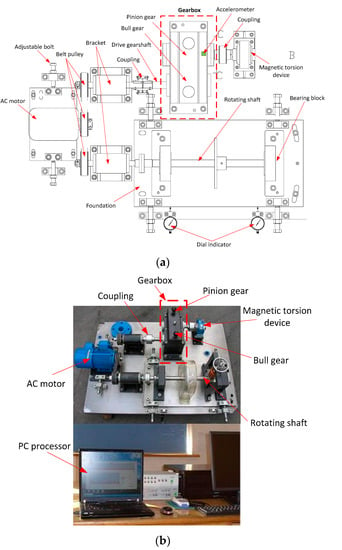
Figure 16.
Gearbox test rig; (a) The engineering drawing of gearbox test rig; (b) The equipment layout figure of real gearbox test rig.
5.4. Case 2—Results and Discussion of Gearbox Multiple-Fault
Figure 17a illustrates the time domain signal of gear pair without any preprocessing. Figure 17b shows envelope spectrum of the raw signal. From Figure 17b, it has no distinctive fault frequency, which was buried in the strong background noise.
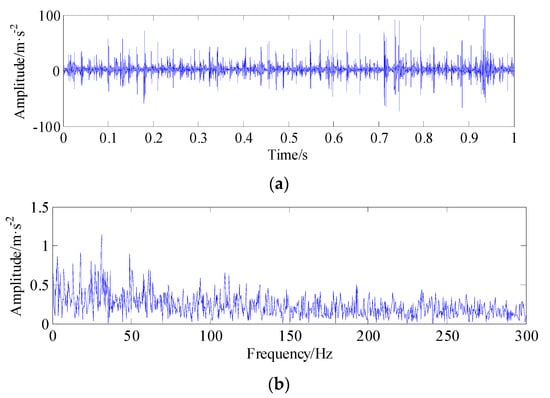
Figure 17.
Raw vibration signal and its envelope spectrum. (a) Raw vibration signal; (b) Envelope spectrum of the raw fault signals.
In order to accurately extract multiple fault impulses from the raw signal, the proposed improved AR-MED method was used to the raw signal, and the result of improved AR-MED denoising signal is given in Figure 18a, where the filtered signal clearly shows multiple impulses that are near the harmonics of the defect frequencies. Moreover, from Figure 18a, we also can see that the interval between the two periodic impulses is approximately equal to 0.0562 s, which is roughly equal to the pitting fault frequency (17.96 Hz) of the tested gear.Then the VMD method is utilized to analyze the filtered signal. Figure 18b,c show the spectrum of IMF modes extracted by VMD, where it is quite clear that the center frequencies coincide, a phenomenon (mode duplication) that emerged in model number K = 20, which demonstrate that model number K = 19 is better than K = 20.
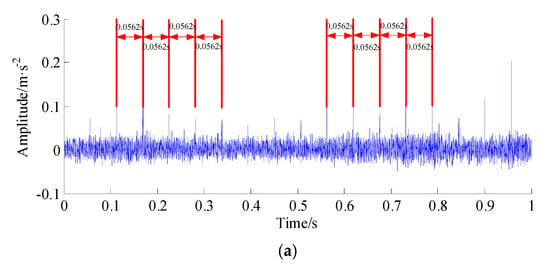
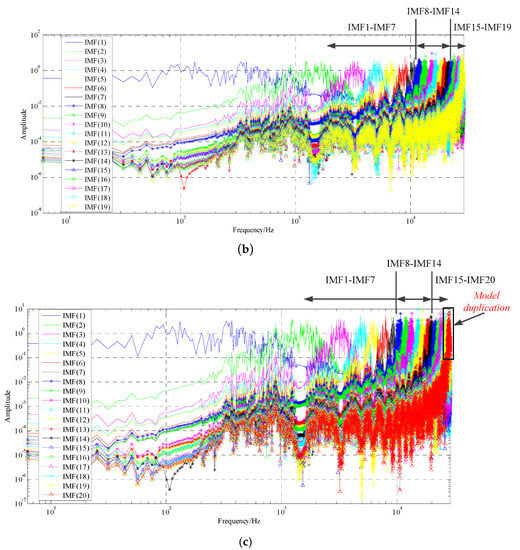
Figure 18.
AR-MED filtered signal and comparison of spectrum of modes extracted by VMD. (a) Filtered signal with improved AR-MED method. (b) The spectrum of modes extracted by VMD, K = 19, = 2000. (c) The spectrum of modes extracted by VMD, K = 20, = 2000.
19 IMF components generated by VMD are given in Figure 19a. The corresponding envelope spectrum of IMF4 component (maximum kurtosis component, kurtosis = 6.0070) is shown in Figure 19b. It can be found the fault frequency 17.81Hz (it is roughly equal to the bull fitting fault frequency ffitting = 17.96 Hz) and its harmonic components (49.06 Hz ≈ 3 × ffitting, the pinion gear wear fault frequency (31.25 Hz ≈ fwear) are clearly observed in the envelope spectrum. The result indicates that there are local defects on the gear pair that match with the engineering application. Therefore, it can be concluded that the proposed hybrid method is able to accurately identify the multiple weak faults caused by a gear-pair, which is particularly appropriate for incipient multiple fault feature extraction.
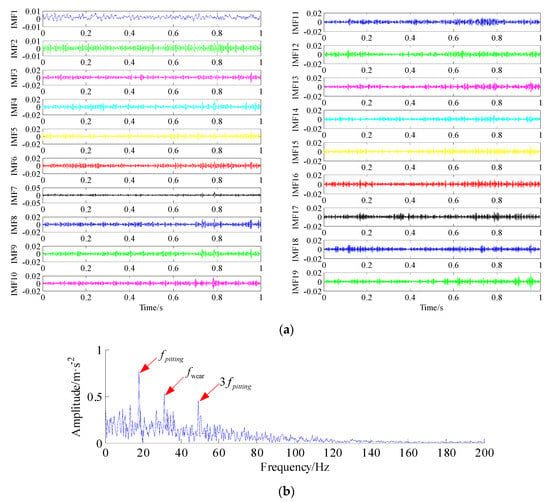
Figure 19.
Results obtained by the proposed method. (a) 19 IMF components of improved AR-MED filtered signal decomposed by using VMD; (b) Envelope spectrum of the IMF4 component.
6. Conclusions
In this paper, the single- and multiple-fault feature extraction based on an improved AR-minimum entropy deconvolution and variational mode decomposition algorithm for rotating machinery equipment is proposed. The results obtained from this research are as follows:
- (1)
- Improved AR-minimum entropy deconvolution provides a solution for the filter that is an optimal solution, which can filter out the high-frequency and background noise and enhance the peak value of the multiple transient impulses. With the improved AR-Minimum entropy deconvolution method, the location of multiple transient impulses can be deconvolved effectively, which is well-suited for the fault nature of rotating machinery.
- (2)
- As a new adaptive decomposition technique, the filtered signal is further decomposed by the VMD method, and the illusive components and model mixing problems are eliminated based upon the VMD method. Moreover, the VMD is more robust to analyze noisy signal on numerical simulation and actual data than the EEMD and LMD approach.
- (3)
- The proposed method has then been applied to experimental and engineering application signals obtained by accelerometers. Both the single-fault of bearing outer race and multiple-fault of gearboxes have proven the validity of the proposed method compared to other conventional methods. Meanwhile, the number of IMF modes requires predetermining before VMD decomposition, which leads to a lot of inconvenience in the engineering application, so an adaptive calculation algorithm should be established in this regard in future works.
Acknowledgments
This research was funded by the Fundamental Research Funds for the Central Universities (Grant No. CUSF-DH-D-2017059) and the National Natural Science Foundation of China (Grant No. 51675096). The authors wish to express their sincere gratitude for this support.
Author Contributions
Conceptualization, formal analysis, investigation and writing the original draft is done by Qing Li. Validation, review and editing is done by Steven Y. Liang. Xia Ji and Steven Y. Liang supervised the work at every stage. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Peng, Z.; Tse, P.W.; Chu, F. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Z.L.; Lu, C.; Wang, Z.P. Bearing diagnostics: A method based on differential geometry. Mech. Syst. Signal Process. 2016, 80, 377–391. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, Z.X.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Measurement 2016, 90, 4–19. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Kim, J.M. High-performance and energy-efficient fault diagnosis using effective envelope analysis and denoising on a general-purpose graphics processing unit. IEEE Trans. Power Electron. 2015, 30, 2763–2776. [Google Scholar] [CrossRef]
- Cattani, C.; Yang, J.G. Detecting singularities with Harmonic wavelets. J. Donghua Univ. 2009, 26, 544–548. [Google Scholar]
- Cattani, C. Harmonic wavelet approximation of random, fractal and high frequency signals. Telecommun. Syst. 2010, 43, 207–217. [Google Scholar] [CrossRef]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Yu, D.J.; Cheng, J.S.; Yang, Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mech. Syst. Signal Process. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Wang, H.C.; Chen, J.; Dong, G.M. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Amarnath, M.; Krishna, I.R.P. Detection and diagnosis of surface wear failure in a spur geared system using EEMD based vibration signal analysis. Tribol. Int. 2013, 61, 224–234. [Google Scholar] [CrossRef]
- Yang, C.Y.; Wu, T.Y. Diagnostics of gear deterioration using EEMD approach and PCA process. Measurement 2015, 61, 75–87. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Jiang, H.K.; Li, C.L.; Li, H.X. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mech. Syst. Signal Process. 2013, 36, 225–239. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 11–14. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, D.J.; Yu, Y. Application of support vector regression machines to the processing of end effects of Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 1197–1211. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2009, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liang, S.Y.; Song, W.Q. Revision of bearing fault characteristic spectrum using LMD and interpolation correction algorithm. Procedia CIRP 2016, 56, 182–187. [Google Scholar] [CrossRef]
- Liu, Z.W.; He, Z.J.; Guo, W.; Tang, Z.C. A hybrid fault diagnosis method based on second generation wavelet de-noising and local mean decomposition for rotating machinery. ISA Trans. 2016, 61, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.L.; He, Q.B.; Zhang, H.B.; Kong, F.R. Rotating machine fault diagnosis through enhanced stochastic resonance by full-wave signal construction. Mech. Syst. Signal Process. 2017, 85, 82–97. [Google Scholar] [CrossRef]
- Kaltungo, A.Y.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Kaltungo, A.Y.; Sinha, J.K.; Nembhard, A.D. Use of composite higher order spectra for faults diagnosis of rotating machines with different foundation flexibilities. Measurement 2015, 70, 47–61. [Google Scholar] [CrossRef]
- Kaltungo, A.Y.; Sinha, J.K.; Nembhard, A.D. A novel fault diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef]
- Konstantin, D.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar]
- Wang, K.D.; Wu, Y.X.; Gao, Y.F.; Li, Y. New methods to estimate the observed noise variance for an ARMA model. Measurement 2017, 99, 164–170. [Google Scholar] [CrossRef]
- Bengtsson, T.; Cavanaugh, J.E. An improved Akaike information criterion for state-space model selection. Comput. Stat. Data Anal. 2006, 50, 2635–2654. [Google Scholar] [CrossRef]
- Kizilkaya, A.; Kayran, A.H. ARMA model parameter estimation based on the equivalent MA approach. Digit. Signal Process. 2006, 16, 670–681. [Google Scholar] [CrossRef]
- Kruczek, P.; Wyłomańska, A.; Teuerle, M.; Gajda, J. The modified Yule-Walker method for image-stable time series models. Physica A 2017, 469, 588–603. [Google Scholar] [CrossRef]
- Wiggins, R.A. Minimum entropy deconvolution. Geoexplorafion 1978, 16, 21–35. [Google Scholar] [CrossRef]
- Endo, H.; Randall, R.B. Application of a minimum entropy deconvolution filter to enhance autoregressive model based gear tooth fault detection technique. Mech. Syst. Signal Process. 2007, 21, 906–919. [Google Scholar] [CrossRef]
- Cabrelli, C.A. Minimum entropy deconvolution and simplicity: A noniterative algorithm. Geophysics 1985, 50, 394–413. [Google Scholar] [CrossRef]
- Wang, J.J.; Wen, S.W. An algorithm twisted from generalized ADMM for multi-block separable convex minimization models. J. Comput. Appl. Math. 2017, 309, 342–358. [Google Scholar] [CrossRef]
- Li, K.Z.; Sundin, M.; Rojas, C.R.; Chatterjee, S.; Jansson, M. Alternating strategies with internal ADMM for low-rank matrix reconstruction. Signal Process. 2016, 121, 153–159. [Google Scholar] [CrossRef]
- Meissen, C.; Lessard, L.; Arcak, M.; Packard, A.K. Compositional performance certification of interconnected systems using ADMM. Automatica 2015, 61, 55–63. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J. Wavelet filter-based weak signature detection method and its application on roller bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Yang, J.G.; Li, B.Z. Long range dependence prognostics for bearing vibration intensity chaotic time series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).