CSL Collapse Model Mapped with the Spontaneous Radiation
Abstract
:1. The CSL Collapse Model
2. The Collapse Rate Parameter
3. A New Limit on
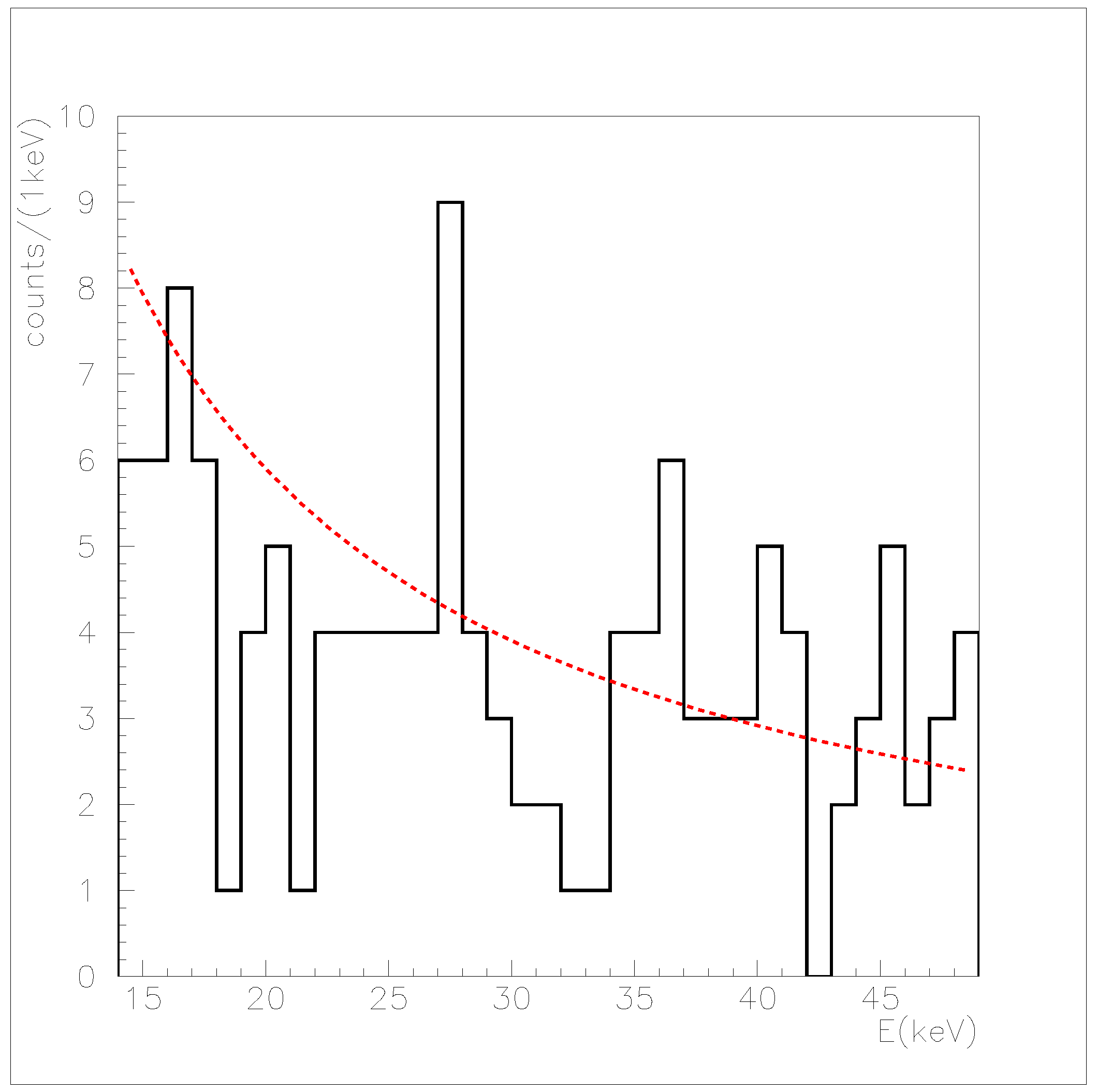
3.1. The Data Analysis: Procedure and Results
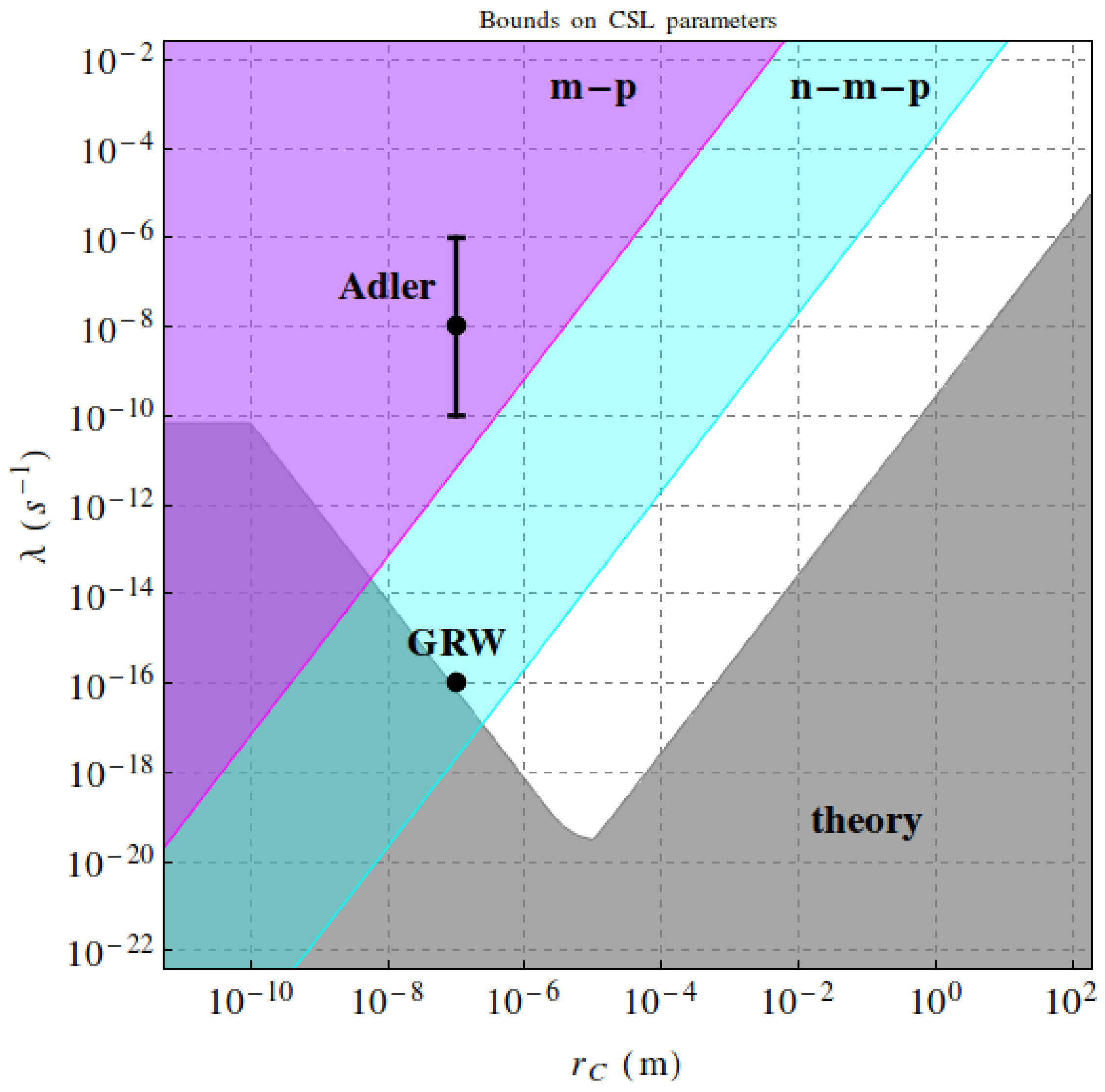
4. Mapping CSL Parameters Space
5. Conclusions and Perspectives
- the non-mass proportional model for a white noise scenario can be excluded by our analysis,
- the higher value on [11] can be excluded for a white noise scenario, in both mass proportional and non-mass proportional models,
- the measurement of the spontaneous radiation allows the obtainment of the most stringent limits on the CSL collapse model parameters, with respect to any other method, in a broad range of the parameter space (see also Ref. [22] for comparison).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bassi, A.; Ghirardi, G.C. Dynamical reduction models. Phys. Rep. 2003, 379, 257–426. [Google Scholar] [CrossRef]
- Pearle, P. Collapse Models Open Systems and Measurements in Relativistic Quantum Field Theory; Lecture Notes in Physics; Breuer, H.-P., Petruccione, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 526. [Google Scholar]
- Diósi, L. Models for Universal Reduction of Macroscopic Quantum Fluctuations. Phys. Rev. A 1989, 40, 1165. [Google Scholar] [CrossRef]
- Bassi, A. Collapse Models: Analysis of the Free Particle Dynamics. Available online: https://arxiv.org/abs/quant-ph/0410222.pdf (accessed on 25 March 2009).
- Adler, S.L. Quantum Theory as an Emergent Phenomenon; Cambridge University Press: Cambridge, UK, 2004; Charpter 6. [Google Scholar]
- Weber, T. Quantum mechanics with spontaneous localization revisited. Il Nuovo Cimento B 1991, 106, 1111–1124. [Google Scholar] [CrossRef]
- Fu, Q. Spontaneous radiation of free electrons in a nonrelativistic collapse model. Phys. Rev. A 1997, 56, 1806. [Google Scholar] [CrossRef]
- Ghirardi, G.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470. [Google Scholar] [CrossRef]
- Pearle, P. Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 1989, 39, 2277. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Pearle, P.; Rimini, A. Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A 1990, 42, 78. [Google Scholar] [CrossRef] [PubMed]
- Adler, S.L. Lower and Upper Bounds on CSL Parameters from Latent Image Formation and IGM Heating. J. Phys. A 2007, 40, 2935–2958. [Google Scholar] [CrossRef]
- Curceanu, C.; Hiesmayr, B.C.; Piscicchia, K. X-rays help to unfuzzy the concept of measurement. J. Adv. Phys. 2015, 4, 263–266. [Google Scholar] [CrossRef]
- Adler, S.L.; Ramazanoglu, F.M. Photon emission rate from atomic systems in the CSL model. J. Phys. A 2007, 40, 13395–13406. [Google Scholar] [CrossRef]
- Adler, S.L.; Bassi, A.; Donadi, S. On spontaneous photon emission in collapse models. J. Phys. A 2013, 46, 245304. [Google Scholar] [CrossRef]
- Donadi, S.; Bassi, A.; Deckert, D.-A. On the spontaneous emission of electromagnetic radiation in the CSL model. Ann. Phys. 2014, 340, 70–86. [Google Scholar] [CrossRef]
- Miley, H.S.; Avignone, F.T.; Brodzinski, R.L., III; Collar, J.I.; Reeves, J.H. Suggestive evidence for the two neutrino double beta decay of Ge-76. Phys. Rev. Lett. 1990, 65, 3092. [Google Scholar] [CrossRef] [PubMed]
- Laloë, F.; Mullin, W.J.; Pearle, P. Heating of trapped ultracold atoms by collapse dynamics. Phys. Rev. A 2014, 90, 52119. [Google Scholar] [CrossRef]
- Collett, B.; Pearle, P.; Avignone, F.; Nussinov, S. Constraint on collapse models by limit on spontaneous X-ray emission in Ge. Found. Phys. 1995, 25, 1399–1412. [Google Scholar] [CrossRef]
- Aalseth, C.E.; Avignone, F.T., III; Brodzinski, R.L.; Collar, J.I.; Garcia, E.; González, D.; Hasenbalg, F.; Hensley, W.K.; Kirpichnikov, I.V.; Klimenko, A.A.; et al. Neutrinoless double-beta decay of Ge-76: First results from the International Germanium Experiment (IGEX) with six isotopically enriched detectors. IGEX Collab. Phys. Rev. C 1999, 59, 2108. [Google Scholar] [CrossRef]
- Morales, A.; Aalseth, C.E.; Avignone, F.T.; Brodzinski, R.L., III; Cebrian, S.; Garcia, E.; Irastorza, I.G.; Kirpichnikov, I.V.; Klimenko, A.A.; Miley, H.S.; et al. Improved constraints on WIMPs from the international Germanium experiment IGEX. IGEX Collab. Phys. Lett. B 2002, 532, 8–14. [Google Scholar] [CrossRef]
- Toroš, M.; Gasbarri, G.; Bassi, A. Bounds on Collapse Models from Matter-Wave Interferometry. Available online: https://arxiv.org/pdf/1601.03672.pdf (accessed on 31 May 2017).
- Carlesso, M.; Bassi, A.; Falferi, P.; Vinante, A. Experimental bounds on collapse models from gravitational wave detectors. Phys. Rev. D 2016, 94, 124036. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piscicchia, K.; Bassi, A.; Curceanu, C.; Grande, R.D.; Donadi, S.; Hiesmayr, B.C.; Pichler, A. CSL Collapse Model Mapped with the Spontaneous Radiation. Entropy 2017, 19, 319. https://doi.org/10.3390/e19070319
Piscicchia K, Bassi A, Curceanu C, Grande RD, Donadi S, Hiesmayr BC, Pichler A. CSL Collapse Model Mapped with the Spontaneous Radiation. Entropy. 2017; 19(7):319. https://doi.org/10.3390/e19070319
Chicago/Turabian StylePiscicchia, Kristian, Angelo Bassi, Catalina Curceanu, Raffaele Del Grande, Sandro Donadi, Beatrix C. Hiesmayr, and Andreas Pichler. 2017. "CSL Collapse Model Mapped with the Spontaneous Radiation" Entropy 19, no. 7: 319. https://doi.org/10.3390/e19070319
APA StylePiscicchia, K., Bassi, A., Curceanu, C., Grande, R. D., Donadi, S., Hiesmayr, B. C., & Pichler, A. (2017). CSL Collapse Model Mapped with the Spontaneous Radiation. Entropy, 19(7), 319. https://doi.org/10.3390/e19070319



