1. Introduction
Since the observation of the Hurst effect [
1] in the Nile river, a huge number of dynamical systems whose observable outputs are time series with complex long-range power-law correlations and scaling properties have been identified. The diversity of such time series include meteorological data, physiological signals such as heart rate, brain activity, gait or postural system, biological signals as DNA sequences, stock market activity, seismic signals and many others. In order to properly analyze this great variety of (possibly non-stationary) signals, several techniques were proposed. In this work, we consider two of them: Fluctuation Analysis (FA) [
2] and Detrended Fluctuation Analysis (DFA) [
3]. Both are based on similar grounds, and try to characterize the scaling properties of the fluctuations of a signal. In particular, DFA has probably become the standard method of choice when analyzing complex time series and it has been used in hundreds of scientific articles.
Often, given a non-stationary strongly correlated time series
i.e., of fractional Brownian motion type, its increment time series
given by
is more informative and can be easier to analyze than the original series itself. On the one hand, the dynamical properties of the increments can shed light on the underlying dynamics of the system. On the other hand, the increment series is very likely (quasi)stationary, i.e., of fractional Gaussian noise type. However, for nonlinear systems, it is worth going beyond the study of linear correlations since they do not account for all the dynamical properties of the systems. For example, increment time series with identical linear correlations may well correspond to systems with different nonlinear and multifractal behavior [
4,
5]. To overcome this problem and break the possible degeneration, the magnitude and sign decomposition method was proposed [
4], consisting of studying separately the correlation properties of the magnitude and sign of the increment time series, typically using DFA or FA. The correlations in the magnitude series (termed volatility series in Economics contexts) are usually related to nonlinear correlations and multifractal properties [
4,
5,
6,
7]. Intuitively, the magnitude series carries the information on how big are the changes in the original signal. In contrast, the correlations in the sign series are uniquely determined by the linear correlations [
4,
6] and, from an intuitive point of view, the sign series provide the information of the direction of the changes of the original signal. The applications of the magnitude and sign decomposition method include heart rate analysis [
8,
9], fluid dynamics [
10], geological [
11,
12], geophysical [
13,
14], and economical time series [
15].
In this work, we use fractional Gaussian noises with different correlation strengths as a model for typical increment time series, apply to them the magnitude and sign decomposition method and study their correlations by using both FA and DFA. We obtain that, below a certain degree of the strength of the correlations (different for sign and magnitude series), FA and DFA interpret that the magnitude and sign series are purely uncorrelated. However, by studying analytically and numerically the corresponding autocorrelation functions, we show that, in all cases, the magnitude and sign series are power-law correlated, and therefore that FA and DFA provide spurious results. Finally, we explain the origin of these spurious results by obtaining analytically the FA and DFA scaling properties when applied to sign and magnitude series.
The paper is organized as follows: in
Section 2, we introduce FA and DFA, and the analytical relationship between both techniques and the autocorrelation function is presented in
Section 3. The magnitude and sign decomposition method is described in
Section 4, and the results of FA and DFA when analyzing magnitude and sign series obtained from fractional Gaussian noises are presented in
Section 5. In
Section 6, we obtain the exact autocorrelation functions of the magnitude and sign series analyzed in
Section 5 and show that the FA and DFA scaling results are spurious, and the reason for these results is analyzed in
Section 7. Finally, we present our conclusions.
2. Fluctuation Analysis and Detrended Fluctuation Analysis
Let us consider a stationary time series
(
. The autocorrelation function
of
can be calculated as
where
denotes average over the whole time series, and
is the variance of the time series. Without loss of generality, in the following, we assume that
. When the time series
is long-range power-law correlated, such as, for example, in fractional Gaussian noises (fGn), then its autocorrelation function,
behaves asymptotically as a power law of the lag
r [
16]:
where
H is the well-known Hurst exponent with values in the range
, and then the autocorrelation exponent
given by
, must be in the range
. For
(
), the correlations are positive, while for
the time series is anticorrelated. Note that, for the special case
(
), the autocorrelation function vanishes, and the time series is uncorrelated (white noise behavior).
However, in many cases, the autocorrelation function is not convenient to determine the exponent
, since
is noisy and very sensitive to the time series size
N [
16,
17], and it is only properly estimated for large
N, very often not available in real experiments. This is the reason motivating the use of indirect methods to quantify correlations and scaling, being paradigmatic examples Fluctuation Analysis and Detrended Fluctuation Analysis.
Fluctuation Analysis (FA) [
2,
18] is a technique aimed at calculating the scaling properties of the fluctuations of a given stationary signal. It works as follows: the time series is interpreted as the steps of a walk in a diffusion process, and then consider the “accumulated walk”
of the signal as
The FA method tries to determine the averaged diffused distance in
ℓ steps as the Mean Square Distance
obtained as:
Scaling is present when
Typically,
is estimated as the slope of a linear fitting of
vs.
. The exponent
quantifies the strength of the correlations present in the time series. The exponents
and
are related via [
19,
20,
21]
Then, for stationary correlated signals,
and it coincides with the Hurst exponent
H (Equation (
2)).
indicates absence of correlations (white noise),
indicates positive power-law correlations which are stronger as
increases, and
indicates anticorrelations, stronger as
decreases.
Detrended Fluctuation Analysis was created [
3] to solve some drawbacks of FA, especially the ones related to the presence of non-stationarities in the time series. The behavior of DFA when applied to signals with different characteristics (trends, nonlinear filters, etc.) has been intensively studied [
22,
23] and, since then, DFA has become one of the standard methods used to analyze complex time series in many scientific fields [
15,
24,
25]. DFA works as follows: (i) calculate the “accumulated walk”
(
3) of the analyzed time series
of length
N; (ii) divide the walk
into boxes of equal length
ℓ (the scale of observation); (iii) In each box of length
ℓ, calculate a linear fit of
to determine the
linear trend within that box. The
Y coordinate of the fit line in each box is denoted by
; (iv) the walk
is detrended by subtracting the local trend
in each box of length
ℓ; and (v) for a given box size
ℓ, the root mean-square (r.m.s.) fluctuation for the detrended walk is calculated:
and (vi) the above computation is repeated for a broad range of scales (box sizes
ℓ) in order to provide a relationship between
and the scale
ℓ. As in the case of FA, scaling is present when
This equation is identical to Equation (
5), and the exponent
is also the same and with the same interpretation as the one in Equation (
5) when the analyzed signal is stationary and power-law correlated (
), i.e., of fractional Gaussian noise type. However, DFA can be also applied to non-stationary long-range correlated signals of fractional Brownian motion type, and in this case,
. For example, for the standard Brownian motion,
.
In this work, we restrict ourselves to the case of stationary long-range correlated signals (), where both FA and DFA can be applied.
3. The Relationship of the Autocorrelation Function with FA and DFA
When the analyzed time series
is stationary, then it is possible to obtain analytical equations relating the autocorrelation function
and the FA and DFA fluctuation functions
and
. In the case of FA, the calculation is simpler. Let us consider that
has zero mean and variance
. Starting from Equation (
4), note first that
After expanding the square in the R.H.S. of Equation (
9), we obtain
and then, noting that the series is stationary with 0 mean and variance
, we can evaluate the averages to get
in agreement with [
26].
For the case of DFA, the relationship between
and
is more complicated with an elaborated derivation recently obtained by Höll and Kantz [
27]. The final result is
with
and
We note that, although expressed in a different manner as in Equation (
11), the relation between
and
was also obtained by Talkner and Weber [
28].
We end this section with two important remarks on Equations (
10) and (
11). First, the variance
of the time series
appears as a multiplicative constant in both equations, and then from now on, we can consider without loss of generality that
. Secondly, we want to stress that Equations (
10) and (
11) are exact results, and therefore independent of the particular behavior of the autocorrelation function
of
. Then, provided that
is stationary, no matter whether the correlations are short- or long-ranged, positive or negative, power-law (with scaling) or exponentially decaying, etc., both equations hold.
4. Magnitude and Sign Decomposition. Volatility
As we mentioned above, the observable output of many complex systems, from heart rate to seismic signals, consists of time series with scaling properties. In many cases, such time series are non-stationary (of fractional Brownian motion type) and are originated as a consequence of the coupling of different underlying mechanisms. In order to shed light on the possible mechanisms responsible for the observed dynamics, the magnitude and sign decomposition method [
4,
6] is used. The method works as follows: given a non-stationary time series
(
), first we obtain its increments time series
as
Typically, the increment time series is stationary and approximately Gaussian, i.e., of fractional Gaussian noise type. Then, the increment time series is decomposed into the sign
and the magnitude
time series defined as:
The sign series carries the information about the direction of the increments (positive or negative) and the magnitude time series, the information about the size of the increments, i.e., whether the increment is big or small. The utility of the magnitude and sign decomposition method is then the possibility of studying independently both types of information [
4,
5,
6,
7,
8,
10]. In addition, the correlations of the sign series is associated with the linear correlations of the original signal [
4,
6], and the sign series contains also important information related to the recurrence intervals of the original signal [
29]. In addition, the correlations in the magnitude series are usually associated with nonlinear correlations and multifractal properties [
4,
5,
6,
7].
In the particular case of financial time series, which are strongly correlated and non-stationary, a convenient way to make stationary the time series consists of a logarithmic transformation. For example, let us consider a stock prize time series
, (
), where the index
i defines a time unit (minute, hour, day, etc.). For these series, instead of the increments of
, the returns time series
is defined as [
15]
Typically, the return time series
is correlated and approximately Gaussian with zero mean, and therefore of fractional Gaussian noise type. Then, in a similar way to Equation (
15), one could analyze separately the sign and the magnitude series obtained from
. In economics, the magnitude of the returns time series
is known as volatility [
7,
15] time series
, i.e.,
Then, in general, both the increment
and the return
time series are stationary and can be modeled to a first approximation by fractional Gaussian noises. Therefore, the correlation properties of their corresponding sign and magnitude (or volatility) [
7] time series can be studied by decomposing fGns as in Equation (
15). In the next section, we study the scaling properties of the sign and magnitude of fGns by applying FA and DFA.
5. Magnitude and Sign Study Using FA and DFA
Gaussian linear noises of fGn type can be generated using the Fourier Filtering Method (FFM) [
30,
31]. FFM works as follows: (i) generate a Gaussian white noise in the time domain
; (ii) Fourier-transform
to obtain a white noise
in the frequency domain; (iii) multiply
by a power-law of the type
; and (iv) Fourier-transform the result back to time domain to obtain
. Then, the power spectrum
of the final time series
behaves by constructions as:
with
for stationary time series. Since
behaves as a power-law, then according to the Wiener–Khinchim theorem,
behaves also as a power law (see Equation (
2)), with the exponents
and
related via
. Then, using Equation (
6), the three exponents
,
and
are related as [
21]
Due to the relation (
19), we use for convenience the FA and DFA exponent
as the input parameter of FFM, which we term
from now on. Then, we choose a large time series size
N to avoid as much as possible finite-size effects. For any
value, using FFM, we generate a large number of correlated time series
, each one with an exponent
by construction. Then, we decompose any individual series into its sign series
and its magnitude series
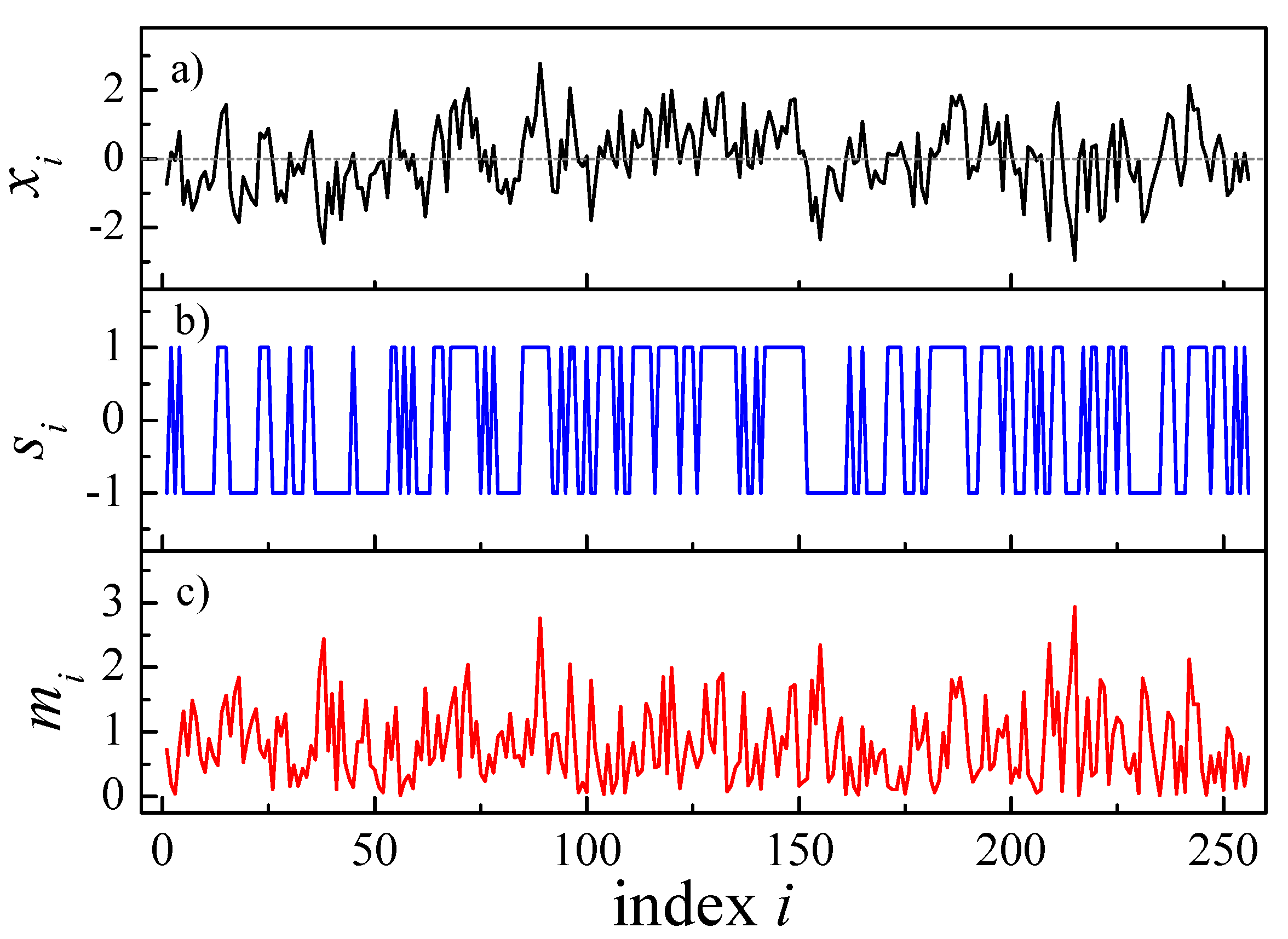
(see
Figure 1 for an example with small
N) according to (
15) and apply FA and DFA to
and
to obtain the sign
and magnitude
scaling exponents. Then, we average the sets of individual
and
values to obtain
and
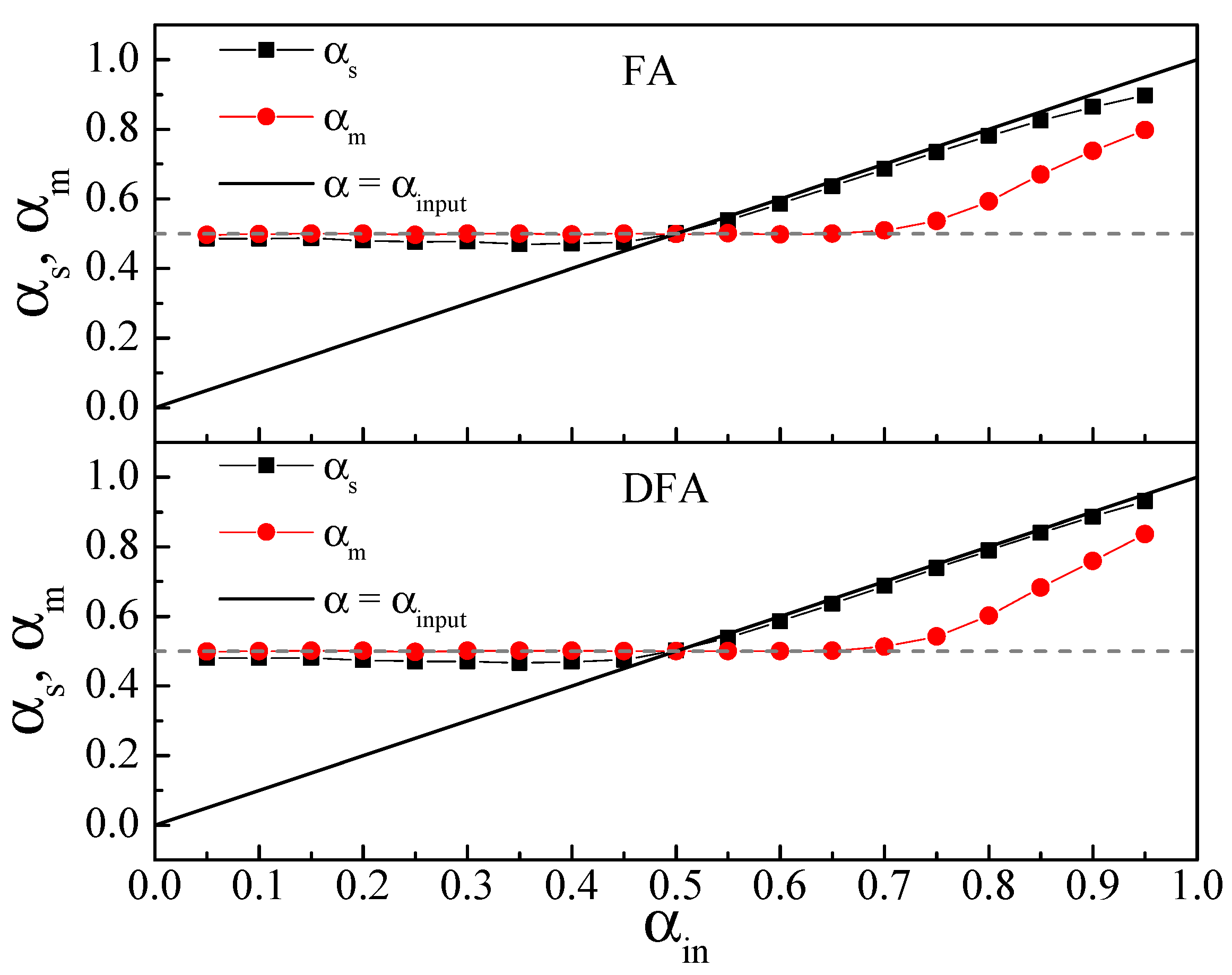
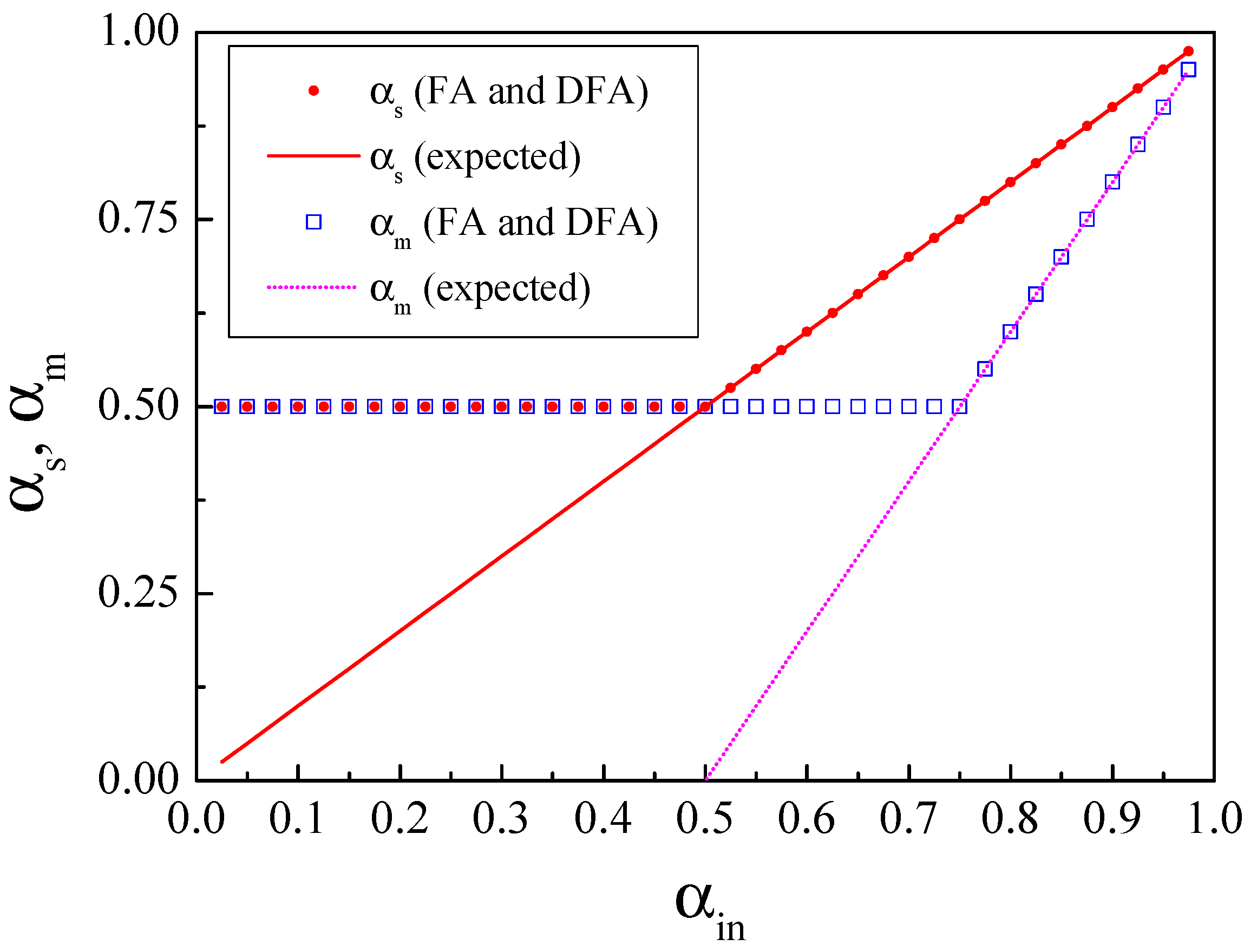
. The behavior of
and
as a function of
is shown in
Figure 2. We note that both FA and DFA provide very similar scaling exponents
and
. For the sign series,
for
, and
when
. In the magnitude series case, we observe that
for
, and
when
. In both cases, the approximate equality ’≃’ tends to the strict equality as the series size
N increases. In the particular case of DFA, these results are in agreement with previous works [
5,
7]. The most noticeable difference between FA and DFA is that, for a given large series size
N, the former presents larger deviations from the asymptotic behaviors (
20) and (
21) than the latter when
(
Figure 2). Note that the limiting value
corresponds to a non-stationary time series where FA is not applicable, and therefore a slower convergence of FA to the asymptotic results for
close to 1 is expected.
In the asymptotic limit
, the
and
results provided by both FA and DFA can be summarized as follows:
The common interpretation of these results is the following: (i) the sign series of fractional Gaussian noises with is uncorrelated (white noise behavior) because in that case = 0.5. However, when , the scaling properties of the time series and of its sign series are the same since for that range . Note that this interpretation precludes the existence of anticorrelations in the sign series, for which are expected; and (ii) the magnitude series of fractional Gaussian noises with is uncorrelated (white noise behavior) since . In contrast, for > 0.75, the magnitude scaling exponent depends linearly on as . According to this, the magnitude time series should behave randomly and thus without correlations for .
However, in the next sections, we show that the above interpretation is misleading: on the one hand, the sign series presents power-law anticorrelations for . On the other hand, the magnitude series is power-law correlated for . The problem is that both FA and DFA do not work properly in the sign and magnitude series, and therefore the scaling provided by both methods is spurious for in the sign case and for in the magnitude case.
6. Exact Autocorrelation Function of Magnitude and Sign Series
The correlations in the sign and magnitude series obtained from correlated and stationary time series of fractional Gaussian noise type can be derived analytically. Let
x and
y be two stochastic Gaussian variables, and let us assume that the linear correlation between both variables is
C, i.e.,
where
denotes the standard deviation. Without loss of generality, from now on, we consider that
and
, i.e.,
x and
y are of
type. Note that Equation (
22) is equivalent to affirm that the joint probability density of
x and
y,
, is the bivariate Gaussian distribution. If
x and
y are
variables, then
. Now, let us consider the pairs of stochastic variables
and
, and
and
. Then, the correlation
of the pair
and
, and the correlation
of the pair
and
are given by
where we have used that, as
x and
y are
variables, then
=
and
=
. In addition,
=
=
, and
=
=
.
Interestingly, both
and
are determined exactly by
C. For
, Apostolov et al. have shown [
32] that
In the
case, we have obtained recently [
9] that
In the time series language, Equations (
25) and (
26) can be easily written in terms of autocorrelation functions. Note that for a stationary and correlated Gaussian time series
, just replacing
x by
and
y by
in Equation (
22), we obtain the autocorrelation function
(Equation (
1)). Similarly, replacing
and
by
and
, we obtain the autocorrelation function of the sign series
. Finally, just replacing
and
by
and
in Equation (
23), we obtain the autocorrelation function of the magnitude series,
. Then, from (
25) and (
26), we can write directly
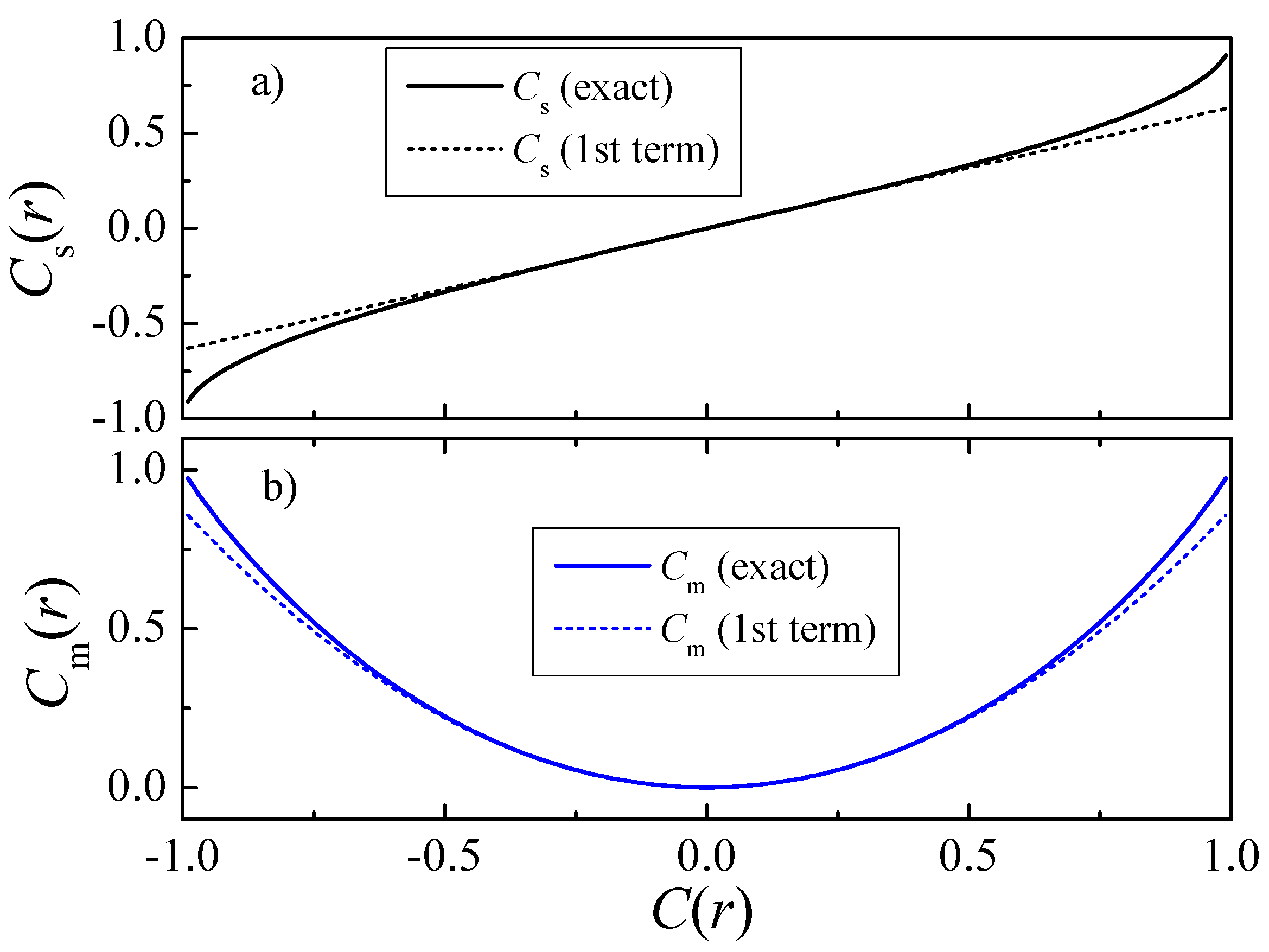
As
, we can plot
and
for any
, and both curves are shown in
Figure 3. The sign autocorrelation
is an odd function of
, and then negative values of
produce negative values of
. In other words, when the time series is (anti)correlated, the sign series is also (anti)correlated. In contrast,
is an even function of
, and then no matter the sign of
, the correlations in the magnitude series,
, are always positive. In addition, note that both (
27) and (28) are exact, independently of the behavior of
(positive or negative, power-law or exponentially decaying, etc.).
Very typically,
is a decaying function of the lag
r and then small for large enough
r. Therefore, in these conditions, we can expand Equations (
27) and (28) in a Taylor series of
and, considering only the first term in the expansions, we get
These two approximations are also shown in
Figure 3 (dashed lines), and are fairly precise for
. According to Equations (
29) and (30), the correlations in the sign series behave as a linear function of
, while the correlations in the magnitude series are quadratic with
.
These last results have profound implications, especially when the analyzed time series are stationary Gaussian power-law correlated (fGns), as the cases studied in
Section 5. Indeed, in that case,
behaves as a decaying power-law of
r (Equation (
2)) and for large enough
r, using Equations (
29) and (30), we obtain finally:
where, for convenience, we have used the FA and DFA exponents
characterizing the original time series instead of
H since they are equivalent in this case. Note that Equations (
31) and (32) are valid for
and then for
. The consequences of these two equations are important: given a power-law correlated time series characterized by an exponent
(or by
), the corresponding sign and magnitude series are also power-law correlated. In the sign series, its autocorrelation function exponent is identical to that of the original series,
(Equation (
31)). In the magnitude series, the exponent characterizing
is given by twice the exponent
of the original series (Equation (32)). The only case in which there is absence of correlations in the three time series corresponds to
or
, where the three autocorrelation functions,
,
and
, vanish.
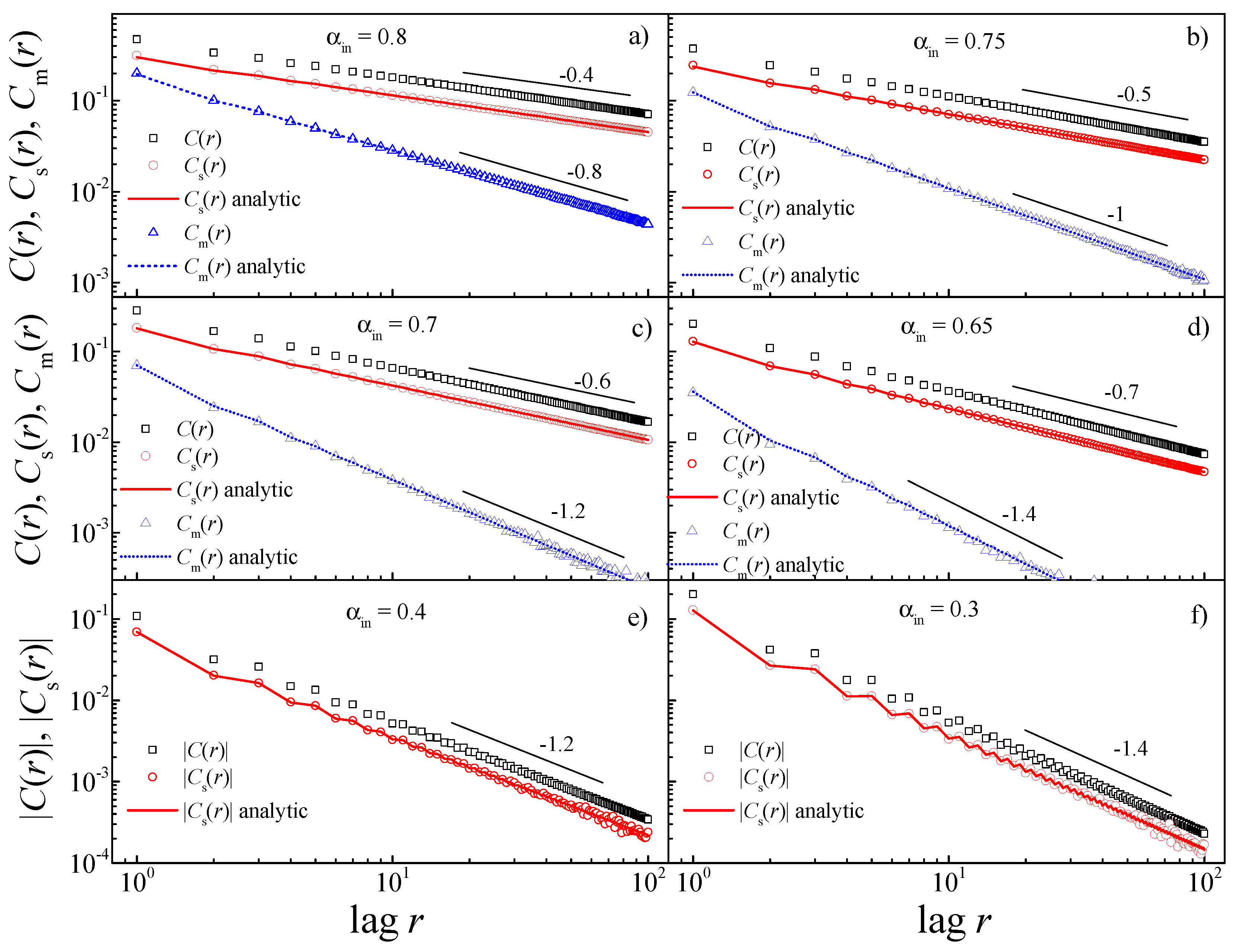
To show the validity of these results, in
Figure 4, we show the autocorrelation functions
,
and
obtained numerically for power-law correlated synthetic
fractional Gaussian noises generated using FFM with different
values. We observe that Equations (
31) and (32) provide correct results: on the one hand, the sign autocorrelation function
behaves as a power law with the same exponent as the original time series. Indeed, both
and
behave as parallel power-laws and then differ essentially in a multiplicative constant, in agreement with Equation (
29). This last equation has been used to plot the solid lines representing
in
Figure 4. On the other hand, the magnitude autocorrelation function
behaves as a power-law with an exponent twice the exponent
of the original series, and the results for
are also in perfect agreement with Equation (30), which has been used to plot the dotted lines for
in
Figure 4. One last remark concerning the results on
Figure 4: for
, both the original and the sign series are power-law anticorrelated, i.e.,
, and, for this reason, we use the absolute values
and
in panels (e) and (f) to produce a log-log plot.
6.1. Spurious Results and Misinterpretations of FA and DFA on Sign and Magnitude Series
According to our analytical (Equations (
29)–(32)) and numerical results (
Figure 4), the sign and magnitude series from power-law correlated fractional Gaussian noises are also power-law correlated. However, when FA and DFA are applied to these series, then the results shown in
Figure 2 and summarized in Equations (
20) and (
21) spuriously indicate a different behavior.
For the sign series, since both
and
are power-laws with the same exponent
, then one should expect that
in the whole range
. FA and DFA provide the correct result
only in the case
. However, both FA and DFA predict
(white noise behavior) when
or, in other words, the two techniques consider that the sign series is completely uncorrelated in this case, which is clearly not the case (see
Figure 4e,f).
For the magnitude series,
behaves as a power-law with an exponent
, twice the exponent
of
(in
Figure 4a–d). Then, according to Equation (
6), one has
for the original series and
for the magnitude series. Combining both expressions, we get that the relation between
and
should be
, and this relation holds for
. Both FA and DFA predict (correctly)
only in the case
. However, the two techniques wrongly estimate that
when
(
Figure 2 and Equation (
21)). In other words, FA and DFA consider that, for
, the magnitude series in completely uncorrelated (white noise behavior), which is clearly false (see
Figure 4b–d).
Then, according to the autocorrelation function behavior, the results for
and
can be summarized as
The discrepancies between the values of
and
predicted using FA and DFA (Equations (
20) and (
21) and
Figure 2 ) and the correct expected values for
and
given by Equation (
33) are shown in
Figure 5. Indeed, both expected values are linear functions of
, and lack of the abrupt corners exhibited by the FA and DFA results.
Before concluding this section, we add a final remark on the behavior of
: the correct result
indicates that, for
, then
. Traditionally, values of the FA and DFA scaling exponent
smaller than 0.5 are interpreted as an indicator of anticorrelations. However, this is not the case: we have proved above (Equations (28) and (30)) that, in general, the correlations in the magnitude series are always positive (see also
Figure 3 and
Figure 4) even in the case
.
In the next section, we derive an analytical explanation for the spurious scaling results of FA and DFA on sign and magnitude series.
7. Analytical FA and DFA Scaling on Sign and Magnitude Series
Let us consider a fractional Gaussian noise with
, and with an autocorrelation function given in terms of
by
For this signal, by construction both FA and DFA give a scaling of the type:
We analyze first the FA and DFA scaling properties of the sign series. We recall Equation (
10) establishing the relationship between
and
. Since the sign series is also stationary, from Equation (
10), we can also write
where
is the FA fluctuation function for the sign series. As
decays as a power-law, for large enough
ℓ, we can use the approximation (
29) to write Equation (
36) in terms of
:
Note that the sum in Equation (
37) also appears in Equation (
10) and then, combining both equations, we finally obtain
This equation establishes the relationship between the FA fluctuation functions of the original series,
, and of the sign series,
, and explains perfectly the (spurious)
value provided by FA. Indeed, for an fGn, Equation (
35) holds and then
. Thus, obviously for
, the second term in the sum inside the square root dominates for large
ℓ and then
, i.e.,
. In contrast, for
, the first term dominates for large
ℓ and then
, i.e.,
. In other words, we recover exactly the numerical results in Equation (
20).
Similar calculations can be carried out for DFA: in this case, starting from Equation (
11) and using Equation (
29), we get:
where
is the DFA fluctuation function for the sign series. Again, the sum in Equation (
39) also appears in Equation (
11) and, combining both equations and using the definition of
in Equation (
12), we obtain
This equation relates the DFA fluctuation function of the sign series,
, to the DFA fluctuation function of the original series,
. Similarly to the FA case,
presents two terms inside the square root, which can explain the
value provided by DFA. Indeed, when the original series is a fGn, then Equation (
35) holds and
. Thus, for
, the second term inside the square root dominates for large
ℓ, and, therefore,
, i.e.,
. In contrast, for
, for large
ℓ, the first term dominates and is proportional to
ℓ, thus implying
, i.e.,
. In other words, we also recover the numerical results in Equation (
20), which are spurious for
.
In conclusion, the reason behind the spurious FA and DFA result
for
is the presence of a first term proportional to
ℓ inside the square root of Equations (
38) and (
40), which dominates for large
ℓ when
. Note that this
ℓ term should be absent in order to obtain the correct result
for
, but it is an intrinsic property of the FA and DFA techniques.
Next, we study the FA and DFA scaling properties of the magnitude series. Concerning FA, since the original series is an fGn, then the magnitude series is stationary and, from Equation (
10), we can write
with
the variance of the magnitude series. Noting that we are considering fGns with
, then
. For large
ℓ, we can use the approximation in Equation (30) to obtain
Contrary to the sign case, in this last equation the sum is not the same as the one in Equation (
10) because we have the square of
. Then, to evaluate Equation (
42), we proceed as follows: first, we note that
is given by Equation (
34) and insert it in Equation (
42). Then, in order to evaluate the sum, we substitute it by a definite integral that we solve and simplify by keeping only the highest powers of
ℓ with constant and non-constant exponents. In this way, after regrouping terms, we get finally:
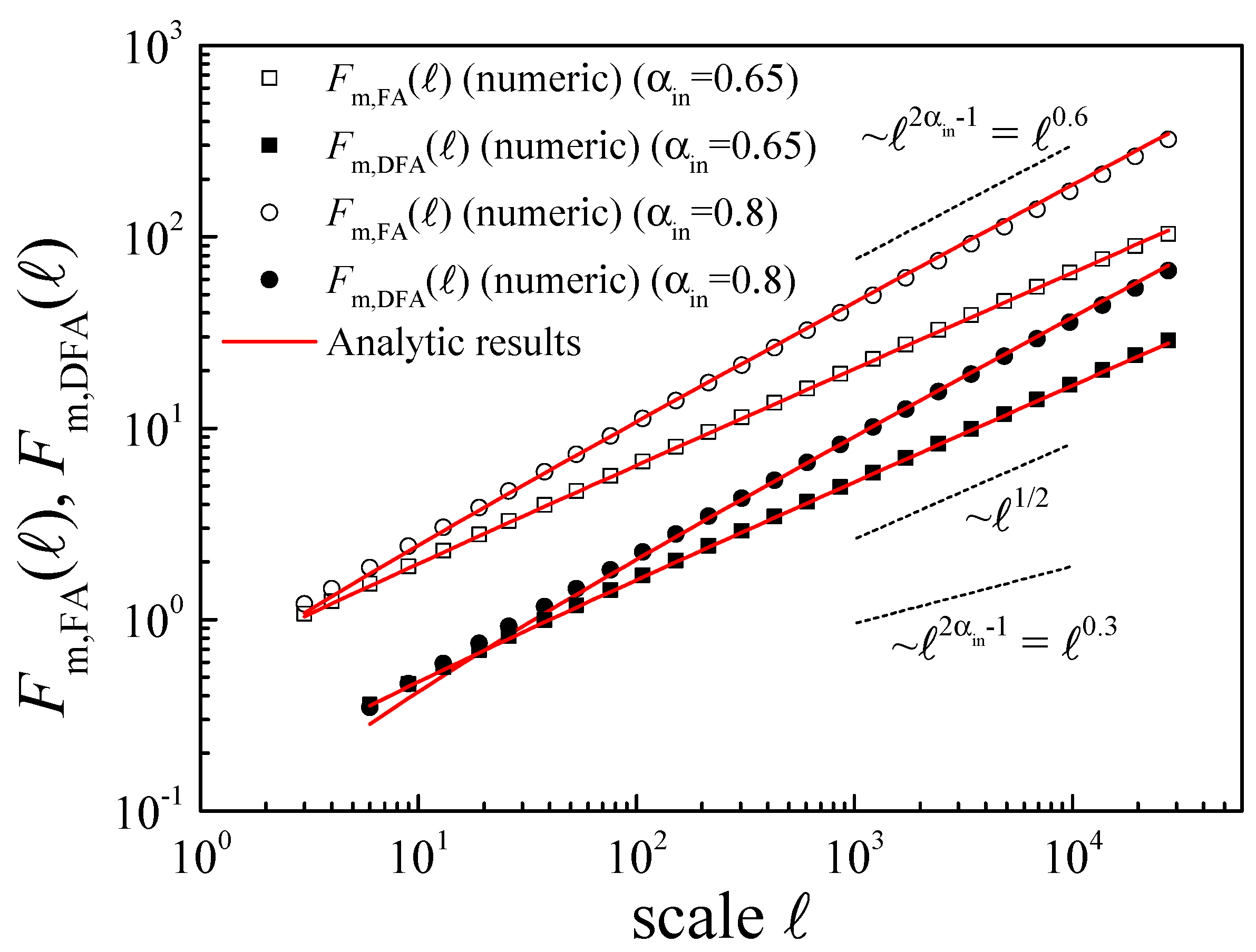
The validity of this analytic result is shown in
Figure 6, where we plot
obtained numerically in magnitude time series from fGns generated using FFM for two values of
(open symbols), and also the corresponding analytical values using Equation (
43), shown in solid lines. Equation (
43) explains the
results obtained using FA (
21): for
, i.e.,
, the second term in the sum dominates asymptotically and then
leading to
(see the case
in
Figure 6). In contrast, for
, i.e.,
, the first term in the sum is the dominant one and
from where
, as the case
in
Figure 6.
A similar, though more elaborated calculation can be carried out for the scaling of the magnitude series using DFA. In this case, starting from Equation (
11), we write for the magnitude series
where, as before,
. Using Equation (30), we get:
To evaluate this equation, we insert the expression of
(Equation (
34)), use the definitions of
(Equation (
12)) and
(Equation (
13)), substitute the sum by a definite integral and calculate it, and simplify the results by keeping the highest powers of
ℓ to get the (asymptotically correct) result:
The validity of this last equation is also shown in
Figure 6, where we plot for two different
values the numerical
functions provided by DFA (solid symbols) and the corresponding analytic
functions from Equation (
46) (solid lines). Similarly to the FA case, Equation (
46) allows for understanding the spurious
results (
21) obtained using DFA. As before, for
, i.e., for
(see the case
in
Figure 6), the second term in the sum dominates for large
ℓ and then
, or
. For
, i.e.,
(see the case
in
Figure 6), the first term in the sum is the dominant one and
from where
.
We conclude that the spurious FA and DFA result
for
is due to the existence of a first term proportional to
ℓ in Equations (
43) and (
46), which dominates asymptotically when
. The correct result
for
could only be obtained by FA and DFA without such
ℓ-term in Equations (
43) and (
46), which, regrettably, is an intrinsic property of both techniques.