Projection to Mixture Families and Rate-Distortion Bounds with Power Distortion Measures

Abstract

The explicit form of the rate-distortion function has rarely been obtained, except for few cases where the Shannon lower bound coincides with the rate-distortion function for the entire range of the positive rate. From an information geometrical point of view, the evaluation of the rate-distortion function is achieved by a projection to the mixture family defined by the distortion measure. In this paper, we consider the $\beta$-th power distortion measure, and prove that $\beta$-generalized Gaussian distribution is the only source that can make the Shannon lower bound tight at the minimum distortion level at zero rate. We demonstrate that the tightness of the Shannon lower bound for $\beta =1$ (Laplacian source) and $\beta =2$ (Gaussian source) yields upper bounds to the rate-distortion function of power distortion measures with a different power. These bounds evaluate from above the projection of the source distribution to the mixture family of the generalized Gaussian models. Applying similar arguments to $ϵ$-insensitive distortion measures, we consider the tightness of the Shannon lower bound and derive an upper bound to the distortion-rate function which is accurate at low rates.

1. Introduction

The rate-distortion function, $R(D)$, shows the minimum achievable rate to reproduce source outputs with the expected distortion not exceeding D. The Shannon lower bound (SLB) has been used for evaluating $R(D)$ [1,2]. The tightness of the SLB for the entire range of the positive rate identifies the entire $R(D)$ for pairs of a source and distortion measure such as the Gaussian source with squared distortion [1], the Laplacian source with absolute magnitude distortion [2], and the gamma source with Itakura–Saito distortion [3]. However, such pairs are rare examples. In fact, for a fixed distortion measure, there exists only a single source that makes the SLB tight for all D, as we will prove in Section 2.3. The necessary and sufficient condition for the tightness of the SLB was first obtained for the squared distortion [4], discussed for a general difference distortion measure d [2], and recently described in terms of d-tilted information [5]. While these results consider the tightness of the SLB for each point of $R(D)$ (i.e., for each D), we discuss the tightness for all D in this paper. More specifically, if we focus on the minimum distortion at zero rate (denoted by $D_{max}$), the tightness of the SLB at $D_{max}$ characterizes a condition between the source density and the distortion measure.

If the SLB is not tight, the explicit evaluation of the rate-distortion function has been obtained only in limited cases [6,7,8,9]. Little is inferred on the behavior of $R(D)$ when the distortion measure is varied from a known case, since $R(D)$ does not continuously change even if the distortion measure is continuously modified. Although the SLB is easily obtained for difference distortion measures, it is unknown how accurate the SLB is without the explicit evaluation, upper bound, or numerical calculation of the rate-distortion function.

In this paper, we consider the constrained optimization of the definition of $R(D)$ from an information geometrical viewpoint [10]. More specifically, we show that it is equivalent to a projection of the source distribution to the mixture family defined by the distortion measure. If the source is included in the mixture family, the SLB is tight; if it is not tight, the gap between $R(D)$ and its SLB evaluates the minimum Kullback–Leibler divergence from the source to the mixture family (Lemma 1). Then, using the bounds of the rate-distortion function of the $\beta$-th power difference distortion measure obtained in [11], we evaluate the projections of the source distribution to the mixture families associated with this distortion measure (Theorem 3).

Operational rate-distortion results have been obtained for the uniform scalar quantization of the generalized Gaussian source under the $\beta$-th power distortion measure [12,13]. We prove that only the $\beta$-generalized Gaussian distribution has the potential to be the source whose SLB is tight; that is, identical to the rate-distortion function for the entire rage of positive rate. This fact brings knowledge on the tightness of the SLB of an $ϵ$-insensitive distortion measure, which is obtained by truncating the loss function near zero error [14,15,16]. The above result implies that the SLB is not tight if the source is the $\beta$-generalized Gaussian and the distortion has another power $\gamma \ne \beta$. We demonstrate that even in such a case, a novel upper bound to $R(D)$ can be derived from the condition for the tightness of the SLB. The fact that the Laplacian ($\beta =1$) and the Gaussian ($\beta =2$) sources have the tight SLB specifically derives a novel upper bound to $R(D)$ of $\gamma (\ne \beta )$-th power distortion measure, which has a constant gap from the SLB for all D. By the relationship between the SLB and the projection in the information geometry, the gap evaluates the projections of the $\beta$-generalized Gaussian source to the mixture families of $\gamma$-generalized Gaussian models. Extending the above argument to $ϵ$-insensitive loss, we derive an upper bound to the distortion-rate function, which is tight in the limit of zero rate.

2. Rate-Distortion Function and Shannon Lower Bound

2.1. Rate-Distortion Function

Let X and Y be real-valued random variables of a source output and reconstruction, respectively. For the distortion measure between x and y, $d(x,y)$, the rate-distortion function $R(D)$ of the source $X\sim p(x)$ is defined by

$$R(D)=\underset{q(y|x):E[d(X,Y)]\le D}{inf}I(q),$$

where

$$\begin{array}{ccc}\hfill I(q)& =& I(X;Y)\hfill \\ & =& \int \int q(y|x)p(x)log\frac{q(y|x)}{\int q(y|x)p(x)dx}dxdy\hfill \end{array}$$

(1)

is the mutual information and E denotes the expectation with respect to $q(y|x)p(x)$. $R(D)$ shows the minimum achievable rate R to reconstruct source outputs with average distortion not exceeding D under the distortion measure d [2,17]. The distortion-rate function, $D(R)$, is the inverse function of the rate-distortion function.

If the conditional distribution $q_s(y|x)$ achieves the minimum of the following Lagrange function parameterized by $s\ge 0$,

$$L(q)=I(q)+s\left(E[d(X,Y)]-D\right),$$

then the rate-distortion function is parametrically given by

$$\begin{array}{ccc}\hfill R(D_s)& =& I(q_s),\hfill \\ \hfill D_s& =& \int q_s(y|x)p(x)d(x,y)dxdy.\hfill \end{array}$$

The parameter s corresponds to the (negated) slope of the tangent of $R(D)$ at $(D_s,R(D_s))$, and hence is referred to as the slope parameter [2]. Alternatively, the rate-distortion function is given by ([18], Theorem 4.5.1):

$$R(D)=\underset{s\ge 0}{sup}\underset{q(y)}{min}\left\{E\left[-log\int e^{-sd(X,y)}q(y)dy\right]-sD\right\}.$$

(2)

If the marginal reconstruction density $q_s(y)$ achieves the minimum above, the optimal conditional reconstruction distribution is given by

$$q_s(y|x)=\frac{e^{-sd(x,y)}{q}_s(y)}{\int e^{-sd(x,y)}{q}_s(y)dy},$$

(3)

(see, for example, [2,19]).

From the properties of the rate-distortion function $R(D)$, we know that $R(D)>0$ for $0<D<D_{max}$, where

$$D_{max}=\underset{y}{inf}\int p(x)d(x,y)dx,$$

(4)

and $R(D)=0$ for $D\ge D_{max}$ [2] (p. 90). Hence, $D_{max}={lim}_{R\to 0}D(R)$.

2.2. Shannon Lower Bound

In this paper, we focus on difference distortion measures,

$$d(x,y)=\rho (x-y),$$

(5)

for which Shannon derived a general lower bound to the rate-distortion function [1] ([2], Chapter 4).

Throughout this paper, we assume that the function $\rho$ is nonnegative and satisfies

$$C_s\equiv \int e^{-s\rho (z)}dz<\infty ,$$

(6)

for all $s>0$. It follows that

$$C_s=\int e^{-s\rho (z)}dz=\int e^{-sd(z,0)}dz=\int e^{-sd(x,\mu )}dx=\int e^{-s\rho (x-\mu )}dx,$$

for all $\mu \in \mathbb{R}$.

Let

$$K(p||r)=\int p(x)log\frac{p(x)}{r(x)}dx$$

denote the Kullback–Leibler divergence from p to r, which is non-negative and equal to zero if and only if $p(x)=r(x)$ almost everywhere. We define the distribution

$$g_s(x)=\frac{1}{C_s}{e}^{-s\rho (x)}.$$

(7)

Then, the Shannon lower bound (SLB) is defined by

$$\underline{R}(D)\equiv h(p)-h(g_s),$$

(8)

where $h(p)$ is the differential entropy of the probability density p, and s is related to D by

$$D=\int \rho (x)g_s(x)dx.$$

(9)

The next lemma shows that the SLB is in fact a lower bound to the rate-distortion function and that the difference between them is lower bounded by the Kullback–Leibler divergence.

Lemma 1.

For a source with probability density function $p(x)$ and the difference distortion measure (5),

$$R(D)-\underline{R}(D)\ge \underset{q(y)}{min}K(p||m_s)\ge 0,$$

(10)

where s and D are related to each other by (9) and

$$m_s(x)=(g_s*q)(x)=\int g_s(x-y)q(y)dy$$

is the convolution between $g_s$ and q.

Proof. 

Let $\underline{s}$ be the slope parameter s satisfying (9) for D. From (2), we have

$$\begin{array}{ccc}\hfill R(D)& \ge & \underset{q(y)}{min}\left\{E\left[-log\int e^{-\underline{s}d(X,y)}q(y)dy\right]-\underline{s}D\right\},\hfill \\ & =& \underset{q(y)}{min}\left\{K(p||m_{\underline{s}})-log{C}_{\underline{s}}+h(p)-\underline{s}D\right\}\hfill \\ & =& \underset{q(y)}{min}K(p||m_{\underline{s}})+h(p)-h(g_{\underline{s}})\hfill \\ & =& \underset{q(y)}{min}K(p||m_{\underline{s}})+\underline{R}(D),\hfill \end{array}$$

which completes the proof. ☐

In the information geometry, for a family of distributions $\mathcal{M}$ and a given distribution p, the distributions that achieve the minimums

$$\underset{r\in \mathcal{M}}{min}K(p||r)\mathrm{and}\underset{r\in \mathcal{M}}{min}K(r||p)$$

are called the m-projection and e-projection of p to $\mathcal{M}$, respectively [10]. As a family of distributions, the ($M-1$)-dimensional mixture family spanned by $\{p_1(x),\cdots ,p_M(x)\}$ is defined by

$$\mathcal{M}=\left\{\sum _{i=1}^M{q}_i{p}_i(x)|q_i\ge 0,i=1,\cdots ,M,\sum _{i=1}^M{q}_i=1\right\}.$$

Hence, from the information geometrical viewpoint, the above lemma shows that the difference between $R(D)$ and $\underline{R}(D)$ evaluates the m-projection

$$\underset{r\in {\mathcal{M}}_s}{min}K(p||r)$$

of the source distribution p to

$${\mathcal{M}}_s=\left\{m_s(x)=(g_s*q)(x)|q(y)\ge 0(\forall y),\int q(y)dy=1\right\},$$

the (infinite-dimensional) mixture family defined by $\left\{g_s(x-y)|y\in \mathbb{R}\right\}$.

It is also easy to see from the lemma that the SLB coincides with $R(D)$ (that is, $R(D)=\underline{R}(D)$ holds in (8)) if and only if the source random variable X with density $p(x)$ can be represented as the sum of two independent random variables, one of which is distributed according to the probability density function $g_s(x)$ in (7). This condition is referred to as the “backward channel” condition, and is equivalent to the fact that the integral equation

$$p(x)=\int g_s(x-y)q_s(y)dy$$

(11)

has a solution $q_s(y)$ which is a valid density function ([2], Chapter 4). This condition is also equivalent to the fact that $p\in {\mathcal{M}}_s$.

2.3. Probability Density Achieving Tight SLB for All D

The following theorem claims that for a difference distortion measure, there is at most a unique source for which $\underline{R}(D)$ is tight at $D=D_{max}$.

Theorem 1.

Assume that the source distribution has a finite $D_{max}$ achieved by a reconstruction μ; that is, $E[d(X,\mu )]=D_{max}<\infty$. The rate-distortion function is strictly greater than the SLB at $D=D_{max}$, $R(D_{max})>\underline{R}(D_{max})$, unless the following holds for the source density almost everywhere:

$$p(x)=\frac{exp\left\{-s^{*}d(x,\mu )\right\}}{C_{s^{*}}},$$

where $C_s$ is defined in (6), and $s^{*}$ is determined by the relation

$$-{\left.\frac{\partial log{C}_s}{\partial s}\right|}_{s=s^{*}}=D_{max}.$$

(12)

Proof. 

Let Z be the random variable such that $Z-\mu$ has the density $g_{s^{*}}$. As a functional of the source density $p(x)$, the SLB at $D=D_{max}$ is expressed as

$$\begin{array}{ccc}\hfill \underline{R}(D_{max})& =& h(p)-h(g_{s^{*}})\hfill \\ & =& h(p)-log{C}_{s^{*}}-s^{*}E[d(Z,\mu )]\hfill \\ & =& -K(p(x)||g_{s^{*}}(x-\mu ))+s^{*}\left\{D_{max}-E[d(Z,\mu )]\right\}.\hfill \end{array}$$

(13)

From the non-negativity of the divergence, $\underline{R}(D_{max})$ is maximized to 0 only if $p(x)=g_{s^{*}}(x-\mu )$ holds almost everywhere. ☐

The tightness of the SLB for each D characterizes the form of the backward channel $p(x|y)$ as discussed for example in ([5], Theorem 4). The above theorem focuses on $D=D_{max}$ and characterizes the relation between the form of the source density $p(x)$ and the distortion measure.

The tightness of the SLB at $D=D_{max}$ is relevant to the tightness for all $0<D\le D_{max}$. For some distortion measures (e.g., the squared and absolute distortion measures), the random variable $Z_s\sim g_s$ is decomposable into the sum of two independent random variables

$$Z_s=Z_{s^{\prime }}+N,$$

where $Z_{s^{\prime }}\sim g_{s^{\prime }}$ and some random variable N for any $s^{\prime }>s$. The backward channel condition (11) means that in such a case, the tightness of the SLB at $D=D_{max}$ implies the tightness of the SLB for all $0<D<D_{max}$. The condition (11) is closely related to the closure property with respect to convolution. If $g_s(x-y)$ is a kernel function associated with a reproducing kernel Hilbert space, such a closure property is studied in detail [20].

3. Generalized Gaussian Source and Power Distortion Measure

3.1. $\beta$-th Power Distortion Measure

We examine the rate-distortion trade-offs under the $\beta$-th power distortion measure

$$d_{\beta }(x,y)={|x-y|}^{\beta },$$

(14)

where $\beta >0$ is a real exponent. In particular, $\beta =2$ corresponds to the squared error criterion and $\beta =1$ to the absolute one. The corresponding noise model given by (7) is

$$g_s(x)=\frac{1}{C_s}{e}^{-{s|x|}^{\beta }},$$

where $C_s=\frac{2}{\beta }\frac{1}{s^{1/\beta }}\Gamma \left(\frac{1}{\beta }\right)$ and $\Gamma$ is the gamma function. This model is the $\beta$-th-order generalized Gaussian distribution including the Gaussian ($\beta =2$) and the Laplace ($\beta =1$) distributions as special cases. Its differential entropy is

$$h(g_s)=log{C}_s+\frac{1}{\beta }.$$

(15)

For a difference distortion measure, we can assume that the $\mu$ in Theorem 1 is zero without loss of generality. Thus, as a source, we assume the generalized Gaussian random variable with the density,

$$p(x)=p_{\beta }(x)=\frac{1}{C_{\frac{\alpha }{\beta }}}exp\left(-\frac{\alpha }{\beta }{|x|}^{\beta }\right),$$

(16)

where $0<\alpha <+\infty$, which is a versatile model for symmetric unimodal probability densities. Here the scaling factor $\alpha /\beta$ is chosen so that

$$D_{max}=E_p{[|X|}^{\beta }]=\frac{1}{\alpha }>0$$

holds.

The SLB for the source (16) with respect to the distortion measure (14) is

$$\underline{R}(D)=\left\{\begin{array}{cc}-\frac{1}{\beta }log\alpha D,\hfill & (0<D\le \frac{1}{\alpha }),\hfill \\ 0,\hfill & (D>\frac{1}{\alpha }),\hfill \end{array}\right.$$

which follows from (8), (15), and the relation between the slope parameter s and the average distortion $D_s$ given by (9),

$$D_s=E_{g_s}{[|Z|}^{\beta }]=\frac{\Gamma (1+1/\beta )}{s\Gamma (1/\beta )}=\frac{1}{s\beta }.$$

It is well known that when $\beta =2$ (Gaussian source and the squared distortion measure), the SLB is tight; that is, $\underline{R}(D)=R(D)$ for all D [1,2,17]. The optimal reconstruction distribution minimizing (2) for this case is given by

$$q_{1/(2D)}(y)=\frac{1}{\sqrt{2\pi (1/\alpha -D)}}exp\left\{-\frac{y^2}{2(1/\alpha -D)}\right\},$$

for $0<D<1/\alpha$. Additionally, when $\beta =1$ (Laplacian source and the absolute distortion measure), the SLB is tight for all D ([2], Example 4.3.2.1), which is attained by

$$q_{1/D}(y)={\alpha }^2{D}^2\delta (y)+(1-{\alpha }^2{D}^2)\frac{\alpha }{2}{e}^{-\alpha |y|},$$

for $0<D<1/\alpha$, where $\delta$ is Dirac’s delta function.

3.2. Tightness of the SLB

From Theorem 1, we immediately obtain the following corollary, which shows that the $\beta$-generalized Gaussian source is the only source that can make the SLB tight at $D=D_{max}$ under the $\beta$-th power distortion measure (14).

Corollary 1.

Assume that the source distribution has mean 0 and a finite β-th moment, $E_p{[|X|}^{\beta }]=1/\alpha <\infty$. Under the β-th power distortion measure (14), the rate-distortion function is strictly greater than the SLB at $D=D_{max}$, $R(D_{max})>\underline{R}(D_{max})$, unless the source distribution is the β-generalized Gaussian with the density (16).

In the case of $\beta =1$, the rate-distortion function of the $ϵ$-insensitive distortion measure,

$$d(x,y)=max\{0,|x-y|-ϵ\},$$

(17)

was studied [16]. It was proved that a necessary condition for $R(D_s)=\underline{R}(D_s)$ at a slope parameter s is that $R(D_s)=\underline{R}(D_s)$ also holds for $ϵ=0$. According to Theorem 1, this fact derives a contradiction if there is a source that makes the SLB of the distortion measure (17) tight at $D=D_{max}$. Thus, we have the following corollary.

Corollary 2.

Under the ϵ-insensitive distortion measure (17) with $ϵ>0$, no source makes the SLB tight at $D=D_{max}$.

4. Rate-Distortion Bounds for Mismatching Pairs

From Corollary 1, the SLB cannot be tight for all D if the distortion measure $d_{\gamma }$ has a different exponent $\gamma$ from that of the source $p_{\beta }$ (i.e., $\gamma \ne \beta$). In this section, we show that even in such a case, accurate upper and lower bounds to $R(D)$ of Laplacian and Gaussian sources can be derived from the fact that $\underline{R}(D)=R(D)$ for $\beta =1$ and $\beta =2$.

We denote the rate-distortion function and bounds to it by indicating the parameters $\beta$ and $\gamma$ of the source and the distortion measure. More specifically, $R_{\beta }^{[\gamma ]}(D)$ denotes the rate-distortion function for the source $p_{\beta }$ with respect to the distortion measure $d_{\gamma }$.

We first prove the following lemma:

Lemma 2.

If ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$ for all D, then

$$E_{q_{1/(\beta D)}{p}_{\beta }}\left[d_{\gamma }(X,Y)\right]=\frac{\Gamma \left(\gamma /\beta +1/\beta \right)}{\Gamma \left(1/\beta \right)}{(\beta D)}^{\gamma /\beta },$$

holds for $\gamma >0$, where $E_{q_{1/(\beta D)}{p}_{\beta }}$ denotes the expectation with respect to $q_{1/(\beta D)}(y|x)p_{\beta }(x)$, and

$$D=E_{q_{1/(\beta D)}{p}_{\beta }}\left[d_{\beta }(X,Y)\right]$$

is satisfied for the optimal conditional reproduction distribution $q_s$ in(3).

Proof. 

${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$ implies that

$$q_s(y|x)p_{\beta }(x)=g_s(x-y)q_s(y)$$

for the optimal reproduction distribution $q_s(y|x)$ in (3) and $q_s(y)$ minimizing (2), and $D=1/(\beta s)$. It follows that

$$\begin{array}{ccc}\hfill E_{q_{1/(\beta D)}{p}_{\beta }}\left[d_{\gamma }(X,Y)\right]& =& {\int |x-y|}^{\gamma }{q}_{1/(\beta D)}(y|x)p_{\beta }(x)dydx\hfill \\ & =& E_{g_{1/(\beta D)}}{[|Z|}^{\gamma }]=\frac{\Gamma \left(\gamma /\beta +1/\beta \right)}{\Gamma \left(1/\beta \right)}{(\beta D)}^{\gamma /\beta }\hfill \end{array}$$

☐

Let $D^{[\gamma ]}\equiv \frac{\Gamma \left(\gamma /\beta +1/\beta \right)}{\Gamma \left(1/\beta \right)}{(\beta D)}^{\gamma /\beta }$, which is equivalent to

$$D=\frac{1}{\beta }{\left\{\frac{\Gamma \left(1/\beta \right)}{\Gamma \left(\gamma /\beta +1/\beta \right)}{D}^{[\gamma ]}\right\}}^{\frac{\beta }{\gamma }}.$$

(18)

The above lemma implies that $q_{1/(\beta D)}(y|x)$ achieving $R_{\beta }^{[\beta ]}(D)$ has the expected $d_{\gamma }$-distortion,

$$D^{[\gamma ]}=E[d_{\gamma }(X,Y)]$$

with the rate $R=R_{\beta }^{[\beta ]}(D)=-\frac{1}{\beta }log(\alpha D)$ if ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$ for all D.

Thus, we obtain the following upper bound to $R_{\beta }^{[\gamma ]}(D)$ if ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$.

$$\begin{array}{ccc}\hfill {\overline{R}}_{\beta }^{[\gamma ]}(D)& \equiv & -\frac{1}{\beta }log\left[\frac{\alpha }{\beta }{\left\{\frac{\Gamma \left(1/\beta \right)}{\Gamma \left(\gamma /\beta +1/\beta \right)}{D}^{[\gamma ]}\right\}}^{\frac{\beta }{\gamma }}\right]\hfill \\ & =& -\frac{1}{\gamma }log\left[{\left(\frac{\alpha }{\beta }\right)}^{\frac{\gamma }{\beta }}\frac{\Gamma (1/\beta )}{\Gamma (\gamma /\beta +1/\beta )}D\right]\hfill \end{array}$$

(19)

We also have the SLB for $R_{\beta }^{[\gamma ]}$,

$$\begin{array}{ccc}\hfill {\underline{R}}_{\beta }^{[\gamma ]}(D)& \equiv & h(p_{\beta })-h(g_{1/\gamma D}^{[\gamma ]})\hfill \\ & =& -\frac{1}{\gamma }log\left[{\left(\frac{\alpha }{\beta }\right)}^{\frac{\gamma }{\beta }}\frac{\Gamma {(1/\gamma )}^{\gamma }}{\Gamma {(1/\beta )}^{\gamma }}\frac{{\beta }^{\gamma }{e}^{1-\gamma /\beta }}{{\gamma }^{\gamma -1}}D\right]\hfill \end{array}$$

(20)

Therefore, we arrive at the following theorem:

Theorem 2.

If ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$, for $0<D\le D_{max}$, the rate-distortion function $R_{\beta }^{[\gamma ]}(D)$ is lower- and upper-bounded as

$${\underline{R}}_{\beta }^{[\gamma ]}(D)\le R_{\beta }^{[\gamma ]}(D)\le {\overline{R}}_{\beta }^{[\gamma ]}(D),$$

where the lower and upper bounds are given by (20) and (19). The left inequality becomes equality only for $\gamma =\beta$. The gap between the bounds is

$$\begin{array}{ccc}\hfill {\delta }_{\beta }^{[\gamma ]}& \equiv & {\overline{R}}_{\beta }^{[\gamma ]}(D)-{\underline{R}}_{\beta }^{[\gamma ]}(D)\hfill \\ & =& -\frac{1}{\gamma }log\left[\frac{{\gamma }^{\gamma -1}}{{\beta }^{\gamma }}\frac{\Gamma {(1/\beta )}^{\gamma +1}}{\Gamma {(1/\gamma )}^{\gamma }}\frac{e^{\gamma /\beta -1}}{\Gamma (\gamma /\beta +1/\beta )}\right],\hfill \end{array}$$

(21)

which is constant with respect to D. Furthermore, the upper bound is tight at $D=D_{max}={(\beta /\alpha )}^{\gamma /\beta }\Gamma (\gamma /\beta +1/\beta )/\Gamma (1/\beta )$; that is,

$$R_{\beta }^{[\gamma ]}(D_{max})={\overline{R}}_{\beta }^{[\gamma ]}(D_{max})=0.$$

Since the upper bound is tight at $D=D_{max}$, it is the smallest upper bound that has a constant deviation from the SLB. In addition, the SLB is asymptotically tight in the limit $D\to 0$ for the distortion measure $d_{\gamma }$ in general [2,21], and the condition for the asymptotic tightness has been weakened recently [22]. These facts suggest that the rate-distortion function $R_{\beta }^{[\gamma ]}(D)$ is near the SLB at low distortion levels and then approaches the upper bound ${\overline{R}}_{\beta }^{[\gamma ]}(D)$ as the average distortion D grows to $D_{max}$. In terms of the distortion-rate function, the theorem also implies that the encoder $q_{1/(\beta D)}(y|x)$ designed for $d_{\beta }$-distortion has the loss in $d_{\gamma }$-distortion, due to the mismatch of the orders, at most by the constant factor $e^{\gamma {\delta }_{\beta }^{[\gamma ]}}$.

From Lemma 1 in Section 2.2, by examining the correspondence between the slope parameter $0<s<\infty$ and the distortion level D, we obtain the next theorem, which evaluates the m-projection of the source to the mixture family,

$${\mathcal{M}}_s^{[\gamma ]}\equiv \left\{m_s^{[\gamma ]}(x)=(g_s^{[\gamma ]}*q)(x)|q(y)\ge 0(\forall y),\int q(y)dy=1\right\}.$$

If the upper bound ${\overline{R}}_{\beta }^{[\gamma ]}$ is replaced by the asymptotically tight upper bound [2,21], asymptotically tighter bounds to the m-projection are obtained.

Theorem 3.

If ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$, for $0<D\le D_{max}$, the m-projection of the generalized Gaussian source $p_{\beta }$ to the mixture family ${\mathcal{M}}_s^{[\gamma ]}$ of $g_s^{[\gamma ]}(x)\propto e^{-{s|x|}^{\gamma }}$ is evaluated as

$$\underset{r\in {\mathcal{M}}_s^{[\gamma ]}}{min}K(p_{\beta }||r)\le {\delta }_{\beta }^{[\gamma ]},$$

for $s\ge s^{*}$ related to $0\le D\le D_{max}$ by (9), where ${\delta }_{\beta }^{[\gamma ]}$ is given by (21). For $0<s\le s^{*}$, the m-projection is upper bounded as

$$\underset{r\in {\mathcal{M}}_s^{[\gamma ]}}{min}K(p_{\beta }||r)\le K(p_{\beta }||g_s^{[\gamma ]}).$$

(22)

Furthermore, the inequality (22) holds with equality for $0<s\le s_{min}$, where $s_{min}={lim}_{h\to -0}{R}_{\beta }^{[\gamma ]}(D_{max}+h)/h$ is the slope parameter of $R_{\beta }^{[\gamma ]}(D)$ at $D=D_{max}$.

Proof. 

The first part of the theorem is a corollary of Theorem 2 and Lemma 1. The second part corresponds to the case of $D\ge D_{max}$, since D monotonically decreases as s grows. Because $q(y)=\delta (y)$ yields $m_s^{[\gamma ]}=g_s^{[\gamma ]}$, we have (22). It follows from (13) that $K(p_{\beta }||g_{s^{*}}^{[\gamma ]})={\delta }_{\beta }^{[\gamma ]}$.

Since for $0\le s\le s_{min}$, the optimal reconstruction distribution is given by $q_s(y)=\delta (y)$, (22) holds with equality. ☐

Since we know that if $\beta =1$ and $\beta =2$, the SLB is tight for all D, we have the following corollaries.

Corollary 3.

The rate-distortion function of the Laplacian source, $R_1^{[\gamma ]}(D)$, is lower- and upper-bounded as

$$-\frac{1}{\gamma }log\left[\frac{{\alpha }^{\gamma }\Gamma {(1/\gamma )}^{\gamma }}{{(e\gamma )}^{\gamma -1}}D\right]\le R_1^{[\gamma ]}(D)\le -\frac{1}{\gamma }log\left[\frac{{\alpha }^{\gamma }}{\Gamma (\gamma +1)}D\right].$$

Corollary 4.

The rate-distortion function of the Gaussian source, $R_2^{[\gamma ]}(D)$, is lower- and upper-bounded as

$$-\frac{1}{\gamma }log\left[{\left(\frac{2\alpha }{\pi }\right)}^{\gamma /2}\frac{\Gamma {(1/\gamma )}^{\gamma }}{{\gamma }^{\gamma -1}{e}^{\gamma /2-1}}D\right]\le R_2^{[\gamma ]}(D)\le -\frac{1}{\gamma }log\left[{\left(\frac{\alpha }{2}\right)}^{\gamma /2}\frac{\sqrt{\pi }}{\Gamma (\gamma /2+1/2)}D\right].$$

Example 1.

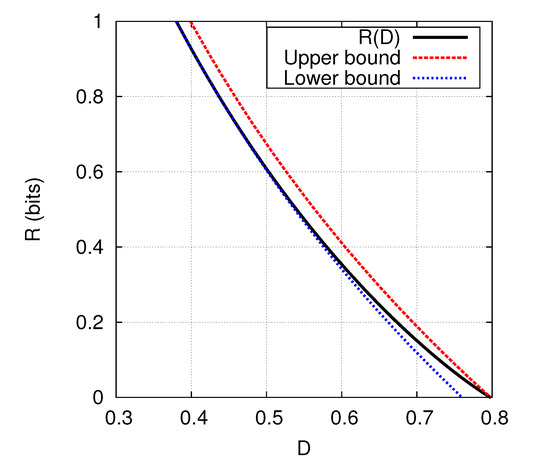
If we put $\gamma =1$ in Corollary 4 ($\beta =2$), we have

$$-log\left(\sqrt{\frac{2e\alpha }{\pi }}D\right)\le R_2^{[1]}(D)\le -log\left(\sqrt{\frac{\pi \alpha }{2}}D\right).$$

(23)

The explicit evaluation of $R_2^{[1]}(D)$ is obtained through a parametric form using the slope parameter s [6]. While the explicit parametric form requires evaluations of the cumulative distribution function of the Gaussian distribution, the bounds in (23) demonstrate that it is well approximated by an elementary function of D. In fact, the gap between the upper and lower bounds is ${\delta }_2^{[1]}=-log\frac{\pi }{2\sqrt{e}}=0.070$ (bit). The bounds in (23) are compared with $R_2^{[1]}(D)$ for $\alpha =\sqrt{2}$ in Figure 1.

Figure 1. Rate-distortion function $R_2^{[1]}(D)$ [6] and its lower and upper bounds in (23).

Example 2.

If we put $\gamma =2$ in Corollary 3 ($\beta =1$), we have

$$-\frac{1}{2}log\left(\frac{{\alpha }^2\pi }{2e}D\right)\le R_1^{[2]}(D)\le -\frac{1}{2}log\left(\frac{{\alpha }^2}{2}D\right)$$

for the Laplacian source and the squared distortion measure $d_2(x,y)={|x-y|}^2$. The gap between the bounds is ${\delta }_1^{[2]}=-\frac{1}{2}log\frac{e}{\pi }=0.104$ (bit).

The upper bound in Theorem 2 implies the following:

Corollary 5.

Under the γ-th power distortion measure, if${\underline{R}}_{\gamma }^{[\gamma ]}(D)=R_{\gamma }^{[\gamma ]}(D)$ for all D, the γ-generalized Gaussian source has the greatest rate-distortion function among all β-generalized Gaussian sources with a fixed $E[|X{|}^{\gamma }]$, satisfying ${\underline{R}}_{\beta }^{[\beta ]}(D)=R_{\beta }^{[\beta ]}(D)$ for all D.

Proof. 

Since $E_{p_{\beta }}{[|X|}^{\gamma }]=D_{max}={(\beta /\alpha )}^{\gamma /\beta }\Gamma (\gamma /\beta +1/\beta )/\Gamma (1/\beta )$, the upper bound in (19) is expressed as $-(1/\gamma )log\left(D/D_{max}\right)$, which is equal to the rate-distortion function of the $\gamma$-generalized Gaussian source under the $\gamma$-th power distortion measure if its SLB is tight for all D. ☐

The preceding corollary is well-known in the case of the squared distortion measure, while the Gaussian source has the largest rate-distortion function not only among all $\beta$-generalized Gaussian sources, but also among all the sources with a fixed variance ([2], Theorem 4.3.3).

5. Distortion-Rate Bounds for $\mathit{ϵ}$-Insensitive Loss

As another example of a distortion measure that is not matching with the $\beta$-generalized Gaussian source in the sense of Theorem 1, we consider the following $\gamma$-th power $ϵ$-insensitive distortion measure generalizing (17),

$$d(x,y)={\rho }_{ϵ}{(x-y)}^{\gamma },$$

(24)

where ${\rho }_{ϵ}(z)=max\{|z|-ϵ,0\}$. Such distortion measures are used in support vector regression models [14,15].

In this section, we focus on the Laplacian source ($\beta =1$), for which similarly to Section 4, we can evaluate

$$E_{g_s}\left[{\rho }_{ϵ}{(Z)}^{\gamma }\right]=D^{\gamma }\Gamma (\gamma +1)exp\left(-\frac{ϵ}{D}\right),$$

where $g_s(z)=\frac{s}{2}{e}^{-s|z|}$ and $s=1/D$. Such an explicit evaluation appears to be prohibitive for $\beta \ne 1$. The above expected distortion is achievable by $q_{1/D}(y|x)$ with the rate $R=-log(\alpha D)$ since $R_1^{[1]}(D)={\underline{R}}_1^{[1]}(D)$ holds for all D. Thus, we obtain the following upper bound, which is expressed by a closed form in the case of the distortion-rate function.

Theorem 4.

The distortion-rate function $D_1^{[ϵ,\gamma ]}(R)$ of the Laplacian source under the γ-th power ϵ-insensitive distortion measure (24) is upper-bounded as

$$D_1^{[ϵ,\gamma ]}(R)\le {\overline{D}}_1^{[ϵ,\gamma ]}(R)\equiv \frac{\Gamma (\gamma +1)}{{\alpha }^{\gamma }}exp\left(-\gamma R-\alpha ϵe^R\right).$$

(25)

In addition, the upper bound is tight at $R=0$; that is,

$$D_1^{[ϵ,\gamma ]}(0)={\overline{D}}_1^{[ϵ,\gamma ]}(0)=E_{p_1}[{\rho }_{ϵ}{(X)}^{\gamma }]=\frac{\Gamma (\gamma +1)}{{\alpha }^{\gamma }}{e}^{-\alpha ϵ}.$$

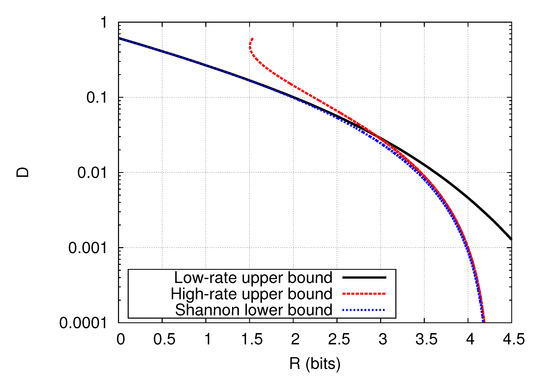
Upper and (Shannon) lower bounds which are accurate asymptotically as $D\to 0$ have been obtained for the distortion measure (24) [16]. They are proved to have approximation error at most $O({ϵ}^2)$ as $D\to 0$. Combined with these bounds, the upper bound (25), being accurate at high distortion levels, provides a good approximation of the rate-distortion function for the entire range of D. This is demonstrated in Figure 2 for the case of $ϵ=0.1$, $\gamma =1$, and $\alpha =\sqrt{2}$, where the upper bound (25) and that in [16] are referred to as low-rate and high-rate upper bounds because they are effective at low and high rates, respectively. Although the rate-distortion function of this case is still unknown, it lies between the upper bounds and the SLB. Hence, the figure implies that the SLB is accurate for all R, and the rate-distortion function is almost identified except for the region around $R=3$ (bits) where there is a relatively large gap between the upper bounds and the SLB.

Figure 2. Distortion-rate bounds for the Laplacian source with $\alpha =\sqrt{2}$ under the $ϵ$-insensitive distortion measure (24) ($ϵ=0.1$, $\gamma =1$). The upper bound (25) (solid), the asymptotic upper bound obtained in [16] (dashed), and the Shannon lower bound (SLB, dotted).

6. Conclusions

We have shown that the generalized Gaussian distribution is the only source that can make the SLB tight for all D under the power distortion measure if the orders of the source and the distortion measure are matched. We have also derived an upper bound of the rate-distortion function for the cases when the orders are mismatched, which together with the SLB provides constant-width bounds sandwiching the rate-distortion function, and hence evaluates the m-projection of the source to the mixture family associated with the distortion measure. The derived bounds demonstrate the possibility that the condition for the tightness of the SLB implies knowledge on the behavior of the rate-distortion function of other distortion measures; for example, those defined by composition of functions. In fact, we have obtained an upper bound to the distortion-rate function of $ϵ$-insensitive distortion measures in the case of the Laplacian source. It is an important undertaking to investigate the geometric structure of the mixture family associated with the distortion measure and its relationship to the m-projection; that is, the optimal reconstruction distribution.