Abstract
Alzheimer’s disease (AD) is a degenerative brain disorder leading to memory loss and changes in other cognitive abilities. The complexity of electroencephalogram (EEG) signals may help to characterise AD. To this end, we propose an extension of multiscale entropy based on variance (MSEσ2) to multichannel signals, termed multivariate MSEσ2 (mvMSEσ2), to take into account both the spatial and time domains of time series. Then, we investigate the mvMSEσ2 of EEGs at different frequency bands, including the broadband signals filtered between 1 and 40 Hz, θ, α, and β bands, and compare it with the previously-proposed multiscale entropy based on mean (MSEµ), multivariate MSEµ (mvMSEµ), and MSEσ2, to distinguish different kinds of dynamical properties of the spread and the mean in the signals. Results from 11 AD patients and 11 age-matched controls suggest that the presence of broadband activity of EEGs is required for a proper evaluation of complexity. MSEσ2 and mvMSEσ2 results, showing a loss of complexity in AD signals, led to smaller p-values in comparison with MSEµ and mvMSEµ ones, suggesting that the variance-based MSE and mvMSE can characterise changes in EEGs as a result of AD in a more detailed way. The p-values for the slope values of the mvMSE curves were smaller than for MSE at large scale factors, also showing the possible usefulness of multivariate techniques.
1. Introduction
Alzheimer’s disease (AD) is a progressive neurodegenerative disease and the most common form of dementia in the elderly population, affecting intellectual, behavioural, and functional abilities [1,2,3]. A positive diagnosis of AD allows the patient and his/her family time to be informed about the disease, to make life and financial decisions, and to plan for the future. In contrast, a negative diagnosis may reduce worry about memory loss associated with ageing. Moreover, it permits for early treatments of reversible conditions with similar symptoms (like depression and nutrition or medication problems) [2]. Medical-based diagnosis of AD is not fully reliable and symptoms are frequently dismissed as normal consequences of healthy ageing. Spinal fluid analysis and signal and image processing methods are used to increase the confidence of the diagnosis of AD [2,3].
As AD progresses, there are changes in the dynamical brain activity that can be recorded in electroencephalogram (EEG) signals [1,2]. The EEG is an affordable, portable, and non-invasive tool to assess brain activity [4]. In addition, in comparison with other non-invasive brain imaging approaches, EEG has high temporal resolution and includes essential information about abnormal brain dynamics in AD subjects [2]. The studies show that AD causes a spectral slowdown and alterations in the non-linear dynamics of the brain signal [5,6].
A prevailing approach to diagnose of AD is to consider specific frequency bands in EEG, such as δ (1–4 Hz), θ (4–8 Hz), α (8–13 Hz), β (13–30 Hz), and γ (30–40 Hz) [2,7,8]. AD affects these different frequency bands in different ways. An increase of power in δ, θ, and γ, and a decrease of power in higher frequencies α and β have been reported in AD patients in comparison with healthy age-matched control subjects [2,7,8,9].
In recent years, because of the non-linearity in the brain, even at the neuronal level [10], there has been an increasing interest in non-linear techniques for the analysis of EEGs for diagnosis of AD [1,2,11,12,13]. One of the most popular non-linear concepts used to assess the dynamical characteristics of signals is that of entropy [14,15]. This concept measures the uncertainty and irregularity of a time series [14,15]. Higher entropy normally stands for higher uncertainty, whereas lower entropy shows more regularity and certainty in a signal [14,16]. Thus, it can be considered as an indicator of dynamical changes along the temporal evolution of EEG signals.
Entropy approaches have been broadly used to characterise different kinds of signals. However, they achieve their maxima for signals with no structure (random) and are defined only for a single temporal scale: the one associated with the original sampling of the time series [17,18]. This can be considered as a limitation to investigate dynamics at longer time scales. Accordingly, multiscale entropy (MSE) was proposed to define entropy values for a range of scales to evaluate the complexity of signals at different time scales [17]. Thus, MSE quantifies signal complexity, which may remain hidden for basic entropy approaches [19].
Complexity indicates a degree of structural richness [19]. In fact, neither completely regular (periodic) nor completely irregular (uncorrelated random) time series are truly complex, because none of them is structurally rich at a global level. Thus, the concept of irregularity and complexity are not the same. For example, white Gaussian noise (WGN) is more irregular than 1/f noise, although the latter is more complex. It is in agreement with this fact that the WGN does not have a rich structure and shows a rapid drop in entropy with an increase in time scale factor [19,20,21].
The MSE algorithm at the temporal scale factor λ includes two main steps [17]. First, in the coarse-graining process, the original signal is divided into non-overlapping segments with length λ, and then the average of each segment is calculated. Second, the sample entropy (SampEn) [15] of the coarse-grained time series is computed [17].
For multi-channel signals, the MSE algorithms, though powerful and broadly-used, treat individual time series separately. Therefore, this method is appropriate for the components of multi-channel time series that are statistically independent. However, real multivariate physiological signals are simultaneously recorded and the time series are statistically dependent [22,23]. To this end, multivariate MSE using the mean in the coarse-graining process, named mvMSEµ, has been recently introduced [22]. The mvMSEµ algorithm was validated on both illustrative benchmark signals and on real-world multivariate physiological and non-physiological datasets [22,24].
However, the dynamics of the volatility (variance) of a time series over multiple temporal scales to extract dynamical properties of spread also need to be inspected. To this end, Costa and Goldberger have recently proposed a modified MSE where the variance is used in the coarse-graining process [25]. The mean- and variance-based MSE would be referred to as MSEµ and MSEσ2, respectively. MSEσ2 was used to analyse heartbeat signals from healthy young and older subjects and patients with congestive heart failure syndrome. It was demonstrated that the dynamics of the volatility of heartbeat signals obtained from healthy young subjects are highly complex. The results also showed that MSEσ2 values decrease with ageing and pathology [25].
EEG irregularity and complexity analyses have been successfully and widely employed and provide a new view to understand physiological processes in both healthy and pathological conditions in AD [1,11,13,26,27,28]. The MSE- and mvMSE-based methods have been successfully used to characterise biomedical signals to detect different pathological states like epilepsy, schizophrenia, Parkinson’s disease, and AD [13,29,30,31,32].
Escudero et al. used multiscale entropy with a coarse-graining process based on the mean to characterise EEGs in AD [11]. Later, Morabito et al. analysed EEGs in AD patients with multivariate entropy techniques based on the mean [13]. However, since the dataset included few subjects and channels, the results may not be completely reliable [13]. Azami and colleagues used only mvMSEµ for magnetoencephalograms (MEGs) in AD [32]. They consider five subsets of channels and not all the channels as a whole. Multiscale approaches using the variance in the coarse-graining process have yet to be applied to EEG analysis. Therefore, there is a need to investigate the usefulness of MSEσ2 and mvMSE where the coarse graining process uses variance (mvMSEσ2) in comparison with the more broadly used methods based on mean (MSEµ and mvMSEµ) to characterise EEGs in AD.
The aim of this research is to investigate the first and second moments (mean and variance) for the coarse-graining process of MSE and mvMSE to characterise EEGs to discriminate age-matched control subjects from AD patients. We want to evaluate the differences between results obtained by the multiscale entropy methods and their corresponding multivariate versions. We also test the hypothesis that AD patients’ signals are less complex than controls’ recordings [13,19]. In addition, the changes in entropy values for different frequency bands are investigated to understand the effect of AD and entropy-based methods on each frequency band.
2. Materials and Methods
2.1. Subjects
Eleven AD patients (five men; six women; age: 72.5 ± 8.3 years, mean ± standard deviation (SD)) and 11 age-matched control subjects (seven men; four women; age: 72.8 ± 6.1 years, mean ± SD) took part in this study. All 22 subjects were recruited from the Alzheimer’s Patients’ Relatives Association of Valladolid, Spain, and fulfilled the criteria of probable AD [33]. The EEG signals were recorded in the University Hospital of Valladolid, Spain, after all of the subjects had undergone a careful clinical assessment which included clinical history, neurological and physical examinations, brain scans and a mini mental state examination (MMSE), as a commonly accepted, simplified, scored form of the cognitive mental status examination [34].
The average of MMSE scores for the AD patients was 13.1 ± 5.9 points (mean ± SD), demonstrating that the mean of the disease degree is moderate, but five patients had an MMSE score below 12 points and, therefore, severe AD dementia. Two subjects were taking lorazepam at the time of the recording, which may improve the beta activity with therapeutic doses, although no prominent fast rhythms were seen in the visual inspection of their EEG signals. The other patients did not use any medication that could be expected to affect the EEG recordings [35,36]. The MMSE score value for 11 age-matched elderly control subjects without past or present neurological disorders was 30 ± 0. Informed consent was obtained for all 22 subjects and the local ethics committee approved the study.
2.2. EEG Recordings
More than 5 min of EEG time series were recorded from each subject with a Profile Study Room 2.3.411 EEG equipment (Oxford Instruments) at electrodes F3, F4, F7, F8, Fp1, Fp2, T3, T4, T5, T6, C3, C4, P3, P4, O1, O2, Fz, Cz, and Pz of the international 10–20 system with a linked ear lobes reference. The signals have a sampling frequency of 256 Hz, with a 12-bit analog-to-digital precision. The EEGs from all 22 subjects were recorded when they were awake and eyes-closed to obtain less noisy signals. A specialist clinician selected 5 s epochs (1280 sample points) with minimal artefacts to be appropriately used for analysis. For each subject, 30.0 ± 12.5 (mean ± SD) artefact-free epochs were chosen from each electrode. Before analysis, all EEG time series were digitally band-pass filtered in both forward and reverse directions to avoid net phase shift with a Hamming window FIR filter of order 200 and cut-off frequencies at 1 Hz and 40 Hz to remove residual electromyographic activity.
2.3. Methods
2.3.1. Multiscale Entropy Based on Mean and Variance
MSE methods include two steps: (I) coarse-graining process and (II) calculation of SampEn at each scale factor.
- (I)
- Assume we have a signal with length C. Each element of the coarse-grained time series for MSEµ and recently proposed MSEσ2 are respectively calculated as:where λ, , and N denote the scale factor, the coarse-grained signal, and its length, respectively [17,25]. In fact, the coarse-grained time series of MSEµ and MSEσ2 are respectively the mean and variance values of consecutive sample points [17,25]. Note that the coarse-graining process based on the mean and variance start from scale factor 1 and 2, respectively [17,25].
- (II)
- At each scale factor, the SampEn of the coarse-grained signal is calculated in the next step. For the sake of conciseness, here, we use yi for both the coarse-grained signals and . At each time t of y, a vector for t = 1, 2, …, N−(m−1), including the m-th subsequent values is constructed, where m, named embedding dimension, stands for how many samples are contained in each vector. Next, the distance between such vectors as the maximum difference of their corresponding scalar components, are calculated. A match happens when the distance is smaller than a predefined tolerance r. The probability Bm(r) shows the total number of m-dimensional matched vectors [15]. Similarly, Bm+1(r) is defined for embedded dimension of m + 1. Finally, the SampEn is defined as follows [15]:where m and r for SampEn were, respectively, chosen as 2, and 0.15 multiplied by the SD of the original time series following recommendations in [15].
2.3.2. Multivariate Multiscale Entropy Based on Mean and Variance
Like MSE, mvMSE includes two main steps: (I) coarse-graining process and (II) calculation of multivariate SampEn (mvSE) at each scale factor.
- (I)
- Assume we have a p-channel (multivariate) time series , q = 1, …, p, where C is the length of each channel’s signal. Each element of the coarse-grained time series is calculated as follows:where λ is the time scale factor [17,22,37]. As an extension of MSEσ2 [25] to multi-channel signals, we propose to use variance, instead of mean value, in the coarse-graining process as follows:
- (II)
- Second, for the defined scale factor λ, the mvSE of the coarse-grained signal is calculated [24,37,38]. To calculate the mvSE, multivariate embedded vectors are initially generated [24]. In [39], the Takens embedding theorem for multivariate concept is described. Using the p-channel signal where N is the length of each coarse-grained time series , the multivariate embedded reconstruction is defined as:where and are the embedding and the time lag vectors, respectively.
For p-variate time series , the mvSE algorithm, as a natural extension of standard SampEn, is described as follows [24]:
- Form multivariate embedded vectors where and .
- Calculate the distance between any two composite delay vectors and as the maximum norm.
- For a given and a threshold r, count the number of instances Pi where . Next, calculate the frequency of occurrence as and define a global quantity .
- Extend the dimensionality of the multivariate delay vector in (6) from m to (m + 1) (keep the dimension of the other variables unchanged).
- Repeat steps 1–4 and find . Next, calculate which denotes the average over all n of . Finally, find which stands for the average over all i of in an (m + 1)-dimensional space.
- Finally, mvSE is defined as:where mk, τk, and r for all of the approaches were, respectively, chosen as 2, 1, and 0.15 multiplied by the SD of the original time series according to [15,24]. Note that the number of sample points is at least 10m, or preferably at least 30m, to robustly estimate SampEn and mvSE, according to [24,40,41].
Since multivariate time series may have different amplitude ranges, the distances calculated from embedded vectors obtained with Takens embedding theorem may be dominated by components of the vectors coming from the time series with the largest amplitudes. Thus, we scale all of the data channels to the same amplitude range and normalise each data channel to unit SD so that the total variation becomes equal to the number of channels or variables [24].
2.4. Experimental Procedures
In addition to the original EEG signals band-pass filtered between 1 Hz and 40 Hz, we investigate the MSEµ, mvMSEµ, MSEσ2, and mvMSEσ2 on different EEG frequency bands, including θ, α, and β. Note that δ and γ, respectively, have too low and high frequency to be considered here based on the fact that the MSEµ and mvMSEµ methods at scale factor λ can be considered as a low-pass filter with cut-off frequency [42].
Another powerful strategy to discriminate the controls from AD subjects is to use the slope values as features of the MSE and mvMSE profiles [11]. The MSE and mvMSE profiles, showing, respectively, the SampEn and mvSE values of each coarse-grained time series versus the scale factor, were visually inspected to determine the range of scales over which the slope would be calculated. A nonparametric test, namely the Mann–Whitney U-test, was used to evaluate the differences between results for AD patients versus controls, as the entropy values at each scale factor did not follow a normal distribution. The scales with the p-values between 0.01 and 0.05 (significant), and less than 0.01 (very significant) are shown with + and *, respectively, in this study.
3. Results
3.1. Global Evaluation of Multivariate and Univariate Multiscale Entropies
The results obtained by the MSEµ, mvMSEµ, MSEσ2, and mvMSEσ2 methods are, respectively, shown in Figure 1, Figure 2, Figure 3 and Figure 4. For each of Figure 1, Figure 2, Figure 3 and Figure 4, (a)–(d) show the results at frequency bands 1–40 Hz, θ, α, and β, respectively. As can be seen in (b)–(d) of Figure 1, Figure 2, Figure 3 and Figure 4, the results obtained at frequency bands θ, α, and β do not show that controls’ signals are more complex than AD patients’ ones. This fact suggests that complexity changes are best highlighted considering broadband activity.
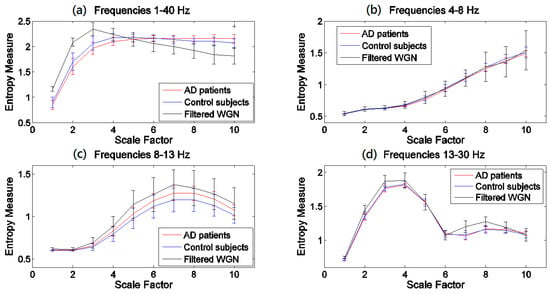
Figure 1.
Plots illustrating the mean ± SD (as error bars) of the MSEµ values computed from 11 AD, 11 control subjects’ signals, and 40 filtered univariate WGN time series at frequency bands (a) 1–40 Hz; (b) θ (4–8 Hz); (c) α (8–13 Hz); and (d) β (13–30 Hz). The scales with the p-values between 0.01 and 0.05, and less than 0.01, are shown with + and *, respectively.
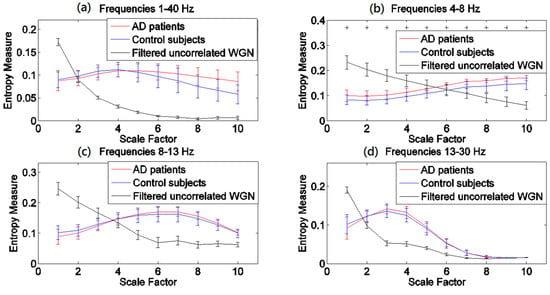
Figure 2.
Plots illustrating the mean ± SD (as error bars) of the mvMSEµ values computed from 11 AD, 11 control subjects’ signals, and 40 filtered uncorrelated sixteen-channel WGN time series at frequency bands (a) 1–40 Hz; (b) θ (4–8 Hz); (c) α (8–13 Hz); and (d) β (13–30 Hz). The scales with the p-values between 0.01 and 0.05, and less than 0.01, are shown with + and *, respectively.
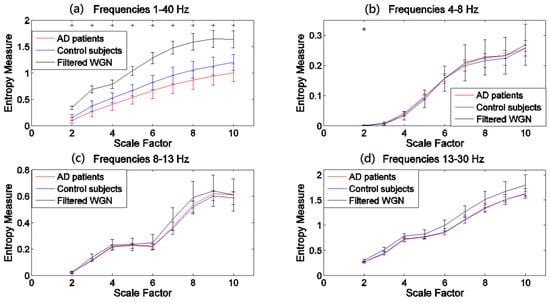
Figure 3.
Plots illustrating the mean ± SD (as error bars) of the MSEσ2 values computed from 11 AD, 11 control subjects’ signals, and 40 filtered univariate WGN time series at frequency bands (a) 1–40 Hz; (b) θ (4–8 Hz); (c) α (8–13 Hz); and (d) β (13–30 Hz). The scales with the p-values between 0.01 and 0.05, and less than 0.01, are shown with + and *, respectively.
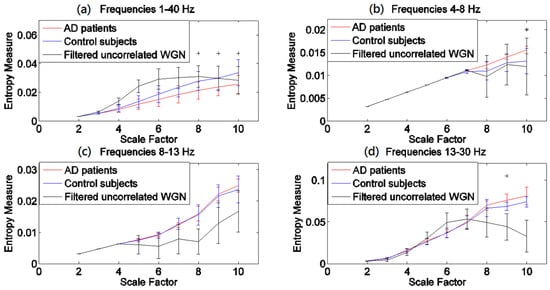
Figure 4.
Plots illustrating the mean ± SD (as error bars) of the mvMSEσ2 values computed from 11 AD, 11 control subjects’ signals, and 40 filtered uncorrelated sixteen-channel WGN time series at frequency bands (a) 1–40 Hz; (b) θ (4–8 Hz); (c) α (8–13 Hz); and (d) β (13–30 Hz). The scales with the p-values between 0.01 and 0.05, and less than 0.01, are shown with + and *, respectively.
In Figure 1a and Figure 2a, the profiles of the mvMSEµ and mvMSEµ are different for the control individuals and AD patients at short- and long-time scale factors. In comparison with the AD group, controls’ signals have more irregularity at short-time scales, whereas the AD patients’ time series are more irregular at long-time scales.
Comparing Figure 1 with Figure 2 demonstrates that mvMSEµ highlights differences between groups at individual scales better than the averaging of univariate MSEµ profiles. However, the opposite seems to happen for MSEσ2 (Figure 3) when compared with mvMSEσ2 (Figure 4). This might be because the variance coarse-grained sequences have too little variability and the multivariate implementation leads to values that are too low (notice that the output values are in 1/100s of the unit).
The results obtained using the variance-based coarse graining process (Figure 3a and Figure 4a), unlike the mean-based ones (Figure 1a and Figure 2a), show that for all the scale factors, the controls’ EEGs have a higher complexity. This is in agreement with findings that controls’ time series are more complex than AD patients’ [11,19,25,32,35,38,43,44]. Of note is that the ranges of entropy values for Figure 1 and Figure 2, and similarly Figure 3 and Figure 4, indicate that the larger the number of channels, the smaller the multivariate entropy values. For more information, please refer to Appendix A.
The p-values for MSEσ2- and mvMSEσ2-based profiles show that MSEσ2 leads to significant differences at all scale factors, while the significant differences based on mvMSEσ2 are seen at scale factors 8 and 10. In comparison with MSEµ, MSEσ2 discriminates better AD group and controls, while compared with mvMSEσ2, mvMSEµ discriminates better these two groups. It shows that the mean- and variance-based complexity measures can complement each other to characterise EEGs in AD. It is worth noting that the results obtained by different values of r (0.2, 0.25, and 0.3) and m (1 and 2) employed in other complexity studies are similar to our results [11,32,44,45].
Note that all channels are considered as a multivariate whole for multivariate entropy techniques although for the univariate ones, the entropy value is computed for each channel. Since the average is reported for MSE-based methods, the results are probably expected to have lower coefficients of variations, although these methods cannot take into account the dynamics across the channels (spatial domain).
In the light of a recently published article providing guidelines on the interpretation of MSEµ results of brain signals [46], we evaluated all MSE and mvMSE methods on 40 different univariate and uncorrelated multivariate WGN time series band-pass filtered at 1–40 Hz, 4–8 Hz, 8–13 Hz, and 13–30 Hz, to investigate whether the entropy profiles of brain signals are linked to their power content. The length of the time series and the number of channels of the filtered multivariate WGN were respectively 1280 sample points (equal to the length of the EEG time series) and 16 (equal to the number of channels of EEG time series), and the parameter values for the multiscale methods were equal to those used for the EEG dataset. The results, shown in Figure 1, Figure 2, Figure 3 and Figure 4, show that the shape of MSEµ and MSEσ2 curves are linked to the power spectral density of the corresponding filtered signals. In fact, to some extent, the MSE curves are determined by the (low and high cut-offs of the) filtering process, especially for frequency bands 4–8 Hz, 8–13 Hz, and for 13–30 Hz to a lesser extent. However, it is important to note that the entropy profiles for EEG signals of AD patients and controls do not overlap with the curves of the filtered WGN at most scale factors for the frequency band of 1–40 Hz. It also evidences the need to have broadband EEGs, instead of narrow band activity, for the evaluation of multiscale complexity. In contrast with the results of univariate entropy techniques, the mvMSEµ- and mvMSEσ2-based curves for AD patients and controls have clearly dissimilar shapes with those for filtered uncorrelated multichannel WGN, suggesting that the multivariate entropy-based values of AD patients’ and controls’ time series are completely different to those of filtered uncorrelated sixteen-channel WGN.
The computation times of the MSEµ, mvMSEµ, MSEσ2, and mvMSEσ2 methods for one of the 16-channel AD signals with the length of 1280 sample points are shown in Table 1. Note that the running time for the MSE-methods is the sum of computation time values for each of the 16 channels. In this study, the simulations have been carried out using a PC with Intel (R) Xeon (R) CPU, E5420, 2.5 GHz and 8-GB RAM by MATLAB R2010a. Since the MSEσ2 and mvMSEσ2 start from scale factor 2 and SampEn has a computational cost of O(N2), the computation time of this kind of algorithms is noticeably smaller than that of the MSEµ or mvMSEµ algorithms. The mvMSE methods deal with both the spatial and time domains, albeit the MSE algorithms consider only the time domain. Thus, as can be seen in Table 1, the MSE techniques are significantly faster than their corresponding mvMSE methods.

Table 1.
The computation time of the univariate and multivariate multiscale entropy based on the mean and variance.
3.2. Regional Evaluation with Univariate Metrics
To evaluate the complexity of the signal of each channel of AD patients’ and controls’ EEGs, we employ univariate MSE methods. The MSEµ and MSEσ2 values and their p-values for each channel of EEGs, band-pass-filtered between 1 and 40 Hz, are presented in Figure 5 and Figure 6, respectively. The p-values show the superiority of MSEσ2 over MSEµ for characterising AD. Moreover, the lowest p-values for MSEσ2 that obtained by the channels O1, O2, and P3 were equal to 0.0058, 0.0086, and 0.0087, respectively, in agreement with [11].
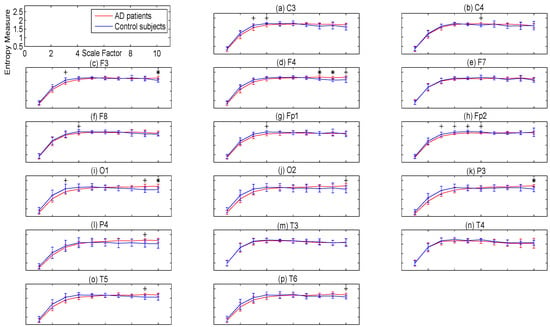
Figure 5.
Plots illustrating the mean ± SD (as error bars) of the MSEµ values computed from 11 AD and 11 control subjects for each channel of 1–40 Hz band-pass-filtered EEG signals. Sixteen electrodes of the international 10–20 system were analysed. (a) C3; (b) C4; (c) F3; (d) F4; (e) F7; (f) F8; (g) Fp1; (h) Fp2; (i) O1; (j) O2; (k) P3; (l) P4; (m) T3; (n) T4; (o) T5; and (p) T6. The scales with the p-values between 0.01 and 0.05, and less than 0.01 are shown with + and *, respectively.
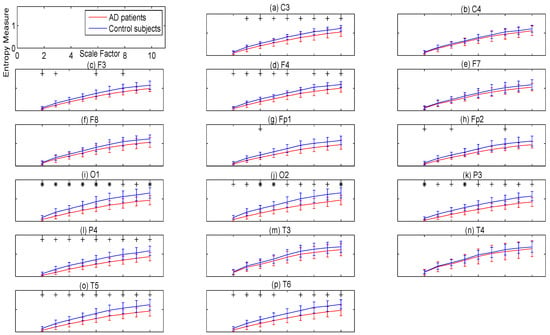
Figure 6.
Plots illustrating the mean ± SD (as error bars) of the MSEσ2 values computed from 11 AD and 11 control subjects for each channel of 1–40 Hz bandpass filtered EEG signals. Sixteen electrodes of the international 10–20 system were analysed. (a) C3; (b) C4; (c) F3; (d) F4; (e) F7; (f) F8; (g) Fp1; (h) Fp2; (i) O1; (j) O2; (k) P3; (l) P4; (m) T3; (n) T4; (o) T5; and (p) T6. The scales with the p-values between 0.01 and 0.05, and less than 0.01 are shown with + and *, respectively.
3.3. Features (Slopes) from Univariate and Multivariate Multiscale Profiles
As mentioned before, a powerful strategy to distinguish different kinds of dynamics consists in using the slopes as features from multivariate and univariate multiscale entropy profiles. As can be seen in Figure 1a and Figure 2a, for MSEµ and mvMSEµ methods, the curves increase until a scale factor of 4. Then, the slope decreases and the SampEn and mvSE values are nearly constant or decrease slightly. Therefore, we can divide each of the MSE and mvMSE curves into two segments: (I) the first part corresponds to the steep increasing slope (small scale factors, i.e., ), and (II) the second one contains the scale factors in which the slope of the SampEn and mvSE values is smoother (large scale factors, i.e., ). For MSEσ2 and mvMSEσ2 profiles, because the curves are always ascending and their slope values do not change noticeably, we consider one slope from the scale factor 2–10 (the entropy values for MSEσ2 and mvMSEσ2 methods are undefined at a scale factor of 1). Note that the slope values of both parts were calculated based on the least-square approach.
Table 2 shows the average ± SD of slope values of the MSE and mvMSE profiles for small and large time scales. We also calculate the p-values of the Mann–Whitney U-test to investigate whether there is any significant difference between the AD and control groups. Like Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, the scales with the p-values between 0.01 and 0.05, and less than 0.01, are denoted by + and *, respectively. For small scale factors, no significant differences between both groups can be found with the MSEµ and mvMSEµ, whereas the differences between these groups are significant (MSEµ) and very significant (mvMSEµ) when we consider the large scale factors. This demonstrates the importance of mvMSE method to characterise EEG signals in AD. Moreover, both the MSEσ2 and mvMSEσ2 methods lead to the significant differences for AD patients and controls.

Table 2.
Average ± SD of slope values of the MSE and mvMSE profiles, and p-values and classification accuracies for AD patients versus controls over all channels and subjects. The scales with the p-values between 0.01 and 0.05, and less than 0.01 are shown with + and *, respectively.
The slopes were also computed for each channel to investigate which channels discriminate better the two subject groups. All results at scale factors did not lead to significant differences. Table 3 summarises the average ± SD of slope values of the MSEµ profiles with scale factors . Table 3 also shows that the p-values for all channels at large scale factors leads to (very) significant differences for several channels. The average ± SD of slope values for MSEσ2 curves are shown in Table 4. The p-values derived by electrodes O1, O2, F4, P3, and T5 for both the MSEµ with scale factors and MSEσ2 profiles are (very) significant. The p-values for F4 and O1 are smaller than 0.05 for MSEµ with scale factors , while electrode O2 leads to the significant difference using the MSEσ2 method. This suggests that variance- and mean-based MSE offer complementary approaches to characterise AD.

Table 3.
Average ± SD of slope values of the MSEµ profiles and p-values for controls versus AD patients at scale factors for each channel. The scales with the p-values between 0.01 and 0.05, and less than 0.01 are shown with + and *, respectively.

Table 4.
Average ± SD of slope values of the MSEσ2 profiles and p-values for controls versus AD patients at scale factors for each channel. The scales with the p-values between 0.01 and 0.05, and less than 0.01 are shown with + and *, respectively.
We also classified the controls versus AD subjects using a naive Bayes method [47]. The slope values across the scale factors were used rather than the entropy values of all scale factors, because a slope value can be considered as a representative value of a complexity-based curve [11]. We ran 50 repetitions of a 10-fold cross-validation using the WEKA data mining software [48]. The average classification values are reported in Table 2. As expected intuitively, the highest and lowest classification accuracies are associated with the largest and smallest p-values, respectively.
4. Discussion and Conclusions
4.1. Global Evaluation of Multivariate and Univariate Multiscale Entropies
We compared the ability of MSEµ, mvMSEµ, MSEσ2, and mvMSEσ2 to characterise the complexity of EEG signals in AD. This was done for conventional frequency bands θ, α, and β, and also for the broadband EEG signals after band-pass filtering between 1 and 40 Hz. The results obtained for frequency bands θ, α, and β were in contradiction with the widely reported higher complexity in control subjects than in AD patients, which could nevertheless be observed when estimating the complexity of the broadband EEGs. This suggests that the presence of broadband activity of EEGs may be needed for a comprehensive evaluation of complexity with multiscale entropy-based methods. Furthermore, we have related these findings with a very recent article providing guidelines on the interpretation of MSE results of brain signals [46] and showed that the profile of multivariate multiscale entropy of EEG signals at different frequency bands is not determined by the band-pass filtering process in comparison with the univariate multiscale entropy.
For the MSEµ and mvMSEµ curves, the slope of the curve increasing or decreasing at different bands can be predicted based on the sampling frequency and the effect of coarse-graining process on the frequency of signals. Since MSEµ and mvMSEµ at scale factor λ can be considered as a low-pass filter with cut-off frequency [42], scales 9 and 10, and 4–10 of the broadband analysis corresponds with α and β, respectively, with θ falling off the range.
The mvMSEµ-based profiles (Figure 2a) were similar to MSEµ-based ones (Figure 1a), although the crossing point for mvMSEµ results was located at a smaller scale factor compared with that obtained by MSEµ. These results are in agreement with [11,32,35,38,43,44]. Unlike MSEµ and mvMSEµ, MSEσ2, and mvMSEσ2 of the controls’ EEGs had more complexity values at all scale factors and smaller p-values. This suggests that both the multivariate and univariate multiscale methods based on the variance may characterise changes in EEGs in AD patients in a more detailed way than methods based on the mean.
The irregularity or complexity decrease in the EEG signals of AD patients could be described by a reduction of dynamical complexity of part of the brain [45]. Nevertheless, the pathophysiological implications of the reduction of EEGs complexity or irregularity are not quite clear. Among others, three mechanisms can take into account it: neuronal death, a general effect of lack of neurotransmitter, and loss of connectivity of local neural networks as a consequence of nerve cell death [12,49]. However, ageing and age-dependent diseases frequently go together with a broad-ranging loss of physiological complexity or irregularity [50].
4.2. Regional Evaluation with Univariate Metrics
The mvMSE methods reveal the dynamics across the channels and consider the information in both the time and spatial domains, while the MSE approaches only consider the time domain. However, the MSE methods, unlike the mvMSE algorithms, can be used to better understand the behaviour of each channel separately, which could highlight complexity changes that are specific to certain electrodes. To this end, we employed MSEσ2 and MSEµ to characterise EEGs in each channel. The lowest p-values for MSEσ2 and MSEµ were obtained for the channels O1, O2, P3, and P4 and O1, P3, F3, and F4, respectively. This shows that when MSEμ (or mvMSEμ) cannot distinguish different types of dynamics of a particular time series (channel), MSEσ2 (or mvMSEσ2) may do so, and vice versa. It is worth noting that the electrodes with the lowest p-values are similar to most of our previous research using this database, such as [36,51].
4.3. Features (Slopes) from Univariate and Multivariate Multiscale Profiles
Finally, we studied the slope values of MSE and mvMSE profiles to check whether they could be used to distinguish AD patients from controls. The p-values for the slopes of the complexity curves showed the importance of this tool to discriminate different kinds of dynamics and demonstrated when the differences between AD patients’ and controls’ signals at some scale factors are not significant, their slopes of complexity curves may lead to significant differences. At small scale factors, significant differences were not found with the mean coarse-gaining-based approaches, while the differences between these groups were significant (MSEµ) and very significant (mvMSEµ) when the large scale factors were considered. This also illustrates the prominence of the mvMSEµ approach over MSEµ. In addition, significant differences between AD patients and controls were found with both the MSEσ2 and mvMSEσ2. The p-values at electrodes O1, O2, F4, P3, and T5 for both the MSEµ and MSEσ2 were significant or very significant.
4.4. Limitations
In spite of the promising results aforementioned, the number of subjects in this pilot study was relatively small. To ascertain the usefulness of these methods, these novel signal processing approaches should be used on a larger database of AD patients and controls subjects, potentially including subjects with mild cognitive impairment. Moreover, the subjects had their eyes closed during the recording of the EEG signals to obtain less noisy signals. However, the eyes closed condition increases frequency content in the alpha range. This increase could have induced a bias in the findings, especially when the alpha range was specifically studied. Thus, investigations under the eyes open condition are also required. In addition, the detected regularity increase in the EEG might not be exclusive to AD and supplementary work should be carried out to analyse whether these EEG complexity changes also happen in other types of dementia. The area under the complexity profiles is another potential feature of interest for future studies. Finally, a comprehensive comparison among all employed non-linear techniques should be done in the future.
5. Conclusions
In this pilot study, the ability of MSEµ, mvMSEµ, MSEσ2, and mvMSEσ2 to characterise the complexity of different frequency bands of EEG signals in AD was investigated. MSEμ and mvMSEμ, MSEσ2, and mvMSEσ2 quantify the dynamical properties of average and spread, respectively, over multiple time scales. They extract different kinds of information from signals. The results indicated that when MSEμ or mvMSEμ cannot distinguish different types of dynamics of a particular time series, MSEσ2 or mvMSEσ2 may do so, and vice versa. The multivariate entropy methods may lead to more significant differences between groups by taking into account both the spatial and time domains. However, they cannot characterise the multivariate time series for single channels. Our results also evidenced that the presence of broadband activity in EEGs is required for a comprehensive evaluation of complexity with univariate and multivariate multiscale entropy approaches. From a clinical perspective, MSEσ2 and mvMSEσ2 results were associated with a loss of complexity in AD time series and showed that the variance-based MSE and mvMSE better discriminate the AD patients’ signals from the controls’ ones in comparison with mean-based multiscale methods. The p-values for the slope values of mvMSE curves were smaller than for MSE, showing the possible usefulness of multivariate approaches. Overall, our results support the relevance of multivariate and univariate multiscale complexity analyses for the characterisation of EEG signals in AD.
Acknowledgments
We would like to thank Pedro Espino (Hospital Clinico San Carlos, Madrid, Spain) for his help in the recording and selection of EEG epochs.
Author Contributions
Hamed Azami and Javier Escudero conceived and designed the methodology. Hamed Azami was responsible for analysing and writing the paper. Daniel Abásolo, Samantha Simons, and Javier Escudero contributed critically to revise the results and discussed them. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Sample entropy and multivariate sample entropy are used in the second step of the algorithms to quantify the complexity of univariate and multivariate time series, respectively. Sample entropy is based on the conditional probability that sequences close to each other for m consecutive data points will also be close to each other when one more point is added to each sequence. Thus, the proportion of unseen, new samples over the number of samples included in the previous pattern for the embedding dimension m = 2 is 50%. However, in multivariate sample entropy, multivariate embedded vectors are initially generated with the length of m1 + m2 + ... + mp, where p denotes the number of channels of a time series. For example, for a trivariate time series with the embedding dimension m = [2, 2, 2], the length of embedded vectors is 6. Then, the conditional probability that sequences with the embedding dimension m = [2, 2, 2] close to each other for six data points will also be close to each other for seven data points, associated with the embedding dimensions [2, 2, 3], [2, 3, 2], or [3, 2, 2], is calculated. Note that the length of the newly embedded vectors is 7. Therefore, the proportion of unseen samples over the number of total samples in previous patterns for the embedding dimension m = [2, 2, 2] is 16.66%. Likewise, for a four-channel time series with the embedding dimension m = [2, 2, 2, 2], the proportion of unseen samples over the number of samples of previous patterns is 12.5%. Consequently, the proportion of new samples decreases proportionally to the number of channels, thus decreasing the likelihood of the longer new pattern not being a match with the shorter ones.
To investigate the changes in multivariate entropy values when the number of channels increases, we used an uncorrelated multivariate WGN time series that the number of its channels changes from 1 to 16 and the length of each of them is 1280 samples (equal to the length of EEG time series). Figure A1 shows how the number of channels affects the mvMSE output values. It can be seen that the larger the number of channels, the smaller the multivariate entropy values, something that agrees with our results, where the multivariate measures result in lower entropy values.
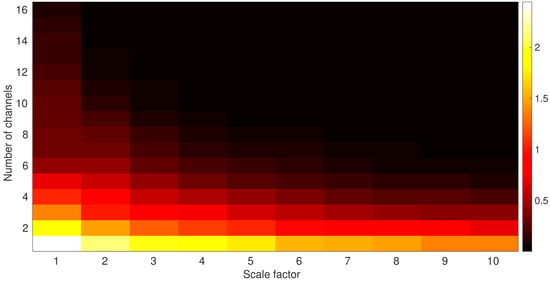
Figure A1.
Multivariate Multiscale entropy values for the uncorrelated 1- to 16-channel WGN noise time series.
References
- Bhat, S.; Acharya, U.R.; Dadmehr, N.; Adeli, H. Clinical neurophysiological and automated EEG-based diagnosis of the Alzheimer’s disease. Eur. Neurol. 2015, 74, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Vialatte, F.; Cichocki, A. Diagnosis of Alzheimer’s disease from eeg signals: Where are we standing? Curr. Alzheimer Res. 2010, 7, 487–505. [Google Scholar] [CrossRef] [PubMed]
- Alzheimer’s Association. 2016 Alzheimer’s disease facts and figures. Alzheimers Dement. 2016, 12, 459–509. [Google Scholar]
- Sanei, S. Adaptive Processing of Brain Signals; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Stam, C. Use of magnetoencephalography (MEG) to study functional brain networks in neurodegenerative disorders. J. Neurol. Sci. 2010, 289, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Escudero, J.; Fernández, A.; Poza, J.; Gómez, C. Spectral and nonlinear analyses of MEG background activity in patients with Alzheimer’s disease. IEEE Trans. Biomed. Eng. 2008, 55, 1658–1665. [Google Scholar] [CrossRef] [PubMed]
- Van der Hiele, K.; Vein, A.; Reijntjes, R.; Westendorp, R.; Bollen, E.; Van Buchem, M.; Van Dijk, J.; Middelkoop, H. EEG correlates in the spectrum of cognitive decline. Clin. Neurophysiol. 2007, 118, 1931–1939. [Google Scholar] [CrossRef] [PubMed]
- Czigler, B.; Csikós, D.; Hidasi, Z.; Gaál, Z.A.; Csibri, É.; Kiss, É.; Salacz, P.; Molnár, M. Quantitative EEG in early Alzheimer’s disease patients—Power spectrum and complexity features. Int. J. Psychophysiol. 2008, 68, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Moretti, D.; Fracassi, C.; Pievani, M.; Geroldi, C.; Binetti, G.; Zanetti, O.; Sosta, K.; Rossini, P.; Frisoni, G. Increase of theta/gamma ratio is associated with memory impairment. Clin. Neurophysiol. 2009, 120, 295–303. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Escudero, J.; Abásolo, D.; Hornero, R.; Espino, P.; López, M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J. EEG dynamics in patients with Alzheimer’s disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; La Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of EEG complexity in Alzheimer’s disease through a multivariate multiscale approach. IEEE Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Sanei, S.; Chambers, J. EEG Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Ahmed, M.; Rehman, N.; Looney, D.; Rutkowski, T.; Mandic, D. Dynamical complexity of human responses: A multivariate data-adaptive framework. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 433–445. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.E.V.; Cabella, B.C.T.; da Costa Neves, U.P.; Junior, L.O.M. Multiscale entropy-based methods for heart rate variability complexity analysis. Phys. A Stat. Mech. Its Appl. 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Fogedby, H. On the phase space approach to complexity. J. Stat. Phys. 1992, 69, 411–425. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. Multivariate refined composite multiscale entropy analysis. Phys. Lett. A 2016, 380, 1426–1431. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.; Montez, T.; Jones, B.; Rombouts, S.; Van Der Made, Y.; Pijnenburg, Y.; Scheltens, P. Disturbed fluctuations of resting state EEG synchronization in Alzheimer’s disease. Clin. Neurophysiol. 2005, 116, 708–715. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, T.; Takahashi, T.; Cho, R.Y.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Assessment of EEG dynamical complexity in alzheimer’s disease using multiscale entropy. Clin. Neurophysiol. 2010, 121, 1438–1446. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Takahashi, T.; Cho, R.Y.; Mizuno, T.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Antipsychotics reverse abnormal EEG complexity in drug-naive schizophrenia: A multiscale entropy analysis. Neuroimage 2010, 51, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Dang, C.; Li, X. Multiscale entropy analysis of EEG recordings in epileptic rats. Biomed. Eng. Appl. Basis Commun. 2009, 21, 169–176. [Google Scholar] [CrossRef]
- Chung, C.-C.; Kang, J.-H.; Yuan, R.-Y.; Wu, D.; Chen, C.-C.; Chi, N.-F.; Chen, P.-C.; Hu, C.-J. Multiscale entropy analysis of electroencephalography during sleep in patients with parkinson disease. Clin. EEG Neurosci. 2013. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Smith, K.; Fernandez, A.; Escudero, J. Evaluation of resting-state magnetoencephalogram complexity in Alzheimer’s disease with multivariate multiscale permutation and sample entropies. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 5–29 August 2015; pp. 7422–7425.
- McKhann, G.; Drachman, D.; Folstein, M.; Katzman, R.; Price, D.; Stadlan, E.M. Clinical diagnosis of Alzheimer’s disease: Report of the nincds-adrda work group* under the auspices of department of health and human services task force on Alzheimer’s disease. Neurology 1984, 34, 939. [Google Scholar] [CrossRef] [PubMed]
- Folstein, M.F.; Folstein, S.E.; McHugh, P.R. “Mini-mental state”: A practical method for grading the cognitive state of patients for the clinician. J. Psychiatr. Res. 1975, 12, 189–198. [Google Scholar] [CrossRef]
- Abásolo, D.; Escudero, J.; Hornero, R.; Gómez, C.; Espino, P. Approximate entropy and auto mutual information analysis of the electroencephalogram in alzheimer’s disease patients. Med. Biol. Eng. Comput. 2008, 46, 1019–1028. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Espino, P.; Alvarez, D.; Poza, J. Entropy analysis of the EEG background activity in Alzheimer’s disease patients. Physiol. Meas. 2006, 27, 241. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. Multivariate generalized multiscale entropy analysis. Entropy 2016, 18, 411. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Phys. D Nonlinear Phenom. 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1643–H1656. [Google Scholar]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Phys. A Stat. Mech. Its Appl. 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdú, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Morabito, F.C.; Labate, D.; Bramanti, A.; La Foresta, F.; Morabito, G.; Palamara, I.; Szu, H.H. Enhanced compressibility of EEG signal in Alzheimer’s disease patients. IEEE Sens. J. 2013, 13, 3255–3262. [Google Scholar] [CrossRef]
- Yang, A.C.; Wang, S.-J.; Lai, K.-L.; Tsai, C.-F.; Yang, C.-H.; Hwang, J.-P.; Lo, M.-T.; Huang, N.E.; Peng, C.-K.; Fuh, J.-L. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer’s disease. Prog. Neuro Psychopharmacol. Biol. Psychiatry 2013, 47, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Abásolo, D.; Escudero, J.; Gómez, C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Courtiol, J.; Perdikis, D.; Petkoski, S.; Müller, V.; Huys, R.; Sleimen-Malkoun, R.; Jirsa, V.K. The multiscale entropy: Guidelines for use and interpretation in brain signal analysis. J. Neurosci. Methods 2016, 273, 175–190. [Google Scholar] [CrossRef] [PubMed]
- Rish, I. An empirical study of the naive bayes classifier. In IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence; IBM: New York, NY, USA, 2001; pp. 41–46. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The weka data mining software: An update. ACM SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Jelles, B.; Van Birgelen, J.; Slaets, J.; Hekster, R.; Jonkman, E.; Stam, C. Decrease of non-linear structure in the EEG of alzheimer patients compared to healthy controls. Clin. Neurophysiol. 1999, 110, 1159–1167. [Google Scholar] [CrossRef]
- Kyriazis, M. Practical applications of chaos theory to the modulation of human ageing: Nature prefers chaos to regularity. Biogerontology 2003, 4, 75–90. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Gómez, C.; García, M.; López, M. Analysis of EEG background activity in Alzheimer’s disease patients with lempel–ziv complexity and central tendency measure. Med. Eng. Phys. 2006, 28, 315–322. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).