Abstract
On the basis of introducing the origin and development of finite time thermodynamics (FTT), this paper reviews the progress in FTT optimization for internal combustion engine (ICE) cycles from the following four aspects: the studies on the optimum performances of air standard endoreversible (with only the irreversibility of heat resistance) and irreversible ICE cycles, including Otto, Diesel, Atkinson, Brayton, Dual, Miller, Porous Medium and Universal cycles with constant specific heats, variable specific heats, and variable specific ratio of the conventional and quantum working fluids (WFs); the studies on the optimum piston motion (OPM) trajectories of ICE cycles, including Otto and Diesel cycles with Newtonian and other heat transfer laws; the studies on the performance limits of ICE cycles with non-uniform WF with Newtonian and other heat transfer laws; as well as the studies on the performance simulation of ICE cycles. In the studies, the optimization objectives include work, power, power density, efficiency, entropy generation rate, ecological function, and so on. The further direction for the studies is explored.
1. Introduction
Internal combustion engines (ICEs) are widely used in industry, agriculture, communication and transport, as well as national defense equipment. It is the main power source of automobiles, tractors, agricultural machinery, engineering machinery, shipping, locomotives, military vehicles, moving and emergency electric stations and so on. Since the number and distribution of ICEs are numerous and extensive, the ICE has a significant influence on energy and the environment. From the point of view of saving energy and protecting the environment against pollution, more and more strict requirements have been imposed on ICEs, such as large power output, little specific fuel consumption, low pollution and even zero emissions.
The ICE cycle is a thermodynamic cycle. Using thermodynamics to analyze the performance of the ICE cycle is not only the basis for improving and exploiting new ICE technologies, but also the main method of perfecting and developing ICE cycles. Using classical thermodynamics to perform the first law analysis for ICE cycles can study the quantitative relation between the efficiency and different losses [,,,]. Using the second law of thermodynamics to analyze ICE cycle performance allows the study of the work capacity loss due to various irreversible losses during the energy transformation process [,,,]. Using simulation studies based on the first law and irreversible thermodynamics to analyze the performance of ICE cycles can provide the law of state parameter variation with space-time of the cycle process [,]. Simulation studies only focus on the local differential properties of a system, but the variable net effect of some procedure functions during specific processes cannot be obtained by using irreversible thermodynamics.
Finite time thermodynamics (FTT) is a new branch of modern thermodynamic theory that can answer some global questions which classical thermodynamics do not try to answer and conventional irreversible thermodynamics cannot answer because of its micro and differential viewpoint. The performance analysis of ICE cycles using thermodynamic theory follows the development of thermodynamics from traditional to modern times. The performance optimization of ICE cycles by using FTT which can obtain the performance limits and optimum path of cycles and provide a scientific basis and theoretical guidelines for the optimum design and operation of practical ICEs is becoming a new subject of FTT study.
2. The Historical Background of FTT
The application of classical thermodynamic principles and the solution of thermodynamic bounds for finite time or finite size thermodynamic processes, which are characterized by a finite exchange rate that happens between the system and the environment, were the first step toward the field of FTT. In 1975, Curzon and Ahlborn [] derived the efficiency () at maximum power output (MP) point of a Carnot engine which was called CA efficiency when finite heat transfer rate between working fluid (WF) and heat reservoir was considered. The CA efficiency was an important symbol of FTT’s birth and provided a new analysis method for heat engine which was characterized by finite rate and finite period. This is the first and perhaps best known FTT study result. Since the mid-1970s, studies seeking thermodynamic process performance limits and achieving thermodynamic process optimization have made important progress in the fields of physics and engineering. In physics, Chicago scholars [,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,] named it FTT.
Determining the optimum performance or the optimum thermodynamic process for a given thermodynamic system or a given optimization objective (OPB) are two basic problems of FTT. The studies for the above two basic problems focus on the following four aspects: studies on the influence of OPB on the optimum performance and configuration [,,,], studies on the influence of loss models on the optimum performance and configuration [,,,], studies on the influence of heat reservoir models on the optimum performance and configuration [,,,], and studies on the optimum performance and configuration for practical heat engine plants and thermodynamic processes [,,,,].
3. Progress in FTT Studies for ICE Cycles
The ICE cycle is a thermodynamic cycle and can also be studied by using FTT. The studies on ICE cycles focus on the following four aspects: the optimum performances of air standard (AS) ICE cycles, the OPM path of ICE cycles, the performance limits of ICE cycles with non-uniform WF, and performance simulation of ICE cycles.
3.1. The Progress in Optimum Performance Studies for AS ICE Cycles
3.1.1. The Study Features
Studies on the optimum performance of AS ICE cycles focus on the following five aspects:
- (1)
- The influences of optimization objectives (OPBs) on cycle optimum performance.
Analyzing and optimizing thermodynamic process by using different OPBs is a very active research field of FTT. The main OPBs used in ICE cycles analysis and optimization include power (work) and efficiency [,,], power density [], effective power [], EF [,,,,,], ecological coefficient of performance (ECOP) [] and so on.
- (2)
- The influences of specific heat (SH) models of WF on cycle optimum performance.
In the early studies, the SH of WF was usually assumed to be constant. For practical cycles, however, the properties and composition of the WF will change as combustion reactions occur, so the SH of WF will also change with the combustion reactions and these changes will have a great influence on cycle performance. Refs. [,] first advanced the variable specific heat (VSH) model in which the SH was assumed to change with the WF component. This model was relatively simple and didn’t consider the influences of VSH on cycle process. Ref. [] first advanced the SH varied with temperature with linear relation model:
where ap, bv and K are constants, Cp and Cv are SH of isobaric process and isochoric process, respectively. According to the relation of Cp and Cv, one has:
where R is the gas constant. Refs. [,,,] advanced the SH model varied with temperature with nonlinear relation which was closer to practice:
The variation of SH of WF would inevitably cause the variation of specific heat ratio (SHR), Refs. [,,] advanced the SHR model varied with temperature with linear [,] and nonlinear [] relation, respectively:
where k is the SHR and k0, u, u1, u2, u3 are constants.
- (3)
- The influences of loss models on cycle optimum performance.
According to the different losses existed in the cycle, thermodynamic cycles can be classified as endoreversible cycles and irreversible cycles. The main losses existing in ICE cycles include heat transfer loss (HTL), friction loss (FL), internal irreversible loss (IIL) and mechanical loss. The cycle with only HTL is an endoreversible cycle, while the cycle with other losses is an irreversible cycle. There exist two models which reflect the influence of HTL on optimum cycle performance. The first is that the cycle maximum temperature is unfixed [,] and must be solved by combining the value of heat addition in the cycle and HTL. The second is that the cycle maximum temperature is fixed [] and needn’t be solved.
There have three methods to define the cycle IIL. The first definition is that Angulo-Brown et al. [] used the ratio of entropy change in heat addition process to that in heat rejection process to define the IIL of Otto cycle. Because the SH of heat addition and rejection processes are different, entropy changes for these two processes are different. The SH in the heat addition process are smaller than those in the heat rejection process. The p − v diagram for AS Otto cycle model established in [] is shown in Figure 1. Processes 1 → 2 and 3 → 4 are reversible adiabatic compression process and expansion process. Process 2 → 3 is constant volume heat addition process with Cv1 and process 4 → 1 is constant volume heat rejection process with Cv2 (where Cv1 and Cv2 are SH at constant volume and Cv1 is smaller than Cv2). The IIL of cycle is defined as:
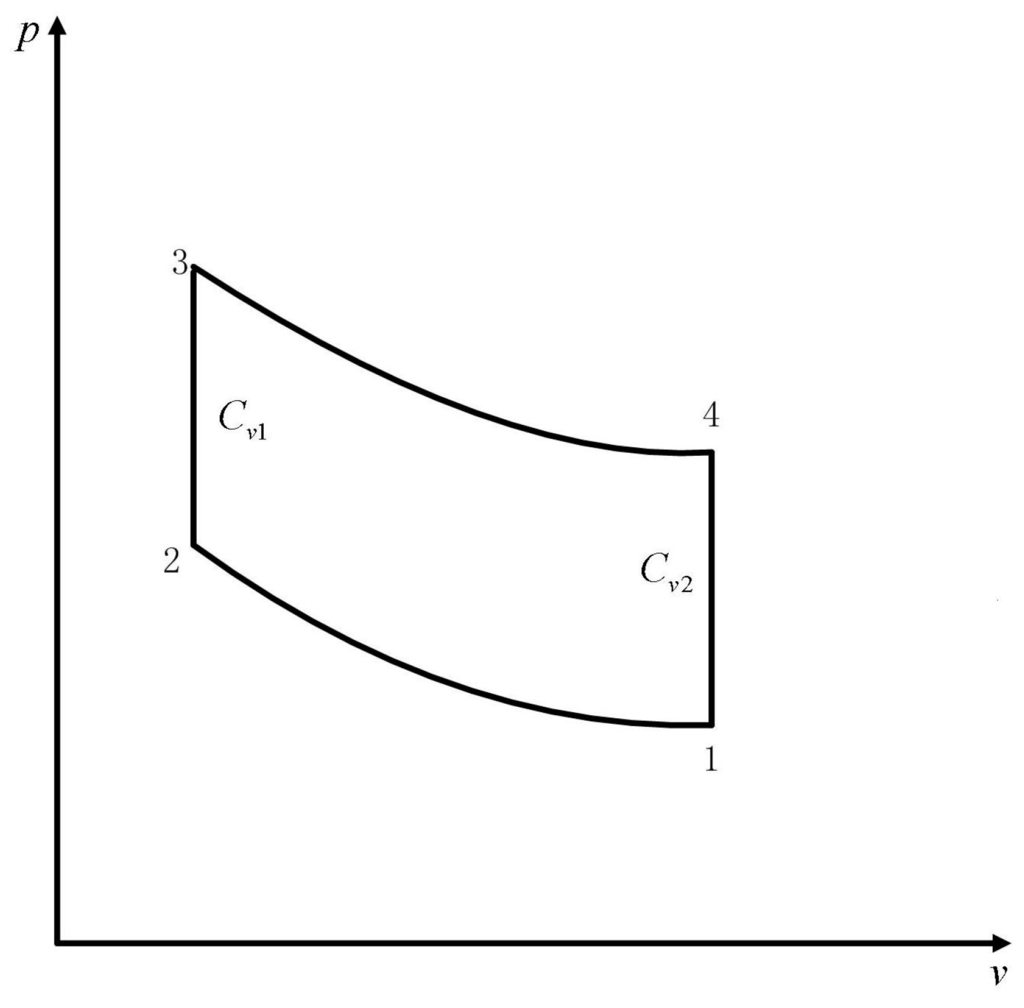
Figure 1.
p − v diagram for the Otto cycle model.
The second definition is that Ust et al. [] used the ratio of entropy change in heat addition process to that in heat rejection process to define the IIL of a Dual cycle. Because the compression and expansion processes are irreversible, the entropy change in heat addition process is different from that in heat rejection processes. The T − s diagram for an irreversible Dual cycle model is shown in Figure 2. Processes 1 → 2S and 4 → 5S are reversible an adiabatic compression process and expansion process. Processes 1 → 2 and 4 → 5 are an irreversible adiabatic compression process and expansion process. Processes 2 → 3 and 3 → 4 are heat addition processes with constant volume and constant pressure. Process 5 → 1 is a heat rejection process with constant volume. The cycle IIL is defined as
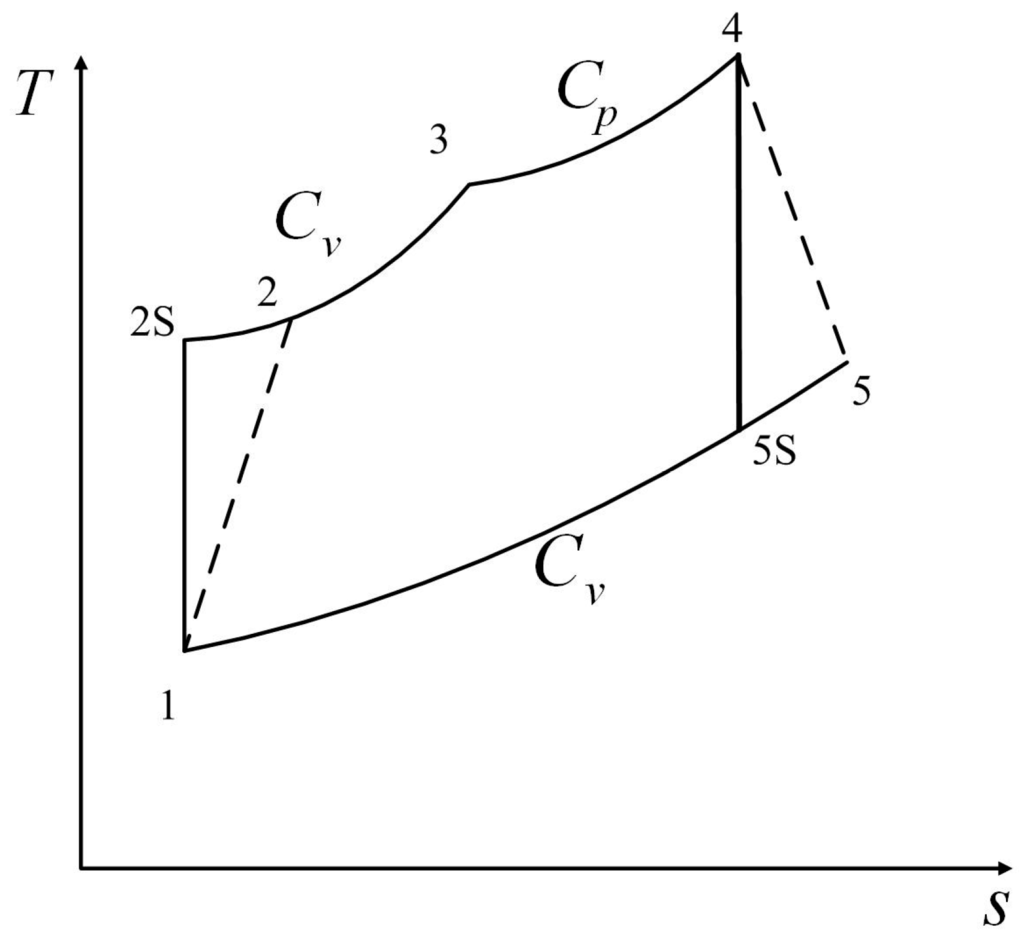
Figure 2.
T − s diagram for the Dual cycle model.
The third definition is that the IIL was defined by using irreversible compression and expansion efficiencies in []. All irreversible losses which included FL in these two strokes could be described by these two efficiencies. Considering the irreversible Dual cycle model in Figure 2, the cycle IIL is defined as:
According to the published literatures, there are two FL models. In the first model which was established in [], FL was converted to the pressure drop loss of WF. In the second model which was established in [], friction force was a linear function of the piston velocity. The computations for piston velocity also have two methods. One is that the velocity is equal to stroke length divided by stroke time and the piston velocities in the four strokes are the same []. Another is that the velocity is sinusoidal relation with the crankshaft rotation angle []. In [], the mechanical loss power was computed by using an empirical equation of mean mechanical loss pressure. The mechanical losses related to construction of combustion chamber and rotating part loss of crankshaft connecting rod have been included in this loss.
- (4)
- The influences of WF characteristics on the cycle optimum performance.
For some special fields and systems, such as superconductivity systems, magnetic systems, laser systems and the cryogenic field, in which WF obeys quantum statistical law, classical thermodynamics based on phenomenological law and classical statistical mechanics based on equilibrium statistical mechanics are inapplicable. The quantum characteristics of WF should be considered in the study. Some researchers have considered the quantum characteristics of WF, extended WF in ICE cycle from classical WF to quantum WF, and obtained many meaningful and new results which were different from those of cycles working with classical WF [,,].
- (5)
- The optimum performances of universal cycle.
The universal laws and results are the aim of pursuing FTT, and it is the same for the optimum performance study of ICE cycles. There are two universal cycle models for ICE cycles. The first universal model which was established in [] and shown in Figure 3 consisted of a heat addition process with constant thermal-capacity, a heat rejection process with constant thermal-capacity and two adiabatic processes.
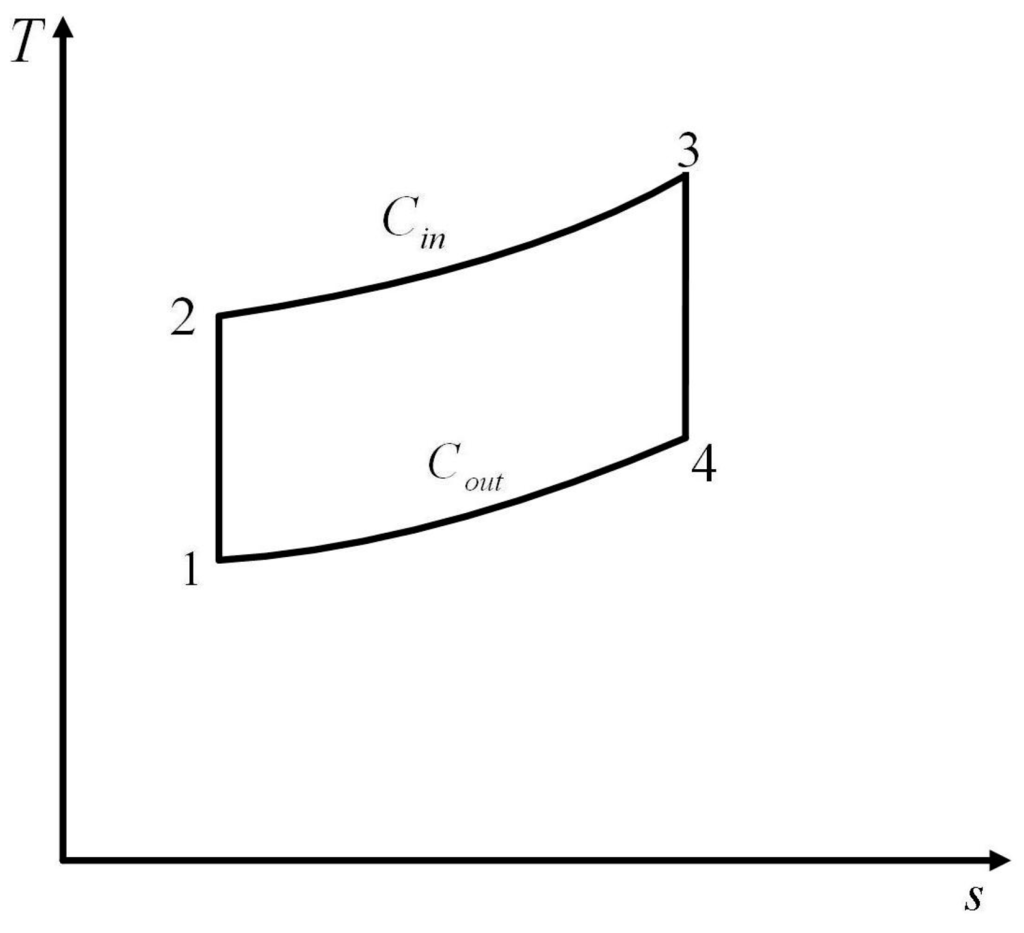
Figure 3.
T − s diagram for the first universal cycle model [].
The second universal model which was established in [,] and shown in Figure 4 consisted of two heat addition processes with constant thermal-capacity, two heat rejection processes with constant thermal- capacity and two adiabatic processes.
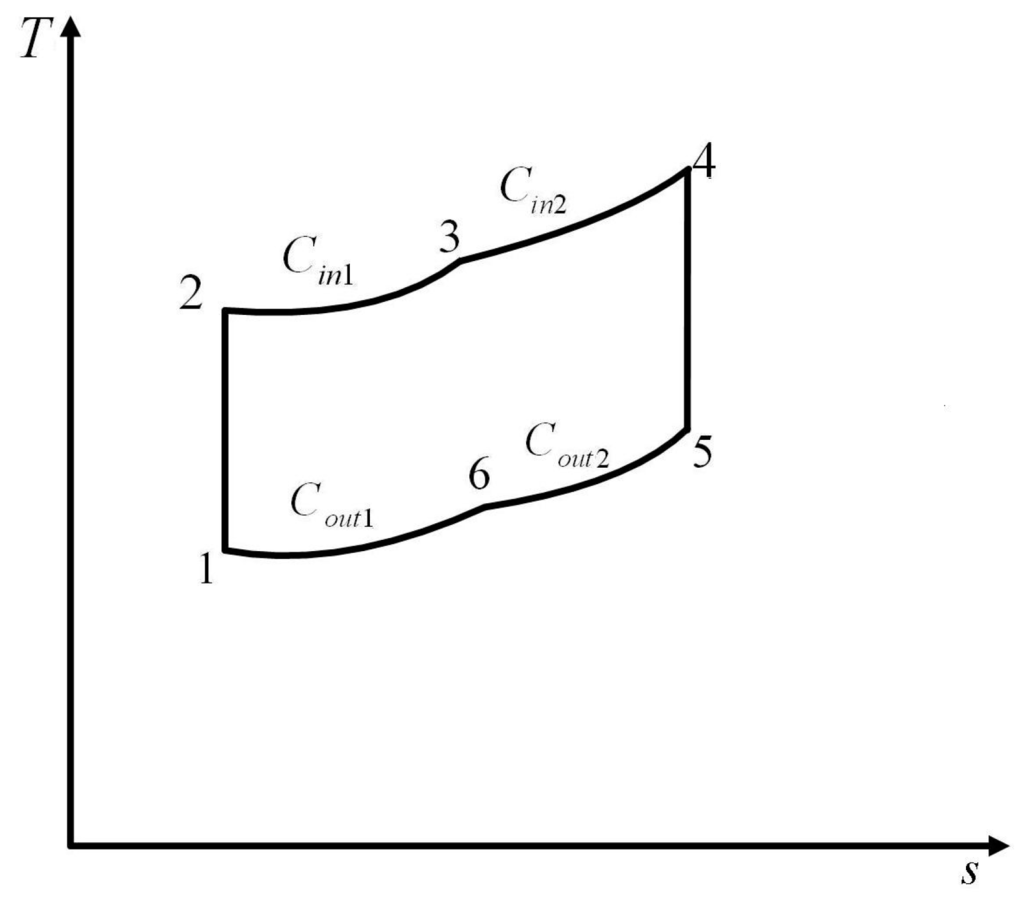
Figure 4.
T − s diagram for the second universal cycle model [,].
3.1.2. The Progress in Optimum Performance Studies for AS Otto Cycles
The Optimum Performance with Constant Specific Heats (CSH) of WF
Rashidi and Hajipour [] obtained the work output and efficiency performance characteristics of reversible Otto cycles, and investigated the influence of cycle maximum temperature and compression ratio (CR) on cycle performance. Considering HTL, Klein [] obtained the work output and CR characteristics and investigated the influence of HTL on cycle performance. Considering the influence of combustion, Wu and Blank [] obtained the relation of the optimum CR varied with the cycle maximum temperature of an endoreversible Otto cycle when the work output was the maximum. Blank and Wu [] optimized the power output and mean effective pressure of an endoreversible Otto cycle. Unfixing the cycle maximum temperature (in the following parts, the cycle maximum temperatures are all unfixed if not explained otherwise), Chen et al. [] obtained the work output and efficiency performance characteristics of endoreversible Otto cycles, and examined the effects of HTL and initial temperature on cycle performance. Ficher and Hoffman [] studied whether an endoreversible Novikov engine model [] with heat leakage could quantitatively reproduce the performance of an endoreversible Otto cycle and found that the power output and efficiency performance characteristics of endoreversible Otto cycles could be reproduced well by the Novikov model with heat leakage. Considering HTL as a part of fuel energy, Ozsoysal [] derived the effective ranges of HTL coefficients of endoreversible Otto cycles and found that cycle performance analysis would be closer to practical results and also more accurate when HTL coefficients were chosen according to the ranges. Comparing the work output and efficiency performance characteristics of an endoreversible Otto cycle with those of an endoreversible Atkinson cycle, Hou [] found that the performance of the endoreversible Atkinson cycle is higher than that of the endoreversible Otto cycle under the same CR, and the CR which maximized work output of an endoreversible Otto cycle is bigger than that of an endoreversible Atkinson cycle. Ozcan [] performed an exergy analysis of an endoreversible Otto cycle by using FTT and found that power output and exergy efficiency would increase when the HTL decreased. Based on the second law efficiency criteria, Rashidi et al. [] optimized the performance of an endoreversible Otto cycle and investigated the influences of HTL on cycle performance.
Considering FL, Angulo-Brown et al. [] established an irreversible Otto cycle model, and optimized the power output and efficiency performance characteristics. Chen et al. [] established an irreversible Otto cycle model when HL and FL were considered based on [,], derived the power output and efficiency performance characteristics, and investigated the influences of above two losses on cycle performance characteristics. Lan et al. [,] pointed out the development direction of the FTT studies for the theoretical ICE cycle, introduced FTT into the thermodynamics analysis of working process of an Otto cycle, and analyzed and compared the thermodynamic process of the Otto cycle from the point of view of energy and available energy, respectively.
Angulo-Brown et al. [] used the ratio of entropy change in a heat addition process to that in a heat rejection process to define the IIL, and analyzed the power output and efficiency performance characteristics of irreversible Otto cycles when both IIL and FL were considered. Using the definition of IIL advanced in [] and considering HTL, Chen et al. [] established an irreversible Otto cycle model, derived the power output and efficiency performance characteristics with the fixed cycle maximum temperature, and investigated the influences of IIL and HTL on cycle performance. Using the definition of IIL advanced in [] and considering HTL and FL, Zhao and Chen [] established an irreversible Otto cycle model, derived the power output and efficiency performance characteristics with the fixed cycle maximum temperature, and investigated the influences of three losses on cycle performance. Fixing the fuel consumption per cycle and cycle maximum temperature, Feidt [] optimized the terminal temperature in compression stroke of an irreversible Otto cycle with the maximum work output (MW) as the OPB. Ebrahimi [] used the ratio of heat addition in the cycle to heat released by fuel combustion to define the combustion efficiency, derived the power output and efficiency performance characteristics of an irreversible Otto cycle when IIL and HTL were considered, and investigated the influence of combustion efficiency on cycle performance. Considering air-fuel mass ratio, Ozsoysal [] investigated the influence of combustion efficiency on the power output and efficiency performance characteristics of irreversible Otto cycles. Considering HTL, FL and IIL, Ebrahimi [] investigated the influence of equivalence ratio on the power output and efficiency performance characteristics of irreversible Otto cycles. Ebrahimi [] used the ratio of volume flow rate to piston displacing volume to define the volumetric efficiency, investigated the power output and efficiency performance characteristics of an irreversible Otto cycle when HTL, FL and IIL were considered, and examined the influence of volumetric efficiency on cycle performance. Considering HTL and IIL, Huleihil [] defined the pressure drop coefficient, examined the influence of pressure drop on the power output and efficiency performance characteristics of an irreversible Otto cycle, and found that the efficiency would decrease by about 15% when the pressure dropped by about 60%. Hu et al. [] studied the power output and efficiency performance characteristics of the irreversible Otto cycle when only IIL was considered, optimized the performance parameters, and examined the influences of IIL and temperature ratio of highest to lowest on cycle performance. Under different performance criteria (maximum power output (MP), maximum efficiency (ME) and maximum mean effective pressure), Ust et al. [] performed the performance optimization of an irreversible Otto cycle with the sole loss of IIL, respectively, compared the optimization results under the MEP with those obtained under the MP and ME, and analyzed the influences of temperature ratio and pressure ratio on cycle performance. Ebrahimi [] compared the performances of an irreversible Otto cycle with ethanol and gasoline fuels, and found that the MP, the cycle working range, the power output at the ME, the efficiency at the MP would increase, while the compression ratios at the MP and the ME would decrease when the fuel was changed from ethanol to gasoline. Huleihil and Mazor [] used polytropic processes to replace the reversible adiabatic processes to consider the losses existing in real Otto engines and investigated the performance characteristics of an irreversible Otto cycle. In order to obtain alternative expressions of performance characteristics, Ladino-Luna and Paez-Hernandez [] proposed a procedure including the time spent on adiabatic processes in an irreversible Otto cycle and the theoretical results obtained were more aligned with the practical results after taking into account these times. Considering fuel incomplete combustion and HTL, Joseph and Thampi [] compared the performance of an irreversible Otto cycle obtained by using FTT with that of an actual Otto cycle and found that the performance obtained by using FTT deviated from that of the actual Otto cycle by 0%–10%.
Gumus et al. [] made a performance comparison for an Otto cycle with three different performance criteria, i.e., MP, maximum power density (MPD) and maximum efficient power (MEP). Only considering FL, Angulo-Brown et al. [] investigated the EF performance of irreversible Otto cycles. The entropy generation rate generated by different SH in heat addition and rejection processes was computed, while the entropy generation rate generated by FL had not been included in []. The entropy generation rate generated by irreversible heat transfer between WF and heat reservoirs was computed, and the optimum EF of the closed Otto cycle was studied in [,]. Considering HTL, FL and IIL, Ge et al. [,] used an AS cycle model to replace the open cycle model, established an irreversible Otto cycle model with CSH of WF, computed the entropy generation rate generated by various losses, studied the cycle optimum EF performance, and examined the influences of three losses on cycle EF performance. Based on EF and ECOP performance criteria, Moscato et al. [] optimized the performance of an irreversible Otto cycle with HTL and IIL, and investigated the influences of the two losses on cycle performance.
The works mentioned above were based on the WF assumed as conventional WF. So in [,,,,,,], the power output and efficiency performance characteristics [,,,,,], as well as the EF performance characteristic [] of irreversible Otto cycles were studied when the quantum characteristic of WF was considered, and the influence of the quantum characteristic on cycle performance was investigated.
The Optimum Performance with VSH of WF
Rocha-Martinez et al. [,] investigated the influence of cyclic variability (VSH of WF) on the power output and efficiency performance characteristics of the Otto cycle. In [,], the authors only considered the SH of WF varied with the component and did not consider the SH varied with temperature. Furthermore, only the SH empirical equations were substituted into the final power output and efficiency performance characteristics equations, and the influence of VSH on the adiabatic process equation was not considered. Ge et al. [,,] adopted the model of SH varied with linear function of the temperature in proposed in [], considered the influences of VSH on cycle process, and investigated the power output and efficiency performance characteristics of an endoreversible Otto cycle [,] and an irreversible Otto cycle [,]. Using the VSH model established in [,,,], Zhao et al. [] studied the power output and efficiency performance characteristics of irreversible Otto cycles with HTL and IIL and the fixed cycle maximum temperature. The Otto cycle models established in [,,] and [] were different, in that the cycle maximum temperature in [,,] was unfixed and should be solved by combining the value of heat addition in the cycle and HTL, so HTL would influence the cycle power output and efficiency. While the cycle maximum temperature in [] was fixed, so HTL only influenced the cycle efficiency and did not influence the cycle power output. The different cycle models should adopt different efficiency definitions, so the efficiency definitions in [,,] and [] were all appropriate and correct. Lin and Hou [] studied the influences of HTL as a part of fuel energy, FL and VSH on the power output and efficiency performance characteristics of irreversible Otto cycles when SH of WF varied with temperature with a linear function. Najad et al. [] investigated the performance of irreversible Otto cycles when HTL and FL were considered, and examined the influences of HTL, FL and VSH on cycle performance when SH of WF varied with temperature with linear function. Ebrahim et al. [] investigated the influence of the equivalence ratio of ethanol to air on the power output and efficiency performance characteristics of an endoreversible Otto cycle with SH of WF varied with temperature with a linear function and found that the MP, the optimum compression ratios at the MP and ME points and the cycle working range would first increase and then decrease when the ethanol-air equivalence ratio increase. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [,] used VSH model established in [,,,,,], studied the optimum EF performance of an irreversible Otto cycle, and analyzed the influences of the three losses and VSH on cycle performance.
Abu-Nada et al. [,,,] established different VSH model in which the SH of WF varied with temperature with nonlinear functions when they studied the performances of ICE cycles. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [,] adopted the VSH model advanced in [,,,], investigated the optimum power and efficiency performance [,], as well as the optimum EF performance [] of an irreversible Otto cycle, and examined the influences of the three losses on cycle optimum performance.
Figure 5, Figure 6 and Figure 7 show the influences of HTL, FL and IIL on Otto cycle performance []. The influences of HTL, FL and IIL on the power output and efficiency performance characteristics are shown in Figure 5. Curve 1 is the power output and efficiency performance characteristics of a reversible Otto cycle, where the shape of curve 1 is a parabolic shape (the efficiency at the MP is not zero, while the power output at the ME is zero), while the shapes of else curves are loop-shaped (both the efficiency at the MP and the power output at the ME are not zero) with one or more irreversible loss. Figure 6 shows the influences of HTL, FL and IIL on the EF and power output performance characteristics. One can see that the power output (except the MP) at a given EF has two values, and heat engine should work at larger power output point. Figure 7 shows the influences of HTL, FL and IIL on EF and efficiency performance characteristics. Curve 1 is the EF and efficiency performance characteristic of a reversible Otto cycle and is a parabolic shape (the efficiency at the maximum ecological function (MEF) is not zero, while the EF at the ME is zero), while the shapes of else curves are loop-shaped (both the efficiency at the MEF and the EF at the ME are not zero) with one or more irreversible loss. The efficiency (except the ME) at a given EF has two values, and heat engine should work at larger efficiency point. From Figure 5, Figure 6 and Figure 7, one can see that the EF, the power output and the efficiency decrease with the increase of HTL, FL and IIL.
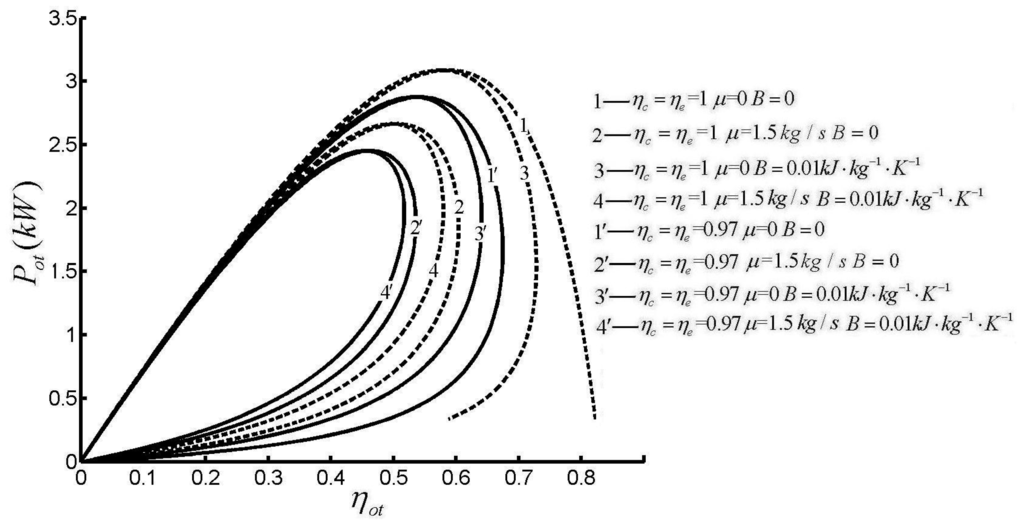
Figure 5.
Effects of ηc, ηe, B and μ on P versus η.
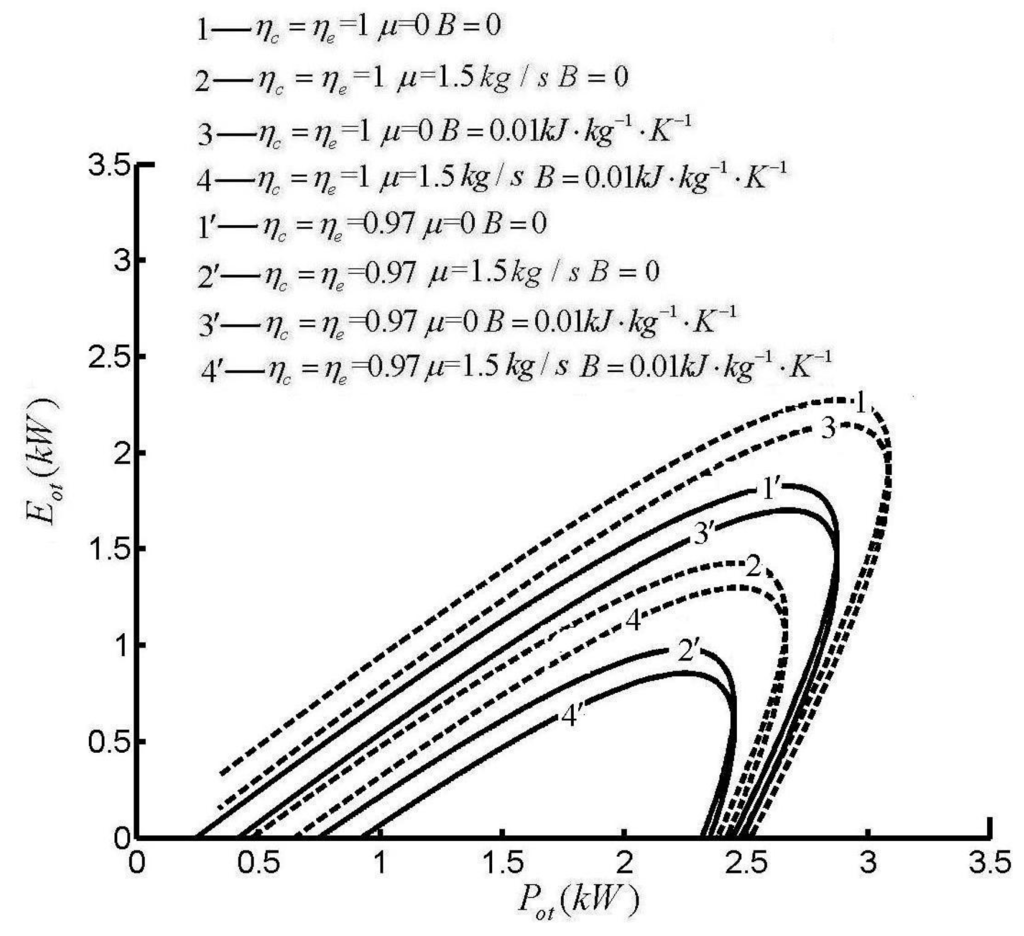
Figure 6.
Effects of ηc, ηe, B and μ on E versus P.
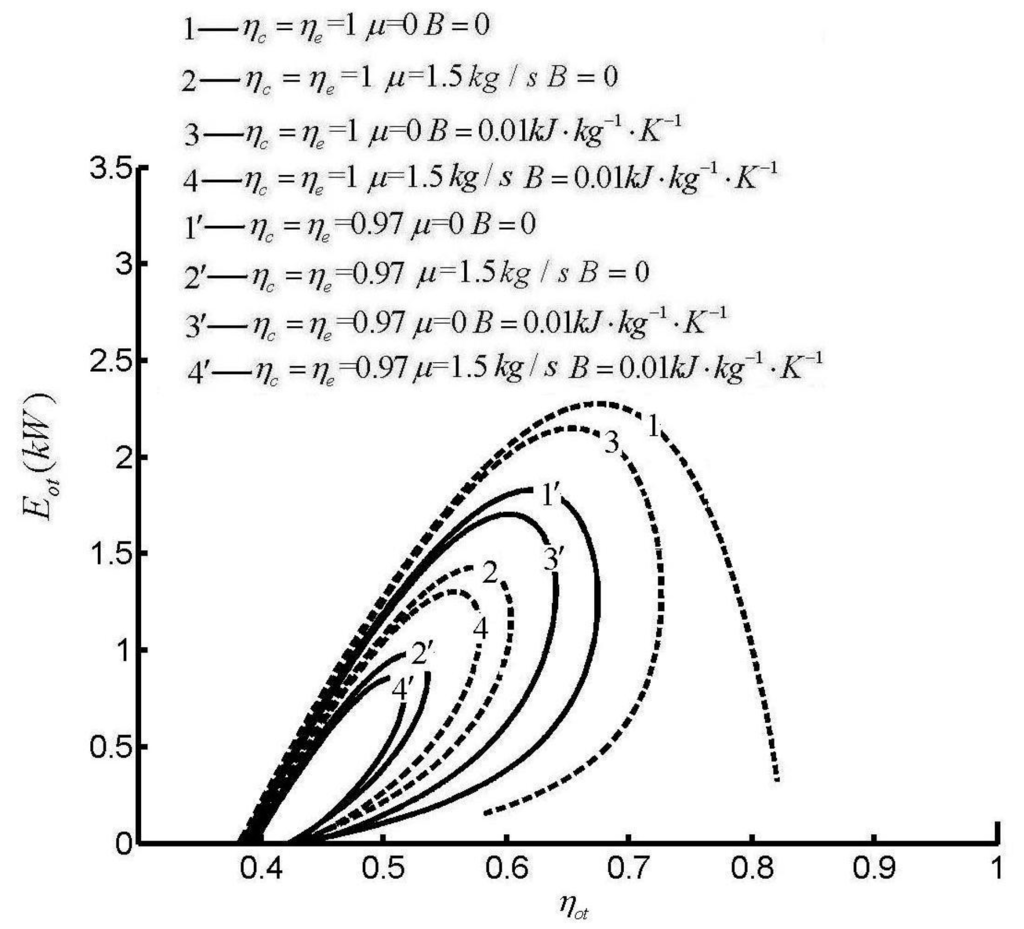
Figure 7.
Effects of ηc, ηe, B and μ on E versus η.
Figure 8 and Figure 9 show the influences of SH models on Otto cycle performance []. Figure 8 and Figure 9 show that SH models have no qualitative influence and only have quantitative influence on cycle performance. The extreme values of EF, efficiency and power output are the maximum when SH are linear function of the temperature. The extreme values of EF, efficiency and power output are the minimum when SH are constant. While the extreme values of EF, efficiency and power output lie between the maximum and minimum values when SH are nonlinear functions of the temperature. In Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, P is the power output, η is the efficiency, μ is the friction coefficient, B is a constant related to heat transfer, and E is the EF.
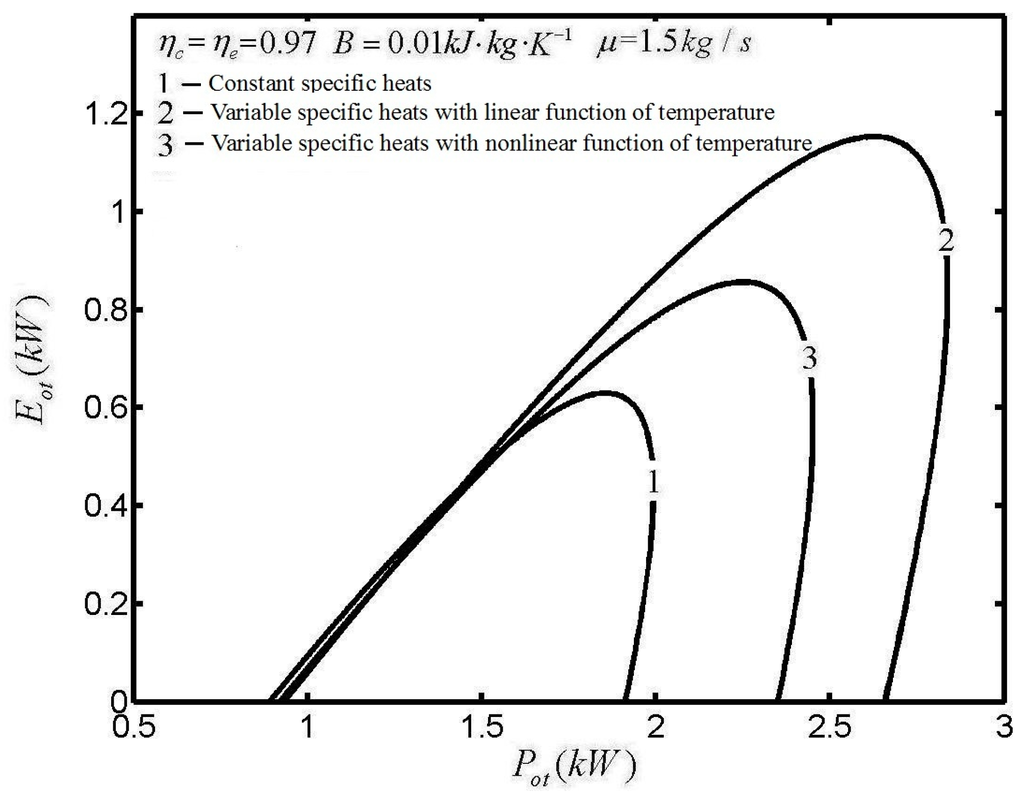
Figure 8.
Effects of specific heat models on E versus P.
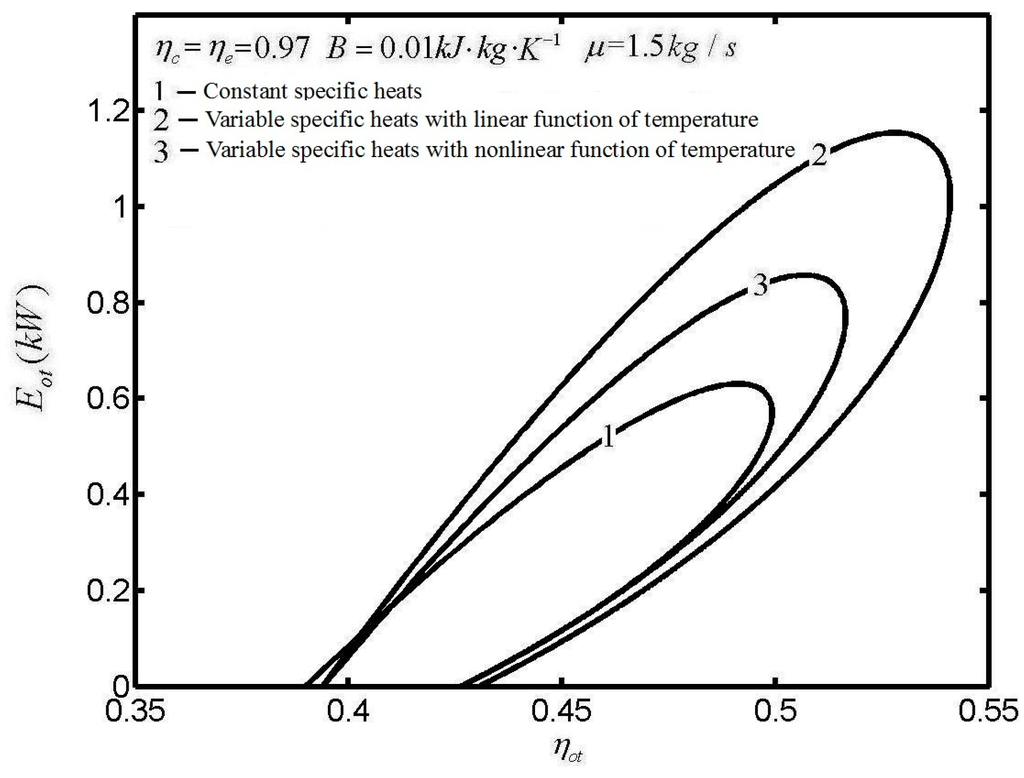
Figure 9.
Effects of specific heat models on E versus η.
The Optimum Performance with Variable Specific Heat Ratio (VSHR) of WF
Considering HTL, Ebrahimi [] investigated the power output and efficiency performance characteristics of an endoreversible Otto cycle with SHR of WF varied as a linear function of temperature. Using the VSHR of WF model advanced in [], Ebrahimi [,] studied the power output and efficiency performance characteristics of irreversible Otto cycles with HTL, FL and IIL considered. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [] modeled a universal cycle model when SHR of WF is linear function of temperature, and investigated the optimum power and efficiency performance, as well as the optimum EF performance of the cycle. The results obtained in [] included the Otto cycle performance, and the optimum power and efficiency performance included the results of [,].
3.1.3. The Progress in Optimum Performance Studies for AS Diesel Cycle
The Optimum Performance with CSH of WF
Rashidi and Hajipour [] obtained the work output and efficiency performance characteristics of reversible Diesel cycles, investigating the influence of cycle maximum temperature and CR on cycle performance. Atmaca and Gumus [] investigated and compared the performances under the MP, MEP and MPD conditions of reversible Diesel cycles and found that design parameters under MEP conditions were better that those under MP and MPD conditions. Considering HTL, Klein [] obtained the work output versus CR characteristics, investigated the influence of HTL on cycle performance, compared the optimum CR and efficiency at the MW of an endoreversible Diesel cycle with those of an endoreversible Otto cycle, and found that the CR at the MW of the endoreversible Diesel cycle was higher than that of the endoreversible Otto cycle, while the efficiencies at the MW of the two cycles were equal. Considering the influence of combustion, Blank and Wu [] obtained the relation of the optimum CR variation with the cycle maximum temperature of an endoreversible Diesel cycle when the work output was the maximum. Chen et al. [] optimized the work output and efficiency performance characteristics of the endoreversible Diesel cycle, and examined the influences of HTL and initial temperature on cycle performance. Parlak et al. [,] investigated the influence of HTL on the performance of the endoreversible Diesel cycle, and performed an exergy analysis for the exhaust of low heat rejection and standard heat engine cycles. Considering HTL as a part of fuel energy, Ozsoysal [] derived the effective ranges of HTL coefficients of endoreversible Diesel cycles, and found that the analysis for cycle performance would be closer to the practical results and also more accurate when HTL coefficients were chosen according to the ranges. Ai-Hinti et al. [] investigated the influences of the air-fuel mass ratio and fuel mass flow rate on the performance of endoreversible Diesel cycles, and found that power and efficiency would increase when the air-fuel mass ratio increased and fuel mass flow rate was given and power would increase and efficiency would remain unchanged when fuel mass flow rate increased and air-fuel mass ratio was given.
With consideration of FL, Chen et al. [], Chen and Sun [] established an irreversible Diesel cycle model, derived the power output and efficiency performance characteristics, and investigated the influence of FL on cycle performance. The difference between these two works was the different computation methods of the mean piston velocity. The mean piston velocity of [] was equal to the stroke length divided by stroke time, while the mean piston velocity in [] was equal to double the stroke length divided by the total time spent on heat addition and rejection processes with constant pressure and constant volume. Refs. [,] obtained the power output and efficiency performance characteristics of irreversible Diesel cycles when HTL and FL were considered and investigated the influences of HTL and FL on cycle performance.
Based on the MP and ME criteria, Parlak et al. [] used the irreversible compression and expansion efficiencies to define the IIL, optimized the performance of an irreversible Diesel cycle, and investigated the influence of IIL on cycle performance. Considering IIL and HTL and fixing the cycle maximum temperature, Zhao et al. [] investigated the power output and efficiency performance characteristics of an irreversible Diesel cycle and examined the influences of two losses on cycle performance. Zheng et al. [,,] investigated the influence of temperature ratio on the power output and efficiency performance characteristics of irreversible Diesel cycles with only IIL [,] and with IIL and HTL [], respectively, and obtained the bounds of some performance parameters and the working range of optimum CR. Ebrahimi et al. [] studied the power output and efficiency performance characteristics of irreversible Diesel cycles with consideration of IIL and FL, and investigated the influence of SHR on the power output and efficiency performance characteristics of the cycle. Fixing the cycle maximum temperature, Ozsoysal [] investigated the effect of air-fuel mass ratio on the power output and efficiency performance characteristics of an irreversible Diesel cycle.
Ge [] introduced the EF into optimum performance analysis for the Diesel cycle, used AS cycle model to replace open cycle model, established an irreversible Diesel cycle model with HTL, FL and IIL considered, computed the entropy generation rate generated by various losses, studied the optimum EF performance of the irreversible Diesel cycle, and investigated the influences of the three losses on cycle EF performance.
The Optimum Performance with VSH of WF
Rocha-Martinez et al. [] investigated the influence of cyclic variability (VSH of WF) on the power output and efficiency performance characteristics of Diesel cycles. In [], the authors only considered that the SH of WF varied with the component and did not consider the SH varied with temperature. Furthermore, only the SH empirical equations were substituted into the final power output and efficiency performance characteristics equations, and the influences of VSH on the adiabatic process equation were not considered. Using the model of SH variation as a linear function of the temperature from [], Refs. [,,,,] considered the influence of VSH on the cycle process, derived the power output and efficiency performance characteristics of an endoreversible Diesel cycle [,,] and an irreversible Diesel cycle [,,], and investigated the influences of VSH, HTL and FL on cycle performance. Considering HTL and using the VSH model established in [,,,,,], Jeshvaghani et al. [] studied the work output and efficiency performance characteristics of an endoreversible Diesel cycle and investigated the influences of fuel types (including Diesel, biodiesel and B20) on cycle performance. Fixing the cycle maximum temperature and using the VSH model established in [,,,,,,], Zhao and Chen [] studied the power output and efficiency performance characteristics of an irreversible Diesel cycle and examined the effects of VSH, HTL and IIL on cycle performance. Considering HTL, FL and IIL, He and Lin [] established an irreversible Diesel cycle model when the SH of WF varied with the temperature as a linear function, derived the power output and efficiency performance characteristics, and investigated the influences of the three losses and VSH on cycle performance.
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] used the VSH model established in [,,,,,,,,], studied the optimum EF performance of an irreversible Diesel cycle, and analyzed the influences of the three losses and VSH on cycle EF performance.
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [,] adopted the VSH model advanced in [,,,], investigated the optimum power and efficiency performance [,], as well as the optimum EF performance [] of an irreversible Diesel cycle, and examined the influences of the three losses on cycle performance. Furthermore, Aithal [,] studied the influence of exhaust gas recycle on the power output and efficiency performance characteristics of an irreversible Diesel cycle when the SH of WF were nonlinear functions of the temperature. Considering IIL and fixing the cycle maximum temperature, Açıkkalp and Yamık [] used the VSH model advanced in [,,,], optimized the maximum available work output of an irreversible Diesel cycle with CR and pressure ratio as optimization parameters, and derived the optimum CR and pressure ratio.
The Optimum Performance with VSHR of WF
Considering the SHR varied as a linear function of temperature, Ebrahimi [,] and Sakhrieh et al. [] investigated the power output and efficiency performance characteristics (work output and efficiency performance characteristics) of an endoreversible Diesel cycle [,] with HTL and an irreversible Diesel cycle [] with HTL and FL, respectively, and investigated the influences of VSHR and loss coefficients on cycle performance. Considering HTL and FL, Ebrahimi [] advanced the SHR varied with temperature with nonlinear function model, studied the power output and efficiency performance characteristics of an irreversible Diesel cycle, and investigated the influence of stroke length on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] established a universal cycle model when SHR of WF was linear function of temperature, and investigated the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance. The results obtained in [] included the Diesel cycle performance, and the power output and efficiency performance characteristics included the results of [,].
3.1.4. The Progress in Optimum Performance Studies for AS Atkinson Cycles
The Optimum Performance with CSH of WF
Chen et al. [] derived the efficiency at the MPD of a reversible Atkinson cycle and found that the efficiency at the MPD was higher than that at the MP, and the design parameters at the MPD were smaller than those at the MP. Rashidi and Hajipour [] obtained the work output and efficiency performance characteristics of a reversible Atkinson cycle, investigated the influence of cycle maximum temperature and CR on cycle performance, compared the performance of Otto, Diesel and Atkinon cycles, and found that the performance of the Atkinson cycle was better than that of the other two cycles. Hou et al. [] obtained the work output and efficiency performance characteristics of an endoreversible Atkinson cycle, investigated the effect of HTL on cycle performance, compared the performances of Atkinson and Otto cycles, and found that the performance of the Atkinson cycle was better than that of an Otto cycle under the same conditions Refs. [,] obtained the power output and efficiency performance characteristics of irreversible Atkinson cycles when HTL and FL were considered and investigated the influences of two losses on cycle performance. Wang et al. [] investigated and compared the performances at the MP and MPD conditions of an irreversible Atkinson cycle which was coupled to variable-temperature heat reservoirs. Considering IIL and HTL and fixing the cycle maximum temperature, Zhao and Chen [] studied the power output and efficiency performance characteristics of irreversible Atkinson cycles, and investigated the influences of the two losses on cycle performance. Ust [] compared the performances of an irreversible Atkinson cycle with IIL at the MP condition with that at the MPD condition, investigated the influences of temperature ratio and IIL on cycle performance, and found that the optimization with the MPD as the OPB was better than that with the MP as the OPB from the point of view of size and efficiency. Ebrahimi [] derived power output and efficiency performance characteristics of an irreversible Atkinson cycle, investigated the influence of air-fuel ratio, fuel mass flow rate and residual gas on cycle performance, and found that the performances would increase with increase in air-fuel ratio and residual gas when the CR was less than certain value, the performances would decrease with increase in air-fuel ratio and residual gas when the CR exceeded certain value, and the performance would increase with increase in fuel mass flow rate throughout the CR working range.
Lin [] computed the entropy generation rate generated by finite rate heat transfer between WF and heat reservoirs, and investigated the optimum EF performance of a closed Atkinson cycle. Considering HTL, FL and IIL, Ge [] used AS cycle model to replace open cycle model, established an irreversible Atkinson cycle model, computed the entropy generation rate generated by various losses, studied the cycle optimum EF performance, and analyzed the effects of the three losses on the cycle EF performance.
The Optimum Performance with VSH of WF
Using the model of SH varied with linear function of the temperature in [], Patodi and Maheshwari [] investigated and compared the performances under the MP, MEP and MPD conditions of a reversible Atkinson cycle and found that design parameters under MEP conditions were better that those of under MP and MPD conditions. Using the model of SH varied with linear function of the temperature in [], Ge et al. [,,] considered the influence of VSH on the cycle process, investigated the power output and efficiency performance characteristics of an endoreversible Atkinson cycle [,] and an irreversible Atkinson cycle [,], and examined the effects of VSH, HTL and FL on cycle performance. Considering HTL as a part of fuel energy and FL, Lin and Hou [] investigated the power output and efficiency performance characteristics of an irreversible Atkinson cycle when SH of WF were linear functions of the temperature, and obtained more accurate relation between heat released by combustion and HTL coefficient which was limited by the cycle maximum temperature. Al-Sarkhi et al. [] investigated the efficiency at the MPD of an Atkinson cycle when the SH of WF varied with temperature with linear function, compared the results obtained with those obtained when SH were constants in [], and found that VSH influenced the power density characteristics. Considering SH of WF varied with temperature in a linear way and fixing the cycle maximum temperature, Ye and Liu [] investigated the power output and efficiency performance characteristics of an irreversible Atkinson cycle with IIL and HTL considered, and analyzed the influences of VSH, the two losses and the cycle maximum temperature on cycle performance.
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] used VSH model established in [,,,,,,], studied the optimum EF performance of an irreversible Atkinson cycle, and analyzed the influences of three losses and VSH on the EF performance. Based on efficient power criteria, Patodi and Maheshwari [] studied the Atkinson cycle performance when SH of WF varied linearly with temperature and analyzed the effects of some design parameters (including maximum temperature ratio, maximum volume ratio and maximum pressure ratio) on cycle performance under MP, MPD and MEP conditions. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [,] adopted the VSH model advanced in [,,,], investigated the optimum power and efficiency performance [,], as well as the optimum EF performance [] of an irreversible Atkinson cycle, and examined the influences of the three losses on cycle performance.
The Optimum Performance with VSHR of WF
Considering SHR varied with temperature with linear function, Ebrahimi [] studied the work output and efficiency performance characteristics of an endoreversible Atkinson cycle and investigated the influences of VSHR and loss coefficient on cycle performance. Considering HTL, FL and IIL, Ebrahimi [,] advanced SHR varied with temperature with nonlinear relation model, studied the power output and efficiency performance characteristics of an irreversible Atkinson cycle, and investigated the influence of piston mean velocity, cylinder wall temperature, stroke length and volume efficiency on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] established a universal cycle model when SHR of WF was a linear function of temperature, and investigated the power output and efficiency performance characteristics, as well as the cycle optimum EF performance. The results obtained included the Atkinson cycle performance, and the power output and efficiency performance characteristics included the results of Ref. [].
3.1.5. The Progress in Optimum Performance Studies for AS Brayton Cycles
Many authors have studied the performance of open and closed, simple, regenerated, intercooled, intercooled and regenerated Brayton cycles with steady flow [,,,,,]. But the performance of reciprocating AS Brayton cycle has not been studied.
The Optimum Performance with CSH of WF
Refs. [,] obtained the power output and efficiency performance characteristics of an irreversible Brayton cycle when HTL and FL were considered and investigated the influences of the two losses on cycle performance. Considering HTL, FL and IIL, Ge [] introduced the EF into the optimum performance analysis of a Brayton cycle, used AS cycle model to replace open cycle model, established irreversible Brayton cycle model, computed the entropy generation rate generated by various losses, studied the cycle optimum EF performance, and analyzed the effects of the three losses on cycle EF performance.
The Optimum Performance with VSH of WF
Using the model of SH variation as a linear function of the temperature given in [], Ge et al. [,,] considered the influence of VSH on the cycle process, derived the power output and efficiency performance characteristics (work output and efficiency performance characteristics) of an endoreversible Brayton cycle (EBC) [,] and an irreversible Brayton cycle [,], and investigated the influences of VSH, HTL and FL on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] used the VSH model established in [,,], studied the optimum EF performance of an irreversible Brayton cycle, and analyzed the influences of the three losses and VSH on cycle EF performance.
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] adopted the VSH model advanced in [,,,], investigated the optimum power output and efficiency performance characteristics, as well as the optimum EF performance of an irreversible Brayton cycle, and examined the influences of the three losses on cycle performance.
The Optimum Performance with VSHR of WF
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] modeled a universal cycle model when SHR of WF was a linear function of temperature, and investigated the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance. The results obtained included the performance of a Brayton cycle.
3.1.6. The Progress in Optimum Performance Studies for AS Dual Cycles
The Optimum Performance with CSH of WF
Sahin et al. [] investigated the power density performance of a reversible Dual cycle, obtained the optimum performance and design parameters of the cycle under MPD conditions, and found that the heat engine design with the MPD as the OPB was better from the point of view of size and efficiency. Atmaca et al. [] investigated the efficient power characteristic of a reversible Dual cycle, examined the influences of design parameters (including volume ratio and extreme temperature ratio) on cycle performance under MP, MPD, MEP and ME conditions, and found that the design parameters under MEP condition were better than those under MP and MPD conditions. Blank and Wu [] obtained the relation of the optimum CR varied with the cycle maximum temperature of an endoreversible Dual cycle when the work output was the maximum, and found that the optimum CR would increase when the cycle maximum temperature increased and would be not influenced by fuel-air mass ratio. Refs. [,] obtained the work output and efficiency performance characteristics of an endoreversible Dual cycle, investigated the influences of HTL and initial temperature on cycle performance, and found that the cycle maximum temperature and pressure would decrease when HTL and initial temperature increase, and that the same was true for the work output and efficiency. Qiu et al. [] proved that the performance of a Dual cycle with constant pressure heat addition process when the temperature and pressure were constrained was more perfect, derived the computation equations of work output and efficiency limits, and gave the conditions when the work output was the maximum and the relation between the efficiency at the MW and Carnot efficiency. Qin [] used FTT to analyze the performance of an endoreversible Dual cycle cycle, compared the results with those obtained by using classic thermodynamics, and found that the cycle parameters which were closer to the practical ICE cycle could be obtained by correctly using FTT to analyze the Dual cycle. Ebrahim et al. [] obtained the work output and efficiency performance characteristics of an endoreversible Dual cycle, investigated the influences of cut-off ratio on cycle performance, and found that the performances would first decrease and then increase as cut-off ratio increased when CR was less than a certain value, while the performances would increase as cut-off ratio increased when the CR exceeded a certain value. Considering HTL, Rashidi et al. [] investigated the performance of an endoreversible Dual cycle by using the first and second laws and examined the influences of HTL and initial temperature on cycle performance.
Considering FL, Wang et al. [] established an irreversible Dual cycle model, derived the power output and efficiency performance characteristics, and investigated the influence of FL on cycle performance. Considering HTL and FL, Zheng et al. [] established an irreversible Dual cycle model, derived the power output and efficiency performance characteristics, and investigated the influences of the two losses on cycle performance. Parlak et al. [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle and gave the corresponding experiment results. Ebrahimi et al. [] derived the power output and efficiency performance characteristics of an irreversible Dual cycle, investigated the influence of SHR on cycle performance, and found that the performances would increase with increased SHR when the CR was less than a certain value, and the performances would decrease with increased SHR when the CR exceeded a certain value. Considering HTL as a part of fuel energy and FL, Nejad and Alaei [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle, and investigated the influences of both losses on cycle performance.
Using irreversible compression and expansion efficiencies, Parlak et al. [] defined the IIL, optimized the irreversible Dual cycle performance with the MP and ME criteria, investigated the influence of IIL on cycle performance, compared the irreversible Dual cycle performances with those of an irreversible Diesel cycle under the MP condition, and found that the MP and corresponding efficiency of an irreversible Dual cycle were higher than those of an irreversible Diesel cycle. Parlak and Sahin [] adopted the definition of IIL in [], studied the optimum performances under the MP and ME conditions, and gave the performance characteristics of Otto and Diesel cycles which were two special examples of a Dual cycle. Considering IIL and HTL and fixing the cycle maximum temperature, Zhao and Chen [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle, and investigated the influences of the two losses on cycle performance. Ozsoysal et al. [] used combustion efficiency to reflect the process of combustion reaction when air-fuel mass ratio was considered, investigated the influence of combustion efficiency on the power output and efficiency performance characteristics of an irreversible Dual cycle considering IIL. Ozsoysal et al. [] investigated the relation between the energy loss of the exhaust gas and the cycle maximum temperature and air excess coefficient of an irreversible Dual cycle with IIL considered. Considering HTL, FL, IIL and combustion efficiency, Ebrahimi [] investigated the power output and efficiency performance characteristics of an irreversible Dual cycle, investigated the influences of equivalent ratio and mean velocity of piston on cycle performance. Furthermore, there existed mechanical losses in practical ICE. With different performance criteria, i.e., MP and ME, Gonca et al. [] performed the performance optimization of an irreversible Dual–Miller cycle with the sole loss of IIL defined in [], and investigated the influences of temperature ratio and pressure ratio on cycle performance. Considering HTL and IIL, Ust et al. [] optimized the performance of an irreversible Dual cycle based on MP, ME and MEP performance criteria and investigated the influences of CR, pressure ratio and the two losses on cycle performance. Based on ECOP, Gonca and Sahin [] optimized the performance of an irreversible Dual–Atkinson cycle with HTL and IIL and investigated the influences of the two losses, CR, cut-off ratio and pressure ratio on cycle performance. Zi et al. [] used an empirical equation of mean mechanical loss pressure to compute the mechanical loss which included the losses related to construction of combustion chamber and rotating part loss of crankshaft connecting rod, and investigated the influence of mechanical loss on the power output and efficiency performance characteristics of an irreversible Dual cycle.
Ust et al. [] computed the entropy generation rate generated by finite rate heat transfer between WF and heat reservoirs, and investigated the optimum EF performance of a closed Dual cycle. Considering HTL, FL and IIL, Ge [] used AS cycle model to replace open cycle model, established an irreversible Dual cycle model, computed the entropy generation rate generated by various losses, studied the cycle optimum EF performance and analyzed the influences of the three losses on cycle EF performance.
The Optimum Performance with VSH of WF
Nejad [] considered the variation of SH of WF due to residual gases, imperfect combustion and other reasons and investigated the influence of the fluctuation (VSH of WF) on the power output and efficiency performance characteristics of a Dual cycle. Ghatak and Chakraborty [] first advanced a VSH model in which SH varied with temperature as a linear function, considered the influence of VSH on the cycle process, investigated the work output and efficiency performance characteristics of an endoreversible Dual cycle with the cycle maximum temperature fixed, and investigated the influence of HTL on cycle performance. Using the model of SH variation as a linear function of the temperature in [], Chen et al. [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle with HTL and FL considered, and investigated the influences of VSH and the two losses on cycle performance. Considering HTL and FL, Wang et al. [,] studied the power density characteristics of an irreversible Dual cycle when SH of WF varied as a linear function of the temperature and investigated the influences of VSH on cycle performance. Considering HTL and IIL, Ye et al. [] investigated the power output and efficiency performance characteristics of an irreversible Dual cycle when SH of WF varied with temperature as a linear function, gave the optimum operating regions of parameters, and investigated the influences of the two losses on cycle performance. Considering HTL and FL, Lin [] used the model of linear SH variation as a function of the temperature in [,], derived the power output and efficiency performance characteristics of an irreversible Dual cycle, and investigated the influences of the two losses and VSH on cycle performance. Using the model of SH variation as a linear function of temperature in [,,,,,], Gahruei et al. [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle and an irreversible Dual–Atkinson cycle with HTL and FL considered, investigated the influences of VSH, and the two losses on cycle performances, compared the performances of the two cycles, and found that the performance of the Dual–Atkinson cycle is higher than that of an irreversible Dual cycle.
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] used the VSH model established in [,,,,,,,] to study the optimum EF performance of an irreversible Dual cycle, and analyzed the influences of the three losses and VSH on cycle EF performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge et al. [,] adopted the VSH model advanced in [,,,], and investigated the optimum power and efficiency performance [,], as well as the optimum EF performance [] of an irreversible Dual cycle, and examined the influences of the three losses on cycle optimum performance. Ebrahimi et al. [] adopted the VSH model in [] and investigated the influence of mean piston motion velocity on the power output and efficiency performance characteristics of an irreversible Dual cycle. Considering HTL, FL and IIL, Ebrahim and Sherafati [] studied the power output and efficiency performance characteristics of an irreversible Dual cycle when SH of WF varied with temperature as a nonlinear function, analyzed the influences of stroke length and volumetric efficiency on cycle performance, and found that the influences of the two factors on cycle performance were obvious. Considering HTL, FL and IIL, Asghari et al. [] obtained power output and efficiency performance characteristics of an irreversible Dual cycle when SH of WF varied with temperature in a nonlinear way and investigated the effects of the three losses, pressure ratio and cut-off ratio on cycle performance.
The Optimum Performance with VSHR of WF
Ebrahimi [,] modeled the linear relation of SHR with the temperature, studied the power output and efficiency performance characteristics (work output and efficiency performance characteristics) of an endoreversible Dual cycle [] with HTL and of an irreversible Dual cycle [] with HTL and FL, respectively, and investigated the influences of VSHR and loss coefficients on cycle performance. Ebrahimi [,] derived the power output and efficiency performance characteristics (work output and efficiency performance characteristics) of an endoreversible Dual cycle [] with HTL and of irreversible Dual cycle [] with HTL and IIL, respectively, when the SHR of WF varied as a nonlinear function of temperature, and analyzed the influence of pressure ratio on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] modeled a universal cycle model when SHR of WF was a linear function of temperature, and investigated the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance. The results obtained included the Dual cycle performance, and the optimum power and efficiency performance included the results of [,].
3.1.7. The Progress in Optimum Performance Studies for AS Miller Cycles
The Optimum Performance with CSH of WF
Al-Sarkhi et al. [] investigated the efficiency at the MPD of a reversible Miller cycle. Considering HTL, Mousapour and Rashidi [] obtained the work output and efficiency performance characteristics of EMC and investigated the influences of HTL, CR and initial temperature on the cycle. Considering HTL and FL, Ge et al. [] established an irreversible Miller cycle model, derived the power output and efficiency performance characteristics, and examined the influences of the two losses on cycle performance. Considering IIL and HTL and fixing the cycle maximum temperature, Zhao and Chen [] derived the power output and efficiency performance characteristics of an irreversible Miller cycle, and investigated the influences of the two losses on cycle performance. Based on MP, ME and MPD performance criteria, Gonca et al. [] optimized the performance of an irreversible Miller cycle with IIL and investigated the influences of design parameters (including CR, pressure ratio, stoke ratio and temperature ratio) on cycle performance. Considering HTL, FL and IIL, Ge [] used an AS cycle model to replace an open cycle model, established an irreversible Miller cycle model, computed the entropy generation rate generated by various losses, studied the cycle optimum EF performance, and investigated the influences of the three losses on cycle EF performance.
The Optimum Performance with VSH of WF
Considering that the SH varied with components, Ebrahimi [] obtained the power output and efficiency performance characteristics of an irreversible Miller cycle with HTL and FL and investigated the influence of residual gas and equivalence ratio on cycle performance. Using the model of SH varied as a linear function of the temperature in [], the authors of [,,,,] studied the power output and efficiency performance characteristics (work output and efficiency performance characteristics) of EMC [,,] and an irreversible Miller cycle [,,], and investigated the influences of VSH and the two losses on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Yang and He et al. [] optimized the power output and efficiency performance characteristics of an irreversible Miller cycle when SH of WF varied with temperature as a linear function. Lin and Hou [] considered HTL as a part of fuel energy, investigated the power output and efficiency performance characteristics of an irreversible Miller cycle with HTL and FL when SH of WF varied linearly as a function of temperature. Considering HTL and IIL, Liu [] and Liu and Chen [] investigated the power output and efficiency performance characteristics of an irreversible Miller cycle when SH of WF varied as a linear function with temperature. Considering HTL and IIL and fixing the cycle maximum temperature, Ye [] studied the work output and efficiency performance characteristics of an irreversible Miller cycle when SH of WF varied with temperature as a linear function and investigated the influences of two losses and VSH on cycle performance. Considering HTL, FL and IIL, Lin et al. [], Mousapour and Rezapour [] and Mousapour et al. [] used the model of SH varying as a linear function of the temperature in [,,,,,,,,,], obtained the power output and efficiency performance characteristics of an irreversible Miller cycle, and investigated the influences of their design parameters on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] used the VSH model established in [,,,,,,,,,,,,,], studied the optimum EF performance of an irreversible Miller cycle, and analyzed the influences of the three losses and VSH on cycle EF performance.
Considering HTL and FL, Al-Sarkhi [] established an irreversible Miller cycle model with different VSH models and obtained the power output and efficiency performance characteristics. Considering HTL, FL and IIL and fixing the maximum cycle temperature, Ge [] and Chen et al. [] adopted a VSH model advanced in [,,,], investigated the optimum power and efficiency performance [,], as well as the optimum EF performance [] of an irreversible Miller cycle, and examined the influences of the three losses on cycle optimum performance. Considering FL and HTL, Ebrahimi [] investigated the optimum power and efficiency performance of an irreversible Miller cycle when SH of WF varied with temperature in a non-linear fashion, examined the influence of the ratio of expansion to compression on cycle performance, and found that the power output would first increase and then decrease when expansion-compression ratio increased. Considering HTL and FL, Ebrahimi and Hoseinpour [] obtained the power output and efficiency performance characteristics of an irreversible Miller cycle when SH of WF varied non-linearly with temperature, and investigated the influences of combustion chamber volume and piston displacement volume on cycle performance.
The Optimum Performance with VSHR of WF
Considering that the SHR varied as a linear function with temperature, Ebrahimi [] investigated the power output and efficiency performance characteristics of an irreversible Miller cycle with HTL and FL, and examined the influences of VSHR and loss coefficients on cycle performance. Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] modeled a universal cycle model when SHR of WF was a linear function of temperature, and investigated the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance. The results obtained included Miller cycle performance, and the optimum power and efficiency performance included the results of [].
3.1.8. The Progress in Optimum Performance Studies for AS Porous Medium (PM) Cycles
The Optimum Performance with CSH of WF
Liu et al. [] analyzed the work output and efficiency performance characteristics of an endoreversible PM cycle. Considering HTL and FL, Ge et al. [] investigated the power output and efficiency performance characteristics of an irreversible porous medium cycle, and investigated the influences of the losses and volume ratio on cycle performance.
Based on [], Ge [] used as AS cycle model to replace the open cycle model, established an irreversible porous medium cycle model when HTL, FL and IIL were considered, and studied the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance.
The Optimum Performance with VSH of WF
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] adopted the SH of a WF model varied with temperature with linear [,] and non-linear [,,,] functions, investigated the optimum power and efficiency performance, as well as the optimum EF performance of an irreversible porous medium cycle, and examined the influences of VSH and the three losses on cycle optimum performance.
The Optimum Performance with VSHR of WF
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] established a universal cycle model when SHR of WF was a linear function of temperature, and studied the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance. The results obtained included the performance of PM cycle.
3.1.9. The Progress in Optimum Performance Studies for AS Universal Cycles
The Optimum Performance with CSH of WF
Considering HTL and FL, Qin et al. [] proposed a universal irreversible reciprocating heat engine cycle model which was shown in Figure 3 and consisted of a heat addition process with constant thermal-capacity, a heat rejection process with constant thermal-capacity and two adiabatic processes, derived the power output and efficiency performance characteristics of the universal cycle. Based on [], Ge et al. [] proposed a more generalized irreversible reciprocating heat engine cycle model which was shown in Figure 4 and consisted of two heat addition processes with constant thermal-capacity, two heat rejection processes with constant thermal-capacity and two adiabatic processes when HTL and FL were considered, derived the power output and efficiency performance characteristics of the generalized cycle, and compared the performance differences of various special cycles. Based on [], Ge [] introduced the EF into the optimum performance analysis of a generalized cycle, used an AS cycle model to replace the open cycle model, established an irreversible generalized cycle model when HTL, FL and IIL were considered, studied the cycle optimum EF performance, and compared the EF performance of various special cycles.
The Optimum Performance with VSH of WF
Based on [], Chen et al. [] modeled a generalized AS ICE cycle with FL and HTL when SH of WF varied with temperature as a linear function, derived the power output and efficiency performance characteristics, and compared the performances of various special cycles under CSH and VSH conditions. Based on [], Ge [] established a generalized cycle model when HTL, FL and IIL were considered and SH of WF varied as a linear function of temperature, studied the cycle optimum EF performance, and compared the EF performance of various special cycles.
Considering HTL, FL and IIL, Ge [] adopted the VSH model advanced in [,,,], investigated the optimum power and efficiency performance, as well as the optimum EF performance of the generalized cycle, and compared the performances of special cycles. The power output, efficiency and EF of the generalized cycle when SH of WF varies with temperature with a non-linear function are as follows []:
where Qin is the heat rate of addition; Qout is the heat rate of rejection; Qleak is the heat leakage; Pμ is the lost power due to friction; ein1, ein2, eout1 and eout2 are constants which equal to 1.3303 or 1.0433; M is the mass flow rate; L is the stoke length; n is the cycles running per second.
Figure 10 and Figure 11 show performance characteristics of special cycles []. From Figure 10 and Figure 11, on can see that the order of the MEF performance is Ebr > Eat > Edi > Epm > Edu > Emi > Eot, the order of the MP is Pbr > Pdi > Pdu > Pat > Ppm > Pmi > Pot and the order of the ME is ηbr > ηpm > ηat > ηdi > ηmi > ηdu > ηot.
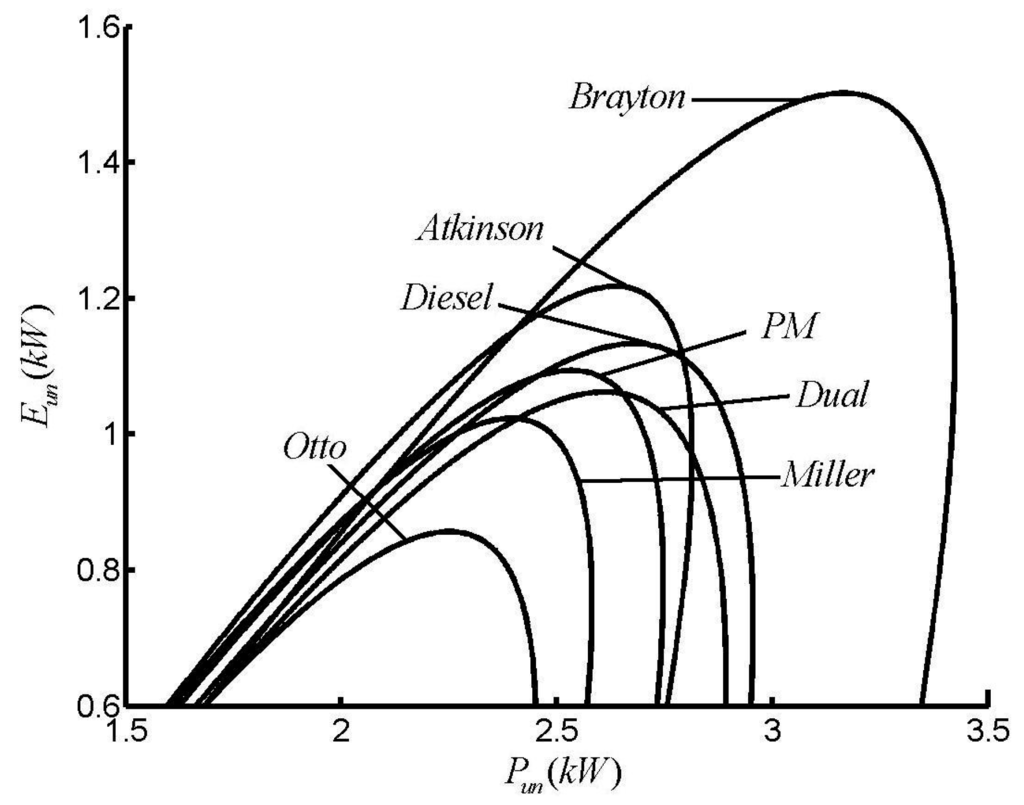
Figure 10.
Comparison of E versus P of different cycles.
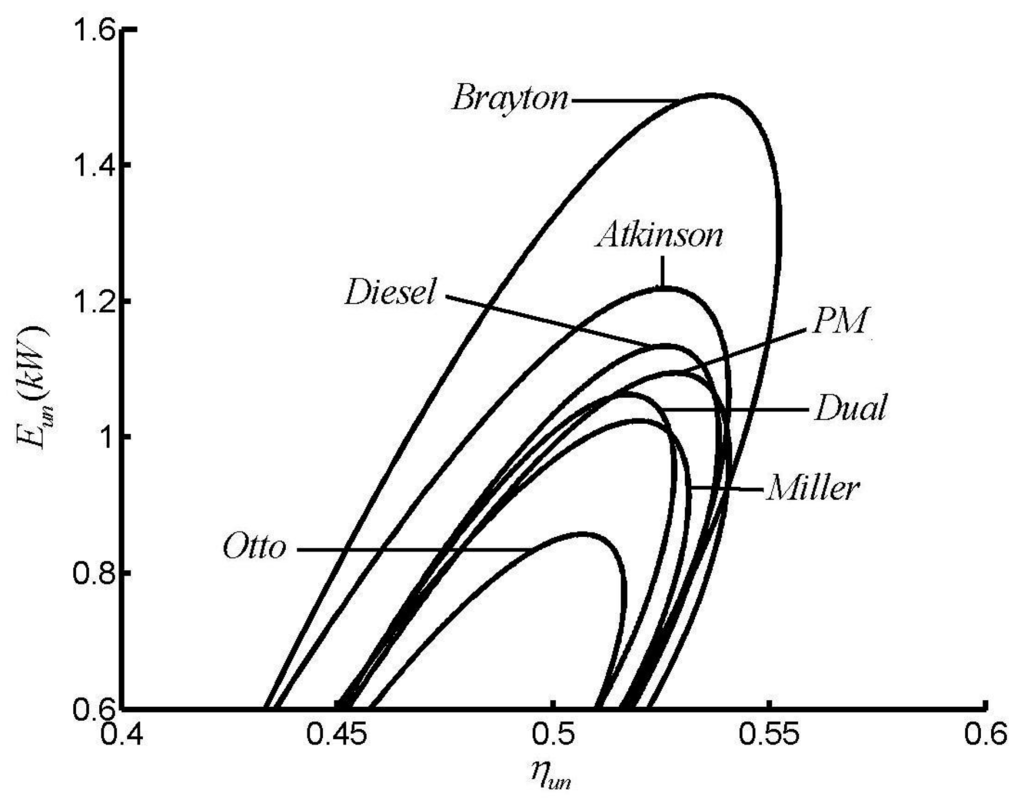
Figure 11.
Comparison of E versus η of different cycles.
The Optimum Performance with VSHR of WF
Considering HTL, FL and IIL and fixing the cycle maximum temperature, Ge [] established a universal cycle model when SHR of WF was a linear function of temperature, and investigated the cycle optimum power and efficiency performance, as well as the cycle optimum EF performance.
3.2. The Progress in Studies of the Optimum Piston Motion Configuration for ICE Cycles
The study of the optimum configuration problem aims to solve the following question: What is the optimum time pathway to obtain the maximum or minimum values of a given performance objective for a system which satisfies some constraint conditions and boundary conditions? Determining control variables and sampling limits of a system, selecting OPB, finding constraint conditions and establishing control equation are all the necessary conditions for solving the optimum configuration problem. Compared with the optimum performance problem, the optimum configuration problem is more complex, and the solution method is more difficult. Under most conditions, this problem has no analytical solution and one can only obtain numerical solutions by numerical calculation. From the above analysis, one can conclude that answering the optimum configuration problem requires a larger calculation workload compared with the optimum performance problem. There are three methods to solve the optimum configuration problem: Euler–Lagrange equation, optimal control theory (OCT) and Hamilton–Jacobi–Bellman (HJB) equation. Euler–Lagrange equation and OCT are often two tools used in optimum configuration problem studies of ICE cycles. The studies on optimum configuration of ICE cycle focus on the influences of heat transfer law (HTA) and OPB on the optimum configuration.
3.2.1. The Optimum Path with Newton’s Heat Transfer Law (HTA) (q ≈ Δ(T))
Considering piston FL and HTL, Mozurkewich and Berry [,] investigated the optimal piston motion (OPM) of a four stroke Otto cycle engine with the MW per cycle as the OPB. The efficiency of the engine would be improved by about 10% after optimizing the piston motion path. Considering fuel finite combustion rate, piston FL and HTL, Hoffmann and Berry [] investigated the OPM of a four stroke Diesel cycle engine with the MW as the OPB. Using a Monte Carlo simulation method, Blaudeck and Hoffman [] investigated the optimum configuration of a four stroke Diesel cycle. Considering the main losses (including chemical reaction loss and heat leakage) in ICE, Teh et al. [,,] investigated the ICE OPM with the MW [] and ME [,] as the objectives. Without considering the entropy generation which was generated by FL, HTL and pressure drop loss in practical ICE, Teh et al. [,] took combustion as the sole source of entropy generation and studied the OPM of an adiabatic ICE for minimum generation (MEG) [] as well as the OPM for MEG when CR was constrained [].
Band et al. [,] investigated optimum configuration of irreversible expansion process for MW obtained from an ideal gas inside a cylinder with a movable piston, and discussed the optimum configuration with eight different constraints. Using the results obtained in [,], the optimum configuration of the expansion process for MP [] and for MW with fixed power output [], respectively, were further studied. Refs. [,] further optimized the configurations of ICE [] and external combustion engine (ECE) [], respectively, by applying the results obtained in [,].
Considering the entropy generation which was excluded in [,], Ge et al. [,] used the heat engine models established in [,], derived the OPM trajectories of an Otto cycle for MEG [,] which was generated by FL, HTL and pressure drop loss, as well as for MEF [], respectively, investigated the influences of OPBs on the OPM trajectories, and compared the results obtained with those obtained for MW [,]. Considering piston FL and HTL, Ge et al. [,] derived the OPM trajectories of a Diesel cycle engine for MEG [,] and MEF [] per cycle with the finite combustion rate model advanced in [].
3.2.2. The Influence of HTA on the Optimum Cycle Path
HTA does not always obey Newton’s HTA and also obeys other laws. HTA affects the optimum configuration of heat engine cycles remarkably. Considering the influences of convective-radiative HTA (q ≈ Δ(T) + Δ(T4)), Burzler and Hoffman [,] derived the OPM in compression and power strokes of a four stroke Diesel engine with MP as the OPB when the WF was non-ideal. Fixing total cycle time and fuel consumed per cycle, Xia et al. [] investigated the OPM trajectory of an Otto cycle engine for MW when HTA between WF and the environment obeys a linear phenomenological HTA (q ≈ Δ(T−1)), and found that work output and efficiency could improve by more than 9% after optimizing the piston motion. Xia et al. [] and Chen et al. [] applied the finite combustion rate model in [], derived the OPM trajectories of irreversible Diesel cycle engine for MW when HTA between WF and the environment obeys a linear phenomenological HTA [] and generalized radiative HTA [], respectively, and examined the influence of HTA on the OPM trajectories.
Chen et al. [] studied the optimum configuration of expansion processes with linear phenomenological HTA. Using the results obtained in [], the configuration of ECE [] and ICE [] with linear phenomenological HTA was optimized. Using Taylor series expansion means, Refs. [,,] investigated the optimum configuration of expansion process with generalized radiative HTA (q ∝ Δ(Tn)) [], Dulong–Petit HTA (q ∝ Δ(T)5/4) [] and convective-radiative HTA [], obtained the first-order approximate analytical solutions for the Euler–Lagrange arcs. Using elimination means, Ma et al. [,] investigated the optimum configuration of the expansion process with generalized radiative HTA. Using the results obtained in [,], Ma et al. [,] optimized the configuration of ECE with radiative HTA (q ≈ Δ(T4)) [,], generalized radiative HTA [] and convective-radiative HTA [], respectively. Considering the influences of piston motion on heat conductance, [,] advanced a model which was closer to realitywith the generalized radiative HTA and time-dependent heat conductance, and investigated the optimum configuration of expansion process for MW.
Using the heat engine models established in [,,,], Ge [] obtained the OPM trajectories of an Otto cycle for MEG which was generated by FL, HTL and pressure drop loss, as well as for MEF, respectively, when the HTA obeys generalized radiative HTA, and the results obtained included the OPM trajectories for MEG [,] and MEF with linear phenomenological HTA [] and radiative HTA []. The OPM trajectories on power strokes of an irreversible Otto cycle for MEG and MEF when HTA obeys generalized radiative HTA are determined by following differential equations []:
where N is number of moles of WF; C is specific heat; X is the displacement; K is the heat transfer coefficient; b is the cylinder bore; Tw is the environment temperature; sign is the sign function; v is the speed; and λ is the Lagrange multiplier.
According to [,,,,,], the conventional piston motion of irreversible Otto cycle is determined by:
where θ is the crankshaft rotation angle; τ is the cycle period; l is the connecting rod length; r is the crank length. The conventional piston linkage is shown in Figure 12. When r/l = 0, the piston motion is a pure sinusoidal shape; when r/l ≠ 0, the piston motion is a modified sinusoid. The OPM trajectory for MEF of the whole cycle when HTA obeys Newton’s HTA is shown in Figure 13. There are in fact several ways of achieving those pathways of which we point out just two: one mechanical solution is using a contoured plate to guide the piston on the desired path, and the other completely different way to transform the optimized paths is the use of an electrical coupling [].Compared with the conventional piston motion, one can see that the piston motion after optimization changes greatly. OPM trajectories on power strokes of irreversible Otto cycle heat engines for different OPBs with different HTAs are shown in Figure 14 []. The results obtained in Figure 14 included the OPM trajectories for MW with Newton’s and phenomenological HTAs, and the OPM for MEG [,] and MEF with Newton’s HTA [], linear phenomenological HTA [] and radiative HTA [].
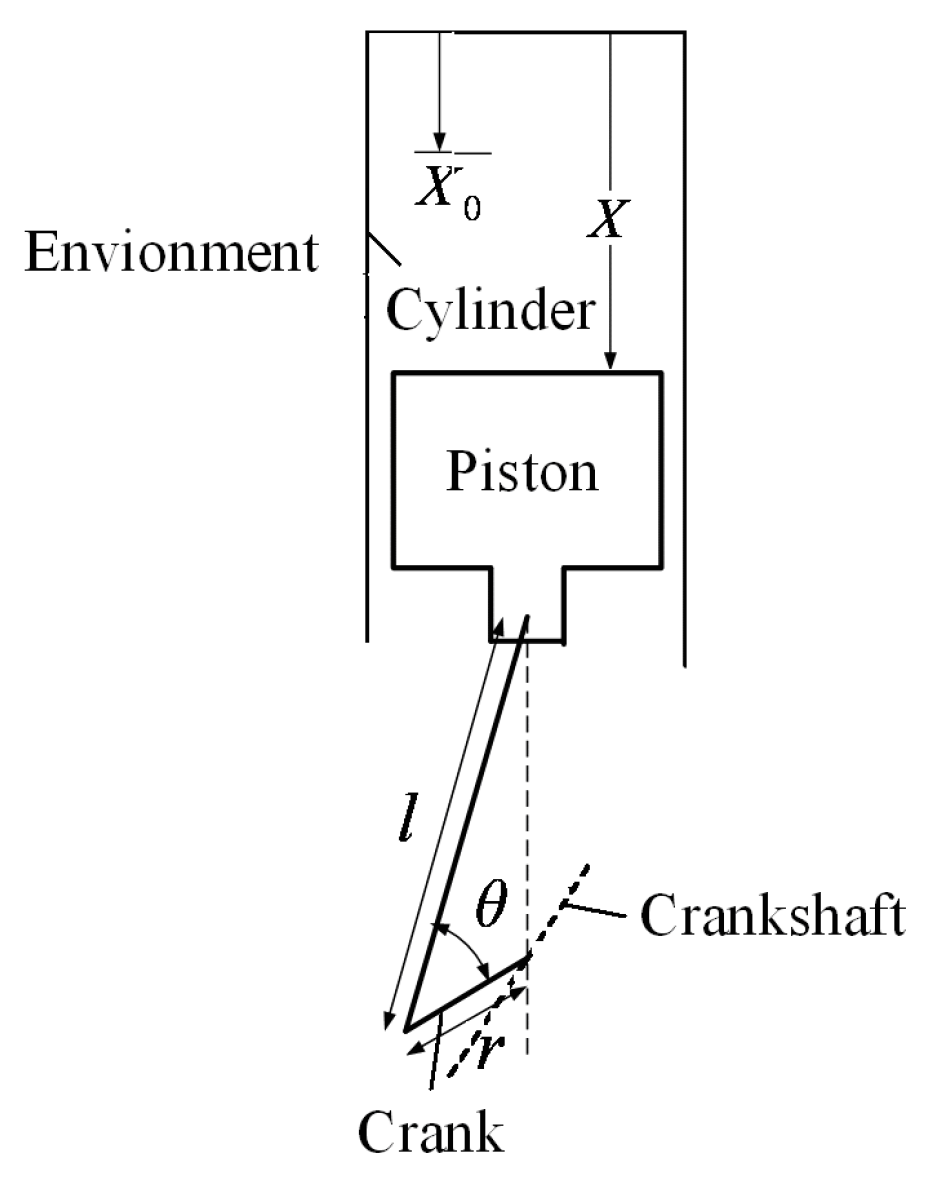
Figure 12.
Conventional piston linkage.
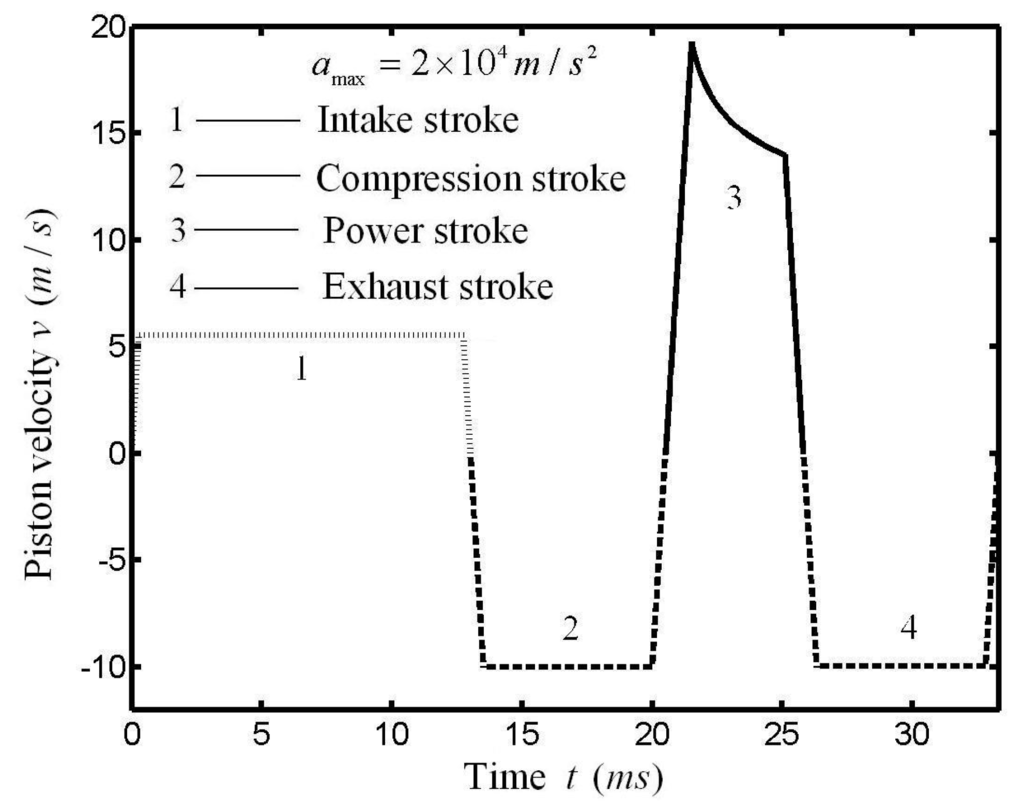
Figure 13.
OPM trajectory for MEF of the whole cycle when HTA obeys Newton’s HTA.
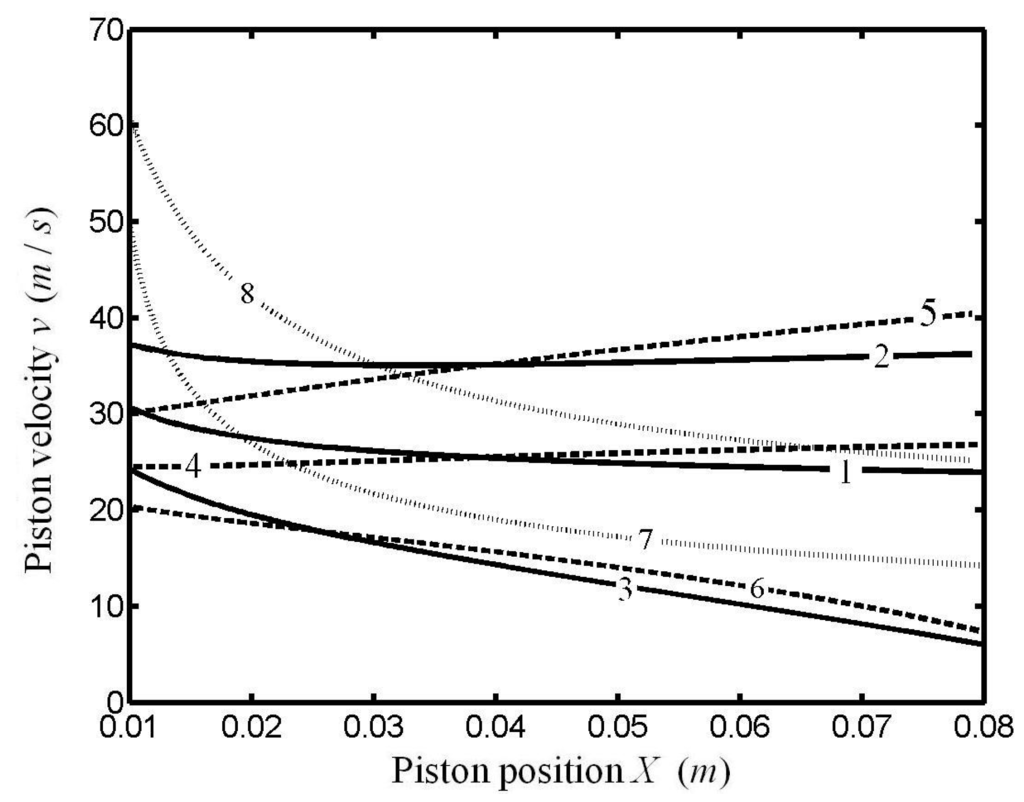
Figure 14.
OPM trajectories on the power stroke with different HTAs and OPBs. 1.MEF, Newton’s heat transfer law; 2. MEG, Newton’s heat transfer law; 3. MW, Newton’s heat transfer law; 4. MEF, linear phenomenological heat transfer law; 5. MEG, linear phenomenological heat transfer law; 6. MW, linear phenomenological heat transfer law; 7. MEF, radiative heat transfer law; 8. MEG, radiative heat transfer law.
Considering the finite combustion rate model in [], Ge [] studied the OPM trajectories of an irreversible Diesel cycle engine for MEG and MEF when HTA obeys the generalized radiative HTA, and examined the influences of HTA and OPB on the OPM trajectories. The results obtained included the OPM trajectories for MEG [] and MEF with linear phenomenological [] HTA and radiative HTA. The OPM trajectories on power strokes of an irreversible Diesel cycle for MEG and MEF when HTA obeys a generalized radiative HTA are determined by following differential equations:
Optimum piston trajectories on power stroke of irreversible Diesel cycle heat engines for different OPBs with different HTAs are shown in Figure 15, Figure 16 and Figure 17 []. The results obtained in Figure 15, Figure 16 and Figure 17 include the OPM trajectories for MW with Newton’s HTA, and the OPM trajectories for MEG [,] and MEF with Newton’s HTA [], linear phenomenological HTA [] and radiative HTA.
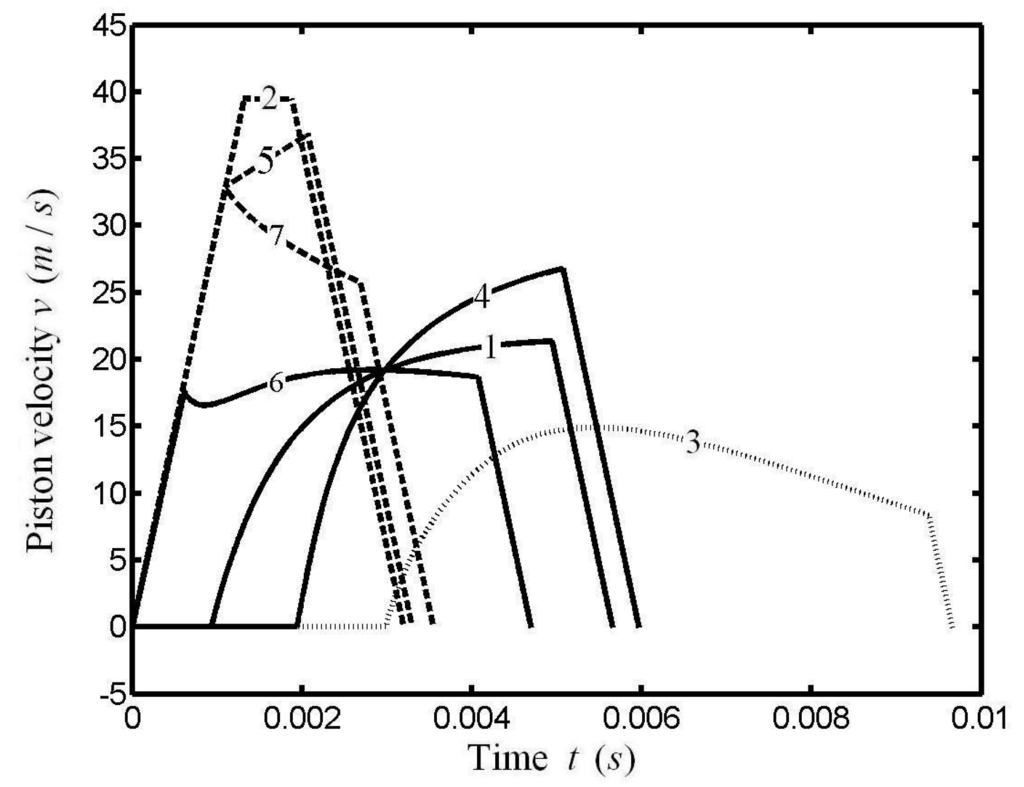
Figure 15.
Comparison of OPM trajectories with different HTAs and OPBs (velocity). 1. MEF, Newton’s heat transfer law; 2. MEG, Newton’s heat transfer law; 3. MW, Newton’s heat transfer law; 4. MEF, linear phenomenological heat transfer law; 5. MEG, linear phenomenological heat transfer law; 6. MW, linear phenomenological heat transfer law; 7. MEF, radiative heat transfer law; 8. MEG, radiative heat transfer law.
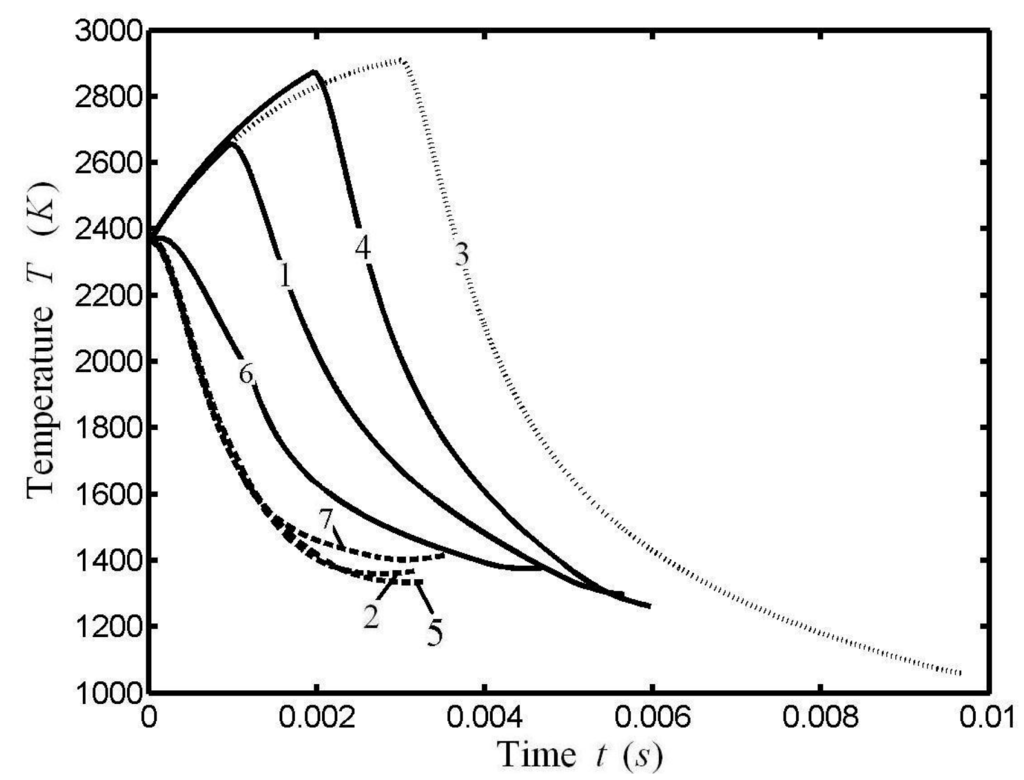
Figure 16.
Comparison of OPM trajectories with different HTAs and OPBs (temperature). 1. MEF, Newton’s heat transfer law; 2. MEG, Newton’s heat transfer law; 3. MW, Newton’s heat transfer law; 4. MEF, linear phenomenological heat transfer law; 5. MEG, linear phenomenological heat transfer law; 6. MW, linear phenomenological heat transfer law; 7. MEF, radiative heat transfer law; 8. MEG, radiative heat transfer law.
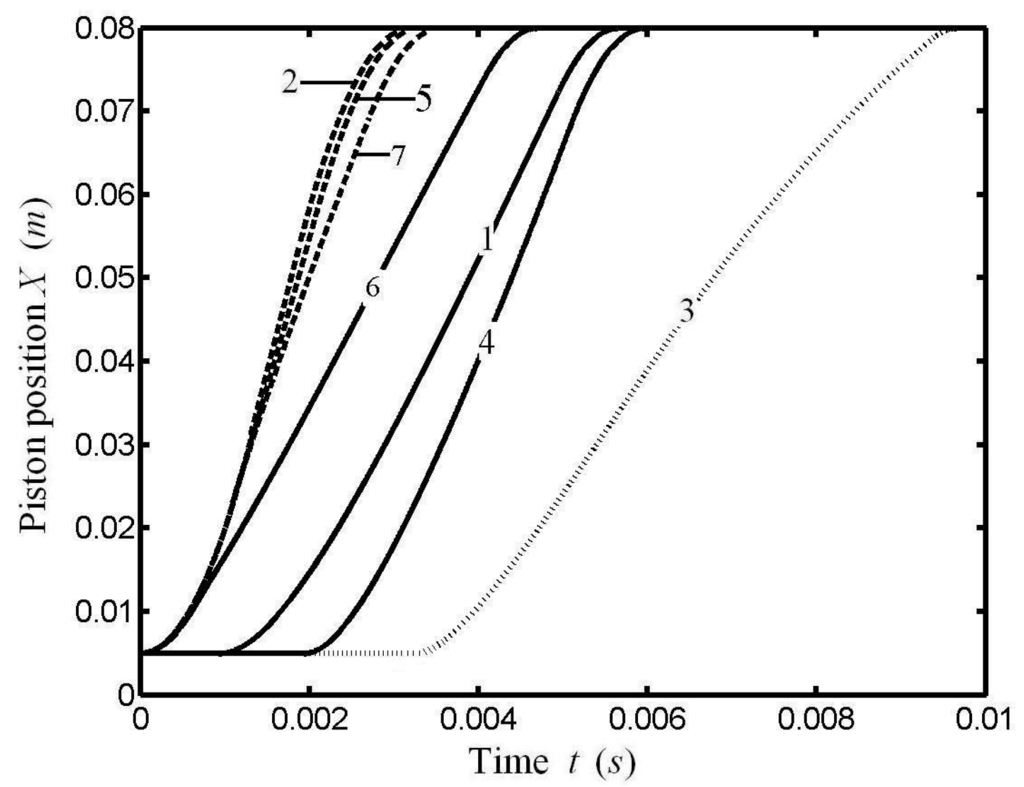
Figure 17.
Comparison of OPM trajectories with different HTAs and OPBs (displacement). 1. MEF, Newton’s heat transfer law; 2. MEG, Newton’s heat transfer law; 3. MW, Newton’s heat transfer law; 4. MEF, linear phenomenological heat transfer law; 5. MEG, linear phenomenological heat transfer law; 6. MW, linear phenomenological heat transfer law; 7. MEF, radiative heat transfer law; 8. MEG, radiative heat transfer law.
3.3. The Progress in Performance Limit Studies for ICE Cycles
3.3.1. The Performance Limit with Newton’s HTA (q ≈ Δ(T))
Considering the WF was non-uniform, Orlov and Berry [] studied the power output performance limit of a class of irreversible non-regeneration heat engines, gave out the lumped-parameter model with uniform temperature and the distributed-parameter model described by using partial differential equations, and found that the MP of the heat engine in the distributed-parameter model was less than or equal to that of in the lumped-parameter model. Based on [], Orlov and Berry [] studied the efficiency performance limit of a class of irreversible non-regeneration heat engines. Considering a finite rate heat transfer obeyed Newton HTA and nonzero entropy generation by combustion chemical reactions, Orlov and Berry [] advanced an open ICE model, obtained the power and efficiency upper limits for ICE model, and found that it might be stimulus for research in the field of constructing highly efficient nonconventional ICE by using heating systems to replace cooling systems.
3.3.2. The Influence of HTA on the Cycle Performance Limit
Xia et al. [] derived the MP of a class of irreversible non-regeneration heat engines with non-uniform WF and linear phenomenological HTA based on []. The upper limits of power for the lumped-parameter model and the distributed-parameter model were determined by using OCT, respectively. The results showed that the MP in the distributed-parameter model was less than or equal to that of in the lumped-parameter model, which could provide more realistic guidelines for real heat engines. Based on [], Chen et al. [] studied the ME of an irreversible heat engine with distributed WF and linear phenomenological HTA. The upper limit of efficiency for various cases was determined by using OCT. Based on [], Chen et al. [] considered a finite rate heat transfer obeyed linear phenomenological HTA and nonzero entropy generation by combustion chemical reactions in the cylinder, investigated a class of irreversible open ICE, obtained the upper limits for power output and efficiency by applying OCT. The upper limits for the power output and efficiency when heat transfer obeys linear phenomenological HTA are as follows []:
where JΔh is the difference between the enthalpy flow rate of inlet and outlet of cylinder; JΔs is the difference between the entropy flow rate of inlet and outlet of cylinder; h specific enthalpy; and γ is the custom constant.
3.4. The Progress in Simulation Studies for ICE Cycles
Descieux et al. [,] studied the simulation for spark ignition engine cycles with HTL [], and with HTL and FL [], respectively, analyzed the effects of cylinder volume, the ratio of stroke length to cylinder diameter, CR, cylinder temperature and the mass ratio of fuel to air on the simulation results. Using a two-zone combustion model, Curto-Risso et al. [] studied the simulation for a practical Otto cycle, compared the simulation results with those of obtained by using FTT, and found that if the cycle maximum temperature, the minimum temperature, the mass of WF, FL and HTL were considered as the functions of piston velocity, the simulation results would completely match with those of obtained by using FTT, otherwise the simulation results would partly match with those obtained by using FTT. Using computer simulation and FTT, Curto-Risso et al. [,] investigated the influences of combustion advance angle and cylinder temperature on the performance of a spark ignition engine, obtained the relation between combustion advance angle and crankshaft angular velocity when the efficiency was the maximum and the power output was fixed, compared the optimization results with those of obtained when combustion advance angle and cylinder temperature were fixed, and found that the cycle performance could be improved by using the optimization parameters. At last, the effects of CR, cylinder temperature and the mass ratio of fuel to air on the simulation results were analyzed. Curto-Risso et al. [] optimized the design parameters of a spark ignition engine by using computer simulation, analyzed the effect of the ratio of stroke length to cylinder inside diameter on the performance, and found that there existed an optimum ratio of stroke length to cylinder inside diameter which would maximize the power output and efficiency.
4. Conclusions
Finite time thermodynamics (FTT) has been a powerful tool in studies of various thermodynamic processes and cycles since its naissance in 1975. Roundly and systematically using FTT to study the optimum performances and configurations of various ICE cycles not only has important significance for decreasing energy consumption, protecting the ecological environment and providing guidelines for the design and operation of practical ICEs, but also can answer some global questions about ICE cycles which classical thermodynamics and conventional irreversible thermodynamics cannot answer, and further continually impel FTT progress in the engineering application fields.
In the future, the analysis and optimization of ICE cycles by using FTT can further progress in the following aspects: the first is to perform FTT performance analysis and optimization for various new single cycles and combined reciprocating cycles, such as the Meletis–Georgiou cycle (Figure 18 shows the T − s diagrams for Meletis–Georgiou cycle model, the isentropic compression processes are shown as 1 → 2S and 3 → 4S; the process of mixing between the working fluid at state 2 with part of the expanding working fluid at state 6 is shown as process 2 → 3; the isochoric heat addition process is 4 → 5; the isentropic expansion processes are shown as 5 → 6S and 7S → 8S; the separation process of the working fluid in expansion volume is shown as 6 → 7; the isochoric and isobaric heat rejection processes are shown as 8 → 9 and 9 → 1) [,,,,,,], rectangular cycle (Figure 19 shows p − v diagram for the rectangular cycle model, the isochoric and isobaric heat addition processes are shown as 1 → 2 and 2 → 3; the isochoric and isobaric heat rejection are shown as 3 → 4 and 4 → 1) [,,,,,,], Lenoir cycle (Figure 20 shows T − s diagram for the Lenoir cycle model, the isochoric heat addition process is shown as 1 → 2; the isentropic expansion processes is shown as 2 → 3; the isobaric heat rejection is shown as 3 → 1) [,,,,,], Dual–Atkinson combined cycle [,,,], Dual–Miller combined cycle [,,] and Otto–Miller combined cycle []. The second is to establish new cycle models which are closer to practical cycles. The third is to adopt more comprehensive and effective OPBs in the analysis and optimization of ICE performance, especially, multi-objective optimization procedures will be utilized.
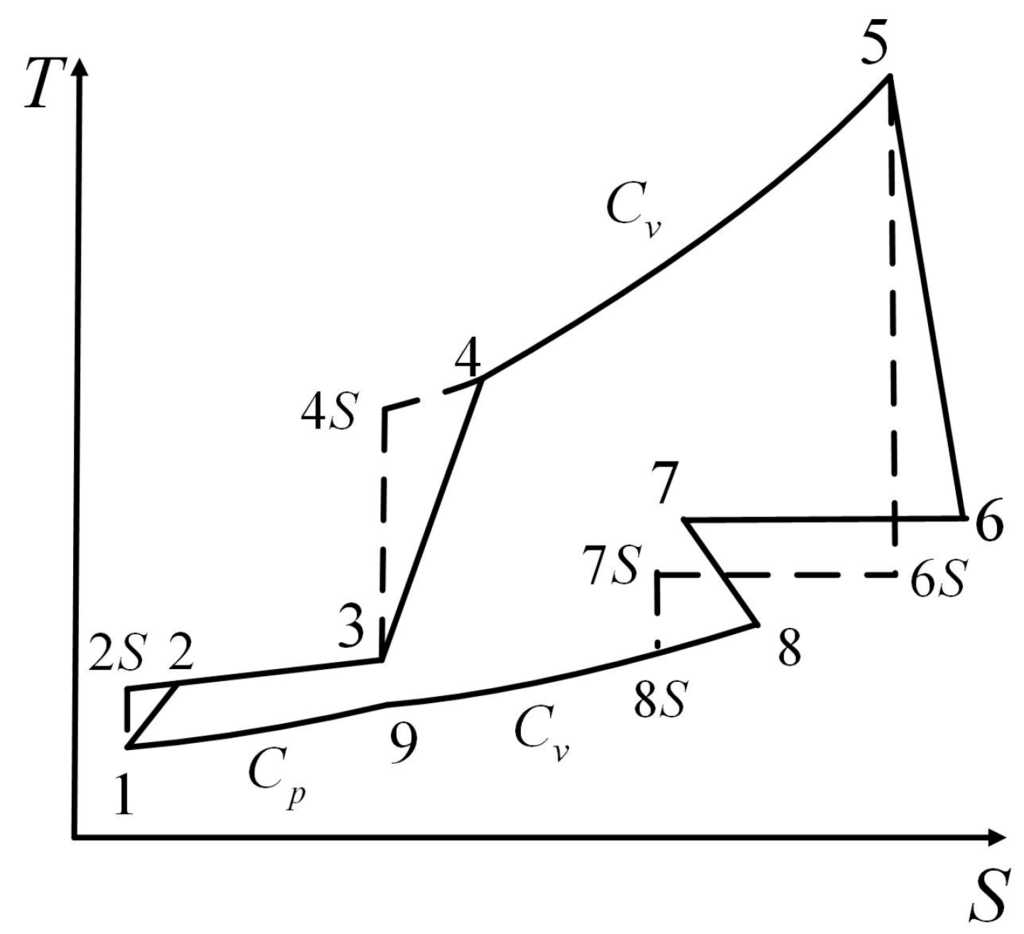
Figure 18.
T − s diagram for irreversible Meletis–Georgiou cycle model [,].
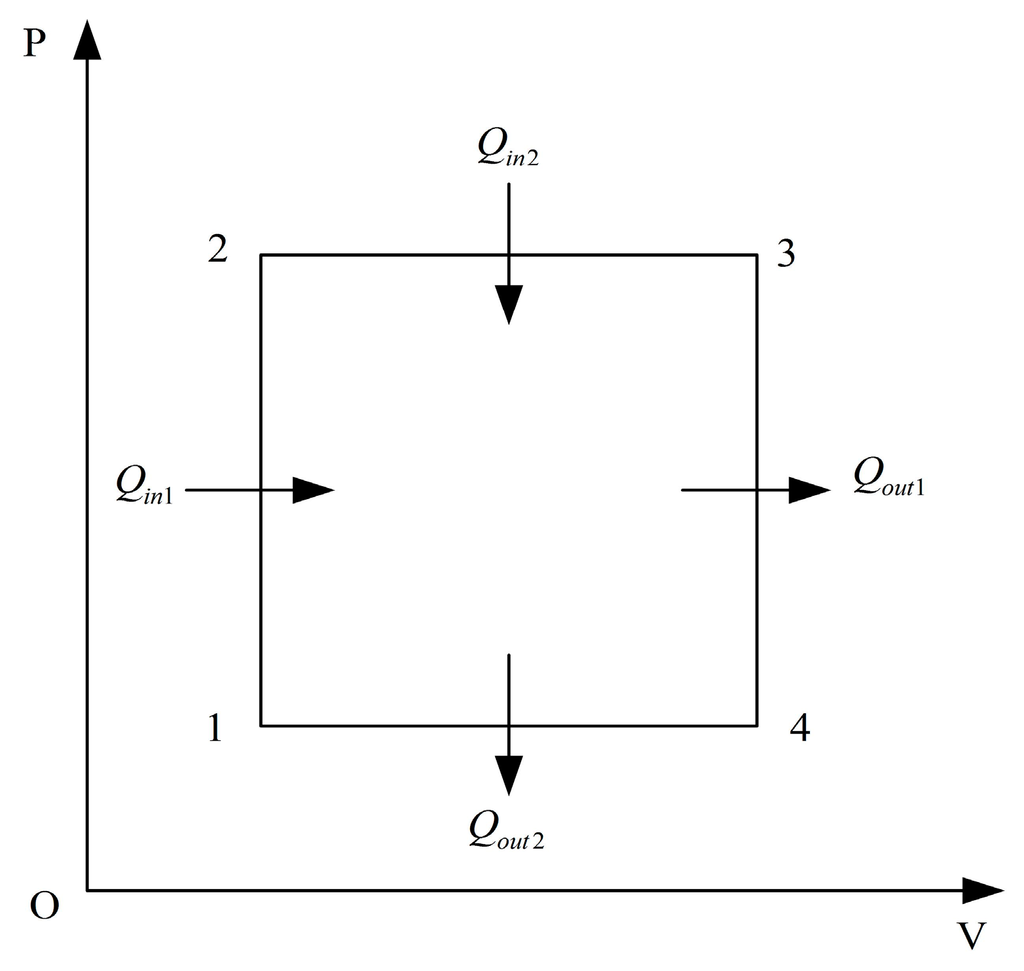
Figure 19.
p − v diagram for the rectangular cycle model [,].
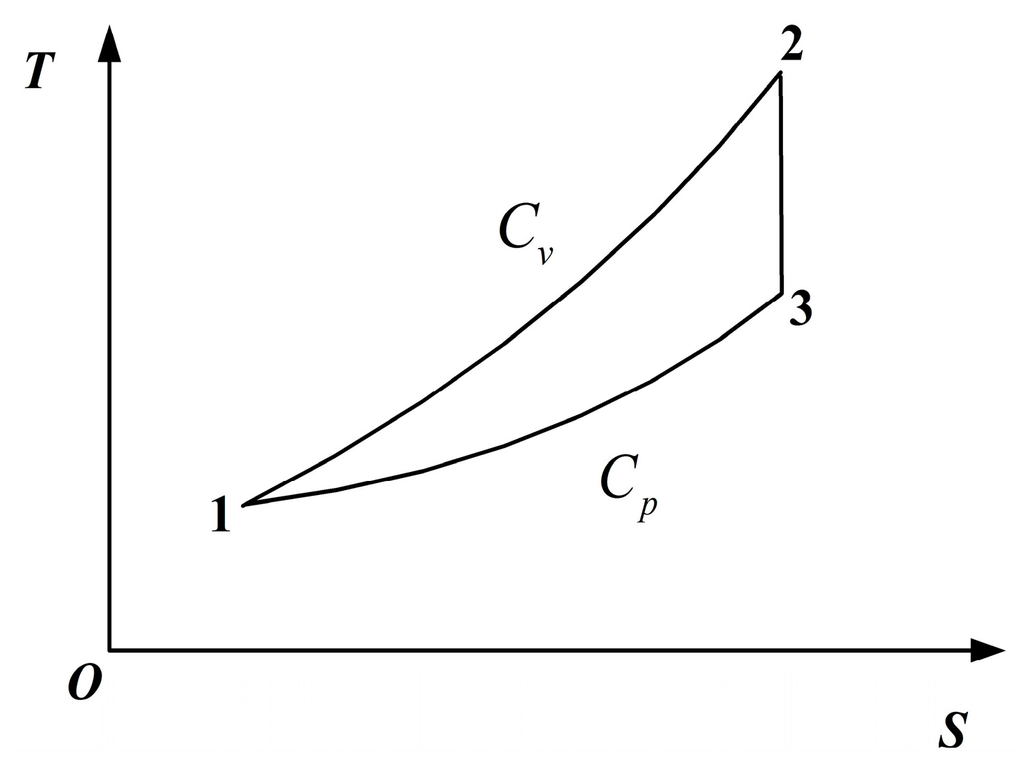
Figure 20.
T − s diagram for the Lenoir cycle model [,].
Acknowledgments
This paper is supported by The National Natural Science Foundation of P.R. China (Project No. 51576207). The authors wish to thank four reviewers for their careful, unbiased and constructive suggestions, which led to this revised manuscript.
Author Contributions
Yanlin Ge, Lingen Chen and Fengrui Sun common finished the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | acceleration |
| B | constant related to heat transfer |
| b | cylinder bore (m) |
| C | specific heat |
| E | ecological function |
| h | specific enthalpy |
| JΔh | the difference between the enthalpy flow rate of inlet and outlet of cylinder |
| JΔs | the difference between the entropy flow rate of inlet and outlet of cylinder |
| K | heat transfer coefficient; coefficient of specific heats varied with temperature |
| k | adiabatic exponent |
| L | stroke length |
| l | connecting rod length |
| m | mass flow rate |
| N | number of moles of working fluid |
| n | cycles running per second |
| P | power output |
| Q | Heat rate of addition or rejection by the working fluid |
| R | gas constant |
| r | crank length |
| S | specific entropy |
| sign | sign function |
| T | temperature |
| t | time |
| u | coefficient of specific heat ratio varied with temperature |
| V | volume |
| v | speed |
| X | displacement |
| Greek symbol | |
| γ | compression ratio; custom constant |
| ηC | Carnot efficiency |
| ηCA | CA efficiency |
| ηc | compression efficiency |
| ηe | expansion efficiency |
| θ | crankshaft rotation angle |
| λ | Lagrange multiplier |
| μ | friction coefficient |
| σ | entropy generation rate |
| τ | cycle period |
| subscript | |
| at | Atkinson cycle |
| br | Brayton cycle |
| di | Diesel cycle |
| du | Dual cycle |
| in | head addition |
| mi | Miller cycle |
| ot | Otto cycle |
| out | heat rejection; outlet |
| p | constant pressure process |
| pm | PM cycle |
| un | universal cycle |
| v | constant volume process |
| 0 | environment |
| 1-6, 2S, 4S, 5S | state points |
Abbreviations
The following abbreviations are used in this manuscript:
| AS: | air standard |
| CR: | compression ratio |
| CSH: | constant specific heats |
| ECOP: | ecological coefficient of performance |
| EF: | ecological function |
| FL: | friction loss |
| FTT: | finite time thermodynamics |
| HTA: | Heat transfer law |
| HTL: | heat transfer loss |
| IIL: | internal irreversibility loss |
| ME: | maximum efficiency |
| MEF: | maximum ecological function |
| MEG: | minimum entropy generation |
| MEP: | maximum efficient power |
| MP: | maximum power output |
| MPD: | maximum power density |
| MW: | maximum work output |
| OCT: | optimal control theory |
| OPB: | optimization objective |
| OPM: | optimization piston motion |
| SH: | specific heats |
| SHR: | specific heat ratio |
| VSH: | variable specific heats |
| VSHR: | variable specific heat ratio |
| WF: | working fluid |
References
- Kanoglu, M.; Kazim, S.I.; Abusoglu, A. Performance characteristics of a Diesel engine power plant. Energy Convers. Manag. 2005, 46, 1692–1702. [Google Scholar] [CrossRef]
- Qiao, A.P.; Li, Y.Q.; Gao, F. Improving the theoretical cycles of four-stroke ICE and their simulation calculations. Proc. IMechE Part D 2006, 220, 219–227. [Google Scholar] [CrossRef]
- Ramesh, C.V. Valved heat engine working on modified Atkinson cycle. J. Energy Resour. Technol. 2010, 132, 015001. [Google Scholar] [CrossRef]
- Nakonieczny, K. Entropy generation in a diesel engine turbocharging system. Energy 2002, 27, 1027–1056. [Google Scholar] [CrossRef]
- Yoshida, S. Exergy analysis of a diesel engine cycle and its performance improvement. Int. J. Exergy 2005, 2, 284–298. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Giakoumis, E.G. The influence of cylinder wall temperature profile on the second-law diesel engine transient response. Appl. Therm. Eng. 2005, 25, 1779–1795. [Google Scholar] [CrossRef]
- Ribeiro, B.; Martins, J.; Nunes, A. Generation of entropy in spark ignition engines. Int. J. Thermodyn. 2007, 10, 53–60. [Google Scholar]
- Caton, J.A. Comparisons of instructional and complete version of thermodynamic engine cycle simulations for spark-ignition engines. Int. J. Mech. Eng. Educ. 2001, 29, 283–306. [Google Scholar] [CrossRef]
- Caton, J.A. Illustration of the use of an instructional version of a thermodynamic cycle simulation for a commercial automotive spark-ignition engine. Int. J. Mech. Eng. Educ. 2002, 30, 283–297. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B. Finite-Time Thermodynamics; University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Salamon, P. Finite-Time Thermodynamics and Thermoeconomics; Taylor & Francis: New York, NY, USA, 1990. [Google Scholar]
- Chen, L.G.; Sun, F.R.; Chen, W.Z. The present state and trend of finite time thermodynamics. Adv. Mech. 1992, 22, 479–488. (In Chinese) [Google Scholar]
- Sieniutycz, S.; Shiner, J.S. Thermodynamics of irreversible processes and its relation to chemical engineering: Second law analyses and finite time thermodynamics. J. Non-Equilib. Thermodyn. 1994, 19, 303–348. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- Berry, R.S.; Kazakov, V.A.; Sieniutycz, S.; Szwast, Z.; Tsirlin, A.M. Thermodynamic Optimization of Finite Time Processes; Wiley: Chichester, UK, 1999. [Google Scholar]
- Wu, C.; Chen, L.G.; Chen, J.C. Recent Advances in Finite Time Thermodynamics; Nova Science Publishers: New York, NY, USA, 1999. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Sieniutycz, S. Hamilton–Jacobi–Bellman framework for optimal control in multistage energy systems. Phys. Rep. 2000, 326, 165–285. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Andresen, T.R.; Limon, A. Principles of control thermodynamics. Energy 2001, 26, 307–319. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. The recent advances in finite time thermodynamics and its future application. Int. J. Energy Environ. Econ. 2001, 11, 69–81. [Google Scholar]
- Hoffmann, K.H. Recent developments in finite time thermodynamics. Technol. Mech. 2002, 22, 14–25. [Google Scholar]
- Hoffman, K.H.; Burzler, J.; Fischer, A.; Schaller, M.; Schubert, S. Optimal process paths for endoreversible systems. J. Non-Equilib. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Sieniutycz, S. Thermodynamic limits on production or consumption of mechanical energy in practical and industry systems. Prog. Energy Combust. Sci. 2003, 29, 193–246. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R. Advances in Finite Time Thermodynamics: Analysis and Optimization; Nova Science Publishers: New York, NY, USA, 2004. [Google Scholar]
- Chen, L.G. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; Higher Education Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Muschik, W.; Hoffmann, K.H. Endoreversible thermodynamics: A tool for simulating and comparing processes of discrete systems. J. Non-Equilib. Thermodyn. 2006, 31, 293–317. [Google Scholar] [CrossRef]
- Wu, F.; Chen, L.G.; Sun, F.R.; Yu, J.Y. Finite Time Thermodynamic Optimization for Stirling Machines; Chemical Industry Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems; Elsevier: Oxford, UK, 2009. [Google Scholar]
- Feidt, M. Optimum thermodynamics-New upperbounds. Entropy 2009, 11, 529–547. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Edit. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.L.; Chen, L.G.; Han, W.W.; Wu, Z.W. Advances in finite time thermodynamic studies for analyses and optimizations of direct/inverse Brayton cycles. Gas Turbine Technol. 2012, 25, 1–11. (In Chinese) [Google Scholar]
- Wang, W.H.; Chen, L.G.; Ge, Y.L.; Sun, F.R. New advances in finite time thermodynamic studies for gas turbine cycles. Therm. Turbine 2012, 41, 171–178. [Google Scholar]
- Chen, L.G. Progress in entransy theory and its applications. Chin. Sci. Bull. 2012, 57, 4404–4426. [Google Scholar] [CrossRef]
- Tlili, I. Finite time thermodynamic evaluation of endoreversible Stirling heat engine at maximum power conditions. Renew. Sustain. Energy Rev. 2012, 16, 2234–2241. [Google Scholar] [CrossRef]
- Tlili, I. Thermodynamic study on optimal solar Stirling engine cycle taking into account the irreversibilities effects. Energy Procedia 2012, 14, 584–591. [Google Scholar] [CrossRef]
- Tlili, I. A Numerical investigation of an Alpha Stirling engine using the Ross Yoke linkage. Heat Technol. 2012, 30, 23–36. [Google Scholar]
- Tlili, I.; Musmar, S.A. Thermodynamic evaluation of a second order simulation for Ross Stirling engine. Energy Convers. Manag. 2013, 68, 149–160. [Google Scholar] [CrossRef]
- Qin, X.Y.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Finite time thermodynamic studies on absorption thermodynamic cycles: A state of the arts review. Arab. J. Sci. Eng. 2013, 38, 405–419. [Google Scholar] [CrossRef]
- Ngouateu, W.P.A.; Tchinda, R. Finite-time thermodynamics optimization of absorption refrigeration systems: A review. Renew. Sustain. Energy Rev. 2013, 21, 524–536. [Google Scholar] [CrossRef]
- Li, J.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Progress in the study on finite time thermodynamic optimization for direct and reverse two-heat-reservoir thermodynamic cycles. Acta Phys. Sin. 2013, 62, 130501. (In Chinese) [Google Scholar]
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoit. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems and Fuel Cells; Elsevier: Oxford, UK, 2013. [Google Scholar]
- Sarkar, J. A review on thermodynamic optimization of irreversible refrigerator and verification with transcritical CO2 system. Int. J. Thermodyn. 2014, 17, 71–79. [Google Scholar] [CrossRef] [Green Version]
- Medina, A.; Curto-Risso, P.L.; Calvo-Hernández, A.; Guzmán-Vargas, L.; Angulo-Brown, F.; Sen, A.K. Quasi-Dimensional Simulation of Spark Ignition Engines: From Thermodynamic Optimization to Cyclic Variability; Springer: London, UK, 2014. [Google Scholar]
- Chen, L.G. Progress in optimization of mass transfer processes based on mass entransy dissipation extremum principle. Sci. China Technol. Sci. 2014, 57, 2305–2327. [Google Scholar] [CrossRef]
- Vaudrey, A.V.; Lanzetta, F.; Feidt, M.H.B. Reitlinger and the origins of the efficiency at maximum power formula for heat engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–204. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Andresen, B.; Salamon, P. Finite-Time Thermodynamics Tools to Analyze Dissipative Processes. In Proceedings of the 240 Conference: Science’s Great Challences; Dinner, A.R., Rice, S.A., Eds.; Wiley: Hoboken, NJ, USA, 2014; Volume 157, pp. 57–67. [Google Scholar]
- Ding, Z.M.; Chen, L.G.; Wang, W.H.; Sun, F.R. Progress in study on finite time thermodynamic performance optimization for three kinds of microscopic energy conversion systems. Sci. Sin. Technol. 2015, 45, 889–918. [Google Scholar]
- Ahmadi, M.H.; Ahmadi, M.A.; Sadatsakkak, S.A. Thermodynamic analysis and performance optimization of irreversible Carnot refrigerator by using multi-objective evolutionary algorithms (MOEAs). Renew. Sustain. Energy Rev. 2015, 51, 1055–1070. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Processes; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chen, L.G.; Xia, S.J.; Li, J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chen, L.G.; Meng, F.K.; Sun, F.R. Thermodynamic analyses and optimizations for thermoelectric devices, the state of the arts. Sci. China Technol. Sci. 2016, 59, 442–455. [Google Scholar] [CrossRef]
- Yan, Z. The relation between optimum efficiency and power output of a Cannot engine. Chin. J. Eng. Thermophys. 1985, 6, 1–6. (In Chinese) [Google Scholar]
- Ma, K.; Chen, L.G.; Sun, F.R. Profit performance optimization for a generalized irreversible combined Carnot refrigeration cycle. Sadhana Acad. Proc. Eng. Sci. 2009, 34, 851–864. [Google Scholar]
- Rubin, M.H. Optimum configuration of a class of irreversible heat engines. Phys. Rev. A 1979, 19, 1272–1287. [Google Scholar] [CrossRef]
- Badescu, V. Optimum strategies for steady state heat exchanger operation. J. Phys. D 2004, 37, 2298–2304. [Google Scholar] [CrossRef]
- Salamon, P.; Nitzon, A. Finite time optimization of a Newton’s law Carnot cycle. J. Chem. Phys. 1981, 74, 3546–3560. [Google Scholar] [CrossRef]
- Li, J.; Chen, L.G.; Sun, F.R. Heating load vs. COP characteristic of an endoreversible Carnot heat pump subjected to heat transfer law q ∝ (ΔTn)m. Appl. Energy 2008, 85, 96–100. [Google Scholar] [CrossRef]
- Rubin, M.H. Optimum configuration of an irreversible heat engine with fixed compression ratio. Phys. Rev. A 1980, 22, 1741–1752. [Google Scholar] [CrossRef]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Optimization for minimizing entropy generation during heat transfer processes with heat transfer law q ∝ (ΔTn)m. J. Therm. Sci. Technol. 2008, 7, 226–230. (In Chinese) [Google Scholar]
- Chen, W.Z.; Sun, F.R.; Chen, L.G. Finite time thermodynamic criteria for parameter choice of heat engine operating between heat reservoirs. Chin. Sci. Bull. 1991, 36, 763–768. (In Chinese) [Google Scholar]
- Wu, C.; Chen, L.G.; Sun, F.R. Optimization of steady flow refrigeration cycles. Int. J. Ambient Energy 1996, 17, 199–206. [Google Scholar] [CrossRef]
- Ondrechen, M.J.; Rubin, M.H.; Band, Y.B. The generalized Carnot cycles: A working fluid operating in finite-time between finite heat sources and sinks. J. Chem. Phys. 1983, 78, 4721–4727. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhou, S.B.; Sun, F.R.; Wu, C. Optimum configuration and performance of heat engines with heat leak and finite heat capacity. Open Sys. Inf. Dyn. 2002, 9, 85–96. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C.; Ni, N. A generalized model of a real combined power plant and its performance. Int. J. Energy Environ. Econ. 1999, 9, 35–49. [Google Scholar]
- Kan, X.X.; Wu, F.; Chen, L.G.; Sun, F.R.; Guo, F.Z. Exergy efficiency optimization of a thermoacoustic engine with a complex heat transfer exponent. Int. J. Sustain. Energy 2010, 29, 220–232. [Google Scholar] [CrossRef]
- Meng, F.K.; Chen, L.G.; Sun, F.R. Extreme working temperature differences for thermoelectric refrigerating and heat pumping devices driven by thermoelectric generator. J. Energy Inst. 2010, 83, 108–113. [Google Scholar] [CrossRef]
- Chen, L.G.; Ding, Z.M.; Sun, F.R. Performance analysis of a vacuum thermionic refrigerator with external heat transfer. J. Appl. Phys. 2010, 107, 104507. [Google Scholar] [CrossRef]
- Ma, K.; Chen, L.G.; Sun, F.R. Optimum paths for a light-driven engine with linear phenomenological heat transfer law. Sci. China Chem. 2010, 53, 917–926. [Google Scholar] [CrossRef]
- Klein, S.A. An explanation for observed compression ratios in international combustion engines. J. Eng. Gas Turbine Power 1991, 113, 511–513. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Rocha-Martinez, J.A.; Navarrete-Gonzalez, T.D. A non-endoreversible Otto cycle model: Improving power output and efficiency. J. Phys. D 1996, 29, 80–83. [Google Scholar] [CrossRef]
- Chen, L.G.; Ge, Y.L.; Sun, F.R. Unified thermodynamic description and optimization for a class of irreversible reciprocating heat engine cycles. Proc. IMechE Part D 2008, 222, 1489–1500. [Google Scholar] [CrossRef]
- Chen, L.G.; Lin, J.X.; Sun, F.R.; Wu, C. Efficiency of an Atkinson engine at maximum power density. Energy Convers. Manag. 1998, 39, 337–341. [Google Scholar] [CrossRef]
- Gumus, M.; Atmaca, M.; Yilmaz, T. Efficiency of an Otto engine under alternative power optimizations. Int. J. Energy Res. 2009, 39, 745–752. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Fernandez-Betanzos, J.; Diaz-Pico, C.A. Compression ratio of an optimized Otto-cycle model. Eur. J. Phys. 1994, 15, 38–42. [Google Scholar] [CrossRef]
- Ust, Y. Ecological performance analysis of irreversible Otto cycle. J. Eng. Nat. Sci. 2005, 3, 106–117. [Google Scholar]
- Mehta, H.B.; Bharti, O.S. Performance analysis of an irreversible Otto cycle using Finite Time Termodynamics. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009.
- Lin, J.C. Ecological optimization for an Atkinson engine. JP J. Heat Mass Transf. 2010, 4, 95–112. [Google Scholar]
- Ust, Y.; Sahin, B.; Sogut, O.S. Performance analysis and optimization of an irreversible dual-cycle based on an ecological coefficient of performance criterion. Appl. Energy 2005, 82, 23–39. [Google Scholar] [CrossRef]
- Ge, Y.L. Finite Time Thermodynamic Analysis and Optimization for Irreversible ICE Cycles. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2011. [Google Scholar]
- Gonca, G.; Sahin, B. Performance optimization of an air-standard irreversible Dual–Atkinson cycle engine based on the ecological coefficient of performance criterion. Sci. World J. 2014, 2014, 815787. [Google Scholar] [CrossRef] [PubMed]
- Rocha-Martinez, J.A.; Navarrete-Gonzalez, T.D.; Pava-Miller, C.G.; Ramirez-Rojas, A.; Angulo-Brown, F. Otto and Diesel engine models with cyclic variability. Revista Mexicana de Física 2002, 48, 228–234. [Google Scholar]
- Rocha-Martinez, J.A.; Navarrete-Gonzalez, T.D.; Pava-Miller, C.G.; Ramirez-Rojas, A.; Angulo-Brown, F. A simplified irreversible Otto engine model with fluctuations in the combustion heat. Int. J. Ambient Energy 2006, 27, 181–192. [Google Scholar] [CrossRef]
- Ghatak, A.; Chakraborty, S. Effect of external irreversibilities and variable thermal properties of working fluid on thermal performance of a Dual ICE cycle. J. Mech. Energy 2007, 58, 1–12. [Google Scholar]
- Abu-Nada, E.; Al-Hinti, I.; Al-Aarkhi, A.; Akash, B. Thermodynamic modeling of spark-ignition engine: Effect of temperature dependent specific heats. Int. Commun. Heat Mass Transf. 2005, 33, 1264–1272. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Al-Hinti, I.; Al-Aarkhi, A.; Akash, B. Thermodynamic analysis of spark-ignition engine using a gas mixture model for the working fluid. Int. J. Energy Res. 2007, 37, 1031–1046. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Al-Hinti, I.; Al-Aarkhi, A.; Akash, B. Effect of piston friction on the performance of SI engine: A new thermodynamic approach. ASME Trans. J. Eng. Gas Turbine Power 2008, 130, 022802. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Akash, B.; Al-Hinti, I.; Al-Sarkhi, A. Performance of spark-ignition engine under the effect of friction using gas mixture model. J. Energy Inst. 2009, 82, 197–205. [Google Scholar] [CrossRef]
- Ebrahimi, R. Effects of variable specific heat ratio on performance of an endoreversible Otto cycle. Acta Phys. Pol. A 2010, 117, 887–891. [Google Scholar] [CrossRef]
- Ebrahimi, R. Engine speed effects on the characteristic performance of Otto engines. J. Am. Sci. 2009, 5, 25–30. [Google Scholar]
- Ebrahimi, R. Performance of an irreversible Diesel cycle under variable stroke length and compression ratio. J. Am. Sci. 2009, 5, 58–64. [Google Scholar]
- Ge, Y.L. The Effects of the Variable Specific Heats of Working Fluid on the Performance of ICE Cycles. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2005. [Google Scholar]
- Zhao, Y.; Lin, B.; Chen, J. Optimum criteria on the important parameters of an irreversible Otto heat engine with the temperature-dependent heat capacities of the working fluid. ASME Trans. J. Energy Res. Technol. 2007, 129, 348–354. [Google Scholar] [CrossRef]
- Parlak, A. Comparative performance analysis of irreversible Dual and Diesel cycles under maximum power conditions. Energy Convers. Manag. 2005, 46, 351–359. [Google Scholar] [CrossRef]
- Petrescu, S.; Harman, C.; Costea, M.; Petre, C.; Dobre, C. Irreversible finite speed thermodynamics (IFST) in simple closed systems. I. Fundamental concepts. Termotehnica 2009, 13, 8–18. [Google Scholar]
- Zhao, Y.; Chen, J. Irreversible Otto heat engine with friction and heat leak losses and its parametric optimum criteria. J. Energy Inst. 2008, 81, 54–58. [Google Scholar] [CrossRef]
- Zi, K.; Yang, X.; Jiang, P. Power and efficiency characteristics of engine with mechanical losses. J. Harbin Inst. Technol. 2009, 41, 209–212. (In Chinese) [Google Scholar]
- Wu, F.; Chen, L.G.; Sun, F.R.; Wu, C. Quantum degeneracy effect on performance of irreversible Otto cycle with deal Bose gas. Energy Convers. Manag. 2006, 47, 3008–3018. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; He, J. Performance analysis and parametric optimum criteria of a quantum Otto heat engine with heat transfer effects. Appl. Therm. Eng. 2009, 29, 706–711. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Du, J. Performance analysis and parametric optimum criteria of a regeneration Bose–Otto engine. Phys. Scr. 2009, 79, 055004. [Google Scholar] [CrossRef]
- Qin, X.Y.; Chen, L.G.; Sun, F.R. The universal power and efficiency characteristics for irreversible reciprocating heat engine cycles. Eur. J. Phys. 2003, 24, 359–366. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Reciprocating heat-engine cycles. Appl. Energy 2005, 81, 180–186. [Google Scholar]
- Rashidi, M.M.; Hajipour, A. Comparison of performance of air-standard Atkinson, Diesel and Otto cycles with constant specific heats. Int. J. Adv. Des. Manuf. Technol. 2013, 6, 57–62. [Google Scholar]
- Wu, C.; Blank, D.A. The effect combustion on a work-optimized endoreversible Otto cycle. J. Energy Inst. 1992, 65, 86–89. [Google Scholar]
- Blank, D.A.; Wu, C. Optimization of the endoreversible Otto cycle with respect to both power and mean effective pressure. Energy Convers. Manag. 1993, 34, 1255–1209. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Heat transfer effects on the net work output and efficiency characteristics for an air standard Otto cycle. Energy Convers. Manag. 1998, 39, 643–648. [Google Scholar] [CrossRef]
- Ficher, A.; Hoffman, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Novikov, I.I. The efficiency of atomic power stations (a review). Atommaya Energiya 1957, 3, 409–412. [Google Scholar] [CrossRef]
- Ozsoysal, O.A. Heat loss as a percentage of fuel’s energy in air standard Otto and Diesel cycles. Energy Convers. Manag. 2006, 47, 1051–1062. [Google Scholar] [CrossRef]
- Hou, S.S. Comparison of performances of air standard Atkinson and Otto cycles with heat transfer considerations. Energy Convers. Manag. 2007, 48, 1683–1690. [Google Scholar] [CrossRef]
- Ozcan, H. The effects of heat transfer on the exergy efficiency of an air-standard otto cycle. Heat Mass Transf. 2011, 47, 571–577. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Hajipour, A.; Baziar, P. Influence of heat loss on the second-law efficiency of an Otto cycle. Int. J. Mechatron. Electr. Comput. Technol. 2014, 4, 922–933. [Google Scholar]
- Chen, L.G.; Zheng, T.; Sun, F.R.; Wu, C. The power and efficiency characteristics for an irreversible Otto cycle. Int. J. Ambient Energy 2003, 24, 195–200. [Google Scholar] [CrossRef]
- Lan, X.; Zi, K. Finite time thermodynamic theory and applications of ICE: State of the arts. J. Kunming Univ. Sci. Technol. 2002, 27, 89–94. (In Chinese) [Google Scholar]
- Lan, X. The Thermodynamics Study on the Working Process of Diesel Engine. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2002. [Google Scholar]
- Chen, J.; Zhao, Y.; He, J. Optimization criteria for the important parameters of an irreversible Otto heat-engine. Appl. Energy 2006, 83, 228–238. [Google Scholar] [CrossRef]
- Ebrahimi, R. Theoretical study of combustion efficiency in an Otto engine. J. Am. Sci. 2010, 6, 113–116. [Google Scholar]
- Ozsoysal, O.A. Effects of combustion efficiency on an Otto cycle. Int. J. Exergy 2010, 7, 232–242. [Google Scholar] [CrossRef]
- Ebrahimi, R. Effects of gasoline-air equivalence ratio on performance of an Otto engine. J. Am. Sci. 2010, 6, 131–135. [Google Scholar]
- Ebrahimi, R.; Ghanbarian, D.; Tadayon, M.R. Performance of an Otto engine with volumetric efficiency. J. Am. Sci. 2010, 6, 27–31. [Google Scholar]
- Huleihil, M. Effects of pressure drops on the performance characteristics of air standard Otto cycle. Phys. Res. Int. 2011, 2011, 496057. [Google Scholar] [CrossRef]
- Hu, H.; Xu, H.; Liu, J.; Xie, W.; Wei, J.; Zhou, J.; Zhang, Y. Optimum analysis of the performance of an irreversible Otto cycle. J. Southwest Univ. Nat. Sci. Edit. 2011, 33, 57–60. (In Chinese) [Google Scholar]
- Ust, Y.; Sahin, B.; Safa, A. The effects of cycle temperature and cycle pressure ratios on the performance of an irreversible Otto cycle. Acta Phys. Pol. A 2011, 120, 413–416. [Google Scholar] [CrossRef]
- Ebrahimi, R. Performance analysis of an Otto engine with ethanol and gasoline fuels. Appl. Mech. Mater. 2012, 110–116, 267–272. [Google Scholar] [CrossRef]
- Huleihil, M.; Mazor, G. Irreversible performance characteristics of air standard Otto cycles with polytropic processes. J. Appl. Mech. Eng. 2012, 1, 1000111. [Google Scholar] [CrossRef]
- Ladino-Luna, D.; Paez-Hernandez, R.T. Otto and Diesel Cycles Modeled by Considering Non-Instaneous Adiabats. In Proceedings of the 6th International Workshop on Nonequilibrium Thermodynamics (IWNET 2012), Røros, Norway, 19–24 August 2012.
- Joseph, A.; Thampi, G.K. Finite time thermodynamic analysis of an irreversible Otto cycle. J. Chem. Pharm. Sci. 2015, 6, 14–18. [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Ecological optimization of an irreversible Otto cycle. Arab. J. Sci. Eng. 2013, 38, 373–381. [Google Scholar] [CrossRef]
- Moscato, A.L.S.; del Rio Oliveira, S. Net power optimization of an irreversible Otto cycle using ECOP and ecological function. Int. Rev. Mech. Eng. 2015, 9, 10–20. [Google Scholar] [CrossRef]
- Mao, Z.; He, J.; Zhou, F. Performance analysis of an irreversible quantum Otto power cycle. J. Nanchang Univ. Eng. Technol. 2007, 29, 126–130. (In Chinese) [Google Scholar]
- Mao, Z. Optimum Analysis of Irreversible Quantum Thermodynamics. Master’s Thesis, Nanchang University, Nanchang, China, 2007. [Google Scholar]
- Nie, W.; Liao, Q.; Zhang, C.; He, J. Micro-/nanoscaled irreversible Otto engine cycle with friction loss and boundary effects and its performance characteristic. Energy 2010, 35, 4658–4662. [Google Scholar] [CrossRef]
- Wu, F.; Chen, L.G.; Sun, F.R.; Wu, C. Ecological optimization performance of an irreversible quantum Otto cycle working with an ideal Fermi gas. Open Sys. Inf. Dyn. 2006, 13, 55–66. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Thermodynamic simulation of performance of an Otto cycle with heat transfer and variable specific heats of working fluid. Int. J. Therm. Sci. 2005, 44, 506–511. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. The effects of variable specific heats of working fluid on the performance of an irreversible Otto cycle. Int. J. Exergy 2005, 2, 274–283. [Google Scholar] [CrossRef]
- Lin, J.C.; Hou, S.S. Effects of heat loss as percentage of fuel’s energy, friction and variable specific heats of working fluid on performance of air standard Otto cycle. Energy Convers. Manag. 2008, 49, 1218–1227. [Google Scholar] [CrossRef]
- Nejad, R.M.; Marghmaleki, I.S.; Hoseini, R.; Alaei, P. Effects of irreversible different parameters on performance of air standard Otto cycle. J. Am. Sci. 2011, 7, 248–254. [Google Scholar]
- Ebrahimi, R.; Tadayon, M.R.; Gandomkari, F.T.; Mahbobian, K. Effect of ethanol-air equivalence ratio on performance of an end reversible Otto engine. Appl. Mech. Mater. 2012, 110–116, 273–277. [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Ecological Optimization of an Irreversible Otto Cycle With Variable Specific Heats of Working Fluid. In Proceedings of the Chinese Society of Engineering Thermophysics on Engineering Thermophysics and Energy Utility, Wuhan, China, 5–7 November 2011. (In Chinese)
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Finite time thermodynamic modeling and analysis for an irreversible Otto cycle. Appl. Energy 2008, 85, 618–624. [Google Scholar] [CrossRef]
- Ebrahimi, R. Thermodynamic simulation of performance of an irreversible Otto cycle with engine speed and variable specific heat ratio of working fluid. Arab. J. Sci. Eng. 2014, 39, 2091–2096. [Google Scholar] [CrossRef]
- Atmaca, M.; Gumus, M. Power and efficiency analysis of Diesel cycle under alternative criteria. Arab. J. Sci. Eng. 2014, 39, 2263–2270. [Google Scholar] [CrossRef]
- Blank, D.A.; Wu, C. The effects of combustion on a power-optimized endoreversible Diesel cycle. Energy Convers. Manag. 1993, 34, 493–498. [Google Scholar] [CrossRef]
- Chen, L.G.; Zen, F.M.; Sun, F.R.; Wu, C. Heat transfer effects on the net work output and power as function of efficiency for air standard Diesel cycle. Energy 1996, 21, 1201–1205. [Google Scholar] [CrossRef]
- Parlak, A. The effect of heat transfer on performance of the Diesel cycle and exergy of the exhaust gas stream in a LHR Diesel engine at the optimum injection timing. Energy Convers. Manag. 2005, 46, 167–179. [Google Scholar] [CrossRef]
- Parlak, A.; Yasar, H.; Eldogan, O. The effect of thermal barrier coating on a turbo-charged Diesel engine performance and exergy potential of the exhaust gas. Energy Convers. Manag. 2005, 46, 489–499. [Google Scholar] [CrossRef]
- Al-Hinti, I.; Akash, B.; Abu-Nada, E.; Al-Sarkhi, A. Performance analysis of air-standard Diesel cycle using an alternative irreversible heat transfer approach. Energy Convers. Manag. 2008, 49, 3301–3304. [Google Scholar] [CrossRef]
- Chen, L.G.; Lin, J.X.; Sun, F.R. Friction effects on power vs. efficiency characteristics for air-standard Diesel cycles. J. Eng. Thermophys. 1997, 18, 533–535. (In Chinese) [Google Scholar]
- Chen, W.Z.; Sun, F.R. New solutions of power and efficiency for Diesel cycles with friction. J. Naval Univ. Eng. 2001, 13, 24–26. (In Chinese) [Google Scholar]
- Zhao, Y.; Lin, B.; Zhang, Y.; Chen, J. Performance analysis and parametric optimum design of an irreversible Diesel heat engine. Energy Convers. Manag. 2006, 47, 3383–3392. [Google Scholar] [CrossRef]
- Zheng, S.; Xia, Z.; Zhou, Y.; Lin, G. Optimization on the work output, wfficiency and other performance parameters of an irreversible Diesel heat engine. J. Xiamen Univ. Nat. Sci. 2006, 45, 182–185. (In Chinese) [Google Scholar]
- Zheng, S. The effect of ratio of high temperature to low temperature on the performance of Diesel engine cycle. Energy Environ. 2009, 1, 18–19. (In Chinese) [Google Scholar]
- Zheng, S.; Lin, G. Optimization of power and efficiency for an irreversible Diesel heat engine. Front. Energy Power Eng. China 2010, 4, 560–565. (In Chinese) [Google Scholar] [CrossRef]
- Ebrahimi, R. Performance optimization of a Diesel cycle with specific heat ratio. J. Am. Sci. 2009, 5, 59–63. [Google Scholar]
- Ozsoysal, O.A. Effects of varying air-fuel ratio on the performance of a theoretical Diesel cycle. Int. J. Exergy 2010, 7, 654–666. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of an endoreversible Diesel cycle with variable specific heats of working fluid. Int. J. Ambient Energy 2008, 29, 127–136. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of Diesel cycle with heat transfer, friction and variable specific heats of working fluid. J. Energy Inst. 2007, 80, 239–242. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Jaber, J.O.; Abu-Qudais, M.; Probert, S.D. Effects of friction and temperature-dependent specific-heat of the working fluid on the performance of a Diesel-engine. Appl. Energy 2006, 83, 153–165. [Google Scholar] [CrossRef]
- Fallahipanah, M.; Ghazavi, M.A.; Hashemi, M.; Shahmirzaei, H. Comparison of the performance of Biodiesel, Diesel, and their compound in Diesel air standard irreversible cycles. In Proceedings of the 2011 International Conference on Environment Agriculture Engineering (IPCBEE), Chengdu, China, 29–31 July 2011; Volume 15, pp. 7–13.
- Jeshvaghani, H.S.; Fallahipanah, M.; Gahruei, M.H.; Chen, L. Performance analysis of a Diesel engines fueled by biodiesel blends via thermodynamic simulation of an air-standard Diesel cycle. Int. J. Environ. Sci. Technol. 2014, 11, 139–148. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. Optimum performance analysis of an irreversible Diesel heat engine affected by variable heat capacities of working fluid. Energy Convers. Manag. 2007, 48, 2595–2603. [Google Scholar] [CrossRef]
- He, J.; Lin, J. Effect of multi-irreversibilities on the performance characteristics of an irreversible air-standard Diesel heat engine. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4.
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Finite time thermodynamic modeling and analysis for an irreversible Diesel cycle. Proc. IMechE Part D 2008, 222, 887–894. [Google Scholar] [CrossRef]
- Aithal, S.M. Impact of EGR fraction on diesel engine performance considering heat loss and temperature-dependent properties of the working fluid. Int. J. Energy Res. 2009, 33, 415–430. [Google Scholar] [CrossRef]
- Aithal, S.M. Effect of EGR fraction on Diesel engine cycle efficiency considering thermophysical properties of the gas mixture. Int. J. Therm. Sci. 2016. submitted for publication. [Google Scholar]
- Açıkkalp, E.; Yamık, H. Modeling and optimization of maximum available work for irreversible gas power cycles with temperature dependent specific heat. J. Non-Equilib. Thermodyn. 2015, 40, 25–39. [Google Scholar] [CrossRef]
- Ebrahimi, R. Effects of variable specific heat ratio of working fluid on performance of an endoreversible Diesel cycle. J. Energy Inst. 2010, 83, 1–5. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Chen, L.G. Effects of variable specific heat ratio of working fluid on performance of an irreversible Diesel cycle. Int. J. Ambient Energy 2010, 31, 101–108. [Google Scholar] [CrossRef]
- Sakhrieh, A.; Abu-Nada, E.; Akash, B.; Al-Hinti, I.; Al-Ghandoor, A. Performance of a Diesel engine using a gas mixture with variable specific heats model. J. Energy Inst. 2010, 83, 217–224. [Google Scholar] [CrossRef]
- Wang, P.Y.; Hou, S.S. Performance analysis and comparison of an Atkinson cycle coupled to variable temperature heat reservoirs under maximum power and maximum power density conditions. Energy Convers. Manag. 2005, 46, 2637–2655. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. Performance analysis and parametric optimum criteria of an irreversible Atkinson heat-engine. Appl. Energy 2006, 83, 789–800. [Google Scholar] [CrossRef]
- Ust, Y. A comparative performance analysis and optimization of irreversible Atkinson cycle under maximum power density and maximum power conditions. Int. J. Thermophys. 2009, 30, 1001–1013. [Google Scholar] [CrossRef]
- Ebrahimi, R. Thermodynamic modeling of an Atkinson cycle with respect to relative air-fuel ratio, fuel mass flow rate and residual gases. Acta Phys. Pol. A 2013, 124, 29–34. [Google Scholar] [CrossRef]
- Patodi, K.; Maheshwari, G. Performance analysis of an Atkinson cycle with variable specific-heats of the working fluid under maximum efficient power conditions. Int. J. Low-Carbon Technol. 2013, 8, 289–294. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of an endoreversible Atkinson cycle. J. Energy Inst. 2007, 80, 52–54. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of Atkinson cycle with heat transfer, friction and variable specific heats of working fluid. Appl. Energy 2006, 83, 1210–1221. [Google Scholar] [CrossRef]
- Lin, J.C.; Hou, S.S. Influence of heat loss on the performance of an air-standard Atkinson cycle. Appl. Energy 2007, 84, 904–920. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Akash, B.; Abu-Nada, E.; Al-Hinti, I. Efficiency of Atkinson engine at maximum power density using temperature dependent specific heats. Jordan J. Mech. Ind. Eng. 2008, 2, 71–75. [Google Scholar]
- Ye, X.; Liu, J. Optimum performance of an irreversible Atkinson heat engine with the working substance having temperature-dependent heat capacities. J. Yunnan Univ. Nat. Sci. Edit. 2010, 32, 542–546. (In Chinese) [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Finite time thermodynamic modeling and analysis for an irreversible Atkinson cycle. Therm. Sci. 2010, 14, 887–896. [Google Scholar] [CrossRef]
- Ebrahimi, R. Performance of an endoreversible Atkinson cycle with variable specific heat ratio of working fluid. J. Am. Sci. 2010, 6, 12–17. [Google Scholar]
- Ebrahimi, R. Effects of mean piston speed, equivalence ratio and cylinder wall temperature on performance of an Atkinson engine. Math. Comput. Model. 2011, 53, 1289–1297. [Google Scholar] [CrossRef]
- Ebrahimi, R. Performance analysis of irreversible Atkinson cycle with consideration of stroke length and volumetric efficiency. J. Energy Inst. 2011, 84, 38–43. [Google Scholar] [CrossRef]
- Wu, C.; Kiang, R.L. Work and power optimization of a finite-time Brayton cycle. Int. J. Ambient Energy 1990, 1, 129–136. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Yu, J. Effect of heat resistance on the performance of closed gas turbine regenerated cycle. J. Eng. Thermophys. 1995, 16, 401–404. (In Chinese) [Google Scholar]
- Chen, L.G.; Zheng, J.L.; Sun, F.R.; Wu, C. Power density analysis and optimization of a regenerated closed variable-temperature heat reservoir Brayton cycle. J. Phys. D 2001, 34, 1727–1739. [Google Scholar] [CrossRef]
- Chen, L.G.; Zheng, J.L.; Sun, F.R.; Wu, C. Power density analysis for a regenerated closed Brayton cycle. Open Sys. Inf. Dyn. 2001, 8, 377–391. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Power optimization of a regenerated closed variable -temperature heat reservoir Brayton cycle. Int. J. Sustan. Energy 2007, 26, 1–17. [Google Scholar] [CrossRef]
- Chen, L.G.; Wang, J.H.; Sun, F.R. Power density analysis and optimization of an irreversible closed intercooled regenerated Brayton cycle. Math. Comput. Model. 2008, 48, 527–540. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of a reciprocating endoreversible Brayton cycle with variable specific heats of working fluid. Termotehnica 2008, 12, 19–23. [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Performance of reciprocating Brayton cycle with heat transfer, friction and variable specific heats of working fluid. Int. J. Ambient Energy 2008, 29, 65–75. [Google Scholar] [CrossRef]
- Sahin, B.; Kesgin, U.; Kodal, A.; Vardar, N. Performance optimization of a new combined power cycle based on power density analysis of the Dual cycle. Energy Convers. Manag. 2002, 43, 2019–2031. [Google Scholar] [CrossRef]
- Atmaca, M.; Gumus, M.; Demir, A. Comparative thermodynamic analysis of Dual cycle under alternative conditions. Therm. Sci. 2011, 15, 953–960. [Google Scholar] [CrossRef]
- Blank, D.A.; Wu, C. The effects of combustion on a power-optimized endoreversible Dual cycle. Energy Convers. Manag. 1994, 14, 98–103. [Google Scholar]
- Lin, J.X.; Chen, L.G.; Wu, C.; Sun, F. Finite-time thermodynamic performance of Dual cycle. Int. J. Energy Res. 1999, 23, 765–772. [Google Scholar] [CrossRef]
- Hou, S.S. Heat transfer effects on the performance of an air standard Dual cycle. Energy Convers. Manag. 2004, 45, 3003–3015. [Google Scholar] [CrossRef]
- Qiu, W. Performance limits for international combustion engine cycle within temperature and pressure restraints. Chin. Intern. Combust. Engine Eng. 2004, 25, 66–68. (In Chinese) [Google Scholar]
- Qin, J. Study on FTT of Dual cycle in internal-combustion engine. Intern. Combust. Engines 2007, 4, 12–13. (In Chinese) [Google Scholar]
- Ebrahim, R.; Mahbobian, K.; Gandomkari, F.T. Effects of cut-off ratio on performance of an endoreversible Dual cycle. Appl. Mech. Mater. 2011, 110–116, 2847–2853. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Hajipour, A.; Fahimirad, A. First and second-laws analysis of an air-standard Dual cycle with heat loss consideration. Int. J. Mech. Electr. Comput. Technol. 2014, 4, 315–332. [Google Scholar]
- Wang, W.H.; Chen, L.G.; Sun, F.R.; Wu, C. The effects of friction on the performance of an air stand Dual cycle. Exergy Int. J. 2002, 2, 340–344. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.G.; Sun, F.R. The Power and Efficiency Characteristics for Irreversible Dual Cycles. Trans. CSICE 2002, 20, 408–412. (In Chinese) [Google Scholar]
- Parlak, A.; Sahin, B.; Yasar, H. Performance optimization of an irreversible Dual cycle with respect to pressure ratio and temperature ratio-experimental results of a ceramic coated IDI Diesel engine. Energy Convers. Manag. 2004, 45, 1219–1232. [Google Scholar] [CrossRef]
- Ebrahimi, R. Effects of specific heat ratio on the power output and efficiency characteristics for an irreversible Dual cycle. J. Am. Sci. 2010, 6, 181–184. [Google Scholar]
- Nejad, R.M.; Alaei, P. Effects of irreversible different parameters on performance of air standard dual-cycle. J. Am. Sci. 2011, 7, 608–613. [Google Scholar]
- Parlak, A.; Sahin, B. Performance optimisation of reciprocating heat engine cycles with internal irreversibility. J. Energy Inst. 2006, 79, 241–245. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. An irreversible heat engine model including three typical thermodynamic cycles and their optimum performance analysis. Int. J. Therm. Sci. 2007, 46, 605–613. [Google Scholar] [CrossRef]
- Ozsoysal, O.A. Effects of combustion efficiency on a Dual cycle. Energy Convers. Manag. 2009, 50, 2400–2406. [Google Scholar] [CrossRef]
- Ozsoysal, O.A. Waste energy depending on the maximum temperature and the excess air coefficient in an irreversible Dual cycle. ASCE J. Energy Eng. 2016. submitted for publication. [Google Scholar]
- Ebrahimi, R. Effects of equivalence ratio and mean piston speed on performance of an irreversible Dual cycle. Acta Phys. Pol. A 2011, 120, 384–389. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B.; Ust, Y. Performance maps for an air-standard irreversible Dual–Miller cycle (DMC) with late inlet valve closing (LIVC) version. Energy 2013, 54, 285–290. [Google Scholar] [CrossRef]
- Ust, Y.; Sahin, B.; Kayadelen, H.K.; Gonca, G. Heat transfer effects on the performance of an air-standard irreversible dual cycle. Int. J. Veh. Des. 2013, 63, 102–116. [Google Scholar] [CrossRef]
- Nejad, R.M. Power output and efficiency of international combustion engine based on the FTT theory. Life Sci. J. 2012, 9, 387–390. [Google Scholar]
- Chen, L.G.; Ge, Y.L.; Sun, F.R.; Wu, C. Effects of heat transfer, friction and variable specific heats of working fluid on performance of an irreversible Dual cycle. Energy Convers. Manag. 2006, 47, 3224–3234. [Google Scholar] [CrossRef]
- Wang, F.; Huang, Y.; Gao, W. The effect of variable specific heats of working fluid on the power density characteristic of Dual cycle. Energy Environ. 2010, 2, 4–6. (In Chinese) [Google Scholar]
- Wang, F. Thermodynamics Optimization Sudy for Dual Cycle. Master’s Thesis, Donghua University, Shanghai, China, 2010. [Google Scholar]
- Ye, X. Performance characteristics of an irreversible Dual heat engine under the variable heat capacities. J. Zhangzhou Normal Univ. Nat. Sci. 2011, 24, 26–30. (In Chinese) [Google Scholar]
- Lin, J.C.; Hou, S.S.; Li, S.J. The effects of temperature-dependent specific heats of the working fluid on the performance of a Dual cycle with heat loss and friction. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 5378–5381.
- Gahruei, M.H.; Jeshvaghani, H.S.; Vahidi, S.; Chen, L.G. Mathematical modeling and comparison of air standard Dual and Dual–Atkinson cycles with friction, heat transfer and variable specific-heats of the working fluid. Appl. Math. Model. 2013, 37, 7319–7329. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Finite time thermodynamic modeling and analysis for an irreversible Dual cycle. Comput. Math. Model. 2009, 50, 101–108. [Google Scholar] [CrossRef]
- Ebrahimi, R. Thermodynamic modeling of an irreversible dual cycle: Effect of mean piston speed. Rep. Opin. 2009, 1, 25–30. [Google Scholar]
- Ebrahim, R.; Sherafati, M. Thermodynamic simulation of performance of a Dual cycle with stroke length and volumetric efficiency. J. Therm. Anal. Calorim. 2013, 111, 951–957. [Google Scholar] [CrossRef]
- Asghari, N.; Mousavi Seyedi, S.R. Performance of Dual cycle with variables heats capacity of working fluid. Int. Res. J. Appl. Basic Sci. 2013, 4, 2544–2552. [Google Scholar]
- Ebrahimi, R. Thermodynamic simulation of performance of an endoreversible Dual cycle with variable specific heat ratio of working fluid. J. Am. Sci. 2009, 5, 175–180. [Google Scholar]
- Ebrahimi, R. Effects of cut-off ratio on performance of an irreversible Dual cycle. J. Am. Sci. 2009, 5, 83–90. [Google Scholar]
- Ebrahimi, R. Effects of pressure ratio on the net work output and efficiency characteristics for an endoreversible Dual cycle. J. Energy Inst. 2011, 84, 30–33. [Google Scholar] [CrossRef]
- Ebrahimi, R. Performance analysis of a dual cycle engine with considerations of pressure ratio and cut-off ratio. Acta Phys. Pol. A 2010, 118, 534–539. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Akash, B.; Jaber, J.O.; Mohsen, M.S.; Abu-Nada, E. Efficiency of Miller engine at maximum power density. Int. Commun. Heat Mass Transf. 2002, 29, 1159–1157. [Google Scholar] [CrossRef]
- Mousapour, A.; Rashidi, M.M. Performance evalution of an air-standard Miller cycle with consideration of heat losses. Int. J. Mechatron. Electr. Comput. Technol. 2014, 4, 1175–1191. [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Effects of heat transfer and friction on the performance of an irreversible air-standard Miller cycle. Int. Commun. Heat Mass Transf. 2005, 32, 1045–1056. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. Performance analysis of an irreversible Miller heat engine and its optimum criteria. Appl. Therm. Eng. 2007, 27, 2051–2058. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B.; Ust, Y.; Parlak, A. Comprehensive performance analyses and optimization of the irreversible thermodynamic cycle engines (TCE) under maximum power (MP) and maximum power density (MPD) conditions. Appl. Therm. Eng. 2015, 85, 9–20. [Google Scholar] [CrossRef]
- Ebrahimi, R. Power optimization of a Miller thermal cycle with respect to residual gases and equivalence ratio. Acta Phys. Pol. A 2013, 124, 6–10. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R.; Wu, C. Effects of heat transfer and variable specific heats of working fluid on performance of a Miller cycle. Int. J. Ambient Energy 2005, 26, 203–214. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Jaber, J.O.; Probert, S.D. Efficiency of a Miller engine. Appl. Energy 2006, 83, 343–351. [Google Scholar] [CrossRef]
- Chen, L.G.; Ge, Y.L.; Sun, F.R.; Wu, C. The performance of a Miller cycle with heat transfer, friction and variable specific heats of working fluid. Termotehnica 2010, 14, 24–32. [Google Scholar]
- Doric, J.Z.; Klinar, I.J. The realization and analysis of a novel thermodynamic cycle in internal combustion engine. Therm. Sci. 2011, 15, 961–974. [Google Scholar] [CrossRef]
- Yang, B.; He, J. Performance optimization of a generalized irreversible Miller heat engine cycle. J. Nanchang Univ. Eng. Technol. 2009, 31, 135–138. (In Chinese) [Google Scholar]
- Lin, J.C.; Hou, S.S. Performance analysis of an air standard Miller cycle with considerations of heat loss as a percentage of fuel’s energy, friction and variable specific heats of working fluid. Int. J. Therm. Sci. 2008, 47, 182–191. [Google Scholar] [CrossRef]
- Liu, J. Influence of multi-irreversibilities on the performance of a Miller heat engine. J. Zhangzhou Normal Univ. Nat. Sci. 2009, 22, 48–52. (In Chinese) [Google Scholar]
- Liu, J.; Chen, J. Optimum performance analysis of a class of typical irreversible heat engines with temperature-dependent heat capacities of the working substance. Int. J. Ambient Energy 2010, 31, 59–70. [Google Scholar] [CrossRef]
- Ye, X.M. Effect of the variable heat capacities on the performance of an irreversible Miller heat engine. Frontiers Energy 2012, 6, 280–284. [Google Scholar] [CrossRef]
- Lin, J.; Xu, Z.; Chang, S.; Hao, Y. Finite-time thermodynamic modeling and analysis of an irreversible Miller cycle working on a four-stroke engine. Int. Commun. Heat Mass Transf. 2014, 54, 54–59. [Google Scholar] [CrossRef]
- Mousapour, A.; Rezapour, K. Effects of variable specific heats of the working fluid, internal irreversibility, heat transfer and friction on performance of a Miller cycle. Int. J. Mechatron. Electr. Comput. Technol. 2014, 4, 886–909. [Google Scholar]
- Mousapour, A.; Hajipour, A.; Rashidi, M.M.; Freidoonimehr, N. Performance evaluation of an irreversible Miller cycle comparing finite-time thermodynamics analysis and ANN prediction. Energy 2016, 94, 100–109. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Al-Hinti, I.; Abu-Nada, E.; Akash, B. Performance evaluation of irreversible Miller engine under various specific heat models. Int. Commun. Heat Mass Transf. 2007, 34, 897–906. [Google Scholar] [CrossRef]
- Chen, L.G.; Ge, Y.L.; Sun, F.R.; Wu, C. Finite time thermodynamic modeling and analysis for an irreversible Miller cycle. Int. J. Ambient Energy 2011, 32, 87–94. [Google Scholar] [CrossRef]
- Ebrahimi, R. Effect of expansion-compression ratio on performance of the Miller cycle. Acta Phys. Pol. A 2012, 122, 645–649. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Hoseinpour, M. Performance analysis of irreversible Miller cycle under variable compression ratio. J. Thermophy. Heat Transf. 2013, 27, 542–548. [Google Scholar] [CrossRef]
- Ebrahimi, R. Thermodynamic modeling of performance of a Miller cycle with engine speed and variable specific heat ratio of working fluid. Comput. Math. Appl. 2011, 62, 2169–2176. [Google Scholar] [CrossRef]
- Liu, H.; Xie, M.; Chen, S. Finite-time thermodynamic analysis of porous medium combustion engine. J. Dalian Univ. Technol. 2008, 48, 14–18. (In Chinese) [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Thermodynamic modeling and parametric study for porous medium engine cycles. Termotehnica 2009, 13, 49–55. [Google Scholar]
- Mozurkewich, M.; Berry, R.S. Finite-time thermodynamics: Engine performance improved by optimized piston motion. Proc. Natl. Acad. Sci. USA 1981, 78, 1986–1988. [Google Scholar] [CrossRef] [PubMed]
- Mozurkewich, M.; Berry, R.S. Optimum paths for thermodynamic systems: The ideal Otto cycle. J. Appl. Phys. 1982, 53, 34–42. [Google Scholar] [CrossRef]
- Hoffman, K.H.; Berry, R.S. Optimum paths for thermodynamic systems: The ideal Diesel cycle. J. Appl. Phys. 1985, 58, 2125–2134. [Google Scholar] [CrossRef]
- Blaudeck, P.; Hoffman, K.H. Optimization of the power output for the compression and power stroke of the Diesel engine. In Proceedings of the International Conference ECOS ’95, Istanbul, Turkey, 11–14 July 1995; Volume 2, p. 754.
- Teh, K.Y.; Edwards, C.F. Optimizing piston velocity profile for maximum work output from an IC engine. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006.
- Teh, K.Y.; Miller, S.L.; Edwards, C.F. Thermodynamic requirements for maximum international combustion engine cycle efficiency Part 1: Optimum combustion strategy. Int. J. Engine Res. 2008, 9, 449–465. [Google Scholar] [CrossRef]
- Teh, K.Y.; Miller, S.L.; Edwards, C.F. Thermodynamic requirements for maximum international combustion engine cycle efficiency Part 2: Work extraction and reactant preparation strategies. Int. J. Engine Res. 2008, 9, 467–481. [Google Scholar] [CrossRef]
- Teh, K.Y.; Edwards, C.F. An optimum control approach to minimizing entropy generation in an adiabatic international combustion engine. J. Dyn. Sys. Meas. Control 2008, 130, 041008. [Google Scholar] [CrossRef]
- Teh, K.Y.; Edwards, C.F. An optimum control approach to minimizing entropy generation in an adiabatic IC engine with fixed compression ratio. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006.
- Band, Y.B.; Kafri, O.; Salamon, P. Maximum work production from a heated gas in a cylinder with piston. Chem. Phys. Lett. 1980, 72, 127–130. [Google Scholar] [CrossRef]
- Band, Y.B.; Kafri, O.; Salamon, P. Finite time thermodynamics: Optimum expansion of a heated working fluid. J. Appl. Phys. 1982, 53, 8–28. [Google Scholar] [CrossRef]
- Salamon, P.; Band, Y.B.; Kafri, O. Maximum power from a cycling working fluid. J. Appl. Phys. 1982, 53, 197–202. [Google Scholar] [CrossRef]
- Aizenbud, B.M.; Band, Y.B. Power considerations in the operation of a piston fitted inside a cylinder containing a dynamically heated working fluid. J. Appl. Phys. 1981, 52, 3742–3744. [Google Scholar] [CrossRef]
- Aizenbud, B.M.; Band, Y.B.; Kafri, O. Optimization of a model international combustion engine. J. Appl. Phys. 1982, 53, 1277–1282. [Google Scholar] [CrossRef]
- Band, Y.B.; Kafri, O.; Salamon, P. Optimization of a model external combustion engine. J. Appl. Phys. 1982, 53, 29–33. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Optimum paths of piston motion of irreversible Otto cycle heat engines for minimum entropy generation. Sci. China Ser. G Phys. Mech. Astron. 2010, 40, 1115–1129. (In Chinese) [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Optimum paths of piston motion of irreversible Diesel cycle for minimum entropy generation. Therm. Sci. 2011, 15, 975–993. [Google Scholar] [CrossRef]
- Burzler, J.M. Performance Optima for Endoreversible Systems. Ph.D. Thesis, University of Chemnitz, Chemnitz, Germany, 2002. [Google Scholar]
- Burzler, J.M.; Hoffman, K.H. Optimum Piston Paths for Diesel Engines. In Thermodynamics of Energy Conversion and Transport; Sienuitycz, S., De vos, A., Eds.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Optimum path of piston motion for Otto cycle with linear phenomenological heat transfer law. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 708–719. [Google Scholar] [CrossRef]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Engine performance improved by controlling piston motion: linear phenomenological law system Diesel cycle. Int. J. Therm. Sci. 2012, 51, 163–174. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J.; Sun, F.R. Optimizing piston velocity profile for maximum work output from a generalized radiative law Diesel engine. Math. Comput. Model. 2011, 54, 2051–2063. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Optimum expansion of a heated working fluid with phenomenological heat transfer. Energy Convers. Manag. 1998, 39, 149–156. [Google Scholar] [CrossRef]
- Song, H.J.; Chen, L.G.; Sun, F.R. Optimization of a model external combustion engine with linear phenomenological heat transfer law. J. Energy Inst. 2009, 82, 180–183. [Google Scholar] [CrossRef]
- Chen, L.G.; Song, H.J.; Sun, F.R.; Wu, C. Optimization of a model ICE with linear phenomenological heat transfer law. Int. J. Ambient Energy 2010, 31, 13–22. [Google Scholar] [CrossRef]
- Song, H.J.; Chen, L.G.; Sun, F.R. Optimum expansion of a heated working fluid for maximum work output with generalized radiative heat transfer law. J. Appl. Phys. 2007, 102, 94901. [Google Scholar] [CrossRef]
- Ma, K.; Chen, L.G.; Sun, F.R. Optimum expansion of a heated gas under Dulong–Petit heat Transfer law. J. Eng. Therm. Energy Power 2009, 24, 447–451. (In Chinese) [Google Scholar]
- Chen, L.G.; Song, H.J.; Sun, F.R.; Wu, C. Optimum expansion of a heated working fluid with convective-radiative heat transfer law. Int. J. Ambient Energy 2010, 31, 81–90. [Google Scholar] [CrossRef]
- Ma, K. Optimum Configurations of Engine Piston Motions and Forced Cool-down Processes. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2010. [Google Scholar]
- Ma, K.; Chen, L.G.; Sun, F.R. New solution to optimum expansion of heated gas under generalized radiative heat transfer law. Chin. J. Mech. Eng. 2010, 46, 149–157. (In Chinese) [Google Scholar] [CrossRef]
- Ma, K.; Chen, L.G.; Sun, F.R. Optimization of a model external combustion engine for maximum work output with radiative heat transfer law. J. Eng. Therm. Energy Power 2011, 26, 533–537. (In Chinese) [Google Scholar]
- Chen, L.G.; Ma, K.; Sun, F.R. Optimum expansion of a heated working fluid for maximum work output with time-dependent heat conductance and generalized radiative heat transfer law. J. Non-Equilib. Thermodyn. 2011, 36, 99–122. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. The optimum path of piston motion of irreversible Otto cycle for minimum entropy generation with radiative heat transfer law. J. Energy Inst. 2012, 85, 140–149. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Optimum paths of piston motion of irreversible Diesel cycle heat engines for minimum entropy generation with linear phenomenological heat transfer law. In Proceedings of the Chinese Society of Engineering Thermophysics on Engineering Thermophysics and Energy Utility, Nanjing, China, 8–10 November 2010. (In Chinese)
- Orlov, V.N.; Berry, R.S. Power output from an irreversible heat engine with a non-uniform working fluid. Phys. Rev. A 1990, 42, 7230–7235. [Google Scholar] [CrossRef] [PubMed]
- Orlov, V.N.; Berry, R.S. Analytical and numerical estimates of efficiency for an irreversible heat engine with distributed working fluid. Phys. Rev. A 1992, 45, 7202–7206. [Google Scholar] [CrossRef] [PubMed]
- Orlov, V.N.; Berry, R.S. Power and efficiency limits for international combustion engines via methods of FTT. J. Appl. Phys 1993, 74, 4317–4322. [Google Scholar] [CrossRef]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Maximum power output of a class of irreversible non-regeneration heat engines with a non-uniform working fluid and linear phenomenological heat transfer law. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1961–1970. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J.; Sun, F.R. Maximum efficiency of an irreversible heat engine with a distributed working fluid and linear phenomenological heat transfer law. Revista Mexicana de Física 2010, 56, 231–238. [Google Scholar]
- Chen, L.G.; Xia, S.J.; Sun, F.R. Performance limits for a class of irreversible international combustion engines. Energy Fuels 2010, 24, 295–301. [Google Scholar] [CrossRef]
- Descieux, D.; Feidt, M. Modelling of a spark ignition engine for power-heat production optimization. Oil Gas Sci. Technol. 2011, 66, 737–745. [Google Scholar] [CrossRef]
- Descieux, D.; Feidt, M. One zone thermodynamic model simulation of an ignition compression engine. Appl. Therm. Eng. 2007, 27, 1457–1466. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C. Theoretical and simulated models for an irreversible Otto cycle. J. Appl. Phys. 2008, 104, 094911. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C. Optimizing the operation of a spark ignition engine: Simulation and theoretical tools. J. Appl. Phys. 2009, 105, 094904. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C. Thermodynamic optimization of a spark ignition engine. In Proceedings of the 22nd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2009), Foz do Iguaçu, Brazil, 31 August–3 September 2009; pp. 1979–1987.
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C. Optimizing the geometrical parameters of a spark ignition engine: simulation and theoretical tools. Appl. Therm. Eng. 2011, 31, 803–810. [Google Scholar] [CrossRef]
- Georgiou, D.P.; Theodoropoulos, N.G.; Milidonis, K.F. Ideal thermodynamic cycle analysis for the Meletis–Georgiou vane rotary engine concept. J. Thermodyn. 2010, 2010, 130692. [Google Scholar] [CrossRef]
- Liu, C. Finite Time Thermodynamic Analysis and Optimization for Meletis–Georgiou Cycle. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2011. [Google Scholar]
- Liu, C.; Chen, L.G.; Sun, F.R. Performance analysis and optimization of an irreversible Meletis–Georgiou cycle. In Proceedings of the 7th National Academic Conference on Engineering Thermophysics in Higher Education Institutions, Daqing, China, 19–21 June 2011. (In Chinese)
- Liu, C.; Chen, L.G.; Sun, F.R. Endoreversible Meletis–Georgiou cycle. Int. J. Energy Environ. 2012, 3, 305–322. [Google Scholar]
- Liu, C.; Chen, L.G.; Sun, F.R. Influence of variable specific heats of working fluid on performance of an endreversible Meletis–Georgiou cycle. Int. J. Ambient Energy 2012, 33, 9–22. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.G.; Sun, F.R. Modelling and performance analysis for endreversible Meletis–Georgiou cycle with non-linear relation between specific heat of working fluid and its temperature. J. Energy Inst. 2013, 86, 49–59. [Google Scholar] [CrossRef]
- Chen, L.G.; Liu, C.; Sun, F.R. Performance of irreversible Meletis–Georgiou vane rotary engine cycle with variable specific heats of working fluid. Int. J. Sustan. Energy 2014, 33, 76–95. [Google Scholar] [CrossRef]
- Da Silva, M.F.F. Some considerations about thermodynamic cycles. Eur. J. Phys. 2012, 33, 13–42. [Google Scholar] [CrossRef]
- Liu, X.; Chen, L.G.; Qin, X.Y.; Ge, Y.L.; Sun, F.R. Finite-time thermodynamic analysis for an endoreversible rectangular cycle. Energy Conserv. 2013, 32, 19–21. (In Chinese) [Google Scholar]
- Liu, C.X.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Power and efficiency characteristics for an irreversible rectangular cycle. Power Energy 2013, 34, 113–117. (In Chinese) [Google Scholar]
- Wang, C.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Effects of variable specific heats of working fluid on perfromace of irreversible rectangular cycle. Energy Conserv. 2014, 33, 18–22. (In Chinese) [Google Scholar]
- Wang, C.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Performance analysis of an endoreversible rectangular cycle considering non-linear variable specific heats of working fluid. Int. J. Energy Environ. 2015, 6, 73–80. [Google Scholar]
- Wang, C.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Performance analysis of an irreversible rectangular cycle considering non-linear variable specific heats of working fluid. In Proceedings of Chinese Society Engneering Thermophyscis on Engneering Thermdynamics & Energy Utility, Xian, China, 1–2 November 2014. (In Chinese)
- Wang, C.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Performance analysis of an endoreversible rectangular cycle with heat transfer loss and variable specific heats of working fluid. Int. J. Energy Environ. 2015, 6, 73–80. [Google Scholar]
- Lichty, C. Combustion Engine Processes; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Georgiou, D.P. Useful work and the thermal efficiency in the ideal Lenoir with regenerative preheating. J. Appl. Phys. 2008, 88, 5981–5986. [Google Scholar] [CrossRef]
- Gong, S.W.; Chen, L.G.; Sun, F.R. Performance analysis and optimization of endoreversible Lenoir cycle with polytropic process. Energy Conserv. 2013, 32, 22–26. (In Chinese) [Google Scholar]
- Zhang, Z.Y.; Chen, L.G.; Qin, X.Y.; Sun, F.R. Effects of variable specific heats of working fluid on perfromace of endoreversible Lenori cycle. Energy Conserv. 2013, 32, 14–19. (In Chinese) [Google Scholar]
- Zhou, J.L.; Chen, L.G.; Sun, F.R. Thermodynamic analysis of an air-standard Lenoir cycle with linear variable specific heats of working fluid. Power Energy 2014, 35, 678–682. (In Chinese) [Google Scholar]
- Zhou, J.L.; Chen, L.G.; Sun, F.R. Performance analysis of an air-standard Lenoir cycle with non-linear variable specific heats of working fluid. Energy Conserv. 2015, 34, 19–23. (In Chinese) [Google Scholar]
- Gonca, G. Thermodynamic analysis and performance maps for the irreversible Dual–Atkinson cycle engine (DACE) with considerations of temperature-dependent specific heats, heat transfer and friction losses. Energy Convers. Manag. 2016, 111, 205–216. [Google Scholar] [CrossRef]
- Gonca, G. Performance analysis and optimization of irreversible Dual–Atkinson cycle engine (DACE) with heat transfer effects under maximum power and maximum power density conditions. Appl. Math. Modell. 2016, in press. [Google Scholar] [CrossRef]
- Ust, Y.; Arslan, F.; Ozsari, I.; Cakir, M. Thermodynamic performance analysis and optimization of DMC (Dual Miller Cycle) cogeneration system by considering exergetic performance coefficient and total exergy output criteria. Energy 2015, 90, 552–559. [Google Scholar] [CrossRef]
- Wu, Z.X.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Ecological objective function optimization of an irreversible Dual–Miller cycle with nonlinear variable specific heat ratio of the working fluid. Energy Conserv. 2016. in press (In Chinese) [Google Scholar]
- Cakir, M. The numerical thermodynamic analysis of Otto–Miller cycle (OMC). Therm. Sci. 2016, 20, 363–369. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).