Correction: Jacobsen, C.S., et al. Continuous Variable Quantum Key Distribution with a Noisy Laser. Entropy 2015, 17, 4654–4663

Christian S. Jacobsen; Tobias Gehring; Ulrik L. Andersen

doi:10.3390/e18100373

,

and

Department of Physics, Technical University of Denmark, Fysikvej, 2800 Kongens Lyngby, Denmark

^*

Author to whom correspondence should be addressed.

Entropy2016, 18(10), 373;https://doi.org/10.3390/e18100373

Version Notes

Order Reprints

This is a correction to the manuscript [1]. Due to misprints in Equations (31) and (43) of [2], the results in Figures 2a and 4a in [1] were incorrectly calculated. In Equation (31) of [2], the matrix

C

reads,

C = [\begin{matrix} \sqrt{T (W^{2} - 1)} (2 - \frac{V}{T V + W - T W}) & 0 \\ 0 & - \sqrt{T (W^{2} - 1)} \end{matrix}],

(1)

but it should in fact read,

C = [\begin{matrix} \sqrt{T (W^{2} - 1)} (\frac{V}{T V + W - T W}) & 0 \\ 0 & - \sqrt{T (W^{2} - 1)} \end{matrix}] .

(2)

This misprint propagated such that in Equation (43) of [2], the parameter c reads,

c = \sqrt{W^{2} - 1} (2 - \frac{1 + V}{1 + T V + (1 - T) W}),

(3)

when it should have been

c = \sqrt{W^{2} - 1} (\frac{1 + V}{1 + T V + (1 - T) W}) .

(4)

This errata contains the mentioned plots where the revised expressions have been applied, such that the replacement for Figure 2 in [1] is shown in Figure 1, and Figure 4 in [1] is shown in Figure 2. We keep the corresponding (b) panels for comparison. We note that the corrections only reinforce the conclusions of our paper, which are that reverse reconciliation is vulnerable to preparation noise, while direct reconciliation is not.

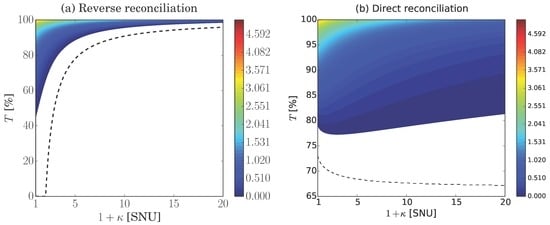
Figure 1. Contour plots of the secure key generation rate for varying preparation noise in shot-noise units (SNUs) and transmission T for (a) reverse reconciliation and (b) direct reconciliation. The error reconciliation efficiency was set to

β = 95 %

, the modulation variance was 32 SNUs, and the channel excess noise

0.11

. The dashed lines indicate the minimal possible transmission of a channel where a positive secret key rate can still be obtained, in the ideal case for

β = 1

, no channel excess noise, and in the limit of high modulation variance. (a) For no preparation noise (

κ = 0

), the rate decreases asymptotically to zero as the transmission approaches zero. When the preparation noise increases, the security of reverse reconciliation is quickly compromised, to the point where almost unity transmission is required to achieve security. (b) For heterodyne detection and no preparation noise, the rate goes to zero at about

79 %

transmission, due to the extra unit of vacuum introduced by heterodyne detection. The plot shows the robustness of direct reconciliation to preparation noise.

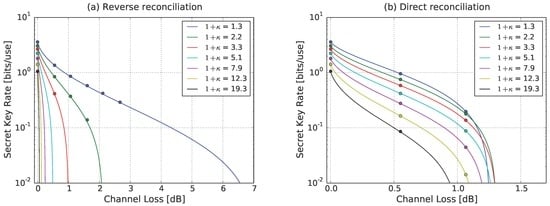
Figure 2. Measured data and theory curves for different levels of preparation noise using (a) reverse reconciliation and (b) direct reconciliation in the post-processing. Error reconciliation efficiency

β = 95 %

. Due to our simulation of losses (see main text), the error bars on the channel loss are negligibly small, and thus not shown in the figure.

Acknowledgments

The authors would like to thank Carlo Ottaviani and Panagiotis Papanastasiou for finding this error.

Conflicts of Interest

The authors declare no conflict of interest.

References

Jacobsen, C.S.; Gehring, T.; Andersen, U.L. Continuous Variable Quantum Key Distribution with a Noisy Laser. Entropy 2015, 17, 4654–4663. [Google Scholar] [CrossRef]
Weedbrook, C.; Pirandola, S.; Ralph, T. Continuous-variable quantum key distribution using thermal states. Phys. Rev. A 2012, 86, 022318. [Google Scholar] [CrossRef]