Abstract
We present a theoretical study of new families of stochastic complex information modules encoded in the hypergraph states which are defined by the fractional entropic descriptor. The essential connection between the Lyapunov exponents and d-regular hypergraph fractal set is elucidated. To further resolve the divergence in the complexity of classical and quantum representation of a hypergraph, we have investigated the notion of non-amenability and its relation to combinatorics of dynamical self-organization for the case of fractal system of free group on finite generators. The exact relation between notion of hypergraph non-locality and quantum encoding through system sets of specified non-Abelian fractal geometric structures is presented. Obtained results give important impetus towards designing of approximation algorithms for chip imprinted circuits in scalable quantum information systems.
1. Introduction
The field of algebraic topology has passed an essential evolution in attaching algebraic objects to topological spaces starting from the simple graph models associated to vertices and edges in terms of Laplacian matrices, leading to higher-order dimensional structures modified through simplices or cliques, finalizing with an elegant mature representation of non-local hypergraph states [1]. From the aspect of the algebraic topology, the dimension of the specific measure for the hypergraph (set system) is a function of the corresponding metric [2]. As a natural extension former implicates that for algebraic dynamical system the entropy of the measure depends on set system evolution process upon its metric spaces [3], i.e., the metric space represents the natural constituent assembly of the set system dimension in dynamical framework. Moreover, for algebraic dynamical systems the dimension directly relates to entropy via geometric concept of the Lyapunov exponents [4,5], which can be successfully applied to quantify the set system complexity in a sense of the topological [6,7] as well as the metric entropy [8].
In general sense the topological entropy represents quantitative measure of complexity for continuous map defined on compact metric spaces of dynamical system [2]. While the metric entropy quantifies the number of typical orbits, the topological entropy represents the exponential growth rate of the number of orbit segments that are distinguishable with finite resolution. Hence, dynamical property of the maps is regulated by the topological entropy, i.e., between distinguishable orbits it measures growth rate of the number of different orbits of length n in infinite limit. Specifically, topological entropy as a non-causal measure of exponential increase of the number of maximal intervals of monotonicity is introduced for a piecewise interval monotone map [9,10].
Important feature of the set system topological entropy is its close relation to periodic orbits. For each periodic orbit P of continuous map f [11] given on the interval I, it can be assigned a corresponding “local pointwise” topological entropy h(P) [12] representing the connection map between distinct points of periodic orbit [13], and at the same time representing the infimum of the entropies of all corresponding maps which display orbits of the same configuration as P. On the other hand, for the piecewise monotone interval, the entropy of each continuous map f corresponds to the supremum of the number h(P), relating in that way to sum of all periodic orbits P of f [14].
In this study we introduce certain situations where the non-local correlations arise from the non-Abelian structure of topological algebraic set systems, addressing at the same time the divergence in dimension and complexity measures of classical and quantum hypergraph representation. In particular, connection between the periodic orbits and the topological entropy for continuous maps on specific fractal hypergraph sets, realized by the action of the free group on two generators F2 [15,16], is analyzed in Section 2. Geometric measure of exponential divergence between nearby orbits of F2 free group is represented via fractional entropic descriptor [17] where action of two generators on a free group corresponds to iteration on two Lyapunov scales. In Section 3, we further exploit generalization of the Shannon measure entropy in order to assess relation between the Lyapunov exponents and the Rényi entropy [18], addressing at the same time some of the unique properties of the presented fractal set. The Rényi entropy as a measure of complexity of dynamical system is analyzed in a sense of correlation of probability distribution function to its local expansion rate, defined by the Lyapunov exponents. Dynamical features of trajectory based metric are further compared to topological entropy equivalent in order to fully quantify the parameters of complexity and characterize combinatorics of dynamical self-organization for the case of fractal system of free group on finite generators. Finally, in Sections 4 and 5, using the underlying fractal structure of the free group on two generators we construct the quantum hypergraph state [1] and demonstrate essential relation between its non-local correlations and the system complexity. Using the stabilizer formalism, the hypergraph states are defined as a class of multiqubit quantum states which generalizes graph states [19]. Obtained results allow efficient mapping of the quantum hypergraph states into corresponding logic circuits. Namely, in scope of the stabilizer formalism [20], in terms of a group theory, it is possible to efficiently implement topological logic gates [21], using operations, such as controlled-NOT, Phase, Hadamard gates. In particular, a stabilizer code on n qubits (a quantum error-correcting code [22]) uses Pauli operators as stabilizer generators. For instance, in order to stabilize a subspace of 2s dimension which belongs to the 2n dimensional Hilbert space, in total s stabilizer generators are required. In that case, k = n − s logical qubits will be encoded into 2n−s dimensional logical subspace. The space stabilized by the generators does not necessarily have to form an Abelian subgroup of the Pauli group over qubits [23]. In particular case of generators, where non-Abelian group is of size s + 2e = n − k (k is notation of the number of qubits, codeword length is denoted as n ; e denotes ebits and s denotes the code ancilla qubit) the non-Abelian subgroup can be decomposed into two subgroups: the commuting isotropic group and the entanglement subgroup with anticommuting pairs [24].
2. Non-Abelian Statistics over Hypergraph Fractal Set
As we introduce some of the basic notations related to the hypergraph based fractal set, without loss of generality we assume topology embedded in ℝ3, where a hypergraph [25] represents a compact connected Hausdorff space represented by a subset G(V, E) of vertex elements V = {v1,v2,…,vn} and edges E ⊂ V,
, where E = {e1,e2,…,em}. Considering a point x ∈ V, the number of edges which contain x will be denoted as the valence, v, of x. In case of a tree configuration where v ≥ 2, we have the set of branching points B(G)which coincide with the spatial hypergraph coordinates.
We shall first introduce some basic definitions related to group-theoretic construction of the specific graph sets. Thus, important property relating to the topological entropy of the special class of hypepergraphs, introduced as a generalization of graphs in which infinite number of infinite clusters appears, is presented. Such geometric structure is the Cayley fractal set Γ = ΓG,H obtained by action of the free group G on finite generators, H ⊆ G.
Let G be a finitely generated group with the finite generating set H = {e1,…,en}, where H ⊆ G. Then, the vertices((x, u) ∈ Γp) ∈ G of corresponding sub-graph Γp, the set of edges G×{e1,…,en} and corresponding mapping functions o and t where o(x,e) = v and t (x,e) = x·e, are all denoted by ΓG,H. Action of the generator elements ei ∈ H over G connects vertices by inserting weighted edges h = g · ei [26].
Consequently, a rank two free group, e.g., a free group G on two generators H = (a±1, b±1), H ⊆ G, forms a 4-valent tree. Detaching any edge from such 4-valent structure parts the underlying graph Γp into disjoint connected sets, resulting in infinitely many self-similar clusters for any p, where parameter p ∈ [0, 1] determines connectivity of each edge of Γp, i.e., to be open with probability p and closed with probability 1 − p. Uniqueness of the infinite cluster only appears when p = 1 and this property is connected to the notion of non-amenability [27], which directly relates to the non-Abelian statistics [28]. Hence, amenability in terms of a group structure directly influences power to determine a specific probability measure on G that is left invariant on subsets of G. Latter gives a clear relation between non-amenability and uniqueness of the fractal set, seen as an infinite cluster, which can be quantitatively assessed from the line of topological entropy and geometric concept of Lyapunov.
Example: Let Γ = ΓG,H be a Cayley tree where Γp ⊂ Γ is its underlying graph structure. As a boundary of Γp we determine the edge-set |∂Γp| which represents the number of edges leaving Γ where ∂Γp = {(e ∈ x,u) | x ∈ Γp, u ∈ Γ \ Γp}.
Definition 1: Amenability [29], in the scope of the set theory, represents a property of possessing an invariant mean for the equivalence classes on almost all scale dimensions with respect to a given measure.
Definition 2: By the Følner condition [30] a set system defined on Cayley tree ΓG,H is amenable if and only if:
where | · | denotes the related set cardinality, Γp ⊂ Γ are finite subsets on a finitely generated group G, and ∂Γp is the edge-set representing the boundary of Γp in reference to a given set of generators acting on G.
Definition 3—Dirichlet’s principle [31]: For each eventual partition of a set X (consisting of n elements, associated to positive integers) there exists a subset x ⊆ X, |x| = N, where N is a positive integer which corresponds to n, such that the mapping П : X → X restricted to the subset x is either a constant or a 1-1 correspondence.
The above definition addresses existence and important relation of topological conjugacy between the set-system partitions and the elements of underlying subset.
Example: Let T (X, E) be a tree with vertex set X (T) and edge set E (T). Partitioning of T (X, E) into P = {X1 (T), X2 (T),…, Xn (T)} corresponds to n sub-trees defined on a subset x ⊆ X, |x| = N, where the number of spanning trees Xi (T) on N elements xi ⊆ Xi is given by a constant NN−2 [32].
Proposition 1: In case of a free group on two generators obtained tree structure ΓG,H is non-amenable, i.e., h(G) ≠ 0 [33], because every step of selection over the tree (vertex) set V (T) = {Xi}, i =1,…,n (in order to form a connected sub-graph Γp) always generates the same number of boundary edges as vertices (due to the self-similar fractal property), i.e., any additional vertex element being appended to a connected sub-graph will create ≥ 2 additional edges |∂Γp|.
Proof: (Erdos-Rado Canonization Lemma [31]) For each
which is the generator of the ith tree on a sub-graph Γp, let the corresponding sub-graph vertex set x (Γp) = {xi ⊆ Xi|xi ∈ (x1,…, xN)} be labeled with x1 = {1}, x2 = {1, 2},…, xN = {1, 2,…,N}. The order of Γp is |x| = N; it is associated to the number of xi elements, which conform with the length-N Cayley permutation (C-permutation) p [34] of ordered set x = {x1,…, xN}, where x1 < x2 < … <xN. Then, for every px:|x| = N it follows that:
converges to a positive limit, where px is the weight probability distribution of each edge-set: ∂Γp = {(ei ∈ xi, ui) | xi ∈ Γp, ui ∈ Γ \ Γp}, where two successive elements from x appear in C-permutation, defined for a stochastic sequence:
,
, and
is the probability distribution of the set x = {xi} on specified hypergraph partition, where ∑|x|=NTx represents a cluster sum of distinguishable hypergraph partitions П:{∑|x|=NTx} [35]. Tx is assigned on time interval: 0 <τx ≤ ∞ which defines exponential growth where τ* <τx is the time of each vertex generation. Tx must be non-negative for each possible sequence of x. Thus, the random variable must have a positive value within the sequence of all |x| = N possible values which are normalized to probability one, i.e., Tx must sum to one (directly addressing that h(G) ≠ 0).
Consequently, the sequence pn,max := max{px:|x| = N} converges to a positive limit, straightforwardly based on the stronger conjecture:
pn,max converges to a positive limit with probability one, where:
is the weight probability distribution of each edge-set: ∂Γp = {(ei ∈ xi, ui) | xi ∈ Γp, ui ∈ Γ \ Γp}, where two successive elements from x appear in N-th level C-permutation for which: if |x| = N (where |x| is associated to the number of xi elements), then the probability
is in total ∑N – measurable (the sum is implicitly over all possible xi) and as a result the denominator converges to a positive limit with probability one, ∑|x|=N Tx =1. Likewise, the numerator Tx : |x| = N must converge to a positive limit with probability one for the maximal time interval τx → ∞, where
.
We focus next on a connection between uniqueness of the ΓG,H free group fractal set and the topological entropy, introducing a key role of non-amenability notion which is a prime characteristic of non-Abelian group topology [36]. Assuming a continuous map f of a compact metric space χ, the topological entropy represents the supremum of the metric entropy, where supremum is taken over all f-invariant Borel probability measures μ [37,38] on a topological space.
This property of the topological entropy can be easily extended for an arbitrary function a(⋅, t) which represents a scale if it is expanding for all intervals t and limt→∞ a(s,t) = ∞ for all scale parameters s. Hence, the topological entropy for a given growth scale a is:
where supremum is taken over all localization parameters represented by the probability measures μ [39]. Now, for N-level Cayley tree ΓG,H, where Γp ⊂ Γ is its underlying graph structure, we define an f -invariant Borel probability measure μ on the finite generating set xi : |x| = N, xi ∈ Γp (where x = {xi ⊆ Xi|xi ∈ (x1,…, xN)} and |x| represents the number of xi elements, which give raise to the length-N Cayley permutation), as:
where
and
are the probability distributions which denote the occurrences of the set system finite spatial partitions.
Example: Let mapping f: M → M define the metric space where λ1 >λ2 > … > λk are the Lyapunov exponents of (f, μ) and Ek are the linear subspaces corresponding to exponents λk so that the dimension D of Ek corresponds to multiplicity of λk. For a hypergraph based fractal set of rank two free group, periodic orbits are defined on a hyperbolic ε = 0 space (due to a tree structure). In particular, geometric measure of the exponential divergence between nearby orbits of given sets is represented by the Lyapunov exponents, which can be successfully embedded into probabilistic framework in the following way.
Action of two generators on a free group corresponds to iteration of two scales which form the fractal set [40,41]. Correspondingly, two scales produce a spectrum of Lyapunov exponents: in this case for the symmetric map, λ (px) = px ln a + (1− px) ln b, with
; m,n ∈ ℤ varying from 0 to 1 in the range: 0 ≤ px ≤ 1 (λ (px = 0) ≤ λmax (px) ≤λ (px =1)), where λ (px = 0) = ln b; and λ (px =1) = ln a.
In presence of the infinite sequences of intervals, which are defined by two scales lm,n = a−m b−n+m where
is fixed, and n takes
values, we have Nn (λmax) = 2n defined intervals and correspondingly Nm (λmin) = n!/m!(n − m)! such defined intervals that determine the fractal dimension D(λk) [17,40] as:
Here
relates directly to Lyapunov coefficients λk.
For the rank two generators F2 {a±1, b±1} action on a free group G, the corresponding Lyapunov coefficients are
. Then, the entropic descriptor [17], i.e., a measure of complexity associated to the fractal dimension D(λk):
quantifies the number of unique sequences produced by the ratio
. Thus x = (xi) (according to i = 1,…, N iterations) determines a periodic point [14] for the shift σ, where for each n ≥1, there are 2n points per period n for σ; this specific property and its relation to topological entropy we discuss in the next section.
Now, the entropy Hn of the probability measure μ, which is defined on the finite (or countable) generating set H {xi : |x| = N}, H ⊆ G (where {Γp ⊂ Γ | xi (Γp) ∈ (x1,…,xN)} and |x| is the number of xi elements, i.e., the order of Γp) for a Cayley fractal tree Γ = ΓG,H obtained after k permutations over elements of N –th sequence (xN), is given by:
where
are the probabilities for occurrence of the partitions:
that are produced by the generating set of H ⊆ G, where
is the probability operator acting over the specified generating set and λk is the Lyapunov coefficient.
2.1. Topological Entropy and Periodic Orbit Growth for Hypergraph Fractal Set
Without loss of generality, topological entropy is defined as a measure of maximal complexity of dynamical system.
Definition 4: Let
be the finite set of n elements (alphabet), describing the discrete topology [42]. The dynamical system consisting of the sets of all bi-infinite symbol sequences
represents the full
-shift over a finite alphabet
, where the shift map
shifts all sequences
to the left,(σx)i = xi+1.
Theorem 1: (Hasselblatt and Katok [43]) Topological entropy and periodic orbit growth coincide for shifts.
Proof: Let σ : ∑k → ∑k be a bilateral k-shift, acting on sequence {1,…,k}, and α = {[1],…,[k]} be a topological generator which transfers the spatial partitions of ∑k into closed cylinders of length 1. Correspondingly,
denotes transformation of spatial partition of ∑k into kn cylinders of length n. As a result we have:
where for n →1 straightforwardly topological entropy for bilateral k-shift coincides with the logarithm of k sequences:
Extension: htop (σk) = p (σk) = log k stems from the restriction of the bilateral k-shift over invariant subset of k sequences, with a property of symbolic system [44].
The above can be easily explained using the following coin experiment.
Example: Let σ,
be the twofold-switch operator acting over all spatial elements of
which denote the symbolic system (subshift) [44], where this operator determines the outcomes of an infinite series of trials (measurements). Then, considering that the sum of all possible outcomes in n trials is given by
, the topological entropy is defined as
.
Thus, specifying the outcomes as P(H) = p and P(T) =1− p in fact determines the metric entropy hμ (σ) = − p log p − (1− p) log(1− p). In case when the output is biased ({H, T} represents the full shift), the number of typical outcomes in n trials is ∼ enh for h < log 2, representing in that way the inequality relation between the topological
and the metric entropy
:
Lemma 1: Extending relation (10) to a hypergraph subset G (V, H) for a finite type subshift [44]:
where M is irreducible n×n transition matrix with entries in {0, 1}, under condition that the largest eigenvalue is always real by the Perron-Frobenius theorem [45], results that the topological entropy htop (σ) is equal to the largest positive eigenvalue of matrix M.
Proof: Let α ={[1],…,[n]} be a topological generator which induces partitions
of space
into a closed cylinders of length n, where σ is a subshift of finite type, and resulting topological entropy coincides with the number of cylinders of length n in
where cylinder set of length n is defined on space
if and only if and the number of length-n cylinders that overlap space
is ‖Mn‖.
As a result, the connection between the topological entropy and the transition matrix [15] is given by:
where the topological entropy equals to the logarithm of the largest eigenvalue of the transition matrix (spectral radius) [46].
2.1. Relations between Lyapunov Spectrum, System Dimension and Measure Entropy for Hypergraph Fractal Set
In case of the systems with infinite degrees of freedom (e.g., the presented fractal system of the free group on two generators, where applies the notion of non-amenability given by Equation (1)) assuming d -dimensional system of linear size Ld, it is possible to establish relation between Lyapunov spectrum, dimension of the system and measure entropy. The first step towards such relation is to resolve the case of ‘thermodynamic’ limit, L → ∞, for the Lyapunov spectrum, which can be assessed by analyzing whether ratio λi : x = i/Ld, x ∈ [0, 1], converges to a density function λi = Λ(x) as L → ∞.
Starting from the Pesin formula [47], where θ is the Heaviside function:
which infers that the Kolmogorov-Sinai entropy [48,49] is in this case proportional to the maximum Lyapunov exponent
. Thus, there is only one positive Lyapunov exponent, as the system size approaches thermodynamic limit L → ∞.
Local entropy hl follows from Equation (14); it is defined for each degree of freedom for the system of linear size Ld, as:
where after setting the existence of bound: λi = Λ(x) as L → ∞, total entropy h is directly related to the dimension of the system. Indeed, using the Kaplan and Yorke formula [50], the fractal dimension D can be estimated from the Lyapunov spectrum as:
Also, under condition: ∑p λi > 0, the dimension of the attractor, Dλ, is proportional to Ld leading to the existence of inherent dimension density
per system degree of freedom.
Now we are ready to elucidate the essential connection between the Lyapunov exponents λi and d-regular hypergraph fractal set. We use the set-theoretic approach, starting from the structure of the Cayley tree. The Cayley tree on a free group G generated by the finite set H ⊆ G is represented by the graph with vertex set V ∈ G and the edge set {(a, b)|a, b ∈ H}. Let G be a free group on two generators where L2 (G) is the function space on G, then L2 (G) can be decomposed into subspaces:
meaning that it has the value 1 on the i-th vertex of a set G and 0 otherwise.
Proposition 2: Assume that the Cayley set satisfies relation: H = H−1. This condition as a result infers existence of orthogonal set of eigenvectors and eigenvalues belonging to the adjacency matrix A. Under constraint that the eigenvalues of A, i.e.,
are bounded by corresponding vector subspaces Ei, the norm of the F -uniform, d-regular (each vertex has degree d) Cayley hypergraph on n vertices is defined as
where
, and Mi,i is a diagonal matrix.
Proof: We first demonstrate that H = H−1 property directly implies that M as a symmetric and a real matrix can be diagonalized by a set of eigenvectors in Rd. Namely, if H is a Hermitian matrix, then H = UMUH, where U is unitary matrix and M is a diagonal matrix (and as such also a symmetric matrix) with real entries λi. Therefore: H−1 = (UMUH)−1 = (UH)−1 M−1U−1 = UM−1UH, since U−1 = UH. Here M−1 is a diagonal matrix with corresponding elements 1/λi. Likewise, H−1 is also a Hermitian matrix where (H−1)H = (UM−1UH)H = U(M−1)H UH = UM−1UH = H−1. Now, let A and F be the adjacency matrix and generating function of the Cayley hypergraph, respectively. A and F are bounded on the vector subspace Ei corresponding to the d dimensional state ρ (where the coefficients of {ρi, j} are given with respect to elements of the basis Ei) as:
leading to:
where δi,k is the Kronecker delta function, ensuing that generating function satisfies:
where Mj,l are elements of the diagonal matrix:
M acts as a diagonal matrix by extending these eigenvectors to the complex basis of Cd. Consequently, as the normalization for each ρi, j element is given by
it follows that for each i, j the coefficients ρi, j represent eigenvectors of the adjacency matrix A with eigenvalue 0 if i ≠ j, and eigenvalue
if i = j.
Now we can easily generalize the concept of the Cayley Γ = ΓG,H graph to the corresponding hypergraph set.
Proposition 3: The eigenvalues of the d-regular Cayley hypergraph can be determined from the Γ = ΓG,H subgraph and from the L2 (G) decomposition.
Proof: Let H be the symmetric set of generators with the vertex set assigned on a finite group G, then the d-regular Cayley hypergraph on G and H is composed of edges E = {(e1,…,ed):e1…ed ∈ H}. Because of its tree character, d-regular Cayley hypergraph has intrinsic Markov property and it can be analyzed in terms of a piecewise linear Markov map f [51] according to the spectral radius of matrix M (whose elements are {0, 1}). Direct consequence is that the topological entropy corresponds to the maximal eigenvalue of the matrix M as it is already shown by Equation (13).
Moreover, taking into account the bound λi = Λ(x) as L → ∞ where
, it follows that Lyapunov spectrum equals to the maximal Lyapunov exponent
. As a result the Kolmogorov-Sinai entropy in case of d-regular Cayley hypergraph is proportional to:
3. Rényi Topological Entropy and Lyapunov Exponents for Non-Abelian Fractal Set
Assume that the fractal set is partitioned into distinguishable clusters of size r. In order to localize a point with a precision r one must determine the partition which contains the point and quantify average data on particular partition. For this one can use the Shannon information formula, and also the topological Rényi entropy of order q, which is directly related to the generalized dimension [52]:
where Pi is the probability measure of the ith partition.
Now, let П be a partition assigned by a free group G on rank two generators H ⊆ G where
are the elements of partitions Пn obtained under measure preserving transformation [53]:
The Rényi entropy of order q is the supremum over all distinguishable partitions Пn:
Next step establishes relation between the topological Rényi entropy of order q and the generalized Lyapunov exponents Λ. By assigning the probability distribution function px (i0…in−1) to the occurrence of distinguishable partitions Пn that are specified in time steps: i0 (t = 0), i1 (t = 1),…,in−1 (t = n −1) as
for which:
and using the generalized measure Λ (ik) which represents the average expansion rate of information given by the building block ik of dimensionε which constituents each partition Пi; the initial building block i0 is defined by the corresponding Lyapunov spectrum Λ(i0). After the initialization is performed, the Lyapunov spectrum is given by: Λ(i0)Λ(i1),⋯,Λ(in−1) from which we obtain the probability rate for the expansion of the spatial partitions building blocks:
Substitution of Equation (26) into Equation (25) gives:
where αn is obtained from the normalization:
and represents the number of various distinguishable clusters (blocks) of length n. Now, from Equation (27) follows the measure:
which establishes the correlation between the topological Rényi entropy of order q and the generalized Lyapunov exponents Λ(ik), for the limit n → ∞ this correlation reads:
Example: Let G(V, H) be a hypergraph defined on a free group G on finite generators H, where vertex set:
, H ⊆ G, and topological order coefficients: qi =(q1,…,qn),
, are assigned on all local partitions Пi, such that:
and defined on a metric space Mx with probability measure μ, where a nonnegative function
is associated to each generator set Hi. Then, under constraint of integrability [38]:
and according to Equation (24) where the Rényi entropy of order q is the supremum over all distinguishable hypergraph partitions, it follows the expression for the fractional Rényi entropy of order q for a hypergraph defined on a free group G with respect to the generator set Hi ⊆ G:
In particular case of two generators, the Rényi’s entropy dependence from the probability measure μx, and the probability rate for the expansion of the spatial partitions (Equation (31)), for different values of order q, is presented in Figure 1 and Figure 2, respectively. Figure 3 shows the maximum allowed correlation between the topological Rényi entropy of order q and the generalized Lyapunov exponents Λ(ik) for the partitioned hypergraph fractal set (Equation (24) obtained by action of the rank -2 free group on finite generators [26].
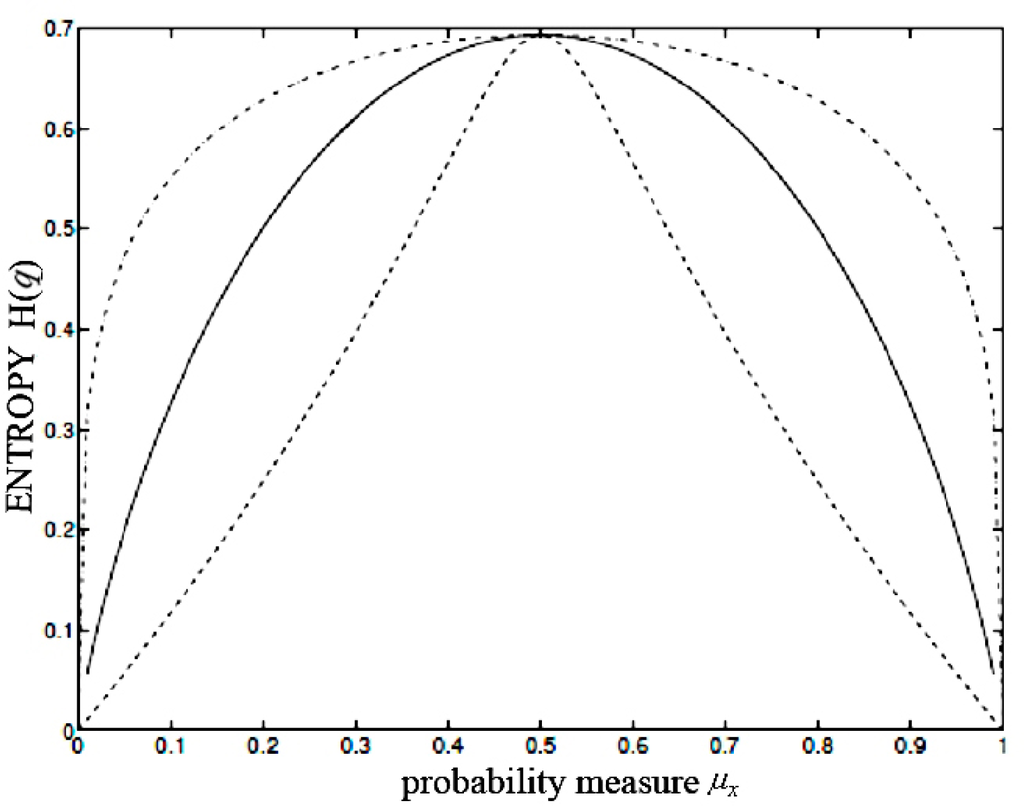
Figure 1.
Topological Rényi entropy as a function of the probability measure μx over hypergraph fractal set of free group on finite generators, according to equation (31), and order: q = 0.4 (dash-dotted), q = 5 (dashed) and q = 1 (full line).
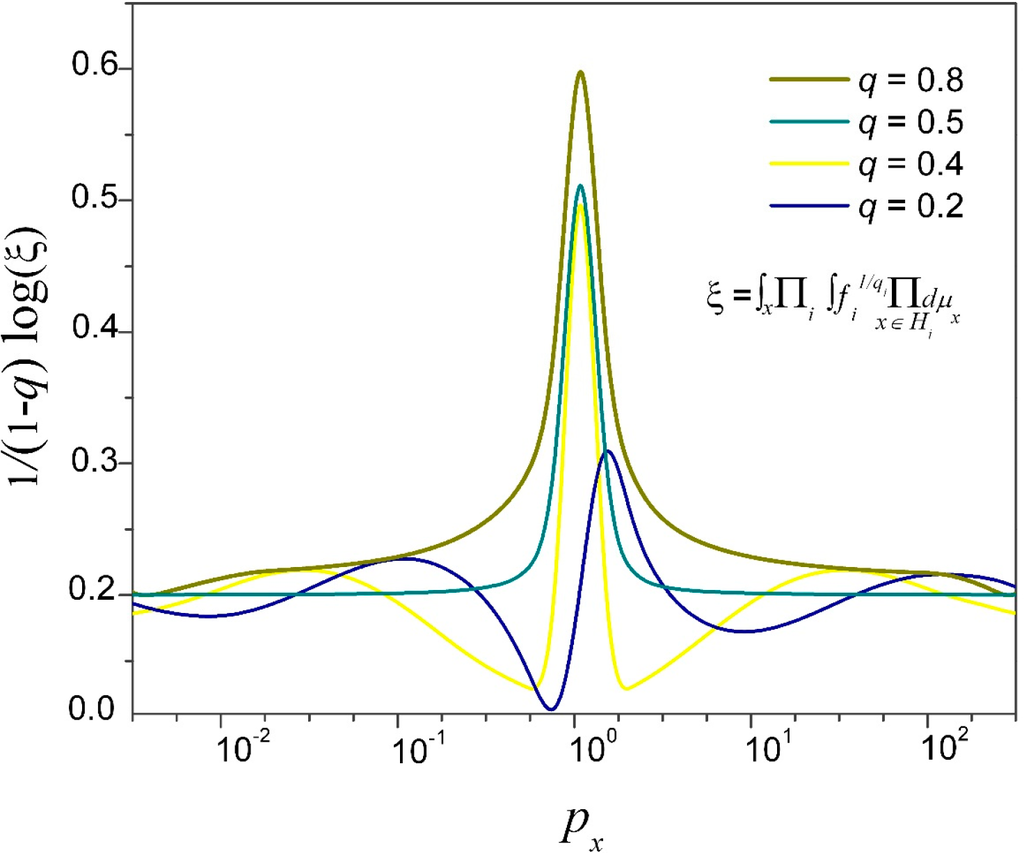
Figure 2.
Plot of the output entropies as functions of probability rate for the expansion of the spatial partitions (Equation (31)) for different input order parameters (designated by solid lines): q = 0.2 (blue), q = 0.4 (yellow), q = 0.5 (dark cyan), q = 0.8 (dark yellow).
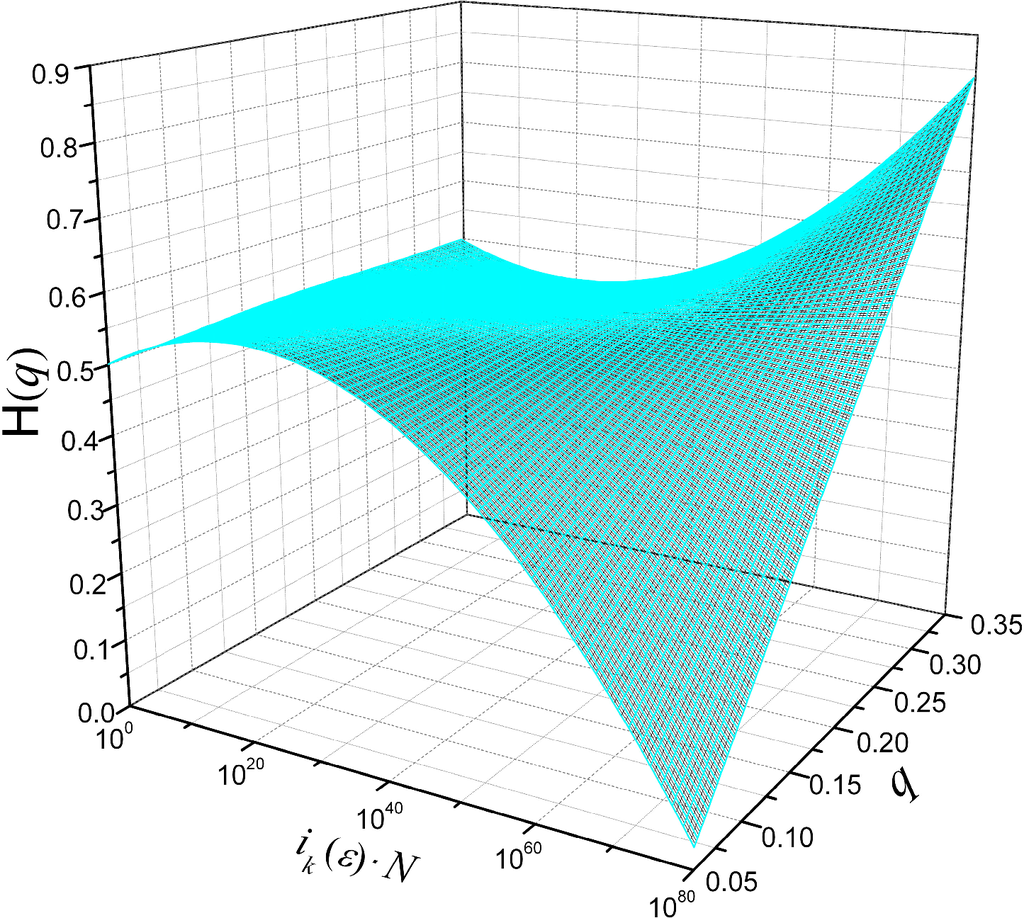
Figure 3.
Maximum allowed correlation between the topological Rényi entropy of order q and the generalized Lyapunov exponents Λ(ik) obtained for the supremum output entropy conjecture over all distinguishable partitions (Equation (24)). The x-y axes are the average expansion rate of information given by the building block ik of dimensionε on N intervals and input order parameters q, respectively.
4. Underlying Non-Locality of F2 —Hypergraph State
In this section we present a more structural understanding of non-locality [54] of a hypergraph state which is obtained by action of the rank two free group, called F2. In particular, we show that intrinsic non-local character of the non-Abelian actions [55] of the free group on two generators is closely tied to notion of the non-amenability.
We consider the algebraic topological structure obtained via generating set HUH−1, H :={a±1,b±1}, where a ; b denote basis of the free group F2 on two generators {a±1,b±1} which realize an infinite 4-regular tree represented as the undirected Cayley set. In this case, the infinite 4-regular structure gives a hypergraph based covering space for the wedge of two circles H1 ^ H1,
which has fundamental (δ = 0) hyperbolic group F2 ≅ ℤ*ℤ where π1 (H1 ^ H1,0) ≅π1 (H1,0) ∗ π1 (H1,0).
Definition 5: Group G is amenable if and only if it does not produce paradoxical decomposition [43].
From the constraint of amenability and Equation (1) it follows that a rank two free group F2 = a,a−1,b,b−1|a,b ∈ H of SO(3) is non-amenable and as a result it is non-Abelian [27] (see fundamental theorem of finitely generated Abelian groups), and there exists a countable subset H on the sphere S such that the decomposition S − H is F -paradoxical [56,57]; a straight repercussion is that SO(3) is paradoxical too. Thus, the elements of the free group of two generators F2 ∈ SO(3) are distance preserving as operators on ℝ3, where they represent a group of nontrivial, independent rotations of the sphere about axis that passes through the sphere center.
Likewise, there are rotations aR, bR of the unit sphere in ℝ3 that generate exactly the free group on two generators. To prove that let us define a group of rotations (aR (φ),bR (φ)) for φ = arccos(1/3) about orthogonal axes:
In this case elements of a group: aR; bR;
;
map vector basis (1,0,0) to a basis
, where x, y, and z as integers, y ≠ 0, and n is the length of the information string.
Proposition 4: Let f: aR → a, f: bR → b, then for a generating set H:{a,b} we can define a rank 2 free group F2 = a,a−1,b,b−1|a,b ∈ H, which determines paradoxical decomposition of S − H, manifesting in this way intrinsic non-local feature of the hypergraph fractal state based on F2 free group. In particular this means that F2 ∈ SO(3) is partitioned into five parts where only four are needed to establish two exact copies of the original sphere S, i.e., to perform the paradoxical decomposition.
Proof: The natural decomposition of F2 ∈ SO(3) is given by:
where for all disjoints sets, ω(·) denotes all possible information strings starting with (·).
The following relations establish correlation between information strings and the set of free group on two generators:
But, another decomposition yields the following property:
where ω(·)c is the complement of the corresponding set ω(·), and where actual multiplying ω(a−1) by a acts like translation over ω(b) and ω(b−1). Here h ∈ F2\ω(a), then a−1h ∈ ω(a−1), and h = a(a−1h) ∈ aω(a−1).
Correspondingly, the third decomposition of F2 is given by:
Now, in order to demonstrate the notion of non-amenability which directly implicates non-locality of the hypergraph quantum states based on the free group F2, one can start by assigning the mean probability distribution m(F2) = 1 that maps subsets of F2 = a,a−1,b,b−1|a,b ∈ H to the unit interval [0, 1] as following:
likewise:
Then, from Equation (33) we have:
Taking into account equation (40), latter also holds for:
Thus, from Equations (37), (38) and right side of Equation (42), directly follows
finally, by inserting into Equation (43) the relations which address the mean probability distribution of F2:
where:
we obtain the characteristic inequality relation for the free group F2 set corresponding to CHSH inequality [58]:
where N is the number of sequences of intervals corresponding to the fractal dimension (see Figure 4.) where uniqueness of the infinite cluster only appears when p =1. Analogue inequality relation can be obtained for all corresponding decomposition elements of F2 ∈ SO(3). Former contraintuitive inequality [54,58] directly provides the resource for analysis of the non-local properties of the hypergraph quantum states [1], defined in this case on the 4-regular subset a,a−1,b,b−1|a,b ∈ H of the free group, F2. Correlation over the elements of the mean probability distribution of F2 corresponds to operations of translation and inversion between information strings starting with: C(ω(a),ω(b)), C(ω(a),ω(b−1)), C(ω(a−1),ω(b)), C(ω(a−1), ω(b−1)). In that context, bound p = 1 on m(F2)CHSH (Equation (44)) establishes demarcation line between the complexity of the classical (local realism) and the quantum counterpart [59] of system state.
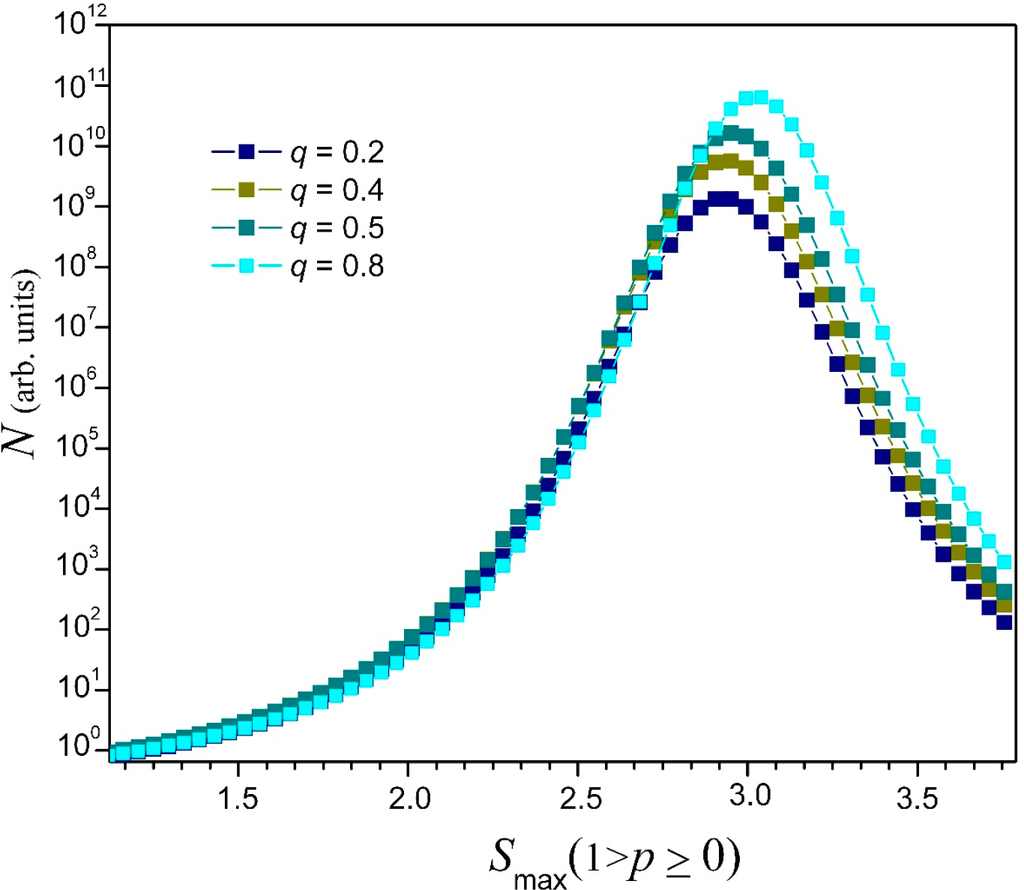
Figure 4.
Maximum violation of m(F2)CHSH inequalities obtained for Smax ≈ 2.82 and p ≥ 0 versus number of interval sequences N (Equation (44)), corresponding to CHSH inequality [58,59], plotted for four order parameters (designated by solid squares): q = 0.2 (blue), q = 0.4 (dark yellow), q = 0.5 (dark cyan), q = 0.8 (cyan).
5. Quantum Hypergraph State
First step towards obtaining the quantum hypergraph state [1, 19, 60] from a mathematical hypergraph G(V, H) based on the free group F2, is to assign qubits to a vertex set elements, V = {x1, x2,…, xn}, and next is to perform initialization of qubits into |+⟩ state [60, 61]. Subsequent control and manipulation over qubit states is achieved through hyperedge controlled-Z operations [1, 60] between specified qubits, which position coincides with underlying geometry of the free group- F2 fractal set. G is the free group on two generators which form a set H = (a±1,b±1), H ⊆ G, where every element g ∈ G can be obtained by the action HUH−1. As a result, a 4-valent hypergraph is generated by action H × G. Qubit states are assigned as:
where measurement basis is specified in exact correspondence to a rank two generating set on a free group F2 = a,a−1,b,b−1|a,b ∈ H, where four basis states are: O = {|00⟩, |01⟩, |10⟩, |11⟩}.
The main prerequisite for encoding is to perform the initialization of the system with probabilities
.
In the first iteration, the probability distribution arising from the corresponding set of measurements
over the Cayley subset {{a,b}, {a,b−1}, {a−1,b}, {a−1,b−1}} is given by:
where action of the measurement is determined by the projective measurement operator PiX = X⟩ ⟨X| over a given generating set (see Equation (46)), producing in that way the state ρ which possesses non-local correlations, representing at the same time the topological state. In particular, the symmetry of the underlying topology is efficiently captured and corresponds exactly to the symmetry of the joint probabilities for each measurement, see Figure 5. In this case the tensor algebra T(V) = ⊕i≥0 V⊗i is represented on a k-module V of a vertex set elements, which is an associative k-algebra spanned by x1x2…xn:= x1 ⊗ x2 ⊗…⊗ xn, where n ∈ ℕ and x1x2…, xn ∈ V. Multiplication is utilized by a k-linear map m(x1x2…xn ⊗ω1ω2…ωm):= x1x2…xnω1ω2…ωm for all n,m ∈ ℕ and x1, x2…, xn,ω1,ω2…,ωm in V.
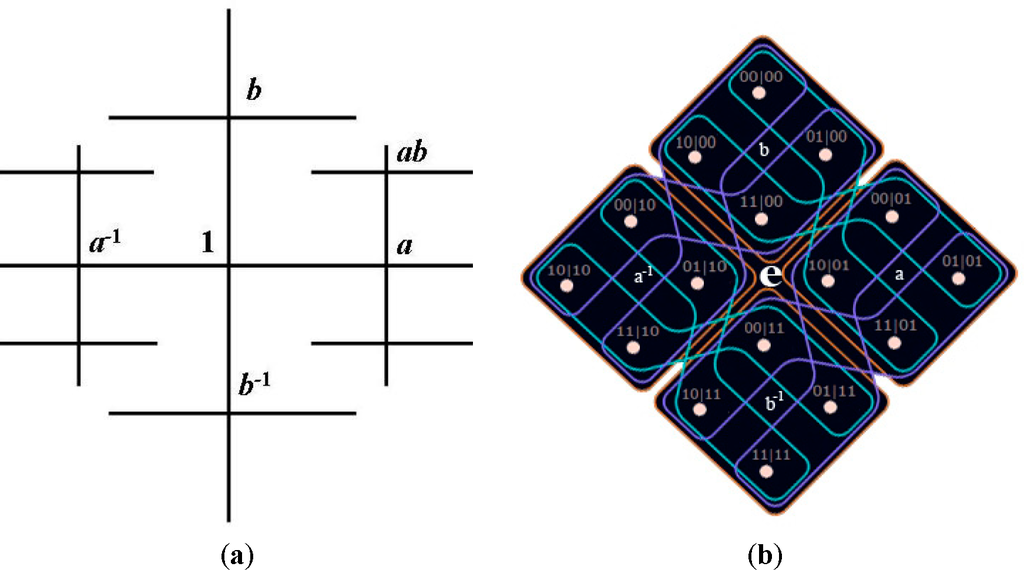
Figure 5.
(a) Geometrical-representation of a rank-2 free group F2 =a,a−1,b,b−1|a,b ∈ H, where H ⊆ G is a generating set. (b) Scheme of the hypergraph state quantum correlations [1,60,62] that reflect exact symmetry of the underlying F2 = a,a−1,b,b−1|a,b ∈ H topology, (Equation (46)).
Likewise, due to a self-similar property, in each subsequent action performed over d-dimensional Cayley fractal structure that corresponds to a rank-d generating set on a free group Fd, probability distributions arising from the corresponding set of measurements determined by the subset H are
Bounds of non-local correlations [63] are closely assessed by determination of observables that influence the maximum of I ~ λi,i max where
[62] with
denoting the Bell operator, and by eigenvalues λi,i max which determine violation of Bell inequality for the concrete joint probabilities.
,
,
,
are the orthonormal eigenvectors of the corresponding observables {A1,…, An} and {B1,…, Bn} defined on a vertex set V ={x1, x2,…, xn} of the free groupG(V, H) on two generators, F2. Consequently, for the d-regular hypergraph state on n vertices, the maximal value for I is bounded with the maximal eigenvalue
of the corresponding diagonal element of d ×d matrix Uρ:
obtained with operator
, where σi,j = −i|i⟩⟨j|+i|j⟩⟨i|, and off-diagonal elements λi, j, λj,i denote rotation and a phase shift, respectively. For the case when Ak = σi,
,
,
; k = 1,…, n, Bell operator,
, corresponds to n2 of the
eigenvalues; as a result,
with multiplicities: 1/4, 1/2, and 1/4, respectively. Labeling states of k =1, …,n vectors from basis sets:
,
,
,
in two dimensional space as |Ф±⟩k and |Ψ±⟩k, after initialization from Equation (46), we obtain:
where for |Ψ±⟩k states the corresponding eigenvalues are
, respectively (with maximal eigenvalue being
). For all |Ф±⟩k states eigenvalues are zero, λ = 0. Consequently, the maximal violation of CHSH inequality is obtained for combinations of |Ψ±⟩k states which yield also maximal value for
[62] equivalent to the maximal eigenvalue
. This result is in agreement with Equation (44) for p = 0, with direct repercussion to notion of the non-local correlations [55] based on non-Abelian set of rank two free group F2.
6. Conclusions
A major advance towards the characterization of complexity of dynamical systems has affected communication complexity as well, offering new paths towards successful implementation of quantum information processing, especially in the field of topological insulators. In particular, the topological Rényi entropy has qualified as a good probe of the topological order, where the amount of fractal distribution present in the system and its scaling are essential for distinguishing between different phases of matter. In addition to former, wide-range implications of here presented results include the fundamental result about distribution and presence of quantum correlation and non-locality in hypegraph state based on free group on two generators, proceeding to direct implementations of underling topology of the free group F2 fractal sets in chip integrated circuits for quantum computing. We have defined the fractional Rényi entropy of order q for the hypergraph fractal sets based on a (non-Abelian) free group on finite generators and shown that intractability of the fractal dynamical processes can be efficiently bypassed using the geometrical concept of Lyapunov, which has proved to be the most viable method for the investigation of the complexity evolution, having its intrinsic relation to the topological and the metric (information) entropy.
Acknowledgments
The author acknowledges partial financial support through the SigmaPhy2014 organization. The author is indebted to Gavin Brennen for fruitful discussions. The work is funded through the grant: ObAd: 1007211.
Conflicts of Interest
The author declares no conflict of interest.
References
- Gühne, O.; Cuquet, M.; Steinhoff, F.E.S.; Moroder, T.; Rossi, M.; Bruß, D.; Kraus, B.; Macchiavello, C. Entanglement and nonclassical properties of hypergraph states. J. Phys. A 2014, 47, 335303. [Google Scholar]
- Katok, A.; Hasselblatt, B. Introduction to the Modern Theory of Dynamical Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hasselblatt, B.; Katok, A. Entropy and Chaos. In A First Course in Dynamics with a Panorama of Recent Developments; Cambridge University Press: Cambridge, UK, 2003; pp. 242–256. [Google Scholar]
- Katok, A. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. IHES 1980, 51, 137–174. [Google Scholar]
- Oseledets, V.I.A. Multiplicative ergodic theorem: Characteristic Lyapunov exponents of dynamical systems. Trans. Moscow Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Adler, R.; Konheim, A.; McAndrew, M. Topological entropy. Trans. Amer. Math. Soc. 1965, 114, 309–319. [Google Scholar]
- Adler, R.; Marcus, B. Topological entropy and equivalence of dynamical systems; Memoirs of the American Mathematical Society: Providence, RI, USA, 1979; Volume 20, p. 219. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Misiurewicz, M.; Szlenk, W. Entropy of piecewise monotone mappings. Studia Math. 1980, 67, 45–63, MR 82a:58030. [Google Scholar]
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar]
- Alsedà, L.; Llibre, J.; Misiurewicz, M. Periodic orbits of maps of Y. Trans. Am. Math. Soc. 1989, 475–538. [Google Scholar]
- Blanchard, F. A disjointness theorem involving topological entropy. Bull. Soc. Math. France. 1993, 121, 465–478, MR1254749 (95e:54050). [Google Scholar]
- Nilson, C.; Bernardes, Jr. On the set of points with a dense orbit. Proc. Am. Math. Soc. 2000, 128, 3421–3423. [Google Scholar]
- Danilenko, A. Entropy theory from the orbital point of view. Monatsh. Math. 2001, 134, 121–141. [Google Scholar]
- Coxeter, H.S.M.; Moser, W.O.J. Generators and relations for discrete groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3rd ed; Springer-Verlag: Berlin, Germany, 1972; Volume 14. [Google Scholar]
- Kharlampovich, O.; Myasnikov, A. Elementary theory of free non-Abelian groups. J. Algebra. 2006, 302, 451–552. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; Wiley: Chichester, UK, 2004; p. 308. [Google Scholar]
- Rényi, A. On measures of entropy and information, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA; University of California Press: Oakland, CA, USA, 1960; 1, pp. 547–561.
- Rossi, M; Huber, M.; Bruß, D.; Macchiavello, C. Quantum hypergraph states. New J. Phys. 2013, 15, 113022. [Google Scholar]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar]
- Raussendorf, R.; Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 2007, 98, 190504. [Google Scholar]
- Gottesman, D. Stabilizer Codes and Quantum Error Correction. Ph.D. Dissertation, California Institute of Technology, Pasadena, CA, USA, 1997. [Google Scholar]
- Brun, T.; Devetak, I.; Hsieh, M.H. Correcting quantum errors with entanglement. Science 2006, 314, 436–439. [Google Scholar]
- Djordjevic, I. Quantum Information Processing and Quantum Error Correction: An Engineering Approach; Academic Press: Oxford, UK, 2012; p. 347. [Google Scholar]
- Berge, C. Graphs and Hypergraphs, 2nd ed; North Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- De la Harpe, P. Topics in Geometric Group Theory; Chicago Lectures in Mathematics;University of Chicago Press: Chicago, IL, USA, 2000. [Google Scholar]
- Runde, V. Lectures on Amenability. Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 2002; Volume 1774. [Google Scholar]
- Stern, A. Non-Abelian states of matter. Nature 2010, 464, 187–193. [Google Scholar]
- Paterson, A.L.T. Amenability, Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 1988; Volume 29. [Google Scholar]
- Følner, E. On groups with full Banach mean value. Math. Scand. 1955, 3, 243–254. [Google Scholar]
- Bollobás, B. (Ed.) Advances in Graph Theory. Annals of Discrete Mathematics; North-Holland: Amsterdam, The Netherlands, 1978; Volume 3.
- Cayley, A. A theorem on trees. Quart. J. Math. 1889, 23, 376–378. [Google Scholar]
- Von Neumann, J. Zur allgemeinen Theorie des Masses. Fundam. Math. 1929, 13, 73–116. [Google Scholar]
- Mor, M.; Fraenkel, A.S. Cayley permutations. Discrete Math. 1984, 48, 101–112. [Google Scholar]
- Lesh, N.; Marks, J.; Patrignani, M. Interactive partitioning system demonstration, short. In Graph Drawing. Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2001; Volume 1984, pp. 31–36. [Google Scholar]
- Brown, R.; Higgins, P.J.; Sivera, R. Nonabelian Algebraic Topology: Filtered spaces, Crossed Complexes, Cubical Homotopy Groupoids, EMS Tracts in Mathematics; European Mathematical Society: Zürich, Switzerland, 2010; Volume 15. [Google Scholar]
- Falconer, K.J. The Geometry of Fractal Sets; Cambridge tracts in mathematics; University of Bangalore Press: Bangalore, India, 1997; Volume 85, p. 120. [Google Scholar]
- Gerald, A.E. Integral, Probability, and Fractal Measures (Mathematics and Theoretical Computer); Springer-Verlag: New York, NY, USA, 1998; p. 3. [Google Scholar]
- Stein, E.M.; Shakarchi, R. Measure Theory, Integration, and Hilbert Spaces; Princeton Lectures in Analysis; Princeton University Press: Princeton, NJ, USA, 2005; pp. 325–327. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Berge, C. Fractional Graph Theory; ISI Lecture Notes; Macmillan of India: New Delhi, India, 1978; Volume 1. [Google Scholar]
- Blanchard, F.; Maass, A.; Nogueira, A. (Eds.) Topics in Symbolic Dynamics and Applications; Cambridge University Press/London Mathematical Society: London, UK, 2000; Volume 279.
- Hasselblatt, B.; Katok, A. (Eds.) Handbook of Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2002; Volume 1A.
- Adler, R.L.; Coppersmith, D.; Hassner, M. Algorithms for sliding block: An application of symbolic dynamics to information theory. IEEE Trans. Inf. Theory 1983, 29, 5–22. [Google Scholar]
- Samelson, H. On the Perron-Frobenius theorem. Michigan Math. J 1957, 4, 57–59. [Google Scholar]
- Bronzi, M.; Tahzibi, A. Homoclinic tangency and variation of entropy. Cad. Mat. 2009, 10, 133–143. [Google Scholar]
- Pesin, Y. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surveys. 1977, 32, 55–114. [Google Scholar]
- Kolmogorov, A.N. Entropy per unit time as a metric invariant of automorphism. Dokl. Acad. Nauk. 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the Notion of Entropy of a Dynamical System. Dokl. Acad. Nauk. 1959, 124, 768–771. [Google Scholar]
- Kaplan, J.L.; Yorke, J.A. Chaotic Behavior of Multidimensional Difference Equations. In Functional Differential Equations and Approximations of Fixed Points; Lecture Notes in Mathematics; Peitgen, H.-O., Walter, H.-O., Eds.; Springer: Berlin, Germany, 1979; Volume 730, p. 204. [Google Scholar]
- MacKernan, D.; Nicolis, G. Generalized Markov coarse graining and spectral decompositions of chaotic piecewise linear maps. Phys. Rev. E 1994, 50, 988. [Google Scholar]
- Sato, S.; Sano, M.; Sawada, Y. Practical methods of measuring the generalized dimension and the largest Lyapunov exponent in high dimensional chaotic systems. Prog. Theor. Phys. 1987, 77, 1–5. [Google Scholar]
- Krieger, W. On entropy and generators of measure-preserving transformations. Trans. Amer. Math. Soc. 1970, 149, 453–464. [Google Scholar]
- Popescu, S.; Rohrlich, D. Quantum non-locality as an axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar]
- Brennen, G.K.; Iblisdir, S; Pachos, J.K.; Slingerland, J.K. Non-locality of non-Abelian anyons. New J. Phys. 2009, 11, 103023. [Google Scholar]
- Ceccherini-Silberstein, T.; Grigorchuk, R.; de la Harpe, P. Amenability and paradoxical decompositions for pseudogroups and for discrete metric spaces. Proc. Stek. Inst. Math. 1999, 224, 57–97. [Google Scholar]
- Wagon, S. The Banach-Tarski Paradox; Cambridge University Press: New York, NY, USA, 1985. [Google Scholar]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar]
- Cirel’son, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93–100. [Google Scholar]
- Wang, R.Q.J.; Li, Z.; Bao, Y. Encoding hypergraphs into quantum states. Phys. Rev. A 2013, 87, 022311. [Google Scholar]
- Berec, V. Phase space dynamics and control of the quantum particles associated to hypergraph states 2014, arXiv, 1411.4059.
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Barrett, J.; Linden, N.; Massar, S.; Pironio, S.; Popescu, S.; Roberts, D. Non-local correlations as an information-theoretic resource. Phys. Rev. A 2005, 71, 022101:1–022101:11. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).