Abstract
In this paper, the exp-function method is improved to construct exact solutions of non-linear lattice equations by modifying its exponential function ansätz. The improved method has two advantages. One is that it can solve non-linear lattice equations with variable coefficients, and the other is that it is not necessary to balance the highest order derivative with the highest order nonlinear term in the procedure of determining the exponential function ansätz. To show the advantages of this improved method, a variable-coefficient mKdV lattice equation is considered. As a result, new exact solutions, which include kink-type solutions and bell-kink-type solutions, are obtained.
1. Introduction
The work of Fermi, Pasta and Ulam in the 1950s [1] has attached much attention on exact solutions of non-linear lattice equations arising different fields which include condensed matter physics, biophysics, and mechanical engineering. In the numerical simulation of soliton dynamics in high energy physics, some non-linear lattice equations are often used as approximations of continuum models. In fact, the celebrated Korteweg–de Vries (KdV) equation can be considered as a limit of the Toda lattice equation [2]. Non-linear lattice equations can provide models for non-linear phenomena such as wave propagation in nerve systems, chemical reactions, and certain ecological systems (for example, the famous Volterra equation). Unlike difference equations which are fully discretized, lattice equations are semi-discretized with some of their spatial variables discretized while time is usually kept continuous. In the past several decades, many effective methods for constructing exact solutions of non-linear partial differential equations (PDEs) have been presented, such as the inverse scattering method [3], Bäcklund transformation [4], Hirota’s bilinear method [5], homogeneous balance method [6], tanh-function method [7], Jacobi elliptic function expansion method [8], Lucas Riccati method [9], differential transform method [10], and others [11–17]. Generally speaking, it is hard to generalize one method for non-linear PDEs to solve non-linear lattice equations because of the difficulty in finding iterative relations from indices n to n ± 1(here n denotes an integer). When the inhomogeneities of media and non-uniformities of boundaries are taken into account, the variable-coefficient equations could describe more realistic physical phenomena than their constant-coefficient counterparts [18], such as seen, e.g., in the super-conductors, coastal waters of oceans, blood vessels, space and laboratory plasmas and optical fiber communications [19]. Therefore, how to solve non-linear lattice equations with variable coefficients is worth studying.
Recently, He and Wu proposed exp-function method [20] to solve non-linear PDEs. It is shown in [20–31] that the exp-function method or its improvement is available for many kinds of nonlinear PDEs, such as Dodd–Bullough–Mikhailov equation [20], sine-Gorden equation [21], combined KdV-mKdV equation [23], Maccari’s system [24], variable-coefficient equation [25], non-linear lattice equation [26], stochastic equation [27], and generalized Klein–Gordon equation [31]. For some recent applications of the method itself, we can refer to Fitzhugh–Nagumo equation [32], extended shallow water wave equations [33] and generalized mKdV equation [34]. In [35–37], there are two remarkable developments of the exp-function method. One is that the exp-function method with a fractional complex transform was generalized to deal with fractional differential equations [35,36], and the other is that the method was hybridized with heuristic computation to obtain numerical solution of generalized Burger–Fisher equation [37]. On the other hand, it is necessary to check the solutions obtained by the exp-function method carefully [38] because some authors have been criticized for incorrect results [39,40]. Besides, for a given non-linear PDEs with independent variables t, x1, x2, ⋯, xs and dependent variable u:
the exp-function method can also be used to construct different types of exact solutions. This is due to its exponential function ansätz:
where an, bm, ki and w are undetermined constants, f, p, g and q can be determined by using Equation (2) to balance the highest order non-linear term with the highest order derivative of u in Equation (1). It is He and Wu [20] who first concluded that the final solution does not strongly depend on the choices of values of f, p, g and q. Usually, f = p = g = q = 1 is the simplest choice. More recently, Ebaid [41] proved that f = p and g = q are the only relations for four types of nonlinear ordinary differential equations (ODEs) and hence concluded that the additional calculations of balancing the highest order derivative with the highest order non-linear term are not longer required. Ebaid’s work is significant, which makes the exp-function method more straightforward. The present paper is motivated by the desire to prove that f = p and g = q are also the only relations when we generalize the exp-function method [20] to solve non-linear lattice equations. Thus, the exp-function method can be further improved because it is not necessary to balance the highest order derivative with the highest order non-linear term in the process of solving non-linear lattice equations.
The rest of this paper is organized as follows. In Section 2, we generalize exp-function method to solve non-linear lattice equations with variable coefficients. In Section 3, a theorem is proved and then used to improve the generalized exp-function method in determining its exponential function ansätz of non-linear lattice equations. In Section 4, we take a variable-coefficient mKdV lattice equation as an example to show the advantages of the improved exp-function method. In Section 5, some conclusions are given.
2. Generalized Exp-Function Method for Non-Linear Lattice Equations
In this section, we outline the basic idea of generalizing the exp-function method [20] to solve a given non-linear lattice equation with variable coefficients, say, in three variables n, x and t:
which contains both the highest order nonlinear terms and the highest order derivatives of dependent variables. Here P is a polynomial of un, un−θ(θ = ±1, ±2, ⋯) and the various derivatives of un. Otherwise, a suitable transformation can transform Equation (3) into such an equation.
Firstly, we take the following transformation:
where d is a constant to be determined, c(x, t) is the undetermined function of x and t, and ω is the phase. Then, Equation (3) can be reduced to a non-linear ODE with variable coefficients:
Secondly, we suppose that the ansätz of Equation (5) can be expressed as:
Thirdly, we substitute Un and Un−θ(θ = ±1, ±2, ⋯) determined by Equation (6) into Equation (5) and then balance the highest order derivative with the highest order nonlinear term in Equation (5) to obtain the integers f, p, g and q. Finally, we determine the coefficients a−f(x, t), ⋯, ag(x, t), b−p, ⋯, bq, d and c(x, t) by solving the resulting equations from the substitution of Un and Un−θ(θ = ±1, ±2, ⋯) along with the obtained values of f, p, g, q into Equation (5).
In order to identify the highest order nonlinear term, we define in this paper the negative order N(·) and the positive order P (·) of ansätz (6) as follows:
under the condition that the functions a−f(x, t) and ag(x, t), and the constants b−p and bq are all nonzero coefficients. Therefore, we can easily obtain N(Un−θ) = p−f and P (Un−θ) = g −q. For the derivatives of Un, we have a general formula:
where τr(x, t) and σr(x, t) are functions of x and t, δr and ςr are constants, and r ≥ 1 is an integer. If τr(x, t), σr(x, t), δr and ςr are nonzero coefficients, then
and
.
Since
we define the product
as the highest order nonlinear term of Equation (5). Here h, i1, j1, i2, j2, ⋯, iz, jz, l1, l2, ⋯, ls are nonnegative integers which satisfy
With above preparations, we can see that Equations (8) and (10) include all possibilities of the highest order derivative and the highest order nonlinear term of Equation (5). In what follows, we shall proof that f = p and g = q are the only relations when using the exponential function ansätz (6) to balance the highest order derivative (8) with the highest order nonlinear term (10).
Remark 1. If we let a−f(x, t), ⋯, ag(x, t) be nonzero constants and take c(x, t) as a linear function kx + lt, k and l are undetermined constants, then the generalized exp-function method described in this section is also effective for non-linear lattice equations with constant coefficients. So the starting point of this paper is to generalize the exp-function method [20] to solve Equation (3) with variable coefficients. In the next section, we shall further improve this generalized exp-function method.
3. Theorem and Improvement
Theorem 1. Suppose that Equations (8) and (10) are respectively the highest order derivative and the highest order nonlinear term of Equation (5), then the balancing procedure using the exponential function ansätz (6) leads to f = p and g = q.
Proof. By contradiction, we suppose that f ≠ p and g ≠ q. Then a computation shows that τr(x, t), σr(x, t), δr, and ςr in Equation (8) are all nonzero coefficients. Using Equations (6) and (8), we have
With the help of Equations (12)–(14), the left hand side and the right hand side of Equation (8) can be respectively written as:
with nonzero coefficients
We further use
to multiply the numerator and denominator of Equation (8), then the left hand side and the right hand side of Equation (8) can be respectively written as:
Balancing the lowest order of the exponential function in Equations (21) and (23) and the highest order of the exponential function in Equations (22) and (24) yields
It is easy to see from Equation (11) that
then Equations (25) and (26) give f = p and g = q. This contradicts with our assumption that f ≠ p and g ≠ q. Thus we complete the proof of Theorem 1. □
Theorem 1 shows that f = p and g = q are the only relations when using the exponential function ansätz (6) to balance the highest order derivative (8) with the highest order nonlinear term (10). Therefore, the simplest choice f = p = g = q = 1 is often selected so that some additional calculations in determining the exponential function ansätz (6) are not longer required. Thus, Theorem 1 improves the generalized exp-function method described in Section 2.
4. Application
To give a concrete application of our improved exp-function method in Sections 2 and 3, we consider in this section the mKdV lattice equation with variable coefficient [42]:
where un = u(n, t), α(t) is an arbitrary differentiable function of t. When α(t) = 0, 1, α(const.), Equation (28) can give three known constant-coefficient versions of the mKdV lattice equation.
Using the transformation
where d is a constant to be determined, c(t) is the undermined function of t, and η0 is the phase, we transform Equation (28) into
According to the exp-function method improved in Sections 1 and 2, we directly suppose that:
Substituting Equations (31)–(33) into Equation (30), and using Mathematica, equating the coefficients of all powers of exp(jηn)(j = 0, ±1, ±2, ±3) to zero yields a set of equations for a1(t), a0(t), a−1(t), b1, b0, b−1 and c(t). Solving the system of equations by the use of Mathematica, we have:
and
where b1 and b−1 are arbitrary constants.
We, therefore, obtain from Equations (29), (31), (34) and (35) a pair of new kink-type solutions of Equation (28):
where ηn = dn + 2 tanh(d) ∫ α(t)dt + η0. If set b1 = 1, then solutions (38) become the known solutions [42].
With the help of Equations (29), (31), (36) and (37), we obtain two pairs of new bell-kink-type solutions of Equation (28):
where
.
In Figure 1, the spatial structures of solutions (38) with (+) branch are shown, where the parameters are selected as α(t) = 1 + 05sintsecht, b1 = −15, b−1 = −2, d = 1, η0 = 0. Figs. 1(a)–(d) show that the amplitude of wave changes periodically in the process of propagation. It is shown in Figure 1c that the “breather”-like phenomena has occurred at the location n = 0. In Figure 2, we show the structures of solutions (39) with (+,+) branch, where α(t) = 1 + secht, b1 = 15 and the other parameters are same as those in Figure 1. From Figure 2c, we can see that u0 has a singularity in the interval t ∈ (0, 1). It is easy to see that when b1 = 15 and b−1 = −2, solutions (39) are unbounded. Such unbounded solutions develop singularity at a finite time, i.e. for any fixed n = n0, there always exists t = t0 at which these solutions “blow-up”. In view of the physical significance, they do not exist after “blow-up”. In the actual experimental physical system, there is no “blow-up”, but a sharp spike [43]. Thus, the finite time “blow-up” can provide an approximation to the corresponding physical phenomenon.
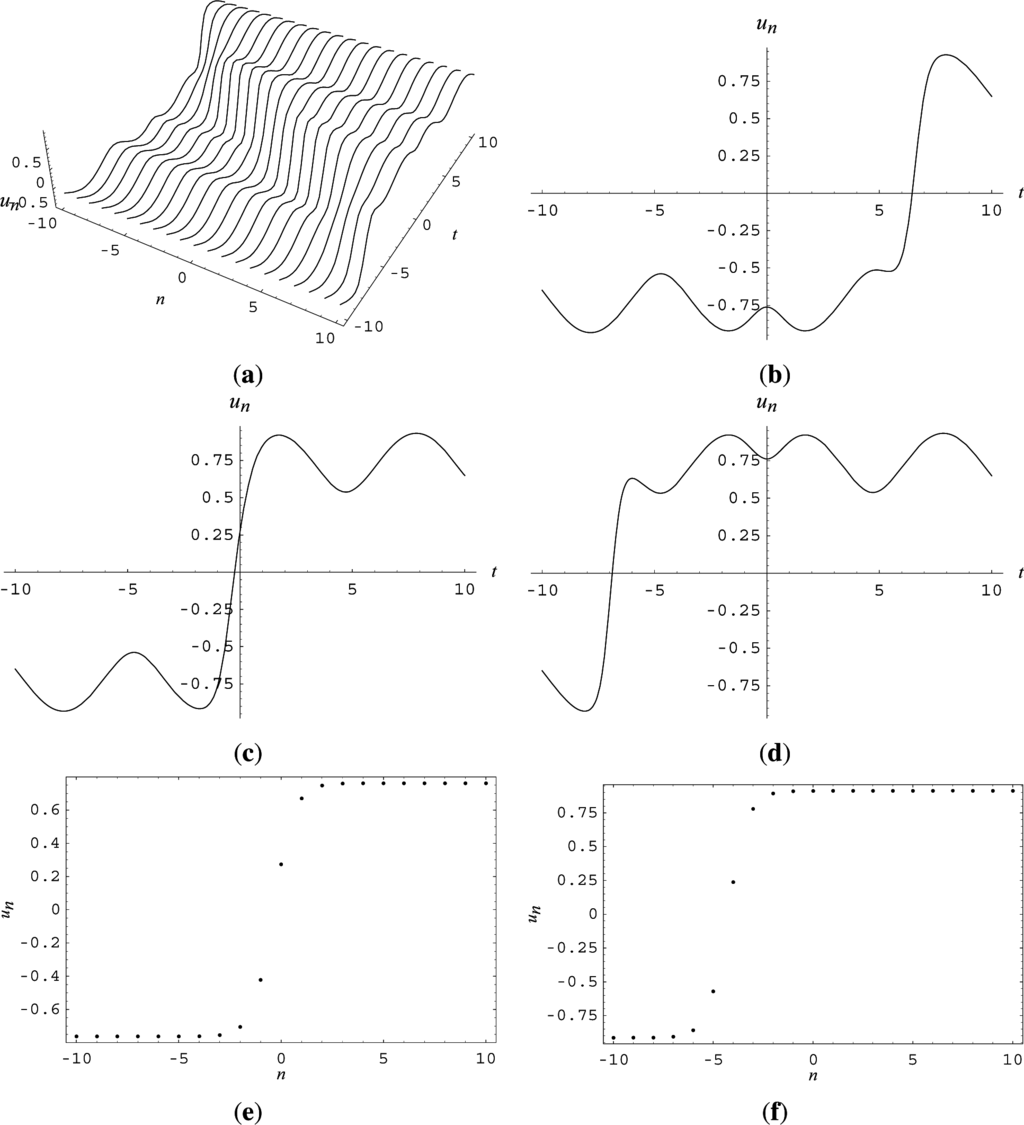
Figure 1.
Spatial structures of solution (38) with (+) branch: (a) n ∈ [−10, 10], t ∈ [−10, 10]; (b) n = −10, t ∈ [−10, 10]; (c) n = 0, t ∈ [−10, 10]; (d) n = 10, t ∈ [−10, 10]; (e) n ∈ [−10, 10], t = 0; (f) n ∈ [−10, 10], t = 2.
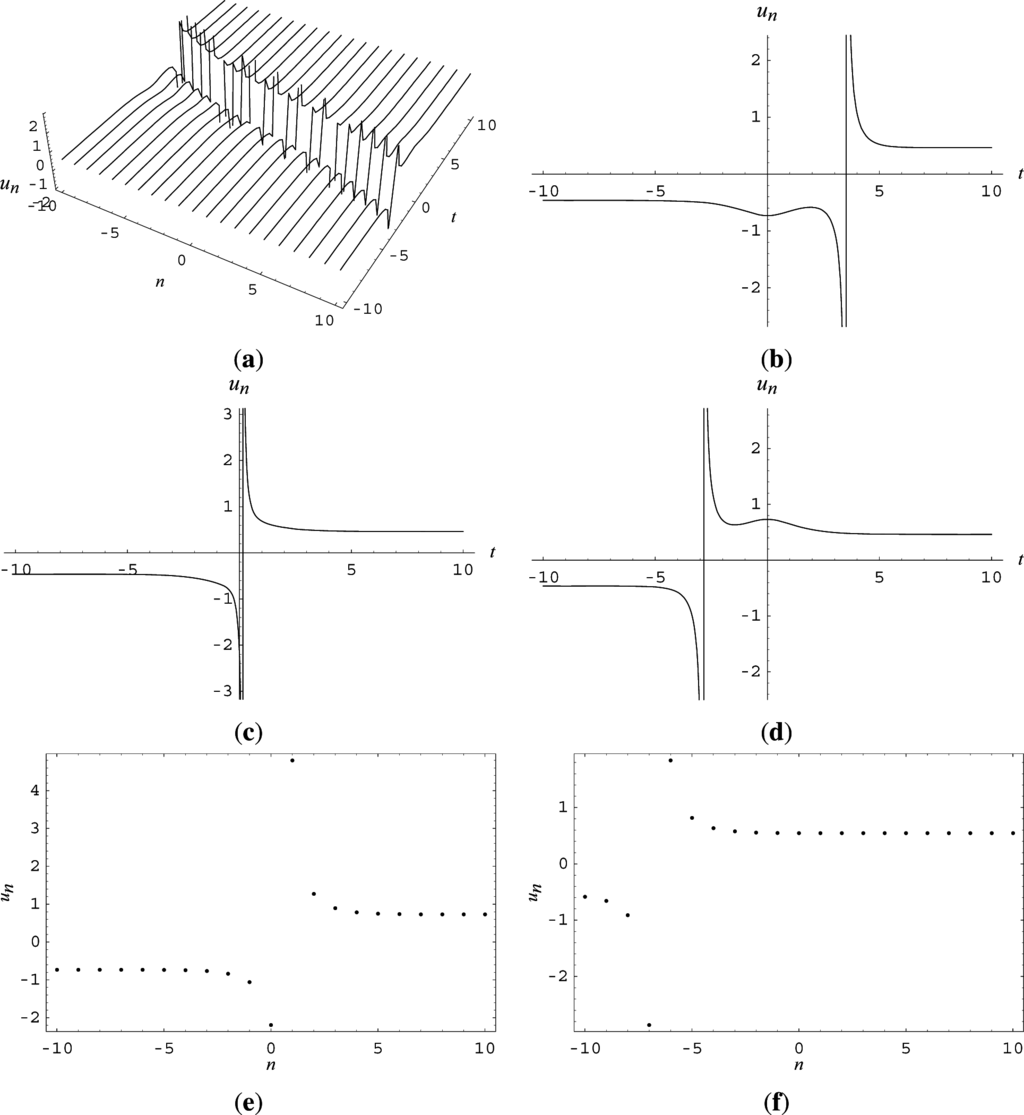
Figure 2.
Spatial structures of solutions (39) with (+,+) branch: (a) n ∈ [−10, 10], t ∈ [−10, 10]; (b) n = −10, t ∈ [−10, 10]; (c) n = 0, t ∈ [−10, 10]; (d) n = 10, t = [−10, 10]; (e) n ∈ [−10, 10], t = 0; (f) n ∈ [−10, 10], t = 2.
5. Conclusions
In summary, we have improved the exp-function method [20] for solving non-linear lattice equations by modifying its exponential function ansätz. In order to show the advantages of the improved method, the variable-coefficient mKdV lattice Equation (28) is considered. As a result, kink-type solutions (38) and bell-kink-type solutions (39) are obtained. To the best of our knowledge, they have not been reported in the literature. Solutions (38) and (39) contain arbitrary function α(t) and arbitrary constants b1 and b−1, which provide enough freedom for us to describe rich spatial structures of these obtained solutions. Applying the improved exp-function method to some other non-linear lattice equations with variable coefficients are worthy of study. This is our task in the future.
Acknowledgments
We would like to express our sincerest thanks to the editor and the referees for their valuable suggestions and comments, and to English teacher Yifei Li at Bohai University for her help in English writing. This work was supported by the PhD Start-up Funds of Liaoning Province of China (20141137) and Bohai University (bsqd2013025), the Natural Science Foundation of Educational Committee of Liaoning Province of China (L2012404), the Liaoning BaiQianWan Talents Program (2013921055) and the Natural Science Foundation of China (11371071).
Author Contributions
Sheng Zhang, Jiahong Li and Yingying Zhou conceived and designed the study. Sheng Zhang and Yingying Zhou wrote the paper. Sheng Zhang and Jiahong Li reviewed and edited the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fermi, E.; Pasta, J.; Ulam, S. Collected Papers of Enrico Fermi II; University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Toda, M. Theory of Nonlinear Lattics, 2nd ed; Springer: Berlin, Germany, 1989. [Google Scholar]
- Garder, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 1965, 19, 1095–1097. [Google Scholar]
- Miurs, M.R. Bäcklund Transformation; Springer: Berlin, Germany, 1978. [Google Scholar]
- Hirota, R. Exact solution of the Korteweg–de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar]
- Wang, M.L. Exact solutions for a compound KdV-Burgers equation. Phys. Lett. A. 1996, 213, 279–287. [Google Scholar]
- Malfliet, M. Solitary wave solutions ofnonlinear wave equations. Am. J. Phys. 1992, 60, 650–654. [Google Scholar]
- Liu, S.K.; Fu, Z.T.; Liu, S.D.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar]
- Abdel-Salam, E.A-B.; Al-Muhiameed, Z.I.A. Exotic localized structures based on the symmetrical lucas function of the (2+1)-dimensional generalized Nizhnik–Novikov–Veselov system. Turk. J. Phys. 2011, 35, 241–256. [Google Scholar]
- Tabatabaei, K.; Celik, E.; Tabatabaei, R. The differential transform method for solving heat-like and wave-like equations with variable coeffcients. Turk. J. Phys. 2012, 36, 87–98. [Google Scholar]
- Fan, E.G. Travelling wave solutions in terms of special functions for nonlinear coupled evolution systems. Phys. Lett. A 2002, 300, 243–249. [Google Scholar]
- Fan, E.G. An algebraic method for finding a series of exact solutions to integrable and nonintegrable nonlinear evolution equations. J. Phys. A: Math. Gen. 2003, 36, 7009–7026. [Google Scholar]
- Dai, C.Q.; Wang, Y.Y.; Tian, Q.; Zhang, J.F. The management and containment of self-similar rogue waves in the inhomogeneous nonlinear Schrödinger equation. Ann. Phys. 2012, 327, 512–521. [Google Scholar]
- Dolapci, I.T.; Yildirim, A. Some exact solutions to the generalized Korteweg–de Vries equation and the system of shallow water wave equations. Nonlinear Anal. Model. Control. 2013, 18, 27–36. [Google Scholar]
- He, J.H. Asymptotic methods for solitary solutions and compactons. Abstr. Appl. Anal. 2012, 2012, 916793, 130pages. [Google Scholar]
- Dai, C.Q.; Wang, X.G.; Zhou, G.Q. Stable light-bullet solutions in the harmonic and parity-time-symmetric potentials. Phys. Rev. A 2014, 89, 013834. [Google Scholar]
- Dai, C.Q.; Zhu, H.P. Superposed Kuznetsov–Ma solitons in a two-dimensional graded-index grating waveguide. J. Opt. Soc. Am. B 2013, 30, 3291–3297. [Google Scholar]
- Liu, Y.; Gao, Y.T.; Sun, Z.Y.; Yu, X. Multi-soliton solutions of the forced variable-coefficient extended Korteweg–de Vries equation arisen in fluid dynamics of internal solitary vaves. Nonlinear Dyn. 2011, 66, 575–587. [Google Scholar]
- Zhang, S.; Cai, B. Multi-soliton solutions of a variable-coefficient KdV hierarchy. Nonlinear Dyn. 2014, 78, 1593–1600. [Google Scholar]
- He, J.H.; Wu, X. H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals. 2006, 30, 700–708. [Google Scholar]
- He, J.H.; Abdou, M.A. New periodic solutions for nonlinear evolution equations using Exp-function method. Chaos Solitons Fractals 2006, 34, 1421–1429. [Google Scholar]
- He, J.H.; Zhang, L.N. Generalized solitary solution and compacton-like solution of the Jaulent–Miodek equations using the Exp-function method. Phys. Lett. A 2008, 372, 1044–1047. [Google Scholar]
- Ebaid, A. Exact solitary wave solutions for some nonlinear evolution equations via Exp-function method. Phys. Lett. A 2007, 365, 213–219. [Google Scholar]
- Zhang, S. Exp-function method for solving Maccari’s system. Phys. Lett. A 2007, 371, 65–71. [Google Scholar]
- Zhang, S. Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365, 448–453. [Google Scholar]
- Zhang, S. Exp-function method for constructing explicit and exact solutions of a lattice equation. Appl. Math. Comput. 2008, 199, 242–249. [Google Scholar]
- Dai, C.Q.; Zhang, J.F. Application of He’s exp-function method to the stochastic mKdV equation. Int. J. Nonlinear Sci. Num. Simul. 2009, 10, 675–680. [Google Scholar]
- Marinakis, V. The exp-function method and n-soliton solutions. Z. Naturforsch. A 2008, 63, 653–656. [Google Scholar]
- Zhang, S. Application of Exp-function method to high-dimensional nonlinear evolution equation. Chaos Solitons Fractals 2008, 38, 270–276. [Google Scholar]
- Ebaid, A. Generalization of He’s exp-function method and new exact solutions for Burgers equation. Z. Naturforsch. A 2009, 64, 604–608. [Google Scholar]
- Ebaid, A. Exact solutions for the generalized Klein–Gordon equation via a transformation and Exp-function method and comparison with Adomian’s method. J. Comput. Appl. Math. 2009, 223, 278–290. [Google Scholar]
- Mohyud-Din, S.T.; Khan, Y.; Faraz, N.; Yildirim, A. Exp-function method for solitary and periodic solutions of Fitzhugh–Nagumo equation. Int. J. Numer. Methods H 2012, 22, 335–341. [Google Scholar]
- Bekir, A.; Aksoy, E. Exact solutions of extended shallow water wave equations by exp-function method. Int. J. Numer. Method. H 2013, 23, 305–319. [Google Scholar]
- Chai, Y.Z.; Jia, T.T.; Hao, H.Q.; Zhang, J.W. Exp-function method for a generalized mKdV equation. Discrete Dyn. Nat. Soc. 2014, 2014, 153974. [Google Scholar]
- He, J.H. Exp-function method for fractional differential equations. Int. J. Nonlinear Sci. Num. Simul. 2013, 14, 363–366. [Google Scholar]
- Yan, L.M. Generalized exp-function method for non-linear space-time fractional differential equations. Therm. Sci. 2014, 18, 1573–1576. [Google Scholar]
- Malik, S.A.; Qureshi, I.M.; Amir, M.; Malik, AN; Haq, I. Numerical solution to generalized Burgers’–Fisher equation using exp-function method hybridized with heuristic computation. PLoS ONE 2015, 10, 1–15. [Google Scholar]
- Kudryashov, N.A.; Loguinova, N.B. Be careful with the Exp-function method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1881–1890. [Google Scholar]
- Aslan, I.; Marinakis, V. Some remarks on exp-function method and its applications. Commun. Theor. Phys. 2011, 56, 397–403. [Google Scholar]
- Aslan, I. Some remarks on exp-function method and its applications-a supplement. Commun. Theor. Phys. 2013, 60, 521–525. [Google Scholar]
- Edaid, A. An improvement on the Exp-function method when balancing the highest order linear and nonlinear terms. J. Math. Anal. Appl. 2012, 392, 1–5. [Google Scholar]
- Zhang, S.; Zhou, Y.Y. Kink-type solutions of the mKdV lattice equation with an arbitrary function. Adv. Mater. Res. 2014, 989–994, 1716–1719. [Google Scholar]
- Zhang, S.; Zhang, H.Q. Discrete Jacobi elliptic function expansion method for nonlinear differential-difference equations. Phys. Scr. 2009, 80, 045002. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).