Image Encryption Using Chebyshev Map and Rotation Equation

1. Introduction

2. Pseudo-Random Bit Generator Based on the Rotation Equations

2.1. Proposed Pseudorandom Scheme

In this section, one real number of rotation formula is preprocessed to a binary pseudo-random sequence.

We are using rotation equations of the form [11,12]

$$\begin{array}{l}{x}_{t+1}=-a-(x_t-a)\cos \theta +y_t\sin \theta /r_t\\ y_{t+1}=-x_t{r}_t\sin \theta -y_t\cos \theta \\ r_t=\sqrt{0.5(x_t^2+\sqrt{x_t^4+4y_t^2}),}\end{array}$$

(1)

where the parameters are θ = 2 and a = 2.8. The rotation Equation (1) with initial conditions x₀ = 0.5, y₀ = 1.0 is graphed in Figure 1. This figure visually shows random-like positions of the points in the set.

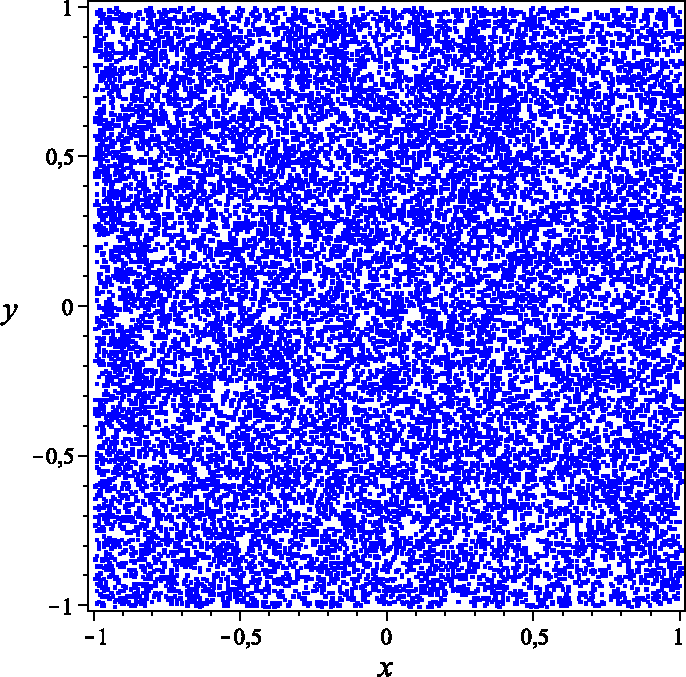
Figure 1. Rotation equations with x₀ = 0.5, y₀ = 1.0, θ = 2, a = 2.8, r_t = 10.3 and 20,000 iterations of Equation (1).

The novel pseudorandom bit generation scheme consists of the following steps:

• Step 1: The initial values x₀ and y₀ from Equation (1) are determined.
• Step 2: The rotation equation, Equation (1), is iterated for L₀ times, where L₀ is a constant.
• Step 3: The iteration of the Equation (1) continues, and as a result, two decimal fractions x_i and y_i are generated.
• Step 4: The number y_i is post-processed as follows:

  $$s_i=mod(abs(integer(y_i\times {10}^5),2),$$

  (2)

  where mod(x, y) returns the reminder after division, abs(x) returns the absolute value of x, and integer(x) returns the integer part of x, truncating the value at the decimal point.
  The output bit s_i is obtained.
• Step 5: Return to Step 3 until pseudo-random bit stream limit is reached.

The rotation equations based pseudo-random bit scheme is implemented softwarely in C++ programming language, using the following initial values: x₀ = 0.2343214592, y₀ = −0.742190593, and L₀ = 140.

2.2. Statistical Test Analysis of the Pseudorandom Bit Generator Based on Rotation Equations

In order to measure randomness of the rotation equation based pseudo-random bit generator, we used NIST [13], DIEHARD [14], and ENT [15] statistical test suites.

Using the novel pseudo-random bit generator were produced 1000 sequences of 1,000,000 bits. The results from all tests are given in Table 1.

Table 1. NIST test suite results.

The entire NIST test is passed successfully: all the p − values are distributed uniformly in the 10 subintervals and the pass rate is also in acceptable range.

The minimum pass rate for each statistical test with the exception of the random-excursion (variant) test is approximately 980 for a sample size of 1000 zero-one sequences. The minimum pass rate for the random excursion (variant) test is approximately 605 for a sample size of 619 binary sequences for Rotation equations based pseudorandom bit generator. The proposed scheme possesses random-like properties.

For the DIEHARD tests, we generated a file with 80 million bits from the proposed pseudorandom bit generator. The results are placed in Table 2. All P-values are in acceptable range of [0, 1).

Table 2. DIEHARD statistical test results.

We tested the output of a string of 125,000,000 bytes of the proposed Rotation equations based pseudorandom bit generation scheme. The results are summarized in Table 3. The proposed pseudorandom bit generator passed all the tests of ENT.

Table 3. ENT statistical test results.

3. Pseudo-Random Bit Generator Based on the Chebyshev Map

4. Image Encryption Algorithm Based on Chebyshev Map and Rotation Equation

4.2. Security Analysis

The proposed image encryption algorithm is implemented in C++ programming language. All statistical results presented have been taken by T = 1.

Twenty eight 8-bit monochrome images and sixteen 24-bit color images have been encrypted for the statistical analysis. The test images are selected from the Miscellaneous volume of USC-SIPI image database. It is available and maintained by the University of Southern California Signal and Image Processing Institute ( http://sipi.usc.edu/database/). The color image names are from 4.1.01 to 4.1.08, size 256 × 256 pixels, from 4.2.01 to 4.2.07, size 512 × 512 pixels, and House, size 512 × 512 pixels. The monochrome images are from 5.1.09 to 5.1.14, size 256 × 256 pixels, from 5.2.08 to 5.2.10, size 512 × 512 pixels, 5.3.01 and 5.3.02, size 1024 × 1024 pixels, from 7.1.01 to 7.1.10, 7.2.01, size 512 × 512 pixels, and Boat, Elaine, Gray21, Numbers, Ruler, size 512 × 512 pixels, and Testpat, size 1024 × 1024 pixels.

4.2.1. Key Space Analysis

The set of all initial numbers compose the key space. The key space of the novel image encryption scheme has six secret key values x₀ = 0.2343214591, y₀ = −0.742190593, T₁(x₁) = 0.702938119500914, T₁(x₂) = −0.3001928364928377, T₁(x₃) = 0.1385946382912478, and T₁(x₄) = −0.2871955600387584, fixed as key K1. As stated in IEEE floating-point standard [21], the computational precision of the 64-bit double-precision number is about 10⁻¹⁵. The key space of the novel scheme is (10¹⁵)⁶ = 10⁹⁰ ≈ 2²⁹⁸. Furthermore, the initial iteration numbers K, L, M and N can also be used as a part of the key size.

Compared with similar image encryption algorithms [22–27], and [28] the proposed one has enough key space size, Table 4. The larger parameter space is based on the proposed combination of two different pseudorandom bit generators.

Table 4. Keyspace comparisons.

4.2.2. Visual Testing

The novel image encryption scheme is tested by using visual review. The inspection does not detect analogy between plain images and their corresponding encrypted images. As an example, Figure 2 shows the image 4.2.06 Sailboat on lake, Figure 2a, and its encrypted version, Figure 2b. The encrypted image doesn’t keep any segmented color clusters and source figures.

Figure 2. Comparison of the plain image and the encrypted image: (a) original picture 4.2.06 Sailboat on lake; (b) encrypted image of 4.2.06 Sailboat on lake.

4.2.3. Histogram Analysis

Histogram analysis of three channels (red, green, and blue) of the plain and encrypted images is given. Figure 3 shows the histograms of the 256 × 256 plain 4.1.08 Jelly beans and encrypted 4.1.08 Jelly beans. It is observed that the histograms of the encrypted image are significantly different from that of the plain image.

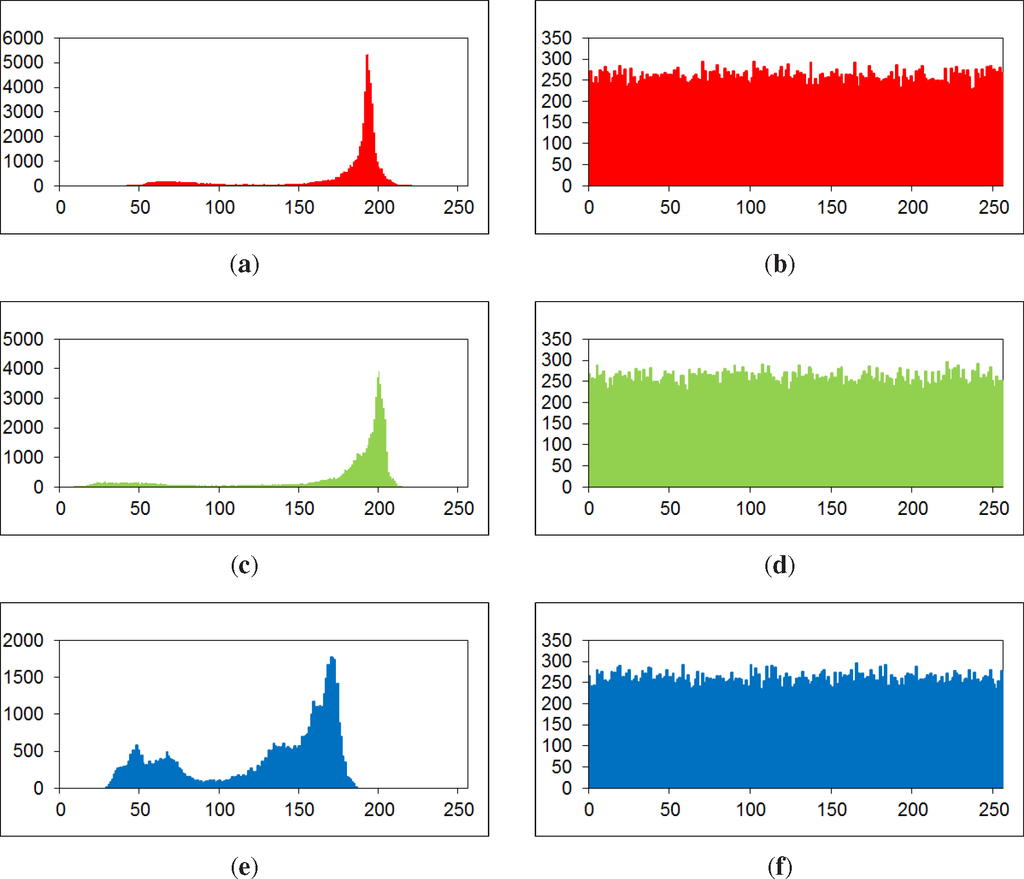
Figure 3. Histogram analysis of plain image and encrypted image: (a), (c), and (e) show the histograms of red, green, and blue channels of the plain picture 4.1.08 Jelly beans; (b), (d), and (f) show the histograms of red, green, and blue channels of encrypted picture 4.1.08 Jelly beans.

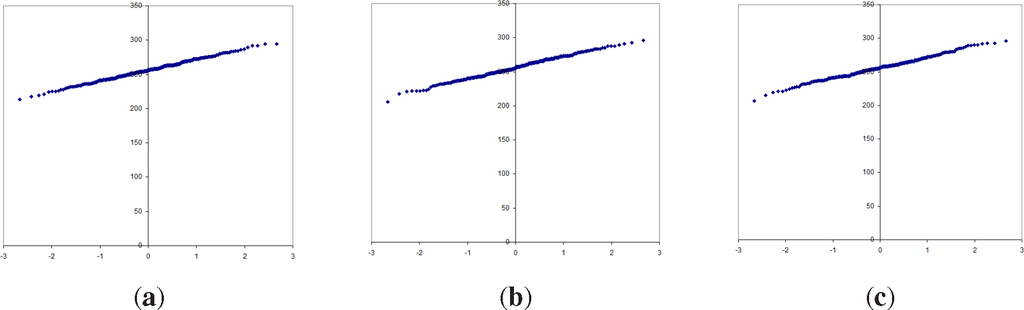
For mathematical quantity analysis of red, green and blue channels of the encrypted image 4.1.08 Jelly beans, we employed Kolmogorov–Smirnov Goodness-of-Fit Test to evaluate an uniformity. The normality was detected with Normal Quantile Plots (NormQuant.xls, Dr Scott Guth at Mt San Antonio College). The Fugure 4 shows the the Normal quantile plots. The obtained correlation coefficients of 0.999198758 (red histogram), 0.998107709 (green histogram), and 0.997868951 (blue histogram) are larger than critical values 0.989519603 (∝ = 0.01), 0.995880763 (∝ = 0.05), and 0.99710484 (∝ = 0.1). Therefore, the data follow the normal distribution. Similar results of uniformity are obtained in [29].

In addition of histogram analysis, the results of the average pixel intensity are given in Tables 5 and 6. They validate the uniformity in distribution of red, green and blue channels of the encrypted images.

Table 5. Average pixel intensity of 24-bit color plain images and encrypted images.

Table 6. Average pixel intensity of 8-bit grayscale plain images and encrypted images.

4.2.4. Information Entropy Analysis

The information entropy H(X) is a statistical measure of uncertainty in communication theory [30]. It is defined as follows:

$$H(X)=-{\displaystyle \sum _{i=0}^{255}p(x_i){\log }_{2}p(x_i),}$$

(5)

where X is a discrete random variable, p(x_i) is the probability density function of the occurrence of the symbol x_i. Let us consider that there are 256 values of the information source in red, green, blue, and grey colors of the image with the same probability. We can get the perfect entropy H(X) = 8, corresponding to a truly random sample.

The information entropy of red, green, blue and grey colors of the plain and their corresponding encrypted images are computed and displayed in Tables 7 and 8.

Table 7. Entropy results of 24-bit plain images and encrypted images.

Table 8. Entropy results of 8-bit plain images and encrypted images.

From the obtained results it is clear that the entropies of red, green, blue, and grey colors of the encrypted images are very close to the ideal value, which is an indication that the new chaos-based image encryption scheme is secure and credible upon information entropy attempt. In addition, Table 9 summarizes the information entropy values for Lena and Peppers encrypted images compared with values in [7,31–33]. As we can see that although they are all close to the ideal entropy value, the results of the novel algorithm are larger than those of corresponding methods.

Table 9. Information entropy comparisons.

4.2.5. Correlation Coefficient Analysis

Because of the existing correlation either in horizontal, vertical, or diagonal direction of the plain image pixels, the correlation coefficient r between two adjacent pixels (a_i, b_i) is computed [35].

$$r=\frac{\mathrm{cov}(a,b)}{\sqrt{D(a)}\sqrt{D(b)}},$$

(6)

where

$$D(a)=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(a_i-\overline{a})}^2,}$$

(7)

$$D(b)=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(b_i-\overline{b})}^2,}$$

(8)

$$\mathit{cov}(a,b)={\displaystyle \sum _{i=1}^M(a_i-\overline{a})(b_i-\overline{b}),}$$

(9)

M is the total number of couples (a_i, b_i), obtained from the image, and ā, $\overline{b}$ are the mean values of a_i and b_i, respectively. Correlation coefficient r can range in the interval of [−1.00, +1.00].

Table 10 shows the results of horizontal, vertical, and diagonal adjacent pixels correlation coefficients computations of the plain images and the corresponding encrypted images. It is clear that the novel chaos based image encryption scheme does not keep any linear dependencies between observed pixels in all three directions: the inspected horizontal, vertical and diagonal correlation coefficients of the encrypted images are close to 0. Overall, the correlation coefficients of the proposed algorithm are analogous with results of four other image encryption schemes [10,25,27–29], Table 11.

Table 10. Horizontal, vertical and diagonal correlation coefficients of adjacent pixels in the plain and encrypted images.

Table 11. Horizontal, vertical and diagonal correlation coefficients comparisons.

In addition, correlation coefficients between the corresponding pixel of the plain and their encrypted images are given in Table 13 (Columns 1, 2, 3, and 4). The computed correlation values are very close to 0.00.

Table 13. Correlation coefficients between the corresponding pixels of the plain and encrypted images—Columns 1, 2, 3, and 4. Correlation coefficients between the corresponding pixels of the encrypted images with keys K1 and K2—Columns 5, 6, 7, and 8.

4.2.6. Differential Attack

In general, a common characteristic of an image encryption scheme is to be sensitive to minor modifications in the plain images. Differential analysis allows that an adversary is able to create small changes in the plain image and revise the encrypted image. The alternation level can be computed by means of two formulae, namely, the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) [35,36].

Let us assume encrypted images before and after one pixel modification in a plain image are C₁ and C₂. The NPCR and UACI are defined as follows:

$$NPCR=\frac{{\displaystyle {\sum }_{i=0}^{W-1}{\displaystyle {\sum }_{j=0}^{H-1}D(i,j)}}}{W\times H}\times 100\%,$$

(10)

$$UACI=\frac{1}{W\times H}\left({\displaystyle \sum _{i=0}^{W-1}{\displaystyle \sum _{j=0}^{H-1}\frac{|C_1(i,j)-C_2(i,j)|}{255}}}\right)\times 100\%,$$

(11)

where D is a two-dimensional set, having the same size as image C₁ or C₂, and W and H are respectively the width and height of the image. The set D(i, j) is defined by C₁(i, j) and C₂(i, j), if C₁(i, j) = C₂(i, j) then D(i, j) = 1; otherwise, D(i, j) = 0. The NPCR and UACI test results from the proposed chaos based algorithm are shown in Tables 12 and 15 (Columns 2 and 3).

Table 12. NPCR and UACI results of encrypted 24-bit plain images and encrypted with one pixel difference 24-bit plain images.

Table 15. NPCR and UACI results of encrypted 8-bit plain images and encrypted with one pixel difference 8-bit plane images—Column 2 and Column 3; NPCR and UACI results of encrypted 8-bit plain images with keys K1 and K2—Column 4 and Column 5.

The obtained NPCR and UACI values for all of the images are larger than the critical values proposed in [36] and similar to the values presented in [10]. The values point out that the novel image encryption algorithm is vastly sensitive regarding to small changes in the plain images and has a vigorous strength of contrary differential cryptanalysis.

4.2.7. Key Sensitivity Test

The strong key sensitivity is another characteristic of the correlation analysis. a good image encryption scheme should be sensitive regarding the secret key i.e. a negligible change of the secret key. We encrypted the 48 images with two similar secret keys: K1 and K2 (x₀ = 0.2343214592, y₀ = −0.742190593, T₁(x₁) = 0.7029381194009314, T₁(x₂) = −0.3001928364928377, T₁(x₃) = 0.1385946382912478, and T₁(x₄) = −0.2871955600387584). The results are shown in Table 13 (Columns 5, 6, 7, and 8). It is clear that the novel image encryption method is strong key sensitive: the correlation coefficients are relatively close to zero.

Moreover, another round of the NPCR and UACI tests are established. In this case, C₁ and C₂ are two encrypted images, obtained from one plain image by the novel encryption scheme using the keys K1 and K2. The results are displayed in Tables 14 and 15 (Columns 4 and 5).

Table 14. NPCR and UACI results of encrypted 24-bit plain images with keys K1 and K2.

In addition, in Figure 5, the results of two tests are shown to decrypt the encrypted with key K1 4.1.07 and 7.1.03 images, Figure 5e and Figure 5f, with the secret key K2.

Figure 5. Key sensitive analysis of the plain images 4.2.07 and 7.1.03, (a) and (b), encrypted with the key K1, (c) and (d), and decrypted with the key K2, (e) and (f).

We observed that the two decrypted images Figure 5e and Figure 5f have no relation with the plain images 4.2.07 and 7.1.03, Figure 5a and Figure 5b, respectively.

4.2.8. Computational and Complexity Analysis

We have measured the average encryption time for 512 × 512 sized grayscale and color images by using the proposed image encryption algorithm. Computational analysis has been done on a 2.40 GHz Intel ® Core™ i7-3630QM Dell Inspiron laptop. The results are provided in Table 16. One can see from Table 16 that the novel image encryption algorithm runs slower only than algorithm in Reference [28]. The novel algorithm needs Θ(n²) of pixel shuffling iterations. For analysis of theoretical complexity in substitutions, the time-consuming parts in computations are Θ(n²) iterations of calculations of a sine and a cosine functions. Therefore, the proposed encryption scheme needs more theoretical time than the algorithms in [27,28].

Table 16. Time complexity comparisons.

Compared to other chaotic image encryption algorithms, we can see that the running speed of the proposed scheme is fast.

5. Conclusions

References

1. Fridrich, J. Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos. 1998, 8, 1259–1284. [Google Scholar]
2. Fu, C.; Wang, P.; Ma, X.; Xu, Z.; Zhu, W. A Fast Pseudo Stochastic Sequence Quantification Algorithm Based on Chebyshev Map and Its Application in Data Encryption, Proceedings of the 6th International Conference on Computational Science, Reading, UK, 28–31 May 2006.Computational Science–ICCS 2006; Alexandrov, V.; Albada, G.; Sloot, P.; Dongarra, J. (Eds.) Springer Verlag: Berlin, Germany, 2006; Lecture Notes in Computer Science 3991; pp. 826–829.
3. Fu, C.; Chen, J.; Zou, H.; Meng, W.; Zhan, Y.; Yu, Y. A Chaos-Based Digital Image Encryption Scheme with an Improved Diffusion Strategy. Opt. Express. 2012, 20, 2363–2378. [Google Scholar]
4. Hung, X. Image encryption algorithm using chaotic Chebyshev generator. Nonlinear Dyn. 2012, 67, 2411–2417. [Google Scholar]
5. Yoon, E.; Jeon, I. An efficient and secure Diffie-Hellman key agreement protocol based on Chebyshev chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2383–2389. [Google Scholar]
6. Wang, X.; Teng, L.; Qin, X. A NovelColour Image Encryption Algorithm Based on Chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar]
7. Fu, C.; Lin, B.; Miao, Y.; Liu, X.; Chen, J. A NovelChaos-Based Bit-Level Permutation Scheme for Digital Image Encryption. Opt. Commun. 2011, 284, 5415–5423. [Google Scholar]
8. Wang, X.-Y.; Yang, L.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar]
9. Wang, X.-Y.; Yu, Q. A block encryption algorithm based on dynamic sequences of multiple chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 574–581. [Google Scholar]
10. Liu, H.; Wang, X. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt. Commun. 2011, 284, 3895–3903. [Google Scholar]
11. Skiadas, C.H. Mathematical models of Chaos. In Chaos Applications in Telecommunications; Stavroulakis, P., Ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 383–413. [Google Scholar]
12. Skiadas, C.H.; Skiadas, C. Chaotic Modelling and Simulation: Analysis of Chaotic Models, Attractors and Forms; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
13. Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Application; NIST Special Publication 800-22; NIST: Gaithersburg, MD, USA, 15 May 2001. [Google Scholar]
14. Marsaglia, G. The Marsaglia Random Number CDROM including the Diehard Battery of Tests of Randomness; Florida State University: Tallahassee, FL, USA, 1995. Available online: http://www.stat.fsu.edu/pub/diehard/ accessed on 8 April 2015.
15. Walker, J. ENT: A Pseudorandom Number Sequence Test Program. Available online: http://www.fourmilab.ch/random/ accessed on 8 April 2015.
16. Hell, M.; Johansson, T.; Meier, W. Grain: A stream cipher for constrained environments. Int. J. Wirel. Mobile Comput. 2007, 2, 86–93. [Google Scholar]
17. Kocarev, L.; Makraduli, J.; Amato, P. Public-Key Encryption Based on Chebyshev Polynomials. Circuits Syst. Signal Process. 2005, 24, 497–517. [Google Scholar]
18. Kordov, K.M. Modified Chebyshev map based pseudo-random bit generator. AIP Conf. Proc. 2014, 1629, 432–436. [Google Scholar]
19. Stoyanov, B.P. Pseudo-random bit generator based on Chebyshev map. AIP Conf. Proc. 2013, 1561, 369–372. [Google Scholar]
20. Stoyanov, B.; Kordov, K. Novel Image Encryption Scheme Based on Chebyshev Polynomial and Duffing Map. Sci. World J 2014. [Google Scholar] [CrossRef]
21. IEEE Computer Society, IEEE Standard for Binary Floating-Point Arithmetic. ANSI/IEEE Std. 754; IEEE: New York, NY, USA, 1985.
22. Chen, J.; Zhu, Z.; Fu, C.; Yu, H. An Improved Permutation-Diffusion Type Image Cipher with a Chaotic Orbit Perturbing. Opt. Express. 2013, 21, 27873–27890. [Google Scholar]
23. Diaconu, A.; Loukhaoukha, K. An Improved Secure Image Encryption Algorithm Based on Rubik’s Cube Principle and Digital Chaotic Cipher. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
24. Gao, H.; Zhang, Y.; Liang, S.; Li, D. A new chaotic algorithm for image encryption. Chaos Solitons Fractals. 2006, 29, 393–399. [Google Scholar]
25. Lian, S.G.; Sun, J.; Wang, Z. A block cipher based on a suitable use of the chaotic standard map. Chaos Solitons Fract. 2005, 26, 117–129. [Google Scholar]
26. Al-Maadeed, S.; Al-Ali, A.; Abdalla, T. A New Chaos-Based Image-Encryption and Compression Algorithm. J. Electr. Comp. Eng. 2012, 2012. [Google Scholar] [CrossRef]
27. Zhang, Y.-Q.; Wang, X.-Y. A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar]
28. Zhu, Z.-L.; Zhang, W.; Wong, K.W.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf. Sci. 2011, 181, 1171–1186. [Google Scholar]
29. Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft. Comput. 2012, 12, 1457–1466. [Google Scholar]
30. Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
31. He, J.; Li, Z.-B; Qian, H.-F. Cryptography based on Spatiotemporal Chaos System and Multiple Maps. J. Softw. 2010, 5, 421–428. [Google Scholar]
32. Liu, L.; Zhang, Q.; Wei, X. A RGB image encryption algorithm based on DNA encoding and chaos map. Comput. Electr. Eng. 2012, 38, 1240–1248. [Google Scholar]
33. Seyedzadeh, S.M.; Mirzakuchaki, S. A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal Process. 2012, 92, 1202–1215. [Google Scholar]
34. Mazloom, S.; Eftekhari-Moghadam, A.M. Color image encryption based on coupled nonlinear chaotic map. Chaos Solitons Fractals. 2009, 42, 1745–1754. [Google Scholar]
35. Chen, G.; Mao, Y.; Chui, C.K. A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps. Chaos Solitons Fractals. 2004, 21, 749–761. [Google Scholar]
36. Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. 2011, 2, 31–38. [Google Scholar]
37. Ghebleh, M.; Kanso, A.; Noura, H. An image encryption scheme based on irregularly decimated chaotic maps. Signal Process. Image Commun. 2014, 29, 618–627. [Google Scholar]
38. Kanso, A.; Ghebleh, M. A novel image encryption algorithm based on a 3D chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2943–2959. [Google Scholar]