Feeding Back the Output or Sharing the State: Which Is Better for the State-Dependent Wiretap Channel?
Abstract
:1. Introduction

2. Capacity-Equivocation Region of the Model of Figure 1
2.1. Definitions of the Model of Figure 1
2.2. Main Result of the Model of Figure 1
- The range of the random variable K satisfies . The proof is standard and easily obtained by using the support lemma (see [15]), and thus, we omit the proof here.
- Corollary 1. The secrecy capacity satisfies:
- Here, note that if is a degraded version of (which implies the existence of the Markov chain ), the capacity-equivocation region still holds. The proof of this degraded case is along the lines of the proof of Theorem 1, and thus, we omit the proof here. In [10,12], an achievable rate-equivocation region is provided for the wiretap channel with noncausal CSI, and it is given by:where the joint probability distribution of satisfies:Here, note that:where (a) is from . Therefore, it is easy to see that the achievable rate-equivocation region of [10] and [12] is enhanced by using this noiseless feedback.
- Proof of the converse: Using the fact that is independent of and , the converse proof of Theorem 2 is along the lines of that of Theorem 1 (see Section A), and thus, we omit the proof here.
- Proof of the achievability: The achievability proof of Theorem 2 is along the lines of the achievability proof of Theorem 1 (see Section B), and the only difference is that for the causal case, there is no need to use the binning technique. Thus, we omit the proof here.
- The range of the auxiliary random variable K satisfies . The proof is standard and easily obtained by using the support lemma (see p. 310 of [16]), and thus, we omit the proof here.
- Corollary 2. The secrecy capacity satisfies:
- Here, note that if is a degraded version of , the capacity-equivocation region still holds. The proof of this degraded case is along the lines of the proof of Theorem 2, and thus, we omit the proof here. In [12], an achievable rate-equivocation region is provided for the wiretap channel with causal CSI, and it is given by:where the joint probability distribution of satisfies:By using (15), it is easy to see that the achievable rate-equivocation region is enhanced by using this noiseless feedback.
3. Examples of the Model of Figure 1
3.1. Gaussian Case of the Model of Figure 1 with Noncausal CSI at the Transmitter
- To the best of the authors’ knowledge, for the case , the bounds on the secrecy capacity of the Gaussian wiretap channel with noncausal CSI at the transmitter are still unknown.
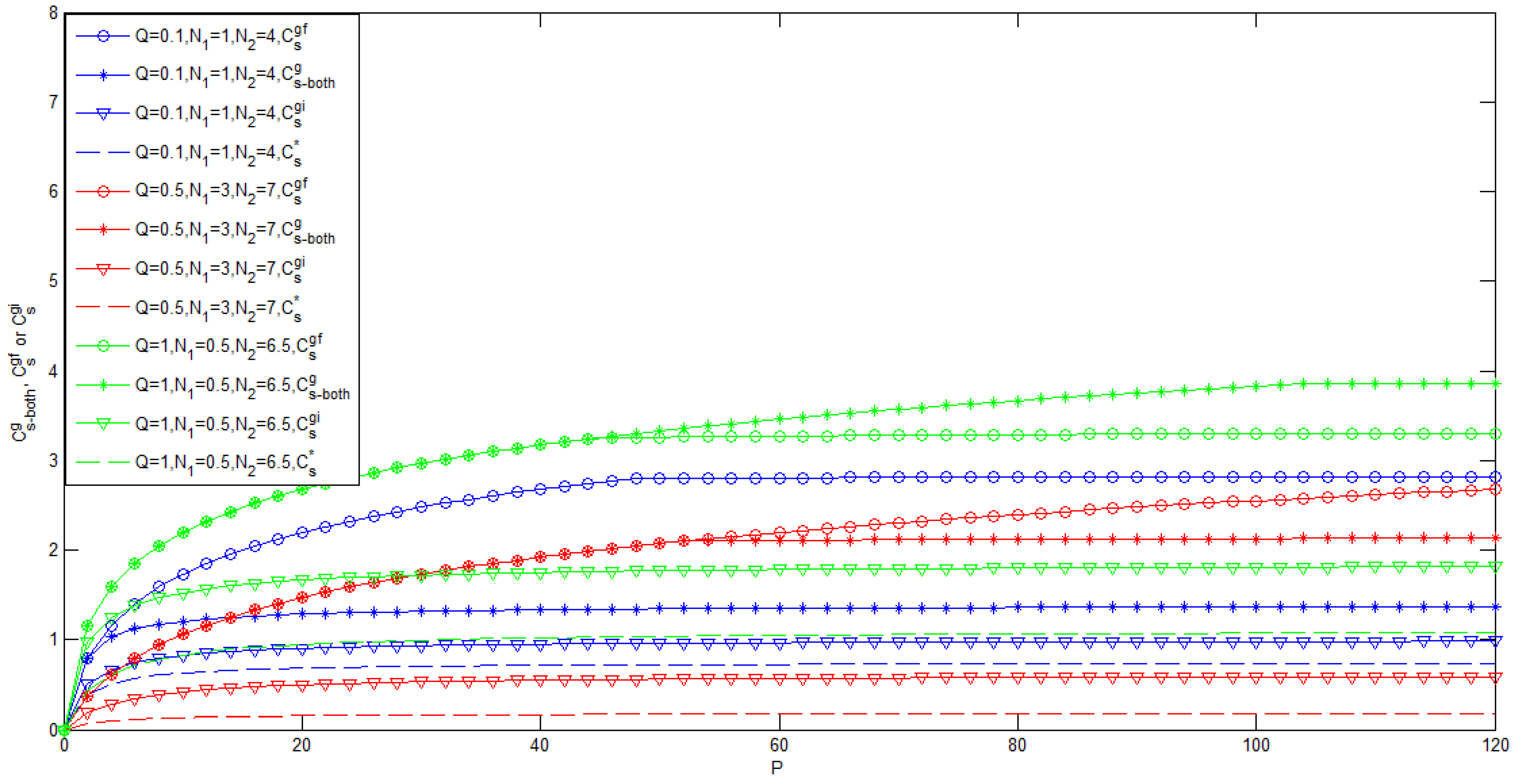

3.2. Binary Case of the Model of Figure 1
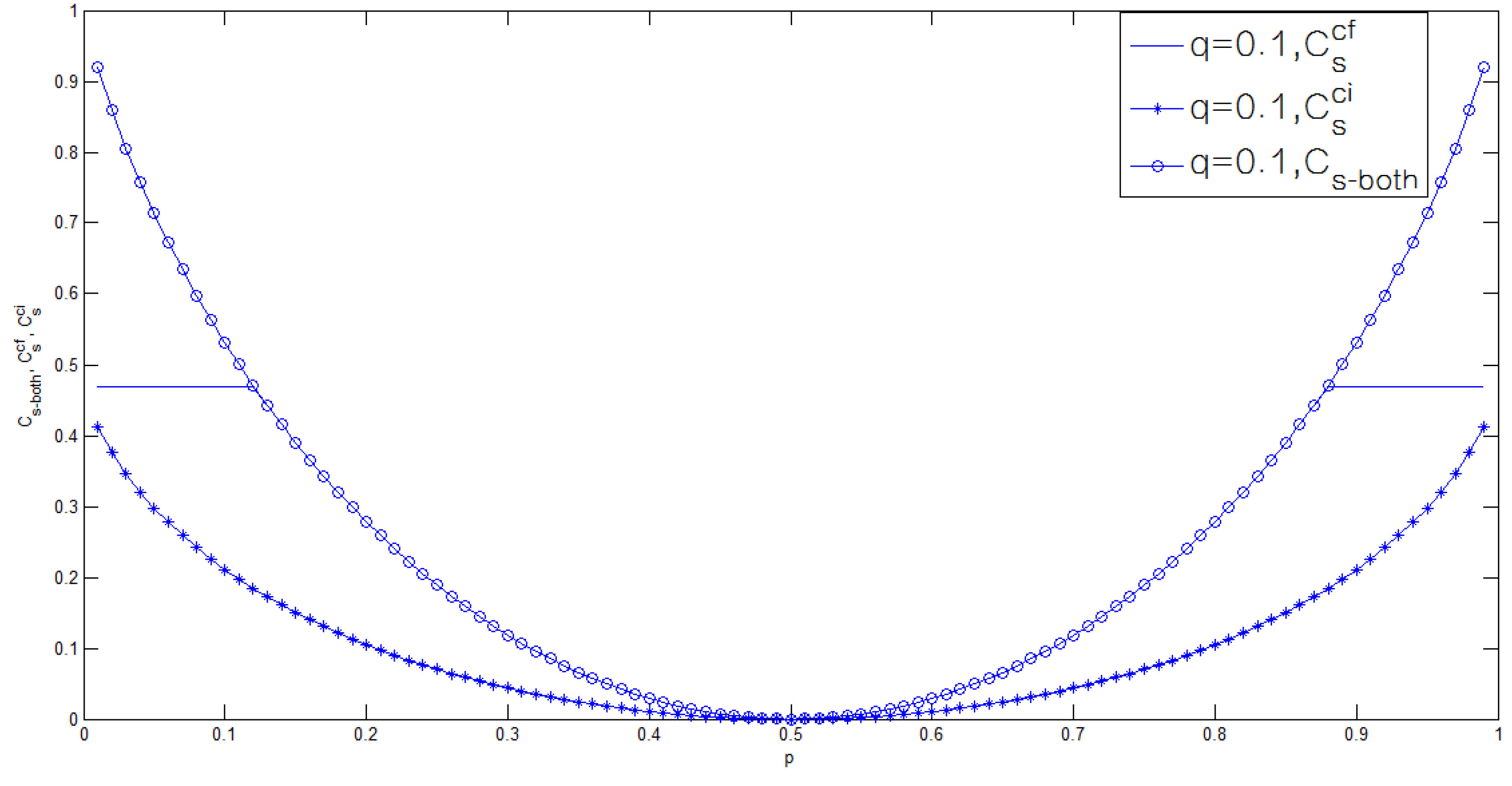

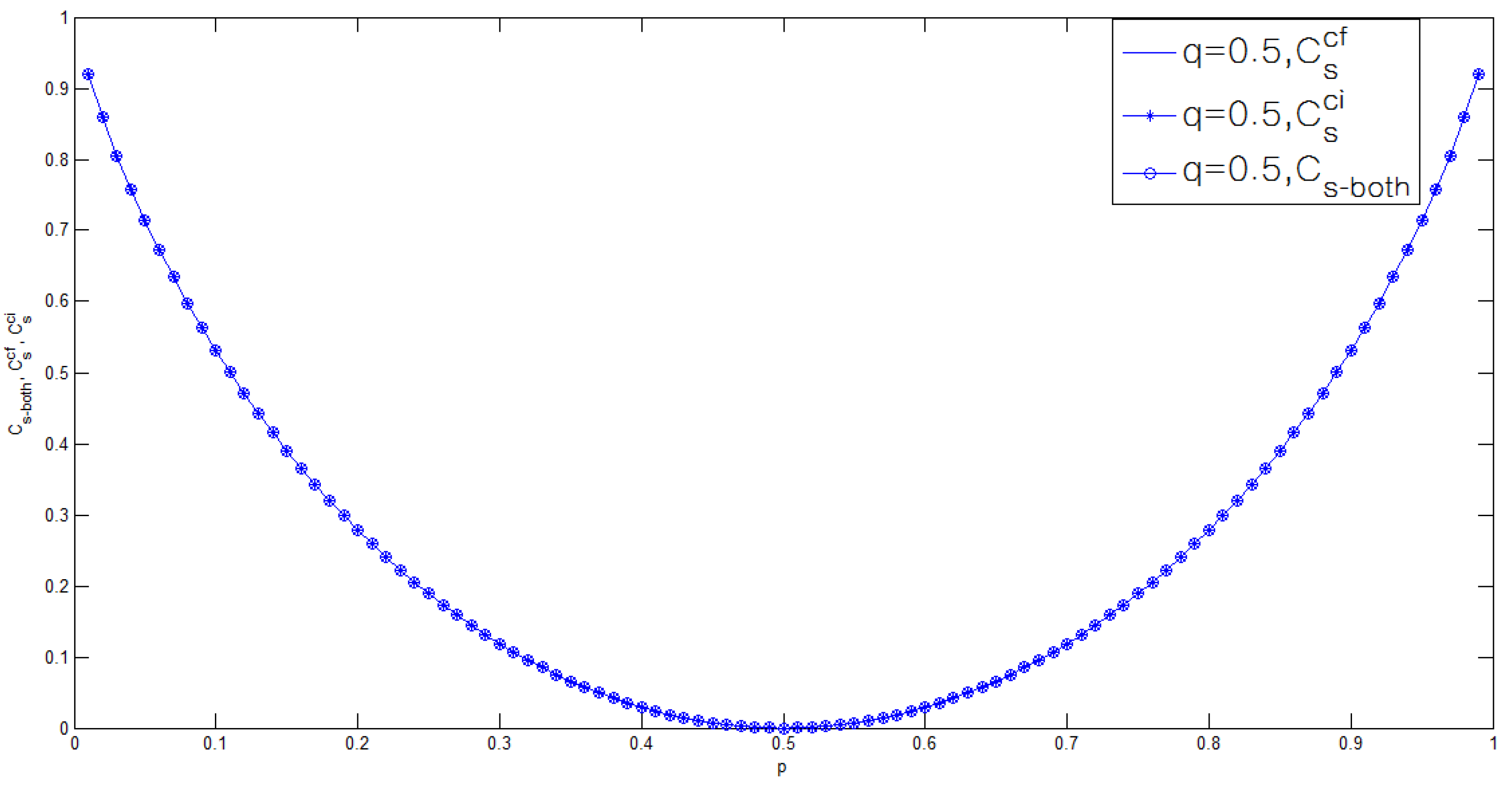
4. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
Appendix
A. Converse Proof of Theorem 1
A.1. Proof of (A.1)
A.2. Proof of (A.2)
A.3. Proof of (A.3)
B. Direct Proof of Theorem 1
- Case 1: If , we need to show that is achievable, where .
- Case 2: If , we need to show that is achievable.
B.1. The Balanced Coloring Lemma
B.2. Code-Book Generation
- Construction of for Case 1:For each block, generate () i.i.d. sequences of , according to . Partition these sequences at random into bins, such that each bin has sequences. Index each bin by .Denote the message () by , where and . Here, note that is independent of .In the first block, for a given side information , try to find a , such that . If multiple sequences exist, randomly choose one for transmission. If there is no such sequence, declare an encoding error.For the i-th block (), the transmitter receives the output of the -th block; he or she gives up if ( as ). It is easy to see that the probability for giving up at the -th block tends to zero as . In the case , generate a mapping . Define a random variable by (), and it is uniformly distributed over the set . is independent of . Reveal the mapping to the legitimate receiver, the wiretapper and the transmitter. Then, since the transmitter gets , he computes . For a given (), the transmitter selects a sequence in the bin (where ⊕ is the modulo addition over ), such that . If multiple sequences in bin exist, choose the sequence with the smallest index in the bin. If there is no such sequence, declare an encoding error. Here, note that since is independent of , is independent of and . The proof is given as follows.Proof. Since:and:it is easy to see that , which implies that is independent of .Analogously, we can prove that , which implies that is independent of . Thus, the proof of is independent of , and is completed.☐
- Construction of for Case 2: The construction of for Case 2 is similar to that of Case 1, except that there is no need to divide into two parts. The detail is as follows. For the i-th block (), if , generate a mapping (note that ). Let (), and it is uniformly distributed over the set . is independent of . Reveal the mapping to the legitimate receiver, the wiretapper and the transmitter. When the transmitter receives the feedback of the -th block, he or she computes . For a given transmitted message (), the transmitter selects a codeword in the bin (where ⊕ is the modulo addition over ), such that . If multiple sequences in bin exist, select the one with the smallest index in the bin. If there is no such sequence, declare an encoding error. Here, note that is independent of and , and the proof is similar to that of Case 1. Thus, we omit the proof here.
B.3. Proof of Achievability
- For Case 1, part of the message is encrypted by . In the analysis of the equivocation, we drop from . Then, the equivocation about is equivalent to the equivocation about . Since , the wiretapper tries to guess from . Note that for a given and sufficiently large N, . Thus, the wiretapper can guess from the conditional typical set . By using the above Lemma 1 and (B.2), the set maps into at least (here, ) (colors). Thus, in the i-th block, the uncertainty about is bounded by:Here, note that is uniformly distributed.
- For Case 2, the alphabet of the secret key equals the alphabet , and the encrypted message is denoted by . Then, by using the above Lemma 1 and (B.2), the set maps into at least (here, ) (colors). Thus, in the i-th block, the uncertainty about is bounded by:
References
- Ahlswede, R.; Cai, N. Transmission, Identification and Common Randomness Capacities for Wire-Tap Channels with Secure Feedback from the Decoder. In General Theory of Information Transfer and Combinatorics; Springer-Verlag: Berlin/Heidelberg, Germany, 2006; Volume 4123, pp. 258–275. [Google Scholar]
- Dai, B.; Vinck, A.J.H.; Luo, Y.; Zhuang, Z. Capacity region of non-degraded wiretap channel with noiseless feedback. In Proceedings of 2012 IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012.
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Ardestanizadeh, E.; Franceschetti, M.; Javidi, T.; Kim, Y. Wiretap channel with secure rate-limited feedback. IEEE Trans. Inf. Theory 2009, 55, 5353–5361. [Google Scholar] [CrossRef]
- Lai, L.; El Gamal, H.; Poor, H.V. The wiretap channel with feedback: Encryption over the channel. IEEE Trans. Inf. Theory 2008, 54, 5059–5067. [Google Scholar] [CrossRef]
- He, X.; Yener, A. The role of feedback in two-way secure communication. IEEE Trans. Inf. Theory 2013, 59, 8115–8130. [Google Scholar] [CrossRef]
- Bassi, G.; Piantanida, P.; Shamai, S. On the capacity of the wiretap channel with generalized feedback. In Processdings of 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015.
- Mitrpant, C.; Vinck, A.J.H.; Luo, Y. An achievable region for the gaussian wiretap channel with side information. IEEE Trans. Inf. Theory 2006, 52, 2181–2190. [Google Scholar] [CrossRef]
- El-Halabi, M.; Liu, T.; Georghiades, C.N.; Shamai, S. Secret writing on dirty paper: A deterministic view. IEEE Trans. Inf. Theory 2012, 58, 3419–3429. [Google Scholar] [CrossRef]
- Chen, Y.; Vinck, A.J.H. Wiretap channel with side information. IEEE Trans. Inf. Theory 2008, 54, 395–402. [Google Scholar] [CrossRef]
- Gel’fand, S.I.; Pinsker, M.S. Coding for channel with random parameters. Probl. Control Inf. Theory 1980, 9, 19–31. [Google Scholar]
- Dai, B.; Luo, Y. Some new results on wiretap channel with side information. Entropy 2012, 14, 1671–1702. [Google Scholar] [CrossRef]
- Chia, Y.K.; El Gamal, A. Wiretap channel with causal state information. IEEE Trans. Inf. Theory 2012, 58, 2838–2849. [Google Scholar] [CrossRef]
- Liu, T.; Mukherjee, P.; Ulukus, S.; Lin, S.; Hong, Y.W.P. Secure degrees of freedom of MIMO Rayleigh block fading wiretap channels with no CSI anywhere. IEEE Trans. Wireless Commun. 2015, 14, 2655–2669. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Academic Press: New York, NY, USA, 1981; pp. 123–124. [Google Scholar]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar]
- Gamal, A.E.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Costa, M.H.M. Writing on dirty paper. IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Leung-Yan-Cheong, S.; Hellman, M.E. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 1978, 24, 451–456. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, B.; Ma, Z.; Yu, L. Feeding Back the Output or Sharing the State: Which Is Better for the State-Dependent Wiretap Channel? Entropy 2015, 17, 7900-7925. https://doi.org/10.3390/e17127852
Dai B, Ma Z, Yu L. Feeding Back the Output or Sharing the State: Which Is Better for the State-Dependent Wiretap Channel? Entropy. 2015; 17(12):7900-7925. https://doi.org/10.3390/e17127852
Chicago/Turabian StyleDai, Bin, Zheng Ma, and Linman Yu. 2015. "Feeding Back the Output or Sharing the State: Which Is Better for the State-Dependent Wiretap Channel?" Entropy 17, no. 12: 7900-7925. https://doi.org/10.3390/e17127852
APA StyleDai, B., Ma, Z., & Yu, L. (2015). Feeding Back the Output or Sharing the State: Which Is Better for the State-Dependent Wiretap Channel? Entropy, 17(12), 7900-7925. https://doi.org/10.3390/e17127852




