Identify the Rotating Stall in Centrifugal Compressors by Fractal Dimension in Reconstructed Phase Space
Abstract
:1. Introduction
2. Numerical Simulations of the Rotating Stall in the Centrifugal Impeller
2.1. The Model and Numerical Method
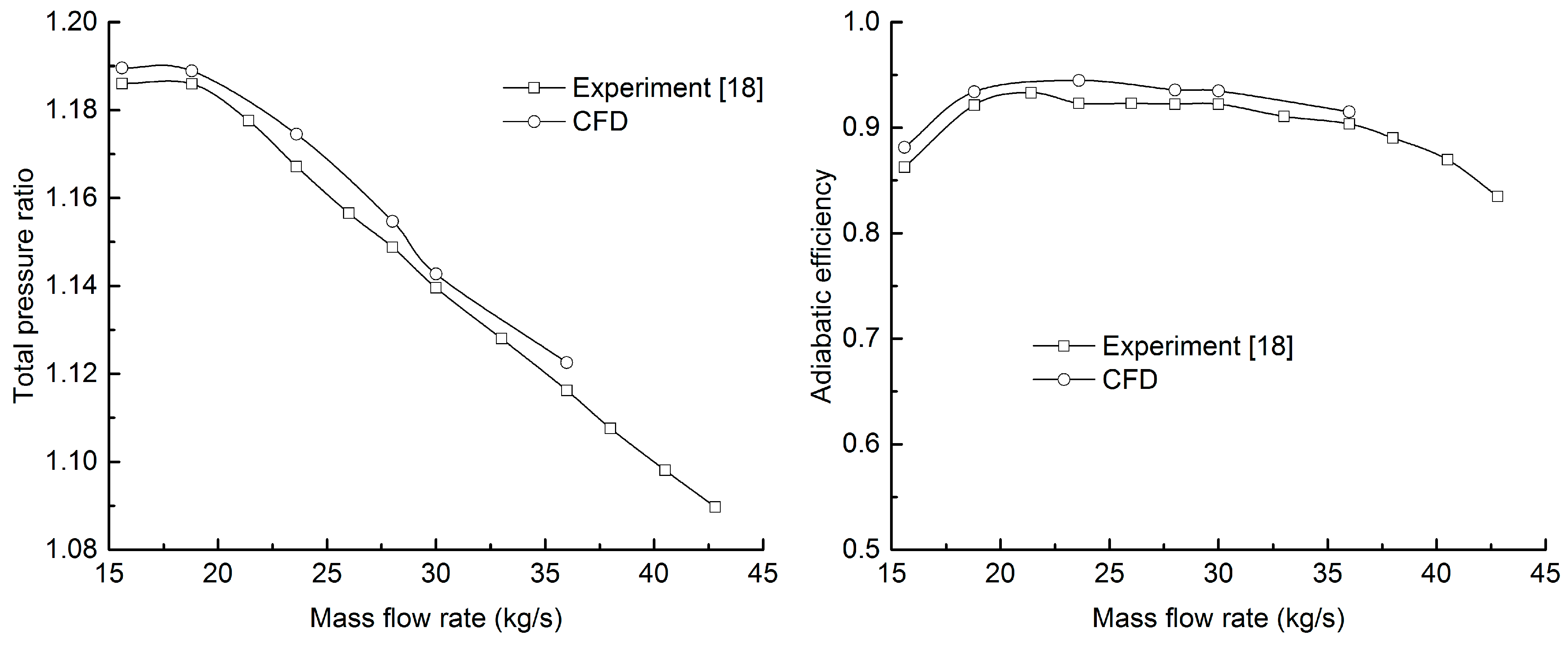
2.2. The Model and Numerical Method
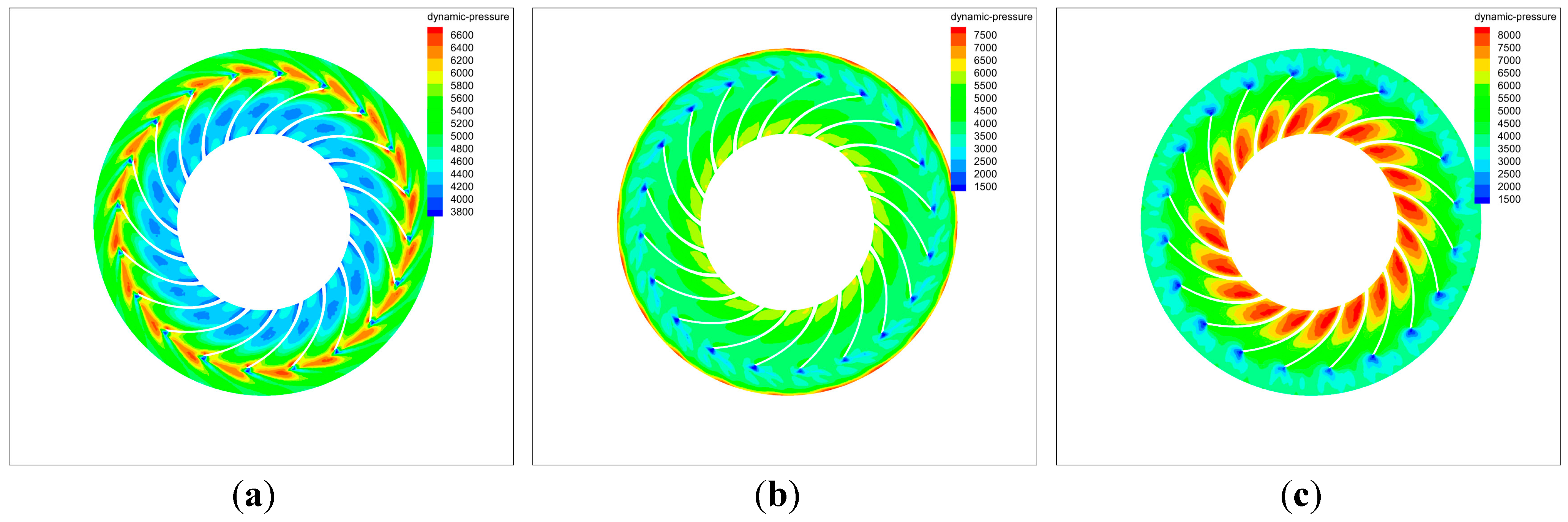
3. Phase Space Reconstruction of Pressure Time Series
3.1. Phase Space Reconstruction
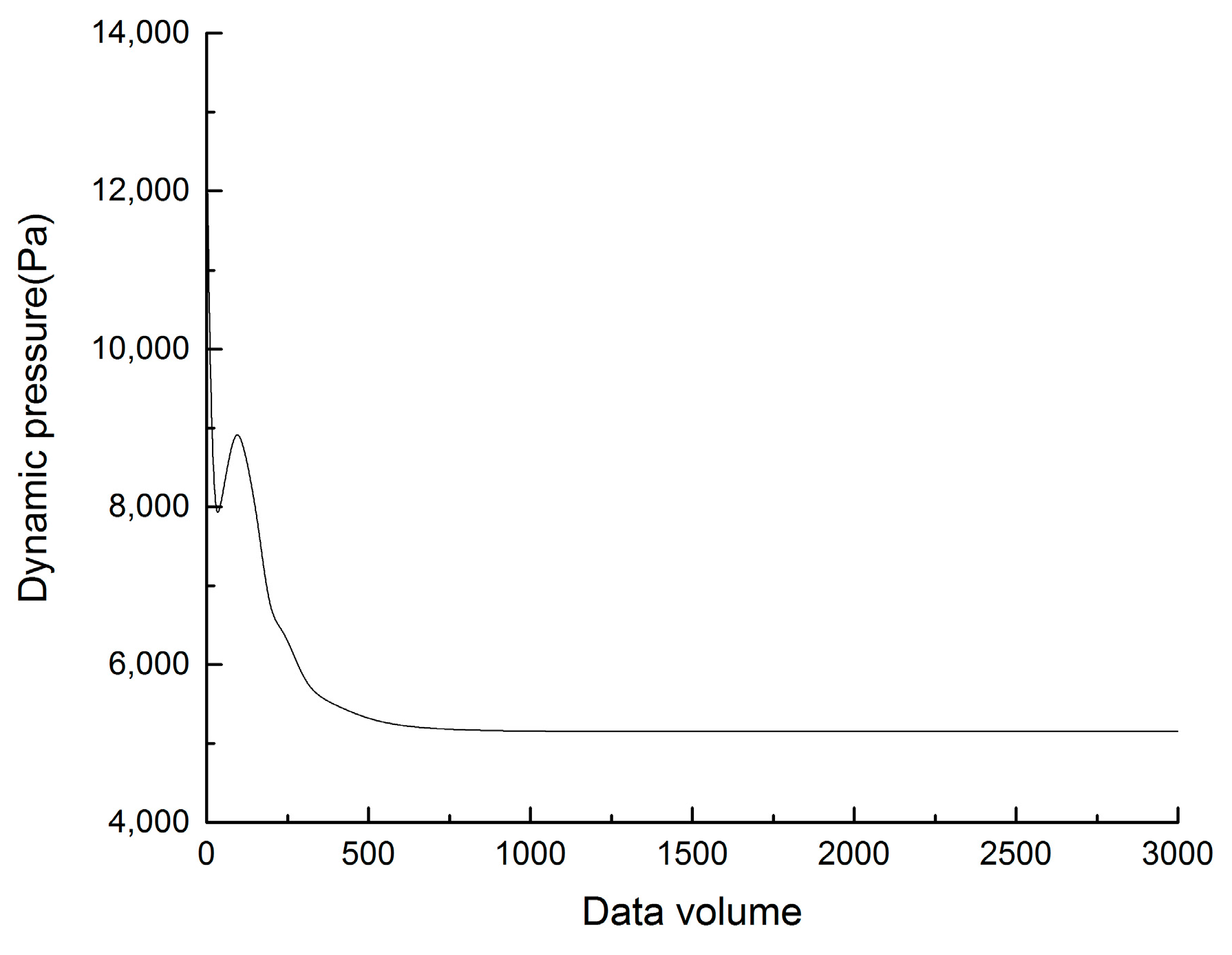
3.2. C–C Method
3.3. Pressure Time Series of the Sampling Points
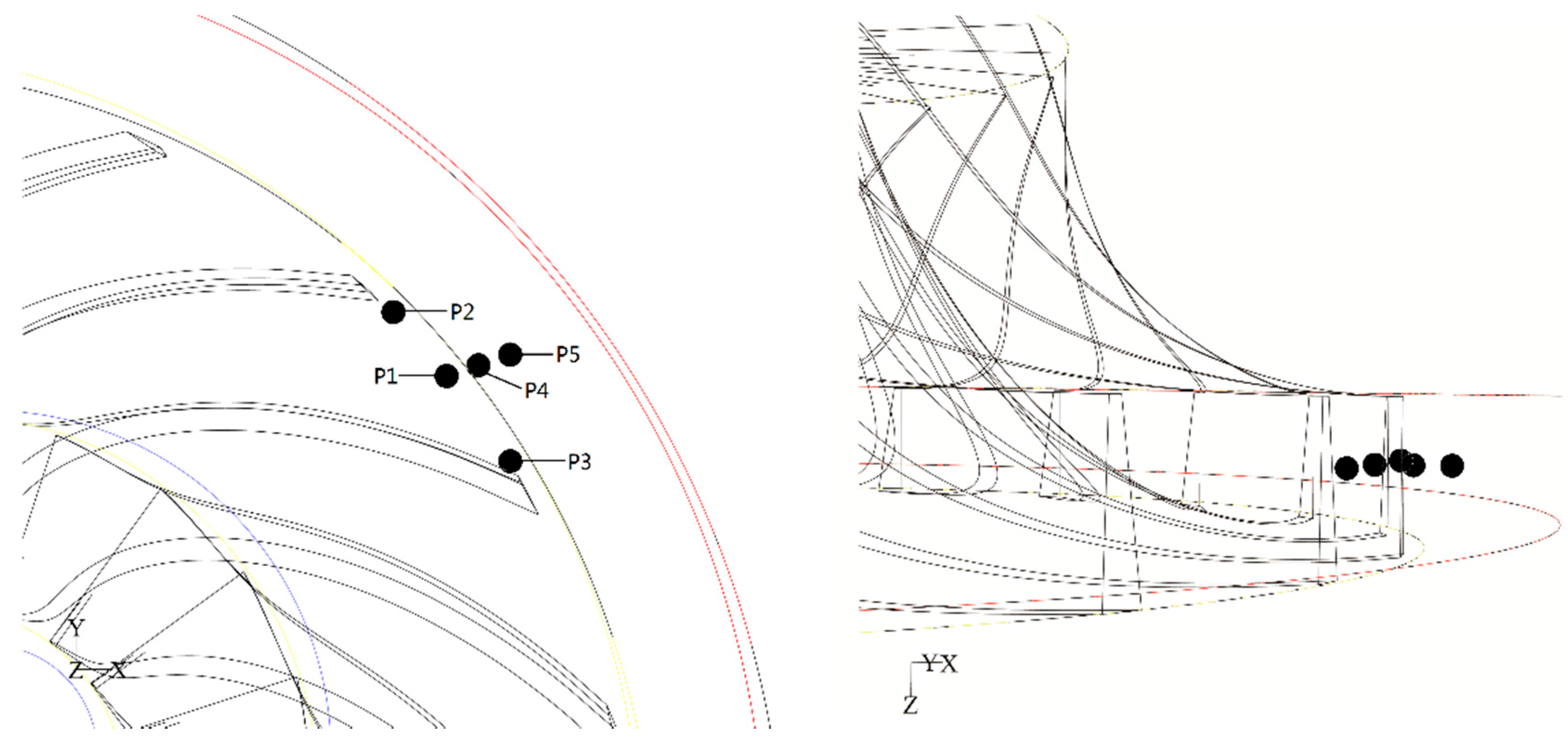
3.4. Phase Space Reconstruction in Pre- and Post- Rotating stalls
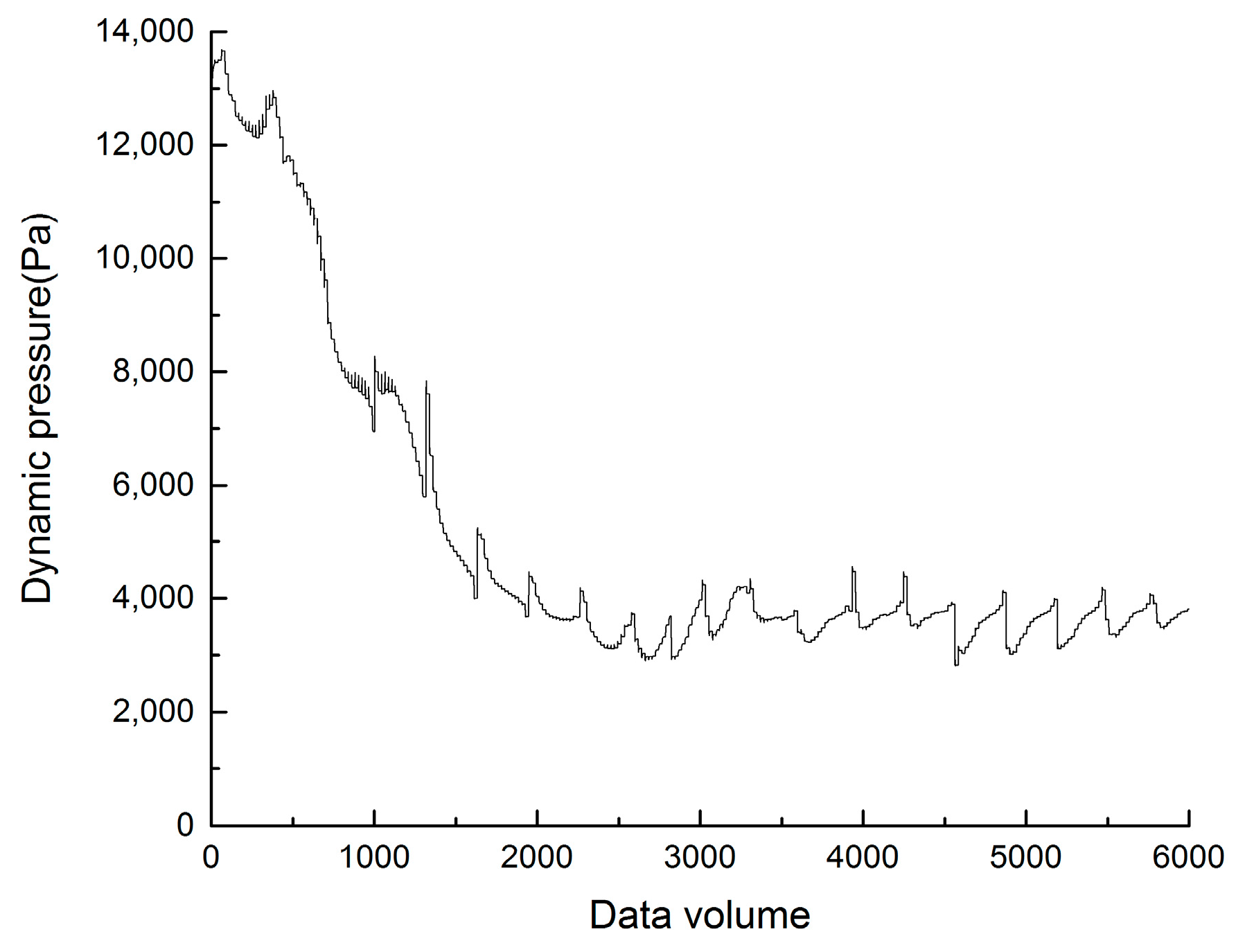
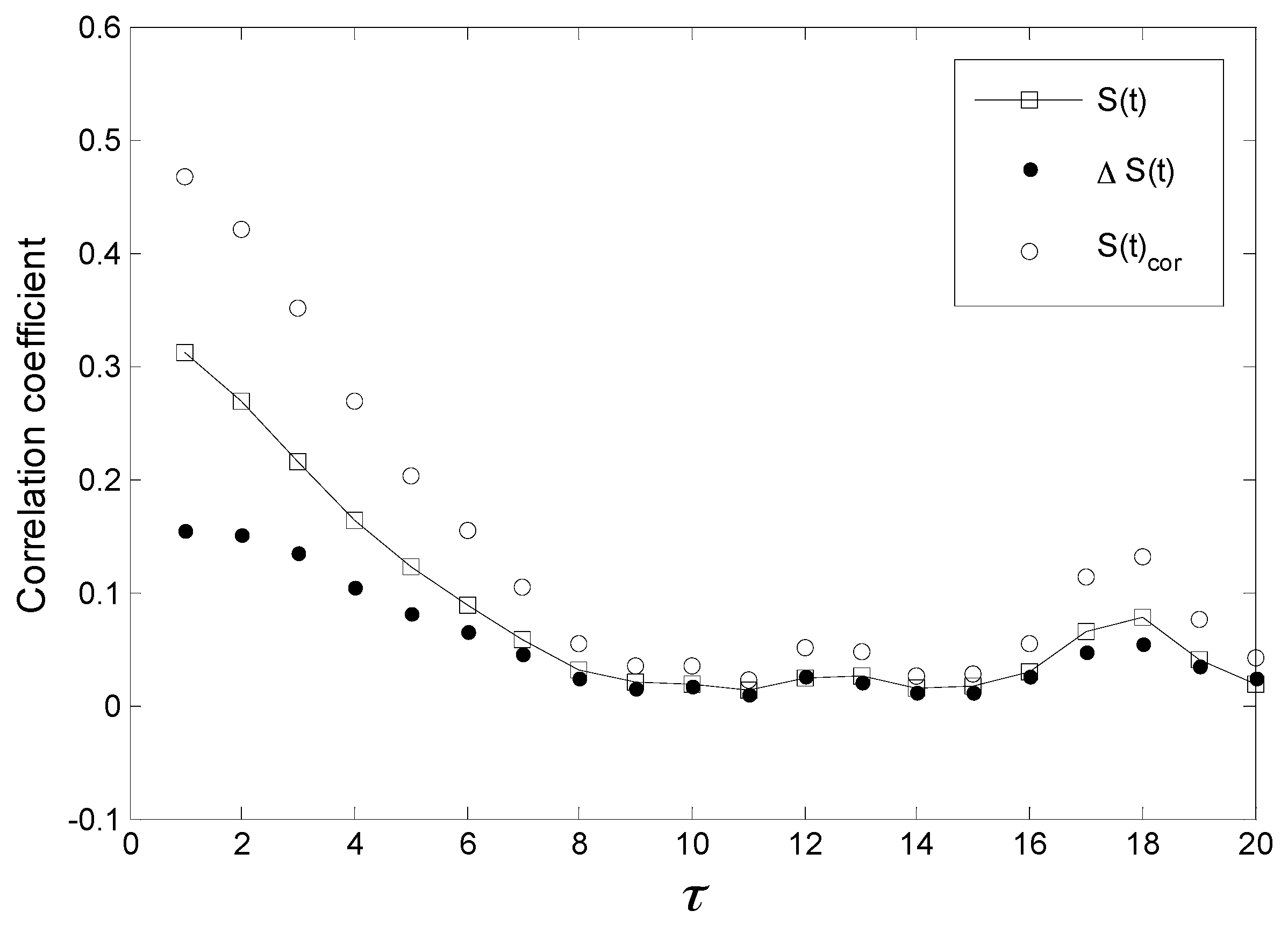
3.4.1. Dynamics Analysis of the Pre- and Post- Rotating stall by Phase Space Reconstruction
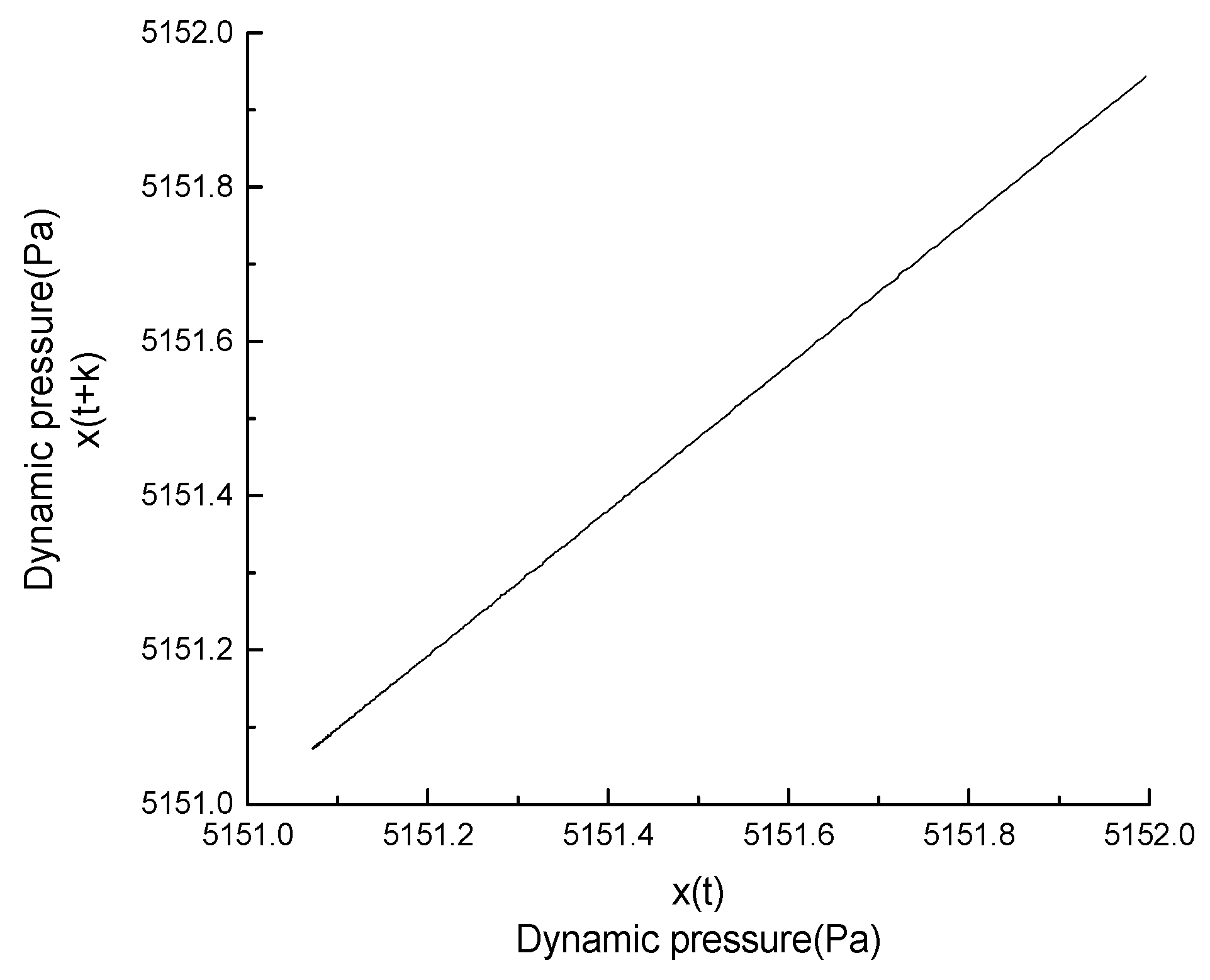
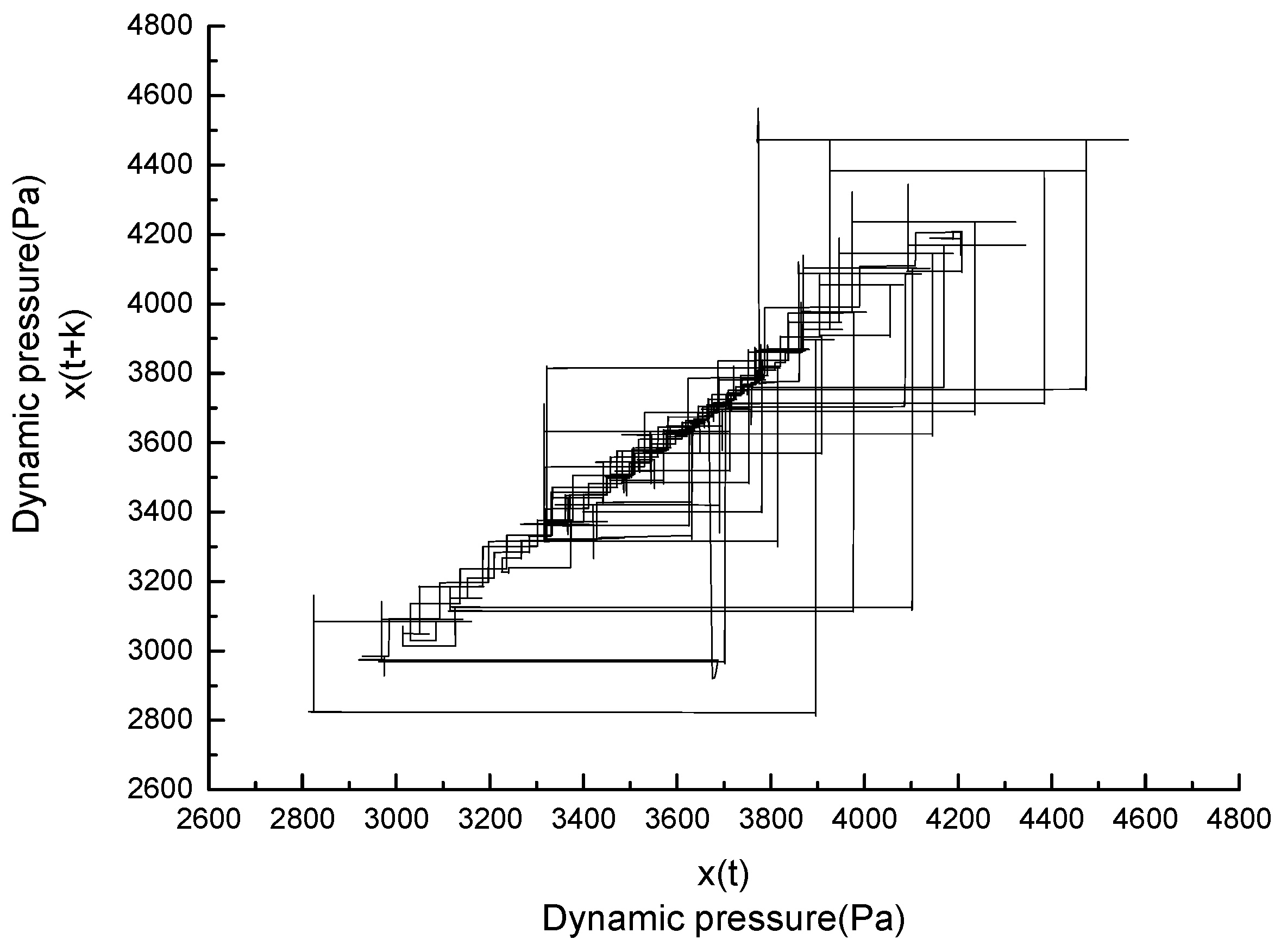
3.4.2. The Fractal Dimension in the Reconstructed Phase Space in the Post-Rotating Stall

4. Phase Space Reconstruction of the Pressure Time Series at Different Locations
4.1. Parameters for Phase Space Reconstruction at Different Locations
| P2 | P3 | P4 | P5 | |
|---|---|---|---|---|
| 12 | 12 | 11 | 10 | |
| 15 | 12 | 14 | 10 | |
| 2.25 | 2.00 | 2.27 | 2.00 |
4.2. Phase Space Reconstruction for Pressure Time Series at Different Locations
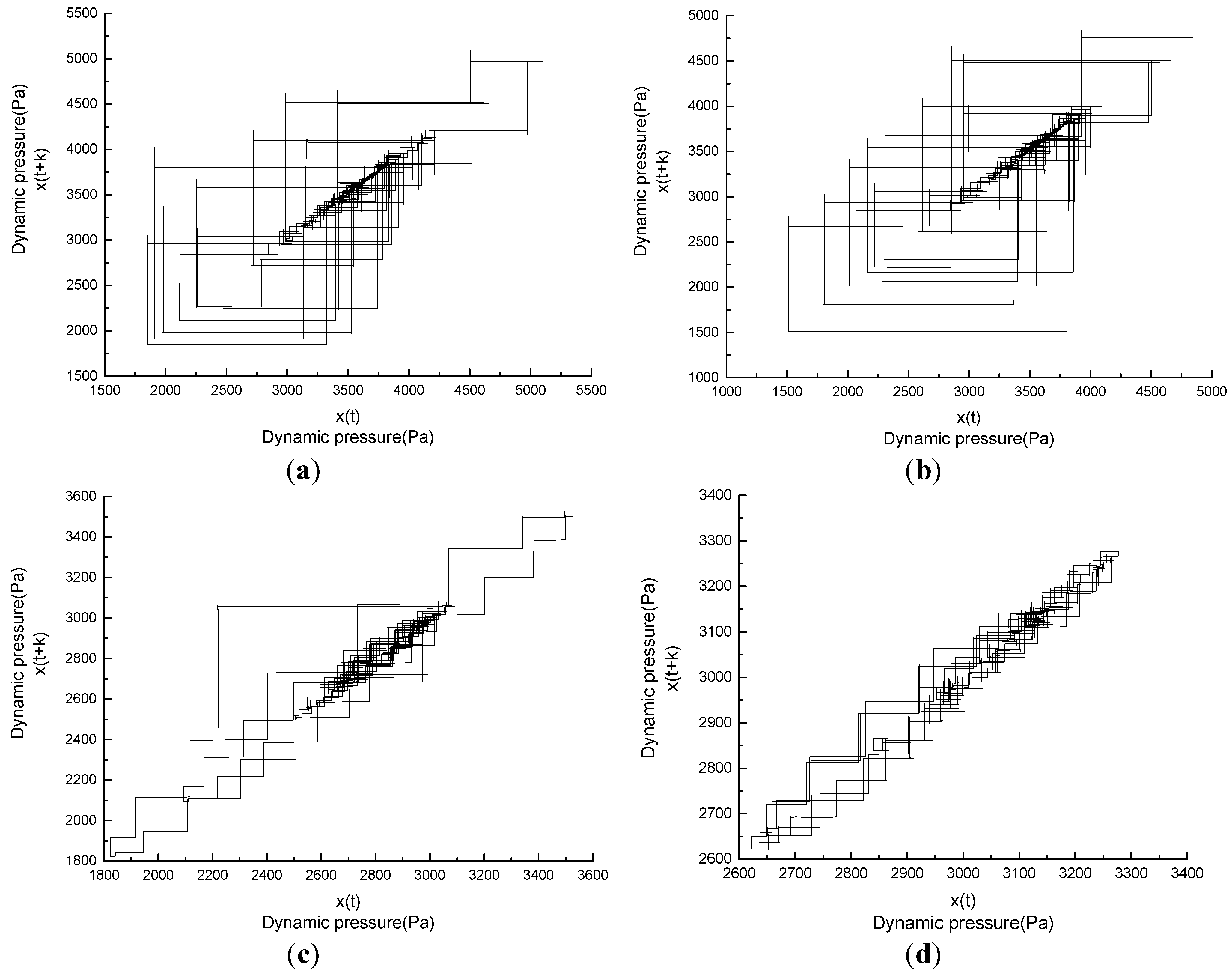
4.3. Fractal Dimension in the Reconstructed Phase Space for Pressure Time Series at Different Locations
4.3.1. Fractal Dimension in the Reconstructed Phase Space at Circumference Locations

4.3.2. Fractal Dimensions in Reconstructed Phase Space at Different Radial Locations
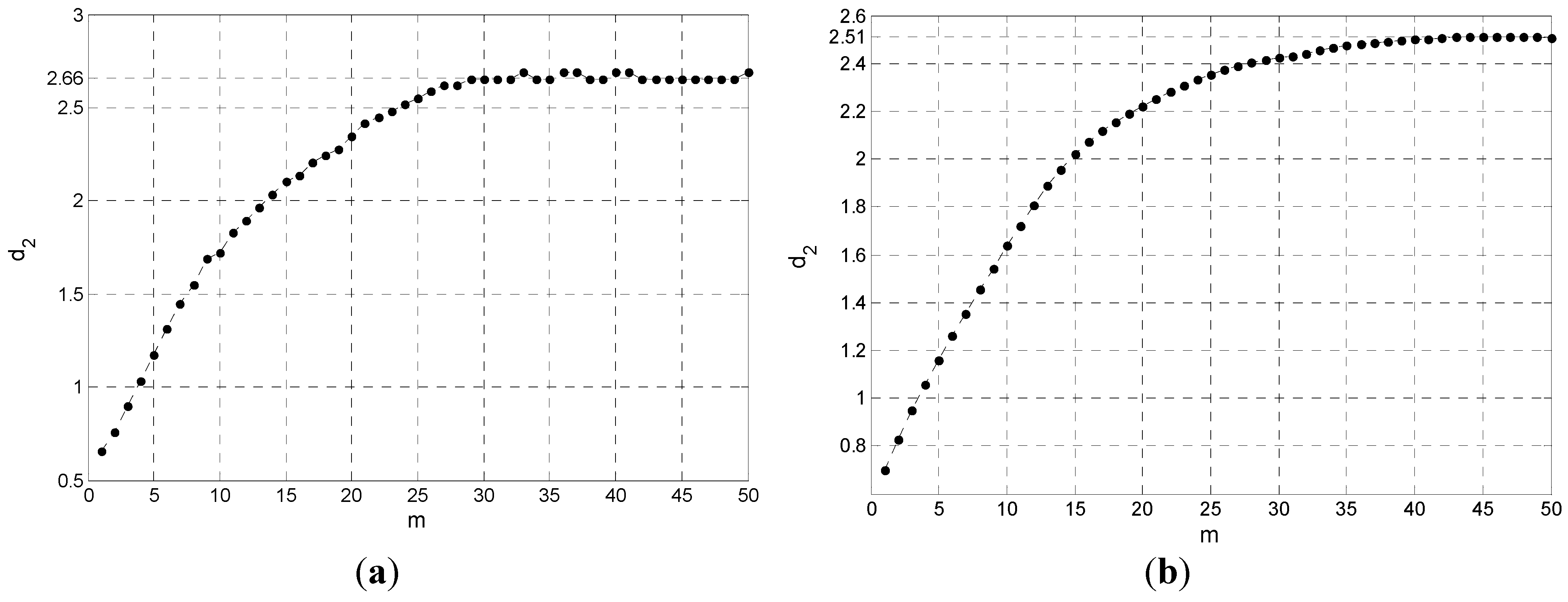
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stein, A.; Niazi, S.; Sankar, L.N. Computational Analysis of Stall and Separation Control in Centrifugal Compressors. J. Propuls. Power 2000, 16, 65–71. [Google Scholar] [CrossRef]
- Stein, A.; Niazi, S.; Sankar, L.N. Computational Analysis of Centrifugal Compressor Surge Control Using Air Injection. J. Aircr. 2001, 38, 513–520. [Google Scholar] [CrossRef]
- Taher, H.; Mohamed, A.; Osama, B.; Mohamed, S.G. Numerical Investigation of The rotating stall Characteristics and Active Stall Control in Centrifugal Compressors. In Proceedings of the ASME 2014 Power Conference, Baltimore, MD, USA, 28–31 July 2014.
- Day, I.J.; Greitzer, E.M.; Cumpsty, N.A. Prediction of Compressor Performance in The rotating stall. J. Eng. Power 1978, 100, 1–14. [Google Scholar] [CrossRef]
- Day, I.J. Stall Inceptionin Axial Flow Compressor. J. Turbomach. 1993, 115, 1–9. [Google Scholar] [CrossRef]
- Tan, C.S.; Day, I.J.; Morris, S.; Wadia, A. Spike-Type Compressor Stall Inception Detection and Control. Annu. Rev. Fluid Mech. 2010, 42, 275–300. [Google Scholar] [CrossRef]
- Greitzer, E.M. Review—Axial Compressor Stall Phenomenon. J. Fluids Eng. 1980, 102, 134–151. [Google Scholar] [CrossRef]
- Fink, D.A.; Cumpsty, N.A.; Greitzer, E.M. Surge Dynamics in a Free-Spool Centrifugal Compressor System. J. Turbomach. 1992, 114, 321–332. [Google Scholar] [CrossRef]
- Chima, R.V.; Yokota, J.W. Numerical Analysis of Three-Dimensional Viscous Internal Flows. AIAA J. 1990, 28, 798–806. [Google Scholar] [CrossRef]
- Xu, C.; Amano, R.S. Study of the Flow in Centrifugal Compressor. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009.
- Liu, Y.; Li, K.; Zhang, J.; Wang, H.; Liu, L. Numerical Bifurcation Analysis of Static Stall of Airfoil and Dynamic Stall under Unsteady Perturbation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3427–3434. [Google Scholar] [CrossRef]
- Seely, A.J.E.; Newman, K.D.; Herry, C.L. Fractal Structure and Entropy Production within the Central Nervous System. Entropy 2014, 16, 4497–4520. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time Series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Joseph, D.D.; Chen, T.S. Friction Factors in theory of Bifurcating Poiseuille Flow through Annular Ducts. J. Fluid Mech. 1974, 66, 189–207. [Google Scholar] [CrossRef]
- Farmer, M.E. Chaotic Phenomena from Motion in Image Sequences. In Proceedings of the International Joint Conference on Neural Networks 2007 (IJCNN 2007), Orlando, FL, USA, 12–17 August 2007.
- Bright, M.M. Chaotic Time Series Analysis Tool for Identification and Stabilization of the Rotating Stall Precursor Events in High Speed Compressor. Ph. D. Thesis, Akron University, Akron, OH, USA, 2000. [Google Scholar]
- Gu, Y.; Zhou, Z.; Li, Y. Characteristic of fan stalling based on correlated dimensions. Trans. Nanjing Univ. Aeronaut. Astronaut. 2011, 28, 362–366. [Google Scholar]
- Hathaway, M.D.; Chriss, R.M.; Strazisar, A.J.; Wood, J.R. Laser Anemometer Measurement of the Three-Dimensional Rotor Flow Field in the NASA Low-Speed Centrifugal Compressor. Available online: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19950025564.pdf (accessed on 17 November 2015).
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Grassgerber, P.; Prociccia, I. Measuring the strangeness of strange attractors. Phys. D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Kugiumtzis, D. State space reconstruction parameters in the analysis of chaotiic time series-the role of the time widow length. Phys. D 1996, 95, 13–28. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay time and embedding windows. Phys. D 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; Wiley: New York, NY, USA, 2004. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, J.; Zhang, W. Identify the Rotating Stall in Centrifugal Compressors by Fractal Dimension in Reconstructed Phase Space. Entropy 2015, 17, 7888-7899. https://doi.org/10.3390/e17127848
Wang L, Zhang J, Zhang W. Identify the Rotating Stall in Centrifugal Compressors by Fractal Dimension in Reconstructed Phase Space. Entropy. 2015; 17(12):7888-7899. https://doi.org/10.3390/e17127848
Chicago/Turabian StyleWang, Le, Jiazhong Zhang, and Wenfan Zhang. 2015. "Identify the Rotating Stall in Centrifugal Compressors by Fractal Dimension in Reconstructed Phase Space" Entropy 17, no. 12: 7888-7899. https://doi.org/10.3390/e17127848
APA StyleWang, L., Zhang, J., & Zhang, W. (2015). Identify the Rotating Stall in Centrifugal Compressors by Fractal Dimension in Reconstructed Phase Space. Entropy, 17(12), 7888-7899. https://doi.org/10.3390/e17127848






