Abstract
The equation that approximately traces the trajectory in the concentration phase space of chemical kinetics is derived based on the rate of entropy production. The equation coincides with the true chemical kinetics equation to first order in a variable that characterizes the degree of quasi-equilibrium for each reaction, and the equation approximates the trajectory along at least final part of one-dimensional (1-D) manifold of true chemical kinetics that reaches equilibrium in concentration phase space. Besides the 1-D manifold, each higher dimensional manifold of the trajectories given by the equation is an approximation to that of true chemical kinetics when the contour of the entropy production rate in the concentration phase space is not highly distorted, because the Jacobian and its eigenvectors for the equation are exactly the same as those of true chemical kinetics at equilibrium; however, the path or trajectory itself is not necessarily an approximation to that of true chemical kinetics in manifolds higher than 1-D. The equation is for the path of steepest descent that sufficiently accounts for the constraints inherent in chemical kinetics such as element conservation, whereas the simple steepest-descent-path formulation whose Jacobian is the Hessian of the entropy production rate cannot even approximately reproduce any part of the 1-D manifold of true chemical kinetics except for the special case where the eigenvector of the Hessian is nearly identical to that of the Jacobian of chemical kinetics.1. Introduction
One of the classical problems in describing the stability of dynamic systems is to find a Lyapunov function for a process in which a chemically reacting system converges to chemical equilibrium. For example, after a pioneering study by Wei [1], who characterized chemically reacting systems by some axioms, Shear [2] and Higgins [3] found and discussed a Lyapunov function for detailed-balanced systems. Krambeck [4] also characterized chemically reacting systems using some axioms with thermodynamic relations instead of a Lyapunov function. Feinberg, Horn, Jackson, and others [5–7] developed “chemical reaction network theory” to give attention to mass-action kinetics; those studies describe the stable dynamic behavior of such systems independently of the values of rate parameters [8–10]. Although the results from [5–7] are summarized in [10] from a modern viewpoint to review recent developments in the theory of chemical reaction networks ([9,11–13] for examples), an important issue in these classical papers is that complex balanced systems (including detailed-balanced systems) have a unique positive equilibrium concentration that is locally asymptotically stable, at least for closed systems with ideal mixing-rules [14]; this mathematically supports that the second law of thermodynamics holds for such systems. Horn and Jackson [7] have shown this using a Lyapunov function similar to that of Shear [2] (though there is another history about this problem, which is briefly reviewed by Powers and Paolucci [15]), whereas Johnston [10] recently showed it by linearizing the mass-action kinetics equation near the equilibrium state. Typically, this illustrates that there are two ways to confirm the existence of an equilibrium state: one is the use of a Lyapunov function and the other is the rather direct use of kinetics equations. However, use of a Lyapunov function provides no trajectories to arrive at equilibrium in the concentration phase space of a chemical reaction system.
In non-equilibrium thermodynamics, Ziegler [16] has postulated that the rate of entropy production is maximized with certain prescribed dissipative forces. The principal results obtained from this hypothesis were known for linear non-equilibrium systems and the second law [17]. However, for chemical reaction systems, there is no example of deriving the equation that describes a chemical change directly based on entropy production or on a Lyapunov function that does not use a chemical kinetics equation. Gorban et al. [18–20] and Lebiedz [21–23] utilized the second law of thermodynamics to determine the so-called slow invariant manifold (SIM) or the so-called low-dimensional manifold (LDM). Gorban et al. [18–20] utilized the basis orthonormal with respect to their “entropic” scalar product that uses the Hessian of a Lyapunov function (the free energy of a perfect gas in a constant volume at constant temperature) because their almost orthogonal “projector” that defines SIM helps convergence to determine SIM [20]. Lebiedz [21–23] proposed a variational principle to identify or approximate SIM as a geodesic to minimize the distance from equilibrium in concentration phase space [22,23], and they [21–23] proposed and compared various types of Riemannian metrics for concentration phase space. Two of these metrics are related to thermodynamics: one [22] is the Hessian of a Lyapunov function, which is the same as used by Gorban et al. [18–20], and the other [23] is the metric of a diagonal matrix whose diagonal components correspond to each species and is defined as the sum of the products of the corresponding stoichiometric coefficients and entropy production rates of respective reactions. The success of these methods in approximating SIM suggests that there might be some thermodynamic equation that determines trajectories for arriving at equilibrium in concentration phase space, although it is uncertain how the thermodynamic methods used by Gorban et al. [18–20] and Lebiedz [21–23] are related to a chemical kinetics equation. Furthermore, Al-Khateeb et al. [24] have concluded that a system’s dynamics cannot be deduced from the Gibbs free energy or entropy production rate (thermodynamic Lyapunov functions) even near the equilibrium state, and they stated that equilibrium thermodynamic potentials do not alone determine the dynamics of a reactive system during the approach to physical equilibrium.
Based on the rate of entropy production in chemical kinetics, this study derives the equation that approximately traces the trajectory in the concentration phase space of chemical kinetics, and argues that the above statement of Al-Khateeb et al. [24] seems to need careful understanding and interpretation. In the derivation, a type of quasi-equilibrium approximation is used in which the difference between the forward and backward rates of each reversible reaction is assumed to be sufficiently small with respect to the backward rate. The equation coincides with the true chemical kinetics equation to first order in a defined variable that characterizes the degree of quasi-equilibrium of each reaction. We call this new equation for the linear non-equilibrium path (ELNEP) because the equation is justified as an approximation to true chemical kinetics for some linear non-equilibrium domain and identifies the trajectory that arrives at equilibrium in concentration phase space for such a domain, although such an approximation is effective only for detailed-balanced quasi-equilibrium and detailed-balanced completely equilibrium state, i.e., complex balancing is not considered below in this paper. (The mathematical difference between detailed balancing and complex balancing has been discussed in [25] based on the theory of chemical reaction networks).
For trajectories to arrive at equilibrium, there is a hierarchy of manifolds of lower dimension that tends to equilibrium [18–23,26–28], i.e., a bundling of trajectories near “manifolds of slow motion” of successively lower dimension (the so-called SIM or LDM already mentioned) as time progresses [21]. The ELNEP reproduces such a bundling into a one-dimensional (1-D) manifold and even higher dimensional manifolds that are almost the same as those of true chemical kinetics when the contour of the entropy production rate in the concentration phase space is not highly distorted.
This paper is organized as follows: Section 2 presents the mathematical foundation for closed spatially homogeneous reaction systems and the ELNEP (including its derivation), together with equations for two artificial paths (the steepest descent and Newton direction paths) in addition to the true chemical kinetics path. Section 3 presents and compares all four types of paths for simple examples of reacting systems, including a non-isothermal case and a practical example used by Al-Khateeb et al. [24]. Section 4 gives a theoretical proof (although not in a mathematically formal fashion) that ELNEP reproduces almost the same LDMs of true chemical kinetics. Section 5 briefly comments on the relevance of ELNEP to Ziegler’s hypothesis [16], and Section 6 summarizes this study.
2. Methodology (Mathematical Basis)
The pure reaction contribution to the entropy production rate of a thermally perfect gas in a closed system is as follows [29]:
where t is time, S is the entropy of the system, is the universal gas constant, V is the volume of the system, and σ is the total reaction contribution to the rate of entropy production.
The latter is minus one times the time derivative of the Lyapunov function found by Shear [2] and used by Gorban et al. [18–20], Lebiedz [22], and many others. Therefore, σ can be interpreted as another Lyapunov function of the system in the linear non-equilibrium regime [30], although this interpretation is not necessarily required for the derivation of ELNEP:
where:
Equation (3) gives the contribution of the l th reaction that has a forward reaction rate Rfl and reverse reaction rate Rbl. Chemical reactions proceed in accordance with the following ordinary differential equation of mass-action kinetics:
where:
Here kfl and kbl are the reaction rate constants of the lth forward and reverse reactions, respectively; yk is the concentration of the kth species; and αkl and βkl are the stoichiometric coefficients of the kth species in the lth forward and reverse reactions, respectively. In Section 2.1, the ELNEP is derived; however, before the derivation, two types of artificial paths that are apparently based on the rate of entropy production in Equation (2) are discussed briefly. These paths can be used to compare with the ELNEP.
Steepest descent path. Ziegler [16] proposed an orthogonality principle for irreversible processes, which is equivalent to a certain extremal principle (i.e., the maximal rate of entropy production). However, the thermodynamic and statistical bases of the principle are not clear, although the second law of thermodynamics can be obtained as a corollary of the principle [17]. In the present study, as a candidate for the uncertain thermodynamic equation that determines trajectories to arrive at equilibrium in concentration phase space, the principle is attempted to apply by assuming that reactions proceed in the direction of steepest descent of the entropy production rate σ given in Equation (1), i.e., in the direction of the maximal rate of entropy production:
where S is the pseudo-time (i.e., an artificial time-marching parameter whose unit is not necessarily that of physical time) and is the vector that consists of the species concentrations chosen as the set of independent variables consistent with element conservation (see Section 2.1). Note that the Jacobian of Equation (8) is the Hessian of σ, and that the Hessian of the Lyapunov function is used by Gorban et al. [18–20] and Lebiedz et al. [22] in their methods for identifying SIM, as described in Section 1. In addition, the left-hand side of Equation (8) would have a different unit from that of the right-hand side if the unit of S were that of physical time. Hereafter, the steepest descent path is termed to be the one that is in accordance with Equation (8).
Newton direction path. Equation (8) for the steepest descent path can be interpreted as a version of a well-known optimization method (i.e., the method of steepest descent or ascent). The standard algorithm uses a line search along a definite length in the search direction, whereas Equation (8) uses the pseudo-time and a differential. Another well-known optimization method is Newton iteration in which the function to be optimized is approximated by a second-order Taylor series expansion in the direction of the line search, the so-called Newton direction [31]. The Newton direction path can be calculated in accordance with:
where:
is the Hessian (matrix of second derivatives) of σ with respect to each component of . Equation (9) might be another candidate for the uncertain thermodynamic equation, although it is rejected, as obviously shown below in this study. In spite of that, the left-hand side of Equation (9) has the same unit as that of right-hand side when the unit of S is that of physical time.
2.1. Derivation of ELNEP (Proof of First-order Coincidence)
First, the form of the ELNEP is introduced, and its derivation is described. The ELNEP is the following:
where Q can be decomposed into the two parts (as the following Equation 12): One appears due to the constraints inherent in chemical kinetics such as element conservation and another is the part independent of the constraints. When the constraints do not exist, the first part disappears and consequently ELNEP becomes essentially equivalent to Equation (8) as explained later in this section:
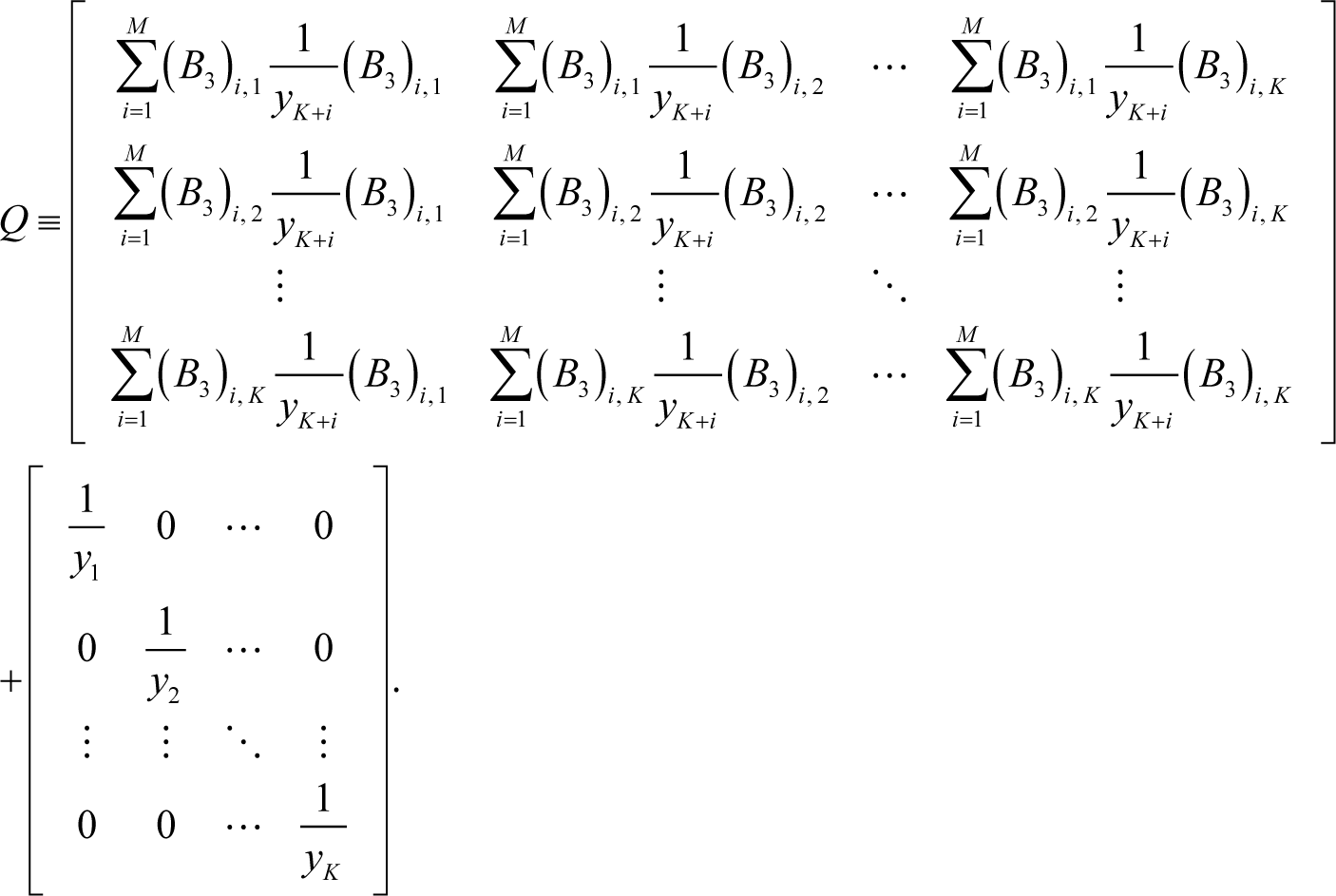
Note that t is not the pseudo-time, and that the matrix Q is symmetric; hence, Q is always invertible because it is positive definite, as proved in Appendix E. The matrix B3 is defined by:
where B2 [32] and B1 are the coefficient matrices of the constraints:
and (B3)i,j is the component in the ith row and jth column of matrix B3. Here:
where K is the number of independent species concentrations (the components of the vector ), M is the number of constraints (such as the number of elements) and also the number of dependent species concentrations (the components of the vector ), N = K + M; and ci for i = 1, ⋯, M is the constants (such as the total number density of the i th element in the system). In principle, the choice of independent and dependent species is arbitrary if the constraints are satisfied. However, the choice may affect the speed or ease of numerical calculation, which is not investigated at present.
It can be proved that Equation (11) coincides with Equation (4) (true chemical kinetics equation) to first order in the variable εl (the difference is in the second order of εl), which is defined by:
Here, it should be noted that sufficiently small |εl| means partial equilibrium or quasi-equilibrium of the lth reaction, and detailed-balanced equilibrium means εl = 0 for every lth reaction in the system. Accordingly, ELNEP is supposed to be applicable to the relaxation process leading to detailed- balanced equilibrium, i.e., a series of successive processes in which the number of elementary reactions that participate in quasi-equilibrium of the system increases (although more careful description of the process is given in Section 4 and Note [33]). In fact, the paths determined by ELNEP trace the low-dimensional manifolds of true chemical kinetics, which is shown in Section 3 and theoretically proved in Section 4; although ELNEP cannot be applied to the complex balancing that does not guarantee εl = 0 and even εl ≈ 0. In brief, the existence of detailed-balanced equilibrium guarantees that each εl approaches zero sooner or later, and the magnitude of each |εl| is a rough indicator how closely ELNEP approximates the path of true chemical kinetics, i.e., ELNEP does not work best in the domain far from equilibrium (large |εl|s). Now, Equation (11) is called as ELNEP, which is derived as follows and its first-order coincidence with Equation (4) is proved.
To begin with, it shall be considered how to properly use −∇σ as a type of thermodynamic “force” to generate paths that are close to the true chemical kinetics path. In such an interpretation, σ would be a thermodynamic “potential” determined by the “position” vector . Such forces are usually employed in optimization techniques, for example, the method of steepest descent or ascent and the Newton iteration, as mentioned earlier for introducing two artificial paths. With respect to this thinking, basic Equations (2) and (3) are calculated to obtain:
Substituting Equation (5) into Equation (18) gives:
At this stage, the constraint must be constituted as follows: As described in Appendix A, the mathematical identity:
holds for an arbitrary function f, whose arguments (xind and xdep) are not independent of each other because of constraints between the xind and xdep variables. Equation (A4) is applied to Equation (19) by treating σ and y in Equation (19) as f and x in Equation (A4), respectively. The result is:
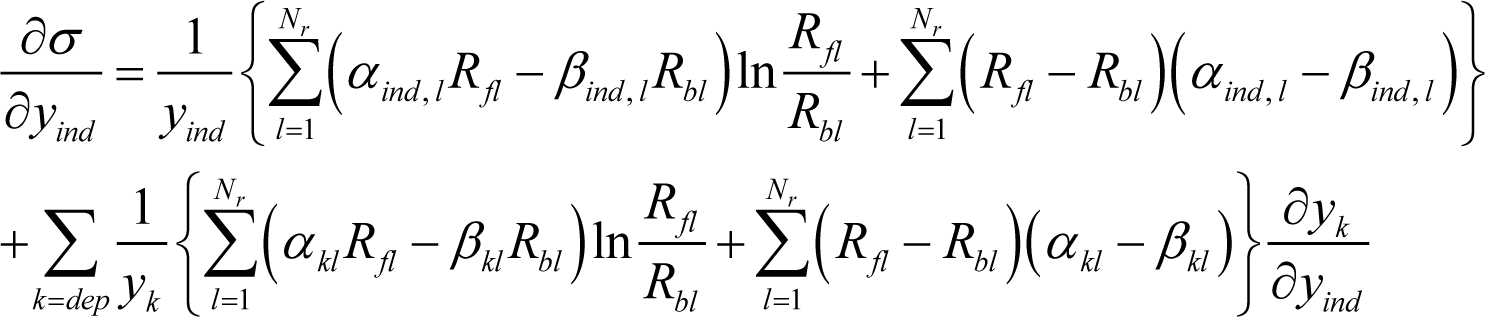
where yind stands for each component of the vector . Since Equation (4) holds, Equation (20) is evidently equivalent to:
In this paper, Equation (14) provides a relation between the two concentration vectors and whose components are the yind and ydep variables in Equation (21), respectively. Accordingly, corresponds to defined by Equation (13), since the derivative of Equation (14):
holds. Thus, Equation (21) becomes:
Furthermore, in Equation (23) can be replaced as follows. From Equation (22), and:
Substituting Equation (24) into Equation (23), the following is obtained:
Equation (25) is equivalent to Equation (4) (true chemical kinetics equation) because Equation (25) is just a variety of Equation (4) based on an identity Equation (20).
The ELNEP is obtained by substituting Equation (17) into Equation (25) as follows. Substituting Equation (17) into the term in Equation (25) gives:
Therefore, Equation (26) is an approximation that is accurate to first order in the variable εl. Then:
Using Equations (24) and (27), Equation (25) becomes:
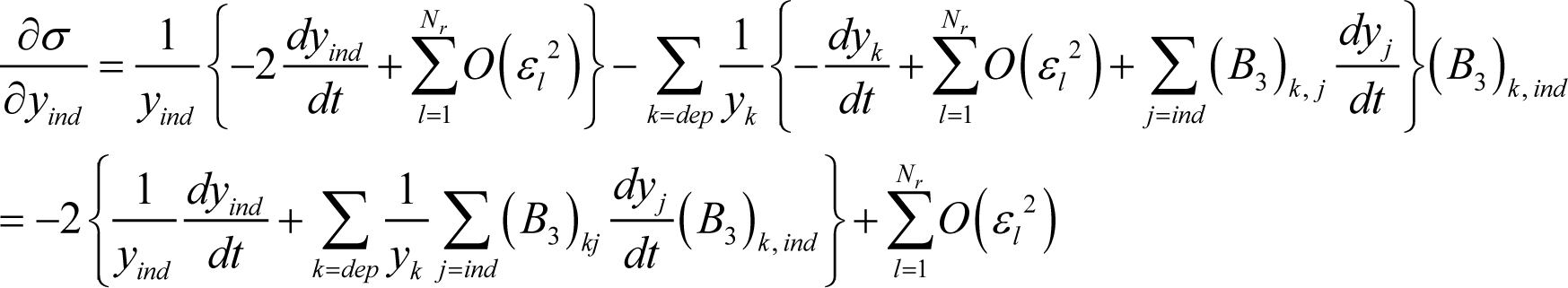
which is the same as Equation (11) except for the second order term of each εl. Accordingly, the ELNEP Equation (11) is equivalent to Equation (4) (true chemical kinetics equation) to first order in each variable εl.
Note that ∇σ on the right-hand side (rhs) of Equations (8), (9), and (11) must also account for the constraints Equation (14) to eliminate ydep in the calculation; whereas Equation (4) intrinsically satisfies the constraints. If any constraint is not considered, Equation (28) can be transformed into the following equation:
which is essentially equivalent to the following Equation (8) for the steepest descent path to first order in each variables εl (as described in Appendix B):
Accordingly, the ELNEP is the equation of the steepest descent path that sufficiently accounts for element conservation. In addition, note that Equation (29) and ELNEP are described with the variable t whose unit is that of physical time, whereas Equation (8) is described with the variable s, pseudo-time whose unit is not that of physical time.
2.2. Relevance to Linear Non-Equilibrium
Since the following Equation (30) also holds to second order in εl, the path that is in accordance with Equation (11) can be termed the path of linear non-equilibrium:
where Jl and Xl are, respectively, interpreted as the thermodynamic flux and thermodynamic force due to the lth reaction.
3. Results: Sample Calculations
In addition to the path of linear non-equilibrium (the path according to ELNEP, Equation 11), the chemical kinetics path (Equation 4) and the paths given by Equations (8) and (9) were calculated for the following examples of simple reaction systems, all of which are detailed-balanced systems with mass-action kinetics because ELNEP is intrinsically based on the reversibility of each reaction and the mass-action law. All calculations in this paper are for a constant volume with fixed or variable (non-isothermal) reaction rate constants, and are dimensionless except for the last example (Section 3.4). In the following, “one-dimensional” is abbreviated as “1-D,” “two-dimensional” is abbreviated as “2-D,” etc.
3.1. A ⇆ 2B ⇆ C: 1-D Manifold
Figures 1 and 2 show the two groups of paths, respectively, for the reactions A⇆2B⇆C projected onto the concentration (yA, yB) phase plane with a contour plot of σ. Figure 1 shows the chemical kinetics and linear non-equilibrium paths, and Figure 2 shows the steepest descent and Newton direction paths. Variable yC is determined by element conservation:
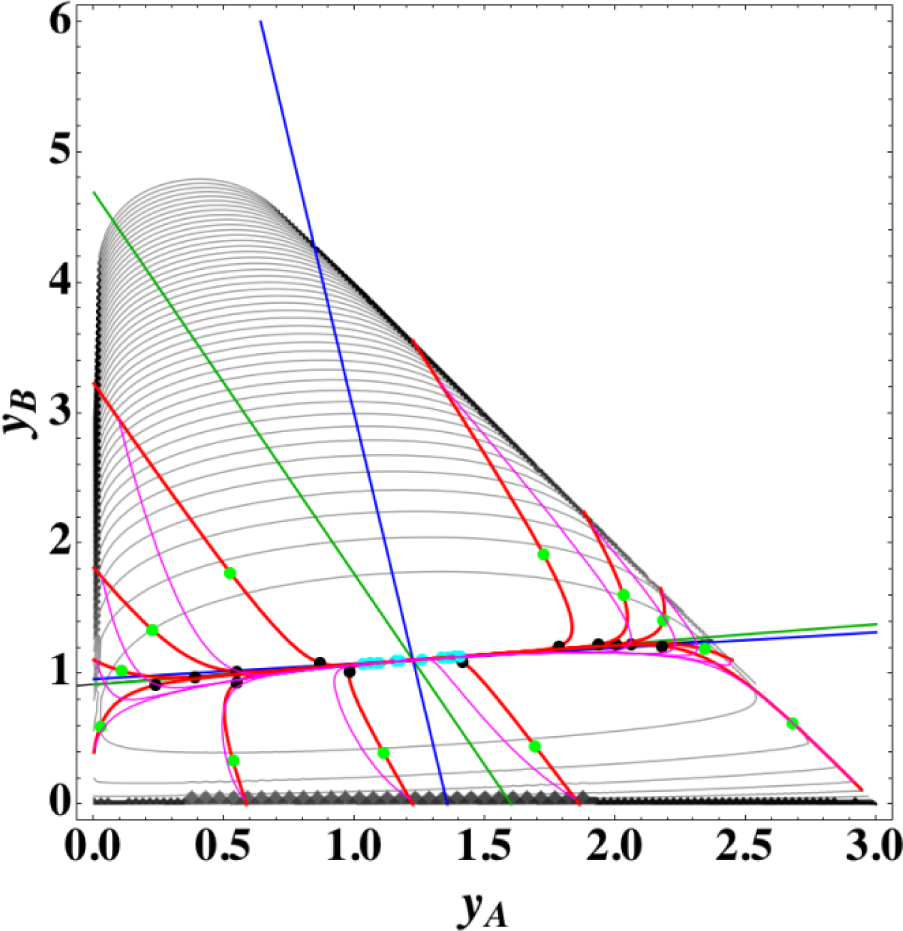
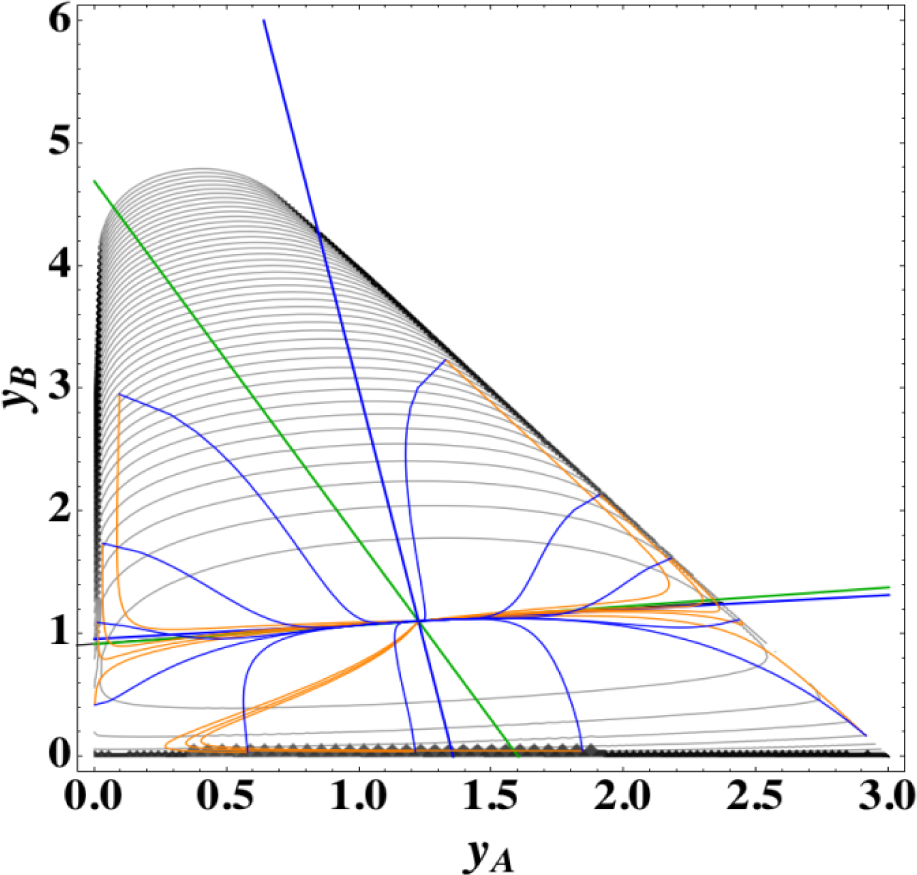
These calculations were performed with the fixed rate constants given in Table 1 for the same equilibrium composition but with different initial compositions (twelve in each figure [34]), and c = 3. The dimensionless equilibrium composition is (yA, yB, yC) = (1.223, 1.106, 1.223). Note that all paths reside in the so-called reaction simplex [35] (kinetics subspace or stoichiometric subspace, both of which coincide [10,36] for the present system) that is determined by c and the stoichiometric coefficients (or the so-called reaction vector [36]) of each reaction. The present reaction simplex is a 2-D plane in the 3-D concentration (yA, yB, yC) phase space. The Following Observations are made from Figures 1 and 2:

- (1)
The paths of linear non-equilibrium (magenta lines in Figure 1) most closely resemble that of chemical kinetics. They have the same 1-D manifold as that of chemical kinetics (one of the eigenvectors of the Jacobian of Equation (4) at equilibrium) expected from the path coinciding with the chemical kinetics path to first order in each variable εl. (The two eigenvectors of the Jacobian of Equation (4) at equilibrium are (1, 0.1544) and (1, −2.928) in the coordinates (yA, yB). The former is the 1-D manifold.)
- (2)
The steepest descent paths (blue lines in Figure 2) have a slightly different 1-D manifold from that of chemical kinetics because the Jacobian of Equation (8) is the Hessian H in Equation (10); this Jacobian differs from that of Equation (4). (The two eigenvectors of the Hessian at equilibrium are (1, 0.1193) and (1, −8.380) in the coordinates (yA, yB).
- (3)
The Newton direction paths (orange lines in Figure 2) have no 1-D manifold or three quasi-1-D manifolds.
It should be noted again that the Jacobian of Equation (8) is the Hessian H, and the difference between ELNEP (Equation 11) and Equation (8) is that Equation (11) does and Equation (8) does not sufficiently account for the constraints such as element conservation, as described in Section 2.1.
Appendix C shows the specific form of the ELNEP (Equation 11) for this case.
3.2. A ⇆ B ⇆ C ⇆ D: 2-D and 1-D Manifolds
Figures 3 and 4 show the two groups of paths, respectively, for the reactions A ⇆ B ⇆ C ⇆ D projected into the concentration (yA, yB, yC) phase space. Figure 3 shows the chemical kinetics and linear non-equilibrium paths, and Figure 4 shows the steepest descent and Newton direction paths. Variable yD is determined by element conservation:
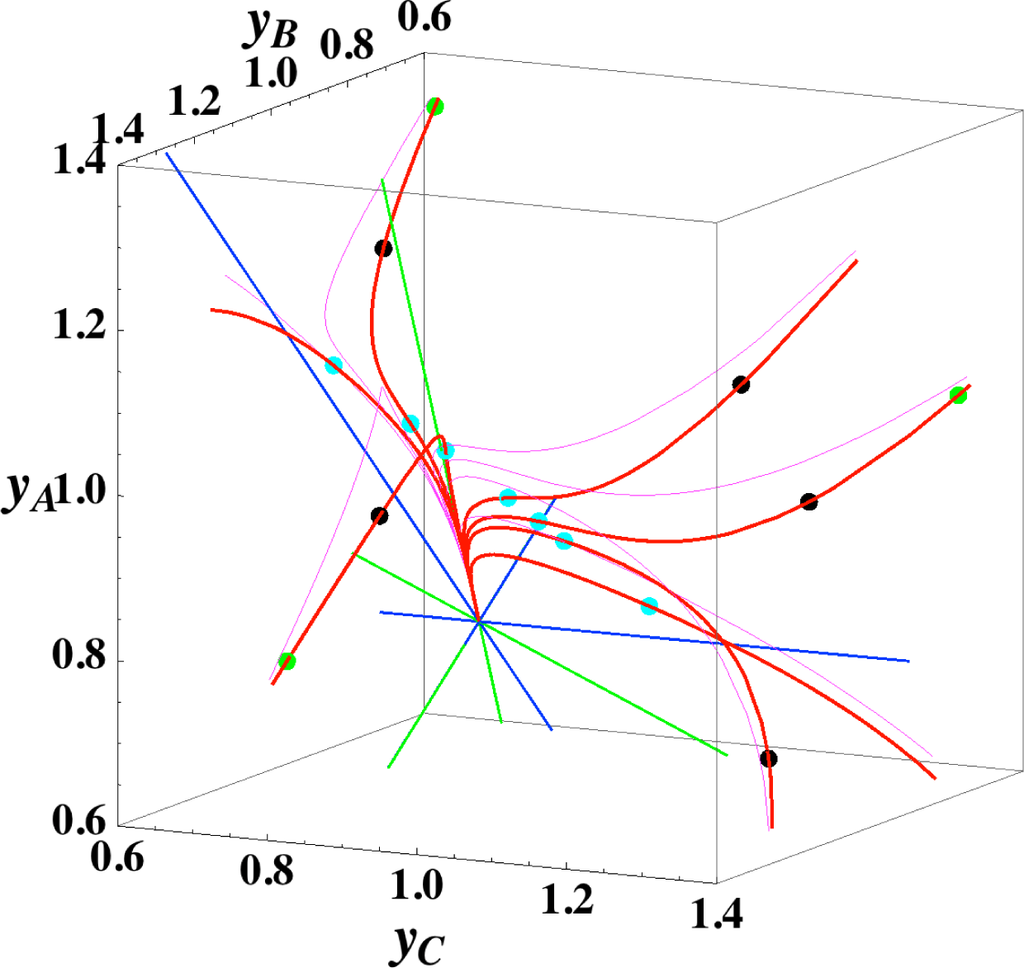
These calculations were performed with the fixed rate constants given in Table 2 for the same equilibrium composition but with different initial compositions (seven in each figure [34]), and c = 3. Each of the seven initial compositions gives all four types of paths plotted in Figures 3 and 7. The dimensionless equilibrium composition is (yA, yB, yC, yD) = (0.75, 0.75, 0.75, 0.75). Note that all paths reside in the reaction simplex determined by c and the stoichiometric coefficients of each reaction, as described in Section 3.1.

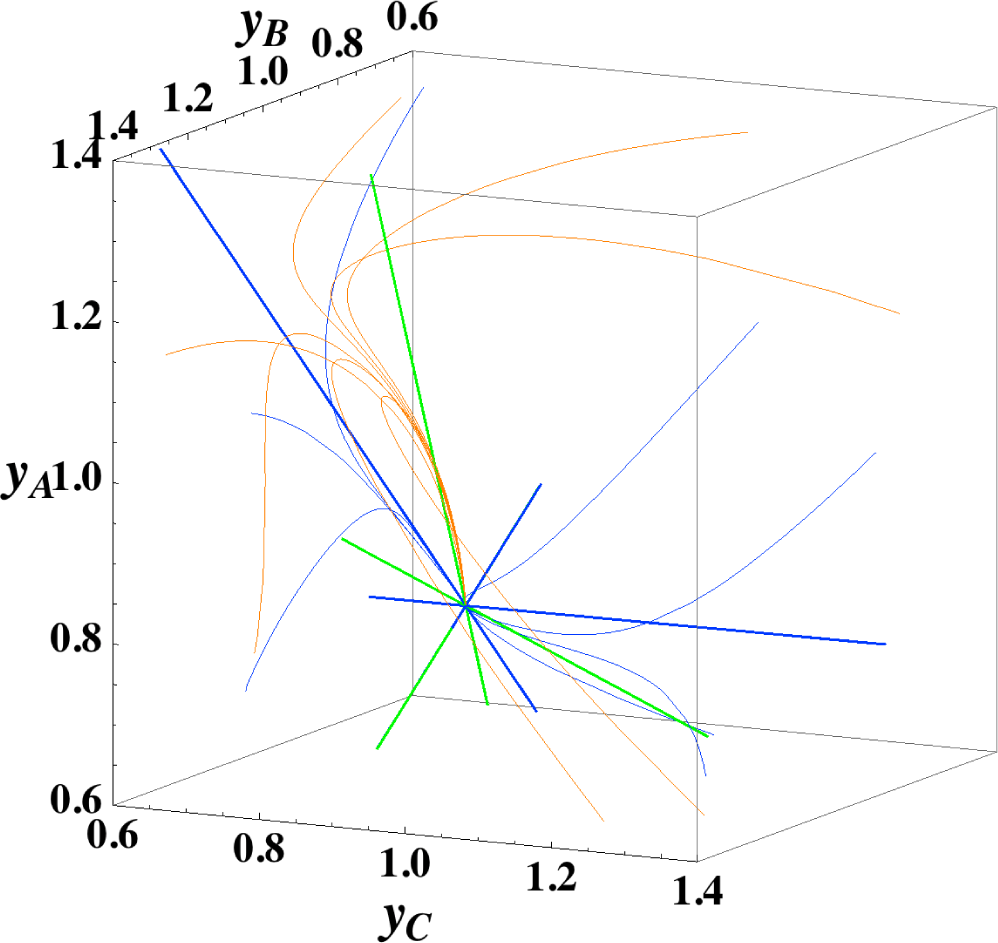
The present reaction simplex is a 3-D space in the 4-D concentration (yA, yB, yC, yD) phase space. Figures 5 and 7 for examining the existence of 2-D manifolds of each path are also shown. The three eigenvectors of the chemical kinetics Jacobian at equilibrium are given in Table 3, and those of the Hessian of σ at equilibrium are given in Table 4.
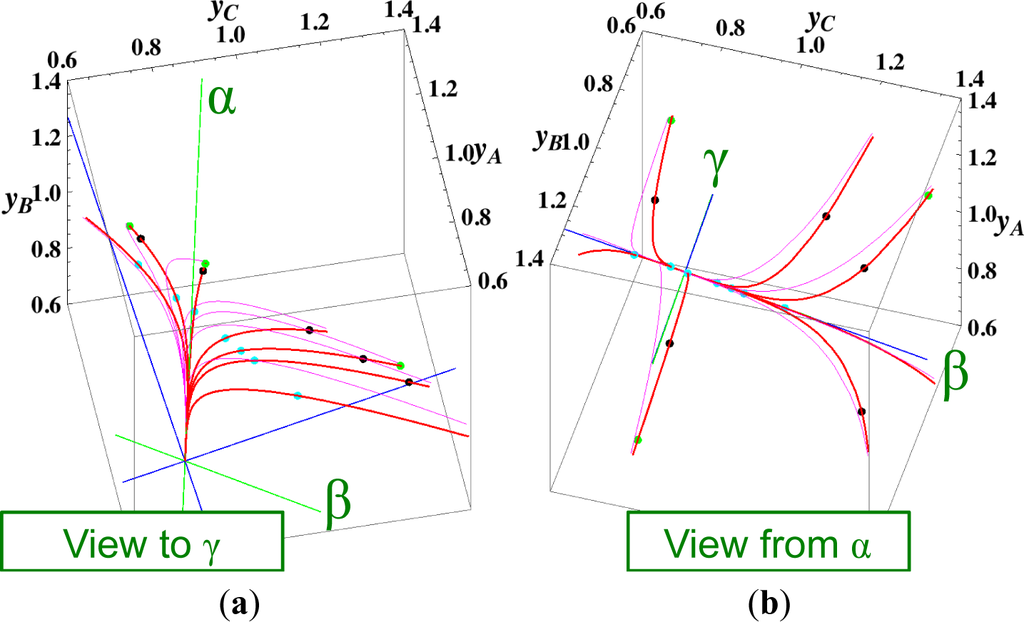
The Following Observations are made from Figures 3 and 7:
- (1)
The paths of linear non-equilibrium (Figure 3) most closely resemble that of chemical kinetics.
- (2)
The path of linear non-equilibrium (Figures 3 and 5) has the same 2-D manifold (the plane formed by the two eigenvectors attached to the equilibrium point, denoted as α and β in Figure 5) and the same 1-D manifold (the eigenvector of the chemical kinetics Jacobian at equilibrium, denoted as α in Figure 5) as those of chemical kinetics. However, the linear non-equilibrium path is considerably different from the chemical kinetics path in the noted 2-D manifold (Figure 5).
- (3)
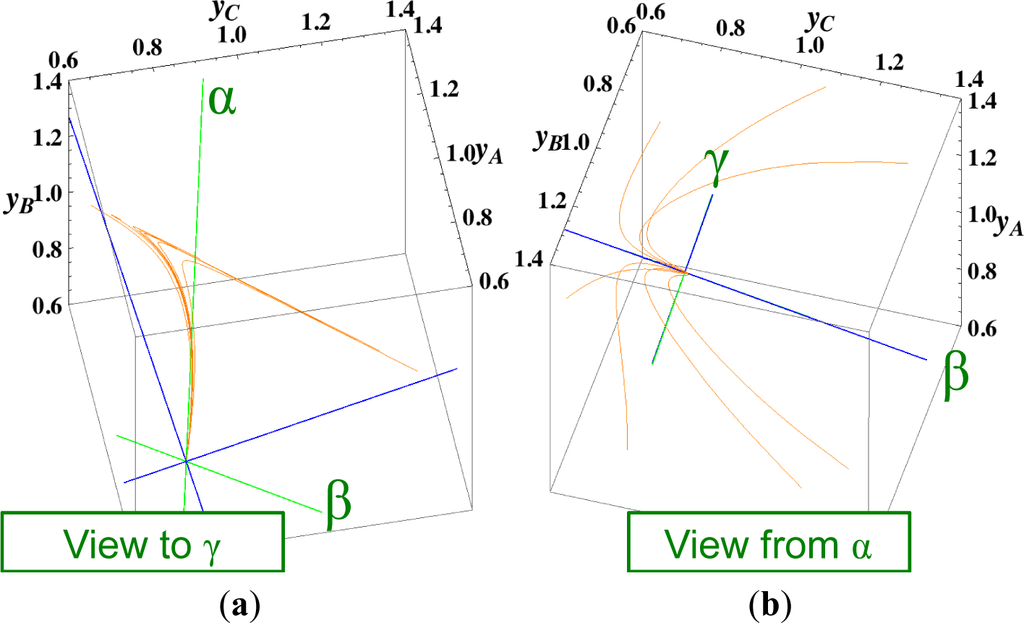
The steepest descent path (Figures 4 and 6) has a 2-D manifold, i.e., the plane formed by the two eigenvectors of the Hessian of σ (blue straight lines); the two eigenvectors are adjacent to the eigenvectors of the chemical kinetics Jacobian, which are denoted as α and β (green straight lines). The plane (in Figure 6) is almost the same as those of chemical kinetics and linear non-equilibrium paths (in Figure 5), but the 1-D manifold is notably different between the steepest descent path (Figure 6) and chemical kinetics (likewise, the path of linear non-equilibrium) (Figure 5). The latter is the eigenvector of the chemical kinetics Jacobian denoted as α (α-eigenvector), whereas the former is the eigenvector of the Hessian of σ that is adjacent to the α-eigenvector.
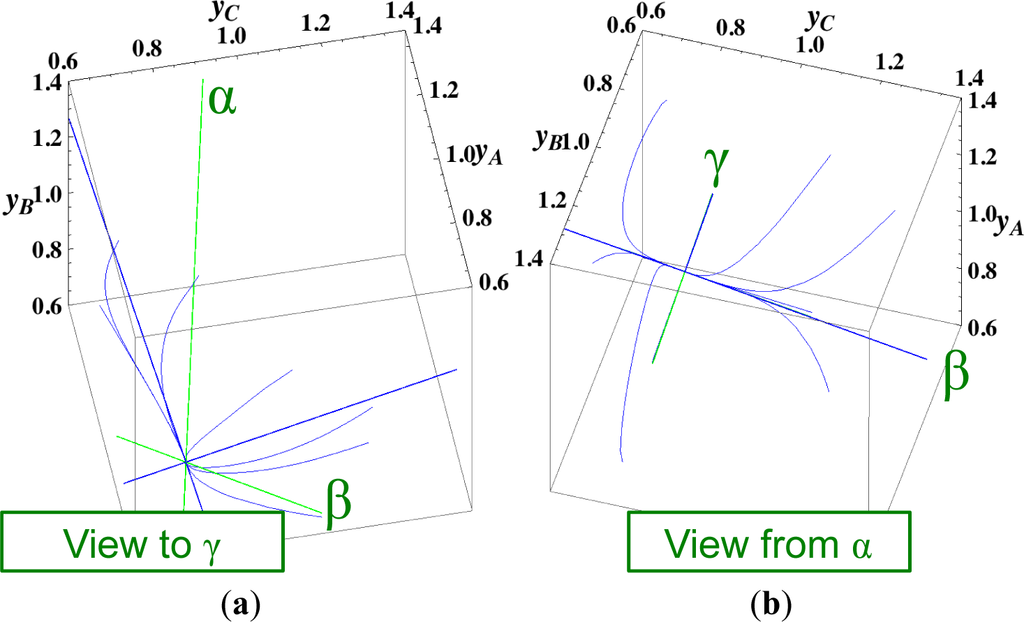 Figure 6. Steepest descent paths of the reactions A ⇆ B ⇆ C ⇆ D projected into the concentration (yA, yB, yC) phase space. All lines and the symbols have the same meanings as described in the captions of Figures 2 and 5. (a) A view of Figure 4 in the direction of the γ-eigenvector of the chemical kinetics Jacobian of Equation (4) (To the point “γ” from the equilibrium point); (b) A view of Figure 4 in the reverse direction of the α-eigenvector of the chemical kinetics Jacobian of Equation (4) (From the point “α” to the equilibrium point”).
Figure 6. Steepest descent paths of the reactions A ⇆ B ⇆ C ⇆ D projected into the concentration (yA, yB, yC) phase space. All lines and the symbols have the same meanings as described in the captions of Figures 2 and 5. (a) A view of Figure 4 in the direction of the γ-eigenvector of the chemical kinetics Jacobian of Equation (4) (To the point “γ” from the equilibrium point); (b) A view of Figure 4 in the reverse direction of the α-eigenvector of the chemical kinetics Jacobian of Equation (4) (From the point “α” to the equilibrium point”).- (4)
The Newton direction path (Figures 4 and 7) is unique and distinct compared to the other paths. A quasi-1-D manifold similar to those of the chemical kinetics path (likewise the path of linear non-equilibrium) and the steepest descent path was observed; however, it could not be described definitely. A quasi-2-D manifold parallel to the γ-eigenvector (Figure 7) was also observed, which is peculiar because this quasi-2-D manifold does not encompass a 1-D manifold.
From these observations and those described in Section 3.1, it is obvious that Equation (9), which governs the Newton direction path, is not the thermodynamic equation (or even its approximation) that is sought, and Equation (8), which governs the steepest descent path, cannot correctly reproduce the 1-D manifold of true chemical kinetics, whereas the ELNEP does. More importantly, point 2 (above) denotes that ELNEP pursues a course in the same LDMs as those of true chemical kinetics but appreciably deviates from the true kinetics path within the noted LDM. The generality of the observation that the ELNEP almost reproduces the higher dimensional manifolds of true chemical kinetics is proved in Section 4. Appendix C shows the specific form of the ELNEP for this case.
3.3. Non-isothermal Case
Observations similar to those previously described for the isothermal case can be expected even for the non-isothermal case because Equation (11) (ELNEP) is an approximation to Equation (4) (to first order in each variable εl); this holds irrespective of variations in temperature. Figure 8 shows the chemical kinetics and linear non-equilibrium paths for the non-isothermal reactions A ⇆ B ⇆ C projected into the phase space (yA, yB, T / 200), where T is the dimensionless temperature of the system. We determined yC by element conservation:
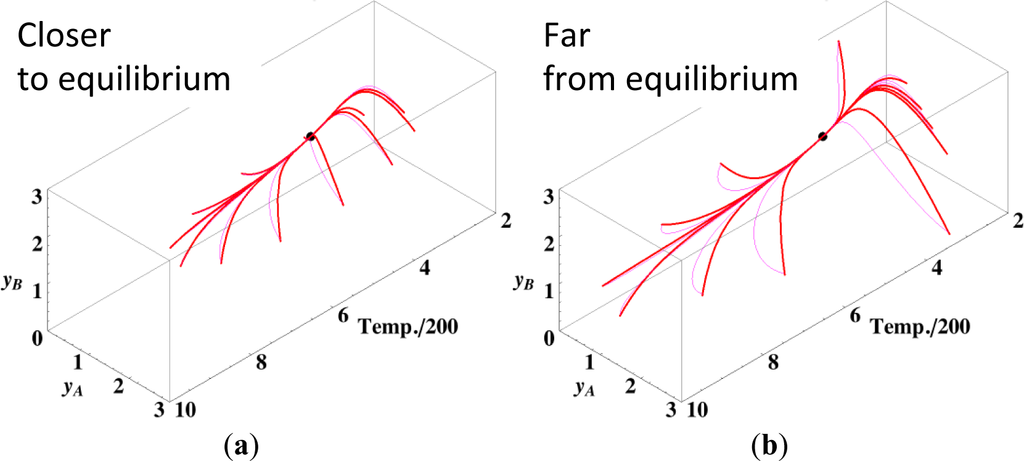
The contour of σ can be plotted on intersections orthogonal to the axis of T in Figure 8, but these intersectional contours are different from each other because the corresponding temperature and reaction rate constants vary. These calculations were performed with the variable rate constants (that must obey the Arrhenius law and hence depends on the gas temperature T) given in Table 5 and c = 3. The dimensionless equilibrium composition and temperature are (yA, yB, yC, T) = (0.7014, 1.597, 0.7014, 850.7).

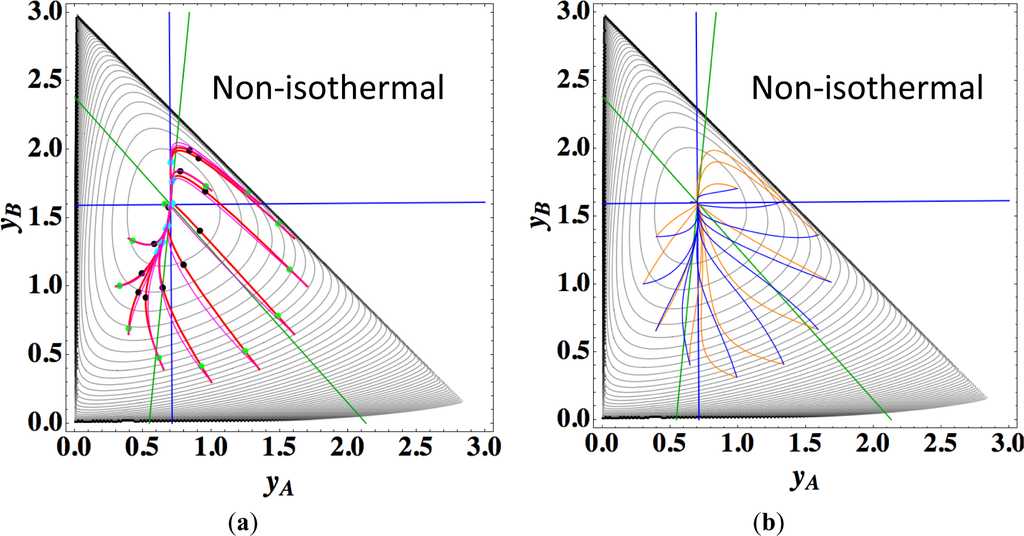
Figures 9a,b show the four paths (chemical kinetics, linear non-equilibrium, steepest descent, and Newton direction) projected onto the concentration (yA, yB) phase plane for the same calculation as for Figure 8a, together with the contour of σ at the final equilibrium temperature. Figures 9c,d also show the paths for the isothermal case, the temperature of which was set as the final equilibrium temperature of the non-isothermal case; therefore, the dimensionless equilibrium composition and temperature are the same as those of the non-isothermal case.
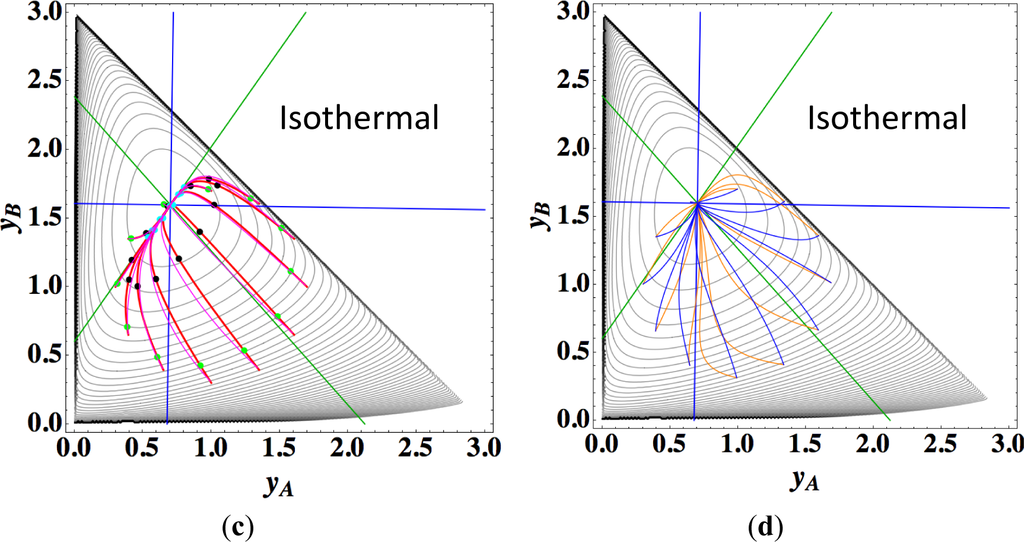
Since the system is considered to be isolated in a constant volume, internal energy is conserved. This constraint can be treated as an equation for just determining the temperature T from the species concentrations (as described in Appendix D), and T disappears in the formulation. Because ∇σ in the rhs of Equation (11) has no derivative with respect to T, the specific form of the ELNEP Equation (11) is the same as that for the isothermal case (Appendix C shows the form for this example).
All species (A, B, and C) are treated as calorically and thermally perfect with one (dimensionless) specific heat of 10−3 at constant volume; Table 5 gives the (dimensionless) heats of reactions. The reaction A→B is neither endothermic nor exothermic, and the reaction B→C is exothermic.
As of yet, the Shear Lyapunov function [2,3] is always applied to isothermal cases [18–20,22,35]; therefore, it is expected that, likewise, the ELNEP cannot be rationalized for non-isothermal cases. However, σ can be deduced from thermodynamic considerations that allow arbitrary rate constants [29], and the mathematical derivation of the ELNEP (in Section 2.1) does not need an interpretation of σ or even its thermodynamic origin. Furthermore, the proof [10] of the Shear Lyapunov function allows variable (i.e., non-isothermal) rate constants, even though the mathematical form of the Shear Lyapunov function coincides, for some reason, with a variant of the Helmholtz free energy of an ideal gas whose usage is physically limited to the isothermal and isochoric condition.
The following observations are made from Figures 8 and 9:
Since the temperature T is determined from the composition through energy conservation, the number of degrees of freedom for this reaction system is two, the same as that for the corresponding isothermal system. Accordingly, the observed LDM is 1-D (Figure 8). Note that all paths reside in the reaction simplex determined by c and the stoichiometric coefficients of each reaction, as described in Sections 3.1 and 3.2. The present reaction simplex is a 2-D space in the 3-D concentration (yA, yB, yC) phase space, although Figure 8 shows the projection into the phase space (yA, yB, T/200) that is a pile (along the axis of T/200) of instantaneous projections at respective instants and temperatures.
Similar results are observed as those found for the examples described in Sections 3.1 and 3.2, but the following results are also noted.
The paths of linear non-equilibrium with their initial compositions closer to equilibrium (Figure 8a) approximate more closely the paths of true chemical kinetics than initial compositions far from equilibrium (Figure 8b). This can be really observed for the previous examples given in Sections 3.1 and 3.2.
The 1-D manifold for the non-isothermal case substantially differs from that of the isothermal case because the temperature dependence of the rate constants distorts the contour of σ for the non-isothermal case (Figure 8 and Figures 9a,b).
In the isothermal case, the steepest descent paths (blue curved lines in Figure 9d) have no LDM, whereas those in the non-isothermal case (blue curved lines in Figure 9b) have a LDM. This indicates that the rate constants employed in this case (Table 5) render the isothermal (non-isothermal) cases insufficiently (sufficiently) to produce the gap in reaction rate between the two reversible reactions, respectively. Nevertheless, the paths of linear non-equilibrium (magenta lines in Figures 9a,c) have a 1-D manifold in each case and approximate the true chemical kinetics irrespective of the difference in the gap.
3.4. An Example of Reference [24]
This example is adopted from Section IV. A of Al-Khateeb et al. [24], where it serves as a simple but realistic reactive system for constructing a 1-D slow invariant manifold (SIM). Also, Al-Khateeb et al. [24] have demonstrated their conclusion (mentioned in Section 1 of this paper) mainly using this example.
The kinetic model of this example is the well-known Zel’dovich mechanism that consists of five species, two elements, and two reversible reactions: N + O2 ⇆ NO + O and N + NO ⇆ N2 + O, which has a 1-D manifold in two-dimensional reaction simplex owing to the following three constraints in its chemistry:
where yNO, yN, yO, , and are concentrations of the species NO, N, O, O2, and N2, respectively. These constraints are the conservations of element oxygen, element nitrogen, and the total number of species in the system, respectively. The calculation is done with:
and Appendix C shows the specific form of the ELNEP for this case.
All the data employed here (including kinetic and thermodynamic data) have been kindly provided by the author of Reference [24], and the calculation in this section is dimensional as in Reference [24]. Figure 10 shows the chemical kinetics, linear non-equilibrium, and the steepest descent paths for twelve initial compositions at constant temperature of 4,000 K in constant volume (the same condition and the same final equilibrium as in Reference [24] except for the initial compositions). The Newton direction path is not shown because of its unimportance indicated by the previous examples.
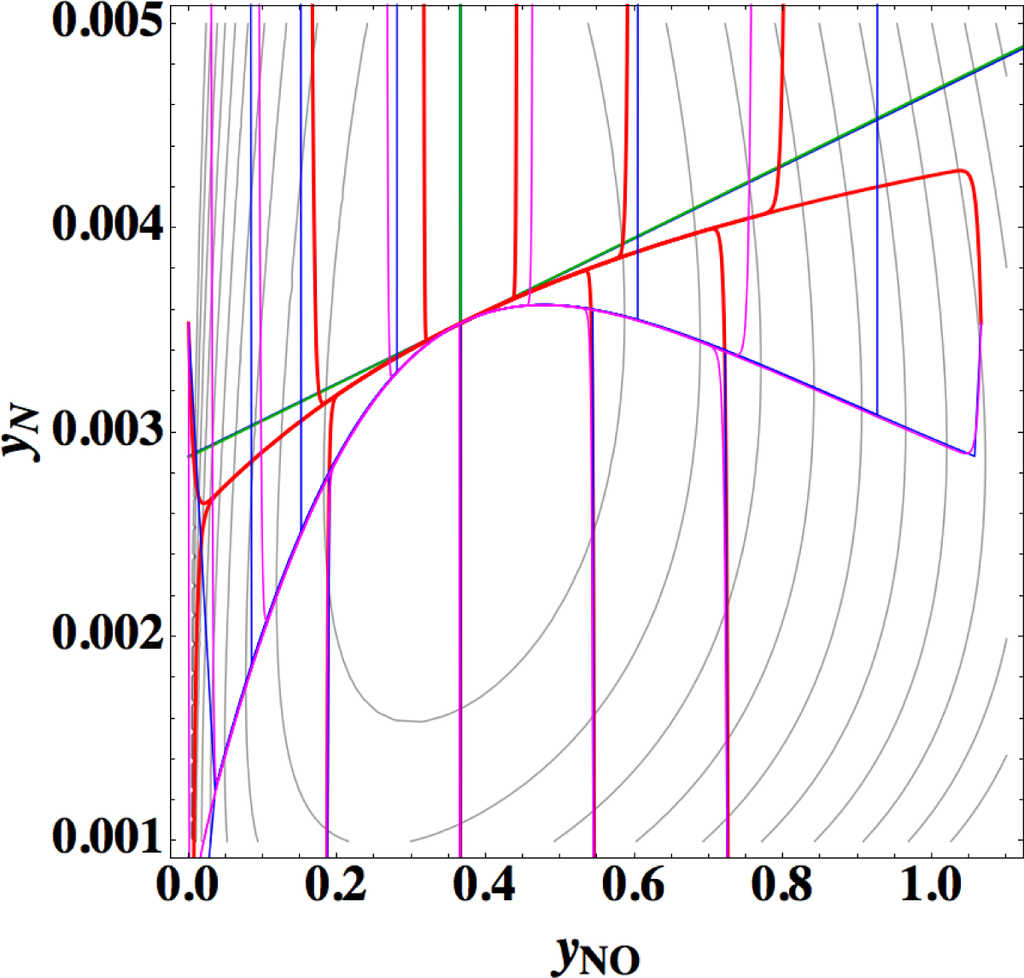
From this figure the following observations are made:
- (1)
1-D manifold of true chemical kinetics is obviously different from those of linear non-equilibrium paths and the steepest descent paths.
- (2)
1-D manifold of linear non-equilibrium paths alomost conincides with that of the steepest descent paths.
- (3)
At equilibrium the eigenvectors of the Jacobian of true chemical kinetics and those of the Hessian of σ are almost the same in agreement with the description in Reference [24].
- (4)
In agreement with the theory given in Section 2, 1-D manifold of linear non-equilibrium paths is tangential to the eigenvectors of the Jacobian of true chemical kinetics. Also, 1-D manifold of the steepest descent paths is tangential to the eigenvectors of the Hessian of σ, which is consistent with Points 2 and 3.
Points 1 and 2 are very striking features that are quite different from those of the previous examples (Sections 3.1–3.3), where 1-D manifold of linear non-equilibrium paths and that of the steepest descent paths are clearly different and 1-D manifold of linear non-equilibrium paths are approximately the same as that of true chemical kinetics. However, Points 2 and 3 seem to have no direct relation to Point 1 [38]. The most important is Point 1, which is directly relevant to the applicability of ELNEP. Since near equilibrium ELNEP is the first order approximation of true chemical kinetics equation, closer look into such domain is helpful to understand this example: Figure 11 shows the paths of true chemical kinetics and linear non-equilibrium for the same condition and initial composition as in Reference [24]. It can be seen from this figure that at the time of 10−5 s the path of linear non-equilibrium starts to nearly ride on the eigenvector of the Jacobian at equilibrium and from this riding point the path of linear non-equilibrium looks very close to the chemical kinetic path, which means that the final part of 1-D manifold of the kinetics is approximated by linear non-equilibrium path (the chemical kinetics path also nearly rides on the eigenvector at the same time 10−5 s, which suggests that the ride on the eigenvector may be one of the topological events that described later, but it needs more evidences). Therefore, it can be said that the linear non-equilibrium path in this example behaves in accordance with the theory, but it is clarified that ELNEP does not necessarily approximate the part of 1-D manifold of true chemical kinetics in some distance away from equilibrium. The reason for the latter is the highly distorted contour of σ whose eigenvectors largely vary from those at equilibrium, and consequently the eigenvector (that defines 1-D manifold) of the Jacobian of ELNEP (described in Appendixes F and I) considerably differs from that of the Jacobian of true chemical kinetics in that part. Also it has been numerically confirmed that for the two paths in Figure 11 the condition [39] that the method of ILDM is safely applicable (mentioned in Appendix F) does not hold at the part of 1-D manifold farther from equilibrium beyond the point of the time 10−5 s at least.
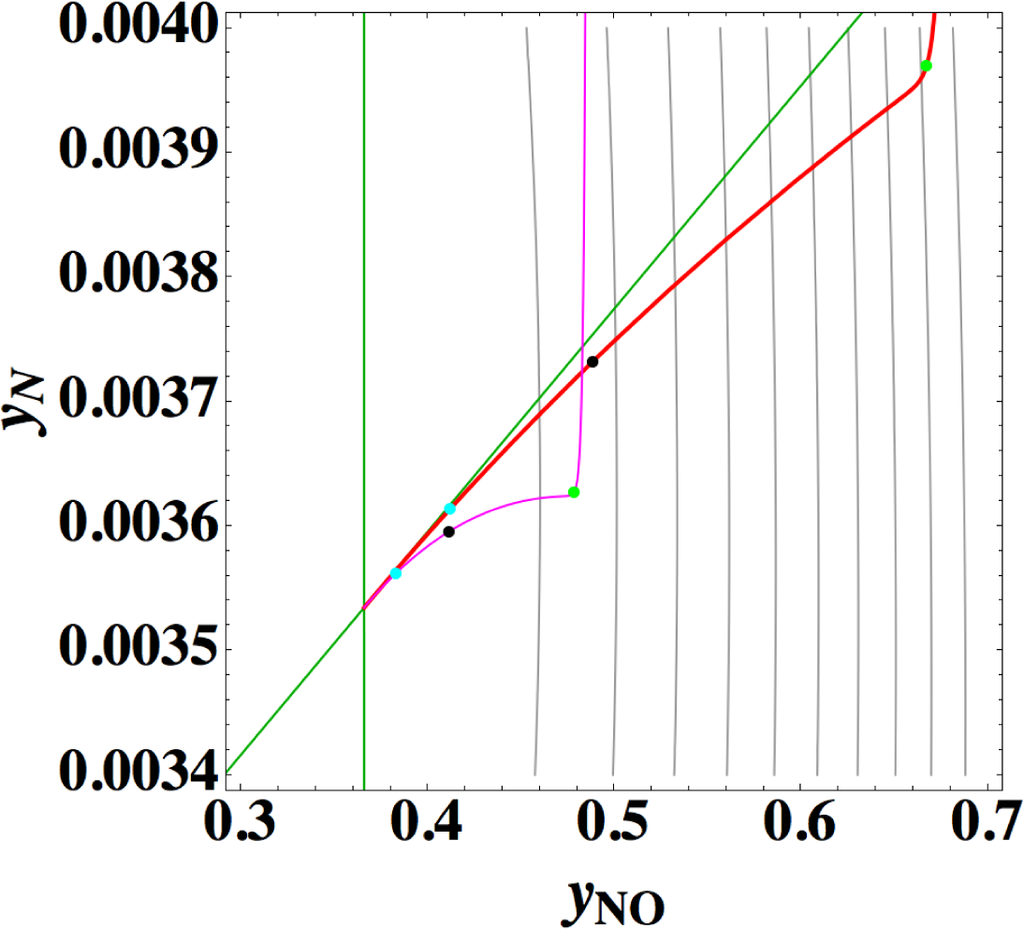
Now the conclusion of Reference [24] is recalled: Reference [24] states that a system’s dynamics cannot be deduced from the Gibbs free energy or entropy production rate even near the equilibrium state. However, ELNEP approximates at least the final part of 1-D manifold of true chemical kinetics as shown above, and ELNEP itself is the near-equilibrium approximation of true chemical kinetics equation, Equation (4) [40]. Accordingly, the statement of Reference [24] should be replaced here by “a system’s dynamics near the equilibrium state can be approximately deduced from the rate of entropy production. The approximation improves as each εl approaches zero.”
4. Relevance to LDMs
The phenomenon in which the concentration phase space of reaction kinetics is progressively reduced to a lower dimensional manifold can be interpreted as successive processes in which the number of quasi-equilibrium reactions increases. For example, Chiavazzo and Karlin [41] devised an algorithm to utilize the so-called quasi-equilibrium manifold as a first approximation to SIM. Regarding this hierarchy of manifolds of lower dimension [18–23,26–28], the observation that the paths determined by ELNEP trace at least final part of the 1-D and (possibly) 2-D manifolds of true chemical kinetics in the samples described in Section 3 is proved or, at least, theoretically justified to hold in more general cases where the method of intrinsic low-dimensional manifolds (ILDM) [26,39] is applicable. However, the proof below might be less formal from a mathematician’s viewpoint.
The coincidence of ELNEP with the true chemical kinetics equation to first order in each variable εl is obviously consistent with the ability of ELNEP to emulate a 0-D manifold, i.e., an equilibrium state, because the variable εl for every reaction vanishes at equilibrium. For higher dimensional manifolds, some elementary reactions participate in quasi-equilibrium (|εl|s are sufficiently small [33]), and the others do not; i.e., for each reduction in dimension of the reaction simplex (each step to descend the hierarchy), a group of elementary reactions constitutes quasi-equilibrium, and the size (number of constituent elementary reactions) of such groups increases as the system approaches its equilibrium. If the ascent on the hierarchy (in a time-reversed way from equilibrium) is observed, the size of such groups decreases as the system moves away from equilibrium because a split in a group occurs. The theoretical proof of the ability of ELNEP to trace every higher dimensional manifold when the method of ILDM is applicable to ELNEP is the following.
At first, ELNEP produces the trajectory that finally reaches the equilibrium state, i.e., a unique solution of ∇σ = 0; this is easily proved on the basis of the fact that the matrix Q of ELNEP is symmetric and positive definite, as described in Appendix E. Therefore, from any initial point in concentration phase space, paths determined by ELNEP reach the same equilibrium point as that of true chemical kinetics. From this starting point, the ability of ELNEP to emulate a 1-D manifold, 2-D manifold, etc. in a time-reversed way from equilibrium (ascent on the hierarchy) is proved inductively.
Base case
Along a 1-D manifold, all elementary reactions constitute one group in quasi-equilibrium and concertedly approach true equilibrium (all εls approach zero). At this stage, the path determined by ELNEP obviously an approximation to the 1-D manifold of true chemical kinetics because otherwise the coincidence to first order in the variable εl for every lth reaction cannot hold between the two.
Inductive case
In the time-reversed way of thinking, at the entry (in ordinary time order) of 1-D manifold a group separates and its |εl|s grow larger. Now, consider the k -D manifold for m ≥ k > 1, where m is the dimension of the reaction simplex, and assume that the (k–1)-D manifold determined by ELNEP is an approximation to the (k–1)-D manifold of true chemical kinetics. Then, it can be proved that the k-D manifold of ELNEP is also an approximation to the k-D manifold of true chemical kinetics. The key to the proof is that the Jacobian and its eigenvectors of ELNEP are exactly the same as those of true chemical kinetics (in the form that explicitly accounts for the constraints inherent in chemical kinetics) at the equilibrium state, as described in Appendix I. Since each eigenvector of the Jacobian constitutes the local basis of the reaction simplex, the k-D manifold of ELNEP is created upon the (k–1)-D manifold when the k th group of reactions that appreciably contributes to a component of the basis (the eigenvector whose direction is the same as that of the most dominant component of acceleration in concentration phase space at this stage) separates (in a time-reversed way) from one of the previous groups that constitute the (k – 1)-D manifold. (The numbering of the groups of reactions also begins in a time-reversed way, i.e., the first group comprises all reactions and corresponds to a 1-D manifold.) The component of the basis is added as one degree of freedom to the trajectories that contract (in ordinary time order) into the (k – 1)-D manifold, and the k-D manifold of ELNEP is an approximation to that of true chemical kinetics because the eigenvector for ELNEP is approximately the same as that for true chemical kinetics even when the system is out of equilibrium, unless the contour of σ is highly distorted as the example in Section 3.4. The latter assumption holds when the method of ILDM is applicable to ELNEP (See Equation F20 and the passage above Equation F21). With this assumption, the respective eigenvectors for ELNEP and for true chemical kinetics are both approximately the same as those at equilibrium (but exactly the same for true chemical kinetics with a constant Jacobian) where the Jacobian and its eigenvectors of ELNEP are exactly the same as those of true chemical kinetics (Appendix I). In addition, since the eigenvalues for ELNEP are also approximately the same as those for true chemical kinetics, the order of the eigenvalues in magnitude and consequently the order of appearance of the manifolds are the same when the gaps among eigenvalues are sufficiently large. Thus, it is proved that the k -D manifold of ELNEP is an approximation to that of true chemical kinetics when the (k – 1)-D manifold does so (as long as the method of ILDM is applicable to ELNEP or the contour of σ is not highly distorted). Since the 1-D manifold (Base case) does so, the proof is inductively completed for all manifolds, although the path itself does not necessarily coincide even approximately with that of true chemical kinetics in manifolds higher than 1-D (as shown in Figures 3 and 5) because, for the k-D manifold (k > 1), the |εl|s of at least the k th group of reactions (that contributes to the basis of k -D manifold) are likely too large to approximate true chemical kinetics.
5. Relevance to Ziegler’s Hypothesis
The present results are nearly (not exactly) in accordance with Ziegler’s hypothesis [16] that the rate of entropy production is maximized with certain prescribed dissipative forces because (a) the path produced by ELNEP is an approximation to the true chemical kinetics path (though in the linear non-equilibrium domain or along at least a final part of the 1-D manifold) and (b) Equations (30)–(32) satisfy the so-called orthogonality conditions [17] that guarantees that the composition of the thermodynamic force Xl, each of which corresponds to the flux Jl, is orthogonal to the surface where σ is constant in the flux space [17].
6. Conclusions
The equation that approximately traces the trajectory in the concentration phase space of chemical kinetics is derived based on the rate of entropy production. In the derivation, a type of quasi-equilibrium approximation, which is automatically fulfilled in the relaxation process leading to detailed-balanced equilibrium, is used. The equation coincides with the true chemical kinetics equation to first order in a defined variable that characterizes the degree of quasi-equilibrium of each reaction. This new equation is named as ELNEP; the equation is justified as an approximation to true chemical kinetics along at least a final part of its 1-D manifold and identifies the trajectory that arrives at equilibrium in concentration phase space. The ELNEP is the equation of steepest descent path that sufficiently accounts for the constraints inherent in chemical kinetics. Although ELNEP is not a technique to extract low-dimensional manifolds, the trajectory of 1-D manifold in the concentration phase space of true chemical kinetics or at least its final part near equilibrium is approximately given by ELNEP because of the first-order coincidence with true chemical kinetics; whereas the simple steepest descent path whose Jacobian is the Hessian of σ does not sufficiently account for the constraints, and consequently cannot reproduce the 1-D manifold of true chemical kinetics except for the cases where the eigenvector of the Hessian of σ is nearly identical to that of the Jacobian of chemical kinetics.
In addition to the 1-D manifold, the paths determined by ELNEP approximately trace every higher dimensional manifold of true chemical kinetics when the contour of σ is not highly distorted or the method of ILDM is applicable to ELNEP, because the Jacobian and its eigenvectors of ELNEP are exactly the same as those of true chemical kinetics (in the form that explicitly accounts for the constraints inherent in chemical kinetics) at the equilibrium state. However, the path itself does not necessarily coincide even approximately with that of true chemical kinetics in manifolds higher than 1-D, as shown in the numerical calculations.
As for the time accuracy of ELNEP, each time of topological events such as the entry of lower dimensional manifold seems to be not badly approximated even in the domain far from equilibrium, but it must be further investigated.
Nomenclature
Here the symbols used only in Appendices D–J are omitted, where their own nomenclatures are consistently given for their respective equations.

| B1, B2, B3 | Matrixes defined by Equations (13) and (14) for element conservation |
| (B3)kj | Component of matrix B3 at the kth row and the jth column |
| c | Constant such as total number of a specified element per volume (a unit of concentration) |
| Vector whose components are the constants such as the total number of respective elements per volume (a unit of concentration) | |
| H | Hessian matrix of σ |
| Jl | Thermodynamic flux due to the lth reaction defined by Equation (31) |
| K | Number of independent species concentrations (the components of the vector ) |
| kbl | Backward reaction rate constant of the lth reaction |
| kfl | Forward reaction rate constant of the lth reaction |
| M | Number of constraints (such as the number of elements) |
| Nr | Number of reactions |
| Q | Matrix defined by Equation (12) |
| Universal gas constant | |
| Rbl | Backward reaction rate of the lth reaction |
| Rfl | Forward reaction rate of the lth reaction |
| S | Entropy |
| s | Pseudo-time (an artificial time-marching parameter) |
| t | Physical time |
| V | Volume |
| X1 | Thermodynamic force due to the lth reaction defined by Equation (32) |
| yA, yB, yC, yD | Concentration of species A, B, C, and D, respectively |
| yk | Concentration of the kth species |
| Vector whose components are concentrations of respective species | |
| Vector whose components are concentrations of respective dependent species | |
| Vector whose components are concentrations of respective independent species | |
| Greek symbols | |
| αkl | Stoichiometric coefficient of the kth species as a reactant in the l th reaction |
| Vector whose components are the stoichiometric coefficients of respective species as reactants in the lth reaction | |
| βkl | Stoichiometric coefficient of the kth species as a product in the lth reaction |
| Vector whose components are the stoichiometric coefficients of respective species as products in the lth reaction | |
| vkl | Difference of the two stoichiometric coefficients βkl − αkl |
| Difference of the two vectors | |
| εl | Quasi-equilibrium parameter of the lth reaction defined by Equation (17) |
| σ | Total reaction contribution to the rate of entropy production |
| σl | Contribution of the lth reaction to the rate of entropy production |
| Ω | Matrix defined by Equation (G2) in Appendix G |
| Suffixes | |
| b | Backward reaction |
| dep | Dependent species |
| f | Forward reaction |
| ind | Independent species |
| l | lth reaction |
| k | kth species |
| • | An arbitrary species common in an equation where this symbol is used |
| (K×1) | Vector with K components for any K |
| (K×N) | Matrix with K rows and N columns for any K and any N |
Appendix A: Considering Constraints
The following simple example may be useful as a reminder of how to consider constraints when function derivatives are calculated. For f = ax + by + cz:
Under the additional constraint z=x2 + y2:
since . However, substituting the relation into , the following is obtained:
which reproduces Equation (A2).
In brief:
and the following relation generally holds:
or:
Appendix B: Equivalence of Equation (29) to Equation (8)
Equation (29) is clearly equivalent to:
Using the identity:
Equation (B1) becomes:
Defining , Equation (B3) is equivalent to Equation (8) to first order in each variable εl when is replaced by and .
Therefore, Equation (29) is essentially equivalent to a scale-transformed version of Equation (8) to first order in each variable εl.
Appendix C: Specific Forms of the ELNEP (Equation (11))
The following are the specific forms of the ELNEP (Equation 11) for the four reaction systems described in Section 3. For the system A ⇆ 2B ⇆ C (in Section 3.1):
For the system A ⇆ B ⇆ C ⇆ D (in Section 3.2):
For the system A ⇆ B ⇆ C (in Section 3.3):
For the Zel’dovich mechanism (in Section 3.4):
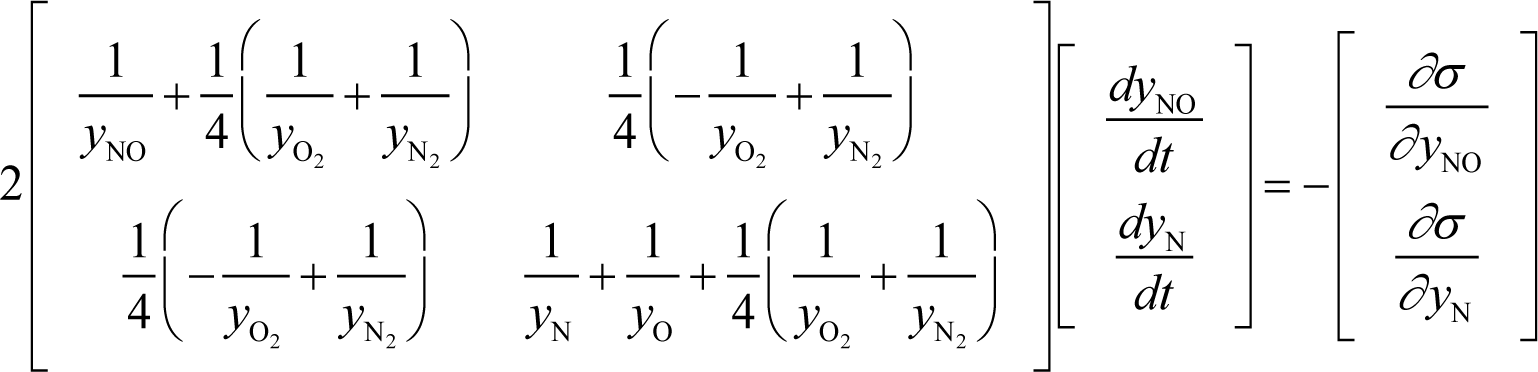
Appendix D: Temperature Determination Based on Internal Energy Conservation
The internal energy of a thermally perfect gas is expressed as:
where U is the internal energy in volume V, is the molar internal energy of the kth species, and yk is the molar concentration of the kth species. When the internal energy is conserved in a constant volume, the following equation holds:
where is the molar heat capacity of the kth species at constant volume, and T is the mixture temperature. From Equation (D2), an increase in the mixture temperature is determined by an increase in the concentration of each species:
Accordingly, variable T can be replaced by variables yks.
Appendix E: Proof that ELNEP gives a unique solution at equilibrium
First, it is proved that the matrix Q of ELNEP is symmetric and positive definite, and that ELNEP gives a unique solution of ∇σ = 0, i.e., the equilibrium state. From Equation (12), it is obvious that the matrix Q of ELNEP is symmetric, and Q can be rewritten as follows:
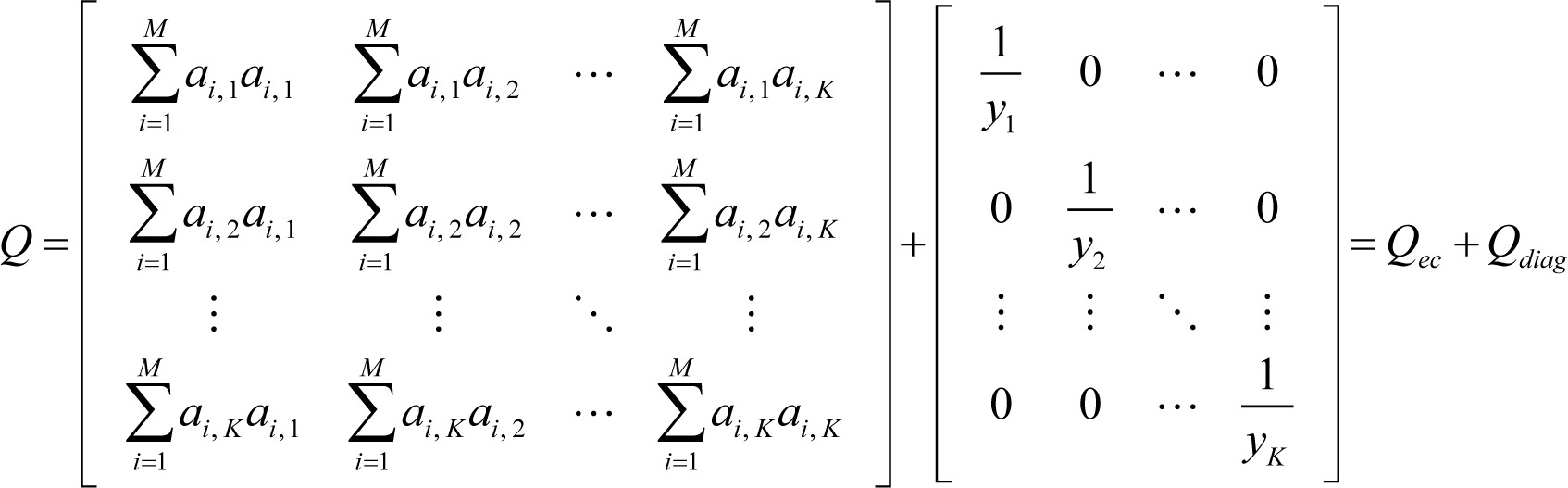
where:
From Equations (E1) and (E2):
Because in the rhs of Equation (E6), and for any vector , the matrix Q is positive definite, and its eigenvalues are all positive. Therefore, Q can be diagonalized as:
where Λ is a diagonal matrix whose components are all positive, and P is an orthogonal matrix (P‒1 = PT) since Q is a real symmetric matrix. Substituting Equation (E7) into ELNEP (Equation (11)), the following is obtained:
which means is always negative except at equilibrium. Together with the fact that σ is always positive except at equilibrium, it is concluded from the Lyapunov theorem [42] that σ is a Lyapunov function of ELNEP, which has an asymptotically stable solution (equilibrium) at ∇σ =0.
Appendix F: LDM and the Jacobian of ELNEP
Here ELNEP (Equation 11) is expressed as follows:
where:
According to Appendix G, Equation (F1) (which is Equation (11)) can be transformed to the following:
where:
Then, the following equation holds:
where:
The left-hand side (lhs) of Equation (F6) becomes:
Then, Equation (F6) becomes:
If the first term on the lhs of Equation (F10) is sufficiently small compared with that on the rhs, Equation (F10) becomes:
The derivation of Equation (F11) is as follows. Neglecting the first term of the lhs of Equation (F10) and multiplying by Q−1, Equation (F10) becomes:
According to Appendix H, the operator Q−1 Ω extracts the first K components of the vector . Then, Equation (F12) becomes Equation (F11), which means that Q−1ΘELNEP is the Jacobian of the vector of Equation (F7) for ELNEP, i.e.:
in accordance with the nomenclature in Appendix I.
However, multiplying the first term of the lhs of Equation (F10) by Q−1 yields:
The derivation of Equation (F14) is as follows. At first, becomes the following:
where the two matrixes on the far rhs of Equation (F15) are diagonal. Multiplying by Q−1 and according to Appendix H, Equation (F15) becomes:
Multiplying and using Equation (F7), Equation (F16) becomes Equation (F14).
Using Equations (F11), (F13), and (F14), Equation (F10) becomes:
Equation (F17) becomes the following when is transformed to , which is defined in Equation (F19):
where P(K×K) is certain K×K matrix. However, when P(K×K) is the left-upper part of the eigenvector matrix of the Jacobian for true chemical kinetics at equilibrium, Equation (F18) at equilibrium becomes:
according to Equation (I21) in Appendix I. Assuming is negligible, as is usual in ILDM applications [39], Equation (F20) becomes the following (at equilibrium) (after multiplying the inverse matrix of P(K×K)):
If the first term on the lhs of Equation (F21) is negligible compared with that on the rhs, Equation (F21) becomes the following (at equilibrium):
which means the LDM of ELNEP is an approximation to that of true chemical kinetics when εl ≈ 0 for every lth reaction. The condition that the first term on the lhs of Equation (F21) is negligible compared with that on the rhs is fulfilled when the eigenvectors of the ELNEP Jacobian JELNEP are almost the same as those of the Jacobian of true chemical kinetics, which has been numerically confirmed in the sample systems described in Section 3. However, the condition that the eigenvectors of the ELNEP Jacobian JELNEP are almost the same as those of the Jacobian of true chemical kinetics does not necessarily hold even in the whole 1-D manifold of true chemical kinetics, such as for the example described in Section 3.4.
Appendix G: Alternative Expression for ELNEP
Owing to Equation (24), the lhs of ELNEP (Equation 11) or Equation (F1) can be transformed as follows:
where:
Appendix H: Extraction of the Independent Parts of Vectors or Matrixes
According to Equation (G1), the following relation holds:
Inspecting the derivation describe d in Appendix G, Equation (H1) holds for any vector or matrix instead of , i.e.:
where and Ψ are any vector and matrix, respectively, and D is any dimension.
Appendix I: Coincidence of the Jacobians of ELNEP and True Chemical Kinetics at Equilibrium
The Jacobian J of true chemical kinetics is derived from Equation (4) as:
At equilibrium (εl = 0 for every lth reaction), the Jacobian of true chemical kinetics becomes:
where J0 is the Jacobian of true chemical kinetics at equilibrium. However, the Jacobian of ELNEP is defined by Equations (F8) and (F13) in Appendix F:
The Hessian to first order in εl can be derived from Equations (10), (2), (3), (5), and (A4) as:
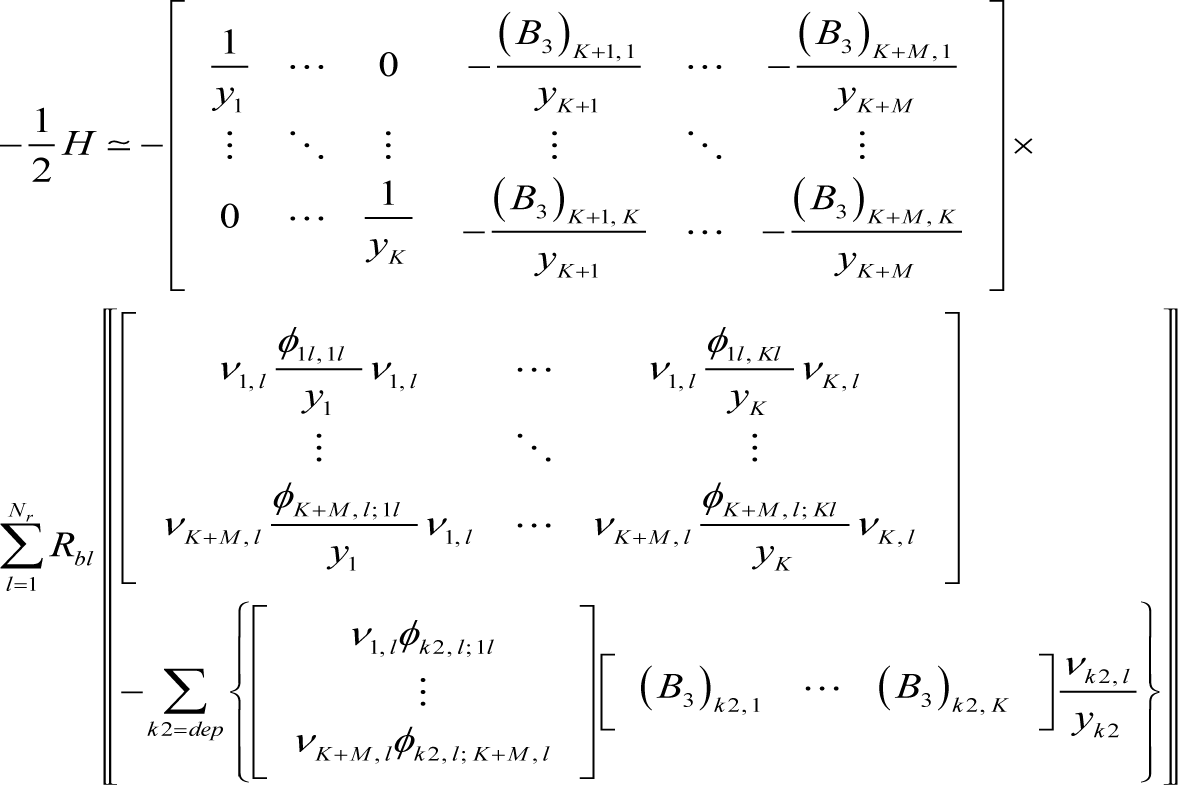
where:
Accordingly, the Hessian at equilibrium becomes:
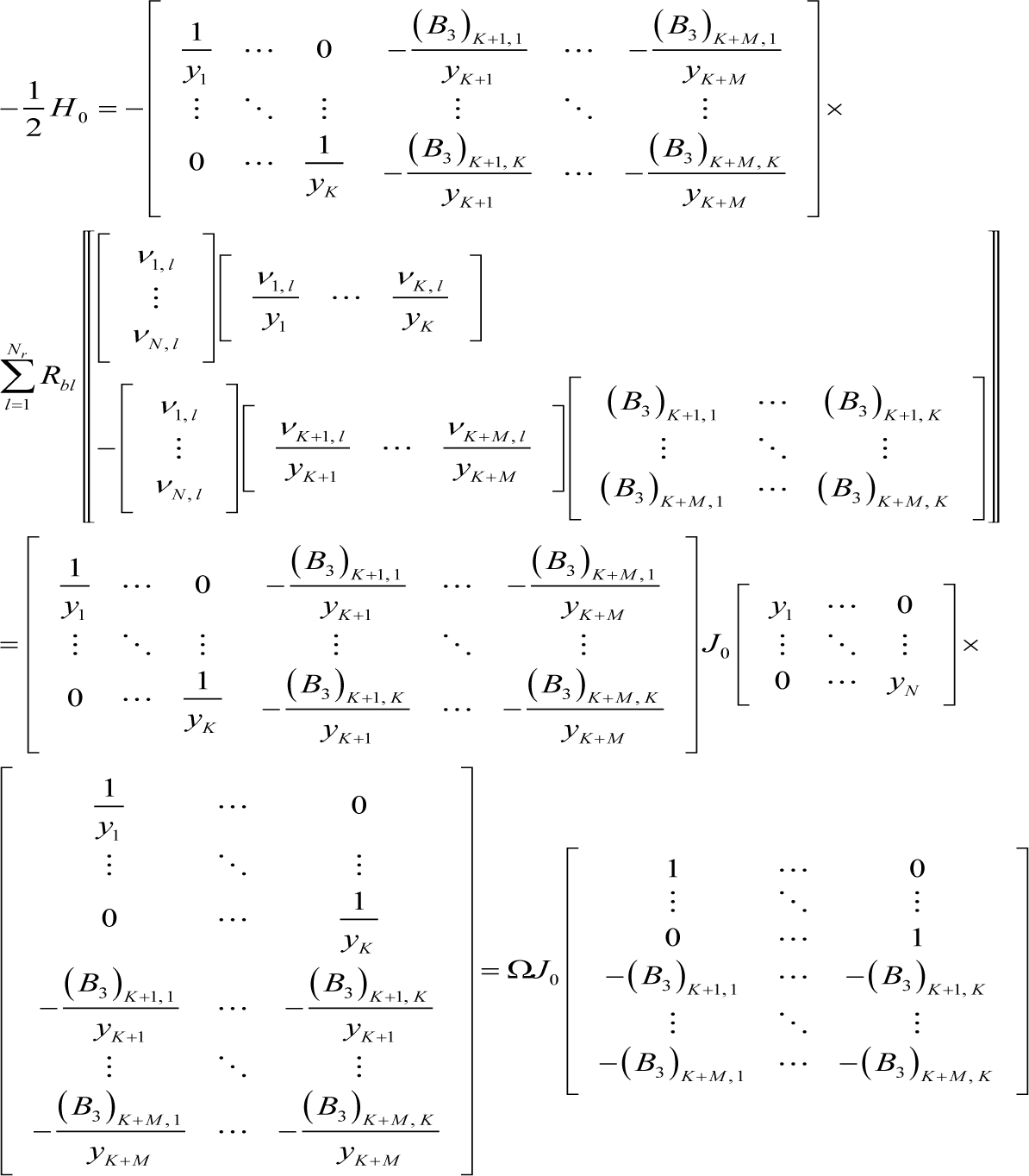
where H0 is the Hessian at equilibrium, and Equation (I7) can be further transformed as follows:
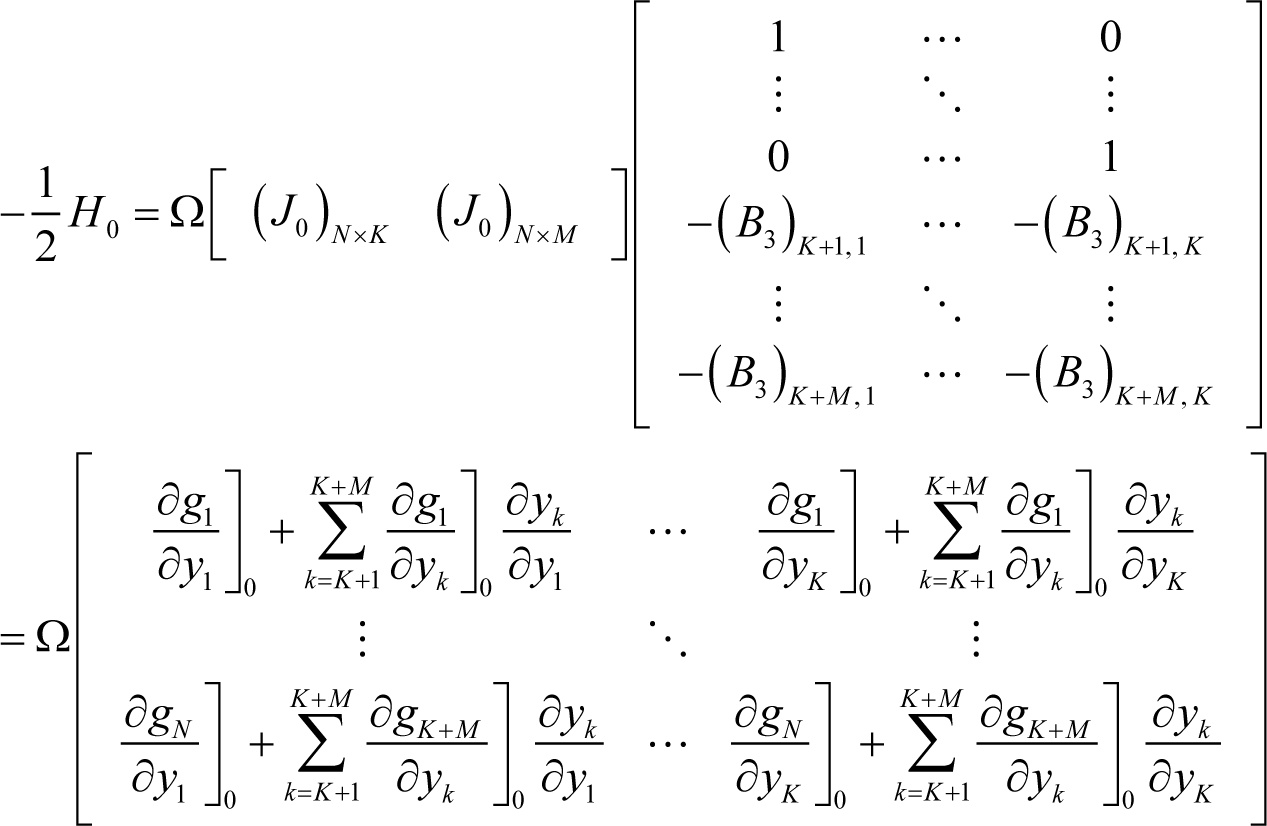
where:
Therefore, according to Equation (I3) and Appendix H, the Jacobian of ELNEP at equilibrium becomes:
which is exactly the Jacobian of true chemical kinetics that explicitly accounts for the constraints inherent in chemical kinetics because:
When Λ0 is defined by the following equation as the diagonalized form of J0 using a matrix P(N×N)
The following equations hold at equilibrium:
where:
Then, from Equation (I10):
where P(K×K) is the left-upper part of P(N×N). However, the following relation also holds:
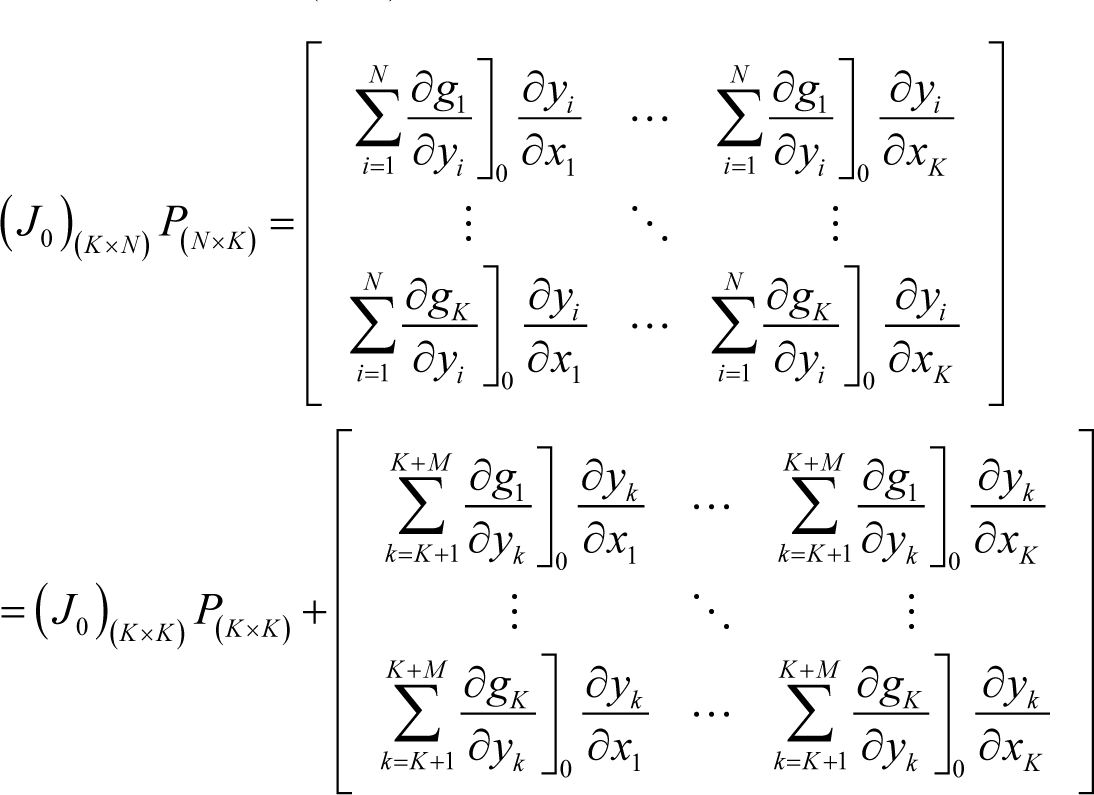
From Equations (I17) and (I18), the following identity is obtained:
Furthermore, the following relation holds, as proved in Appendix J:
Then, from Equations (I19) and (I20), the following identity is obtained:
Using Equation (I21), Equation (F20) in Appendix F is derived.
Appendix J: Proof of a Relation (Equation I20) with regard to Matrix Diagonalization
Consider a general matrix J and its diagonalized form Λ that satisfy the following equation:
On the basis of Equation (J1), the following equations hold:
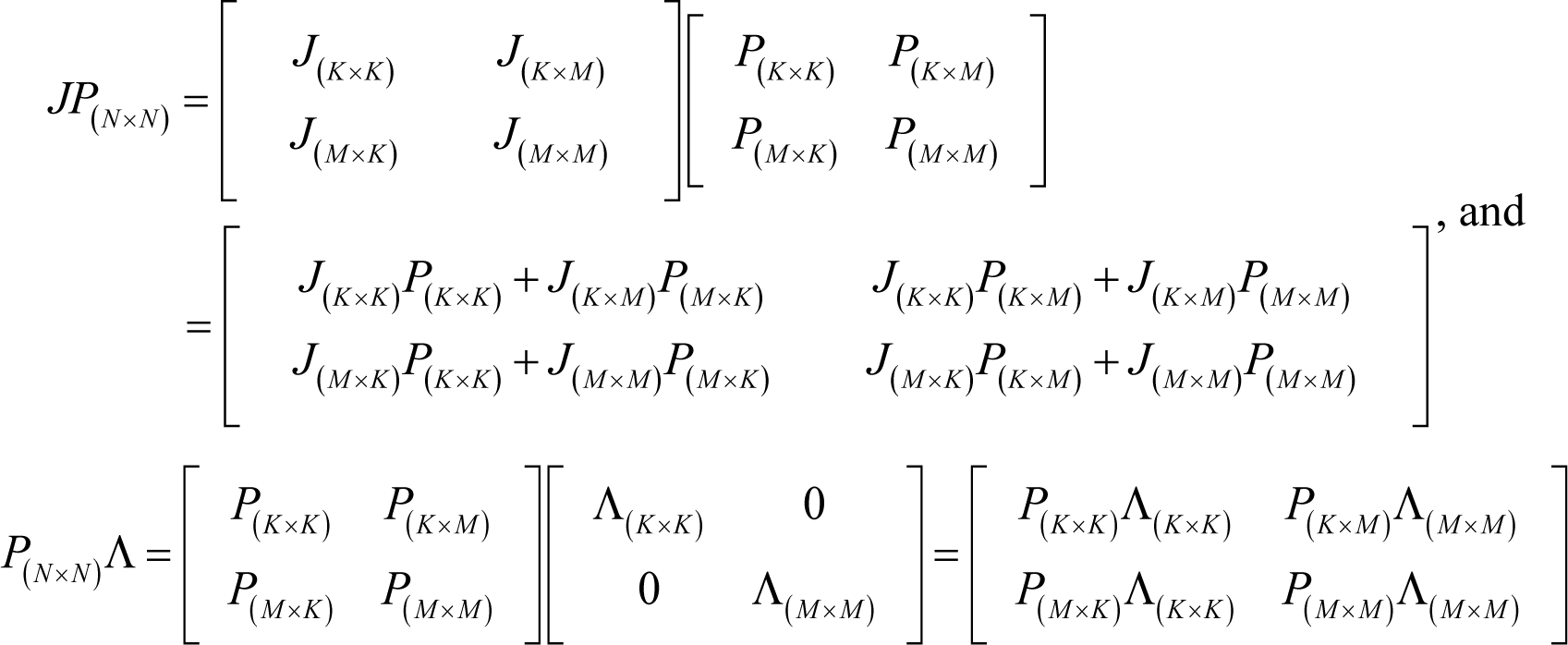
From Equations (J2)–(J4), the following holds:
The lhs of Equation (J5) is indeed J(K×N)P(N×K) because:
Therefore, from Equations (J5) and (J6):
which gives Equation (I20) in Appendix I.
PACS Codes: 05.70.-a; 82.20.-w; 82.40.-g; 82.40.Bj; 05.70.Ln
Conflicts of Interest
The author declares no conflict of interest.
References and Notes
- Wei, J. Axiomatic treatment of chemical reaction systems. J. Chem. Phys 1962, 36, 1578–1584. [Google Scholar]
- Shear, D. An analog of the Boltzmann H-theorem (a Liapunov function) for systems of coupled chemical reactions. J. Theor. Biol 1967, 16, 212–228. [Google Scholar]
- Higgins, J. Some remarks on Shear’s Liapunov function for systems of chemical reactions. J. Theor. Biol 1968, 21, 293–304. [Google Scholar]
- Krambeck, F.J. The mathematical structure of chemical kinetics in homogeneous single-phase systems. Arch. Ration. Mech. Anal 1970, 38, 317–347. [Google Scholar]
- Feinberg, M. Complex balancing in genera kinetic systems. Arch. Ration. Mech. Anal 1972, 49, 187–194. [Google Scholar]
- Horn, F. Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal 1972, 49, 172–186. [Google Scholar]
- Horn, F.; Jackson, R. General mass action kinetics. Arch. Ration. Mech. Anal 1972, 47, 81–116. [Google Scholar]
- Anderson, D. A proof of the global attractor conjecture in the single linkage class case. SIAM J. Appl. Math 2011, 71, 1487–1508. [Google Scholar]
- Pantea, C. On the persistence and global stability of mass-action systems. SIAM J. Math. Anal 2012, 44, 1636–1673. [Google Scholar]
- Johnston, M.D. Topics in Chemical Reaction Network Theory. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2011. [Google Scholar]
- Szederkenyi, G.; Hangos, K. Finding complex balanced and detailed balanced realizations of chemical reaction networks. J. Math. Chem 2011, 49, 1163–1179. [Google Scholar]
- Craciun, G.; Dickenstein, A.; Shiu, A.; Sturmfels, B. Toric dynamical systems. J. Symb. Comput 2009, 44, 1551–1565. [Google Scholar]
- Siegel, D.; Johnston, M.D. A stratum approach to global stability of complex balanced systems. Dyn. Syst 2011, 26, 125–146. [Google Scholar]
- Multiple physical equilibria are available for systems open to mass exchange or the systems that obey non-ideal mixing rules, for which [15] gives a short review in its section of introduction.
- Powers, J.M.; Paolucci, S. Uniqueness of chemical equilibria in ideal mixtures of ideal gases. Am. J. Phys 2008, 76, 848–855. [Google Scholar]
- Ziegler, H. Chemical reactions and the principle of maximal rate of entropy production. J. Appl. Math. Phys. (ZAMP) 1983, 34, 832–844. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in Physics, Chemistry and Biology. Phys. Rep 2006, 426, 1–45. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Method of invariant manifold for chemical kinetics. Chem. Eng. Sci 2003, 58, 4751–4768. [Google Scholar]
- Gorban, A.N.; Karlin, I.V.; Zmievskii, V.B.; Dymova, S.V. Reduced description in the reaction kinetics. Phys. A 2000, 275, 361–379. [Google Scholar]
- Chiavazzo, E.; Gorban, A.N.; Karlin, I.V.; Dymova, S.V. Comparison of invariant manifolds for model reduction in chemical kinetics. Commun. Comput. Phys 2007, 2, 964–992. [Google Scholar]
- Lebiedz, D. Entropy-related extremum principles for model reduction of dissipative dynamical systems. Entropy 2010, 12, 706–719. [Google Scholar]
- Lebiedz, D.; Reinhardt, V.; Siehr, J. Minimal curvature trajectories: Riemannian geometry concepts for slow manifold computation in chemical kinetics. J. Comput. Phys 2010, 229, 6512–6533. [Google Scholar]
- Reinhardt, V.; Winckler, M.; Lebiedz, D. Approximation of slow attracting manifolds in chemical kinetics by trajectory-based optimization approaches. J. Phys. Chem 2008, 112, 1712–1718. [Google Scholar]
- Al-Khateeb, A.N.; Powers, J.M.; Paolucci, S.; Sommese, A.J.; Diller, J.A.; Hauenstein, J.D.; Mengers, J.D. One-dimensional slow invariant manifolds for spatially homogeneous reactive systems. J. Chem. Phys 2009, 131, 024118. [Google Scholar]
- Dickenstein, A.; Millán, M.P. How far is complex balancing from detailed balancing? Bull. Math. Biol 2011, 73, 811–828. [Google Scholar]
- Maas, U.; Pope, S.B. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Combusti. Flame 1992, 88, 239–264. [Google Scholar]
- Goussis, D.; Lam, S. A study of homogeneous methanol oxidation kinetic using CSP. Proc. Combust. Inst 1992, 24, 113–120. [Google Scholar]
- Lam, S.; Goussis, D. The CSP method for simplifying kinetics. Int. J. Chem. Kinet 1994, 26, 461–486. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: New York, NY, USA, 1998; pp. 242–247. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: New York, NY, USA, 1998; pp. 402–404. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization Second Edition; Springer: New York, NY, USA, 2006; pp. 20–25. [Google Scholar]
- The matrix B2 is always invertible. Otherwise the physically measurable concentrations could not be determined from the other physically measurable concentrations .
- Quasi-equilibrium in a reactive system does not necessarily mean the quasi-equilibrium of an elementary reaction. Even |εl| > 1 is accepted in quasi-equilibrium where a combination of elementary reactions constitutes a quasi-equilibrium and |εl|s of the combination concertedly become smaller.
- In Section 3.1–3.3, the initial composition of the paths based on σ (linear non-equilibrium, steepest descent, and Newton direction) is set as the values calculated by true chemical kinetics at the dimensionless time of 0.01. The reason is the numerical difficulty encountered in the edge of physical domain with non-negative concentration. When the denominator in the logarithmic term of Equation (3) is zero, the calculation diverges. Even when the denominator is not zero but too small, the paths may behave abnormally. Section 3.4 does not use such a critical condition and all paths in that section start from the same initial point for each initial composition.
- Hangos, K.M. Engineering model reduction and entropy-based Lyapumov functions in chemical reaction kinetics. Entropy 2010, 12, 772–797. [Google Scholar]
- Feinberg, M.; Horn, F.J.M. Chemical mechanism structure and the coincidence of the stoichiometric and kinetic subspaces. Arch. Ration. Mech. Anal 1977, 66, 83–97. [Google Scholar]
- The original unit of each reaction rate constant depends on the order of reaction, and is not necessarily the same as each other, but the dimensional value of each rate constant is certainly calculable based on the reference length or volume, reference time, and reference number of molecules.
- The Jacobian of Equation (8) (steepest descent path) is the Hessian H, and Equation (8) is essentially equivalent to Equation (29) in the neighborhood of equilibrium. Accordingly, in the neighborhood of equilibrium the Hessian H corresponds to the constraint-independent part of Q in Equation (11) (linear non-equilibrium path). The comparison between the analytic expressions of the constraint-independent part of Q and Q itself (in Equation C4) indicates that the smallness of the concentrations NO and N compared with the other species in the neighborhood of equilibrium produces the situation where Q approximately equal to its constraint-independent part, i.e., the eigenvectors of H are approximately the same as those of the Jacobian of ELNEP and likewise of true chemical kinetics; which is at least one of the reason for the points 2 and 3 in Section 3.4.
- Bykov, V.; Goldfarb, I.; Gol’dshtein, V. On a modified version of ILDM approach: Asymptotic analysis based on integral manifolds. IMA J. Appl. Math 2006, 71, 359–382. [Google Scholar]
- The conclusion of Reference [24] was founded on the difference between (the eigenvectors of) H and (those of) the Jacobian of Equation (4) (true chemical kinetics). The examples described in Section 3.1–3.3 clearly show that H cannot be alternative of the Jacobian of true chemical kinetics, whereas the example in Section 3.4 gives H whose eigenvectors are nearly the same as those of the Jacobian of true chemical kinetics. However, near equilibrium for any detailed-balanced systems including all examples in Section 3, ELNEP (one of the equations based on σ) approximates Equation (4) (true chemical kinetics).
- Chiavazzos, E.; Karlin, I.V. Quasi equilibrium grid algorithm: Geometric construction for model reduction. J. Comput. Phys 2008, 227, 5535–5560. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems, 3rd ed; Springer: New York, NY, USA, 2001; pp. 129–132. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Appendix A: Considering Constraints
The following simple example may be useful as a reminder of how to consider constraints when function derivatives are calculated. For f = ax + by + cz:
Under the additional constraint z=x2 + y2:
since . However, substituting the relation into , the following is obtained:
which reproduces Equation (A2).
In brief:
and the following relation generally holds:
or:
Appendix B: Equivalence of Equation (29) to Equation (8)
Equation (29) is clearly equivalent to:
Using the identity:
Equation (B1) becomes:
Defining , Equation (B3) is equivalent to Equation (8) to first order in each variable εl when is replaced by and .
Therefore, Equation (29) is essentially equivalent to a scale-transformed version of Equation (8) to first order in each variable εl.
Appendix C: Specific Forms of the ELNEP (Equation (11))
The following are the specific forms of the ELNEP (Equation 11) for the four reaction systems described in Section 3. For the system A ⇆ 2B ⇆ C (in Section 3.1):
For the system A ⇆ B ⇆ C ⇆ D (in Section 3.2):
For the system A ⇆ B ⇆ C (in Section 3.3):
For the Zel’dovich mechanism (in Section 3.4):
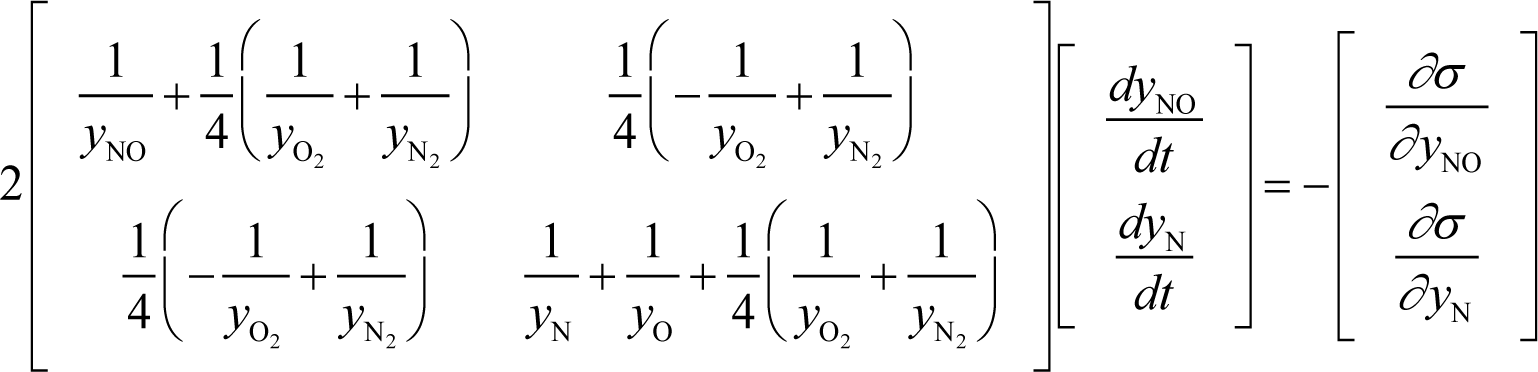
Appendix D: Temperature Determination Based on Internal Energy Conservation
The internal energy of a thermally perfect gas is expressed as:
where U is the internal energy in volume V, is the molar internal energy of the kth species, and yk is the molar concentration of the kth species. When the internal energy is conserved in a constant volume, the following equation holds:
where is the molar heat capacity of the kth species at constant volume, and T is the mixture temperature. From Equation (D2), an increase in the mixture temperature is determined by an increase in the concentration of each species:
Accordingly, variable T can be replaced by variables yks.
Appendix E: Proof that ELNEP gives a unique solution at equilibrium
First, it is proved that the matrix Q of ELNEP is symmetric and positive definite, and that ELNEP gives a unique solution of ∇σ = 0, i.e., the equilibrium state. From Equation (12), it is obvious that the matrix Q of ELNEP is symmetric, and Q can be rewritten as follows:
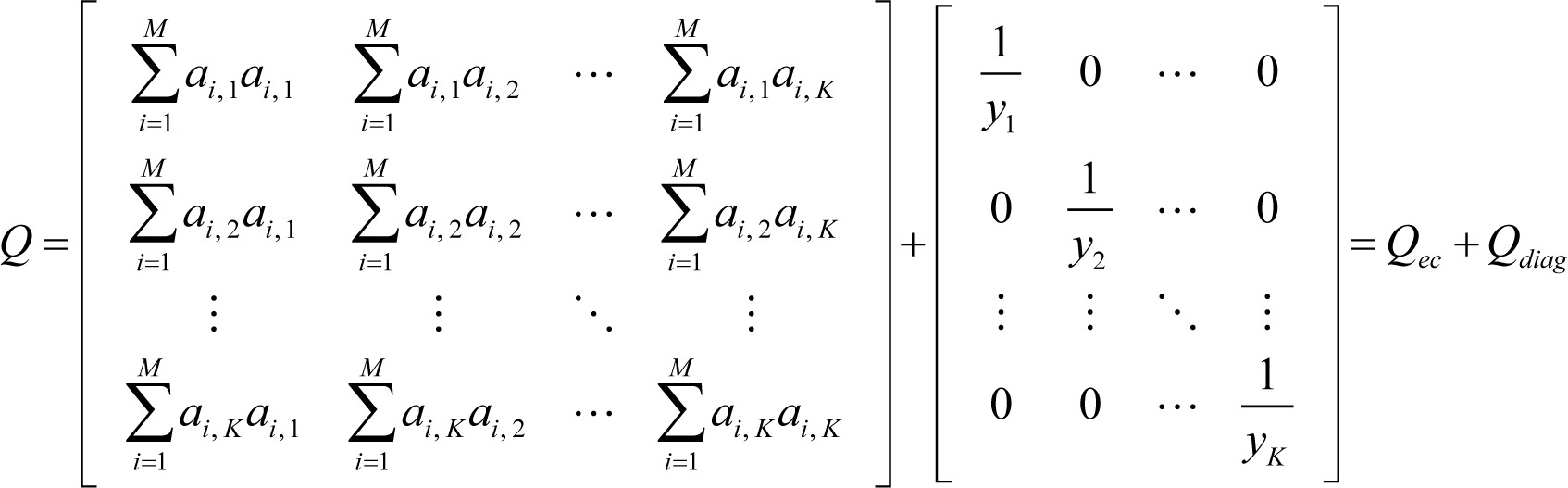
where:
From Equations (E1) and (E2):
Because in the rhs of Equation (E6), and for any vector , the matrix Q is positive definite, and its eigenvalues are all positive. Therefore, Q can be diagonalized as:
where Λ is a diagonal matrix whose components are all positive, and P is an orthogonal matrix (P‒1 = PT) since Q is a real symmetric matrix. Substituting Equation (E7) into ELNEP (Equation (11)), the following is obtained:
which means is always negative except at equilibrium. Together with the fact that σ is always positive except at equilibrium, it is concluded from the Lyapunov theorem [42] that σ is a Lyapunov function of ELNEP, which has an asymptotically stable solution (equilibrium) at ∇σ =0.
Appendix F: LDM and the Jacobian of ELNEP
Here ELNEP (Equation 11) is expressed as follows:
where:
According to Appendix G, Equation (F1) (which is Equation (11)) can be transformed to the following:
where:
Then, the following equation holds:
where:
The left-hand side (lhs) of Equation (F6) becomes:
Then, Equation (F6) becomes:
If the first term on the lhs of Equation (F10) is sufficiently small compared with that on the rhs, Equation (F10) becomes:
The derivation of Equation (F11) is as follows. Neglecting the first term of the lhs of Equation (F10) and multiplying by Q−1, Equation (F10) becomes:
According to Appendix H, the operator Q−1 Ω extracts the first K components of the vector . Then, Equation (F12) becomes Equation (F11), which means that Q−1ΘELNEP is the Jacobian of the vector of Equation (F7) for ELNEP, i.e.:
in accordance with the nomenclature in Appendix I.
However, multiplying the first term of the lhs of Equation (F10) by Q−1 yields:
The derivation of Equation (F14) is as follows. At first, becomes the following:
where the two matrixes on the far rhs of Equation (F15) are diagonal. Multiplying by Q−1 and according to Appendix H, Equation (F15) becomes:
Multiplying and using Equation (F7), Equation (F16) becomes Equation (F14).
Using Equations (F11), (F13), and (F14), Equation (F10) becomes:
Equation (F17) becomes the following when is transformed to , which is defined in Equation (F19):
where P(K×K) is certain K×K matrix. However, when P(K×K) is the left-upper part of the eigenvector matrix of the Jacobian for true chemical kinetics at equilibrium, Equation (F18) at equilibrium becomes:
according to Equation (I21) in Appendix I. Assuming is negligible, as is usual in ILDM applications [39], Equation (F20) becomes the following (at equilibrium) (after multiplying the inverse matrix of P(K×K)):
If the first term on the lhs of Equation (F21) is negligible compared with that on the rhs, Equation (F21) becomes the following (at equilibrium):
which means the LDM of ELNEP is an approximation to that of true chemical kinetics when εl ≈ 0 for every lth reaction. The condition that the first term on the lhs of Equation (F21) is negligible compared with that on the rhs is fulfilled when the eigenvectors of the ELNEP Jacobian JELNEP are almost the same as those of the Jacobian of true chemical kinetics, which has been numerically confirmed in the sample systems described in Section 3. However, the condition that the eigenvectors of the ELNEP Jacobian JELNEP are almost the same as those of the Jacobian of true chemical kinetics does not necessarily hold even in the whole 1-D manifold of true chemical kinetics, such as for the example described in Section 3.4.
Appendix G: Alternative Expression for ELNEP
Owing to Equation (24), the lhs of ELNEP (Equation 11) or Equation (F1) can be transformed as follows:
where:
Appendix H: Extraction of the Independent Parts of Vectors or Matrixes
According to Equation (G1), the following relation holds:
Inspecting the derivation describe d in Appendix G, Equation (H1) holds for any vector or matrix instead of , i.e.:
where and Ψ are any vector and matrix, respectively, and D is any dimension.
Appendix I: Coincidence of the Jacobians of ELNEP and True Chemical Kinetics at Equilibrium
The Jacobian J of true chemical kinetics is derived from Equation (4) as:
At equilibrium (εl = 0 for every lth reaction), the Jacobian of true chemical kinetics becomes:
where J0 is the Jacobian of true chemical kinetics at equilibrium. However, the Jacobian of ELNEP is defined by Equations (F8) and (F13) in Appendix F:
The Hessian to first order in εl can be derived from Equations (10), (2), (3), (5), and (A4) as:

where:
Accordingly, the Hessian at equilibrium becomes:

where H0 is the Hessian at equilibrium, and Equation (I7) can be further transformed as follows:

where:
Therefore, according to Equation (I3) and Appendix H, the Jacobian of ELNEP at equilibrium becomes:
which is exactly the Jacobian of true chemical kinetics that explicitly accounts for the constraints inherent in chemical kinetics because:
When Λ0 is defined by the following equation as the diagonalized form of J0 using a matrix P(N×N)
The following equations hold at equilibrium:
where:
Then, from Equation (I10):
where P(K×K) is the left-upper part of P(N×N). However, the following relation also holds:

From Equations (I17) and (I18), the following identity is obtained:
Furthermore, the following relation holds, as proved in Appendix J:
Then, from Equations (I19) and (I20), the following identity is obtained:
Using Equation (I21), Equation (F20) in Appendix F is derived.
Appendix J: Proof of a Relation (Equation I20) with regard to Matrix Diagonalization
Consider a general matrix J and its diagonalized form Λ that satisfy the following equation:
On the basis of Equation (J1), the following equations hold:
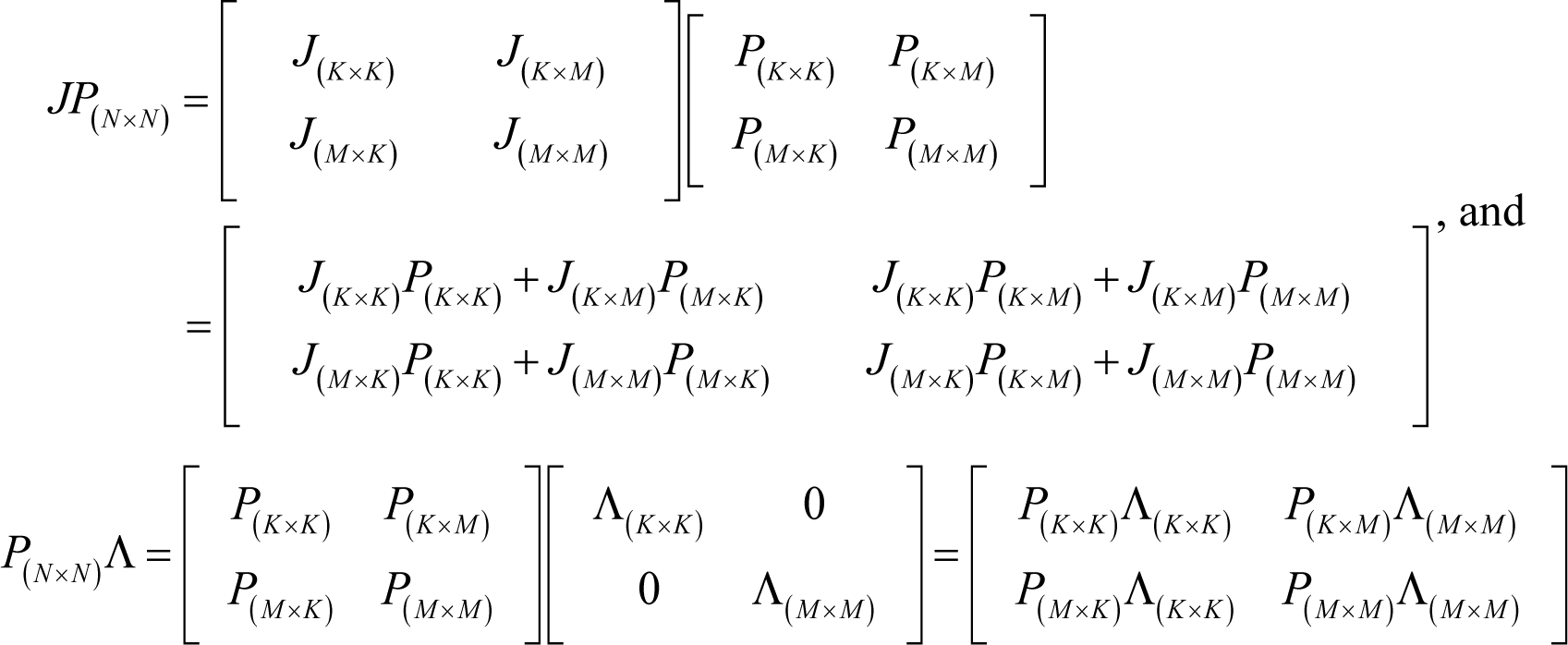
From Equations (J2)–(J4), the following holds:
The lhs of Equation (J5) is indeed J(K×N)P(N×K) because:
Therefore, from Equations (J5) and (J6):
which gives Equation (I20) in Appendix I.
PACS Codes: 05.70.-a; 82.20.-w; 82.40.-g; 82.40.Bj; 05.70.Ln
Conflicts of Interest
The author declares no conflict of interest.
References and Notes
- Wei, J. Axiomatic treatment of chemical reaction systems. J. Chem. Phys 1962, 36, 1578–1584. [Google Scholar]
- Shear, D. An analog of the Boltzmann H-theorem (a Liapunov function) for systems of coupled chemical reactions. J. Theor. Biol 1967, 16, 212–228. [Google Scholar]
- Higgins, J. Some remarks on Shear’s Liapunov function for systems of chemical reactions. J. Theor. Biol 1968, 21, 293–304. [Google Scholar]
- Krambeck, F.J. The mathematical structure of chemical kinetics in homogeneous single-phase systems. Arch. Ration. Mech. Anal 1970, 38, 317–347. [Google Scholar]
- Feinberg, M. Complex balancing in genera kinetic systems. Arch. Ration. Mech. Anal 1972, 49, 187–194. [Google Scholar]
- Horn, F. Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal 1972, 49, 172–186. [Google Scholar]
- Horn, F.; Jackson, R. General mass action kinetics. Arch. Ration. Mech. Anal 1972, 47, 81–116. [Google Scholar]
- Anderson, D. A proof of the global attractor conjecture in the single linkage class case. SIAM J. Appl. Math 2011, 71, 1487–1508. [Google Scholar]
- Pantea, C. On the persistence and global stability of mass-action systems. SIAM J. Math. Anal 2012, 44, 1636–1673. [Google Scholar]
- Johnston, M.D. Topics in Chemical Reaction Network Theory. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2011. [Google Scholar]
- Szederkenyi, G.; Hangos, K. Finding complex balanced and detailed balanced realizations of chemical reaction networks. J. Math. Chem 2011, 49, 1163–1179. [Google Scholar]
- Craciun, G.; Dickenstein, A.; Shiu, A.; Sturmfels, B. Toric dynamical systems. J. Symb. Comput 2009, 44, 1551–1565. [Google Scholar]
- Siegel, D.; Johnston, M.D. A stratum approach to global stability of complex balanced systems. Dyn. Syst 2011, 26, 125–146. [Google Scholar]
- Multiple physical equilibria are available for systems open to mass exchange or the systems that obey non-ideal mixing rules, for which [15] gives a short review in its section of introduction.
- Powers, J.M.; Paolucci, S. Uniqueness of chemical equilibria in ideal mixtures of ideal gases. Am. J. Phys 2008, 76, 848–855. [Google Scholar]
- Ziegler, H. Chemical reactions and the principle of maximal rate of entropy production. J. Appl. Math. Phys. (ZAMP) 1983, 34, 832–844. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in Physics, Chemistry and Biology. Phys. Rep 2006, 426, 1–45. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Method of invariant manifold for chemical kinetics. Chem. Eng. Sci 2003, 58, 4751–4768. [Google Scholar]
- Gorban, A.N.; Karlin, I.V.; Zmievskii, V.B.; Dymova, S.V. Reduced description in the reaction kinetics. Phys. A 2000, 275, 361–379. [Google Scholar]
- Chiavazzo, E.; Gorban, A.N.; Karlin, I.V.; Dymova, S.V. Comparison of invariant manifolds for model reduction in chemical kinetics. Commun. Comput. Phys 2007, 2, 964–992. [Google Scholar]
- Lebiedz, D. Entropy-related extremum principles for model reduction of dissipative dynamical systems. Entropy 2010, 12, 706–719. [Google Scholar]
- Lebiedz, D.; Reinhardt, V.; Siehr, J. Minimal curvature trajectories: Riemannian geometry concepts for slow manifold computation in chemical kinetics. J. Comput. Phys 2010, 229, 6512–6533. [Google Scholar]
- Reinhardt, V.; Winckler, M.; Lebiedz, D. Approximation of slow attracting manifolds in chemical kinetics by trajectory-based optimization approaches. J. Phys. Chem 2008, 112, 1712–1718. [Google Scholar]
- Al-Khateeb, A.N.; Powers, J.M.; Paolucci, S.; Sommese, A.J.; Diller, J.A.; Hauenstein, J.D.; Mengers, J.D. One-dimensional slow invariant manifolds for spatially homogeneous reactive systems. J. Chem. Phys 2009, 131, 024118. [Google Scholar]
- Dickenstein, A.; Millán, M.P. How far is complex balancing from detailed balancing? Bull. Math. Biol 2011, 73, 811–828. [Google Scholar]
- Maas, U.; Pope, S.B. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Combusti. Flame 1992, 88, 239–264. [Google Scholar]
- Goussis, D.; Lam, S. A study of homogeneous methanol oxidation kinetic using CSP. Proc. Combust. Inst 1992, 24, 113–120. [Google Scholar]
- Lam, S.; Goussis, D. The CSP method for simplifying kinetics. Int. J. Chem. Kinet 1994, 26, 461–486. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: New York, NY, USA, 1998; pp. 242–247. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: New York, NY, USA, 1998; pp. 402–404. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization Second Edition; Springer: New York, NY, USA, 2006; pp. 20–25. [Google Scholar]
- The matrix B2 is always invertible. Otherwise the physically measurable concentrations could not be determined from the other physically measurable concentrations .
- Quasi-equilibrium in a reactive system does not necessarily mean the quasi-equilibrium of an elementary reaction. Even |εl| > 1 is accepted in quasi-equilibrium where a combination of elementary reactions constitutes a quasi-equilibrium and |εl|s of the combination concertedly become smaller.
- In Section 3.1–3.3, the initial composition of the paths based on σ (linear non-equilibrium, steepest descent, and Newton direction) is set as the values calculated by true chemical kinetics at the dimensionless time of 0.01. The reason is the numerical difficulty encountered in the edge of physical domain with non-negative concentration. When the denominator in the logarithmic term of Equation (3) is zero, the calculation diverges. Even when the denominator is not zero but too small, the paths may behave abnormally. Section 3.4 does not use such a critical condition and all paths in that section start from the same initial point for each initial composition.
- Hangos, K.M. Engineering model reduction and entropy-based Lyapumov functions in chemical reaction kinetics. Entropy 2010, 12, 772–797. [Google Scholar]
- Feinberg, M.; Horn, F.J.M. Chemical mechanism structure and the coincidence of the stoichiometric and kinetic subspaces. Arch. Ration. Mech. Anal 1977, 66, 83–97. [Google Scholar]
- The original unit of each reaction rate constant depends on the order of reaction, and is not necessarily the same as each other, but the dimensional value of each rate constant is certainly calculable based on the reference length or volume, reference time, and reference number of molecules.
- The Jacobian of Equation (8) (steepest descent path) is the Hessian H, and Equation (8) is essentially equivalent to Equation (29) in the neighborhood of equilibrium. Accordingly, in the neighborhood of equilibrium the Hessian H corresponds to the constraint-independent part of Q in Equation (11) (linear non-equilibrium path). The comparison between the analytic expressions of the constraint-independent part of Q and Q itself (in Equation C4) indicates that the smallness of the concentrations NO and N compared with the other species in the neighborhood of equilibrium produces the situation where Q approximately equal to its constraint-independent part, i.e., the eigenvectors of H are approximately the same as those of the Jacobian of ELNEP and likewise of true chemical kinetics; which is at least one of the reason for the points 2 and 3 in Section 3.4.
- Bykov, V.; Goldfarb, I.; Gol’dshtein, V. On a modified version of ILDM approach: Asymptotic analysis based on integral manifolds. IMA J. Appl. Math 2006, 71, 359–382. [Google Scholar]
- The conclusion of Reference [24] was founded on the difference between (the eigenvectors of) H and (those of) the Jacobian of Equation (4) (true chemical kinetics). The examples described in Section 3.1–3.3 clearly show that H cannot be alternative of the Jacobian of true chemical kinetics, whereas the example in Section 3.4 gives H whose eigenvectors are nearly the same as those of the Jacobian of true chemical kinetics. However, near equilibrium for any detailed-balanced systems including all examples in Section 3, ELNEP (one of the equations based on σ) approximates Equation (4) (true chemical kinetics).
- Chiavazzos, E.; Karlin, I.V. Quasi equilibrium grid algorithm: Geometric construction for model reduction. J. Comput. Phys 2008, 227, 5535–5560. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems, 3rd ed; Springer: New York, NY, USA, 2001; pp. 129–132. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).