Abstract
We show that the thermodynamics of ideal gases may be derived solely from the Democritean concept of corpuscles moving in vacuum plus a principle of simplicity, namely that these laws are independent of the laws of motion, aside from the law of energy conservation. Only a single corpuscle in contact with a heat bath submitted to a z and t-invariant force is considered. Most of the end results are known but the method appears to be novel. The mathematics being elementary, the present paper should facilitate the understanding of the ideal gas law and of classical thermodynamics even though not-usually-taught concepts are being introduced.
1. Introduction
This paper is devoted to an alternative derivation of the ideal gas law, which agrees with the accepted postulates of statistical mechanics, and may present pedagogical and scientific interest. We postulate the law of thermal equilibrium. By ideal gas, we mean a collection of non-interacting corpuscles in some enclosure. These corpuscles may be submitted to an external force, e.g., of electrical or gravitational origin, and the non-relativistic approximation does not have to be made. We will call perfect gas an ideal gas with no external force acting upon the corpuscles and with the non-relativistic approximation being made. There is full agreement between our general results and the first and second laws of thermodynamics as they are spelled out in textbooks such as Callen [1]. There is also full agreement with the usual perfect-gas laws that can be found in the Bernoulli work and elementary text-books, in the limit considered.
The question has been often raised by historians of science as to why the industrial revolution that occurred in the 17th century in Europe did not occur much earlier, for example at the time of Hero of Alexandria (100 BC), who was a disciple of Democritus and invented the first known steam engine called the aeolipile. Some of the possible reasons invoked are lack of interest on the part of the rulers, the paucity of the wood needed to heat water, and the fact that materials, that can withstand high vapor pressures, had not been discovered yet. We will not consider here these sociological or technological problems, but instead concentrate on the conceptual issues. From a pedagogical viewpoint many teachers point out the usefulness of presenting to students the major discoveries in science as they actually occurred, and perhaps also as they could have occurred, from a logical standpoint. On the scientific side, we observe that most text-books reproduce the Bernoulli argument based on Galilei–Newton mechanics. But the ideal gas and the barometric laws are not so restricted. In the present paper, we give a generalized and—at least in our opinion—simplified treatment that accounts for the effect of a constant force acting on the corpuscle and special-relativity effects. Some of the results in those cases are known (but not very well-known). They can be generalized to other situations including various dispersion relations (or Hamiltonians), and z-dependent forces (see the last section of our longer paper in [2,3]).
Let us first quote Feynman [4] “If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the hypothesis that all things are made of atoms. In that one sentence there is an enormous amount of information about the world, if just a little imagination and thinking are applied." In line with this quotation, it seems worthwhile exploring how much physics may be derived from the corpuscular concept. Only some qualitative observations are needed. One is the fact that it takes some time, denoted here , for a corpuscle thrown upward on earth to reach an altitude and come back to the ground level. We have of course . If the corpuscle bounces elastically on the ground, represents the oscillation period. The time during which the corpuscle is located above some altitude during a period is: . Under our assumptions the τ-function does not depend on the initial altitude or initial time. A second observation is that two bodies left in contact for a sufficient period of time tend to reach the same temperature, as one can judge by our senses.
The purpose of the present paper is thus to show that the thermodynamics of ideal gases and in particular the ideal gas law may be obtained on the sole basis of the Democritean model according to which nature consists of corpuscles moving in a vacuum, plus a principle of simplicity: namely that these fundamental laws are independent of the law of corpuscle motion (non-relativistic, special relativistic, or otherwise). According to general relativity, thermal energy has weight. But this so-called Tolman effect that entails a temperature variation on the order of on earth is entirely negligible. The temperature θ enters solely for dimensional reasons. We later show from the general expressions of the gas internal energy and of the force (or pressure) that the heat delivered by the gas is , an expression of the entropy S being given. This result enables us to prove that the formally-introduced temperature θ is a thermodynamic temperature. Indeed, we recover for ideal gases the general Carnot result asserting that the efficiency of reversible thermal engines is , where denotes the cold bath temperature and the hot bath temperature. Since Kelvin time this expression defines the thermodynamics temperature to within an arbitrary proportionality factor, which is fixed by specifying that joules at the water triple point. An alternative derivation of the Carnot result, also solely based on the concept of potential energy, is in [2,5].
In the title of this paper the word “classical” means “non-quantum” (), but the non-relativistic approximation is not made, except in examples. “Ideal Gases” refer to non-interacting identical corpuscles. Accordingly, the corpuscles are independent, and we may consider a single corpuscle. As a result of the slight thermal motion of the container wall, there is an exchange of energy between the corpuscle and the heat bath (for a static wall, even a rough one, the corpuscle energy would be a constant of motion). Thus we are working in the so-called “canonical ensemble". Concretely, the corpuscle may be a cold neutron submitted to the earth gravity and reflected by a diamond at some non-zero temperature [6]. The paper [7] “Microcanonical single-particle distributions for an ideal gas in a gravitational field” is valuable because it establishes (within the non-relativistic approximation) the gas law in the micro-canonical ensemble with the effect of gravity taken into account as in the present paper. These authors find that the micro-canonical result approaches the canonical result for few corpuscles only. However that paper is complicated both from mathematical and physical viewpoints. The reader may wish to compare the micro-canonical many-corpuscle paper just cited with the present canonical single-corpuscle paper in terms of pedagogical value. Of course the final results are the same.
The reader may feel that our statement that the above invariance principle implies the ideal gas laws, without anything else, is surprising. Yet, we hope that we can convince him/her that this is indeed the case. On the other hand, a quick reading of standard books on thermodynamics may lead other readers to believe that this is a well-known fact. For example, Callen [1] states correctly that: “The essence of the ideal-gas law is that molecules of the gas do not interact. This simple fact implies that ”. However, in order to reach this conclusion, the author needs postulate the Newtonian law of motion, quantum theory, and the Boltzmann factor. The claim that corpuscle independence entails the ideal gas law (without anything else) therefore does not appear to have been justified before. For a broad discussion of the laws of thermodynamics, see for example [8].
Let us emphasize that our goal is to derive the ideal gas laws from first principles, only conservation of potential energy and thermal equilibrium being assumed (our model cannot describe directly the so-called “adiabatic atmospheres” that are in mechanical but not thermal equilibrium). We do not use the concept of kinetic energy, nor do we postulate any particular law of corpuscle motion. Accordingly, a given potential for a weight w does not imply any specific law of motion . We call “weight” the downward force exerted on the corpuscle, even though this force does not have to be of gravitational origin. Because the presence of a corpuscle affects negligibly the potential, one may consider the latter to be an external potential. To our knowledge, the concepts presented in this paper have not been considered before. However, the final expressions relating to the relativistic ideal gas law in the presence of gravity are known, see for example [9].
Admittedly the present paper departs much from usually-taught concepts in thermodynamics [10]. We indeed ignore the concepts of kinetic energy, of micro-states, and the laws of Physics that would provide the motion (to within arbitrary t and z translations) of corpuscles of given energy. The temperature θ (to within a constant factor) follows from dimensional considerations and not as usual from the derivative of the average energy with respect to the entropy S at constant volume (here denoted h). Quite to the contrary, an explicit expression of the (classical ideal gas) entropy function is derived from the average force (or pressure) and average energy U. This change of perspective suggests that one should first emphasize, in teaching the subject to students, the Democritean concept of corpuscles moving in vacuum and the concept of potential energy (e.g., from cords and pulleys experiments). Next, consider the up and down motion of a corpuscle thrown upward from in the earth gravitational field (supposed to be static and independent of the vertical z coordinate), the particular function being left undefined. As a result of weak thermal contact with the bath (that does not need to be specified further), the maximum altitude varies slowly in the course of time. This variation is described statistically by some probability law . It should be explained next that a weight measured by a high-inertia balance does not depend on possible up and down motion of the corpuscle. It is intuitive that the up and down motion of a corpuscle cannot modify the average force that it exerts on the ground plate. The formal proof is as follows: The force is the product of twice the momentum p at the collision time and the number of collisions per unit time, that is: . The Hamilton equations of motion of a corpuscle are and for a Hamiltonian . If a uniform time-invariant force is applied to the corpuscle, we have , where represents the potential energy and is an arbitrary function of p. The main contribution of our paper is indeed to show that the barometric and ideal gas laws do not depend on that function. Application of the Hamilton equations just recalled: , with a time translation when w is not strictly equal to zero. If , is of course a constant of motion, but gets reversed in sign upon a collision. Consider now a full oscillation period beginning at and ending up at , the collision with the ground () occurring half-way. Accordingly we have and as asserted. In the non-relativistic approximation, , where m denotes the corpuscle mass. However, since the barometric and ideal gas laws do not depend on , they do not depend on m either. The quantum theory is mathematically feasible for non-relativistic or ultra-relativistic corpuscles, but it becomes very involved for general functions. The semi-classical (Bohr–Sommerfeld) approximation of the quantum theory coincides at the end with our treatment, but it may not be as straightforward.
Accordingly, the impact is equal to w times the motion period. This observation enables us to express the force F in terms of round-trip times when a rigid plate is present at , see Figure 1. The condition that the average force be independent of the function introduced above provides the ideal gas law in full generality.
To conclude, the approach advocated in this paper enables us to recover classical results in thermodynamics in a considerably generalized form (but only for independent classical corpuscles and laws of physics that are independent of time and altitude translations). Admittedly, our presentation goes against the order in which basic concepts are usually taught, but the greater simplicity and generality will perhaps be appreciated.
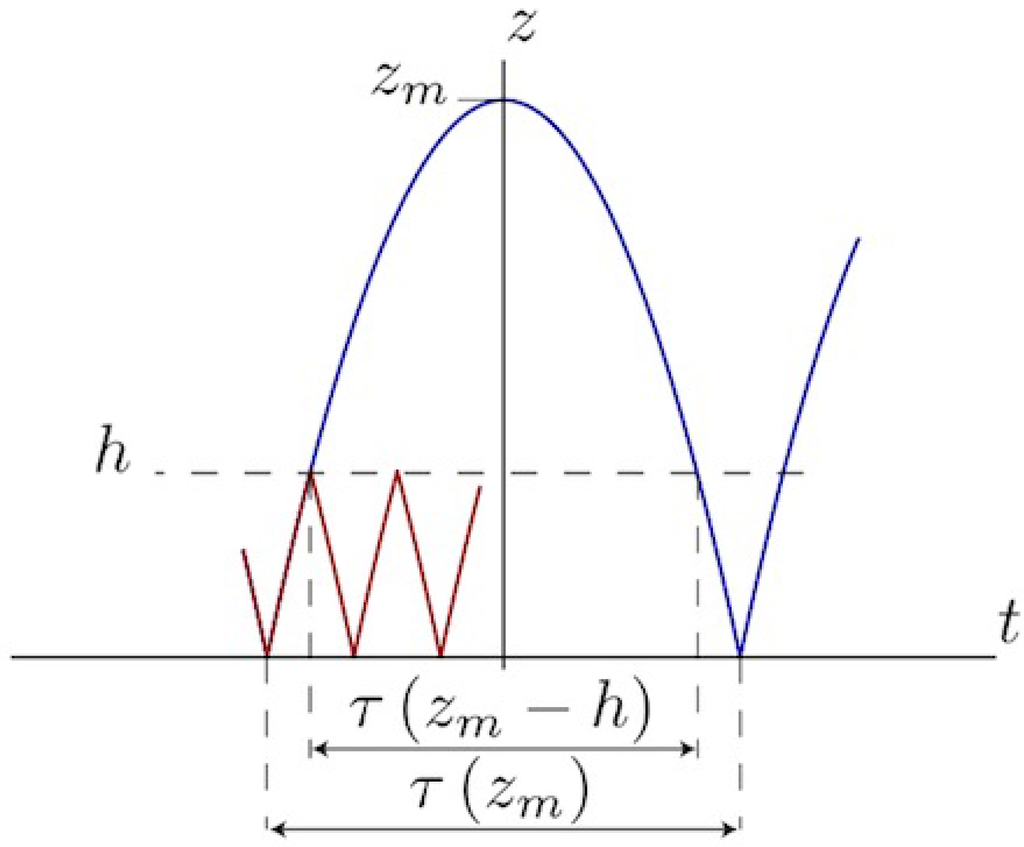
Figure 1.
Space-time () trajectory for a corpuscle of weight w bouncing off the ground (z = 0). The maximum altitude reached by the corpuscle is , where E denotes the energy. The motion is periodic with period , where denotes the corpuscle round-trip time at a distance Z from the top of the trajectory. When the altitude is restricted to h by a plate (dashed horizontal line) the motion remains periodic with a period evidently equal to: . Note that this expression holds even if the motion is not symmetric in time.
2. Average Force Exerted by a Corpuscle on a Piston
We consider a unit-area cylinder with vertical z-axis in uniform gravity resting on the ground () at some temperature. A tight piston is free to move in the vertical direction. The cylinder height is denoted by h and contains a single corpuscle of weight w, or submitted to a force constant in space and time. The motion may be relativistic or not. In our one-dimensional model, the pressure corresponds to the average force , the volume to the height h, and . Our result provides the ideal-gas law in a generalized form, taking into account gravity. In that case, the pressure varies as a function of altitude. More precisely, the force exerted by the corpuscle on the lower end of the cylinder exceeds the force exerted on the upper end (or piston) by the corpuscle weight. But in the absence of gravity, the forces exerted on both ends would be the same. We are introducing (static and uniform) gravity mainly because this helps clarify the concept of corpuscle energy: the corpuscle energy E is the maximum altitude that the corpuscle would reach in the absence of the piston times w. The corpuscle bounces elastically off the ground and off the piston (if it reaches it), that is, without any loss or gain of energy. (Clarification is perhaps needed here. Some quantities in thermodynamics have a clear experimental significance and are unambiguous. Let us first recall that we are considering a single corpuscle. However, an ideal gas, as we define it, is a collection of non-interacting corpuscles. Accordingly, at a given temperature and at a given value of h, for N identical corpuscles the force and the internal energy, and thus the free energy, are simply multiplied by N).
The force (or pressure) and internal energy have clear meanings. This is the case in particular for the average force exerted by the gas on a piston. The word “average” here enters in two ways, as a mechanical average and as a thermal average. This point is clarified below. Consider a purely mechanical problem: the so-called “bouncer". A corpuscle of energy E is submitted to a constant force. The mechanical average referred to above is the product of , that is, twice the corpuscle momentum p when it collides with the plane, times the number of collisions per unit time, which is equal to , where τ denotes the corpuscle round-trip time (or motion period), which is . Physically, it is supposed that the plane (e.g., the earth) has so much inertia that it does not respond to individual collisions. The second averaging refers to thermal averaging. We postulate a distribution of energy, and the second averaging is taken with respect to this distribution. The point of our paper is that this distribution does not have to be postulated (or derived from considerations a la Boltzmann); it follows from our simplicity principle.
Without piston () we obtain the so-called “barometric law", that is, the decay of the average corpuscle density as a function of altitude z. The density decay is found from our simplicity principle to be: . This is of course a well-known result, but here the Boltzmann factor does not have to be postulated. Similar considerations apply to the case where there is a piston at altitude h. Both the piston and the ground are assumed to have great inertia, so that they do not react significantly to individual collisions, and again the mechanical average force for some corpuscle energy E is . In the presence of a force w acting on the corpuscle, p is of course larger at than at . If there is no force acting on the corpuscle, i.e., , p and thus F are the same on the piston and on the ground. The corpuscle energy in the non-relativistic approximation is , and thus the mechanical-average force acting on the piston or on the ground are . Since , we obtain . Performing now a thermal averaging, we finally obtain if we define θ as the average corpuscle energy (which reduces here to the kinetic energy, ). The above discussion applicable to perfect gases, initially due to Bernoulli, is given in elementary textbooks. The purpose of the present note is to clarify that the well-known results applicable to perfect gases are special cases of our more general results, applicable to ideal gases.
Consider first the case where h is infinite, that is, in the absence of a piston. The time period is denoted as before by with . The average force exerted on the ground, equal to the corpuscle weight is the impulse i divided by the period. Thus . In other words, the impulse transmitted to a piston when the corpuscle impacts on it is equal to the motion period. If the piston is located at , the impulse it receives is if , and zero otherwise. On the other hand, the motion period is if and if .
Accordingly, the force F experienced by the piston when the corpuscle energy is is the ratio of the impulse and period:
Because the cylinder lower end is in contact with a bath, there is a slight thermal motion and the corpuscle energy slowly varies in the course of time. Accordingly, the average force experienced by the piston is, if denote the distribution:
Initially, we obtained the form of the force from the Bohr–Sommerfeld approximation of the quantum theory. But this amounts to saying that the corpuscle action (area in the position-momentum z-p phase-space, where here ) is discrete, and evenly spaced in units of the Planck constant. However, because the “bouncer” considered in our paper is not a harmonic oscillator, the discrete corpuscle energies are not evenly spaced. This is why, when going to the continuous limit, converting the sum into an integral, we must introduce the factor in the form given. However, after going through all these semi-classical considerations, we discovered that it was sufficient to postulate the simplicity principle given earlier. The latter concept (unlike the quantum theory) could have been understood at the time of the ancient Greece. Going the opposite way, one may say that the simplicity principle suggests the semi-classical quantum theory. This viewpoint is not discussed further here.
According to our simplicity principle, the average force must be independent of the corpuscle equation of motion, and thus of the function. This condition obtains from Equation (2) if one selects the following distribution:
where θ has the dimension of an energy. The average force becomes, using Equations (2) and (3):
In the above integrals going from h to ∞ we have replaced by and introduced the variable , so that all the integrals go from zero to infinity and cancel out. Note that even though integral signs have been introduced, no integration has been performed. We simply consider an integral as a sum of terms and employ the rule of addition associativity. We have employed also the fact that is the only function such that .
For a collection of N independent corpuscles having weights respectively, the force is a sum of N terms of the form given in Equation (4). In the case of zero gravity (w=0 or more precisely: ), the above expression gives . Thus we have obtained the ideal gas law .
Average force for a three-dimensional space:
We suppose that the cylinder radius is very large compared with h, and we do not consider the force exerted by the corpuscle on the cylinder wall. Motion of the corpuscle along directions perpendicular to z (say, x and y) does affect the round-trip time function . However, since the average force does not depend on this function, the ideal gas law is unaffected. This is so for any physical system involving a single corpuscle provided the physical laws are invariant under a z-translation (besides being static).
The internal energy, to be discussed in the following section, though, is incremented. One can prove that in the non-relativistic approximation and in the absence of gravity the internal energy is multiplied by 3. It would be incremented further by corpuscle rotation or vibration, not considered here. Using conventional methods, Landsberg [9] and Louis-Martinez [11] obtain exactly the same result as given above (except for the factor 3 in the expression of the internal energy, relating to the number of space dimensions considered).
3. Internal Energy
The gas internal energy U is the average value of , the gravitational energy being accounted for. Note that only corpuscle motion along the z-axis is being considered. In the present section, a non-unity (but constant) weight w is considered to clarify the dimensions of the quantities introduced. The expression of U is, using the energy distribution given in Equation (3):
The first term in the final above expression, minus θ, corresponds to the kinetic energy K. The second term, plus θ, corresponds to the potential energy P. In the non-relativistic limit, the first term gives the well-known expression . Without gravity, . In the general case the splitting of U into looks somewhat artificial.
The internal energy divided by the temperature: , thus is the sum of a term function of θ but not of h, and a term that tends to when . To evaluate the first term, we need to know the round-trip time to within an arbitrary proportionality factor, and an integration must be performed in that case.
In order to write the above expression in terms of dimensionless quantities, we introduce the corpuscle rest-mass energy μ. Defining: , , , we have:
where the function depends on the round-trip time.
In the special case of non-relativistic motion , we have . The first term in Equation (6) is then equal to 3/2 (note that ), so that in the absence of gravity the internal energy U is equal to , a well-known result. More generally, we have . A plot of U from low () to high temperatures can be seen in [2]. A three-dimensional expression of U in terms of Bessel functions can be found, for example, in [12], p. 234.
4. The Energy θ is a Thermodynamic Temperature
We prove in this section that θ, introduced in previous sections on dimensional grounds only, is a thermodynamic temperature. We do this by showing that the efficiency of a reversible thermal cycle employing ideal gases is , where is the cold-bath temperature and the hot bath temperature—this is the accepted Kelvin definition of absolute temperatures.
The expressions given earlier for the average force in Equation (4) and the internal energy U in Equation (5) may be written, setting , as:
Z is essentially the quantity called in statistical mechanics the partition function. It becomes dimensionless if it is divided by the reduced Planck constant ℏ, which however plays here no physical role.
If we introduce the Helmholtz free-energy (the letter A is from the German “Arbeit” or work): the expressions in Equation (7) are conveniently written:
We have thus obtained from our simplicity principle both the force function and the internal energy function . We noticed that they follow from the partial derivations of a free-energy function that we denote (as some, but not all, authors do): . This function has exactly the same physical and mathematical content as the usual internal energy function, where S denotes the entropy, since they are related by a Legendre transform. Here is the definition. One can forget for a moment the h-variable. Given some point of the known function, we define a straight line in the plane as: , and obtain in that way (using θ as a parameter) a collection of straight lines whose envelop is the function looked for. Callen [1], for example, shows how the stability condition initially defined for the function may be transformed into two conditions on the free-energy function . Discussing this point would, however, lead us too far astray. The enthalpy follows from the same function through a Legendre transform with respect to h (rather than S). For our problem, this latter transform does not seem to bring anything new.
From Equation (8) we obtain:
where represents the heat released by the gas, from the law of conservation of energy. For any function such as : . Note that we employ only two independent variables, namely θ and h, so that partial derivatives are unambiguous. If the gas is in contact with a thermal bath (θ=constant), is the heat gained by the bath. The quantity S defined above is called “entropy”. In particular, if heat cannot go through the gas container wall (adiabatic transformation) we have , that is, according to the above result, . Thus reversible adiabatic transformations are isentropic. We have obtained an expression for the free-energy for the special case of a single corpuscle submitted to a constant force in the canonical ensemble. This free-energy function has the same physical content as the often-used energy function , or the entropy function , see [1]. The expressions following Equation (8) in this section therefore coincide with the conventional ones, applicable to any working substance, and our entropy S is the same as the one employed, e.g., in [1]. For many corpuscles, the postulate of equi-probability of the microstates may be viewed as implicit.
The Carnot cycle: A Carnot cycle consists of two isothermal transformations at temperatures and , and two intermediate reversible adiabatic transformations (). After a complete cycle, the entropy recovers its original value and therefore . According to Equation (9): , and therefore . Energy conservation gives the work performed over a cycle from: . The cycle efficiency is defined as the ratio of and the heating supplied by the hot bath. We have therefore , from which we conclude that θ is the “thermodynamic temperature”. Since Kelvin time, thermodynamics temperatures are strictly defined from Carnot (or other reversible) cycles efficiency. In practice, temperatures may be measured by other means and employed in other circumstances.
We have implicitly assumed in the above discussion that the working medium (presently an ideal gas) has reached the bath temperature before being contacted with it. Otherwise, there would be at that time a jump in entropy, and the cycle would no longer be reversible. Given initial values, the temperature change for an increment in the isentropic regime () follows from the relation: , where may be expressed in terms of , Equation (7), from the above expressions. The details will be omitted. It suffices to know that θ may be varied by varying h, in a calculable manner, in an isentropic transformation.
Practical units: The energy has been defined so far only to within a multiplicative factor from dimensional considerations. This factor is fixed by agreeing that exactly when the cylinder is in thermal equilibrium with water at its triple point. Here joules is considered as an energy unit (akin to the calorie = 4.182... joules). This manner of defining θ is equivalent to the usual one, though expressed differently. The dimensionless quantity is the usual unit of thermodynamic temperature, expressed in Kelvin.
Next, measurements have shown that the number of atoms in 0.012 kg of carbon 12 is: . For this quantity of matter (called a mole), the ideal gas law therefore reads: , or: , with the ideal gas constant: joules per Kelvin per mole.
5. Conclusions
Let us briefly recall the concepts introduced in the present paper. One can imagine that after having introduced the corpuscular concept, Democritus observed the elastic bounces of a unit weight on a balance and defined the weight “impulse” from the motion period. Not knowing the nature of the motion, he may have thought of introducing a distribution such that the average force does not depend on the law of motion. This, as we have seen, may be done. This distribution involves for dimensional reasons a quantity θ having the dimension of energy. Considering a thermal engine operating between two baths at temperatures one finds on the basis of the principles just stated that the maximum efficiency is . This allows us to call θ the thermodynamic temperature.
The present paper provides a first-principle proof of the ideal gas law, including a possible effect of uniform gravity with no knowledge of the round-trip time function being required. Our thesis is that this law may be obtained on the sole basis of the Democritus model of corpuscles and vacuum. It is indeed unnecessary to specify the law of corpuscle motion, where E denotes the energy. Explicit expressions of the internal energy are obtained provided the round-trip time is known. One can further show that the ideal-gas internal energy depends only on temperature in the absence of gravity. The theory presented is strictly classical. As such, it does not depend on the numerical value of the universal constant ℏ. However, the introduction of this quantity is needed to make the results dimensionless.
References
- Callen, H.C. Thermodynamics and an Introduction to Thermo-Statistics, 2nd ed.; Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
- Arnaud, J.; Chusseau, L.; Philippe, F. Democritus and the motive power of fire, 2011. Available online: http://arxiv.org/abs/1104.0836 (accessed on 12 December 2012).
- Arnaud, J.; Chusseau, L.; Philippe, F. On the ideal gas law, 2011. Available online: http://arxiv.org/abs/1105.2643 (accessed on 12 December 2012).
- Feyman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures in Physics, 6th ed.; Addison-Wesley: Reading, PA, USA, 1977. [Google Scholar]
- Arnaud, J.; Chusseau, L.; Philippe, F. A simple model for Carnot heat engines. Am. J. Phys. 2010, 78, 106–110. [Google Scholar] [CrossRef]
- Kaneko, H.; Tohsaki, A.; Hosaka, A. Thermodynamics of quantum ultra-cold neutron gas under gravity of the earth, 2012. Available online: http://arxiv.org/abs/1205.0378 (accessed on 12 December 2012).
- Roman, F.L.; White, J.A.; Velasco, S. Microcanonical single-particle distributions for an ideal gas in a gravitational field. Eur. J. Phys. 1995. [Google Scholar] [CrossRef]
- Thermodynamics. Available online: http://en.wikipedia.org/wiki/Thermodynamics (accessed on 12 December 20122).
- Landsberg, P.T.; Dunning-Davies, J.; Polland, D. Entropy of a column of gas under gravitation. Am. J. Phys. 1994, 62, 712–717. [Google Scholar] [CrossRef]
- Leinonen, R.; Raesaenen, E.; Asikainen, M.; Hirvonen, P.E. Students’ pre-knowledge as a guideline in the teaching of introductory thermal physics at university. Eur. J. Phys. 2009, 30, 593–604. [Google Scholar] [CrossRef]
- Louis-Martinez, D.J. Classical relativistic ideal gas in thermodynamic equilibrium in a uniformly accelerated reference frame. Class. Quantum Gravity 2011, 28, 035004. [Google Scholar] [CrossRef]
- Greiner, W.; Neise, L.; Stöcker, H. Thermodynamics and Statistical Mechanics; Springer-Verlag: New York, NY, USA, 1997. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).