Abstract
Ecosystem dynamics provides an interesting arena for the application of a plethora concepts and techniques from statistical mechanics. Here I review three examples corresponding each one to an important problem in ecology. First, I start with an analytical derivation of clumpy patterns for species relative abundances (SRA) empirically observed in several ecological communities involving a high number n of species, a phenomenon which have puzzled ecologists for decades. An interesting point is that this derivation uses results obtained from a statistical mechanics model for ferromagnets. Second, going beyond the mean field approximation, I study the spatial version of a popular ecological model involving just one species representing vegetation. The goal is to address the phenomena of catastrophic shifts—gradual cumulative variations in some control parameter that suddenly lead to an abrupt change in the system—illustrating it by means of the process of desertification of arid lands. The focus is on the aggregation processes and the effects of diffusion that combined lead to the formation of non trivial spatial vegetation patterns. It is shown that different quantities—like the variance, the two-point correlation function and the patchiness—may serve as early warnings for the desertification of arid lands. Remarkably, in the onset of a desertification transition the distribution of vegetation patches exhibits scale invariance typical of many physical systems in the vicinity a phase transition. I comment on similarities of and differences between these catastrophic shifts and paradigmatic thermodynamic phase transitions like the liquid-vapor change of state for a fluid. Third, I analyze the case of many species interacting in space. I choose tropical forests, which are mega-diverse ecosystems that exhibit remarkable dynamics. Therefore these ecosystems represent a research paradigm both for studies of complex systems dynamics as well as to unveil the mechanisms responsible for the assembly of species-rich communities. The more classical equilibrium approaches are compared versus non-equilibrium ones and in particular I discuss a recently introduced cellular automaton model in which species compete both locally in physical space and along a niche axis.
1. Introduction
Population dynamics provides an interesting field for the application of a plethora of ideas from statistical mechanics. Here I present applications of statistical mechanics concepts and techniques to three main problems in ecology in which I have been working in collaboration with different groups of ecologists: emergent neutrality or clumpiness vs. limiting similarity [1], regime shifts in ecosystems [2] and modeling of ecosystem assembly [3]. I chose these topics because I think they are examples of fruitful interdisciplinary cooperation between ecologists and physicists to report and serve as a basis to review recent developments on those fields. This special issue of Entropy on Advances in Applied Statistical Mechanics seems to be a very good place to disseminate this kind of material, contributing then to forge new connections between physics and biology by analyzing how some fascinating problems posed by biologists can be approached with tools borrowed from statistical mechanics. Before start let us mention a non exhaustive list of important recent developments that use statistical mechanics in different problems of ecology like demographic stochasticity in predator-prey systems [4,5], evolutionary ecology [6,7], population genetics [8], community assembly and species distributions [9,10,11,12,13,14,15] and complex ecological aggregates and networks [16,17,18,19,20].
Organisms in nature are discrete entities that interact only within its immediate neighborhood and therefore are neither distributed uniformly nor at random. Instead, in general, they are prone to form characteristic spatial patterns like patchy structures or gradients. This spatial variance in the environment creates diversity in communities of organisms, as well as it affects their stability, dynamics and pattern generation [21] (pp. 7–8) and [22]. However these spatial effects have been long ignored by most ecologists because of the difficulties they pose for modeling. Rather a common assumption in ecological modeling is the well mixing hypothesis or, in physics parlance, the mean-field (MF) approximation. The MF assumption is a good approximation when the physical environment is homogeneous and physical forces exist that cause strong mixing of organisms, or when organisms themselves are highly mobile, etc. As conditions depart from those above, the MF assumption becomes less and less appropriate. A lack of mixing generates neighborhoods around individuals that deviate from the spatial averages. Heterogeneity in local environmental conditions becomes especially important if organisms only interact over short distances.
Another important dimension in ecology, besides the physical space, is the abstract niche-space. Each species is thought to have a separate, unique ecological niche that describes how a population responds to the distribution of resources and competitors (e.g., by growing when resources are abundant, and when predators, parasites and pathogens are scarce) and how it in turn alters those same factors (e.g., limiting access to resources by other organisms, acting as a food source for predators and a consumer of prey) [23]. That is, the coordinates of the niche space quantify the phenotypic traits of a species which are relevant for the consumption of resources.
Figure 1 offers a schematic representation of the two dimensions mentioned above, each represented by as a coordinate axis. The ecological topics we will discuss, as well as the corresponding models to address them are represented by big dots. This diagram is intended to serve as a “road map” for the reader. Therefore, in Section 2, I start by providing an analytical derivation of an empirical observation which has puzzled ecologists for decades: the clumpy patterns over niche space for species relative abundances (SRA) in several ecological communities involving a large number n of species (along this review the acronym SRA is used to denote the set of fractions of the total population represented by each species, and this should not be confused with RSA which is commonly used in ecology to denote histograms of the number of species vs. the number of individuals for each species). An interesting fact of this derivation is that, although it is based on the MF Lotka-Volterra Competition Niche Theory (LVCNT), it uses analytical results obtained for a lattice models of magnetic materials . Since physical space is not taking into account in classical LVCNT it is marked by a red dot on the vertical axis of Figure 1.
Figure 1.
A schematic representation of the models considered in terms of two coordinate axis corresponding to physics an niche space.
As it was mentioned, in many circumstances the physical space cannot be neglected. This is the case for instance when analyzing the problems of overgrazing. Hence in Section 3, going beyond the MF approximation, I study the spatial version of a popular ecological model involving just one species representing vegetation. Actually, since what is relevant is the aggregated biomass of all coexisting grass species, this model doesn’t distinguish between grass species and treat them as a unique species. This is represented by a blue dot on the horizontal axis of Figure 1.
The main goal of Section 3 is to address the phenomena of catastrophic shifts—gradual cumulative variations in some control parameter that suddenly lead to an abrupt change in the system—and the early warnings of them provided by statistical mechanics tools. This is illustrated by means of the process of desertification of arid lands. I focus on the aggregation processes and the effects of diffusion that combined lead to the formation of non trivial spatial vegetation patterns. It is shown that different quantities from statistical mechanics—like the two-point correlation function and the patchiness—may serve as early warnings for the desertification of arid lands. Remarkably, it is found that in the onset of a desertification transition the distribution of vegetation patches exhibits scale invariance i.e., the system looks the same way at all scales and so we can zoom in or out and the picture still has the same properties. I comment on similarities of and differences between these catastrophic shifts and paradigmatic thermodynamic phase transitions like the boiling of water.
In Section 4, I analyze a community involving many species interacting in space, represented by a green dot with “coordinates” both on physical and niche axis. I choose tropical forests, which are mega-diverse ecosystems that exhibit remarkable dynamics. Therefore these ecosystems represent a research paradigm both for studies of complex systems dynamics as well as to unveil the mechanisms responsible for the assembly of species-rich communities. I compare equilibrium approaches with a recently introduced non-equilibrium approach involving cellular automata in which species compete both locally in physical space and along a niche axis.
Section 5 is devoted to draw some general conclusions and to make connections between the different topics analyzed throughout this review.
In order to make this review accessible to ecologists unfamiliar with statistical mechanics, I include at the end of each section a glossary of common terms and concepts from statistical mechanics used in that section.
2. Mean Field Competition between Many Species along a Niche Axis: Emergent Neutrality
2.1. The Lotka-Volterra Competition Model and the MacArthur-Levins Niche Overlap Formula
An important problem in ecology is that of how closely species can be packed in a natural environment or the limiting similarity problem [21] (pp. 139–171). Limiting similarity means that there is some maximum level of similarity between competing species (i.e., similar use of resources that are in short supply) beyond which no stable coexistence of them is possible. A usual way to approach this issue is by considering the species distributed along a continuum resource spectrum which can be represented by an hypothetical one-dimensional niche axis [21] (pp. 139–171). To fix ideas we can think on bird species that feed on seeds. The beak size of a bird species determines the utilization ability of resources (seeds): for a given beak size, a bird species can optimally feed on a particular size of seed, and its feeding ability drops off for seeds that depart from this size. Therefore, one may consider the niche axis as a gradient that is related to the size of organisms. Each species is numbered by an index i and is represented by a normal distribution Pi(ξ) = exp[−(ξ − μi)2/(2σi2)] centered at μi, corresponding to its mean size (i.e., its position on this niche axis ξ), and with a standard deviation σi, which measures the width of its niche. The competition for finite resources among the n species can be described by the Lotka-Volterra competition (LVC) equations:
where Ni is the population size of species i, ri is its maximum per capita growth rate, Ki is the carrying capacity of species i (the asymptotic population size it reaches when isolated from the other competing species) and the coefficient αij is the coefficient of competition between species i and j. A measure of the intensity of this competition is provided by their niche overlap, i.e., the overlapping between Pi(ξ) and Pj(ξ). The rationale is that species that are far apart in the niche axis will interact less strongly than those that are closer, and that species with narrower niches will compete with less species than those with wider niches. Therefore the competition coefficients αij can be computed by the MacArthur-Levins niche overlap (MLNO) formula [24]:
and this combination of LVC in Equation (1) with MLNO in Equation (2) results in the Lotka-Volterra Competition Niche Theory (LVCNT). Simulations of LVCNT equations yielded long transients of clumpy distributions of species along the niche axis [25] (see Figure 3 and Figure 4). This phenomenon of spontaneous emergence of self-organized clusters of look-alikes separated by gaps with no survivors was dubbed emergent neutrality (EN). It was recognized as an important new finding in an established model in ecology [26,27] since there is empirical evidence for self-organized coexistence of similar species in communities ranging from mammal [28] and bird communities [29] to plankton [30,31].
However, it wasn’t clear whether this lumpy distribution of species was an artifact of the simulations or either if it was a robust result or it depends strongly on details of the model. In this section I show that the lumpy pattern is a robust phenomenon provided one takes into account the finiteness of the niche axis. Thus, truncation, besides being a realistic assumption which warrants clustering, allows the analytical computation of the eigenvalues and eigenvectors of the competition matrix α with elements αij given by Equation (2). Furthermore, I show that ultimately solving the linear problem is enough to get both the transient pattern for SRA—clumps and gaps between them—as well as the asymptotic equilibrium.
Since an analytic solution for realistic conditions—species randomly distributed along a finite and non-periodic niche axis, each with a different ri, Ki and σi—is not possible, I consider in Section 2.2 a series of simplifications. This simplifying assumptions allow to obtain an analytic expression for SRA, in terms of the dominant eigenvector of α, which provides a qualitatively good description of the system for not too short times and becomes quite good for asymptotic times [32]. Using simulations it can be shown that all these simplifications do not destroy EN: clumps and gaps for SRA remain in the case of a finite linear niche axis no matter whether the niche is non-periodic (i.e., it has borders), or the species are randomly distributed, or when r, K and σ change from species to species [33]. Indeed LVCNT with heterogeneous species-dependent parameters is able to predict quite well the number of lumps for several different ecosystems [30,31,33,34].
A main connection of all this with statistical mechanics relies on the formal equivalence of the simplified ecological model of Section 2.2 with a lattice model for magnetic materials [35,36] (see Box 1). A goal of this review is to remark these formal analogies between problems in ecology and statistical mechanics. Firstly for a methodological reason, since reformulating ecological problems as statistical mechanics ones opens the possibility of using powerful computational techniques developed in statistical mechanics. Secondly, because recognizing that problems that emerged in completely different fields can be formulated as the same mathematical problem would serve to attract scientists from these fields to work together into multidisciplinary collaborations bringing complementary expertise.
2.2. An Analytical Proof of Self-Organized Similarity in a Simplified Case
We start by considering the following simplifications:
- S1. The n species are evenly distributed along a finite niche axis of length L = 1, i.e., their mean sizes are given by μi = (i − 1)/n (i = 1, ..., n).
- S2. To avoid border effects, the niche is defined as circular, i.e., periodic boundary conditions (PBC) are imposed. This is done by just taking the smallest of |μi − μj| and 1 − |μi − μj| as the distance between the niche centers.
- S3. All species have the same niche width: σi = σ ∀i.
- S4. All species have the same per capita growth rate which we take equal to 1: ri = 1 ∀i.
- S5. All species have the same carrying capacity: Ki = K ∀i.
Under the above simplifying conditions the system of Equations (1) reduces to:
where xi = Ni/K. Conditions S1 to S3 allow to write the competition coefficients αij as:
where the upper “circle” denotes that the niche axis is circular i.e., = min{|μi − μj|, 1 − |μi − μj|} and = min{|i − j|, n − |i − j|} and α = . Therefore α becomes a “circulant” matrix [37] whose rows are cyclic permutations of the first one:
An equilibrium of the system in Equation (3) is specified by a set of densities xi* verifying = 0. Linear stability analysis for this equilibrium starts by considering initially small disturbances yi(0) from the equilibrium values xi* and to study their fate as the time grows. Let us take xi* = x* ∀ i which, by virtue of conditions S1 and S2, is an exact equilibrium. The evolution equation for yi(t) can then be written as:
Since the coefficients αij are symmetric, in the eigenvector basis {vi} it becomes diagonal with all its eigenvalues λi real. Hence integrating Equation (6), and using that yi(0) is small, yi(t) can be approximated by:
Thus, for asymptotic times, y becomes proportional to the dominant eigenvector vm, the one associated with the minimum eigenvalue of α, λm, i.e.,
y(t) ∝ e−x*λmt vm (for large times)
I will show that, for most of the range of parameters n and σ, λm(n,σ) is negative (see below). Hence, from Equation (8), y is amplified over time instead of decaying to zero (as it would happen in the case of a positive λm). Therefore, for large times, Equation (8) implies that we can express the time derivative of x as:
and by integration we get the approximated solution given by:
dx/dt = −x(t)λmvm
x(t) ≈ exp (−λmvm t) (for large times)
It turns out that analytic expressions for the eigenvalues and eigenvectors of α are not known in general. However, for the simpler case of circulant matrices we have [35,37]:
From Equations (11) and (12) one can see that, except for k = 1 and k = n/2 + 1, the eigenvalues come in pairs: λn − k + 2 = λk, one corresponding to the sine and the other to the cosine eigenvector. Equation (11) can be used to find numerically the index k = m with the minimal eigenvalue λm(n,σ) (as we have just seen, k = n − m + 2 has the same value). The specific value of this index m is important since, as turns out from Equation (12), the corresponding dominant eigenvector vm has m − 1 peaks and m − 1 valleys.
The minimal eigenvalue λm was determined from Equation (11) from a grid of values of n and σ: 2 ≤ N ≤ 200, and 0.05 ≤ σ ≤ 0.5. The surface depicted in Figure 2 corresponds to λm(n,σ), showing that λm is negative except for small values of n (n < 8) or when σ is below a critical value σc which is approximately 0.075. This means that for higher values of n the equilibrium in which all species have the same biomass is not stable, implying that a pattern can be formed.
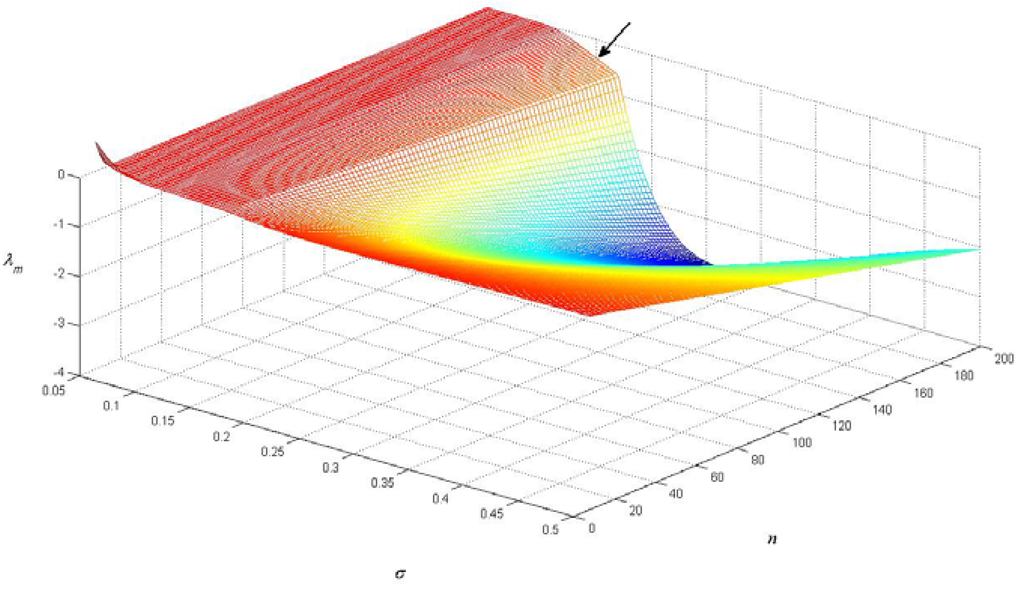
Figure 2.
The minimal eigenvalue λm, determined from Equation (11), as a function of n and σ. The arrow denotes the point n = 200 and σ = 0.15.
The dominant eigenvector vm can also be used to predict the species distribution in time, using Equation (10). In Figure 3 we can see that the clumps and gaps in SRA coincide, respectively, with the m − 1 peaks and valleys of vm.
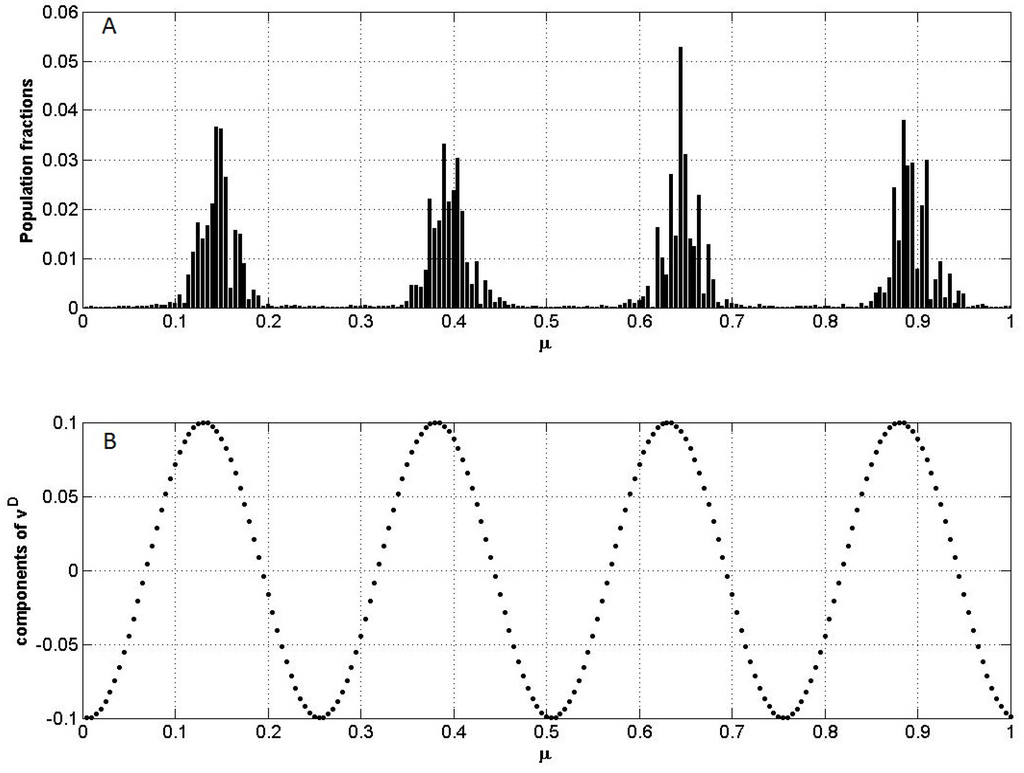
Figure 3.
The coincidence of lumps and gaps of species relative abundances (SRA) with, respectively, the peaks and valleys of the dominant eigenvector for n = 200 and σ = 0.15. (A) Results from numerical integration of Equations (3), with competition coefficients given by Equation (4), after t = 1000 generations. (B) the components of the dominant eigenvector vm.
Figure 4 compares this linearized model in Equation (10) with simulations. For instance, if n = 200 and σ = 0.15, we get m = 5 (and m = 200 − 5 + 2 = 197), and then λm = −0.3938 and is either sin(8πμj)/10 or cos(8πμj)/10. Panel (A) of Figure 4 is a plot of a typical population distribution, produced by simulation, for t = 1000 generations and the expected biomass based on the dominant eigenvector = cos(8πμj)/10 substituted in the linearized model Equation (10). Notice that the agreement is quite good and that the quality of the agreement improves with time (Figure 4B), until it becomes very good when the lumps are thinned to single lines.
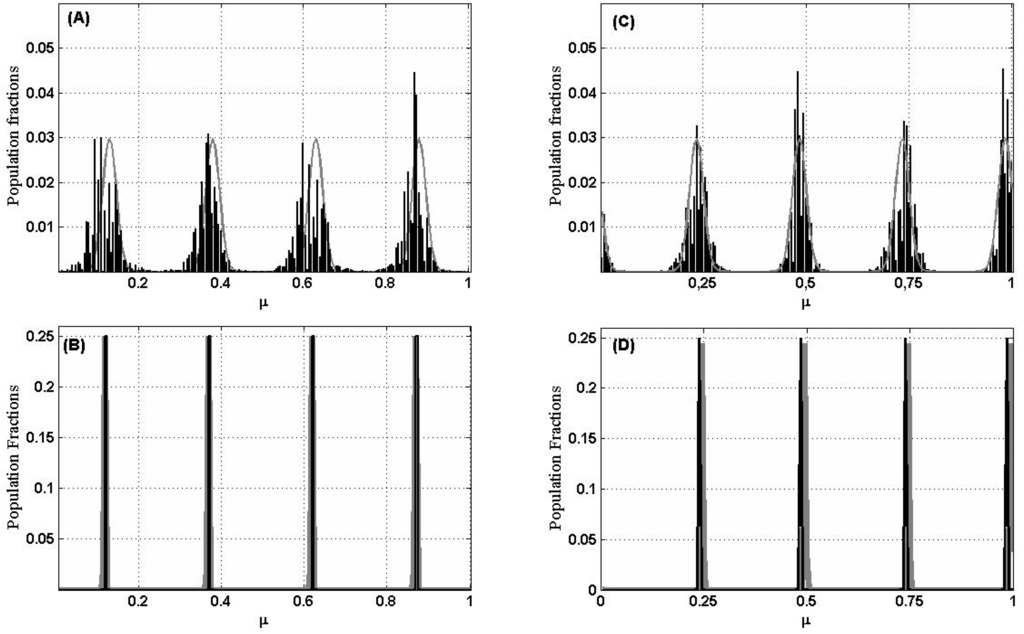
Figure 4.
Distribution of species for n = 200 and σ = 0.15. In black results from a simulation after t generations and in gray exp[λmvmt]. (A,B): Species evenly spaced along the niche axis for t = 1000 and t = 10,000 generations, respectively. (C,D): Species randomly distributed along the niche axis for t = 1000 and t = 10,000. (vm is obtained now numerically from the matrix α).
For other values of σ the number of clumps (or gaps) may change: the smaller σ the greater the number of lumps.
Notice that for a given n even the maximum possible number of peaks is n/2 (one half of the components of the eigenvector pointing up and the other half down).
The integer m that gives the minimal eigenvalue is only a function of the width σ of the niche, m = m(σ), and is independent from n, provided n is large (n/2 ≥ m − 1). It turns out that m is always an odd number (and then the number of clumps is even). The reason for this can be traced from the cosines appearing in Equation (11) making contributions to the eigenvalues of opposite signs: positive for odd k and negative for even k. As a consequence the number of peaks, equal to m − 1, is always even. For σ = 0.15, m − 1 = 4 for all even n ≥ 8. The number of species that survive for asymptotically long times is then given simply by:
n∞(σ) = m(σ) − 1
I conclude this section by remarking that the Hamiltonian of the lattice spherical model of ferromagnetism [35,36] is written in terms of the matrix in Equation (5) and in fact the Equations (11) and (12) for the eigenvalues and eigenvectors for circulant matrices were first derived by Berlin and Kac [35] for this statistical physics system. In the ecological realm the niche plays the role of the physical space in the model for ferromagnetism. This correspondence is pictorially represented in Box 1.
Box 1. Correspondence between niche axis and spherical ferromagnet.
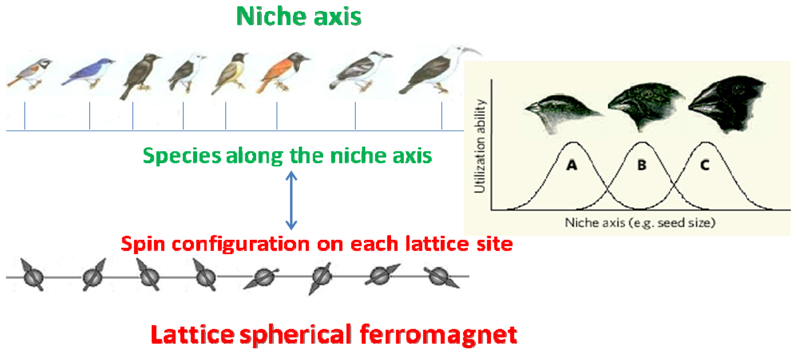
Above: Schematic representation of a niche axis for bird species.
The beak size of a bird species determines the utilization ability of resources (seeds). For a given beak size, a bird species can optimally feed on a particular size of seed, and its feeding ability drops off for seeds that depart from this size. So the intensity of the interaction between two species of birds A and B, αAB, is proportional to their niche overlap: the closer they are in size the stronger their interaction.
Below: Schematic representation of a ferromagnetic material.
A ferromagnetic material (like iron or nickel) can be regarded as a collection of spins, representing tiny magnets, located at the sites of a lattice. The intensity of the interaction between two spins Si and Sj, i.e., their interaction energy εij, is also proportional to their “overlap” or scalar product Si. Sj.
Therefore, we have the correspondence:
species i ↔ spin Si
niche position ↔ lattice position
αij ↔ εij
Glossary of statistical mechanics terms of Section 2
Ferromagnetism: The basic mechanism by which certain materials, such as iron and nickel, form permanent magnets. Microscopically the ferromagnetism is explained in terms of the electrons contained in the material. Specifically, one of the fundamental properties of an electron is that it has a magnetic dipole moment, i.e., it behaves itself as a tiny magnet. When these tiny magnetic dipoles are aligned in the same direction, their individual magnetic fields add together to create a measurable macroscopic magnetic field.
Hamiltonian: The mathematical descriptor for the energy of a given interaction. The total hamiltonian describes all energies of all the interactions that affect the system.
3. The Parallelism between a Spatial Grazing Model and Liquid-Gas Phase Transition: Metastability, Catastrophic Shifts in Ecosystems and Early Warnings [38]
3.1. Catastrophic Shifts beyond Mean Field Theory
It is generally assumed that gradual changes in external conditions such as climate, inputs of nutrients, toxic chemicals, etc. yield also gradual changes in ecosystems. However, quite often sudden catastrophic regime shifts may occur. Examples illustrating such changes are the desertification of arid lands by overgrazing [39] and lakes that shift from clear to turbid [40,41]. A simple explanation for such drastic shifts is that the ecosystem has alternative stable states (ASS) [42,43]. In other words, under the same external conditions the system can be in two or more stable states. Hence, when subjected to a slowly changing external factor (such as climate or human activities), an ecosystem may show little change until it reaches a critical point where a sudden shift to an alternative contrasting state occurs. The presence of ASS implies that if a system has gone through such a state shift, it tends to remain in the new state until the control parameter is changed back to a much lower level. This hysteresis phenomenon of “history dependent” alternative equilibrium states, which is well known in physics, make it very difficult to restore ecosystems to their original “good” equilibrium states. The identification of early warning signals that allow to predict such catastrophic events before they happen is therefore invaluable for making management decisions to avoid or mitigate them.
The simplest approach to address alternative states in ecosystems is by MF models. Neglecting all spatial heterogeneities, these models describe the change over time of some variable that characterizes the state of the ecosystem. MF models are easy to analyze and in cases without significant heterogeneity their predictions are not very different from those of spatial models. However, often spatial dimensions profoundly alter the dynamics and outcomes in the real world [44]. In fact, the oversimplification of MF models casts doubt on whether the occurrence of an alternative stable state could be an artifact. Analyzing spatially explicit models is relevant for other reasons—for example, for understanding phenomena like aggregation and spatial segregation in plant communities [45]. It was shown that vegetation patches, which have been extensively studied for arid lands [46], can be approached as a pattern formation phenomenon [47,48,49,50]. Moreover, it has been hypothesized that vegetation patchiness could be used as a signature of imminent catastrophic shifts between alternative states [51]. Evidences that the patch-size distribution of vegetation follows a power law were later found in arid Mediterranean ecosystems [52]. This implies that vegetation patches were present over a wide range of size scales, thus displaying scale invariance. It was also found that with increasing grazing pressure, the field data revealed deviations from power laws. Hence, the authors proposed that this power law behavior may be a warning signal for the onset of desertification. These spatial early warnings complement temporal ones like the variance of time series introduced to detect trophic shifts in lakes [53] or the impact of pollutants [54].
This section addresses the development of spatial early warnings of catastrophic shifts using tools and ideas borrowed from statistical mechanics. I focus on overgrazing which is one of the greatest causes of a common catastrophic shift: desertification. Worldwide, desertification is making approximately 12 million hectares useless for cultivation every year [55]. The Sahara desert appear to be advancing downward into some places of the Sahel, the semiarid region of 5000 km extending across Africa south of the Sahara desert, at the rate of 18 feet per hour due to overgrazing [56]. I start by introducing the spatial version of a general ecological model in terms of a logistically growing species whose consumption, loss or removal (either by grazing, predation or harvesting) is represented by a saturation curve [57,58]. The MF version of this model, in terms of two parameters, is known to have ASS. In order to take into account the spatial heterogeneity of the landscape, one of the two parameters, the local parameter, is taken as dependent on the position and constant in time. The other parameter, the global or control parameter, is taken as uniform throughout the system and changing slowly with time.
Our goal is to use this framework to address in this section the following questions:
- (i)
- How spatial heterogeneity of the environment and diffusion of matter and organisms affects the existence of alternative stable states.
- (ii)
- Whether emergent characteristic spatial patterns are really useful as early warnings and how they are connected with temporal signs of catastrophic shifts.
- (iii)
- The search for scaling laws underlying spatial patterns and self-organization.
Another goal is to show how the desertification transition can be connected with one of the most widely analyzed phase transition in physics: the boiling of a liquid. I do this by mapping this model into the simplest state equation able to account for the liquid-vapor phase transition, the van der Waals equation of state. This in turn allow us to analyze the above questions by measuring typical observables of statistical mechanics, like the spatial variance, the two-point correlation function and the patchiness.
3.2. The Mean Field Ecological Model
Our starting point is the population model introduced to describe grazing systems [57] and later used in general for several ecosystems [58] and in particular for the case of the spruce budworm [59,60]. It involves the total grass biomass density X which evolves in time according to:
where r is the intrinsic per capita growth rate, K is the carrying capacity or the number of individuals which can be supported in a given area within natural resource limits, c is the maximum consumption rate or grazing pressure (the stress on plant populations due to the grazing of animals) and h is a half-saturation constant, i.e., it corresponds to the value of X such that the effective consumption is half of the maximum consumption rate. We can rewrite Equation (14) in terms of non-dimensional quantities: t’ = rt, X’ = X/h, K’ = K/h and c’ = c/(hr), as:
In what follows, for simplicity, we will omit the primes for the non-dimensional variables. The right hand side (rhs) of Equation (15) may be thought of as the gradient of a potential V associated with the problem:
such that the equilibria correspond to the roots of the first derivative of V:
This equation has one or three real roots (besides the trivial unstable solution X = 0), corresponding to one stable equilibrium state or two alternative stable states (separated by an unstable one). I want to remark that the presence of ASS is linked to the functional form assumed for the density dependent consumption. This can be modeled by different consumption functions, being the most popular: linear (or Holling type I), hyperbolic (or Holling type II) and sigmoidal (or Holling type III) [61]. Only for the sigmoidal consumption of Equation (14) there occur two stable equilibria separated by an unstable one and therefore do we have ASS.
In Figure 5 the response curves obtained from Equation (17) for different values of K are depicted. For K ≤ Kc = 33/2 ≅ 5.196 only one stable solution exists for each c. As long as we consider quasi-stationary evolution for increasing c, the system will exhibit a smooth response. On the other hand, for K > Kc, the response curve is folded backwards at two saddle-node bifurcation points. For certain values of c the system can be found either in the upper or the lower stable branch. If the system starts on the upper branch and c increases slowly, X will vary smoothly until a threshold value is found, where a catastrophic transition to the lower branch occurs. If at this point we want to reverse this transition by decreasing c, the system would not be able to recover its original state. Instead, the system would remain on the lower branch, until we decrease c enough to reach another threshold value and “jump” to the upper branch. From an ecological management viewpoint, it would be desirable to anticipate these transitions.
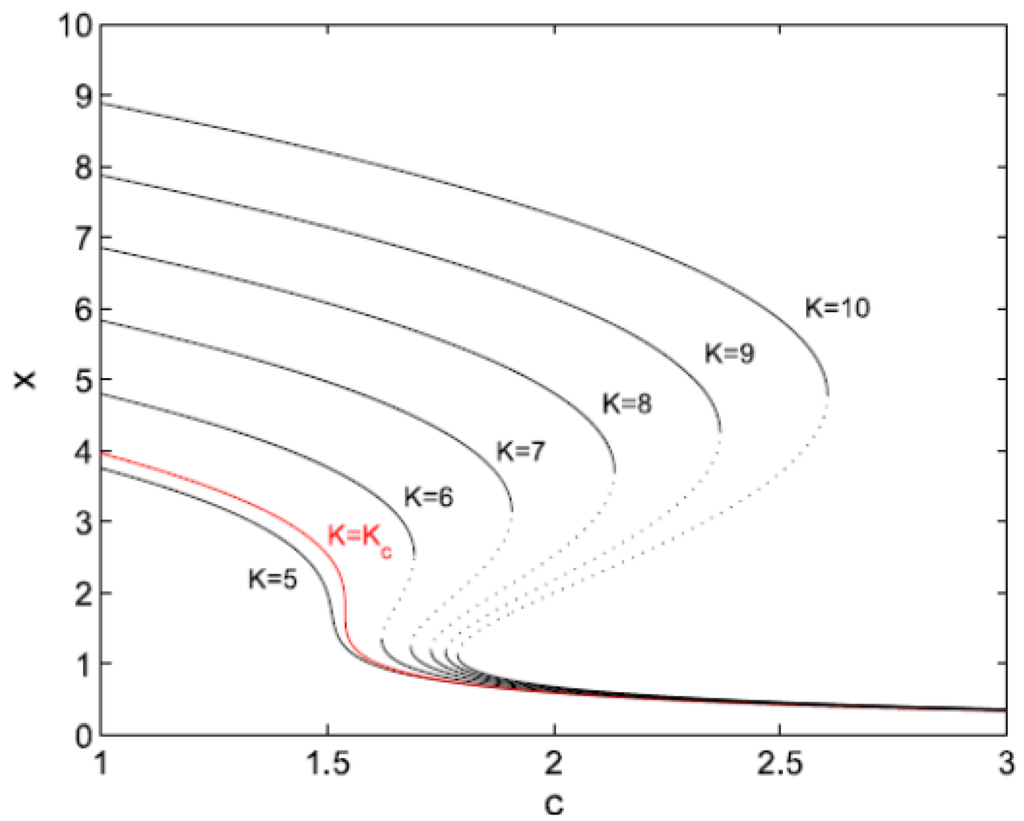
Figure 5.
Folding diagrams for different values of K.
A general formalism for treating these catastrophic regime shifts is the elementary catastrophe theory (ECT) developed by Thom [62]. However, ECT works for static and homogeneous (MF) systems, where there is no time or spatial dependence of the potential. To discuss dynamics or local properties, ECT must be extended by incorporating some external assumptions. A change of the control parameter, reflecting changes of the external conditions, modifies the form of the potential. Therefore, as the shape of the potential changes, an original global minimum in which the system sits may become a metastable local minimum because another minimum assumes a lower value, or it may even disappear. In this case the system must jump from the original global minimum to the new one. ECT does not tell us when, and to which minimum, the jump occurs. The criterion which determines this is called a convention. Before discussing conventions we need to introduce two important sets of points in parameter space which control structural changes of the potential.
The first such set of points is the bifurcation set SB [63], the locus of the points (c,K) such that the second derivative of the potential V vanishes and then an attractor pops out or in. It divides the phase space into two regions corresponding either to single stability or bistability of the system (see Figure 6).
The second set of points is called the Maxwell set SM [63]. On the Maxwell set the values of V at two or more stable equilibria are equal (see the inset of V for K = 7.5, c = 1.91 in Figure 6).
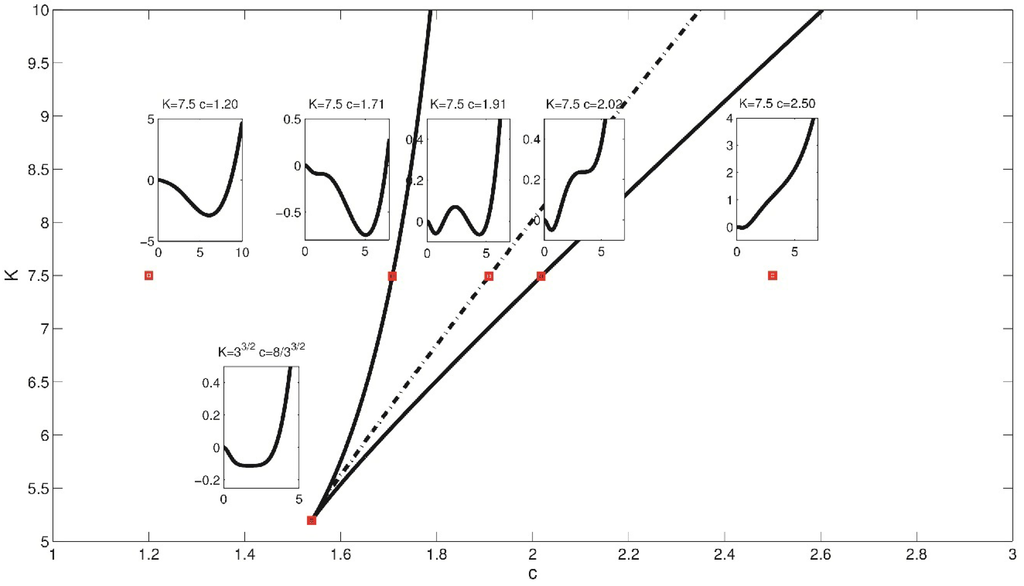
Figure 6.
Bifurcation set (solid line) with a cusp point at c = 8/33/2, K = Kc and the Maxwell set (dashed). The potential V is shown for selected values of c and K.
SB and SM are connected to two commonly applied criteria or conventions. Systems which remain in the equilibrium that they are in until it disappears are said to obey the delay convention. On the other hand, systems which always seek a global minimum of V are said to obey the Maxwell convention. Indeed these two conventions correspond to two extremes in a continuum of possibilities. Furthermore, real systems may obey either of these two conventions depending on the rate of change of the control parameters or on other external conditions. When the control parameters, and so also the shape of V, change very slowly the system tends to follow the delay convention. In contrast, when the control parameters change more quickly or when perturbations on the system are big enough, the Maxwell convention describes the dynamics better (more on this below).
3.3. Spatial Model
A two-dimensional continuum spatial version of the previous mean-field model is given by
where the carrying capacity K(x, y) is a spatial heterogeneous parameter that varies from point to point (while the parameter c is taken as uniform) and D is the diffusion coefficient measuring dispersion of X in space (given in units of the intrinsic growth rate 1/r from Equation (14)). To simulate this model we discretize the system in a L × L regular square lattice of spacing a, so each cell, centered at integer coordinates (i, j), can be associated with a patch of the ecosystem. This resulting cellular automaton (CA) is defined in terms of a von Neumann neighborhood, i.e., each cell is connected to its four nearest neighbors, and periodic boundary conditions (PBC) with L ranging from 100 to 800 (in fact, for different values of L in this range, no important differences were found). The number of time steps is typically 1000.
The ranges of values for the parameters that we use are chosen to contain the region of alternative stable states determined by the MF equations: the carrying capacity K(i, j) varies randomly from cell to cell around a fixed spatial mean <K> = 7.5 in the interval [−δK, δK] where δK = 1.0–2.5. Typical values for the consumption rate c are between 1 and 3 and for d, a reduced diffusion coefficient related to D and the lattice spacing a by d = 4D/a2 are between 0.1 and 0.5.
Several quantities can be measured from the time series produced by the model:
- The spatial mean <X(t)>:
- The spatial variance σ2X:
- The temporal variance σ2t, computed from mean values of X at different times, which is defined as:for temporal bins of size τ (typical values for τ are from 50 to 150).
- The patchiness or cluster structure. Clusters of high (low) X are defined as connected regions of cells with X(i, j, t) > Xm (X(i, j, t) < Xm) where Xm is a threshold value. There are different criteria for defining Xm (see below).
- The two-point correlation function for pairs of cells at (i1, j1) and (i2, j2), separated by a given distance R, which is given by:G2(R) = <X(i1, j1)X(i2, j2)> − <X(i1, j1)><X(i2, j2)>
3.4. Alternative Stable States and Early Warnings
Let us now study the effect of gradually increasing stress on the system, varying c from 1 to 3 in steps of 2/1000. It is important to emphasize that we do not let the system “thermalize”, i.e., each measure is performed for a different value of the control parameter c.
We will see that some characteristics of the spatial structure may serve as early warnings of catastrophic shifts of the system.
- Mean and Variances
Figure 7 presents <X>, σ2X and σ2t in terms of increasing c with <K> = 7.5, d = 0.1 and the initial condition for each X(i, j) in the interval [0, <K>]. The position of the peak for the spatial variance, cm ≅ 2.08, is earlier than the position of the peak for the temporal variance in nearly 110 time steps. So σ2X works better than σ2t as a warning signal for the upcoming transition. The reason for this is clear. When estimating the temporal variance one must consider past values in the time series, which correspond to situations where the ecosystem is far from undergoing a transition. The spatial variance considers only the present values, hence a signal announcing the shift is not blurred by averages including situations where these indications are absent. However, notice that when the peak in σ2X occurs, <X> has already experienced a decrement of almost 50% over its initial value.
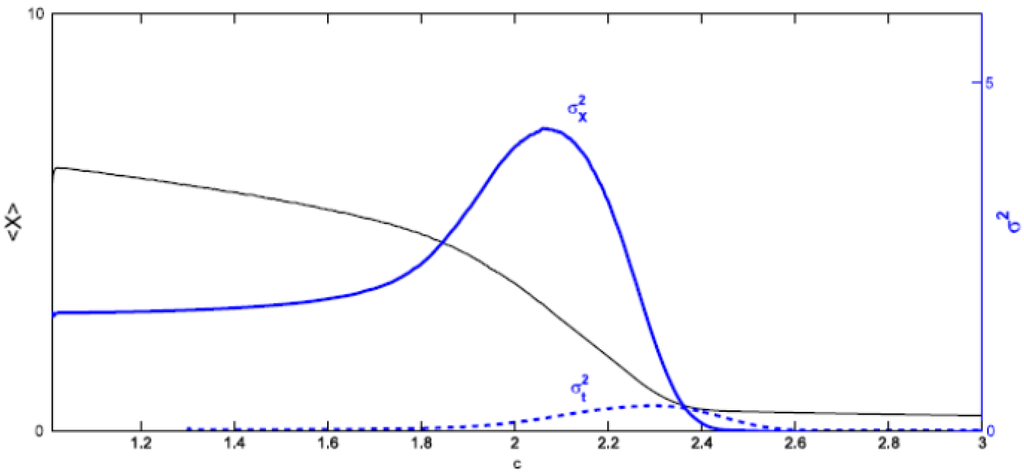
Figure 7.
<X>, σ2X and σ2t for d = 0.1, <K> = 7.5. The peak of σ2X occurs at cm ≅ 2.08 and the peak of σ2t at c ≅ 2.30.
So far we have studied the shift for increasing c. Let us see what happens when c is decreased. In Figure 8 the hysteresis cycles, yielded by these backward shifts, are shown for different values of d. We observe two remarkable things. First, the peak in σ2X is always narrower for the backward transition than for the forward transition. Second, the width of the hysteresis loop decreases with d, so diffusion tends to make the transition more abrupt.
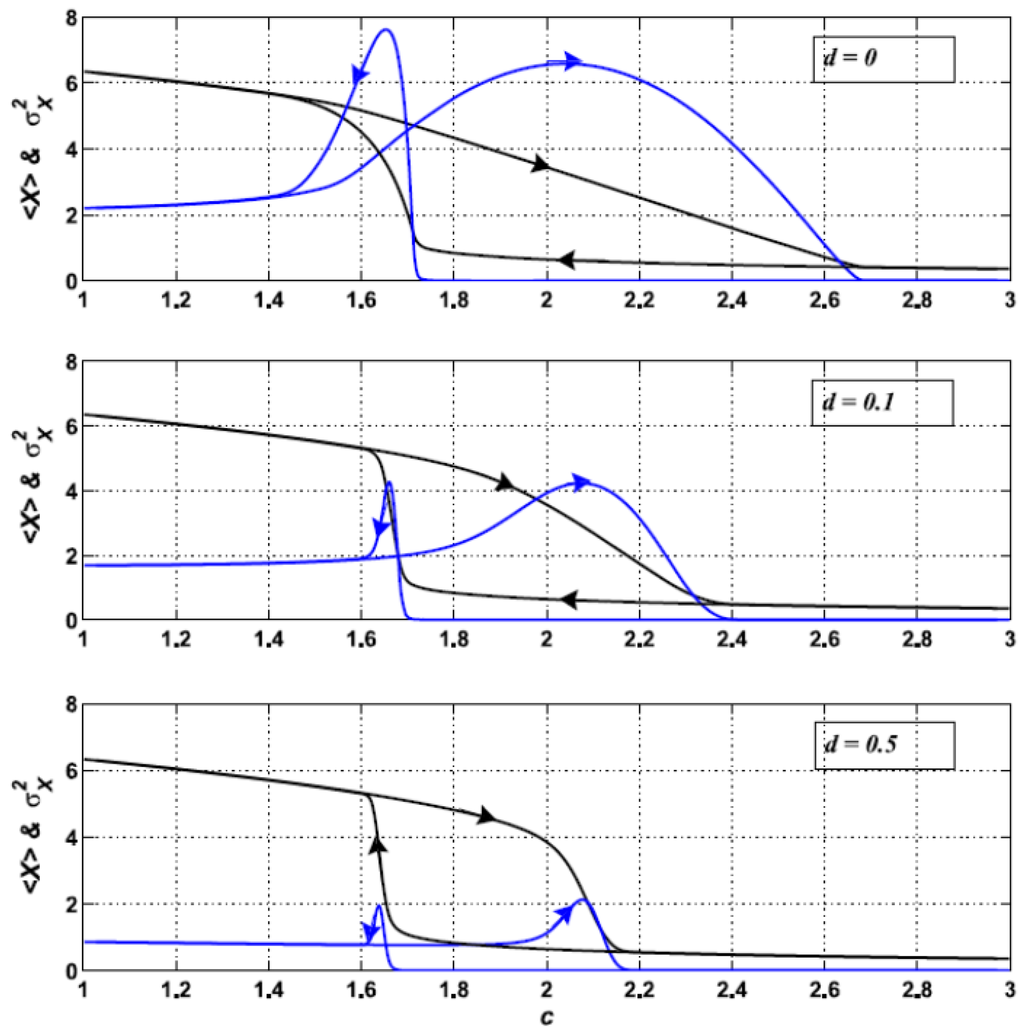
Figure 8.
<X> (black curves) and σ2X (blue curves) for <K> = 7.5 and δK = 2.5, computed for forward and backward changes of the control parameter c. Results for d = 0 (above), d = 0.1 (middle) and d = 0.5 (below).
- Correlation Function
The spatial variance is a particular case (R = 0) of the two-point correlation function in Equation (22). In Figure 9 the two-point correlation is depicted for R = 0, 1, 2, 3 (R is measured along rows or columns of the matrix array of system’s cells). Notice that the peak of the correlation for any R occurs at nearly the same value of the control parameter c ≈ cm = 2.08.
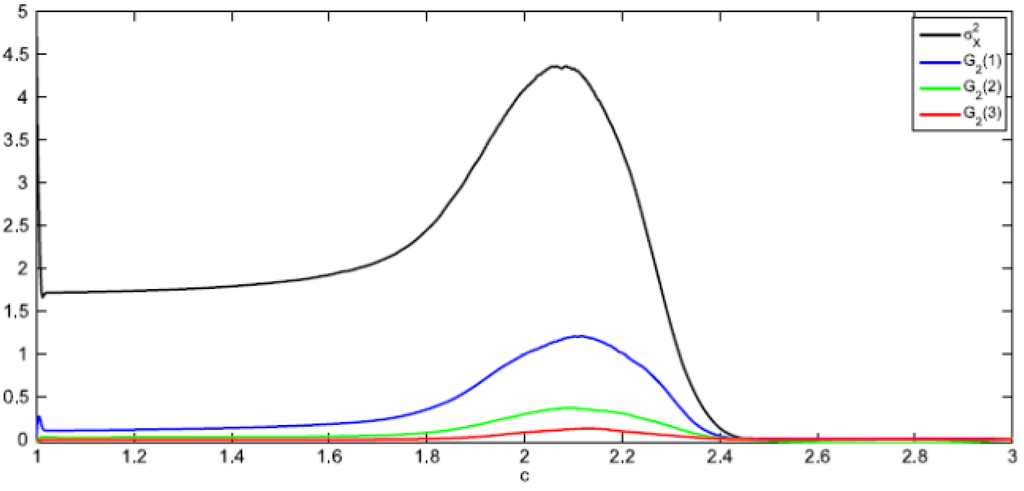
Figure 9.
Two-point correlation function for different lengths R, d = 0.1, <K> = 7.5.
- Patchiness: Cluster Structure
In order to study the cluster structure we must define a threshold Xm as a reference for the grid values X(i, j). For <K> = 7.5 and d = 0.1 the maximum in σ2X is given at cm ≅ 2.08 (Figure 7). The value of <X> corresponding to cm is <K> cm ≅ 2.89 and we will take it as the threshold. In the first column of Figure 10 we include snapshots of typical patch configurations for c = cm − 0.1, c = cm and c = cm + 0.1 and in the second column a binary representation, i.e., dark red (blue) cells correspond to cells for which X > <X> cm (X << X> cm). The plots in the third column are the corresponding cluster distributions. At c = cm the patch-size distribution follows a power law over two decades—with exponent γ ≈ −1.1 for d = 0.1 and γ ≈ −0.9 for d = 0.5—which disappears for smaller or greater value of c. Therefore this particular distribution may be considered as a signature of an upcoming catastrophic shift in the system.
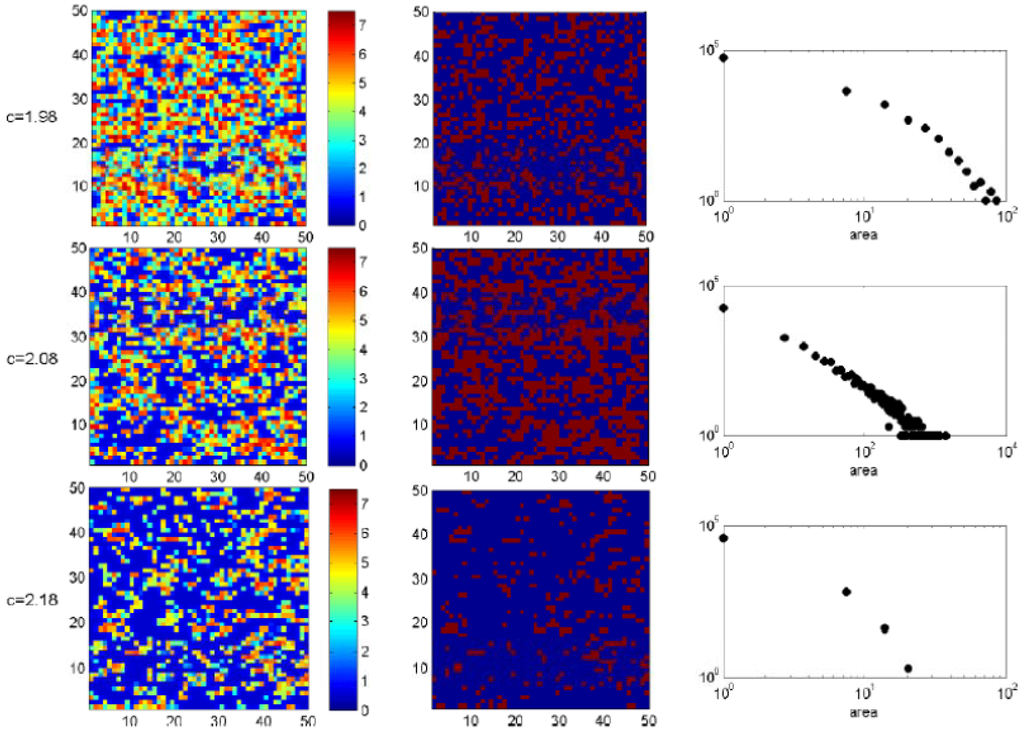
Figure 10.
First column: a portion of 50 × 50 cells from the original 800 × 800 lattice is shown, grids representing the value taken by X(i, j) at each cell for <K> = 7.5, d = 0.1. The rows correspond to c = 1.98, c = 2.08 and c = 2.18. Second column: same as the first, for binarized data (blue: cells with low vegetation density, red: cells with high vegetation density). Third column: number of clusters versus area on a logarithmic scale.
Catastrophes have characteristic fingerprints or “wave flags”. Some of the standard catastrophe flags are: modality, sudden jumps, hysteresis and a large or anomalous variance [63]. These are precisely the signals that we found for the ecological model considered, representing a species subject to exploitation (grazing, harvesting or predation). The development of methods to identify which behavior might be an appropriate signal when encountering a novel system as well as statistical methods that can distinguish between signatures of early warning behaviors and noise was recently discussed in [64].
3.5. Usefulness of the Spatial Early Warnings
To determine the usefulness of the warning indicators presented in the previous section it is necessary to assess (1) their practicality and (2) whether they really allow the implementation of corrective actions to avoid the catastrophic shift.
Calculating variances over grids consisting of a large number of sites (e.g., 400 × 400 or 800 × 800) is easy on a computer but involves a formidable task from a measuring point of view. So, in order to assess the practical difficulty of estimating σ2X, I have performed calculations over sample grids of different sizes Ls < L. In Figure 11 we observe that the signal does not depend qualitatively on the number of points on the grid that are considered for estimating σ2X.
In fact, even for a very small sample of nine points, σ2X still exhibits a noticeable peak. Of course, the quality of the signal improves with the size of the sample.
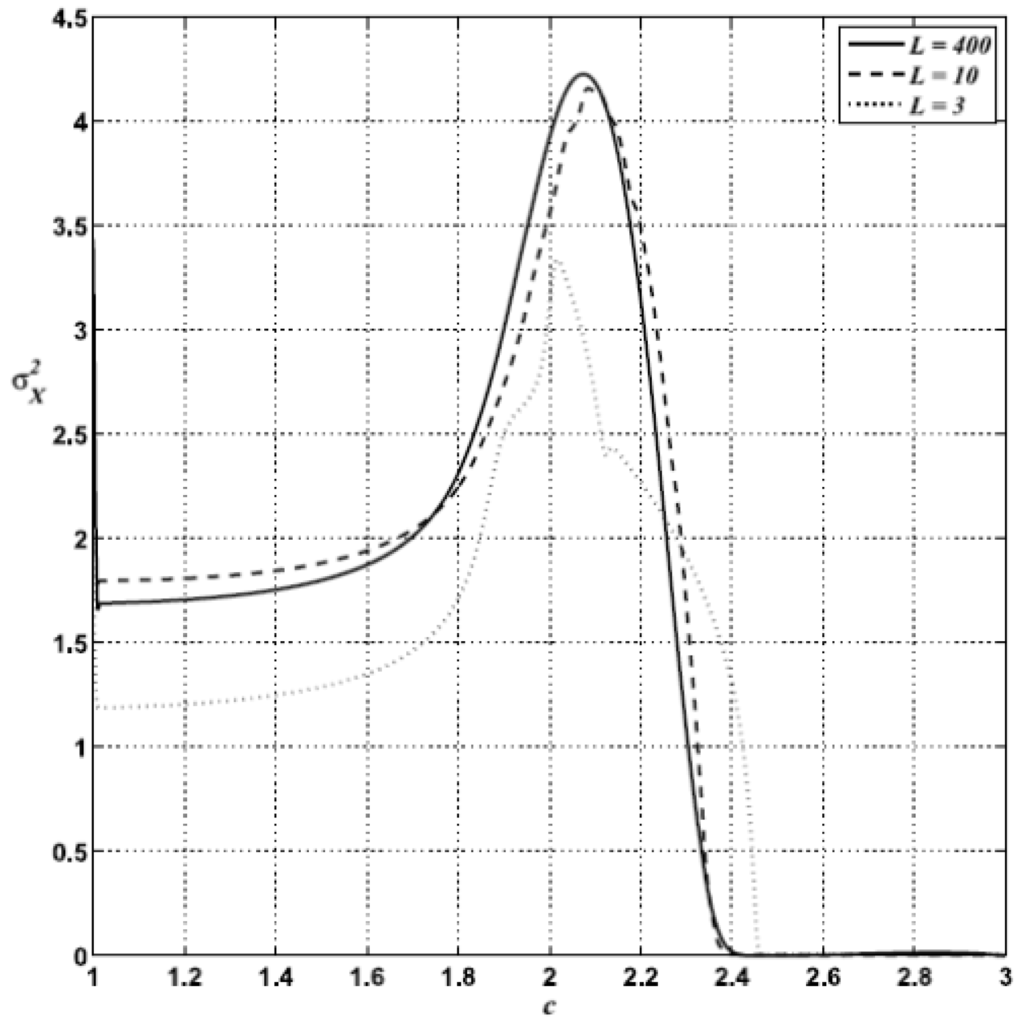
Figure 11.
σ2X for <K> = 7.5, d = 0.1 and δK = 2.5, calculated for lattices of size Ls = 3 (dotted line), 10 (dashed line) and 400 (full line).
Concerning possible remedial actions, we will study the consequences of a simple remedial action consisting in immediately stopping the increase of the control parameter after it reaches some threshold value c*. In Figure 12, I show the effect of keeping c constant at c* for different values of c* and d. For instance, if the measure is applied at the very position of the peak of σ2X, c* = cm ≅ 2.08 (for <K> = 7.5), its usefulness depends on the value of d. For d small (d = 0.1) the decay in <X(t)> stabilizes soon to a value above 2, i.e., the system remains in a mixed state.
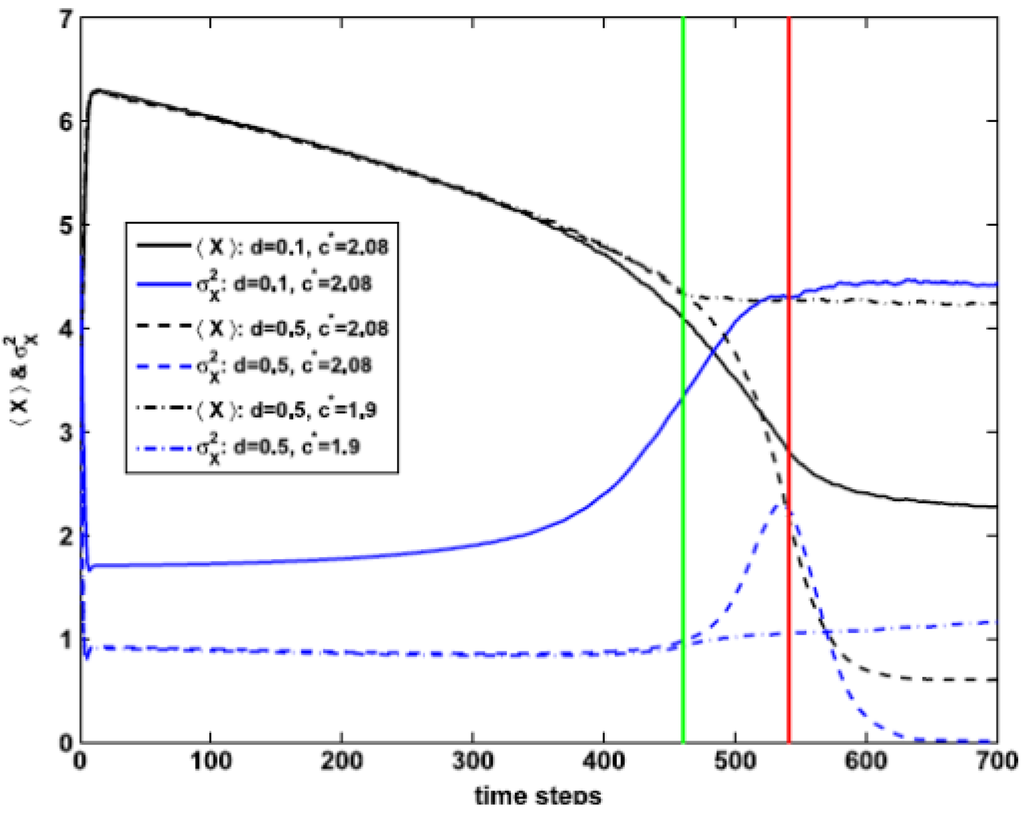
Figure 12.
<X> (black) and σ2X (blue) for <K> = 7.5 in the case of a remedial action consisting in keeping constant the control parameter after it reaches some threshold value c*. The red line indicates a threshold c* coinciding with the peak of σ2X, c* = cm ≅ 2.08. Full (dashed, dash–dotted) curves correspond to d = 0.1 (d = 0.5). The green line corresponds to a value of c* before cm, c* = 1.9.
On the other hand, for larger values of d (d = 0.5) the decay in <X(t)> continues and the ecosystem passes to the alternative state with low biomass, <X(t)> < 1. This figure also shows that, for d = 0.5, the remedial measure is effective when applied before σ2X reaches its maximum at cm, for c* = 1.9. It was checked that, for moderate or high diffusion (up to d = 0.5), this recipe of management works if c* is taken between the line corresponding to SM and the right fold line of SB (closer to the first than to the second one). So a possible criterion for choosing c* is as a point belonging to SM.
3.6. Comparison with the Boiling Phase Transition: From the Delay to the Maxwell Convention
To conclude this section it is enlightening to analyze similarities and differences for these catastrophe flags with those occurring in a liquid-vapor transition in a fluid, like water. In fact, this grazing model can be mapped into the van der Waals model since the right hand of Equation (15) is formally equivalent to the van der Waals equation of state. Indeed the non-dimensional Equation (17) for equilibrium can be mapped into a non-dimensional van der Waals equation assuming constant pressure (see Box 2). Therefore, the biomass density X would correspond to the fluid density, the liquid to the high biomass density attractor and the vapor to the low biomass density attractor. The two spinodal lines, denoting the boundary of instability of pure phases (liquid or gas) to decomposition into a liquid-gas mixture, for the van der Waals gas can then be identified with SB. Within this spinodal curve, infinitesimally small fluctuations in composition and density will lead to rapid phase separation via the mechanism known as spinodal decomposition [65]. Outside of the curve, the solution will be at least metastable with respect to fluctuations. An important remark is that this power law behavior for domains or patches exhibited as early-warning indicators in regime shifts is nothing to do with critical point phenomena. A critical point in statistical mechanics or thermodynamics occurs under conditions, such as specific values of temperature and pressure, at which no phase boundaries exist (e.g., at the critical point of water the properties of liquid and vapor become indistinguishable) and is associated with second order phase transitions. Instead, the transition here is first-order, the two distinguishable phases coexist during the transition, and this behavior arises because the ecosystem is approaching the spinodal line. That is, the transformation from one phase to another at a first-order phase transition usually occurs by a nucleation process. Nucleation near a spinodal appears to be very different from classical nucleation. Droplets appear to be fractal objects and the process of nucleation is due to the coalescence of these droplets, rather than the growth of a single one [66]. As a consequence the domain size grows with a power law for spinodal decomposition [65].
Box 2. Mapping from the grazing model to the van der Waals equation of state.
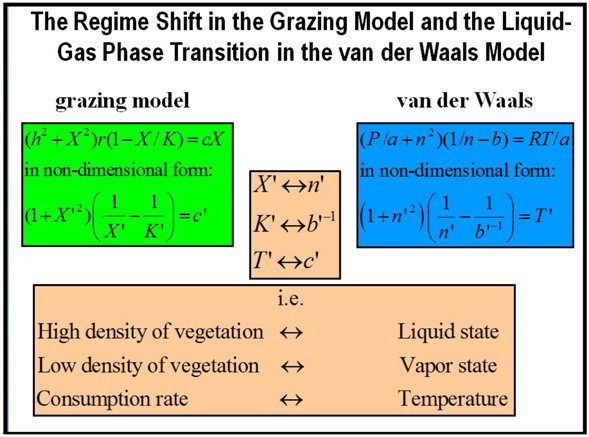
Below I compare the above mentioned signals of catastrophic shifts for both systems.
- Modality: the fluid is bimodal within the coexistence region, having well defined liquid and gas states. Hence in this aspect both systems are similar.
- Sudden jumps: in the case of the fluid it is certainly true that sudden jumps occur, since there is an abrupt increase in volume when a liquid transforms into vapor. However, this large change in volume occurs when a slight change in the temperature and pressure moves the fluid from one side of the coexistence curve to the other. Hence, the liquid-vapor coexistence curve can be identified with SM and the water changes of state obey in general the Maxwell convention. On the other hand, the shift in the ecological model considered always obeys the delay convention: the ecosystem remains in the higher attractor (higher values of X) until the bifurcation set is completely traversed. However as mentioned before that, when perturbations are big enough to allow the switching between equilibriums on different stability branches, the system may follow the Maxwell convention. Hence we will consider the effect of a sudden perturbation of the environment, represented here by a sharp decrease of the average carrying capacity <K> followed by a slow recovery. Figure 13 shows the evolution of the system for such a perturbation in <K>. Instead of remaining close to the initial attractor (upper branch of K = 7.5), the system rapidly falls to the lower branch of K = 6.0 (which corresponds to the minimum value of the potential V). Next it approaches slowly to the lower branch of K = 7.5 until it arrives at it for c ≅ 1.915. So one can conclude that this type of perturbation on the system produces a change of convention: from delay to Maxwell.
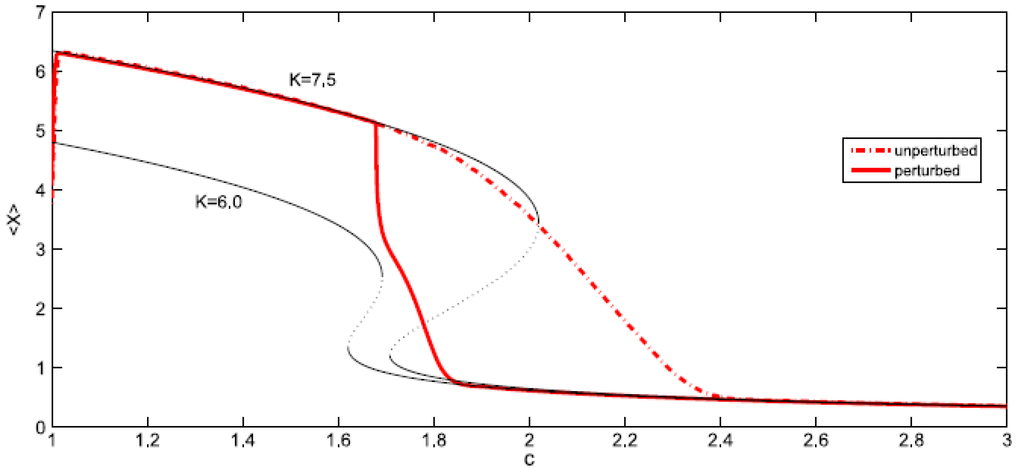 Figure 13. The effect on <X> of a global perturbation on <K> which suddenly decreases from <K> = 7.5 to 6 and slowly recovers later. Thin lines represent “iso-K” curves for K = 7.5 and K = 6.0.
Figure 13. The effect on <X> of a global perturbation on <K> which suddenly decreases from <K> = 7.5 to 6 and slowly recovers later. Thin lines represent “iso-K” curves for K = 7.5 and K = 6.0. - Hysteresis: in everyday situations one does not observe hysteresis in the liquid-gas phase transition of water—the liquid usually boils at the same temperature as the vapor condenses at. In other words, water changes of state obey in general the Maxwell convention. Nevertheless, a careful experimentalist can obtain a hysteresis cycle by first raising the temperature and superheating the liquid, and after evaporation, cooling the gas below the condensation point. Indeed the coexistence curve is surrounded by two spinodal lines which determine the limits to superheating and supersaturation. These spinodal or fold lines can then be identified with SB.
- Anomalous variance: when a fluid condenses (boils) from its gas (liquid) to its liquid (gas) state, small droplets (bubbles) are formed. As a consequence, the variance of the volume may become large, which is similar to what happens for the ecosystem. This study illustrates well that the ultimate cause of the wide variations in patch size, giving rise to scale invariance, is spatial heterogeneity both in the initial conditions and the physical environment (i.e., in K).
Glossary of Statistical Mechanics terms of Section 3
Anomalous variance: a particularly large variance at the onset of a catastrophic shift. A waving flags for such shifts is a sudden increase in the variance of certain relevant variable characterizing the state of the system (like the vegetation density).
Control parameter: a parameter whose variation controls the qualitative properties of the solutions of a differential equation.
Droplets: tiny drops formed by the condensation of a vapor or by atomization of a larger mass of liquid.
Hysteresis: is the dependence of a system not only on its current state but also on its history. This dependence arises because the system can be in more than one equilibrium state i.e., it has alternative stable states. To predict its future development, in addition to its present state, its history must be known.
The canonical example of hysteresis in physics is ferromagnetism. When an external magnetic field is applied to a ferromagnet (see Section 2) such as iron, the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. In biology there are several examples of hysteresis e.g., mitosis in cell biology, the activation of T cells that have been previously activated in immunology, the desertification of semi-arid lands in ecology, etc.
Hysteresis implies that the forward “path” described by the succession of states of a system when a control parameter (the external magnetic field in the case of ferromagnetism or the grazing pressure in desertification) increases is different from the backward path when this parameter is decreased, giving rise to an hysteresis loop.

Long Range order: characterizes physical systems in which remote portions of the same sample exhibit correlated behavior. LRO occurs for example in second order phase transitions (see below) and implies power law behavior (however the reciprocal is not true). LRO can be expressed as a correlation function or two point correlation.
Nucleation process: is the extremely localized budding of a distinct thermodynamic phase. Some examples of phases that may form by way of nucleation in liquids are gaseous bubbles (boiling) or liquid droplets (condensation) in saturated vapor.
Phase transitions: are changes of phase of some substance when the thermodynamic variables reach some critical values, e.g., the transition from liquid to gas in the boiling of water occurs at atmospheric pressure at sea level when the temperature reaches 100 °C.
Order of a phase transition: Phase transitions can be divided in two large groups. First order transitions, in which the phases are distinguishable (for instance liquid and gas have very different densities) and coexist (like boiling in ordinary conditions in which the liquid and vapor coexist) and the transition absorbs or releases energy known as latent heat (e.g., to boil water in a pan the stove provides this latent heat). In second order transitions, on the other hand, the phases are no longer distinguishable and they involve no latent heat. Long range order is an important phenomenon of second order PT.
Spinodal lines: are lines denoting, in a P-V diagram, the boundary of instability of pure phases, liquid or gas, to decomposition into a liquid-gas mixture. That is, the isotherms or lines of constant temperature in the P-V plane (blue curves) produced by the van der Waals equation have a non-physical piece, called “kink”, in which the volume V grows when the pressure is simultaneously P growing. The spinodal lines (red dotted lines) are the locus of the end points (big red dots) delimiting kinks in the van der Waals isotherms. From a mathematical point of view spinodals are the locus of bifurcations.
Turing instability: Reaction-diffusion systems are mathematical models which explain how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reactions in which the substances are transformed into each other, and diffusion which causes the substances to spread out over a surface in space. An important idea that was first proposed by Alan Turing is that a state that is stable in the local system should become unstable in the presence of diffusion.
van der Waals equation: The simplest equation of state for a gas is the ideal gas state equation relating the pressure P, the temperature T and the density of the gas n (number of moles per volume V) by P = nRT, where R is the gas constant. The ideal gas denies the interaction between molecules, which is crucial to yield a phase transition from gas to a liquid state. The van der Waals equation represents a step further since it takes into account molecular interactions and then it is able to model the liquid-gas phase transition (for example water boiling in a pan).
4. Nonequilibrium Dynamics in Cellular Automata Model for the Dynamics of Tropical Forests
A central challenge in ecology is to understand and predict the organization and spatial distribution of biodiversity using mechanistic models. Ecologists have pursued to understand the spatial distribution of species at multiple spatial scales [67,68,69], ranging from species-area relationships SAR, i.e., the number of species in a given area at a coarse scale, to the patchiness or degree of spatial aggregation of individuals of a species at a local scale. This long-lasting interest can be explained because biodiversity patterns provide critical information to grasp the forces that structure and maintain ecological diversity [70,71]. The coexistence of many species of the same trophic level with similar resource needs (and hence substantial niche overlaps) in spatially and temporally homogenous habitats has remained a puzzle in ecology [21,26,72,73]. In this section, first I review the uses of statistical mechanics in the main ecological theories for biodiversity. Next I focus on tropical forests, an example of mega-diverse and out-of-equilibrium community, from a LVCNT point of view. Since they are communities of sessile individuals, it is natural to consider that interspecific competition occurs simultaneously both in niche and physical space. This leads to the formulation of a spatially explicit or cellular automaton (CA) model. I show that this CA, based on Lotka-Volterra competition equations and using a stochastic update rule, describes quite well the biodiversity dynamics found for tropical forests.
4.1. Three Main Theories for Biodiversity—Classical, Neutral and Maxent—and the Use of Statistical Mechanics Methods
Three main alternative theories addressed the challenge posed by biodiversity. Firstly, the classical theoretical framework of ecology, in which interspecific competition is the main processes proposed to explain the main patterns of biodiversity, particularly for species that have overlapping niches because of their sharing of similar resource needs [72]. This is LVCNT introduced and discussed in Section 1. Secondly, the neutral theory of biodiversity (NTB) [74] predicts a set of biodiversity patterns from the ecological drift of functionally equivalent species with identical niches whose individuals have similar prospects of birth, death and dispersal. NTB is able to reproduce the relative species abundances (SRA), the species-area relationship (SAR) and main biodiversity indices in tropical forests with only four parameters with an accuracy and consistency that have elluded the classical niche-based theory [74]. However, NTB has been criticized for ignoring the strong evidence of functional [75] and fitness differences [76] among species. Thirdly, the maximum entropy theory of ecology (METE) [77] based upon an extremum principle. The optimized quantity is the entropy subject to constraints on macroecological “state variables” (the number of species, the total number of individuals in all those species and the total rate of metabolic energy consumed by all those individuals).
There have been important developments based on statistical mechanics for the three main biodiversity theories mentioned above. Indeed METE is an equilibrium statistical mechanics formulation for making inferences in ecology. It is based on the mathematical procedure of Maximum Information Entropy (MaxEnt), developed by Edwin T. Jaynes [78] to make predictions from incomplete information [9]. Numerous tests of METE predictions for spatial abundance distributions, and species-area relationships were presented [79,80]. In the case of NTB, a non exhaustive list of selected examples includes, the mapping of NTB into an urn model or Markovian description by means of an expansion of the master equation [81]; an analytically tractable variant of the voter model that provides quantitatively accurate two-point correlation functions, SRA and SAR in two tropical forests [82]; analytical results for the similarity function, i.e., the probability F(r) that two trees separated by a distance r belong to the same species [83]; the development of technical methods to study SAR from a spatially explicit extension of Hubbell’s neutral model [84]; an explanation of the species coexistence in terms of stochasticity and dispersal-limitation [85]; the study of spatial effects on species persistence and their implications for biodiversity [86].
Statistical mechanics methods have been used to address Lotka-Volterra general competition equations for more than forty years [87,88,89]; competition along a niche axis (see review [90] and references therein); and also there have been many different lattice Lotka-Volterra studies [91,92,93,94]. However the combination of competition simultaneously in niche and physical space, i.e., spatially explicit LVCNT models, is very recent [95,96] and will be the focus of the next subsections.
4.2. Describing Tropical Forests by the Transient Regime of Spatial LVCNT
Tropical forests are mega-diverse communities containing typically several hundreds of species of trees in 50 ha plots, i.e., as many tree species as there are in all of US and Canada combined. These permanent plots of tropical forests which have been exhaustively censused over time show three relevant facts [97]. First, the data clearly reveal that these systems are far from stationary: the Barro Colorado Island (BCI) plot (Panama) has lost 37 species in 23 years, while the Bukit Timah plot (Singapore) had an average rate of species loss of 8% between consecutive censuses [97], etc. Second, besides their non-equilibrium dynamics, the SRA for all tropical plots are very uneven: few common species and many rare species [97]. For example the 1982 census for BCI reveals that ten tree species, of a total of 320 registered species, comprise more than half of the total population of trees. Third, for all the plots for which there is more than one census, the number of coexisting species or species richness, S, always decreases from one census to the next [97].
NTB and METE, at least in their standard original form, both are static theories, focused on steady state and their theoretical predictions are typically compared with census data of large tropical forest plots viewed as snapshots [74,77]. Being systems far from equilibrium, fitting detailed snapshots of tropical forest plots can only describe transitory configurations but cannot help understand the mechanisms underlying the observed dynamics. However, it is worth mentioning that there have been developments to include dynamics for both NTB [98,99,100,101] and METE [102]. By contrast LVCNT intrinsically a dynamic theory. In section 1 we have seen that for a large initial number of species n, LVCNT is able to produce this sort of uneven SRA provided the niche width σ >> 1/n and only for the transient regime (well before equilibrium is reached). In fact the equilibrium state consists in a very small number n∞ of surviving species (e.g., n = 200, σ = 0.1 >> 0.005 = 1/n, then n∞ = 4). Therefore it seems natural to analyze non-equilibrium communities of trees through the transient regime of LVCNT. We will focus on LVCNT and its predictions for tropical forests when analyzed in the transient regime.
Another common assumption of the above three biodiversity theories (at least in their classical formulation) is the well mixing hypothesis or the mean field approximation. This assumption clearly fails for sessile individuals like trees for which there is local recruitment [103] and local competition for resources [104,105]. Therefore, incorporating the spatial setting seems crucial to describe the dynamics of tropical forest plots.
Our aim is thus to formulate a parsimonious model depicting tree competition as a local interaction whose strength depends on the degree of niche overlap between neighboring individuals. This model has to include only the minimal set of realistic biological features sufficient to accurately predict a set of commonly used biodiversity metrics. Hence we will consider a cellular automaton (CA) model with a variable, that take values on a one-dimensional axis, and who lives in a two dimensional regular lattice, representing physical space.
4.3. A Cellular Automaton Model Based on Lotka-Volterra Competition Niche Theory
All the L×L cells of the CA are occupied by one individual, representing a tree belonging to a given species s = 1, 2,...,n. The number of individuals, N = L×L, remains constant (as in the NTB [74]). The entire community is closed to migration from the outside and we consider periodic boundary conditions to avoid border effects. As in section 1, we assume the simplest one-dimensional, finite niche scaled in [0, 1] wherein the resource utilization function of each species s is defined by a normal distribution P(s) whose mean μ(s) and standard deviation σ(s) indicate the position and width of the niche of species s. The positions of the species niches were chosen by randomly drawing the values of μ from a uniform distribution at the beginning of each simulation and were not changed during the simulation. Each focal individual, located at site i, belonging to a species si only interacts with the eight neighbors of its Moore neighborhood Mi. The strength of its competition with a neighbor of species sj, αij, is proportional to the niche overlap between species si and sj. This overlap is determined by a symmetric version of MLNO Equation (2) (the symmetry of the competition coefficients is a neutral assumption in the absence of precise details of the interaction between pairs of species) for a linear niche [34]:
where μk ≡ μ(sk) and σk ≡ σ(sk). We further assume that all species were functionally and demographically equivalent by having the same niche width: σi = σ (which could be regarded as an average niche width). Hence, the fitness f(si) of a focal individual of species si located at site i is given by , where the “8” corresponds to the numbers of neighbors of i and it ensures that fi is always non-negative. Thus, f(si) has its maximum value when the focal species si has minimal overlap with its eight neighbors, and minimal when their niche overlaps are maximal. The functional equivalence between species is consistent with the chosen normalization for the αij (Equation (23)) to assure that the matrix α is symmetric.
The model contains three free parameters: the already mentioned niche width for each species, σ, plus the dispersal rate from outside of each neigborhood, m and a “temperature”, T. Both m and T introduce stochasticity in the local replacement of focal individuals in the model. The dynamics of this stochastic cellular automaton is governed by the popular Glauber update rule [106,107] for lattice models in which the following steps are repeated: (I) A focal individual of species si, located at site i, is randomly chosen (with probability 1/N); (II) This focal individual is replaced with probability m, representing the non-local dispersal of seeds by wind or animals, by another randomly chosen individual of species sk from outside its neighborhood Ωi. And with probability (1 − m)*Pr(s; si → sj) by a randomly chosen neighbor of species sj where . The probability that the focal individual si is replaced by its neighbor sj is greater as the difference between individual fitnesses f(sj) and f(si) increases. If the stochasticity parameter T = 0, then the change from si to sj is accepted if and only if f(si) < f(sj) (I analyzed this update rule for a CA simulating a more general ecological context in which in addition to mutual competition there can be mutual cooperation and competition-cooperation relationships [108]). On the other hand, for very large values of T, Pr(si → sj) approaches to ½, i.e., a totally random process.
4.3.1. Estimation of Parameters
The CA was designed to simulate the spatio-temporal dynamics of all trees of diameter at breast height (dbh) ≥ 1 cm in two large (50 ha), permanent plots of tropical forests; one at Barro Colorado Island (BCI) in Panama and the other at Passoh in Malaysia. For each analyzed plot, L was chosen in such a way that L×L is the closest multiple of ten to the maximum number of trees (with dbh ≥ 1 cm) measured along the different censuses, , while the initial number of species, n, was set equal to the species richness found for the first census, (the subscript e stands for “empirical”). For example, for BCI ( = 244,062 for 1990 and = 320 for 1982 [97]): L = 500 and n = 320.
A sequential procedure was used to estimate the adjustable parameters σ, m, and T whose values provide the best fit to the observed dynamics of the set of censuses of each forest. In contrast to equilibrium systems, for non-equilibrium systems time is an essential degree of freedom. So the question of when to stop simulations and compare with empirical data to estimate the model parameters is not trivial. There is no clear-cut or universally accepted criterion to set the number of evolution steps t. It turns out that while σ and m were enough to reproduce with accuracy the values of all biodiversity metrics found at the first census of each forest plot, T was a “fine tuning parameter” required to improve the agreement between observed and theoretical values of biodiversity metrics calculated for subsequent censuses. Therefore, for each plot, the procedure as follows.
In a first stage, using only data of the first census, σ and m were estimated. To do this an array of values in the plane σ-m, generated by varying σ in [0.05, 0.1] in steps of ∆σ = 0.001 and m in [0.02, 0.12] in steps of ∆m = 0.01, was systematically searched. As mentioned, it is unknowable a priori how many simulation steps are required to yield a configuration comparable to the one observed in the first census starting from random initial conditions. The Shannon equitability index, H = (where Ns is the abundance of species s), was used to decide when to stop simulations. That is, for each given pair (σ, m), 100 simulations (100 different initial conditions) were run until H was equal to the empirical value for the first census with an accuracy of 1%. Replacements of species having only one individual were prevented in order to constrain the CA configuration corresponding to the first census to the observed species. Among all the pairs σ-m it was chosen the one such that the coefficient of determination of the linear regression between the observed and predicted (average over the 100 simulations) RSA distributions, was the highest (in all the cases ≥ 0.95).
In a second stage, the pair of fitted values of σ and m was then used to estimate the other parameter, T. I restarted the simulation at each CA configuration corresponding to the first census now allowing species to become extinct so that the predicted forest dynamics could describe the observed changes in S for the remaining censuses of each forest. Proceeding in a similar way as before, it was systematically searched for the best fitting value of T in [0.5, 5.0] in steps of ∆T = 0.5. For each candidate value of T, the number of simulation steps between consecutive censuses for a given simulation was set whenever the absolute values of (H − )/ or (S − )/ became ≤ 0.01 (the first that was satisfied). As before, the best estimate of T was the one that predicted the highest for all censuses. We obtained the parameters summarized in Table 1.

Table 1.
CA parameters for BCI and Pasoh, values of empirical quantities (in bold) and predicted species richness.
| Forest | L | n | σ, m, T | Species richness, S | |
|---|---|---|---|---|---|
| Pasoh (Malaysia) | 580 | 823 | 0.085, 0.11, 0.5 | 0.842 | 823, 819, 811, 808 823, 821 ± 2, 815 ± 4, 808 ± 5 |
| Barro Colorado (Panamá) | 500 | 320 | 0.077, 0.10, 3.0 | 0.694 | 320, 318, 303, 299, 292, 283 320, 314 ± 4, 300 ± 5, 293 ± 6, 287 ± 7, 281 ± 7 |
In each simulation, the sequence of replacement events led to a different set of values of the biodiversity metrics. Consequently, the matching between theoretical and observed biodiversity metrics occurred after different numbers of individual replacement events in each of the 100 simulations. The average number of steps for BCI and Pasoh corresponding to consecutive censuses were, respectively, <∆tBCI> = 950,000 and <∆tPasoh> = 435,000, i.e., an approximately 2:1 relationship. A higher <∆t> for BCI than for Pasoh reflects the fact that BCI is more dynamic than Pasoh [109]. The value of <∆t> for a forest plot should be proportional to the total number of trees N (the larger the number of trees, the larger the replacement attempts needed) as well as to the fraction of species that went extinct on average between consecutive censuses ∆S (idem), and inversely proportional to the average (over censuses) number of species with one individual Σ1 (which represents the species most likely to become extinct). It turns out that NBCI ∆SBCI/Σ1BCI = 250,000 × 9.8/20.3 = 120,690 [97] while NPasoh ∆SPasoh/Σ1pasoh = 336,400 × 5.0/24.5 = 68,653 [97], which are absolutely consistent with the above 2:1 relationship.
4.4. Results and Discussion
Let’s compare model predictions with data from censuses of plots at BCI (six censuses: 1982, 1985, 1990, 1995, 2000 and 2005) and Pasoh (four censuses: 1987, 1990, 1995 and 2000) [97].
The model is able to fit the main biodiversity metrics used to characterize community structure such as SRA (Figure 14 and Figure 15) and SAR (Figure 16) with similar accuracy as NTB or METE. However, a distinctive feature of this CA competition model is its capacity to accurately predict the observed dynamics of the species richness and of the SRA for subsequent censuses to the first for these two considered plots. Most analyses of tropical forests to date have considered and predicted biodiversity metrics of consecutive censuses as independent, isolated snapshots.
The CA model can also fit and explain other biodiversity metrics related to spatial aggregation that NTB cannot. For example, it reproduces the observed tendency of rarer species to be more strongly aggregated in tropical forests, a feature that neither NTB nor METE can explain. This pattern can be easily understood in terms of local competition and is related to the result for LVCNT analyzed in Section 1: the SRA represented on the niche axis displays a pattern with clumps and gaps (Figure 17). That is, rarer species’ niches are located in the gaps between clumps in the niche space and that these species turn out to be poorer competitiors. The association between rarity and spatial aggregation arose because rare species could only avoid competitive displacement by being surrounded by either conspecifics or by species with which they had a minimal niche overlap.
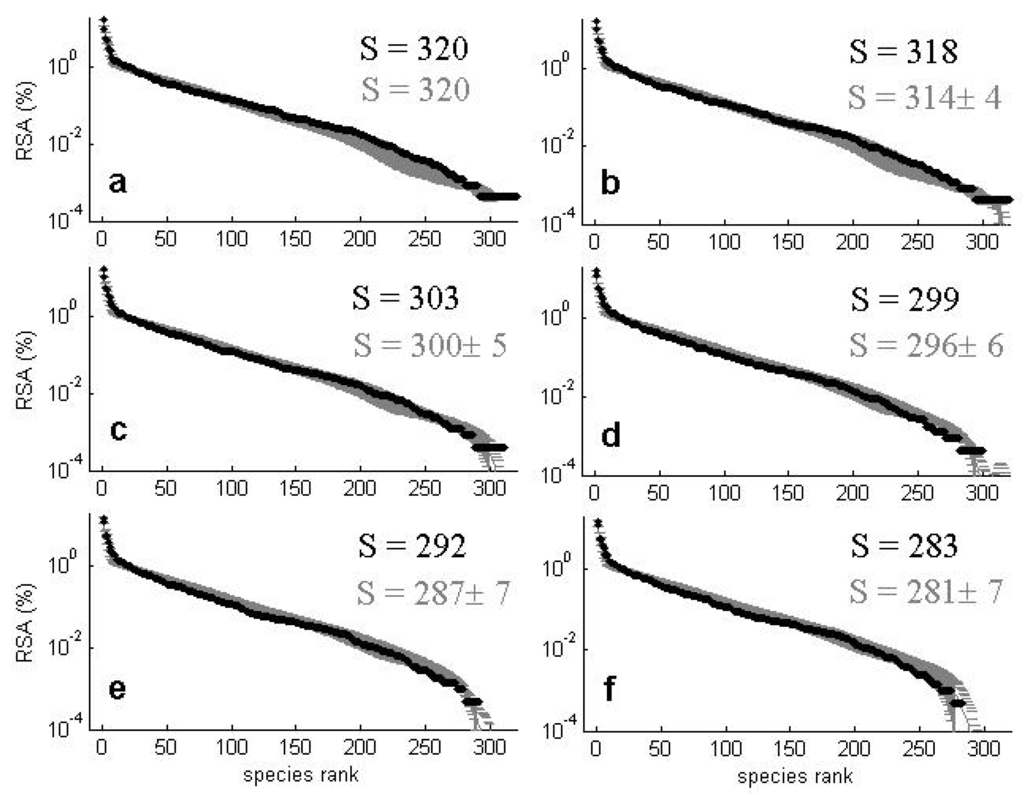
Figure 14.
Observed (black) and predicted (gray) distributions of relative species abundances (RSA): % in log scale vs. species ranked abundance for all trees with dbh ≥ 1 cm in BCI for censuses corresponding to 1982 (a), 1985 (b), 1990 (c), 1995 (d), 2000 (e) and 2005 (f). S denotes the species richness (i.e., the number of coexisting species). The predicted values correspond to averages ± std of 100 model simulations for the best estimates of model parameters.
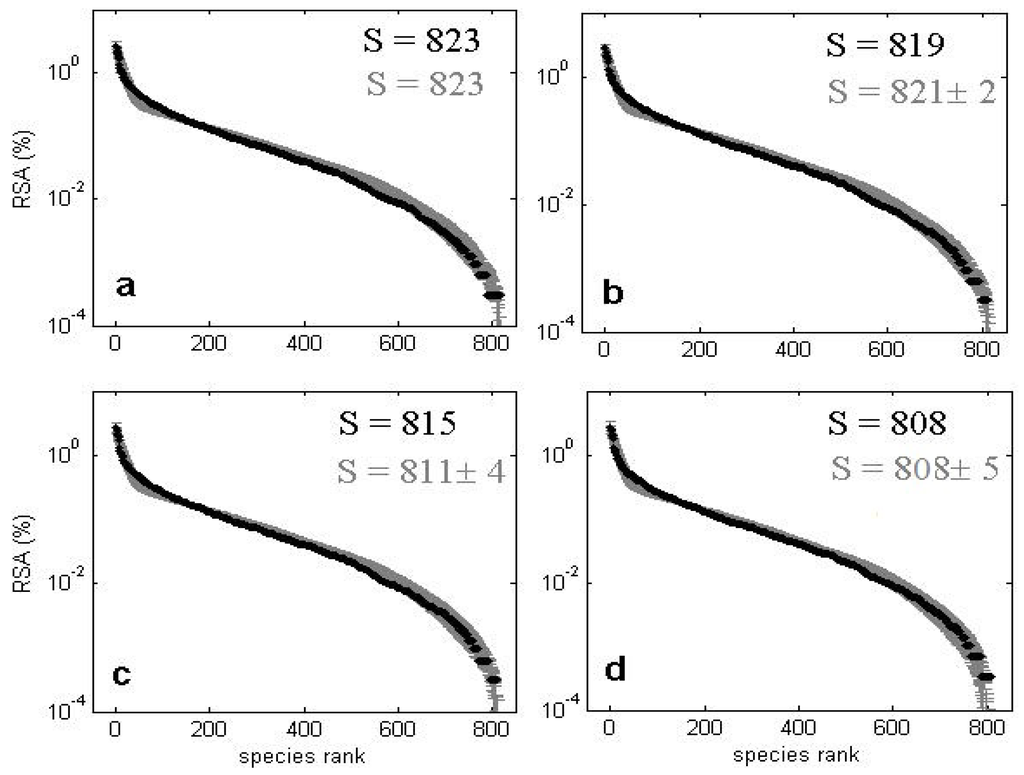
Figure 15.
Observed (black) and predicted (gray) distributions of relative species abundances (RSA): % in log scale vs. species ranked abundance for all trees with dbh ≥ 1 cm in Pasoh for censuses corresponding to 1987 (a), 1990 (b), 1995 (c) and 2000 (d). S denotes the species richness. The predicted values correspond to averages ± std of 100 model simulations for the best estimates of model parameters.
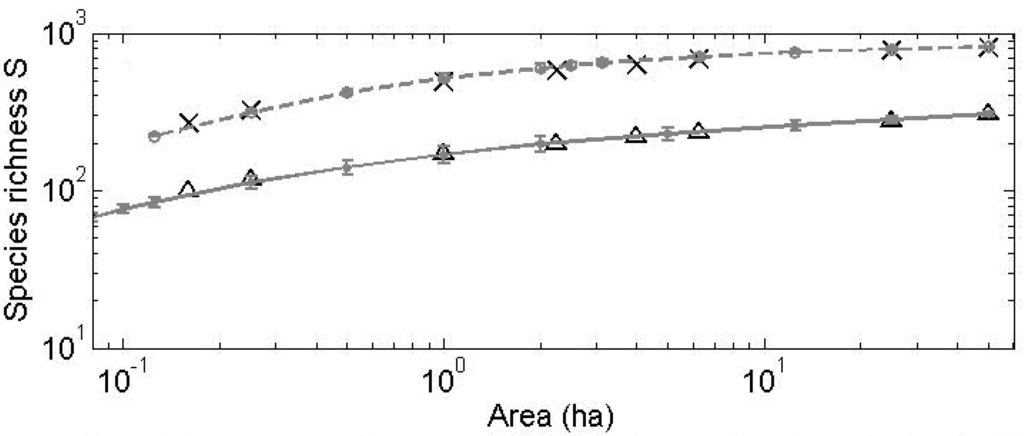
Figure 16.
Species-area relationships (SAR) and for selected censuses of tropical forests. Predicted curves correspond to averages over 100 simulations, and the error bars correspond to one std. Observed and predicted (grey line) number of tree species with dbh ≥ 1 cm for sampling areas of different sizes at BCI 1990 (∆) and Pasoh 1987 (×).
In fact we can’t know a priori the correspondence between each species and its position on the niche axis. Only after leaving the CA evolve we can attempt to map the niche axis by comparing the empirical SRA against the theoretical SRA and matching species in such a way that the theoretical most abundant species corresponds to the most abundant empirically observed, the theoretical second most abundant species corresponds to the second most abundant observed, and so on. Since the SRA are very uneven, this procedure makes sense only for the most abundant species i.e., for the great majority of species the differences in abundances are within the error bars (Figure 14 and Figure 15). In Table 2, I present the list of the ten most abundant species for BCI in the 2005 census together with the ten most abundant theoretical species and their corresponding niche position. I also include the mean and maximal dbh for these tree species [110,111,112] (rows marked in gray correspond to species with relatively low dbh). Figure 17 depicts a tentative identification of the most abundant species at the BCI plot, those belonging to the main clumps at the ends of the niche axis, using the information of Table 2. It turns out that species at the left (right) hand of the niche axis correlate quite well with trees having large (small) dbh [97,110,111,112,113]. This would suggest that the one dimensional niche axis corresponds to a growing function of the dbh of trees.
A remarkable result is that a niche width for both analyzed forest plots of σ ≈ 0.08 implies by Equation (23) that the strength of interspecific interactions is on average <αij> ≈ 0.25. Since, by construction, <αii> = 1 it means that the average interspecific competition strength is one-quarter of the intraspecific competition strength. This factor of 0.25 corresponds to an intermediate value between the extreme claims of the neutral model, where species are functionally identical and have independent dynamics i.e., <αij> = 0, and the classical niche-based model of community assembly, where interspecific competition is dominant i.e., <αij> > 1.

Table 2.
The ten most abundant species of BCI, dbh properties and the niche position according to our CA.
| Genus | Species | <dbh> (cm) * | max dbh (cm) * | Empirical Abundance ** | Theor. Abundance | Niche position |
|---|---|---|---|---|---|---|
| Hybanthus | Prunifolius | 2.24 | 8.8 | 29,846 | 31,115 | 0.008 |
| Faramea | Occidentalis | 4.54 | 23.2 | 26,038 | 29,560 | 0.998 |
| Trichilia | Tuberculata | 5.49 | 65.3 | 11,344 | 13,711 | 0.995 |
| Desmopsis | Panamensis | 2.59 | 13.1 | 11,327 | 13,152 | 0.012 |
| Alseis | Blackiana | 5.64 | 91.1 | 7,754 | 8,013 | 0.993 |
| Mouriri | Myrtilloides | 2.17 | 5.0 | 6,540 | 7,758 | 0.013 |
| Garcinia | Intermedia | 5.68 | 41.5 | 4,602 | 4,707 | 0.988 |
| Hirtella | Triandra | 4.71 | 48.3 | 4,566 | 4,193 | 0.984 |
| Tetragastris | Panamensis | 4.64 | 75.9 | 4,493 | 3,744 | 0.981 |
| Psychotria | Horizontalis | 1.77 | 6.3 | 3,119 | 3,443 | 0.021 |
Gray rows correspond to tree species with small dbh and their theoretical correlates with low niche position. *: [109,110,111], **: [96].
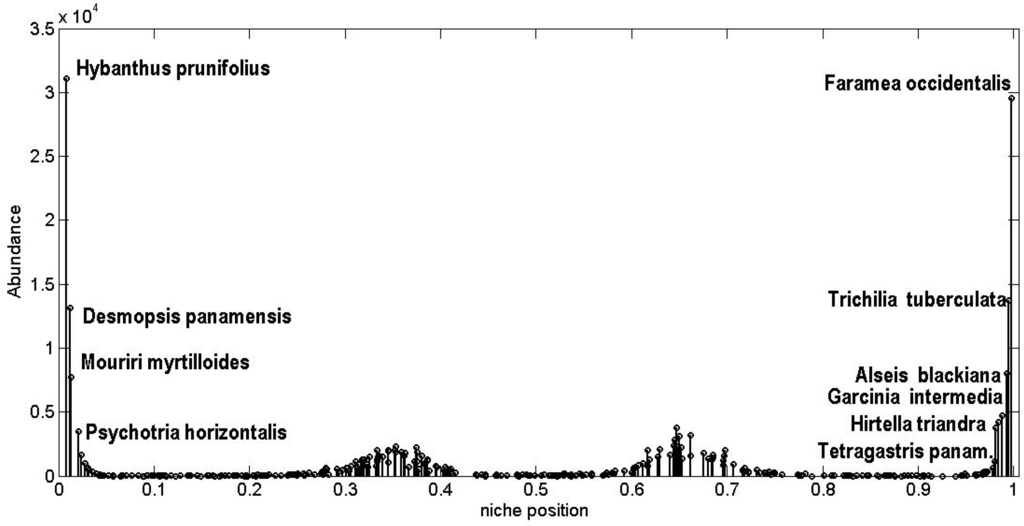
Figure 17.
An attempt to identify the most abundant species found at BCI in 2005 with it corresponding theoretical species (same ranking order) and then to locate them along the niche axis (see Table 2 ).
In the same spirit of statistical mechanics, this CA description shows that it is unnecessary to model the detailed “microscopic” dynamics in a landscape to accurately predict the aggregate, macroscopic variables characterizing the composition and dynamics of large and complex ecosystems such as tropical forests. In fact, it seems that local competitive interactions coupled with limited, stochastic dispersal can give rise to the non-equilibrium dynamics for a niche width identical to all tree species and that takes similar values for the two forests analyzed. This functional similarity among species that can be interpreted as neutrality is not a fundamental building assumption of this CA model but rather an emergent outcome [34]. This emergent neutrality may explain why many results reported here could be indistinguishable from those predicted by the NTB [114] and its CA implementations [115].
Glossary of statistical mechanics terms of Section 4
MaxEnt (maximum entropy principle): A principle that states that the probability distribution which best represents the current state of knowledge on a system is the one with maximizes its entropy subject to the constraints imposed by prior knowledge. It is based on a correspondence between statistical mechanics and information theory. The basic idea is that entropy of statistical mechanics and the information entropy of information theory are the same thing. Consequently, statistical mechanics should be seen just as a particular application of a general tool of logical inference and information theory.
Stochastic Cellular Automata: Stochastic Cellular Automata are CA whose updating rule is a stochastic one, which means the new entities’ states are chosen according to some probability distributions. They are models of “noisy” systems in which processes do not function exactly as expected, like most processes found in natural systems. Stochastic CA are discrete-time random dynamical systems.
5. Concluding Remarks
In Section 2 and Section 4 we addressed community assembling, a central issue of ecology, from a niche theory perspective. In Section 2 the analysis was general, with no reference to any specific ecological community, using the simpler MF approximation. We focused on the so-called emergent neutrality—the appearance of a clumpy pattern in niche space. In Section 4, I chose a specific kind of community, trees in tropical forests, for which interactions are mostly local and thus requires a spatially explicit model, and it was shown how parameters can be estimated from large datasets.
The phenomenon of clumping discussed in Section 2 is related with many interesting issues in Biology. One of them is the possibility of sympatric speciation (the process through which new species evolve from a single ancestral species while inhabiting the same geographic region) driven by competition for resources. For example it was recently shown that an individual-based evolutionary model, involving a population of genetically diverse organisms competing with each other for limited resources, exhibits a pattern-forming instability which is highly amplified by the effects of demographic noise [116]. This mechanism, which leads to the spontaneous formation of genotypic clusters, is a nice example of the application of statistical mechanics beyond mean field theory in ecology supporting the thesis that stochasticity has a central role in the formation and coherence of species. In addition, demographic noise greatly enlarges the region of parameter space where pattern formation very similar to those produced by Turing instability occurs [5]. This result may account for the prevalence of large-scale ecological patterns, beyond that expected from traditional nonstochastic approaches.
It is worth to mention that the clumpiness can also be related to the SAR analyzed in Section 4. It was argued that SARs are a robust consequence of a skewed species abundance distribution resembling a lognormal with higher rarity, together with the fact that individuals of a given species tend to cluster [117]. In Section 4 it was also mentioned that most biodiversity metrics predicted by niche and neutral theories are difficult to distinguish empirically, making it problematic to deduce ecological dynamics from these measures of diversity and community structure. Concerning the niche vs. neutrality issue I would like to point out two interesting recent findings. One is that neutral models are just a subset of the majority of plausible models that lead to the same patterns [118]. The authors arrived to this result by applying MaxEnt, and in turn also providing a link between NTB and MAxEnt. The other finding is related to quantifying the relative roles played by niche and neutral forces. A proposed methodology for addressing this problem in the case of microbial communities, by fusing measures of abundance with phylogenetic information, suggests that apparently neutral patterns of diversity and abundance can arise from niche-dominated dynamics [119]. These results seem consistent with the idea of emergent neutrality as a synthesis of both opposing viewpoints [34].
Another remarkable point is that the success of statistical mechanics in predicting ecological spatio-temporal observables for ecosystems out of equilibrium (Section 3 and Section 4) implies that communities are in dynamic equilibrium and hence that temporal fluctuations on all sorts of scales are likely to be important in community structure [120]. The catastrophe theory approach of Section 3 allows to identify early warning indicators of catastrophic shifts in ecosystems as well as to establish parallels with the well known physics of phase transitions. This relationship in turn opens the use of statistical mechanics techniques to anticipate undesired and often difficult to revert changes in ecosystems.
Acknowledgment
I thank financial support from ANII (SNI), and PEDECIBA Uruguay. Part of the material presented here is based on papers I wrote with various colleagues: Section 2 with M. Scheffer and E. van Nes [33,34], Section 3 with A. Fernández [38] and Section 4 with P. Inchausti [95,96]; I am indebted to all of them. I would like to thank two anonymous referees, I feel that their observations and suggestions greately contributed to improve the paper and to clarify some points, also I would like to thank both of them for their kind comments on our work. The author is grateful to the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute. The BCI forest dynamics research project was made possible by National Science Foundation grants to Stephen P. Hubbell: DEB-0640386, DEB-0425651, DEB-0346488, DEB-0129874, DEB-00753102, DEB-9909347, DEB-9615226, DEB-9615226, DEB-9405933, DEB-9221033, DEB-9100058, DEB-8906869, DEB-8605042, DEB-8206992, DEB-7922197, support from the Center for Tropical Forest Science, the Smithsonian Tropical Research Institute, the John D. and Catherine T. MacArthur Foundation, the Mellon Foundation, the Small World Institute Fund, and numerous private individuals, and through the hard work of over 100 people from 10 countries over the past two decades. The plot project is part the Center for Tropical Forest Science, a global network of large-scale demographic tree plots.
Conflicts of Interest
The author declares no conflict of interest.
References
- Nee, S. The neutral theory of biodiversity: Do the numbers add up? Funct. Ecol. 2005, 19, 173–176. [Google Scholar]
- Scheffer, M. Critical Transitions in Nature and Society; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Cody, M.L.; Diamond, J.M. (Eds.) Ecology and Evolution of Communities; Belknap Press: Cambridge, MA, USA, 1975; pp. 342–444.
- McKane, A.J.; Newman, T.J. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 2005, 94, 218102. [Google Scholar]
- Butler, T.; Goldenfeld, N. Robust ecological pattern formation induced by demographic noise. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Chia, N.; Goldenfeld, N. Statistical mechanics of horizontal gene transfer in evolutionary ecology. J. Stat. Phys. 2011, 142, 1287–1301. [Google Scholar]
- Blythe, R.A.; McKane, A.J. Stochastic models of evolution in genetics, ecology and linguistics. J. Stat. Mech. 2007. [Google Scholar] [CrossRef]
- Vladar, H.P.; Barton, N.H. The contribution of statistical physics to evolutionary biology. Trends Ecol. Evol. 2011, 26, 424–432. [Google Scholar]
- Harte, J.; Zillio, T.; Conlisk, E.; Smith, A.B. Maximum entropy and the state-variable approach to macroecology. Ecology 2008, 89, 2700–2711. [Google Scholar]
- Dewar, R.C.; Porté, A. Statistical mechanics unifies different ecological patterns. J. Theor. Biol. 2008, 251, 389–403. [Google Scholar]
- Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Neutral theory and relative species abundance in ecology. Nature 2003, 424, 1035–1037. [Google Scholar]
- Volkov, I.; Banavar, J.; He, F.; Hubbell, S.P.; Maritan, A. Density dependence explains tree species abundance and diversity in tropical forests. Nature 2005, 438, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Patterns of relative species abundance in rainforests and coral reef. Nature 2007, 450, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Maritan, A.; Volkov, I. Applications of the principle of maximum entropy: From physics to ecology. J. Phys. Condens. Matter 2010, 22. [Google Scholar] [CrossRef] [PubMed]
- Houchmandzadeh, B. Neutral clustering in a simple experimental ecological community. Phys. Rev. Lett. 2008, 101, 078103. [Google Scholar]
- Maurer, B.A. Statistical mechanics of complex ecological aggregates. Ecol. Complex. 2005, 2, 71–85. [Google Scholar]
- Solé, R.V.; Montoya, M. Complexity and fragility in ecological networks. Proc. R. Soc. Lond. B 2001, 268, 2039–2045. [Google Scholar] [CrossRef] [PubMed]
- Montoya, J.M.; Pimm, S.L.; Sole, R.V. Ecological networks and their fragility. Nature 2006, 442, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Bastolla, U.; Fortuna, M.A.; Pascual-García, A.; Ferrera, A.; Luque, B.; Bascompte, J. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature 2009, 458, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; Simini, F.; Banavar, J.R.; Maritan, A. Emergence of structural and dynamical properties of ecological mutualistic networks. Nature 2013, 500, 449–452. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 1974. [Google Scholar]
- Tilman, D.; Lehman, C.L.; Kareiva, P. Population Dynamics in Spatial Habitats. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva, P.M., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 3–20. [Google Scholar]
- Lomolino, M.; Brown, J.; Brown, T.E. Biogeography; Sinauer Associates: Sunderland, MA, USA, 1998. [Google Scholar]
- MacArthur, R.H.; Levins, R. The limiting similarity, convergence and divergence of coexisting species. Am. Nat. 1967, 101, 377–385. [Google Scholar]
- Scheffer, M.; van Nes, E. Self-organized similarity, the evolutionary emergence of groups of similar species. Proc. Natl. Acad. Sci. USA 2006, 103, 6230–6235. [Google Scholar]
- Nee, S.; Colegrave, N. Ecology: Paradox of the clumps. Nature 2006, 441, 417–418. [Google Scholar]
- May, R.M.; Crawley, J.M.; Sugihara, G. Theoretical Ecology Principles and Applications; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Siemann, E.; Brown, J.H. Gaps in mammalian body size distributions reexamined. Ecology 1999, 80, 2788–2792. [Google Scholar]
- Holling, C.S. Cross-scale morphology, geometry and dynamics of ecosystems. Ecol. Monogr. 1992, 62, 447–502. [Google Scholar]
- Segura, A.M.; Kruk, C.; Calliari, D.; García-Rodriguez, F.; Conde, D.; Widdicombe, C.E.; Fort, H. Competition drives clumpy species coexistence in estuarine phytoplankton. Sci. Rep. 2013. [Google Scholar] [CrossRef]
- Segura, A.M.; Calliari, D.; Kruk, C.; Bonilla, S.; Conde, D.; Fort, H. Emergent neutrality drives phytoplankton species coexistence. Proc. R. Soc. B 2011, 278, 2355–2361. [Google Scholar]
- Fort, H.; Scheffer, M.; van Nes, E. The paradox of the clumps mathematically explained. Theor. Ecol. 2009, 2, 171–176. [Google Scholar]
- Fort, H.; Scheffer, M.; van Nes, E. The clumping transition in niche competition: A robust critical phenomenon. J. Stat. Mech. 2010, 2010. [Google Scholar] [CrossRef]
- Vergnon, R.; van Nes, E.H.; Scheffer, M. Emergent neutrality leads to multimodal species abundance distributions. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef]
- Berlin, T.H.; Kac, M. The spherical model of a ferromagnet. Phys. Rev. 1952, 86, 821–835. [Google Scholar]
- Ziman, J.M. Models of Disorder: The Theoretical Physics of Homogeneously Disordered Systems; Cambridge University Press: Cambridge, UK, 1979; pp. 182–186. [Google Scholar]
- Gray, R.M. Toeplitz and Circulant Matrices: A Review; Now Publisher Inc.: Hanover, MA, USA, 2006; pp. 1–5. [Google Scholar]
- Fernández, A.; Fort, H. Catastrophic phase transitions and early warnings in a spatial ecological model. J. Stat. Mech. 2009, 2009. [Google Scholar] [CrossRef]
- Dregne, H.E. Desertification of Arid Lands. In Physics of Desertification; El-Baz, F., Hassan, M.H.A., Eds.; Martinus Nijhoff: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Scheffer, M. Ecology of Shallow Lakes; Chapman and Hall: London, UK, 1998. [Google Scholar]
- Carpenter, S.R.; Ludwig, D.; Brock, W.A. Management of eutrophication for lakes subject to potentially irreversible change. Ecol. Appl. 1999, 9, 751–771. [Google Scholar]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar]
- Carpenter, S. Alternate States of Ecosystems: Evidence and Some Implications. In Ecology: Achievement and Challenge; Huntly, N., Press, M.C., Levin, S., Eds.; Blackwell: Oxford, UK, 2001; pp. 357–383. [Google Scholar]
- Steinberg, E.K.; Kareiva, P. Challenges and Opportunities for Empirical Evaluation of Spatial Theory. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva Princeton, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 318–332. [Google Scholar]
- Levin, S.A.; Pacala, S.W. Theories of Simplification and Scaling of Spatially Distributed Processes. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva Princeton, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 271–296. [Google Scholar]
- Aguiar, M.R.; Sala, O.E. Patch structure, dynamics and implications for the functioning of arid ecosystems. Tree 1999, 14, 273–277. [Google Scholar]
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar]
- Von Hardenberg, J.; Meron, E.; Shachak, M.; Zarmi, Y. Diversity of vegetation patterns and desertification. Phys. Rev. Lett. 2001, 87, 1981011. [Google Scholar] [CrossRef]
- Von Hardenberg, J.; Kletter, A. Y.; Yizhaq, H.; Nathan, J.; Meron, E. Periodic versus scale-free patterns in dryland vegetation. Proc. R. Soc. B 2010, 277, 1771–1776. [Google Scholar] [CrossRef] [PubMed]
- Bel, G.; Hagberg, A.; Meron, E. Gradual regime shifts in spatially extended ecosystems. Theoretical Ecology 2012, 5, 591–604. [Google Scholar]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1928. [Google Scholar]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; ElAich, A.; de Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar]
- Carpenter, S.R.; Brock, W.A. Rising variance: A leading indicator of ecological transition. Ecol. Lett. 2006, 9, 311–318. [Google Scholar]
- Brock, W.A.; Carpenter, S.R. Variance as a leading indicator of regime shift in ecosystem services. Ecol. Soc. 2006, 11. Art. 9. [Google Scholar]
- Noy-Meir, I. Stability of grazing systems: An application of predator-prey graphs. J. Ecol. 1975, 63, 459–481. [Google Scholar]
- World Resources Institute. World Resources 1988–89; Basic Books: New York, NY, USA, 1988. [Google Scholar]
- Wade, N. Sahelian drought: No victory for western aid. Science 1974, 185, 234–237. [Google Scholar]
- May, R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 1977, 269, 471–477. [Google Scholar]
- Ludwig, D.; Jones, D.D.; Holling, C.S. Qualitative analysis of insect outbreak systems: The spruce budworm and forest. J. Anim. Ecol. 1978, 47, 315–322. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer: Berlin, Germany, 1993. [Google Scholar]
- Holling, C.S. The components of predation as revealed by a study of small mammal predation of the European pine sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar]
- Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; Addison-Wesley: Boston, MA, USA, 1975. [Google Scholar]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Dover: New York, NY, USA, 1981. [Google Scholar]
- Boettiger, C.; Ross, N.; Hastings, A. Early warning signals: The charted and uncharted territories. Theor. Ecol. 2013, 6, 255–264. [Google Scholar]
- Goldenfeld, N. Lecture on Phase Transitions and the Renormalization Group; Perseus Books: Reading, MA, USA, 1992; pp. 219–222. [Google Scholar]
- Monette, L.; Klein, W. Spinodal decomposition as a coalescence process. Phys. Rev. Lett. 1992, 68, 2336–2339. [Google Scholar]
- Preston, F.W. The commonness, and rarity, of species. Ecology 1948, 29, 254–283. [Google Scholar]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gaston, K.J.; Blackburn, T.M. Pattern and Process in Macroecology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Brown, J.H. Macroecology; University of Chicago Press: Chicago, IL, USA, 1995. [Google Scholar]
- Harte, J.; Conlisk, E.; Ostling, A.; Green, J.L.; Smith, A.B. A theory of spatial-abundance and species-abundance distributions in ecological communities at multiple spatial scales. Ecol. Monogr. 2004, 75, 179–197. [Google Scholar]
- Begon, M.; Townsend, C.; Harper, J. Ecology: From Individuals to Ecosystems, 4th ed.; Blackwell: New York, NY, USA, 2006. [Google Scholar]
- Hutchinson, G.E. Concluding remarks. Cold Spring Harb. Symp. Quant. Biol. 1957, 22, 415–427. [Google Scholar]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Condit, R.; Hubbell, S.P.; Lafrankie, J.V.; Sukumar, R.; Manokaran, N.; Foster, R.B.; Ashton, P.S. Species-area and species-individual relationships for tropical trees: A comparison of three 50-ha plots. J. Ecol. 1996, 84, 549–562. [Google Scholar]
- Chave, J. Neutral theory and community ecology. Ecol. Lett. 2004, 7, 241–253. [Google Scholar]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Harte, J.; Smith, A.; Storch, D. Biodiversity scales from plots to biomes with a universal species-area curve. Ecol. Lett. 2009, 12, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Notes on Present Status and Future Prospects. In Maximum Entropy and Bayesian Methods; Grandy, W.T., Jr., Schick, L.H., Eds.; Springer: Dordrecht, The Netherlands, 1991; Volume 43, pp. 1–13. [Google Scholar]
- McKane, A.J.; Alonso, D.; Sole, R.V. Analytic solution of Hubbell’s model of local community dynamics. Theor. Popul. Biol. 2004, 65, 67–73. [Google Scholar]
- Zillio, T.; Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Spatial scaling in model plant communities. Phys. Rev. E 2005, 71, 1507–1519. [Google Scholar] [CrossRef]
- Chave, J.; Leigh, E.G., Jr. A spatially explicit neutral model of beta-diversity in tropical forests. Theor. Popul. Biol. 2002, 62, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Rosindell, J.; Cornell, S.J. Species-area relationships from a spatially explicit neutral model in an infinite landscape. Ecol. Lett. 2007, 10, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Etienne, R.S.; Alonso, D. Neutral community theory: How stochasticity and and dispersal-limitation can explain species coexistence. J. Stat. Phys. 2007, 128, 485–510. [Google Scholar] [CrossRef]
- Bertuzzo, E.; Suweis, S.; Mari, L.; Maritan, A.; Rodríguez-Iturbe, I.; Rinaldo, A. Spatial effects on species persistence and implications for biodiversity. Proc. Natl. Acad. Sci. USA 2011, 108, 4346–4351. [Google Scholar] [CrossRef] [PubMed]
- Goel, N.S.; Maitra, S.C.; Montroll, E.W. On the volterra and other nonlinear models of intereacting populations. Rev. Mod. Phys. 1971, 43, 231–276. [Google Scholar] [CrossRef]
- Maynard Smith, J. Models in Ecology; Cambridge University Press: Cambridge, UK, 1974; pp. 90–97. [Google Scholar]
- Wilson, A. Boltzmann, Lotka and Volterra and spatial structural evolution: An integrated methodology for some dynamical systems. J. R. Soc. Interface 2008, 5, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Tainaka, K. Lattice model for the Lotka-Volterra system. J. Phys. Soc. Jpn. 1988, 57, 2588–2590. [Google Scholar] [CrossRef]
- Matsuda, H.; Ogita, N.; Sasaki, A.; Sato, K. Statistical mechanics of population: The lattice Lotka-Volterra model. Prog. Theor. Phys. 1992, 88, 1035–1049. [Google Scholar] [CrossRef]
- Wilson, W.G.; de Roos, A.M.; McCauley, E. Spatial instabilities whitin the diffusive Lotka-Volterra system: Individual-based simulation results. Theor. Popul. Biol. 1993, 43, 91–127. [Google Scholar] [CrossRef]
- Szabó, G.; Czárán, T. Phase transition in a spatial Lotka-Volterra model. Phys. Rev. E 2001, 63, 061904. [Google Scholar] [CrossRef]
- Leimar, O.; Sasaki, A.; Doebeli, M.; Dieckmann, U. Limiting similarity, species packing, and the shape of competition kernels. J. Theor. Biol. 2013, 339, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Fort, H.; Inchausti, P. Biodiversity patterns from an individual-based competition model on niche and physical spaces. J. Stat. Mech. 2012, 2012. [Google Scholar] [CrossRef]
- Fort, H.; Inchausti, P. Tropical forests are non-equilibrium ecosystems governed by interspecific competition based on a universal 1/6 niche width. PLOS One 2013, in press. [Google Scholar] [CrossRef] [PubMed]
- Center for Tropical Forest Science. Available online: http://www.ctfs.si.edu/ (accessed on 25 November 2013).
- Azaele, S.; Pigolotti, S.; Banavar, J.; Maritan, A. Dynamical evolution of ecosystems. Nature 2006, 444, 926–928. [Google Scholar] [CrossRef] [PubMed]
- Vanpeteghem, D.; Haegeman, B. An analytical approach to spatio-temporal dynamics of neutral community models. J. Math. Biol. 2010, 61, 323–357. [Google Scholar] [CrossRef] [PubMed]
- Chisholm, R.A. Time-dependent solutions of the spatially implicit neutral model of biodiversity. Theor. Popul. Biol. 2011, 80, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; Rinaldo, A.; Maritan, A. An exactly solvable coarse-grained model for species diversity. J. Stat. Mech. 2012, 2012. [Google Scholar] [CrossRef]
- Carey, S.; Ostling, A.; Harte, J.; del Moral, R. Impact of curve construction and community dynamics on the species-time relationship. Ecology 2007, 88, 2145–2153. [Google Scholar] [CrossRef] [PubMed]
- Hubbell, S.P. Neutral theory and the evolution of ecological equivalence. Ecology 2006, 87, 1387–1398. [Google Scholar]
- Morin, R.J. Community Ecology, 2nd ed.; John Wiley & Sons: Chichester, West Sussex, UK, 2011; pp. 26–27. [Google Scholar]
- Dieckmann, U.; Law, R.; Metz, J.A. (Eds.) The Geometry of Ecological Interactions; Cambridge University Press: Cambridge, UK, 2000.
- Glauber, R.J. Time-dependent statistics of the ising model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar]
- Krapivsky, P.J.; Redner, S.; Ben Naim, E. A Kinetic View of Statistical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fort, H. A minimal model for the evolution of cooperation through evolving heterogeneous games. Europhys. Lett. 2008, 81. [Google Scholar] [CrossRef]
- Condit, R.; Ashton, P.S.; Manokaran, N.; LaFrankie, J.V.; Hubbell, S.P.; Foster, R.B. Dynamics of the forest communities at Pasoh and Barro Colorado: Comparing two 50-ha plots. Philos. Trans. R. Soc. B 1999, 354, 1739–1748. [Google Scholar]
- Hubbell, S.P.; Condit, R.; Foster, R.B. Forest Census Plot on Barro Colorado Island. Available online: http://ctfs.arnarb.harvard.edu/webatlas/datasets/bci (accessed on 25 November 2013).
- Condit, R. Tropical Forest Census Plots; Springer: New York, NY, USA, 1998. [Google Scholar]
- Hubbell, S.P.; Ahumada, J.A.; Condit, R.; Foster, R.B. Local neighborhood effects on long-term survival of individual trees in a neotropical forest. Ecological Research 2001, 16, 859–875. [Google Scholar]
- O’Brien, S.T.; Hubbell, S.P.; Spiro, P.; Condit, R.; Foster, R.B. Diameter, height, crown, and age relationship in eight neotropical tree species. Ecology 1995, 76, 1926–1939. [Google Scholar]
- Chisholm, R.; Pacala, S. Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proc. Nat. Acad. Sci. USA 2010, 107, 15821–15825. [Google Scholar]
- Seri, E.; Maruvka, Y.E.; Shnerb, N.M. Neutral dynamics and cluster statistics in a tropical forest. Am. Nat. 2012, 180, E161–E173. [Google Scholar]
- Rogers, T.; McKane, A.J.; Rossberg, A.G. Spontaneous genetic clustering in populations of competing organisms. Phys. Biol. 2012, 9. [Google Scholar] [CrossRef]
- García-Martín, H.; Goldenfeld, N. On the origin and robustness of power-law species-area relationships in ecology. Proc. Natl. Acad. Sci. USA 2006, 103, 10310–10315. [Google Scholar]
- Pueyo, S.; He, F.; Zillio, T. The maximum entropy formalism and the idiosyncratic theory of biodiversity. Ecol. Lett. 2007, 10, 1017–1028. [Google Scholar] [CrossRef] [PubMed]
- Jeraldo, P.; Sipos, M.; Chia, N.; Brulc, J.M.; Dhillon, A.S.; Konkel, M.E.; Larson, C.L.; Nelson, K.E.; Qu, A.; Schook, L.B.; et al. Quantification of the relative roles of niche and neutral processes in structuring gastrointestinal microbiomes. Proc. Natl. Acad. Sci. USA 2012, 109, 9692–9698. [Google Scholar] [CrossRef] [PubMed]
- Bowler, M.G.; Kelly, C.K. On the statistical mechanics of species abundance distributions. Theor. Popul. Biol. 2012, 82, 85–91. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).