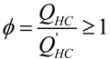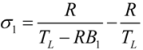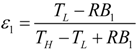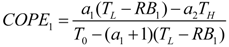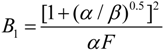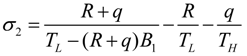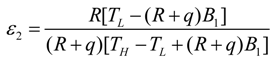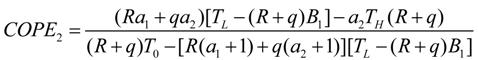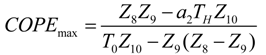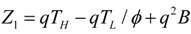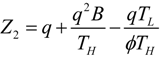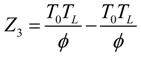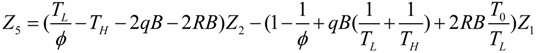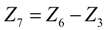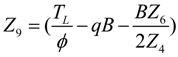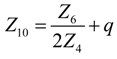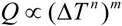Performance Optimization of Generalized Irreversible Refrigerator Based on a New Ecological Criterion
Abstract
:1. Introduction
2. Model and Basic Assumption

- (1)
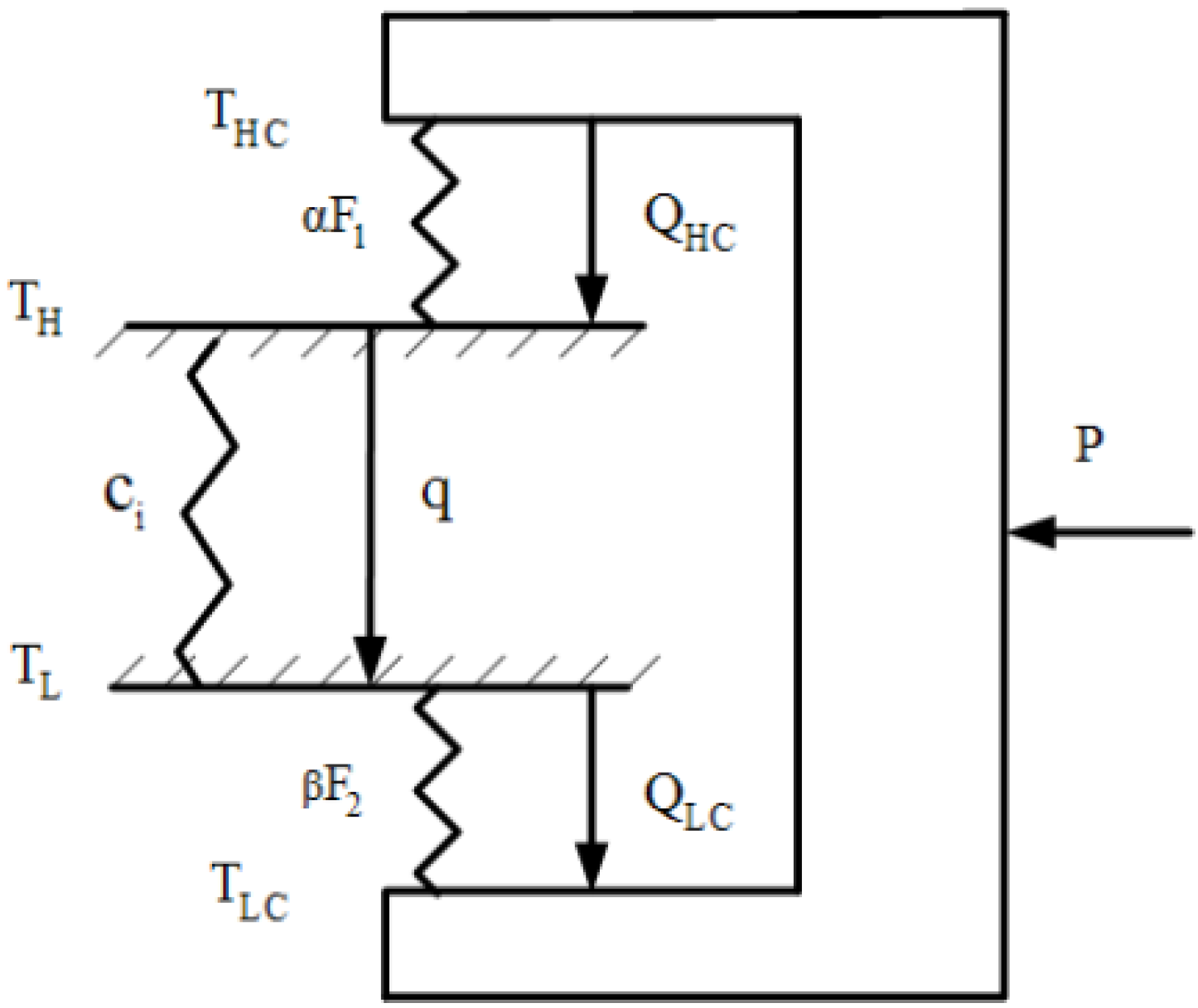
- The working fluid flows through the cycle at a steady state. The cycle consists of two isothermal processes and two adiabatic processes. All four processes are irreversible.
- (2)
- The heat transfer surface areas (F1 and F2) of the high- and low- temperature heat exchangers are finite. The total heat transfer surface area (F) of the two heat exchangers is assumed to be a constant:F = F1 + F2
- (3)
- There exists heat leakage (q) from the heat sink to the heat source. Thus:QH = QHC − qQL = R = QLC − q
- (4)
- There are various irreversibilities in the refrigeration cycle due to: (i) heat resistance between heat reservoirs and working fluid. (ii) heat leakage between heat reservoirs and (iii) miscellaneous factors such friction, turbulence and non-equilibrium activities inside the refrigerator. Therefore, a larger power input is needed when compared with an endoreversible refrigerator. In other words, the rate of heat rejected to the sink (QHC) of the generalized irreversible refrigerator is higher than that of an endoreversible one (Q′HC). To scale these irreversibilities, we introduce a constant factor, ϕ, to characterize the additional internal miscellaneous irreversibility effect:
3. Optimization for Irreversible Refrigerator
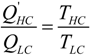

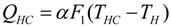
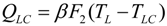


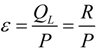
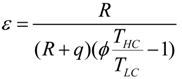
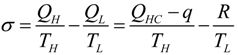
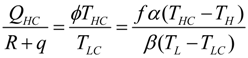
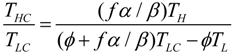




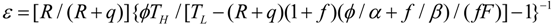

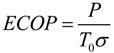
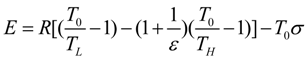
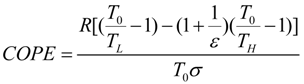

 and
and 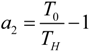 .
.
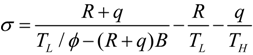

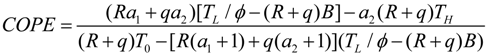
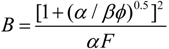 .
.4. Discussion
- (1)
- If q = 0 and ϕ = 1, the model is reduced to the endoreversible refrigerator with external heat resistance as the sole irreversibility in the system, and Equations (29)–(31) become:where
.
- (2)
- If q > 0 and ϕ = 1, the model is reduced to the irreversible refrigerator with heat resistance and heat leak losses, and Equations (29)–(31) become:
- (3)
- If q = 0 and ϕ > 1, the model is reduced to the irreversible refrigerator with heat resistance and internal irreversibilities, and Equations (29)–(31) become:
- (4)
- If q > 0 and ϕ > 1, and in order to find the optimal coefficient of performance of exergy (COPE) for the generalized irreversible refrigerator, letting dCOPE/dR = 0 yields:where:
5. Numerical Examples
5.1. Calculation Conditions
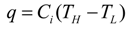
5.2. The Main Influencing Factors on COPE
5.2.1. Cooling Load and Entropy Generation Rate
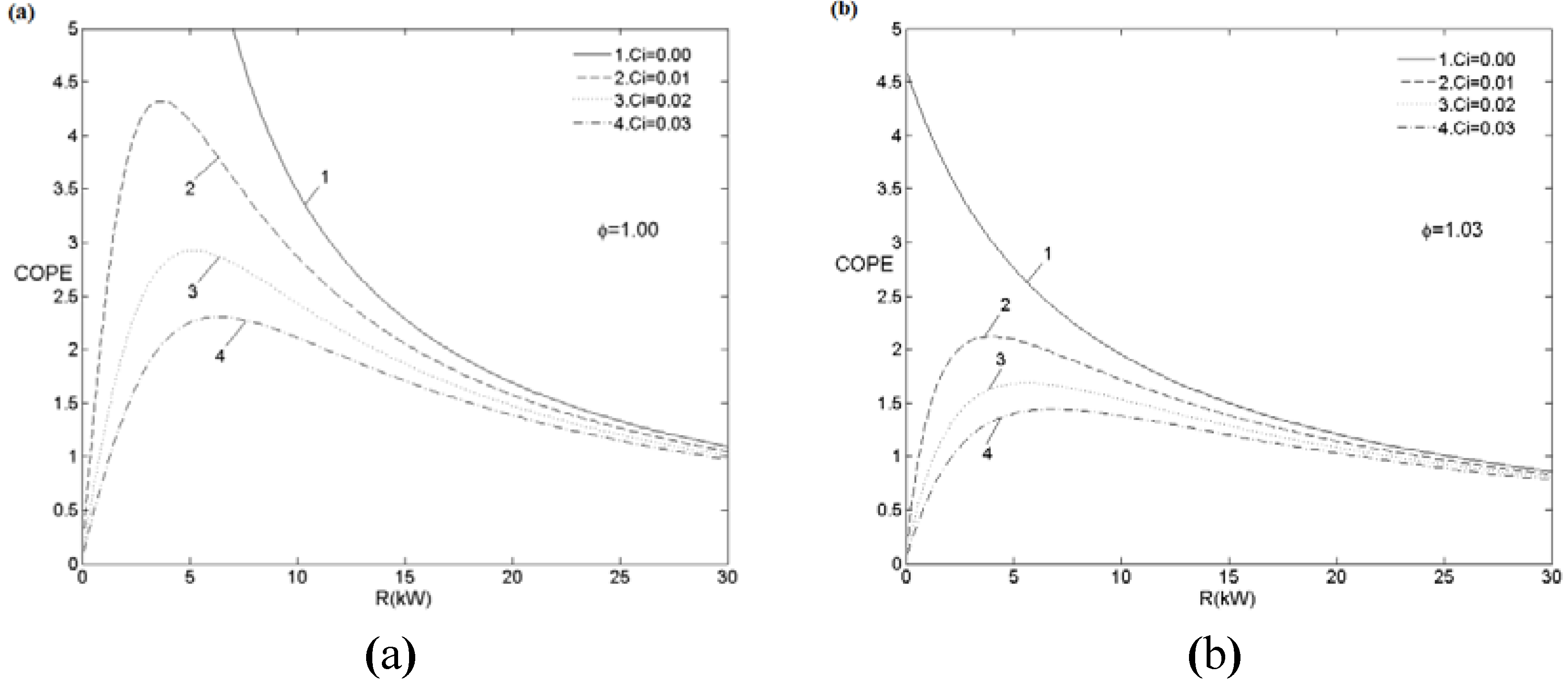
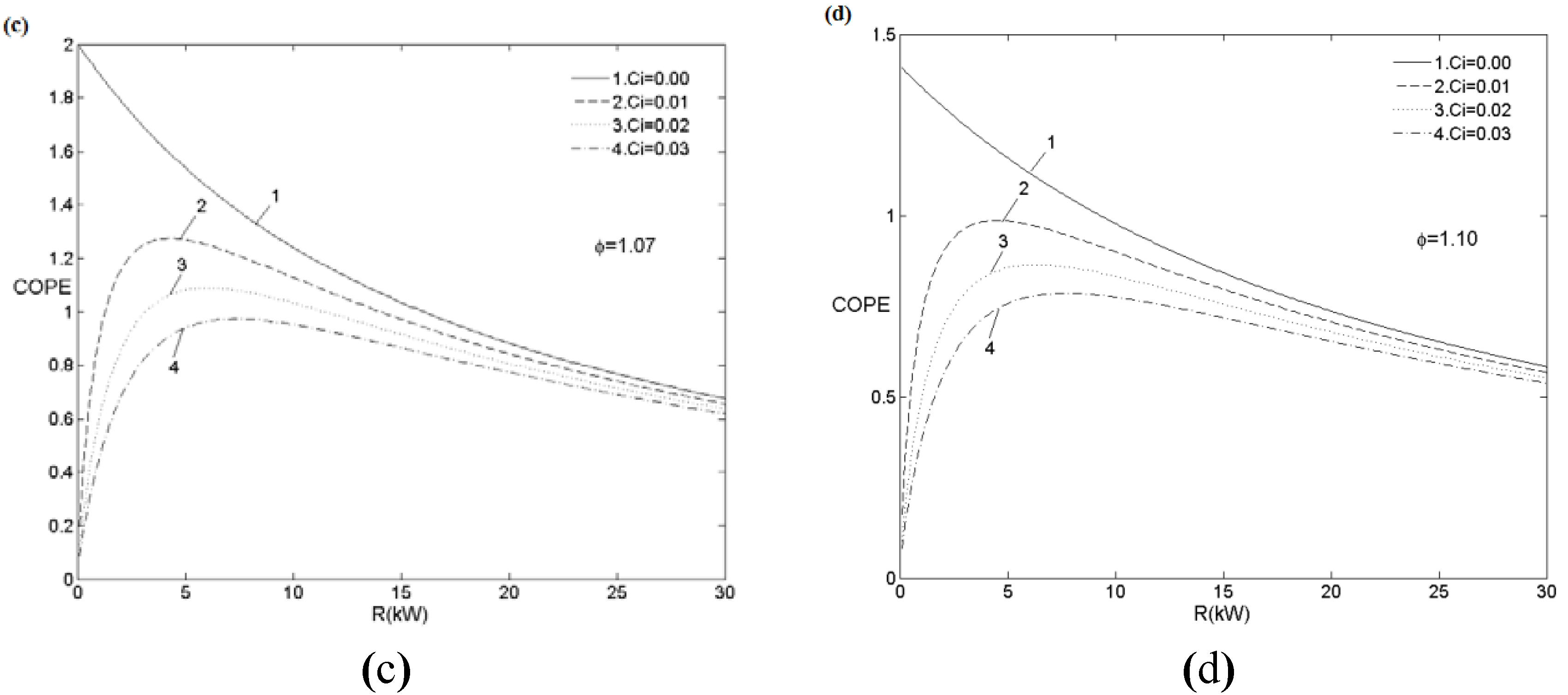
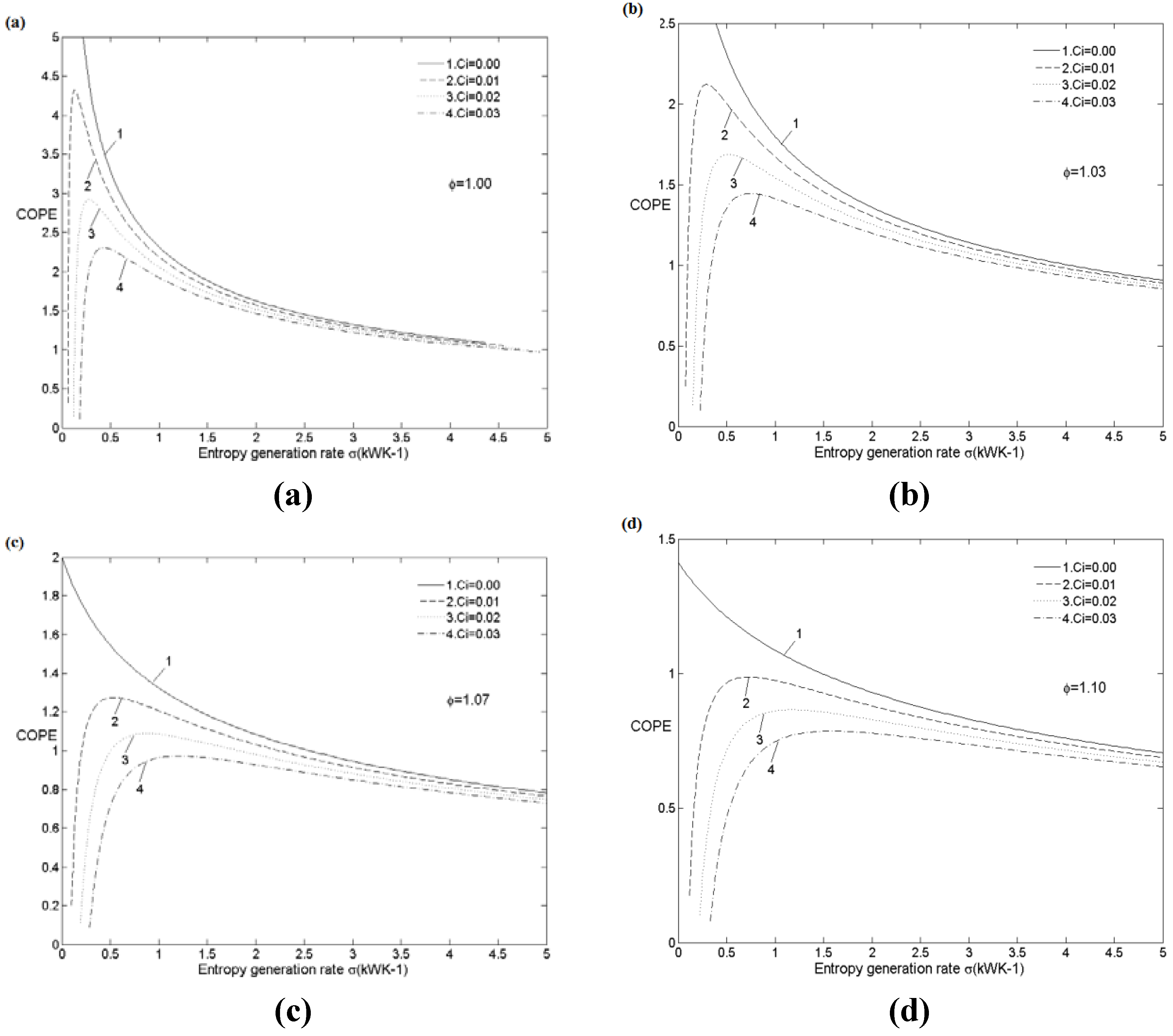
| ϕ | 1.0 | 1.0 | 1.0 | 1.1 | 1.1 | 1.1 |
|---|---|---|---|---|---|---|
| Ci | 0.01 | 0.02 | 0.03 | 0.01 | 0.02 | 0.03 |
| T0σE(kW) | 0.14 | 0.27 | 0.43 | 0.73 | 1.17 | 1.58 |
| εE | 5.23 | 4.78 | 4.46 | 3.11 | 2.89 | 2.73 |
| COPEmax | 4.31 | 2.92 | 2.30 | 0.98 | 0.8644 | 0.79 |
| ECOPm | 27.87 | 18.77 | 14.76 | 6.19 | 5.39 | 4.88 |
| Rm(kW) | 3.68 | 5.2 | 6.356 | 4.51 | 6.34 | 7.72 |
| ϕ | 1.2 | 1.2 | 1.2 | 1.3 | 1.3 | 1.3 |
| Ci | 0.01 | 0.02 | 0.03 | 0.01 | 0.02 | 0.03 |
| T0σE(kW) | 1.47 | 2.26 | 2.92 | 2.21 | 3.37 | 4.36 |
| εE | 2.22 | 2.08 | 1.97 | 1.73 | 1.62 | 1.55 |
| COPEmax | 0.57 | 0.52 | 0.49 | 0.41 | 0.38 | 0.36 |
| ECOPm | 3.49 | 3.16 | 2.93 | 2.43 | 2.24 | 2.10 |
| Rm(kW) | 5.00 | 7.05 | 8.58 | 5.376 | 7.53 | 9.15 |
5.2.2. The Coefficient of Performance (COP)
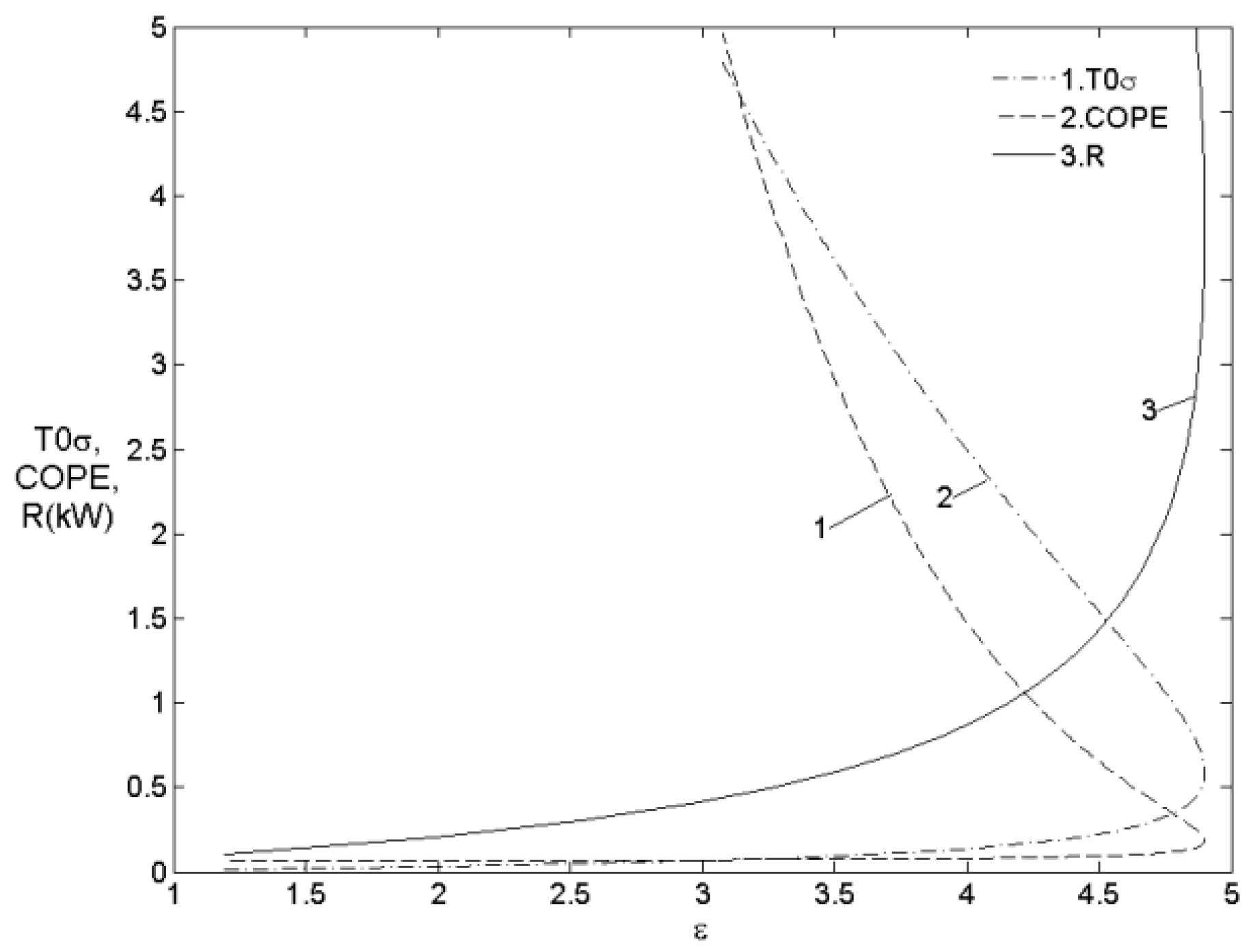
5.2.3. The Irreversibility and Internal Conductance
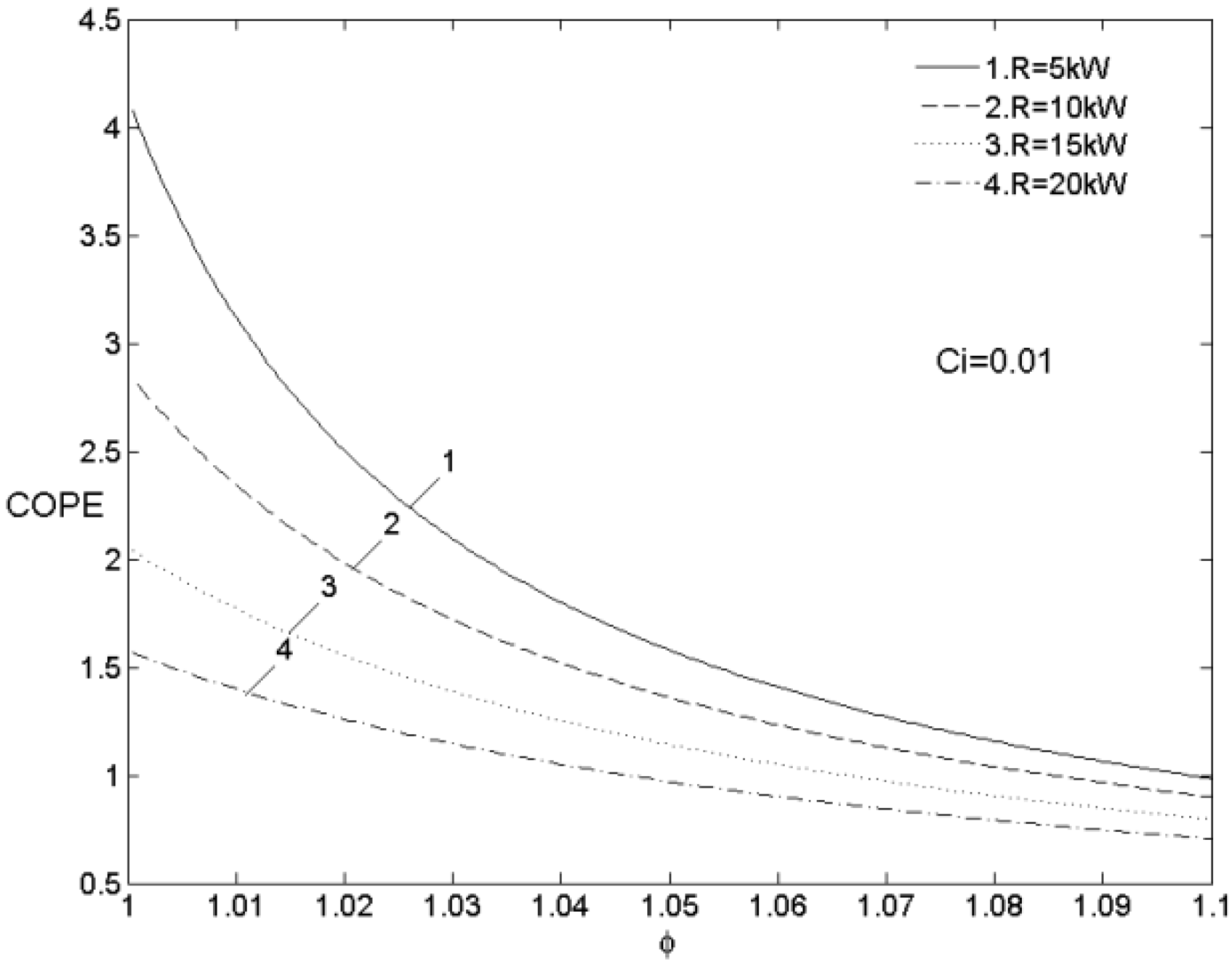
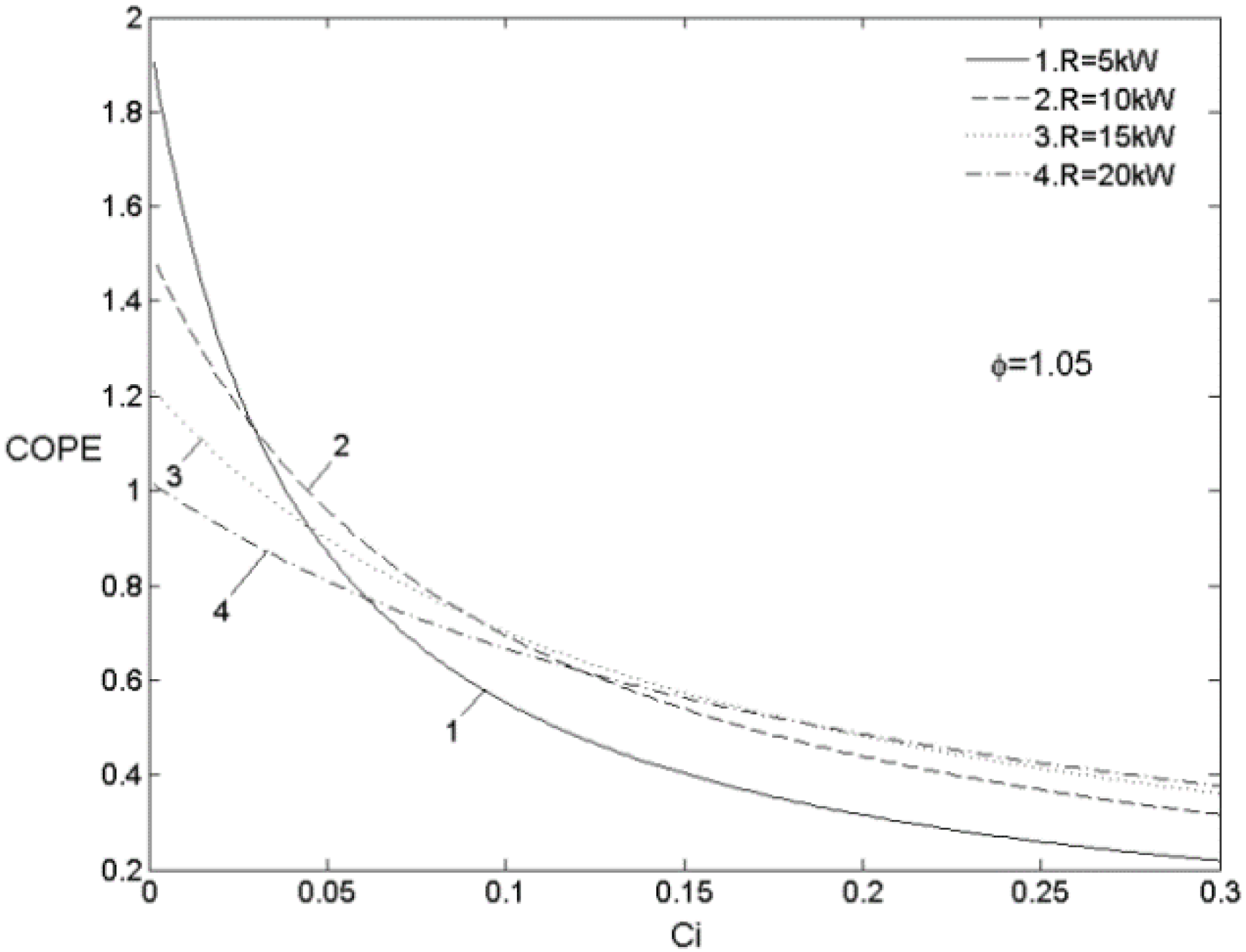
5.3. Optimal Matching Criterion
5.4. Comparison between COPE and ECOP
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow, 1st ed.; Wiley: New York, NY, USA, 1982; pp. 118–152. [Google Scholar]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes, 1st ed.; CRC Press: Boca Raton, FL, USA, 1996; pp. 70–122. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy system. J. Non-Equil. Thermodyn. 2005, 24, 327–359. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhang, L.; Sun, F.R. Power, efficiency, entropy-generation rate and ecological optimization for a class of generalized irreversible universal heat-engine cycles. Appl. Energy 2007, 84, 512–525. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Chen, C.K.; Su, Y.F. Exergetic efficiency optimization for an irreversible Brayton refrigeration cycle. Int. J. Therm. Sci. 2005, 44, 303–310. [Google Scholar] [CrossRef]
- Tu, Y.; Chen, L.G.; Sun, F.R.; Wu, C. Cooling load and efficient of performance optimizations for real air-refrigerators. Appl. Energy 2006, 83, 1289–1306. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. Steady flow combined refrigeration cycle performance with heat leak. Appl. Therm. Eng. 1997, 17, 639–645. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Chen, L.G.; Sun, F.R.; Wu, C. Effect of heat transfer law on the ecological optimization of a generalized irreversible Carnot heat pump. Int. J. Exergy 2005, 2, 423–436. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhu, X.Q.; Sun, F.R.; Wu, C. Ecological optimization of a generalized irreversible Carnot refrigerator for a generalized heat transfer law. Int. J. Ambient Energy 2007, 28, 213–219. [Google Scholar] [CrossRef]
- Chen, L.G.; Li, J.; Sun, F.R. Ecological optimization of a generalized irreversible Carnot refrigerator in case of
. Int. J. Sustain. Energy 2012, 31, 59–72. [Google Scholar] [CrossRef]
- Agnew, B.; Anderson, A.; Frost, T.H. Optimisation of a steady-flow Carnot cycle with external irreversibilities for maximum specific output. Appl. Therm. Eng. 1997, 1, 3–15. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Chen, L.G.; Sun, F.R.; Wu, C. Exergy based ecological optimization for a generalized irreversible Carnot refrigerator. J. Energy Inst. 2006, 79, 42–46. [Google Scholar] [CrossRef]
- Goktun, S. Coefficient of performance for an irreversible combined refrigeration cycle. Energy 1996, 21, 721–724. [Google Scholar] [CrossRef]
- Salah El-Din, M.M. Optimization of totally irreversible refrigerators and heat pumps. Energy Convers. Manag. 1999, 40, 423–436. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Wu, C. Ecological optimization of a multi-stage irreversible combined refrigeration system. Energy Convers. Manag. 2002, 43, 2379–2393. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Bose, S.; Sarkar, J. Exergy maximization of cascade refrigeration cycles and its numerical verification for a transcritical CO2-C3H8 system. Int. J. Refrig. 2007, 30, 624–632. [Google Scholar] [CrossRef]
- Chen, L.G.; Li, J.; Sun, F.R. Generalized irreversible heat-engine experiencing a complex heat-transfer law. Appl. Energy 2008, 85, 52–60. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Influence of heat-transfer law on the performance of a Carnot engine. Appl. Therm. Eng. 1993, 17, 277–282. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Wu, C. Optimisation of rate of exergy output of a multistage endoreversible combined refrigeration system. Exergy 2001, 1, 100–106. [Google Scholar] [CrossRef]
- Morosuk, T.; Tsatsaronis, G. Advanced exergetic evaluation of refrigeration machines using different working fluids. Energy 2009, 34, 2248–2258. [Google Scholar] [CrossRef]
- Koda, A.; Sahin, B.; Yilmaz, T. Effects of internal irreversibility and heat leakage on the finite-time thermoeconomic performance of refrigerators and heat pumps. Energy Convers. Manag. 2000, 41, 607–619. [Google Scholar] [CrossRef]
- Ust, Y. Performance analysis and optimization of irreversible air refrigeration cycles based on ecological coefficient of performance criterion. Appl. Therm. Eng. 2009, 29, 47–55. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Kaushik, S.C.; Salhotra, R. Ecological optimization and performance study of irreversible Stirling and Ericsson heat-engines. J. Phys. D 2002, 35, 2668–2675. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Yan, Z. Comment on “ecological optimization criterion for finite-time heat-engines”. J. Appl. Phys. 1993, 73, 3583. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Ecological optimization criteria for an endoreversible Carnot refrigerator. Nat. J. 1992, 15. No. 8, (in Chinese). [Google Scholar]
- Chen, L.G.; Sun, F.R.; Wu, C. On the ecological figures of merit for thermodynamics cycles. J. Eng. Therm. Energy Power 1994, 9, 374–376. (in Chinese). [Google Scholar]
- Ust, Y.; Sahin, B. Performance optimization of irreversible refrigerators based on a new thermo-ecological criterion. Int. J. Refrig. 2007, 30, 527–534. [Google Scholar] [CrossRef]
- Ust, Y.; Sahin, B.; Sogut, O.S. Performance analysis and optimization of an irreversible dual-cycle based on an ecological coefficient of performance criterion. Appl. Energy 2005, 82, 23–39. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhu, X.; Sun, F.R.; Wu, C. Ecological optimization for generalized irreversible Carnot refrigerators. J. Phys. D 2005, 35, 113–118. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. A generalized model of a real refrigerator and its performance. Appl. Therm. Eng. 1997, 17, 401–412. [Google Scholar] [CrossRef]
- Bejan, A. Theory of heat transfer-irreversible refrigeration plants. Int. J. Heat Mass Trans. 1989, 32, 1631–1639. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. Influence of internal heat leak on the performance of refrigerators. Energy Convers. Manag. 1998, 39, 45–50. [Google Scholar] [CrossRef]
- Gordon, J.M.; Ng, K.C. Thermodynamic modeling of reciprocating chillers. J. Appl. Phys. 1994, 75, 2769–2774. [Google Scholar] [CrossRef]
- Sun, F.R.; Wu, C.; Chen, L.G. Optimal performance and rate of entropy production for forward and reverse irreversible Carnot cycles. Chin. J. Eng. Thermophys. 1991, 12, 357–360. [Google Scholar]
- Ait-Ali, M.M. A class of internally irreversible refrigeration cycles. J. Phys. D 1996, 29, 593–599. [Google Scholar] [CrossRef] [Green Version]
- Ait-Ali, M.M. The maximum coefficient of performance of internally irreversible refrigerators and heat pumps. J. Phys. D 1996, 29, 975–980. [Google Scholar] [CrossRef]
- Ust, Y. Performance analysis and optimization of irreversible air refrigeration cycles based on ecological coefficient of performance criterion. Appl. Therm. Eng. 2009, 29, 47–55. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xu, J.; Pang, L.; Wang, J. Performance Optimization of Generalized Irreversible Refrigerator Based on a New Ecological Criterion. Entropy 2013, 15, 5277-5291. https://doi.org/10.3390/e15125277
Xu J, Pang L, Wang J. Performance Optimization of Generalized Irreversible Refrigerator Based on a New Ecological Criterion. Entropy. 2013; 15(12):5277-5291. https://doi.org/10.3390/e15125277
Chicago/Turabian StyleXu, Jie, Liping Pang, and Jun Wang. 2013. "Performance Optimization of Generalized Irreversible Refrigerator Based on a New Ecological Criterion" Entropy 15, no. 12: 5277-5291. https://doi.org/10.3390/e15125277
APA StyleXu, J., Pang, L., & Wang, J. (2013). Performance Optimization of Generalized Irreversible Refrigerator Based on a New Ecological Criterion. Entropy, 15(12), 5277-5291. https://doi.org/10.3390/e15125277