Abstract
The Maximum Entropy Production (MEP) principle has been remarkably successful in producing accurate predictions for non-equilibrium states. We argue that this is because the MEP principle is an effective inference procedure that produces the best predictions from the available information. Since all Earth system processes are subject to the conservation of energy, mass and momentum, we argue that in practical terms the MEP principle should be applied to Earth system processes in terms of the already established framework of non-equilibrium thermodynamics, with the assumption of local thermodynamic equilibrium at the appropriate scales.
1. Introduction
The proposed Maximum Entropy Production (MEP) principle states that sufficiently complex systems are characterized by a non-equilibrium thermodynamic state in which the rate of thermodynamic entropy production is maximized [1,2,3,4]. Several examples have demonstrated the feasibility of the MEP principle. For example, the prediction of atmospheric heat transport from simple considerations [5,6] and rates of mantle convection within the Earth [7]. The explanatory power of the MEP principle is not always fully appreciated. In the example of planetary heat transport [6] a two-box model is astonishingly simple and yet able to provide predictions of poleward heat transport that are consistent with observations for several planetary settings.
In this paper we attempt to answer the questions: Why does the MEP principle work? How can the MEP principle be used to increase our knowledge of the Earth system? In doing so we will consider the theoretical basis of the MEP principle in the face of what may appear to be two conflicting interpretations: first, that the MEP principle is a natural law that provides a description of real world systems; second, that the MEP principle is an inference procedure that can robustly increase our information about certain systems. We will argue that the inference procedure is the interpretation that is consistent with the existing applications and derivations of the MEP principle recently proposed by Dewar [8]. Much of our argument follows from the theories of E. T. Jaynes and Dewar’s attempted extension of Jaynes’ MaxEnt procedure to non-equilibrium systems. The particular utility of our contribution is to address some of the more conceptual or philosophical aspects and issues that arise when attempting to interpret the MEP principle as an inference procedure. Part of our argument will be to highlight a number of assumptions that may lead one to initially conclude that the MEP principle is a natural law. Making these assumptions explicit will allow us to untangle a number of seemingly confusing aspects of the MEP principle that can only be fully resolved within a conception of science which is centrally about increasing our information about systems and therefore sits naturally within an information theoretic formulation of entropy which can be defined as the amount of information or “surprise” that a message contains.
After these conceptual issues we consider what their significance is for scientists who wish to apply the MEP principle to real world systems. Many systems of the Earth are in non-equilibrium states and therefore ripe for being described in terms of thermodynamics which sets the foundations for the application of the MEP principle. We argue that for physical processes occurring on the Earth, such considerations can be effectively carried out in the absence of informational concepts because when we deal with processes occurring within the Earth system, energy and mass balances are always a central foundation, either to describe the process under consideration directly, and/or to describe the nature of the boundaries and their sensitivity to which the process is subjected to. We argue that this effectively translates the information theory based MEP principle into a thermodynamic MEP principle. In doing so, we acknowledge that there will be instances in which the conservation of energy and mass are of less relevance (for instance in linguistics, or in purely statistical analyses of data in which the MaxEnt approach is also used). In such cases, the purely information theory based MaxEnt approach would not translate into thermodynamics, and the maximization of physical entropy production has little relevance to such applications.
We structure the paper with the following sections. In Section 2 we introduce the concept of entropy in equilibrium systems in terms of the relationship between microscopic and macroscopic properties of systems. We then show how to calculate rates of entropy production for simple non-equilibrium states. In Section 3 we present the MEP principle as a predictive tool that assumes certain systems will be in states of maximum entropy production. We review a number of open issues with the MEP principle, in particular whether the theory can be falsified and consequently whether is it a scientific theory. In Section 4 we continue with the issue of falsification via a discussion of the Popperian formulation of science. In Section 5 we specify what we mean by the term probability and argue that the natural law interpretation of the MEP principle is based on a frequentist interpretation. We present the Bayesian interpretation and outline the process of Bayesian inference. In Section 6 we give an overview of Dewar’s information theoretic derivation of the MEP principle and how it can be seen as extending the MaxEnt inference procedure to a class of systems that have non-equilibrium states. In Section 7 we argue that as all real world systems must conserve energy and matter, we can safely translate information theoretic concepts into thermodynamic ones when modelling the Earth system. We show how systems that have states that are further from thermodynamic equilibrium will require more information in order to model accurately which is equivalent to specifying more boundary conditions for the MEP principle procedure. We propose that the MEP principle can be used to better incorporate sub-grid scale processes without a commensurate increase in computational cost. We conclude the paper in Section 8 with a discussion.
2. What is Entropy and Entropy Production?
2.1. Equilibrium States
Statistical mechanics is the application of probability to physical theories. It explains the macroscopic properties of systems such as temperature and pressure in terms of the microscopic arrangements of the elements that comprise the system. Real world systems typically have a very large number of individual molecules. For an isolated system (a system that does not exchange energy or mass with its surroundings) at equilibrium, we should expect it to be in the most probable macroscopic state which corresponds to the greatest number of different ways that the individual molecules can rearrange themselves. This probabilistic feature becomes effectively a law when we deal with systems that have extremely large numbers of individual elements. The Gibbs configuration entropy of a system is a measure of the number of different ways that the microscopic elements can arrange themselves so as to produce the same macroscopic property [9]. Figure 1 gives a spatial demonstration of this probabilistic basis of entropy during the evolution from an initial low entropy to maximum entropy state in a rigid box that contains a number of gas molecules. It was Bolzmann who showed at thermodynamic equilibrium, one can compute the entropy of a system with:
where is the Boltzmann constant and translates the microscopic energy of particles to the macroscopic property of temperature and Ω is the number of different microstates possible for a particular macrostate. In Figure 1, the two macrostates have all the gas molecules in one side of the box or evenly distributed throughout the box. As the number of molecules increases, the difference in Ω for these two different macrostates increases. When we deal with the number of molecules that would be contained within a litre of air at room temperature and sea level pressure, the difference in entropy becomes extremely large and the probability of all molecules being in one side of the box is so small as to be safely ignored. It is the fact that many real world systems of interest are composed of a very large number of individual elements that leads to the power of statistical mechanics.
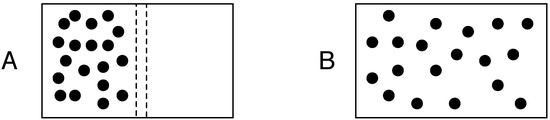
Figure 1.
Entropy at equilibrium in an isolated system. Diagrams A and B represent a rigid box that is isolated from the rest of the universe in that it is impermeable to energy and matter. A similarly impermeable partition bisects the box. To the left of the partition are a number of gas molecules. Diagram A shows the situation immediately after a dividing partition is removed (removed instantaneously and without disturbing any of the molecules). Given the particular properties of the individual gas molecules, there will be a particular number of ways that they can rearrange themselves so that all of them remain in the left hand side of the box. This number will be much less than the different arrangements of having an equal number of molecules in both sides of the box as shown in diagram B which is the expected distribution of molecules at equilibrium.
2.2. Non-Equilibrium States
The situation changes dramatically when we move from isolated systems to closed and open systems that exchange energy and/or matter with their surroundings as shown in Figure 2. Now suppose that the left and right hand sides of the box are connected to heat reservoirs. The left hand side reservoir is hotter than the right hand side. The left hand side will impart energy to gas molecules via conduction when a molecule hits that side of the box (we ignore the effects of radiation). This will produce an energy gradient where heated molecules on the left have more energy and so velocity than the cooler molecules on the right. Rather than an equal number of molecules on each side of the box we will typically observe fewer faster moving molecules on the left and more, slower moving molecules on the right hand side. Now, let us suppose that the temperatures of the hot and cold reservoirs can vary. As the molecules transfer heat, the temperature of the hot reservoir will decrease and the cold reservoir increase. Furthermore let us suppose that we can alter the flux of heat transported by the molecules. This could be achieved in two ways. First, we could vary the physical properties of the molecules so that they conduct more or less heat. Alternatively we could alter the amount of heat that is transferred from the heat reservoir to the molecules. In order to do that, imagine that we have a dial at our disposal that alters the amount of heat delivered from the reservoir to the left hand side of the box by raising or lowering an insulating barrier. The dial can turn from 0 to 10 where 0 represents no heat transferred to 10 where maximum heat is transferred. When the dial is set to 0 the box will be uniformly at the temperature of the cold reservoir. At equilibrium, the molecules will be at a maximum entropy state as the box can be considered an isolated system and so the molecules will be uniformly distributed. We now increase the dial to its maximum value. Furthermore, we assume that the molecules can transfer this heat arbitrarily fast so that there is no temperature difference between left and right sides of the box. This leads to a uniform distribution of molecules as once again there is no heat gradient and so the system has maximum entropy. Processes operating on the Earth are not isolated in that they exchange energy and/or matter with their surroundings. Also, the fluxes of heat through them are finite. Consequently they will be at non-equilibrium states which cannot be predicted from classical thermodynamics as it can no longer be assumed that these states will be maximum entropy states.
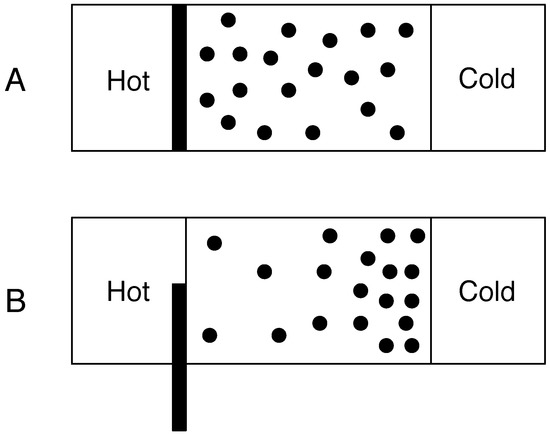
Figure 2.
Entropy in non-isolated systems. A rigid box that contains a number of gas molecules is connected to a hot and cold reservoir. In diagram A, an insulating partition separates the hot reservoir and the box. At equilibrium the molecules will be in a state of maximum entropy. In diagram B the insulating partition is partially raised so that an amount of heat flows from the hot reservoir into the box. This sets up a temperature gradient which results in a decrease in the entropy of the gas molecules. The dissipation of heat gradients keeps the gas molecules away from the maximum entropy equilibrium state. This non-equilibrium state may be a steady state with respect to the temperatures of the hot and cold reservoirs and the configurational entropy of the gas molecules.
3. Entropy production and the MEP principle
In the simple box model, a dial was used to adjust the heat flow such that the gas molecules were not at thermodynamic equilibrium. For the Earth’s atmosphere and other similarly dissipative systems, the system itself adjusts to the thermodynamic gradient. The MEP principle proposes that the Earth’s atmosphere and other complex systems are in particular thermodynamic states of maximum entropy production. The rate of change of entropy, , for these systems can be formulated as
where is the Net Entropy Exchanged across the boundary of the system and σ is the entropy produced within the system. In steady state where , we have
where F is the heat flux (e.g., see [1]) . Consequently, the rate of entropy production within the system can be calculated from the exchange fluxes of entropy into and out of the system. Such fluxes can be easier to compute than the entropy production within the system. Figure 3 shows the different components for the entropy produced within a simple system. In [6], Lorenz et al. formulated a simple 2-box climate model of the Earth, Mars and Titan that was able to accurately predict equatorial and polar temperatures by assuming that the rate of heat flux from the equator to the pole produced maximum rates of entropy production. This model is shown in Figure 4.
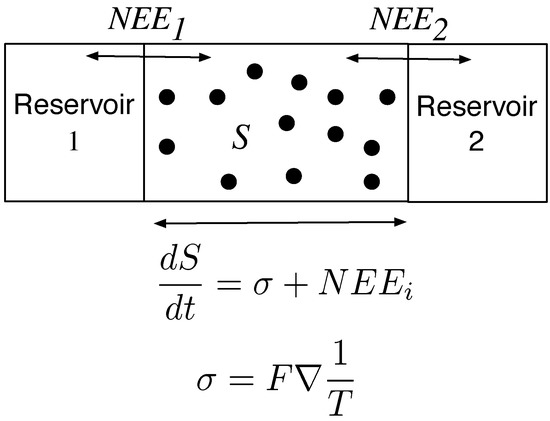
Figure 3.
The rate of change of entropy production of a system over time, is a function of the entropy produced within the system and the entropy that is imported and exported into its surroundings. If Reservoir 1 where hotter than Reservoir 2, there would be a flux of heat through the system from hot to cold. would import entropy into the system and would export entropy while σ would be determined by the temperature gradient and the rate of heat flux.
For Mars and Titan while the amount of insolation at the equator and poles are known, temperatures are not know. The approach was to assume that these atmospheres “select” the rate of heat transport such that σ is at a maximum. This was essentially the same approached adopted by Paltridge in [5] who solved a 10-box Earth climate model by assuming that latitudinal heat transport was at a steady state value that produced maximum rates of entropy production. As with Paltridge’s original study, no explanation was offered as to why these atmospheres were in these MEP states. However, given that there is a very large number of different ways for them to organise themselves, the fact that they are in MEP states seems to suggest that in some respects they “must” be in that state. The hypothesis proposed was that other atmospheres or other similarly complex systems would also be in MEP states and so a new and powerful approach to understanding such systems was possible.
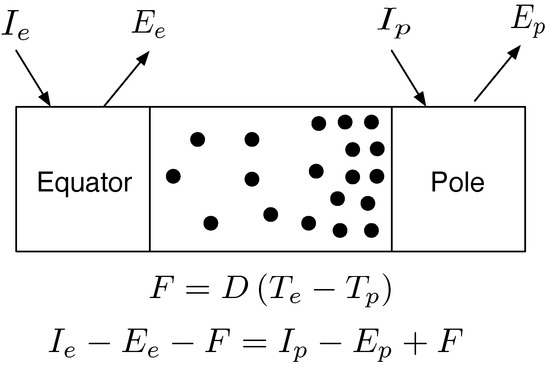
Figure 4.
Two box climate model. A simple two box climate model is shown. The equator receives more energy from the sun (I for insolation) than the poles; . Longwave emissions, E, are also larger; . The difference in insolation sets up a temperature gradient where the equator is hotter than the poles; . A certain amount of heat, F, flows over this gradient with a diffusivity term, D, parameterising how easily this heat flows polewards. Over decadal time scales, the Earth’s climate is in steady state: energy emitted equals energy absorbed.
3.1. Ambiguities of and Objections to the MEP Principle
The MEP principle as proposed faced two objections: First, if the MEP principle was applicable to a range of systems, we should expect empirical confirmation of the MEP principle from other studies. In the absence of other confirmation of MEP principle, we are faced with the possibility that the MEP principle is not a universal principle but something particular to the systems studied or even something particular with how these systems have been modelled. It should also be possible to reproduce them in controlled conditions. Experiments with fluids that have temperature dependent viscosity [10] would initially appear to possess the sufficient conditions to be in MEP states, however to date no such states have been observed [S. Schymanski, personal correspondence]. Second, no mechanism or explanation was proposed as to how the state of MEP was achieved in these or other systems. A number of studies by Dewar [8,11,12] have attempted to derive the MEP principle as an extension of the MaxEnt procedure of Jaynes [13,14]. This is an ongoing project (see Dewar this issue).
A symptom of the absence of an exact analytical understanding of the MEP principle is the inexact specification of when the MEP principle will and will not be applicable. A common expression within MEP studies is that MEP will be observed in systems that are “sufficiently complex”, or have “sufficient degrees of freedom”. Indeed, we began this paper with such an expression. This begs the question: how complex is sufficiently complex? For example, the Earth’s atmosphere is not in a state of MEP with respect to short to long wave radiation absorption and emissions because there are no real degrees of freedom for the system to do otherwise [15]. The question then becomes, what rate of entropy production is being maximised for any particular system? If the MEP principle is a description of some aspect of the real world, then our job is to identify those systems that we suspect are MEP systems. The procedure appears to be that we initially propose some system S1 to be a MEP system. We model this system and in doing so produce a function for the rate of entropy production. By finding those parameter values that maximum this function we are able to produce a set of predictions P1. If P1 are found to agree with observations, then we have at the same time identified S1 to be an MEP system and produced a useful set of predictions (e.g., temperatures on the surface of a planet and amount of heat flux). If P1 turns out to be inaccurate then we conclude that S1 is not an MEP system. The problem then arises of how is the MEP principle falsified? Any particular study that concludes that the MEP principle does not accurately predict some aspect of a system can be explained by claiming that the system is not a MEP system. Consequently, if one requires falsification to be a necessary condition of any scientific theory, the MEP principle is not a scientific theory.
4. Science and Falsification
In order to evaluate the epistemological basis of the MEP principle, we will consider the role of falsification in the formulation of scientific theories. The notion of falsification is central to the Popperian formulation of science [16]. This is how for example, an astronomy theory differs from a astrological one. An astronomy theory will have well defined terms under which observational evidence can be used to show that the theory is false. Popper argued that it is impossible to prove any theory is true. Rather we have a certain degree of confidence that it is true with that confidence being largely based on the quality of its predictions and how readily it is falsifiable. For example, consider two competing theories. Theory T1 produces more predictions that can in principle be falsified than theory T2. By Popper’s account, T1 is the better theory. In a sense it must be better because there is greater opportunity to disprove it. There is then an inverse relationship between information and probability of a theory being true. T1 will have more information than T2 as it provides more routes for falsification. This means that T1 is less likely to survive as it has more possibilities for being shown to be false. This use of survival was used in quite a literal sense as Popper envisaged a form of natural selection operating on scientific theories. Much as natural selection weeds out the weak individuals from a population, so falsification removes poor theories. This is how we can account for the notion of scientific progress which Popper formulates thus:
where PS is a Problem Situation at time 1. TT is the set of different and competing theories that seek to explain or solve PS. EE is the process of error elimination or falsification. Empirical and theoretical data are used to attempt to falsify theories with those theories that survive being part of the process by which new problems are formulated at time 2, PS, and so the process continues. In this fashion, problems beget solutions which beget new problems and scientific progress marches onwards.
PS1 → TT1 → EE1 → PS2
The natural law interpretation of the MEP principle is that it can make a number of accurate predictions for complex systems that defy analysis via other theories. However, as we argued in the previous section, any empirical evidence that does not agree with a MEP principle prediction does not represent any falsification of the theory, rather the identification of the “fact” that the system is not a MEP system. What appears to be required is the formulation of the rules of engagement for the MEP; under what conditions will the MEP apply to certain systems. In the absence of a set of rules or guidelines that allow us to identify MEP systems, then the MEP principle itself cannot be a scientific theory because it will always be possible to explain erroneous predictions as instances where the MEP principle was applied incorrectly. The natural law interpretation solution to this problem is to argue that the MEP principle is a developing theory and that at some point in the future a derivation may be produced that details exactly under what circumstances systems will and will not produce maximum rates of entropy.
While we acknowledge that there is still some way to go before the MEP principle is firmly established on analytical grounds, we believe that seeking a formulation of the principle that will guarantee the production of accurate predictions for the steady states of real world systems to be fundamentally misguided. Rather, the MEP principle is a procedure or method for increasing our information about real world systems. The particular utility of the MEP is not to reveal the “true” steady states of systems, but as a robust inference procedure that allows us to increase the amount of information about the fundamentally probabilistic states of systems. In order to explain this further, we must first clarify what we mean by the term “probability” and how it is related to information.
5. Information, Probability and Inference
The natural law interpretation of the MEP principle is that it is a description of particular systems. There is “something about them” such that they are in particular steady states of entropy production. There is an inherent probabilistic aspect to the MEP principle and we believe that it is a particular interpretation of probability that is largely responsible for the natural law interpretation. This is the “frequentist” interpretation of probability in which the probability of observing an event (e.g., a coin landing heads up) is proportional to the frequency of that event occurring over a very large number of trials. In order to produce an exact value for the probability of flipping a head or a tail we would need an infinite number of trails. That is, the probability of observing a heads or tails is a property of the coin in the same way that is has intensive and extensive properties such as mass or density. Conducting trials are analogous to taking measurements in that they are ways of finding out the properties of a system. Within equilibrium and non-equilibrium statistical mechanics, entropy and rates of entropy production can be regarded as probabilistic descriptions of aspects of the system. Therefore the frequency of observing that particular macroscopic state over a very large number of observations is related the Gibbs configurational entropy of a system:
where is the probability of the ith microstate for a given energy level. The connection to ergodicity comes from the frequentist interpretation of probability so that a system will explore those microstates possible for that energy level. The probability of finding a system in a particular configuration of microstates is proportional to how long it will be in that particular configuration over a very long period of time. One conclusion of this is that a system will, if given sufficient time, explore all possible microstates, no matter how improbable or however long one would need to wait in order to observe such improbable states.
5.1. Inference and Information
There are alternative interpretations of probability. Dewar’s derivations of the MEP principle are ultimately predicated on the Bayesian interpretation. Bayesian probability theories are subject to criticisms that are beyond the scope of this paper. Here we limit our argument to establishing that point that the MEP principle is only a cogent theory when one adopts a Bayesian interpretation of probability.
Rather than say that the probability of observing a Bernoulli trial event such as a coin landing heads up is a property of the coin, we instead say that assigning a probability to observing a heads is a way that we quantify what we know about the coin. For example, given the two possible outcomes (we ignore the possibility that the coin can land on its side), we propose the initial hypotheses of H1 that states that there is a 0.5 probability of the coin landing head’s up and H2 that states there is a 0.5 probability of tails landing. H1 and H2 are mutually exclusive and p(H1) + p(H2) = 1 . Suppose that we now conduct a number of trials and that we repeatedly get more heads than tails. We would being to suspect that the coin is not fair. It may be weighted. H1 and H2 were based on our initial beliefs about the system which we increasingly believe were not correct. However, given no reasons to suspect the coin (unless it was being flipped by a known crook!) there are no reasons to ground our beliefs otherwise. Consequently, the probability we ascribe to events can change as the amount of information we have about a system changes and so our degree of confidence of a particular hypothesis can change. Information can be obtained not only by performing trials (flipping the coin), but also making observations and measurements on the coin. For example we can weigh it, determine its centre of balance, assess how flat it is etc. We can also examine how the coin is flipped. In [17] Jaynes provides a tour de force in considering whether there is in fact such a thing as a random coin flip or any truly random process.
Probability can now be seen as assigning a value to our ignorance about a particular system or hypothesis. Rather than the entropy of a system being a particular property of a system, it is instead a measure of how much we know about a system. For the gas molecules in a box, at thermodynamic equilibrium, the probability of a particular molecule being at a particular place is equal to it being at any other place. We have absolutely no information as to exactly where it and all the other molecules are. The situation changes as we move away from equilibrium. For example, if there is a temperature gradient within the molecules, then it is more probable for a particular molecule to be nearer the cold reservoir rather than the hot reservoir. The more we know about the system, the more information we have on the boundary conditions, the more probable that a particular prediction for the position of a particular molecule becomes. Bayesian inference is the procedure which employs these notions of probability and information. It proceeds on the basis of making predictions about systems which are based on the available information. These initial predictions are then updated as and when information about the system is obtained. For the gas molecules, we could produce a set of predictions PG with each element of PG assigning a probability that the ith molecule was in the jth position (assuming a finite number of discrete positions). If we observe molecule n at position m, then all the probability functions of PG are updated to incorporate that information. In the language of the Bayesian Probability Calculus, an initial hypothesis H has a “prior” probability distribution function. The probability that evidence, E, will be observed that confirms H is the “posterior” probability distribution function. In the gas molecule case, if H is the hypothesis that molecule i is in position j, then the probability that H is true given the current evidence, E, is given with:
The process is essentially iterative as posteriors can inform the construction of new priors as new evidence is obtained and the process is repeated. As our information about systems change, the probabilities that we assign to events or hypotheses change.
6. MaxEnt and the MEP Principle
Bayesian inference can be seen as a procedure to leverage the most amount of information from what is currently known about a system. An important component of that procedure is the formulation of the initial prior functions. That is, given the information to hand, how do we construct initial probability functions for our hypotheses? Jaynes showed that the best position to adopt is one where the Shannon informational entropy of the initial probability density functions is maximised [18]. This will produce prior functions that will make only those assumptions that are justified by the available information. The Shannon Entropy of a message is proportional to the amount of information that the message communicates from sender to receiver [19]. For example if John has rolled a six sided die and sends a message to Jane that the side uppermost is an even number, then Jane has received information that allows her to ignore three possible sides out of six. In the absence of any message, Jane would assign uniform probability functions for the priors to all numbers. By constructing prior probability density functions with the maximum amount of entropy, we ensure that no additional assumptions “sneak in” to our initial beliefs. MaxEnt can be understood as allowing us to make the least worse initial predictions. MaxEnt is not a theory about the behaviour or property of real world systems, but a procedure or algorithm that scientists can use to make the most accurate or probable hypotheses and predictions about systems. As well as applications to equilibrium thermodynamics, MaxEnt has also been used in image reconstruction and spectral analysis. Jaynes’ long term (and unfinished) project was to show how the logic of Bayesian inference underpins all of science.
The MaxEnt approach is briefly illustrated here for the case of the ideal gas. The macroscopic equations that govern the behavior of the ideal gas such as the ideal gas law can be derived from MaxEnt in the scope of statistical mechanics. The derivation requires two, very basic constraints: energy and mass conservation. The energy conservation adds the Lagrange multiplier that yields temperature (or, more precisely , with being the Boltzmann constant), which then forms the basis for deriving the Boltzmann distribution etc. The example of the ideal gas in a state of thermodynamic equilibrium should therefore be the limit case of any non-equilibrium thermodynamic state as the most simple or least constrained.
To describe a state away from thermodynamic equilibrium, we need to add more constraints and information. If exchange of mass takes place, we get chemical potential and alike as additional Lagrange multipliers from these additional constraints. To describe gradients, we need to explicitly represent variables in space and/or time, which adds more and more information. In the context of the ideal gas, we still, however, stay within the well-established framework of thermodynamics, except that the assumption of thermodynamic equilibrium holds only at smaller scales.
Dewar has attempted to show that the MEP principle is an extension of Jaynes’ MaxEnt procedure to non-equilibrium states. Rather than producing predictive hypotheses for their equilibrium states, the MEP principle instead uses the available information in the most effective way in order to produce predictive hypotheses about the trajectories that these systems will take over time. If it is assumed that the systems are in steady state, then such predictions should be in agreement with observations of the system. Dewar has characterised the MEP principle as a procedure that turns information (in the form of constraints) into predictions, perhaps much as a mathematician is a biological machine that turns coffee into theorems. This can be an iterative procedure much in the same way as Popper envisaged scientific progress:
Information at time 1, I, is used to formulate boundary conditions for a model. The MEP principle is employed to produce a set of predictions, P. Observations (empirical and theoretical) at time 1, O, are compared to P with any difference between them being used to update the new boundary conditions at time 2, I. In terms of a procedure that increases information about systems, the MEP principle procedure perhaps somewhat paradoxically produces most information when O ≠ P. Observations can be seen as a message from the real world system to the model of that system. If this message has the same content as the set of predictions, then no additional information about the real world system is communicated. This may appear paradoxical because a correct prediction surely tells us that the information used to formulate the boundary conditions was sufficient for the production of accurate predictions. However, this only confirms the information that was already known. What we are primarily motivated to do is obtain new information. This only happens when the observation contains a certain amount of “surprise”. What is important in this procedure is its repetition which will allow the construction of a gradient which can help guide the formulation of new boundary conditions. This is analogous to the childhood game of “hunt the thimble” in which an object is hidden with the searchers only being told if they are warmer (nearer) or colder (further) to the object with reference to their previous guess. In this respect the MEP principle is conceptually compatible with an inference formulation of science in the terms proposed by Caticha in [20,21]. Indeed there are tantalising analogues between Caticha’s theories and Dewar’s recent attempted derivations of the MEP principle which have alluded to an information theoretic (and we would argue, inference) basis of Hamiltonian dynamics.
I1 → P1 → O1 → I2
7. MEP Principle and the Earth System
When we want to apply MEP to Earth system processes, we first should recognize that we deal with a world of molecules. Whether we discuss the large-scale motion of Earth’s atmosphere, the global hydrologic cycle, plate tectonics, or photosynthesizing organisms, these processes all deal with the transport and transformation of molecules at a highly aggregated scale. These dynamics are all subject to the energy and mass balance constraints of the Earth system. Hence, when we follow the MaxEnt approach and interpret MEP from an information theoretical perspective, then these two basic constraints yield us the classical thermodynamic variables as Lagrange multipliers. The information theory based interpretation quickly translates into a thermodynamic one. If MEP subjected to these two constraints does not yield predictions consistent with observations, it should not be seen as the failure of MEP per se, but rather as the lack of further relevant information, for instance in terms of additional constraints. Hence, there is no conflict between an information theory based derivation of MEP and the thermodynamic applications of MEP (as in e.g., [1,2,3,4]).
7.1. Earth System Processes away from Thermodynamic Equilibrium
As stated above, the state of thermodynamic equilibrium would seem to serve as a reference state that is the most simple in its nature since merely the energy and mass balance contain the relevant information. Imagine Earth in a state of thermodynamic equilibrium. We would need separate energy and mass balances for the different states of matter: the gaseous phase (mostly the atmosphere), the liquid state of water (mostly oceans), and the solid state of water (mostly ice sheets) and of the Earth’s crust and interior. These balances would yield the typical thermodynamic variables as Lagrange multipliers, such as the temperatures and pressures of the atmosphere, oceans, ice sheets etc. The overall state of the Earth would then be characterized by a dozen or so thermodynamic variables in total.
The present-day Earth is far away from thermodynamic equilibrium so we need more information to describe its state. What does this mean? First, we have variations of thermodynamic variables in space and time. To describe such gradients, we clearly require more information to describe these. Examples of such gradients and how these relate to thermodynamic variables are: topographic gradients are reflected in the differences in height between mountains and the sea floor, resulting in gradients in gravitational potential; temperature gradients are maintained between the surface and the air aloft, between the tropics and the poles, and between the oceans and the land. Gradients in relative humidity are gradients in the chemical potential of water vapor. High concentration of reactive oxygen in Earth’s atmosphere and reducing conditions in the Earth’s mantle result in chemical potential gradients.
All of these gradients can be expressed in terms of common variables of equilibrium thermodynamics: radiative temperatures, kinematic temperatures, chemical potentials and so on. The underlying assumption is that the well known laws of equilibrium thermodynamics still hold and can be applied, but at a much smaller scale. To do so, we then introduce the notion of local thermodynamic equilibrium. In other words, to analyse the Earth with equilibrium thermodynamics, we no longer apply equilibrium thermodynamics at the planetary scale, but rather at a much finer scale. It would then seem logical to hypothesize that as a system moves away further and further away from thermodynamic equilibrium, the system would need to be represented at finer and finer scales. Dynamic properties like temporal variability and spatial heterogeneity are then inherently a result of a system that is driven far away from thermodynamic equilibrium. This should, for instance, be reflected in the spatial and temporal autocorrelation structures, as illustrated in Figure 5. At thermodynamic equilibrium, trivially so, we find the highest autocorrelation since the thermodynamic variables are constant in space and time. As the system moves further and further away from thermodynamic equilibrium, these structures should show less and less autocorrelation. Less autocorrelation in turn represents increased “memory” of a system. Since such a state is associated with greater gradients and more irreversibility and entropy production of the fluxes that are driven by these gradients, this would suggest that the thermodynamic state of a system away from equilibrium is directly linked to its memory and its rate of entropy production.
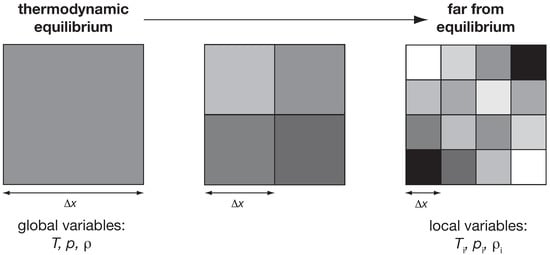
Figure 5.
Illustration of how variables should change as a system is maintained further and further away from thermodynamic equilibrium. The state of thermodynamic equilibrium is characterized by global variables (e.g., ) that are constant in space and time. The further the system is maintained away from equilibrium, the more the state should be associated with larger and larger gradients in space and time. The characteristic spatial scale at which the assumption of thermodynamic equilibrium applies should therefore decrease correspondingly, resulting in local variables (illustrated by ).
7.2. Increasing the Resolution of Earth System Models: a Practical Application of the MEP Principle
We conclude this section with a brief discussion on how the MEP principle can be used to inform Earth System Models and so increase our information about the Earth. The fundamental challenge all Earth System Models face is finding the spatial and temporal resolution that allows the numerical solutions to be computationally tractable with the resources currently available but not to coarse grain the systems so much that important dynamics are lost. There would appear to be an inevitable trade off between model resolution and time required for computation. The lowest level of resolution is the “grid” which is a volume of ocean, land and atmosphere. At the scale of its grid, a model will assume local thermodynamic equilibrium if it parameterizes this grid scale by one set of variables. While there are probably no obvious violations of the second law in such models, there are nevertheless several issues related to the thermodynamic formulation of processes within such models. First, fluxes are not always expressed in terms of thermodynamic gradients that drive fluxes. For instance, it is common to model condensation leading to instantaneous precipitation while such a conversion should be driven by the chemical potential gradient associated with supersaturated vapor. Also, in terrestrial vegetation models, root respiration releases carbon dioxide that quite often is released into the free atmosphere instantaneously instead of being driven by the emergent gradient that drives the flux from the root to the soil to the air. In a thermodynamic context, these models contain the formulation of gradients that do not respond to fluxes and are therefore likely to result in biases in the magnitude of these fluxes.
We propose that the MEP principle applied at the grid scale may help allow better parameterizations of the grid scale behaviour which will include sub-grid scale spatial heterogeneity and variability within time steps of integration. This would then imply that local thermodynamic equilibrium no longer need to be assumed at the grid scale. For example the MEP principle should allow us to derive better parameterizations of subgrid scale processes in numerical simulation models, see [22]. Figure 6 shows how the MEP principle can be used to increase the accuracy of the parameterizations of sub-grid scale processes.
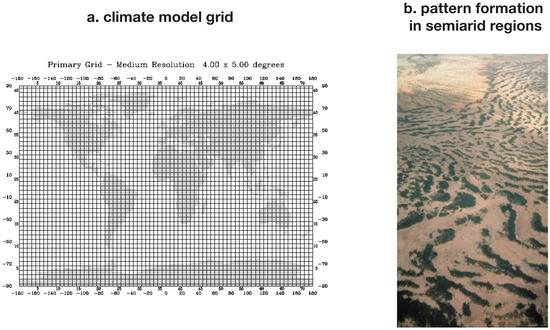
Figure 6.
Illustration of (a) a global grid used in climate models. Such grids are used for a discrete representation of variables, such as temperature, and implicitly assume a state of thermodynamic equilibrium within the grid. Subgrid scale heterogeneity, as found for instance in form of pattern formation of vegetation found in semiarid regions (b), illustrate that subgrid scale processes can operate far from thermodynamic equilibrium. MEP could help to scale up subgrid scale heterogeneity so that this is adequately represented at the grid scale, as for instance shown by [22]. Photo credit: Stephen Prince.
8. Discussion
In this paper we have argued that the MEP principle is not a physical law that describes the properties of a certain class of system, but is instead a potentially widely applicable method of inference which we believe has particular utility for increasing our information about non-equilibrium systems such as the Earth. Our argument required a Bayesian interpretation of probability which centred around our level of ignorance about systems and their dynamics. Probability is not a description of some property of a system, but rather a quantification of how much we know about it. The MEP principle is a potentially iterative procedure in which available information about a system is used to produce predictive hypotheses which are then compared with observations. Any differences between observational data and predictions corresponds to additional information about the system that can then be used to update the model. We argued that the MEP principle procedure is of particular utility because like the MaxEnt procedure that is used to produce the most probable predictions for equilibrium systems, the MEP principle leverages the maximum from the information to hand in order to produce the most probable predictions for the steady state trajectories of non-equilibrium systems. This interpretation of the MEP principle means that it is effectively silent on what information is and is not relevant to the formulation of boundary conditions which are used as Lagrange multipliers within the MEP principle procedure. It is our job as intelligent, inquisitive agents to capture the required information. Consequently, the absence of an exact definition of the “sufficient degrees of freedom that a system needs to possess in order for the MEP principle to be observed” does not represent an outstanding specification or detail of the MEP principle but is rather an unavoidable conclusion of any inference procedure. The procedure itself cannot tell us what is and what is not relevant to formulating a model. It can only use the information that we give it, which it promises to use as effectively as possible.
The other side of this story is that the MEP principle can also be used to find information that is not necessary for the production of accurate predictions. For example, if our initial information or beliefs about a state is that it is far from equilibrium and complex with many processes occurring within it, we may build a commensurately complex model that may produce accurate predictions. Some Earth System Models and General Circulation Models are very complex systems in their own right and they may very accurately predict aspects of the Earth’s climate. The MEP principle shows that some of the information in these models, in fact nearly all the information, is irrelevant when it comes to predicting equatorial and polar temperatures, and rates of latitudinal heat transport. The MEP principle can be applied in conjunction with Occam’s Razor in that we should be motivated to find the model that produces accurate predictions with the minimal amount of information. For example in the 2-box climate model, a single scalar parameter, D, controlled the rate of heat flux from the equator to the poles. Buried within D must be the net effects of the properties of the Earth’s atmosphere and oceans. Not including such details tells us that such information is irrelevant for the purposes of the model. This issue is related to a question that arose during the MEP workshop in Jena 2009: What if the Earth’s sea was made of vinegar? Given that the simple 2-box model has no information about the composition of the oceans, then it would produce exactly the same set of predictions if the oceans were suddenly replaced with vinegar. This question was in part addressed by [6] that showed the MEP principle was able to accurately predict aspects of atmospheres that are in many ways very different to the Earth. This demonstrates that for complex systems such as planetary atmospheres, information that pertains to their composition may not be required for the production of accurate predictions of some of their properties. If we wished to understand the role of the Earth’s oceans in the transport of heat, then it may well be necessary to include more information in our model that may include certain properties of water. The amount of information we provide to a model is not only determined by what we currently know about the system, but what we are hoping to find out.
We argued that when employing the MEP principle in the analysis of the Earth system, the conservation of energy, mass and momentum are unavoidable constraints. This leads to an effective correspondence of the information theoretic interpretation to a non-equilibrium thermodynamic one as energy, mass and momentum conservation will supply Lagrange multipliers to the MEP principle procedure such that the information theoretic aspects can be safely overlaid with physical thermodynamic concepts. This allows a number of simplifications in model formulations which rest ultimately on the MEP principle but which can be formulated in non-information theoretic terms. Given that our motivation in modelling systems is to increase our understanding of them, we believe that this interpretation of the MEP principle best captures what scientists are actually doing when they use it.
Acknowledgements
This essay was motivated by the discussions held at the “Maximum Entropy Production in the Earth system” workshop, held at the Max-Planck-Institute for Biogeochemistry in Jena, Germany in May 2009. The authors thank the Helmholtz-Gemeinschaft as this research has been supported by the Helmholtz Association through the research alliance “Planetary Evolution and Life”. The authors would also like to thank Fabian Gans and Stan Schymanski for their insight and suggestions and the comments from three anonymous reviewers that have greatly improved the manuscript.
References
- Ozawa, H.A.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Kleidon, A.; Lorenz, R.D. Non-Equilibrium Thermodynamics and the Production of Entropy: Life, Earth, and Beyond; Springer, Berlin, 2005; Chapter 1. [Google Scholar]
- Kleidon, A. Non-equilibrium thermodynamics and maximum entropy production in the Earth system: applications and implications. Naturwissenschaften 2009, 96, 635–677. [Google Scholar] [CrossRef]
- Paltridge, G.W. The steady-state format of global climate systems. Quart. J. Royal Meterological Soc. 1975, 104, 927–945. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Lunine, J.I.; Withers, P.G. Titan, Mars and Earth: entropy production by latitudinal heat transport. Geophys. Res. Lett. 2001, 28, 415–418. [Google Scholar] [CrossRef]
- Lorenz, R.D. Planets, life and the production of entropy. Int. J. Astrobiol. 2002, 1, 3–13. [Google Scholar] [CrossRef]
- Dewar, R. Maximum entropy production and the fluctuation theorem. J. Phys. A 2005, 38, 371–381. [Google Scholar] [CrossRef]
- Bumstead, H.A.; Van Name, R.G. (Eds.) The Scientific Papers of J. Willard Gibbs; Dover Publications: New York, NY, USA, 1961.
- Jellinek, A.M.; Lenardic, A.M. Effects of spatially varying roof cooling on Rayleigh-Benard convection in a fluid with temperature-dependent viscosity. J. Fluid Mech. 2008. in revision. [Google Scholar]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A 2003, 36, 631. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum Entropy Production and Non-Equilibrium Statistical Mechanics. In Non-equilibrium Thermodynamics and the Produciton of Entropy; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin, Germany, 2005; pp. 41–53. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics, II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Essex, C. Radiation and the irreversible thermodynamics of climate. J. Atmos. Sci. 1984, 41, 1985–1991. [Google Scholar] [CrossRef]
- Popper, K.R. Conjectures and Refutations: The Growth of Scientific Knowledge; Routledge: Florence, KY, USA, 1963. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Jaynes, E. Where do we stand on Maximum Entropy? In The Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; MIT Press: Cambridge, MA, USA, 1979; p. 15. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Caticha, A. Information and entropy. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering; Knuth, K.H., Ed.; AIP: New York, NY, USA, 2007; Volume 30. [Google Scholar]
- Caticha, A. From Information Geometry to Newtonian Dynamics. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering; Knuth, K.H., Ed.; AIP: New York, NY, USA, 2007; Volume 30. [Google Scholar]
- Schymanski, S.J.; Kleidon, A.; Stieglitz, M.; Narula, J. Maximum Entropy Production allows simple representation of heterogeneity in arid ecosystems. Phil. Trans. Royal Soc. B: Biol. Sci. 2009, in press. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.