Abstract
The steady increase in energy demand for residential consumers requires an efficient energy management scheme. Utility organizations encourage household applicants to engage in residential energy management (REM) system. The utility’s primary goal is to reduce system peak load demand while consumer intends to reduce electricity bills. The benefits of REM can be enhanced with renewable energy sources (RESs), backup battery storage system (BBSS), and optimal power-sharing strategies. This paper aims to reduce energy usages and monetary cost for smart grid communities with an efficient home energy management scheme (HEMS). Normally, the residential consumer deals with numerous smart home appliances that have various operating time priorities depending on consumer preferences. In this paper, a cost-efficient power-sharing technique is developed which works based on priorities of appliances’ operating time. The home appliances are sorted on priority basis and the BBSS are charged and discharged based on the energy availability within the smart grid communities and real time energy pricing. The benefits of optimal power-sharing techniques with the RESs and BBSS are analyzed by taking three different scenarios which are simulated by C++ software package. Extensive case studies are carried out to validate the effectiveness of the proposed energy management scheme. It is demonstrated that the proposed method can save energy and reduce electricity cost up to 35% and 45% compared to the existing methods.
1. Introduction
Energy, a scare resource that needs to be efficiently utilized, is considered the most indispensable component in modern society. For a typical home, energy losses are generally higher due to line losses increased by a factor of double []. These energy losses can be minimized by developing an efficient home energy management scheme (HEMS) that plays a crucial role in our daily life due to increasing energy demand []. The minimization of energy cost and the maximization of user comfort are the typical optimization problems in recent smart homes [,]. The authors in research [] illustrate an aggregator based household energy scheduling plan in the smart grid framework where all home appliances are managed by different power scheduling schemes. However, the backup battery storage system (BBSS) is not considered in that research. Electricity consumers are not permitted to access the grid side mechanisms due to the high voltage grid and sophisticated device operation. They can manipulate on energy consumption to minimize the peak demand while reducing electricity bills [,]. To decrease electricity costs of residential users (RUs), it is important to maintain an energy scheduling plan for electrical appliances concerning the price of the respective time slot. The energy management of home appliances deals with utility tariffs and usages patterns []. Conversely, the smart home energy management scheme within the smart grid environment can integrate the alternative sources of energy and optimize the monetary cost []. Authors in research [] illustrate the impact of the change in users’ behavior in the smart grids framework. The smart consumption and production behaviors are analyzed in this study to assist smart grid diffusion. The energy management is highly dependent on demand response in a smart grid framework which is illustrated by evolutionary analysis in [].
Residential utility management systems have been developed and validated through simulations and several case studies [,]. However, they did not consider the satisfied power demand and power-sharing algorithm to effectively handle the residential consumer’s power demand. Researchers have taken some initiatives to manage a range of household appliances based on energy demand pattern. Most of the literature is related to minimizing the energy cost with carbon emissions and the impact of renewable energy integration in the smart grid []. A real-time energy management problem was solved using a modified particle swarm optimization to investigate the nominal battery state of a microgrid environment while minimizing operating charge. This work was extended to consider the degradation cost of the battery for a two-step ahead energy management scheme []. In [], the authors demonstrated battery degradation costs which solely depends on a day-ahead energy scheduling and on a charging-discharging patterns. The optimization problem is solved using a framework consisting of Rainflow algorithm, particle swarm optimization (PSO), and scenario techniques. However, in these papers, the power-sharing algorithm and backup battery storage system are not taken into account. The authors of [,] provided a compact assessment of home energy management systems (HEMS). They explained the initial challenges of HEMS and then outlined some insights on the existing literature regarding the modeling of demand-side management (DSM) followed by wireless communication infrastructure. An optimization technique is developed through several programming strategies to handle home appliances with a solar system installed at the premises []. However, the impacts of different load patterns such as peak, off-peak and, mid-peak loads on renewable energy and BBSS are not considered. A fuzzy logic-based home energy management system (HEMS) is developed by the authors in [] which is more effective compared to [,] but the lowering of energy cost by applying power-sharing algorithm is not taken into account. The home batteries, monitoring technologies, and smart heat pumps are analyzed in a smart grid architecture to show how the householders participate in HEM [].
While several works deal with the advanced methods, these methods are not typically adopted by industry due to the reliability and security issues of a power system. Therefore, in order to minimize energy consumption and cost for residential consumers, this research develops an efficient energy management scheme using commercial software, C++, considering RESs and a BBSS integrated for smart grid model. The proposed HEMS offers higher customer satisfaction with low energy costs compared to the existing method.
The contributions of this paper can be listed as follows:
- A computationally efficient simulation model for HEM is developed using the C++ software package.
- The proposed model enables a power-sharing strategy in a community being assessed sequentially.
- The power-sharing technique with the proposed model saves energy cost up to 35% and 45% compared to conventional techniques.
- Mathematical modelling is developed to facilitate extensive analysis.
The rest of the paper is organized as follows: Section 2 discusses the problem description, existing power management system, and smart grid architecture including advanced smart metering infrastructure. Section 3 explains the system model, including a solar generator, wind generator, energy storage systems, loads and utility grid. Mathematical modeling of a smart home and the proposed algorithms are also presented in the section. Analysis of the results and graphical representation of simulation results are elaborated in Section 4. Finally, the conclusion this research is depicted in Section 5.
2. Problem Description
In this section, the proposed smart grid architecture and its advanced features with the application of intelligent smart metering infrastructure in the smart grid framework are presented in this section.
Smart Grid Architecture
The rapid growth in household appliances has significantly increased the power demand of residential consumers. Nowadays, most electricity demand is met by fossil fuel-based generation system which heavily pollutes the environment by emitting greenhouse gas [,]. According to the international standards, each country must put a cap on the carbon emission to save the environment. Thus, researchers are working hard to figure out the new means of electricity generation. In this research, the renewable energy sources (RESs) integration is found to be one of the most costs effective and environment-friendly solutions [,]. Normally, residential loads consist of washing machine, freezer, fans, lights, laptops, television, heater, dishwasher, microwave woven, and so on. Most of the residential consumers suffer from load shading, unstable voltage levels, service line loss, higher utility tariff, unscheduled system maintenance, and so on. To overcome these limitations, it is important to build an effective energy optimization method. To address these issues, a smart grid architecture is proposed with an efficient home energy management scheme (HEMS) to provide a profitable and sustainable solution.
The proposed community-based smart grid architecture illustrated in Figure 1, consists of three different scenarios considering local utility supply, renewable energy sources (RESs) such as solar cell and windmill and backup battery storage system (BBSS). It has three different energy communities such as community A, B, and C. To identify residential consumer effectively these communities are considered. Moreover, we have considered three scenarios where scenario 1 considers a residence with local utility supply as the primary source of energy whereas scenario 2 considers renewable energy as the primary source of energy and local utility supply as the secondary source. Besides, scenario 3 uses renewable energy and backup battery storage system (BBSS) as a primary source and local utility as secondary source in case of scarcity. When any particular consumer request power and met by the energy community is called satisfied power demand. In a day, during any particular period if any user requests power to the community and receives sufficient power called satisfied power demand. An efficient power-sharing algorithm is developed to meet user power demand using battery power sharing among the community. The novelty of this research is power-sharing technique for the residential consumers within the community [].
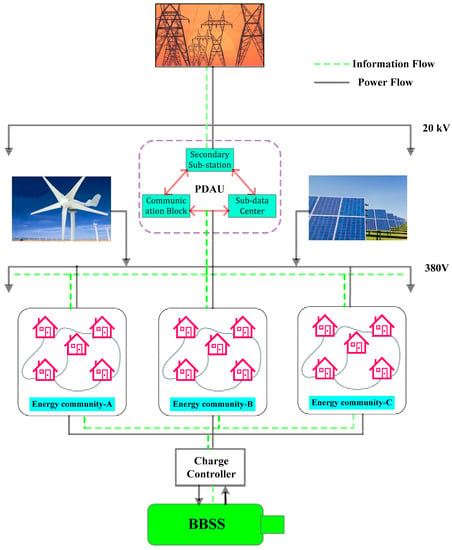
Figure 1.
Proposed community-based smart grid architecture.
A backup battery storage system (BBSS) bank is used to tackle emergency cases while all other power supplies are off. The BBSS charging and discharing are performed based on real-time pricing in order to reduce daily operation cost. Each residence has local utility supply, solar and wind power generation, smart battery, and smart meter. The smart meters are connected with all smart home appliances via a wireless connection. The use of smart meters (SM) in smart grid facilitates to record the exchange of information between utility companies, and electricity consumption. Home appliance usages are managed by scheduling and switching on/off some of them and track consumption over a period [].
A smart home provides an excellent interface between household applicants and home appliances to keep energy use record and take essential and effective decisions []. All home appliances are connected via smart meters and permit a consumer to move energy use from peak-hours to mid-peak or off-peak hours []. It is capable of detecting the energy use charges in real-time by taking some electrical parameters.
The advanced smart metering architecture in the smart grid framework outlined in Figure 2 consists of metering and communication infrastructures. The SM unit includes time-of-use price monitoring, demand-side management, and automatic meter reading.
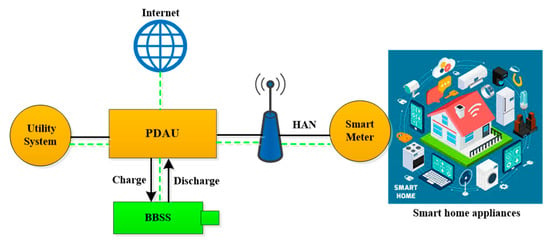
Figure 2.
Advanced smart metering architecture in the smart grid framework.
The wireless communication technologies permit dual flow to enable the smart meter. Thus, smart meter permits exchange information with distant centers and to execute the control instructions. Multiple home appliances are connection with the smart meter in the residential premises by the aid of home area network (HAN). Wireless technologies such as ZigBee, Wi-Fi, and WiMAX [,] are effectively used in the smart grid environment. The benefits of advanced smart metering infrastructure are outlined below:
- Time-of-use pricing information can acquire from the distant consumer price indications.
- Customer’s energy use information can accumulate, store and notify any particular time intervals or real-time.
- A detailed load patterns can develop the energy management process effectively.
- Smart meter can locate and identify the outages of any particular consumer by sharing a control message throughout the entire energy community.
- Power circuit can open or close over a long distance.
- Feasible to identify line losses and stealing exposure.
These meters send and receive information from the power data aggregator unit (PDAU) and permit residential consumers to handle their household appliances distantly. SMs of those communities are designed in such a way that allows them to be monitored by PDAU. If any users have extra demand, the smart meter sends a demand message to PDAU. After receiving the message, PDAU executes a power-sharing algorithm (PSA) to sequentially fulfill the user demand. Frist, PDAU forwards a demand message in the whole community. If the neighbor user can meet the extra demand, PDAU channels the excess stored energy of neighbors to the desired user. If demand cannot be fulfilled by neighbor users within the community, power will be acquired from the local utility companies. Moreover, if all power suppliers are unable to provide power then if any other user who wishes to receive power can take from BBSS by the permission of PDAU. PDAU is the main controller of this infrastructure. The BBSS keeps charging through the charge controller via a local utility supply while energy charges at low price intervals. Besides, BBSS can discharge when the community consumer energy demand is increased or all other supplies are off. To implement this framework, a simulator is designed and developed to evaluate the home user power consumption and cost considering satisfied power demand (hourly & daily basis) for one week. This method can save a significant amount of energy and cost compared to the existing systems.
3. System Modeling
This section deals with system components such as solar and wind generator, energy storage system, loads and utility grid, and a typical energy consumption profile for residential consumer’s and home appliances considering peak-load, mid-peak, and off-peak loads and real-time electricity prices.
3.1. System Components
3.1.1. Solar Generator
Photovoltaic (PV) panels use sunlight to convert solar energy into usable DC electricity. The amount of PV power generated depends on the array size, solar radiance and solar insolation. Solar radiance is emphatically relying on surrounding climate and varies significantly as depicted in Figure 3. In order to gain maximum yield, PV panels are equipped with maximum power point tracking (MPPT) technology []. The performance of a PV system is assessed based on its output power. Output power depends on the size of the array and the overall efficiency of the installed PV system. PV power output as a function of solar irradiance and being operated at MPPT mode is defined using the following equation:
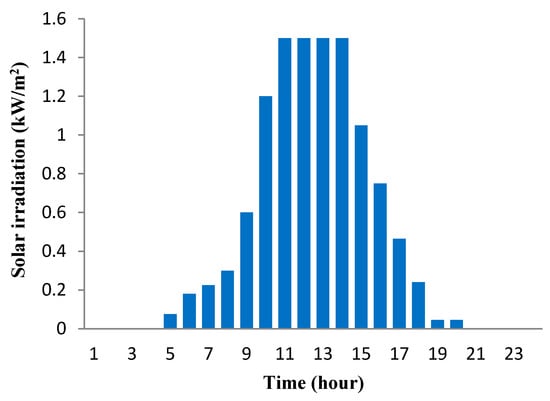
Figure 3.
Predicted solar irradiation over a 24 h horizon.
In Equation (1) above, represents efficiency, and A is the PV panel area. SI is the solar irradiation, t0 is the air temperature, is the temperature coefficient of the maximum output power and is usually denoted as a negative percentage per °C or K. The PV technology and manufacturing parameters have great impact on , this study considers as −0.005/°C. The range of for silicon cells is between 0.004–0.006 per °C []. The expression of power for several solar PV panels is given below:
where Ns is the number of solar generators.
3.1.2. Wind Generator
Wind power is a vital renewable energy resource that continues to thrive around the world due to features such as abundance, clean nature and being readily available. It is the method of power generation by rotating turbine blades installed at an elevated height. However, power generated from wind turbines is highly intermittent and stochastic in nature. It is highly dependent on the available wind speed and significantly varies based on the installation height. Figure 4 below illustrates wind speed over a range of time. The following power-law equation is used to convert wind speed recorded by anemometer (installed at tower heights) and transfer them based on hub heights []:
where velocity at hub height h0 is v0, velocity at hub height h is v, and the power-law exponent, α, depends on several parameters as presented in [] which takes a value of 1/7 for open space. The wind turbine power as a function wind velocity can be represented as a piece-wise function below []:
where the rated power is Pr, the wind rated speed is vr, the cut-in wind speed is vc, and the cut-off wind speed is vf. Turbine manufacturers define a cut-in and cut-off speed for safety issues. The wind generator does not produce any power beyond the cut-off wind speed. The expression of total power for a number of wind turbines is given below []:
where Nw is the number of wind generators.
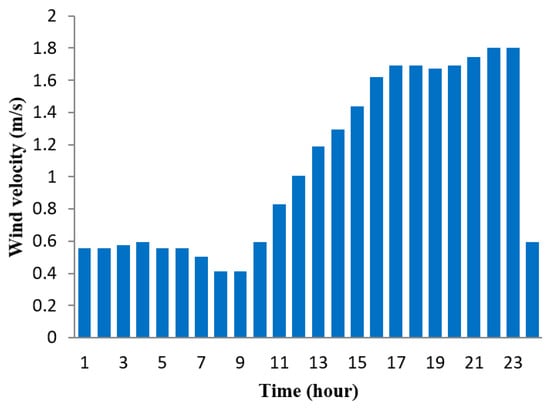
Figure 4.
Predicted wind velocity over a 24 h horizon.
3.1.3. Backup Battery Storage Systems (BBSS)
The different types of energy storages, such as superconducting magnetic energy storage, batteries, flywheel energy storage, and compressed air energy storage, are studied in power system. Each of the energy storage devices has different features such as high-power density, high-energy density, high response time and so on. In this study, electrochemical batteries are used due to its high energy density. The charging and discharging of ESS can reduce the effect of the unpredictable nature of renewable energy sources (RESs) on the smart grid to balance power generation and demand. The expression for charging and discharging of battery is given as below”
Subject to the following constraints:
where the battery charging power at time t is Pc(t), the battery discharging power at time t and Pd(t), the energy storage at time t is BL(t), the time interval is Δt, the charging efficiency is ղc, and the discharging efficiency is ղd. This study considers ղc and ղd as unity for simplicity.
BLmax > BL(t) > BLmin
3.1.4. Loads and Utility Grid
The load profiles of residential users are illustrated in Figure 5, Figure 6 and Figure 7. There are three different load patterns shown in separate figures. The maximum load is approximately 0.43 kW during peak-hours, the mid-peak hour is 0.42 kW during intermediate-hours and the minimum load is 0.32 kW during off-peak hours.
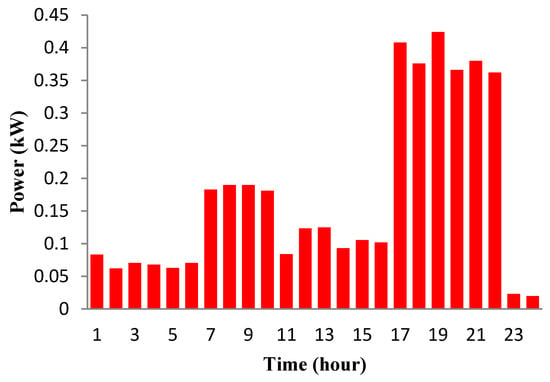
Figure 5.
Predicted load profile of a house during peak hours over a 24 h horizon.
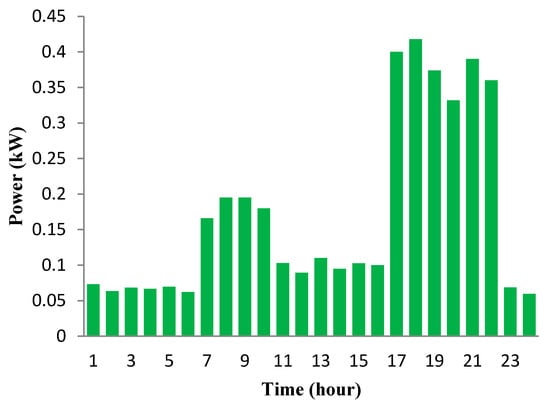
Figure 6.
Predicted load profile of a house during mid-peak hours over a 24 h horizon.
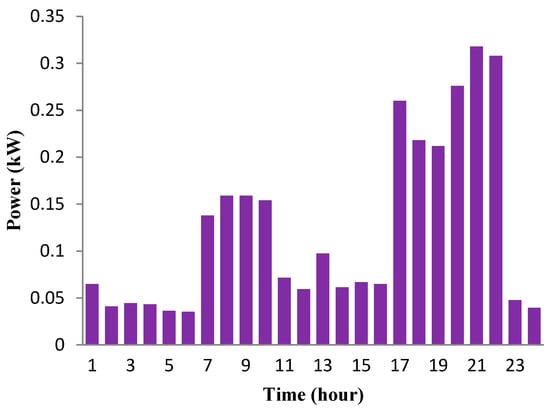
Figure 7.
Predicted load profile of a house during off-peak hours over a 24 h horizon.
The estimated loads can meet the primary home appliances such as washing machine, freezer, fans, lights, laptops, television, heater, dishwasher, microwave woven etc. Home user energy demand patterns are fluctuating with time. It is assumed that the energy demand profiles are same for all residential consumers. Several measurements output values can shape the diverse energy demands for individual consumer.
Figure 8 indicates the real-time electricity prices for energy purchase per unit that is taken as a grid model in this study. These dynamic prices help electricity customers to schedule flexible loads, such as water heaters and washing machines. Electricity prices are generally announced an hour ahead from a distribution management company. We have considered a community smart grid that is connected to the grid.
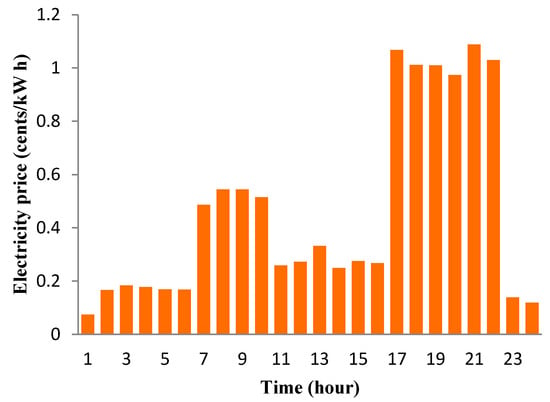
Figure 8.
Predicted average electricity prices of a house over a 24 h horizon.
We have considered that the project is executed in an environment where building renewable energy plant is encouraged by the local government and the generated power can exchange to the utility grid without any transfer threshold. This process is due to insufficient power production, leading to low voltage outlines in the smart grid energy community. As a result, renewable energy owner can add more money on their utility business to help community inhabitants as well as to get profits.
3.1.5. Mathematical Modeling of a Smart Home for the Proposed Power-Sharing Algorithm
In this section, we analyze and model the electrical smart home appliances with renewable energy sources (RESs), backup battery storage system (BBSS), and related mathematical parameters in detail. The mathematical model contains different parts such as photo-voltaic system, small scale windmill, smart battery, backup battery storage system, utility tariffs, home appliances and their expenditure, etc. Renewable energy is generated by the solar cells and windmill that store in a smart battery. Total local renewable energy generation is formulated by the given equation:
where PB is the battery power storage, PPV and PW denote the solar photovoltaic and wind power, respectively. The power generation by photovoltaic solar cell, PPV, and wind mill, PW, are directly stored in a smart battery which is outlined by PB. The total capacity of the battery is greater than sum of solar and wind power in order to save the battery from overcharge.
PB = pPV + pW
A single residential consumer all smart home appliances energy consumption is defined by the given equation:
where ETHA denotes the total energy of home appliances, EL indicates lighting load, EWM illustrates washing machine, ER presents refrigerator load, EC denotes computer load, and EDW is the energy taken by dishwasher and EH is the heating load.
ETHA = ∑ (EL + EWM + ER + EC + EDW + EH)
All home users considered renewable energy as a primary source and utility as a secondary source.
where EU represents the user energy consumption, EB is the battery energy and EBB is the backup battery energy. Similarly, ETHA indicates the total home appliance’s energy of residential consumers. The user energy consumption is equal to the sum of battery and backup battery storage minus the total home appliances energy. Home users extra power demand is meet by the utility system and it is defined by the given Equation (11) and extra energy is formulated by the Equation (12).
EU = (EB + EBB) − ETHA
EEE = ∑ (EUO − EU)
EEEC = ∑ ((EUO − EU) × EUC))
EEE represents the extra energy, EUO is the energy of utility operator and EU is the user power. Similarly, EEEC defines the extra energy cost and EUC illustrates the utility cost. We have considered four user energy communities and the total energy consumption are calculated by the given equation:
where n equals to 4 (the total number of user energy communities) and ETU represents the total user energy. We have considered a group of twenty home users in our proposed community smart grid and the total energy consumption in a community is given by the following equation:
where ETUE represents the total user energy and EU denote the individual user energy. Total users energy cost in a community is carried out by the given equation:
where ETUEC represents the total user energy cost and EU denote the individual user energy and EUC illustrates the individual user energy cost. The total number of hours in a day is given by the given equation which is 24 h.
where T equals to 24 due to 24 h in a day and HTNH represents the total number of hours and EH denote the hourly user energy consumption. Total energy consumption and cost for a week is shown in the given equation:
where W equals to 7 and DTND represents the total number of day and ED denotes the daily user energy consumption. Total satisfied power demands are carried out by the given Equation (18)
where PTSPD denotes the total satisfied power demand and PSPD represents the satisfied power demand. However, the sum of individual satisfied power demand is equal to the total satisfied power demand.
ETUEC = ∑ (EU1 + EU2 + EU3 + EU4 ……….+ EU_N) x EUC
pTSPD = ∑ pSPD
3.2. The Proposed Algorithm and Simulations
In this section, we introduce the simulation framework and proposed a power-sharing algorithm. An advanced and efficient power-sharing algorithm is proposed which defines the step by step simulation execution process and priority basis energy management for residential consumers is placed in the Appendix A.
The Proposed Power-Sharing Algorithm (PSA)
The real-time electricity prices are considered in the simulation process, allowing us to overcome the conventional optimization problems. To resolve these issues an efficient algorithm is designed called power-sharing algorithm (PSA). The PSA is used to optimize the new proposed community- based smart grid model considering a backup battery storage system (BBSS) []. In this study PSA is also discussed to effectively share user battery power and backup energy storage within the community smart grid. The prime objective of the proposed algorithm is to minimize the energy cost with a high level of customer satisfaction. Residential consumers consume most of the energy to meet their smart home appliances. When smart battery and local utility are unable to support, a BBSS is connected with the power data aggregator unit (PDAU) to support the electricity supply. BBSS channels the energy to the respective user by the coordination of PDAU. All decisions including emergency case are made by PDAU. If the residential user (RU) energy consumption is greater than the battery capacity then battery needs to charge. At that time the user sends a demand message to the PDAU. Taking approval of PDAU, the user can receive shared energy from other user battery. Moreover, when all supplies are off, the requested user receives power from the BBSS service.
4. Simulation Results
The proposed energy management procedure and simulation results are outlined in this section to analyze and compare the effectiveness of the proposed HEM scheme. An on-grid tied smart grid framework is taken into account in this research. Sufficient PV solar and wind power generation reduce the utility tariffs. An efficient power-sharing algorithm (PSA) is developed to effectively manage residential consumer’s smart battery power-sharing. We have also considered a backup battery storage system (BBSS) having a group of a battery bank to support residential consumers while all supply is off. The capacity of BBSS is selected as 30 kWh, and the minimum and maximum energy storage margins are taken as 5 kWh and 30 kWh, respectively.
The primary energy level of the BBSS is considered as 10 kWh. The smart grid constraints and the other input values are presented in Table 1. The input data are picked from real-time investigations. However, those are a bit scaled up or down due to precise application of this research. We have considered three smart grid scenarios, one existing and two proposed to compare the percentage of energy and cost savings. The simulation results are used to compare with the existing scenarios to show how the proposed scheme is better for reducing energy demand and cost significantly. It also evaluates the hourly and daily energy consumption and prices considering satisfied power demand to make the comparison effectively to propose an economic solution for residential consumers.

Table 1.
Simulation parameters.
4.1. Case Study
Several case studies are carried out to presents the residential consumer’s energy consumption patterns and compare due to get economic solutions. A group of 20 residential consumers is considered to have several smart grid communities to evaluate energy and cost through some case studies. Besides, we have considered three scenarios one existing and two proposed. In scenario-1, all residential consumers have power supply from local utility only whereas in scenario-2, all residential consumers have a power supply both from the local utility and RESs. Moreover, in scenario-3, all residential consumers have power supply from local utility, renewable energy and, backup battery storage system (BBSS).
- Scenario 1: Residences with local utility support only;
- Scenario 2: Residences with local utility support and RESs;
- Scenario 3: Residences with local utility support, RESs and BBSS.
4.1.1. Case I
In this case, residential consumers considered a local utility as their primary source of energy. There is no renewable energy generator and energy storage system to support while power shortage. This approach is completely unable to manage economic issues and energy minimization due to the absence of RESs and backup battery storage systems (BBSS). All residence appliances receive energy from local utility and use as much as they require and after a certain time pay for the utility bills. Energy consumption and electricity cost management for three scenarios over 24-h time horizon is illustrated in Figure 9. In this research, we have considered scenario 1 as existing whereas scenario 2 is the proposed energy management scheme. Residential consumers have different load patterns such as peak-load, off-peak and mid-peak loads. The load profiles are presented in Figure 5, Figure 6 and Figure 7. To optimize residential consumer’s energy consumption and cost it is necessary to take some efficient initiatives and techniques.
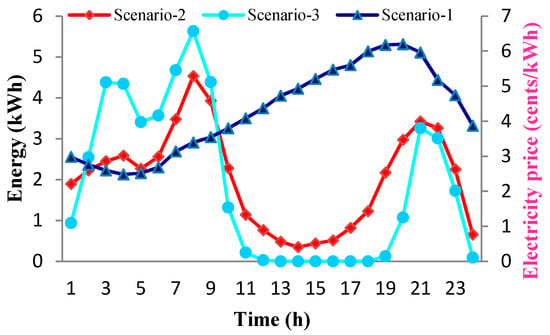
Figure 9.
Energy consumption and electricity cost management for three scenarios over 24 h time horizon.
Some effective strategies and RESs integration are taken in to account in the proposed scheme. From Figure 9 it is clear that the highest energy consumption is attained by scenario 1 and the lowest energy consumption is cut by scenario 3.
4.1.2. Case II
A typical power production using solar panel and wind turbine is considered that are figured in Figure 3 and Figure 4, respectively. The spasmodic power production from wind and solar generators is completely stochastic. Sometimes it is tough to meet residential consumer power demand due to unpredictable power generation. To overcome these issues a backup battery storage system (BBSS) is introduced in the smart grid environment. The comparison of proposed and existing energy and cost management over 24 h time horizon is presented in Figure 10 and the relationship of proposed and existing energy, and cost management for case II is tabulated in Table 2.
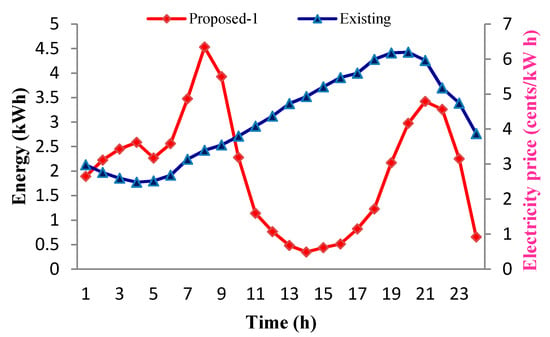
Figure 10.
Comparison between proposed-1 and existing scenario of energy and electricity cost management over 24 h time horizon.

Table 2.
Comparison of the proposed and existing energy, and cost management for case-II.
The comparison between proposed 1 and existing energy and cost management scheme over 24-h time horizon is presented in Figure 10 and solar and wind power generation is presented in Figure 3 and Figure 4, respectively. Renewable energy generation is stored in a smart battery thus residence consumers can use and share battery power when they require. The electricity cost for this case study is 3.60 EUR, which is 35% less than the existing approach. It should be mention that the cost-saving is high due to the power purchasing from grid and RESs power generator. Moreover, during the peak hours, RESs generates the extra power than the exact demand and it is an extra reason behind the dramatic increase in profits.
Satisfied power demand: When residential consumers can not satisfy power demand by local utility supply then RESs can support power demand using an efficient power-sharing algorithm (PSA). Renewable energy generation is stored in a smart battery and residential consumers can use and share their battery power each other when they require. Figure 11 presents the satisfied power demand management between existing and proposed scenarios over 24 h time horizon.
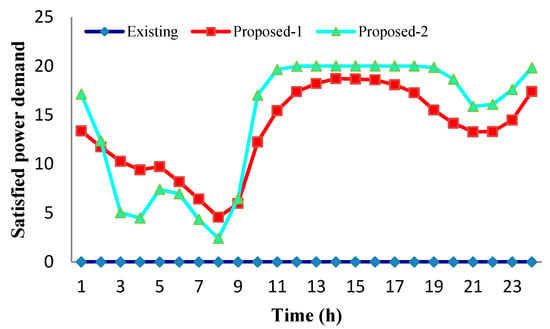
Figure 11.
Satisfied power demand management between existing and proposed scenarios over 24 h time horizon.
Figure 12 presents the satisfied power demand management between existing and proposed 1 scenario over 24 h time horizon. In the case of scenario 1, the total number of satisfied power demand is empty due to local utility supply only. However, scenario 2 has both local utility and renewable energy generation support, for this reason, it can satisfy 18% power demands and tabulated in Table 3.
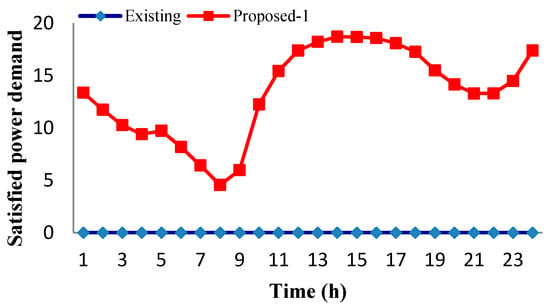
Figure 12.
Comparison of satisfied power demand management between proposed 1 and existing scenario over 24 h time horizon.

Table 3.
Comparison of the proposed and existing satisfied power demand management for case-II.
4.1.3. Case III
To validating the efficiency of the offered method, the simulation procedure is executed to evaluate the daily energy and cost considering a backup battery storage system (BBSS) and power generation from RESs. The day with RESs power generation and BBSS is added to the simulation to notice the retort of the energy and cost minimization. Figure 13 presents the energy consumption and electricity cost management for three scenarios over 24 h time horizon. The electricity charge of the surviving method is 3.60 EUR with a day simulation period. 24-h simulation is observed in the proposed energy management approach where the BBSS is charged from the utility grid up to 30 kWh. Besides, during the high price hours of the electricity, BBSS fully discharged to fulfill the power demand. Again the BBSS consumed electricity for charging itself from the grid during the low price hours and touches the highest level of energy. A comparison between the offered approach and the existing ones is revealed in Table 4. The BBSS takes charge from the RESs and reaches the highest levels of energy in the subsequent time slots. The proposed 2 scenario can save energy and cost up to 45% compared to the existing method.
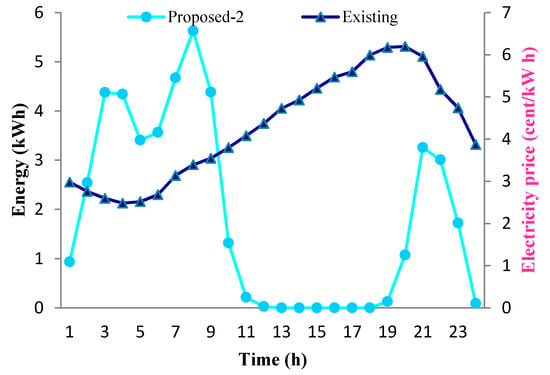
Figure 13.
Comparison between proposed-2 and existing scenario of energy and electricity cost management over 24 h time horizon.

Table 4.
Comparison of the proposed and existing energy, and cost management for case-III.
Satisfied power demand: When residential consumers can not satisfy power demand by local utility supply then an efficient power-sharing algorithm starts to satisfy user power demand using renewable energy sources and BBSS. Figure 14 presents the comparison of the satisfied power demand management between existing and proposed 2 scenarios over 24 h time horizon. In the case of the existing scenario, the total number of satisfied power demand is empty due to local utility supply only. However, the proposed 2 scenario has local utility, renewable energy generation, and BBSS support, for this reason, it can satisfy the highest numbers of power demands which are 22.5% and demonstrated in Table 5.
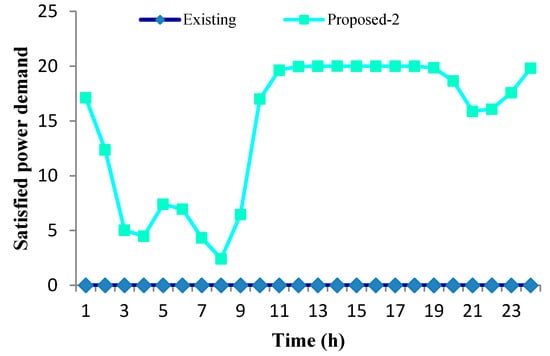
Figure 14.
Comparison of satisfied power demand management between proposed-2 and existing scenario over 24 h time horizon.

Table 5.
Comparison of the proposed and existing satisfied power demand management for case-III.
4.2. Discussion
In this section, the overall energy and cost minimization for the residential consumers is outlined based on several case studies. Case I is completely unable to minimize energy and monetary cost due to the absence of an alternative sources of energy and BBSS. However, case II and case III can save a significant amount of energy and cost considering renewable energy, BBSS and satisfied power demand. Percentage of savings is tabulated in Table 6 to identify the most profitable case.

Table 6.
Comparison of the proposed and existing energy, and cost management within case-I, II, and III.
Figure 15 presents the percentage of energy savings management within different case studies over 24 h time horizon. Case II can save 35% energy consumption whereas case III can save 45%. The pink line indicates the percentage of energy savings which is sharply increasing due to cost-effective energy management.
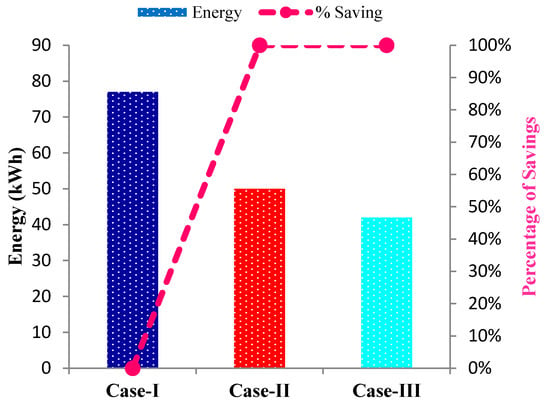
Figure 15.
Percentage of energy savings management within case-I, II, and III over 24 h time horizon.
On the other hand, Figure 16 illustrates the percentage of monetary cost savings management within different case studies over 24 h time horizon. Case II can save 35% energy cost whereas case III can save 45%. The pink line indicates the percentage of energy cost savings which is linearly increasing due to economic energy optimization.
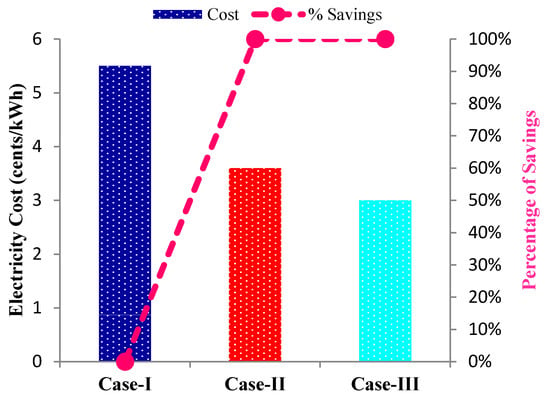
Figure 16.
Percentage of energy cost savings management within case-I, II, and III over 24 h time horizon.
The comparison of average daily energy consumption and cost management within three different cases are tabulated in Table 7. From Figure 17 the daily energy consumption is the greatest in case I whereas in case II and case III is declining. Evaluating several case studies the overall energy and cost reduction is profitably accelerated in case II and case III due to considering RESs, BBSS, and PSA in the smart grid environment. To get dual supply opportunity we have considered an on-grid tied smart grid system.

Table 7.
Comparison of the average daily energy consumption and cost management within three cases.
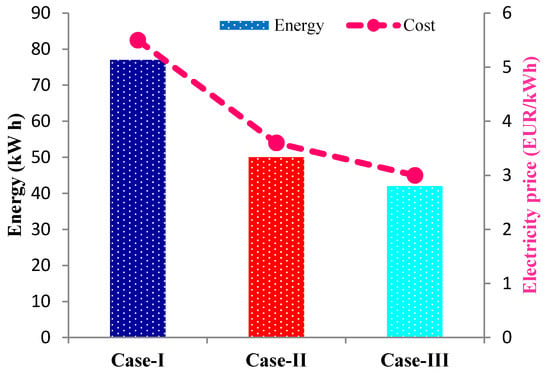
Figure 17.
Comparison of average daily energy consumption and cost management within case-I, II, and III.
In case any load shading due to system maintenance then RESs and BBSS can support a part of the energy community. Sometimes residential consumers cannot estimate load management properly due to unpredictable RESs generation. However, the outlined efficiency is not much due to RESs and BBSS limitations. A large BBSS and the best quality of RESs can significantly increase the percentage of energy and cost savings. However, the residential consumers may not be interested or effort the cost due to huge primary investment.
A comparison of energy consumption and cost for a single residential consumer in a day is illustrates in Figure 18 and Table 8 to get a basic idea regarding energy and respective cost within different scenarios. The highest energy consumption shows in scenario-1 whereas the lowest energy consumption is done by the scenario 3.
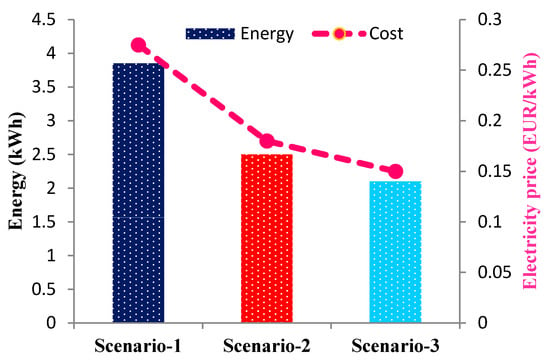
Figure 18.
Comparison of the average daily energy consumption and cost management for a single user within three scenarios.

Table 8.
Comparison of the average daily energy consumption and cost management for single user within three scenarios.
A comparison of the proposed and existing satisfied power demands within different case studies are illustrated in Figure 19 and tabulated in Table 9. In Figure 19 the pink line indicates the percentages of satisfied power demand savings which are 18% and 22.5%, respectively. Case III has 4.5% more satisfied power demand savings than case II and 22.5% more savings than case I. The prescribed percentage of savings is not much and the amount can be accelerated with the aid of a large backup battery bank and RESs system. However, it requires large space and huge primary investment. For this reason, the residential consumers may not effort or interested to invest a large amount of economy. Moreover, the proposed model can be implemented effectively on a small scale micro-grid environment.
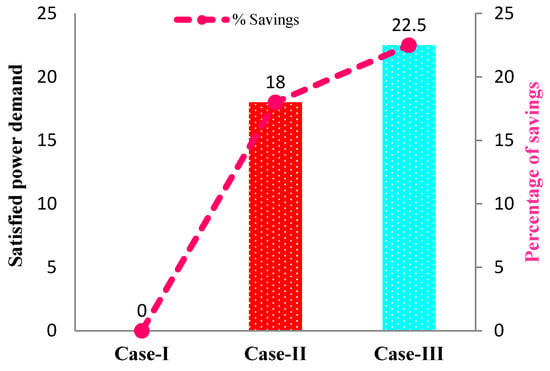
Figure 19.
Percentage of satisfied power demand savings within cases I, II, and III over 24 h time horizon.

Table 9.
Comparison of the proposed and existing satisfied power demands within case-I, II and III.
4.3. Case Comparison
The vital concern of this research is the case comparison to understand and outline the most cost-effective solution to minimize energy and cost for the residential consumers. Case I consider fixed utility tariffs and a nominated kW demand thus the consumer cannot exceed the allocated energy demand which is set by the utility companies. For this reason, the consumer cannot avoid the peak load and higher utility tariffs. Case II demonstrated an idea to overcome these difficulties by installing RESs with a utility grid to compensate the peak load and higher utility costs. However, it is not always possible due to dependency on solar irradiation and wind velocity during cloudy weather and winter season. The compared amount is not much higher due to the moderate size of ESS. However, installing a large BBSS requires a big battery bank, leading greater energy costs which consumers may not effort.
Finally, case III has additional backup battery storage systems (BBSS) compared to case II to eliminate the mentioned difficulties which is presented in Figure 20. The BBSS is charged during low energy cost periods and discharges when peak loads and extra demand arise. We have taken into account the point of view that the initial investment for RESs and BBSS is cost-effective and sustainable. A depreciation cost is considered with RESs and BBSS to make the proposed model more realistic. Government and many energy providers encourage residential consumers by providing home loans for installing small scale renewable energy generators. This may be a flexible opportunity for low-income bracket individuals and mid-category consumers. The proposed model can be implemented effectively on a small scale micro-grid environment.
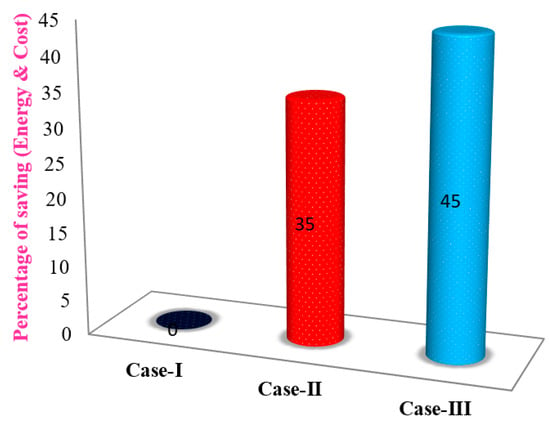
Figure 20.
Comparison of the percentage of energy and cost saving for cases I, II and III.
5. Conclusions
A home energy management scheme for smart grid community with renewable energy sources and backup battery storage system is developed in this paper for a group of residential consumers. The residential energy management (REM) problem with consumer’s energy consumption, cost minimization, and satisfied power demand is modeled. The home appliances’ priorities, energy availability and real-time energy pricing are considered in the proposed power-sharing technique. The offered model with the power-sharing technique is implemented in a practical system considering twenty residential consumers. The economic benefits of the proposed REM scheme with BESS are investigated with three different scenarios. The financial analysis of the proposed technique is conducted to show the monetary savings which is guaranteed in our proposed scheme. It is clear from the simulation results that the recommended scheme can save energy and costs by up to 35% and 45% compared to existing methods. Also, the results outline that the proposed method can save satisfied power demands by up to 16% and 22.5% compared to the existing method. From overall analysis, the proposed REM model can enhance the benefits of the RESs and BBSS integration. Moreover, the simulation outcomes prove the potential benefits of the residential consumers and endorse the green effort to improve the sustainability and effectiveness of the power management infrastructure.
Author Contributions
M.M.U.R, F.G., M.A.H. and M.S.A. initiated the idea, designed the energy management scheme and drafted the article. M.M.U.R., F.S.A.-I., A.K.K. and M.M.R. performed the simulations and formal analysis. All authors made revisions of the articles. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| SG | smart grid | pW | Wind power |
| SM | smart meter | ETHA | total home appliances |
| HEMS | home energy management scheme | EL | lighting load |
| PDAU | power data aggregator unit | EWM | power by washing machine |
| DSM | demand-side management | WR | power taken by refrigerator |
| PSA | power-sharing algorithm | EC | power taken by computer |
| HANs | home area networks | EDW | power taken by dishwasher |
| SMA | smart metering architecture | EH | power taken by heater |
| DSO | distribution system operator | EBB | backup battery storage |
| RESs | renewable energy sources | EEE | users extra energy |
| EMS | energy management system | EEEC | users extra energy cost |
| ESS | energy storage system | PUC | utility company |
| SI | solar irradiation | PUP | utility price |
| PV | photovoltaic | CT | total number of community |
| PwT | total wind power | RUT | total number of residential users |
| PsT | total solar power | ETUE | total users energy |
| BLo | initial battery energy level | ETUEC | total users energy cost |
| BLmax | maximum battery energy level | HTNH | total number of hours |
| BLmin | minimum battery energy level | DTND | total number of days |
| EB | battery storage | pTSPD | total satisfied power demand |
| pS | solar power | IT | total number of iteration |
| REM | residence energy management | ECE | cost of energy |
| BCSB | capacity of smart battery |
Appendix A
| Algorithm A1: Power-Sharing Algorithm (PSA) | |
| 1: | Initialization. |
| 2: | Load data. |
| 3: | Start simulation. |
| 4: | Iteration. |
| 5: | Generate random values. |
| 6: | if user power ≥ battery power then |
| 7: | Charge user battery. |
| 8: | Otherwise, the user battery is the maximum. |
| 9: | end if |
| 10: | else if found healthy battery then |
| 11: | Charge user battery. |
| 12: | Otherwise, search for another healthy battery. |
| 13: | end else if |
| 14: | if all power supply off then |
| 15: | Use a backup battery storage |
| 16: | Otherwise, use the user battery. |
| 17: | end if |
| 18: | Evaluate energy & prices. |
| 19: | Evaluate satisfied power demand. |
| 20: | repeat step 4 |
| 21: | until iteration ≥ 10 |
| 22: | Stop simulation |
References
- Farrokhifar, M.; Momayyezi, F.; Sadoogi, N.; Safari, A. Real-time based approach for intelligent building energy management using dynamic price policies. Sustain. Cities Soc. 2018, 37, 85–92. [Google Scholar] [CrossRef]
- Sharifi, A.H.; Maghouli, P. Energy management of smart homes equipped with energy storage systems considering the PAR index based on real-time pricing. Sustain. Cities Soc. 2019, 45, 579–587. [Google Scholar] [CrossRef]
- Sheikhi, A.; Rayati, M.; Ranjbar, A.M. Demand side management for a residential customer in multi-energy systems. Sustain. Cities Soc. 2016, 22, 63–77. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Guerrero, J.M. Energy scheduling of community microgrid with battery cost using particle swarm optimisation. Appl. Energy 2019, 254, 113723. [Google Scholar] [CrossRef]
- Lezama, F.; Soares, J.; Canizes, B.; Vale, Z. Flexibility management model of home appliances to support DSO requests in smart grids. Sustain. Cities Soc. 2020, 55, 102048. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M. Scheduling deferrable appliances and energy resources of a smart home applying multi-time scale stochastic model predictive control. Sustain. Cities Soc. 2017, 32, 338–347. [Google Scholar] [CrossRef]
- Yigit, K.; Acarkan, B. A new electrical energy management approach for ships using mixed energy sources to ensure sustainable port cities. Sustain. Cities Soc. 2018, 40, 126–135. [Google Scholar] [CrossRef]
- Abushnaf, J.; Rassau, A.; Górnisiewicz, W. Impact of dynamic energy pricing schemes on a novel multi-user home energy management system. Electr. Power Syst. Res. 2015. [Google Scholar] [CrossRef]
- Reynolds, J.; Rezgui, Y.; Hippolyte, J.L. Upscaling energy control from building to districts: Current limitations and future perspectives. Sustain. Cities Soc. 2017, 35, 816–829. [Google Scholar] [CrossRef]
- Perri, C.; Giglio, C.; Corvello, V. Smart users for smart technologies: Investigating the intention to adopt smart energy consumption behaviors. Technol. Forecast. Soc. Chang. 2020, 155, 119991. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.; Wang, W. Evolutionary Analysis for Residential Consumer Participating in Demand Response Considering Irrational Behavior. Energies 2019, 12, 3727. [Google Scholar] [CrossRef]
- López, J.M.G.; Pouresmaeil, E.; Cañizares, C.A.; Bhattacharya, K.; Mosaddegh, A.; Solanki, B.V. Smart Residential Load Simulator for Energy Management in Smart Grids. IEEE Trans. Ind. Electron. 2019, 66, 1443–1452. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. A review of residential demand response of smart grid. Renew. Sustain. Energy Rev. 2016, 59, 166–178. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Rahman, M.M.; Hossain, M.A.; Ahmed, M.R. Exploration and corrective measures of greenhouse gas emission from fossil fuel power stations for Bangladesh. J. Clean. Prod. 2020, 244, 118645. [Google Scholar] [CrossRef]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Muttaqi, K.M. Energy management of community microgrids considering degradation cost of battery. J. Energy Storage 2019, 22, 257–269. [Google Scholar] [CrossRef]
- Di Giorgio, A.; Pimpinella, L. An event driven Smart Home Controller enabling consumer economic saving and automated Demand Side Management. Appl. Energy 2012, 96, 92–103. [Google Scholar] [CrossRef]
- Qayyum, F.A.; Naeem, M.; Khwaja, A.S.; Anpalagan, A.; Guan, L.; Venkatesh, B. Appliance Scheduling Optimization in Smart Home Networks. IEEE Access 2015, 3, 2176–2190. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Mouftah, H.T. Wireless sensor networks for cost-efficient residential energy management in the smart grid. IEEE Trans. Smart Grid 2011, 2, 314–325. [Google Scholar] [CrossRef]
- Mahmood, A.; Khan, I.; Razzaq, S.; Najam, Z.; Khan, N.A.; Rehman, M.A.; Javaid, N. Home appliances coordination scheme for energy management (HACS4EM) using wireless sensor networks in smart grids. Procedia Comput. Sci. 2014, 32, 469–476. [Google Scholar] [CrossRef]
- Smale, R.; Spaargaren, G.; van Vliet, B. Householders co-managing energy systems: Space for collaboration? Build. Res. Inf. 2019, 47, 585–597. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Ahmed, M.R.; Hossain, M.A.; Sikder, M.M. Feasibility assessment & design of hybrid renewable energy based electric vehicle charging station in Bangladesh. Sustain. Cities Soc. 2018, 39, 189–202. [Google Scholar] [CrossRef]
- Alam, M.S.; Abido, M.A.Y.; El-Amin, I. Fault Current Limiters in Power Systems: A Comprehensive Review. Energies 2018, 11, 1025. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Abdou, A.F. Modified PSO algorithm for real-time energy management in grid-connected microgrids. Renew. Energy 2019, 136, 746–757. [Google Scholar] [CrossRef]
- Ur Rashid, M.M.; Hasan, M.M. Simulation based energy and cost optimization for home users in a community smart grid. Int. J. Renew. Energy Res. 2018, 8, 1281–1287. [Google Scholar]
- Lior, N. Sustainable energy development: The present (2009) situation and possible paths to the future. Energy 2010, 35, 3976–3994. [Google Scholar] [CrossRef]
- McDaniel, P.; McLaughlin, S. Security and privacy challenges in the smart grid. IEEE Secur. Priv. 2009, 7, 75–77. [Google Scholar] [CrossRef]
- Zipperer, A.; Aloise-Young, P.A.; Suryanarayanan, S.; Roche, R.; Earle, L.; Christensen, D.; Bauleo, P.; Zimmerle, D. Electric energy management in the smart home: Perspectives on enabling technologies and consumer behavior. Proc. IEEE 2013, 101, 2397–2408. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chow, M.Y.; Chen, J. A survey on demand response in smart grids: Mathematical models and approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.X.; Li, Y.F.; Zio, E.; Kang, R. Smart electricity meter reliability prediction based on accelerated degradation testing and modeling. Int. J. Electr. Power Energy Syst. 2014, 56, 209–219. [Google Scholar] [CrossRef]
- Xiao, W.; Lind, M.G.J.; Dunford, W.G.; Capel, A. Real-time identification of optimal operating points in photovoltaic power systems. IEEE Trans. Ind. Electron. 2006, 53, 1017–1026. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Sizing optimization of grid-independent hybrid photovoltaic/wind power generation system. Energy 2011, 36, 1214–1222. [Google Scholar] [CrossRef]
- Justus, C.G. Wind energy statistics for large arrays of wind turbines (New England and Central U.S. Regions). Sol. Energy 1978, 20, 379–386. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Abbadi, N.M. Wind shear coefficients and energy yield for Dhahran, Saudi Arabia. Renew. Energy 2007, 32, 738–749. [Google Scholar] [CrossRef]
- Borowy, B.S.; Salameh, Z.M. Optimum Photovoltaic Array Size for a Hybrid Wind/PV System. IEEE Trans. Energy Convers. 1994, 9, 482–488. [Google Scholar] [CrossRef]
- Farrugia, R.N. The wind shear exponent in a Mediterranean island climate. Renew. Energy 2003, 28, 647–653. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.S.; Jatskevich, J.; Schober, R. Optimal and autonomous incentive-based energy consumption scheduling algorithm for smart grid. In Proceedings of the Innovative Smart Grid Technologies Conference, ISGT 2010, Gothenburg, Sweden, 22 March 2010. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).