Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming

Abstract

The traveling-salesman problem can be regarded as an NP-hard problem. To better solve the best solution, many heuristic algorithms, such as simulated annealing, ant-colony optimization, tabu search, and genetic algorithm, were used. However, these algorithms either are easy to fall into local optimization or have low or poor convergence performance. This paper proposes a new algorithm based on simulated annealing and gene-expression programming to better solve the problem. In the algorithm, we use simulated annealing to increase the diversity of the Gene Expression Programming (GEP) population and improve the ability of global search. The comparative experiments results, using six benchmark instances, show that the proposed algorithm outperforms other well-known heuristic algorithms in terms of the best solution, the worst solution, the running time of the algorithm, the rate of difference between the best solution and the known optimal solution, and the convergent speed of algorithms.

1. Introduction

With the development of Big Data technology, graphics computing is applied to all kinds of fields. For example, in power-inspection route planning [1,2], all task points and equipment can be regarded as nodes in the graph, and path length between each task point or equipment can be regarded as an edge; thereby, a road graph on power inspection is formed. In another example, an entire social network [3,4,5] is a graph in which the user is the vertex of the graph, and the relationship between the user and another user is regarded as the edge. As can be seen from the above examples, as a storage or presentation form in a specific application, how to mine the knowledge contained in a graph by quickly traversing the vertices in the graph is a research hotspot in the field of graphics computing.

Traversing all the vertices in the graph and repeating is an important application direction in graph-vertex traversal. Traversing all the vertices in the graph is a classical traveling-salesman problem (TSP) in the shortest time. It is well known that TSP is an NP-hard problem [6,7]. To solve the problem, besides traditional backtracking algorithms, branch-and-bound algorithms, and greedy algorithms, we mainly use heuristic search algorithms to optimize. These heuristic algorithms include the simulated annealing algorithm [8,9,10,11,12], tabu-search algorithm [13,14,15], ant-colony optimization algorithm [16,17,18], and genetic algorithm [19,20,21,22,23,24]. However, the optimization time of the simulated annealing algorithm is very long, the tabu-search algorithm has a strong dependence on the initial solution and can only be serialized, genetic algorithm is easy to fall into local optimization and has poor convergence performance, and the ant-colony algorithm also has long optimization time and is also prone to falling into local optimization [25].

Inspired by the characteristics of genetic expression, Candida Ferreira first proposed the concept of gene-expression programming (GEP) in 2001 [26,27,28]. It is a new member of the evolutionary-computing family based on genetic algorithms and genetic programming with a strong-function mining ability and high-function mining efficiency. Compared with traditional genetic algorithms and genetic programming, GEP has the following advantages [29,30,31]: (1) it uses simple encoding to solve a complex problem; (2) its convergent speed is improved by 2–4 times in comparison to genetic algorithms and genetic programming; and (3) it is easy for it to overcome combination exploration and premature phenomena. This paper proposes a traveling-salesman problem based on simulated annealing and GEP (TSP-SAGEP) in order to traverse all cities in the shortest time. The major contributions of our work are listed as follows:

(1)

To better improve the ability to global search, we applied a simulated annealing algorithm to the genetic operation of GEP, and propose an improved GEP algorithm based on simulated annealing (IGEP-SA).

(2)

In order to solve traveling-salesman problems like graph vertex traversal optimization, we present a traveling-salesman optimization algorithm on the basis of IGEP-SA.

(3)

Experimental results show that the proposed algorithm outperforms traditional algorithms in terms of the best solution, the worst solution, the running time of the algorithm, the rate of difference between the best solution and the known optimal solution, and the convergent speed of the algorithms.

The remainder of this paper is organized as follows. Section 2 discusses the related works. Section 3.1 introduces the improved GEP algorithm based on simulated annealing. Section 4 focuses on the traveling-salesman problem based on simulated annealing and GEP. Section 5 conducts detailed comparative experiments. Finally, conclusions are given in Section 6.

2. Related Work

Zhan et al. [8] proposed a new simulated annealing algorithm, called a list-based simulated annealing algorithm, in order to solve the traveling-salesman problem. Experimental results indicated that the proposed algorithm in this paper had competitive performance compared with the other algorithms. Yu et al. [9] presented a hybrid simulated annealing algorithm based on tabu search to solve the traveling-salesman problem. Experimental results demonstrated that the proposed algorithms improved accuracy and efficiency. Absalom et al. [10] presented a simulated annealing algorithm based on symbiotic-organism search in order to better solve the traveling-salesman problem. Comparative results showed that the proposed algorithm had advantages in terms of convergence, average execution time, and percentage deviations. Behnck et al. [11] applied a modified simulated annealing algorithm to SUAVs’ path, planning to find an optimal path that included most of points. Zhao et al. [12] used an improved simulated annealing algorithm to solve the traveling-salesman problem. Results indicated that the proposed algorithm in this paper could obtain the best solutions for most TSPLIB benchmarks. Xu et al. [13] proposed a new tabu-search algorithm based on the evolutionary and ant-colony algorithms to effectively solve the traveling-salesman problem. Archetti et al. [14] proposed an integer linear programming model based on the tabu-search algorithm to solve the vehicle-routing problem. Simulated experiments illustrated that the proposed algorithm had good performance compared with other algorithms. Chiang et al. [15] used a quantum-inspired tabu-search algorithm to optimize the traveling-salesman problem. Experimental results verified effectiveness of the proposed algorithm. Yang et al. [18] proposed an improved ant-colony optimization algorithm based on swarm intelligence to obtain the best solution for the traveling-salesman problem. Comparative results showed that the algorithm had higher accuracy and efficiency compared with classic optimization algorithms. He et al. [16] put forward an improved ant-colony algorithm based on new crossover and mutation operations to find the best solution for the traveling-salesman problem. Simulation results demonstrated that the proposed algorithm had advantages in terms of stability and optimization capacity. Mohsen et al. [17] proposed a hybrid ant-colony optimization algorithm based on the simulated annealing algorithm to solve the traveling-salesman problem. El-Samak et al. [19] applied the affinity propagation clustering technique to optimize the genetic algorithm for finding the best solutions to the traveling-salesman problem. Rani et al. [20] proposed the improved genetic algorithm by a roulette-wheel selection operator with different crossovers and mutation rates to solve the traveling-salesman problem. Experimental results demonstrated that the algorithm in this paper is better than the existing crossover operator in other algorithms. Deng et al. [21] presented the improved genetic algorithm by using k-means to generate a new initial-population strategy for solving the traveling-salesman problem. Wang et al. [22] solved the traveling-salesman problem by merging two optimization strategies into the traditional genetic algorithm. Comparative results showed that the proposed algorithm in this paper could find better solutions than a traditional optimal algorithm. Wang et al. [23] solved the traveling-salesman problem by means of a multioffspring genetic algorithm according to biological evolutionary and mathematical ecological theory. Compared with the traditional genetic algorithm, the proposed algorithm in this paper was faster and decreased the evolutionary time of the best solution. Changdar et al. [24] introduced a multiobjective genetic algorithm into solving a multiobjective solid traveling-salesman problem. In order to compare performance of the genetic algorithm and the simulated annealing ant-colony optimization, Haroun et al. [25] performed a comparative experiment to evaluate the performance of the three algorithms in terms of computational time and the shortest distance in solving the traveling-salesman problem.

GEP [26] is also a kind of heuristic algorithm. Many researchers have already applied GEP to combinatorial optimization. Ferreira et al. [32] applied a new chromosomal organization based on multigenes in GEP to solve the combinatorial optimization problem. Results demonstrated that the algorithm had high efficiency and accuracy. Sabar et al. [33] used gene-expression programming to generate the acceptance criterion for solving an combinational optimization problem. Comparative results showed that the solution was better than the other results obtained from the existing algorithms.

3. Improved GEP Algorithm Based on Simulated Annealing

Although the GEP algorithm can quickly find the solution for combinatorial optimization problems, such as the traveling-salesman problem, GEP is still easy to fall into the local optimum. In order to better solve the problem, this paper proposes an improved GEP algorithm based on simulated annealing (IGEP-SA) to avoid GEP falling into a local optimum.

3.1. Simulated Annealing

Simulated annealing (SA) is an effective and general form of optimization and is based on simulating the annealing of solids [34,35]. It is very useful in finding global optima in the presence of local-optima large numbers. The simulated-annealing algorithm starts from a higher temperature, which is called the initial temperature. When the temperature gradually decreases, the solution of the algorithm tends to be stable. However, the solution may be a local optimal solution. Then in SA, such a local optimal solution is jumped with a certain probability to find the global optimal solution of the objective function. The flow chart of the simulated-annealing algorithm is shown in Figure 1.

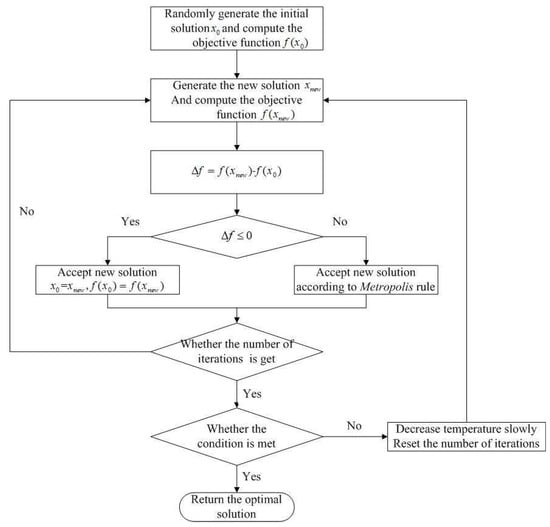
Figure 1. A flowchart of the simulated-annealing algorithm.

From Figure 1, we can see that the Metropolis rule is very important for SA to find the optimal solution. Suppose that state ${\mathrm{x}}_{old}$ becomes a state ${\mathrm{x}}_{\mathrm{new}}$ when the system is subject to some disturbance. Then, in the Metropolis rule, the energy of the system also changes from $\mathrm{E}\left({\mathrm{x}}_{old}\right)$ to $\mathrm{E}\left({\mathrm{x}}_{\mathrm{new}}\right)$, and the acceptance probability of the system changing from state ${\mathrm{x}}_{old}$ to state ${\mathrm{x}}_{\mathrm{new}}$ is $\mathrm{p}$:

$$\mathrm{p}=\left\{\begin{array}{c}1\mathrm{if}E\left({\mathrm{x}}_{new}\right)<\mathrm{E}\left({\mathrm{x}}_{\mathrm{old}}\right)\hfill \\ exp(-\frac{E\left({\mathrm{x}}_{\mathrm{new}}\right)-\mathrm{E}\left({\mathrm{x}}_{\mathrm{old}}\right)}{\mathrm{T}})\mathrm{if}E\left({\mathrm{x}}_{new}\right)\ge \mathrm{E}\left({\mathrm{x}}_{\mathrm{old}}\right)\hfill \end{array}\right.$$

The steps of the simulated-annealing algorithm are as follows (Algorithm 1):

Algorithm 1: SA

Input:    initial temperature ${\mathrm{T}}_0$, minimum temperature ${\mathrm{T}}_{min}$, maximum number of iteration ${\mathrm{K}}_{m\mathrm{ax}}$,

probability of temperature drop $\rho$;

Output: the optimal solution ${\mathrm{x}}_{\mathrm{best}}$;

1. Generating an initial solution ${\mathrm{x}}_0$;

2. ${\mathrm{x}}_{\mathrm{best}}\leftarrow {\mathrm{x}}_0$;

3. Computing the value of the objective function $\mathrm{f}\left({\mathrm{x}}_0\right)$ and $\mathrm{f}\left({\mathrm{x}}_{b}est\right)$;

4. ${\mathrm{T}}_{\mathrm{i}}\leftarrow {\mathrm{T}}_0$;

5. while ${\mathrm{T}}_{\mathrm{i}}>{\mathrm{T}}_{min}$ do

6.     $\Delta \mathrm{f}\leftarrow \mathrm{f}\left({\mathrm{x}}_{\mathrm{new}}\right)-\mathrm{f}\left({\mathrm{x}}_{\mathrm{best}}\right)$;

7.     if $\Delta \mathrm{f}<0$ then

8.         ${\mathrm{x}}_{\mathrm{best}}\leftarrow {\mathrm{x}}_{\mathrm{new}}$;

9.     end if

10.    if $\Delta \mathrm{f}\ge 0$ then

11.        $\mathrm{p}\leftarrow {\mathrm{e}}^{\frac{\Delta \mathrm{f}}{\mathrm{T}}}$;

12.        if $\mathrm{c}\leftarrow \mathrm{random}[0,1]\ge \mathrm{p}$ then

13.             ${\mathrm{x}}_{\mathrm{best}}\leftarrow {\mathrm{x}}_{\mathrm{new}}$;

14.        else

15.             ${\mathrm{x}}_{\mathrm{best}}\leftarrow {\mathrm{x}}_{\mathrm{best}}$;

16.        end if

17.    end if

18.    $\mathrm{i}\leftarrow \mathrm{i}+1$;

19.    ${\mathrm{T}}_{\mathrm{i}}\leftarrow \rho \times {\mathrm{T}}_{\mathrm{i}}$;

20. end while

21. Return ${\mathrm{x}}_{\mathrm{best}}$;

3.2. IGEP-SA

Because the simulated-annealing algorithm has the advantage of jumping out of the local optimum, gene-expression programming was improved by using the simulated-annealing algorithm in this paper. Firstly, this paper used simulated annealing to dynamically generate a GEP population. Then, we applied the simulated-annealing algorithm to the mutation operator of GEP to improve the ability of global search.

3.2.1. New Population Generation Based on Simulated Annealing

In order to improve the diversity of the GEP population, this paper proposes new population-generation algorithm based on SA (NPG-SA). The steps of NPG-SA are shown as follows (Algorithm 2):

Algorithm 2: NPG-SA

Input:     current temperature T, number of population $PopSize$, fitness value of previous

generation population $f\left(old\right)$, and fitness value of population after genetic operations $f\left(new\right)$;

Output: new population $NewPop$;

1. $\mathrm{i}\leftarrow 1$;

2. while $\mathrm{i}<\mathrm{PopSize}$ do

3.       $\Delta \mathrm{f}\leftarrow \mathrm{f}\left(\mathrm{new}\right)\left[i\right]-\mathrm{f}\left(\mathrm{old}\right)\left[i\right]$;

4.       $\mathrm{p}\leftarrow {\mathrm{e}}^{\frac{\Delta \mathrm{f}}{\mathrm{T}}}$;

5.       if $\mathrm{c}\leftarrow \mathrm{random}[0,1]\ge \mathrm{p}$ then

6.           $\mathrm{NewPop}.\mathrm{add}\left(\mathrm{i}\right)$;

7.       end if

8.       $\mathrm{i}\leftarrow \mathrm{i}+1$;

9. end while

10. Return $NewPop$;

3.2.2. New Mutation Operator Based on Simulated Annealing

We know that it is very important for GEP to have a diverse population. A mutation operator is the most efficient way. By mutation operator, the best individual of the population in GEP can be found. However, the existing mutation operator in GEP is implemented according to a certain probability. The way depends on the initialization of mutation probability so that the mutation operator in GEP is strongly subjective. This paper proposes a new mutation operator based on SA (NMO-SA). The steps of NMO-SA are shown in Algorithm 3.

Algorithm 3: NMO-SA

Input:     current temperature T, number of population $PopSize$, fitness value of the previous

generation population $f\left(old\right)$, and fitness value of population after genetic operations $f\left(new\right)$;

Output: new population $NewPop$;

1. $\mathrm{i}\leftarrow 1$;

2. $\mathrm{j}\leftarrow \mathrm{SelectPo}int\left(oldPop\right)$;

3. while $\mathrm{i}<\mathrm{PopSize}$ do

4.       $\Delta \mathrm{f}\leftarrow \mathrm{f}\left(\mathrm{new}\right)\left[i\right]-\mathrm{f}\left(\mathrm{old}\right)\left[i\right]$;

5.       $\mathrm{q}\leftarrow {\mathrm{e}}^{\frac{\Delta \mathrm{f}}{\mathrm{T}}}$;

6.       $\mathrm{p}\leftarrow 0.001;//$initial mutation rate

7.       if $\mathrm{c}\leftarrow \mathrm{random}[0,1]\ge \mathrm{q}$ then

8.           $NewPop\leftarrow \mathrm{Mutation}(oldPop,j,c)$;

9.       else

10.         $NewPop\leftarrow \mathrm{Mutation}(oldPop,j,p)$;

11.     end if;

12.      $\mathrm{j}\leftarrow \mathrm{SelectPo}int\left(NewPop\right)$;

13.      $\mathrm{i}\leftarrow \mathrm{i}+1$;

14. end while

15. Return $NewPop$;

3.2.3. Description of IGEP-SA

To better improve the evolutional efficiency of traditional GEP and avoid falling into the local optimum, we applied Algorithms 2 and 3 to IGEP-SA. The steps of IGEP-SA are shown in Algorithm 4.

Algorithm 4: IGEP-SA

Input:     current temperature T, number of population $PopSize$, fitness value of the previous

generation population $f\left(old\right)$, fitness value of population after genetic operations $f\left(new\right)$, probability

of temperature drop $\rho$, $MaxGen$, $P_t$, and $P_r$;

Output: new population $NewPop$;

1. $Pop\leftarrow InitPop\left(PopSize\right)$;

2. $f\left(old\right)\leftarrow Evaluatefitness\left(Pop\right)$;

3. while $\mathrm{i}<\mathrm{MaxGen}$ do

4.       $f\left(new\right)\leftarrow Evaluatefitness\left(Pop\right)$;

5.       $Pop\leftarrow \mathrm{NPG}-\mathrm{SA}(\mathrm{T},PopSize,f(old),f(new\left)\right)$;

6.       $Pop\leftarrow \mathrm{NMO}-\mathrm{SA}(\mathrm{T},PopSize,f(old),f(new\left)\right)$;

7.       $Pop\leftarrow ISTransposition(P_t,Pop,PopSize)$;

8.       $Pop\leftarrow RISTransposition(P_t,Pop,PopSize)$;

9.       $Pop\leftarrow GeneTransposition(P_t,Pop,PopSize)$;

10.      $Pop\leftarrow OnePointRecombination(P_r,Pop,PopSize)$;

11.      $Pop\leftarrow TwoPointRecombination(P_r,Pop,PopSize)$;

12.      $Pop\leftarrow GeneRecombination(P_r,Pop,PopSize)$;

13. end while

14. $NewPop\leftarrow Pop$;

15. $ReturnNewPop$;

4. Traveling-Salesman Problem Based on Simulated Annealing and GEP

The traveling-salesman problem is a kind of classical combinatorial optimization problem. To simplify the solution of the problem, in this paper, we suppose that the traveling-salesman problem is symmetric. We know that the traveling-salesman problem is an NP-hard problem. For the TSP with N cities, there are $(N-1)!$ solutions. With the increase of N, the number of solutions for TSP grow exponentially. We propose a traveling-salesman problem based on simulated annealing and GEP (TSP-SAGEP) in order to better solve the problem.

4.1. TSP-SAGEP Code

The traveling-salesman problem is a kind of combinational optimization problem. For a combinational optimization problem, a chromosome of GEP is a multigene chromosome composed of one-element genes. However, in a multigene chromosome, one-element genes are very important because they can be organized in multigene families (MGFs). These MGFs are composed of clusters of related-gene encoding. An example is shown as follows:

Example 1.

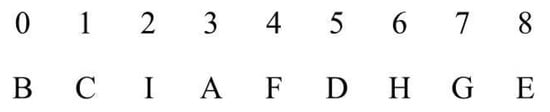
The different cities in the traveling-salesperson problem can be encoded in an MGFs where each gene code represent a particular city visited by the salesman. Consider the simple chromosome below, composed of one MGF with nine cities:

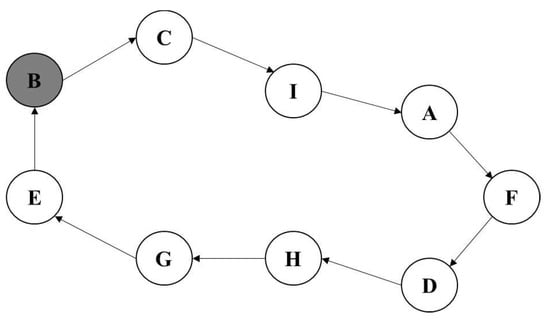
The spatial structure of the chromosome, which is shown in Figure 2, is shown in Figure 3. This is the traveling route of the traveling-salesman problem, where B is both the starting and finishing city and shown in gray.

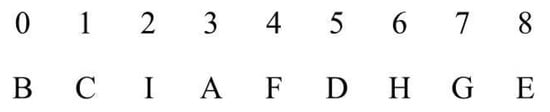
Figure 2. Chromosome of a multigene family.

Figure 3. Expression of the above chromosome.

4.2. Fitness Function of the TSP-SAGEP

The fitness function is very important for GEP to solve the traveling-salesman problem. We know that the objective of the traveling-salesman problem needs to find the shortest route on the condition that we start and lastly finish the city. The fitness function helps algorithm move in the correct direction.

It is obvious that we cannot directly use tour length as a measure of fitness, as the shorter the tour is, the fitter the individual [26]. So, for each generation, fitness $f_i$ of the ith individual in the gth generation is evaluated by the equation:

$$f_i=T_g-t_i+1$$

(1)

where $T_g$ is the length of the largest tour is encoded in the chromosomes of the current population, and $t_i$ is the length of the tour encoded in the ith individual. From Equation (1), we know that the fitness of the worst individual of the population is always equal to one.

4.3. Algorithm Description

In order to better solve graph vertex traversal optimization problems, this paper proposes a traveling-salesman problem based on TSP-SAGEP. The description of TSP-SAGEP is similar to Algorithm 4, but the differences between TSP-SAGEP and Algorithm 4 are as follows:

(1)

In TSP-SAGEP, the population is initialized according to Figure 1.

(2)

In TSP-SAGEP, the fitness value of the individual in the population is evaluated according to Equation (1).

(3)

TSP-SAGEP returns the best graph vertex traversal line.

5. Experiment and Analysis

5.1. Experimental Environment

To better explain the effectiveness and feasibility of the proposed algorithms, we conducted related experiments in a laboratory environment. All experiments were implemented in Java on an Intel Core-i7 PC and Windows 10. All experiments were done by using 6 TSP standard benchmark problems, with different lengths, from TSPLIB [36,37]. Experimental datasets are shown in Table 1. These datasets can be divided into three groups according to their dimension. The first group includes four instances that vary in dimension, between 26 and 70 cities. The second group includes four instances that vary in dimension, between 120 and 442 cities. The last group includes four instances that vary in dimension, between 666 and 1304 cities. Finally, after conducting the experiments 50 times for each instance, the best experimental results were obtained.

Table 1. Datasets used in experiments.

Instance	Cities	Optimal Solution
fri26	26	937
st70	70	675
gr120	120	6942
pcb442	442	50,778
gr666	666	294,358
rl1304	1304	252,948

The optimal solution of each instance is from https://wwwproxy.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/STSP.html.

As a kind of heuristic algorithm, the performance of TSP-SAGEP is affected by the different values of the parameters. Table 2 provides the parameters that the proposed algorithm takes.

Table 2. Parameters of traveling-salesman problem based on simulated annealing and gene-expression programming (TSP-SAGEP).

Parameter Item	Value
Initial temperature	100
Minimum temperature	${10}^{-8}$
The probability of temperature drop	0.98
Population size	500
The number of runs	10
The number of generations	1000
IS Transposition rate	0.3
RIS Transposition rate	0.3
Gene Transposition rate	0.1
One-point recombination rate	0.3
Two-point recombination rate	0.3
Gene recombination rate	0.1

The length of the chromosome in TSP-SAGEP is especially set according to the dimensions in Table 1.

5.2. Experimental Analysis

Experiment 1: To verify the effectiveness of IGEP-SA, we compare dTSP-SAGEP with traditional GEP for all datasets in Table 1. Four measures that include the best solution, the worst solution, number of generations, and the average running time of two algorithms were used to evaluate two algorithms. Table 3 shows that TSP-SAGEP algorithm is better than the traditional GEP algorithm in the above four measures. Meanwhile, we observed the relationship between the number of runs and the tour length for all datasets in Table 1. Results are shown in Figure 4.

Table 3. Comparison of four measures between TSP-SAGEP and a traditional GEP algorithm.

Instances	Optimal	Algorithm	Best	Worst	Average	Generations	Time (s)
fri26	937	TSP-SAGEP	937	971	941	150	7.0671
		GEP	943	1132	961	800	8.1629
st70	675	TSP-SAGEP	675	699	677	150	12.1135
		GEP	698	822	710	800	14.0931
gr120	6942	TSP-SAGEP	6942	7406	6995	200	19.4612
		GEP	7147	10,035	7624	900	22.3573
pcb442	50,778	TSP-SAGEP	50,811	52,147	50,878	300	51.0964
		GEP	51,092	54,113	51,676	900	57.1428
gr666	294,358	TSP-SAGEP	294,419	305,036	295,542	990	79.7853
		GEP	310,982	410,368	328,459	990	85.1204
rl1304	252,948	TSP-SAGEP	253,104	271,582	254,699	990	160.2458
		GEP	281,296	334,871	290,611	990	165.5572

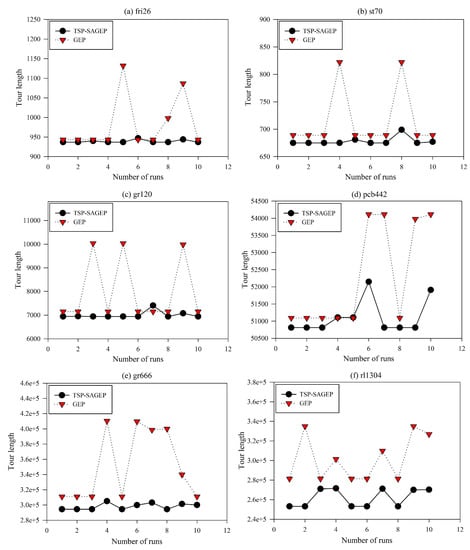
Figure 4. Comparison of tour length based on TSP-SAGEP and GEP for six datasets with an increase in the number of runs.

Table 3 shows that the TSP-SAGEP algorithm is superior over a traditional GEP in computational results for all datasets in Table 1. The best solution based on TSP-SAGEP is better than the solutions based on a traditional GEP for all test instances. In Experiment 1, we used the rate of difference to evaluate the advantages and disadvantages of experiment results based on TSP-SAGEP and traditional GEP. The rate of difference is defined in Equation (2).

$$\rho =\frac{P_{best}-P_{optimal}}{P_{best}}$$

(2)

where $\rho$ represents the rate of difference, $P_{best}$ represents the best solution based on TSP-SAGEP, and $P_{optimal}$ represents the known optimal solution. Rate of difference $\rho$ based on TSP-SAGEP and traditional GEP is 0, 0, 0, 0.00636, 0.033, and 0.0287 for fri26, st70 and gr120 instances. For pcb442, gr666 and rl1304 instances, respectively, and the rate of difference based on TSP-SAGEP and traditional GEP is 0.00065, 0.000207, 0.000616, 0.00615, 0.0535, and 0.1008, respectively. These results illustrate that the best solution based on TSP-SAGEP is better than traditional GEP. This is mainly because new population generation policy and mutation operator based on simulated annealing can improve the diversity of the GEP population and increase the probability of searching for a global solution. Figure 4 demonstrates that, when the number of runs increases from 1 to 10, tour length based on TSP-SAGEP is closer to the optimal tour length than traditional GEP for six instances. From Figure 4, we can also find that, in all 10 runs, the number of solving the best solution based on TSP-SAGEP is 7, 7, 7, 6, 5 and 5 for the fri26, st70, gr120, pcb442, gr666, and rl1304 datasets, respectively.

Experiment 2: In order to better demonstrate the advantage of the proposed algorithm in this paper, we compared TSP-SAGEP with Ezugwu2017 [10], Mohsen2016 [17], and Wang 2016 [23] in terms of the best solution, the worst solution, and rate of difference, which is obtained by the Equation (2). Results are shown in Table 4. Figure 5 shows the comparison of the number of obtaining the best solution based on five algorithms for six instances in all 10 runs. Figure 6 shows comparison of convergent speed between TSP-SAGEP and three other algorithms for six instances. In Experiment 2, we also used convergent speed to evaluate the performance of four algorithms. Convergent speed is defined as follows.

$$C_s=\frac{P_G}{T_G}$$

(3)

where $C_s$ represents the convergent speed of the algorithm, $P_G$ represents the current generation corresponding to the best solution, and $T_G$ represents the total number of generations. From Equation (3), we know that the smaller the $C_s$ value of the algorithm is, the faster the convergence speed of the algorithm.

Table 4. Comparison of three measures between four algorithms.

Instances	Optimal	Algorithm	Best	Worst	Average	Rate	Time (s)
fri26	937	TSP-SAGEP	937	971	941	0	7.0671
		Ezugwu2017	937	1204	951	0	8.5247
		Mohsen2016	937	1299	955	0	8.5916
		Wang2016	937	1151	948	0	8.3103
st70	675	TSP-SAGEP	675	699	677	0	12.1135
		Ezugwu2017	675	846	701	0	14.9045
		Mohsen2016	675	907	715	0	15.1037
		Wang2016	675	831	695	0	14.0985
gr120	6942	TSP-SAGEP	6942	7406	6995	0	19.4612
		Ezugwu2017	6942	11,237	7786	0	25.3581
		Mohsen2016	6942	11,354	7801	0	27.0433
		Wang2016	6942	11,008	7655	0	23.6709
pcb442	50,778	TSP-SAGEP	50,811	52,147	50,878	0.00065	51.0964
		Ezugwu2017	51,107	55,723	51,958	0.00644	61.0876
		Mohsen2016	51,143	56,098	52,044	0.00714	63.9011
		Wang2016	51,097	55,006	51,828	0.00624	59.4571
gr666	294,358	TSP-SAGEP	294,419	305,036	295,542	0.00021	79.7853
		Ezugwu2017	311,855	417,702	331,024	0.05611	90.0014
		Mohsen2016	312,096	420,809	332,528	0.05684	92.0745
		Wang2016	311,003	411,984	329,199	0.05352	88.0163
rl1304	252,948	TSP-SAGEP	253,104	271,582	25,4699	0.00062	160.2458
		Ezugwu2017	288,013	340,015	297,813	0.12175	169.0031
		Mohsen2016	290,057	341,298	299,305	0.12798	170.1165
		Wang2016	286,799	335,990	294,637	0.11803	167.9084

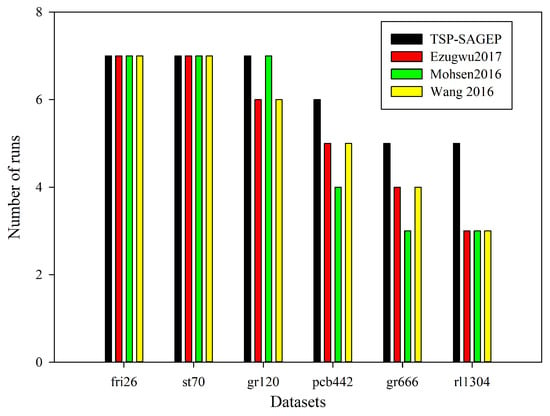
Figure 5. Comparison of the number of the best solutions obtained by four algorithms for six instances in all ten runs.

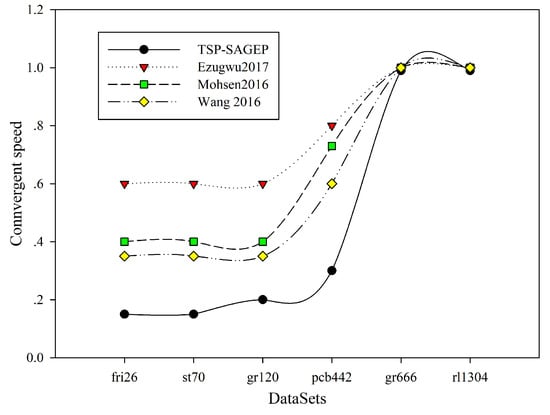
Figure 6. Comparison of convergent speed among four algorithms for six instances.

Table 4 shows that TSP-SAGEP algorithm is superior over Ezugwu2017, Mohsen2016, and Wang 2016 in computational results for all datasets in Table 1. The best solution based on TSP-SAGEP is better than the solutions based on other three algorithms for all test instances. According to Equation (2), we can see that the rate of difference based on TSP-SAGEP is the same as that of the other three algorithms for the fri26, st70 and gr120 instances, while the rate of difference based on TSP-SAGEP is obviously less than the other three algorithms for the pcb442, gr666 and rl1304 instances. Experimental results illustrate that, in comparison to the other three algorithms, the best solution obtained by TSP-SAGEP is the closest to the optimal solution.

According to Figure 5, we know that the number of the best solutions obtained by TSP-SAGEP is obviously more than other algorithms for the pcb442, gr666, and rl1304 instances, and the number of the best solutions obtained by TSP-SAGEP is equal to the number of the best solutions obtained by other algorithms for the fri26 and st70 instances. Generally, for the pcb442, gr666, and rl1304 instances, the number of the best solutions obtained by TSP-SAGEP is improved by 28.57%, 42.86%, and 57.14%, respectively, in comparison to Ezugwu2017 and Wang2016; compared with Mohsen2016, the number of the best solutions obtained by TSP-SAGEP is improved by 28.57%, 42.86%, and 57.14%, respectively. This illustrates that TSP-SAGEP easily solves the best solution on the condition that the number of runs is the same. Figure 6 indicates that convergent speed of TSP-SAGEP is superior over the other three algorithms for six instances. Specifically, compared with Ezugwu2017, Mohsen2016, and Wang2016, the convergent speed of TSP-SAGEP is improved by 75%, 62.5%, and 57.14% for the fri26, st70, and gr120 instances, respectively; for pcb442, the convergent speed of TSP-SAGEP is improved by 62.5%, 58.9%, and 50%, in comparison to Ezugwu2017, Mohsen2016, and Wang2016, respectively. However, when the number of cities increases to 666 and 1304, the convergent speed of four algorithms is almost the same. This is mainly because that the increase in the number of cities cause the increase of solution scale so that it is difficult for the above four algorithms to solve the best solution in the 1000 generations.

6. Conclusions

In this paper, we introduce a traveling salesman problem based on TSP-SAGEP in order to traverse all vertices of a graph in the shortest time. To verify the performance of the proposed algorithm, two experiments were conducted for six benchmark instances obtained from the TSPLIB, and the experimental results of TSP-SAGEP were compared with three other heuristic algorithms. Results show that TSP-SAGEP outperformed the other heuristic algorithms proposed in [10,17,23,26]. Specifically, compared with traditional GEP, Ezugwu2017, Mohsen2016, and Wang2016, TSP-SAGEP had the best solution quality, low error between the best solution, a known optimal solution for all instances, and high convergent speed. In the future, we will enhance the proposed algorithm in this paper by using other GEP operations in order to better solve the problem of large-scale graph vertex traverse. We will also introduce the proposed algorithm into the asymmetric application of graph vertex traverse.