Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming
Abstract
1. Introduction
- (1)
- To better improve the ability to global search, we applied a simulated annealing algorithm to the genetic operation of GEP, and propose an improved GEP algorithm based on simulated annealing (IGEP-SA).
- (2)
- In order to solve traveling-salesman problems like graph vertex traversal optimization, we present a traveling-salesman optimization algorithm on the basis of IGEP-SA.
- (3)
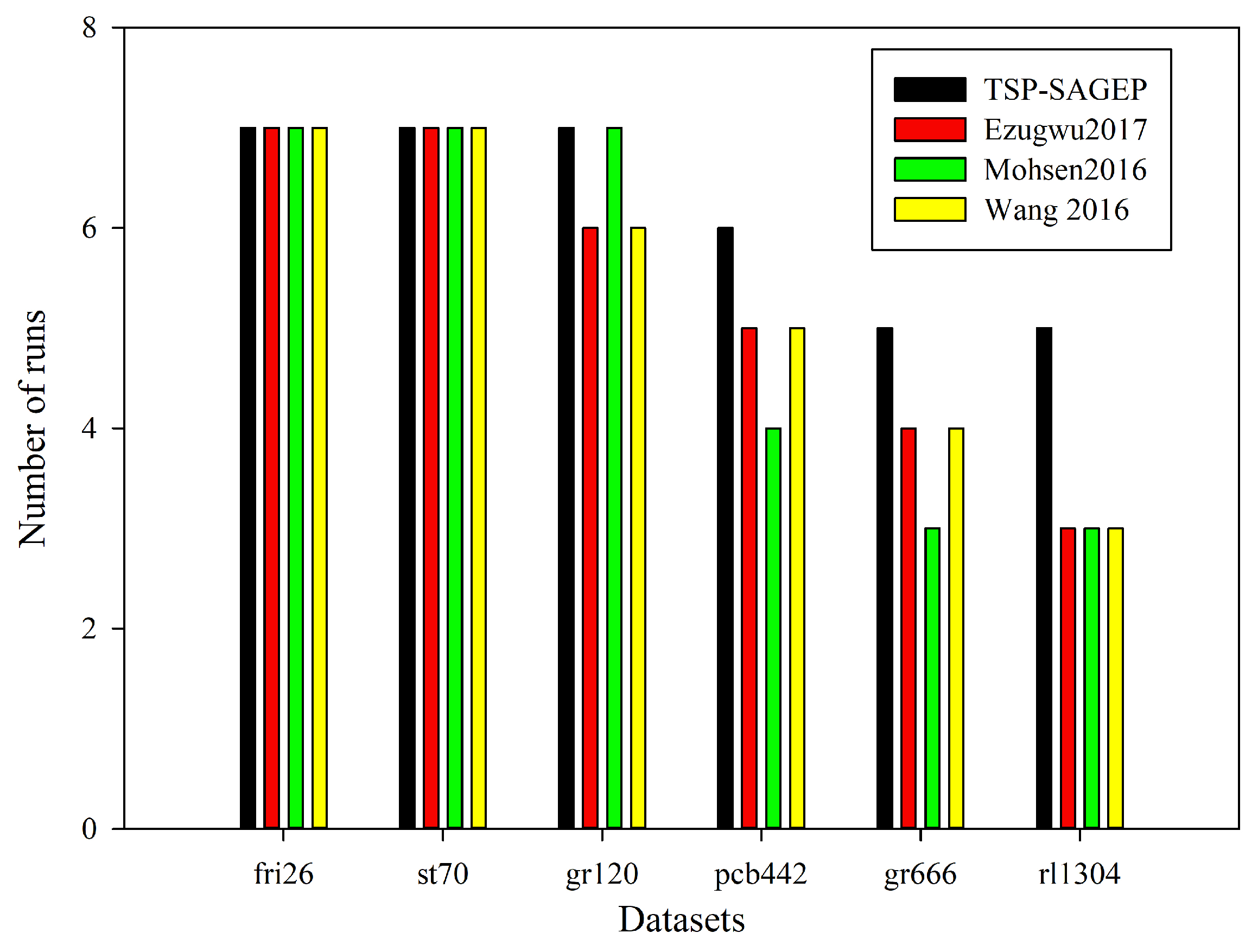
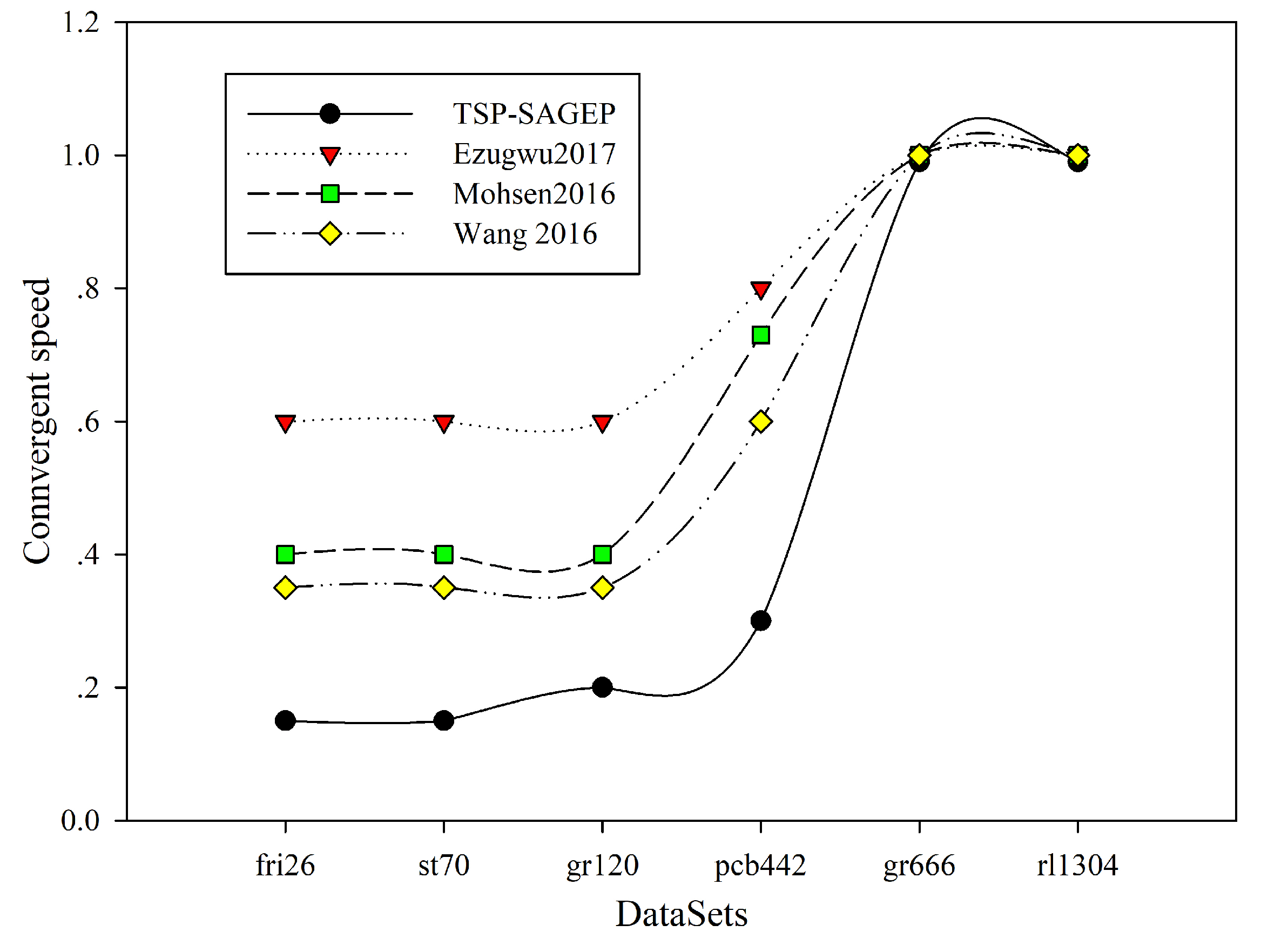
- Experimental results show that the proposed algorithm outperforms traditional algorithms in terms of the best solution, the worst solution, the running time of the algorithm, the rate of difference between the best solution and the known optimal solution, and the convergent speed of the algorithms.
2. Related Work
3. Improved GEP Algorithm Based on Simulated Annealing
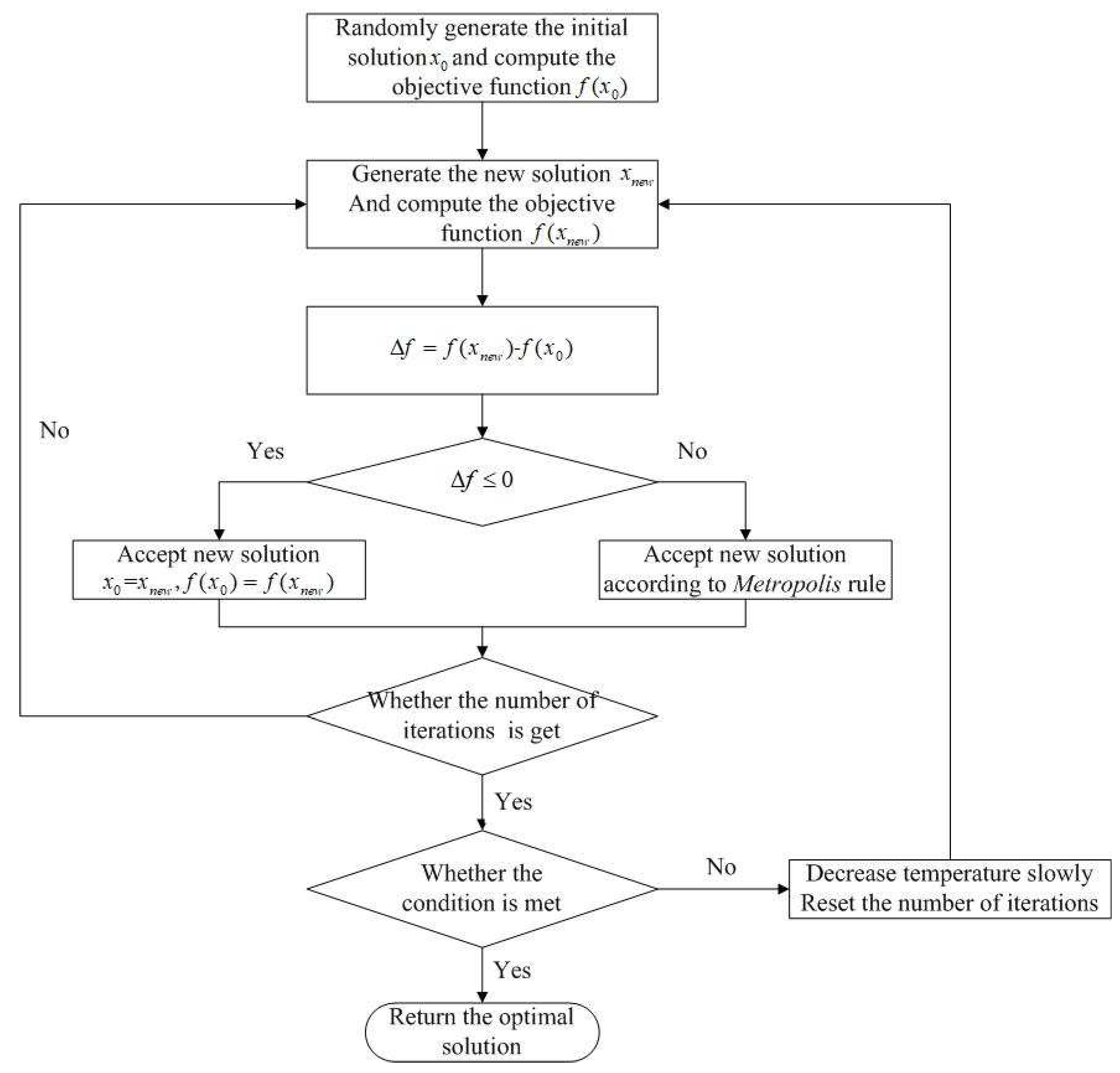
3.1. Simulated Annealing
| Algorithm 1: SA |
| Input: initial temperature , minimum temperature , maximum number of iteration , |
| probability of temperature drop ; |
| Output: the optimal solution ; |
| 1. Generating an initial solution ; |
| 2. ; |
| 3. Computing the value of the objective function and ; |
| 4. ; |
| 5. while do |
| 6. ; |
| 7. if then |
| 8. ; |
| 9. end if |
| 10. if then |
| 11. ; |
| 12. if then |
| 13. ; |
| 14. else |
| 15. ; |
| 16. end if |
| 17. end if |
| 18. ; |
| 19. ; |
| 20. end while |
| 21. Return ; |
3.2. IGEP-SA
3.2.1. New Population Generation Based on Simulated Annealing
| Algorithm 2: NPG-SA |
| Input: current temperature T, number of population , fitness value of previous |
| generation population , and fitness value of population after genetic operations ; |
| Output: new population ; |
| 1. ; |
| 2. while do |
| 3. ; |
| 4. ; |
| 5. if then |
| 6. ; |
| 7. end if |
| 8. ; |
| 9. end while |
| 10. Return ; |
3.2.2. New Mutation Operator Based on Simulated Annealing
| Algorithm 3: NMO-SA |
| Input: current temperature T, number of population , fitness value of the previous |
| generation population , and fitness value of population after genetic operations ; |
| Output: new population ; |
| 1. ; |
| 2. ; |
| 3. while do |
| 4. ; |
| 5. ; |
| 6. initial mutation rate |
| 7. if then |
| 8. ; |
| 9. else |
| 10. ; |
| 11. end if; |
| 12. ; |
| 13. ; |
| 14. end while |
| 15. Return ; |
3.2.3. Description of IGEP-SA
| Algorithm 4: IGEP-SA |
| Input: current temperature T, number of population , fitness value of the previous |
| generation population , fitness value of population after genetic operations , probability |
| of temperature drop , , , and ; |
| Output: new population ; |
| 1. ; |
| 2. ; |
| 3. while do |
| 4. ; |
| 5. ; |
| 6. ; |
| 7. ; |
| 8. ; |
| 9. ; |
| 10. ; |
| 11. ; |
| 12. ; |
| 13. end while |
| 14. ; |
| 15. ; |
4. Traveling-Salesman Problem Based on Simulated Annealing and GEP
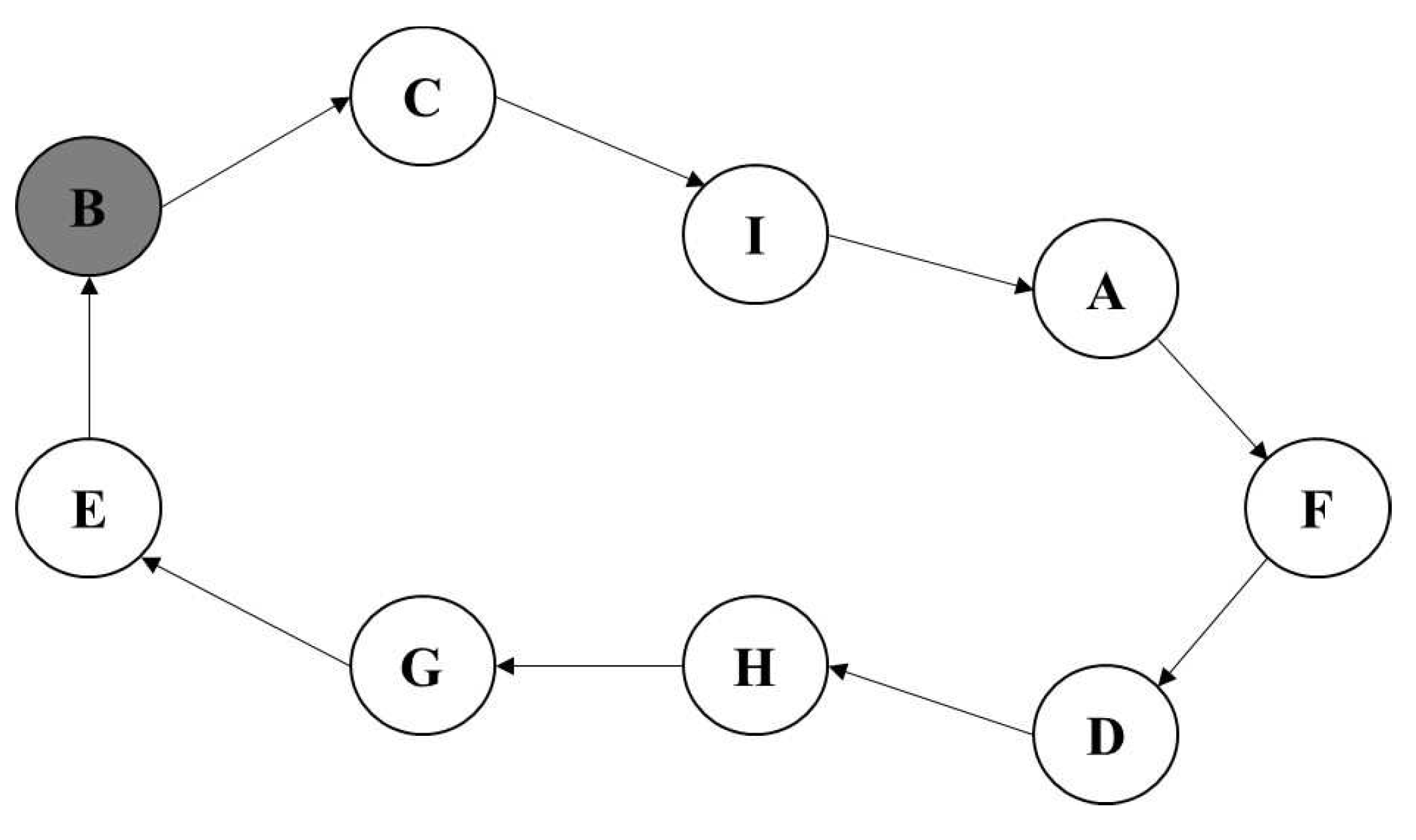
4.1. TSP-SAGEP Code
4.2. Fitness Function of the TSP-SAGEP
4.3. Algorithm Description
5. Experiment and Analysis
5.1. Experimental Environment
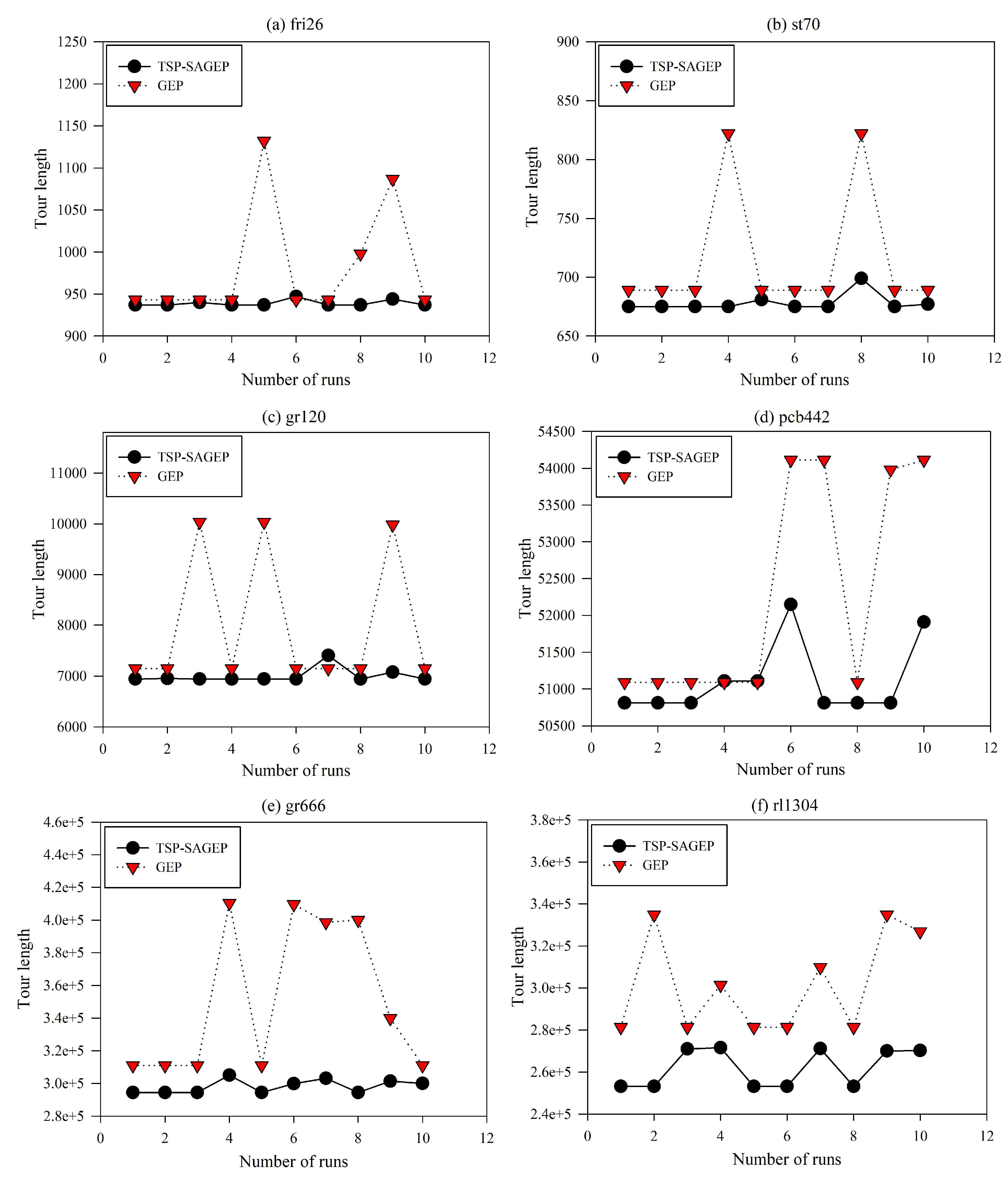
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, Y.; Li, Z.-W. Application of Ant Colony Algorithm to Power Cable Patrol Route Planning. Comput. Syst. Appl. 2015, 5, 135–139. [Google Scholar]
- Wang, J.; Wang, X.; Chen, Y.; Cai, G. Intelligent patrolling robot addressing program based on graph method. Autom. Electr. Power Syst. 2007, 9, 78–81. [Google Scholar]
- Robins, G.; Pattison, P.; Kalish, Y.; Lusher, D. An introduction to exponential random graph (p*) models for social networks. Soc. Netw. 2007, 29, 173–191. [Google Scholar] [CrossRef]
- Soussi, R.; Aufaure, M.-A.; Baazaoui, H. Towards social network extraction using a graph database. In Proceedings of the 2010 Second International Conference on Advances in Databases Knowledge and Data Applications (DBKDA), Menuires, France, 2–6 June 2010; pp. 28–34. [Google Scholar]
- Cattuto, C.; Quaggiotto, M.; Panisson, A.; Averbuch, A. Time-varying social networks in a graph database: A Neo4j use case. In Proceedings of the First International Workshop on Graph Data Management Experiences and Systems, New York, NY, USA, 22–27 June 2013; pp. 1–6. [Google Scholar]
- Arora, S. Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems. J. ACM 1998, 45, 753–782. [Google Scholar] [CrossRef]
- Cook, W.; Espinoza, D.; Goycoolea, M. Computing with Domino-Parity Inequalities for the TSP; Georgia Institute of Technology, Industrial and Systems Engineering: Atlanta, GA, USA, 2007; Volume 19, pp. 356–365. [Google Scholar]
- Zhan, S.; Lin, J.; Zhang, Z.; Zhong, Y. List-based simulated annealing algorithm for traveling salesman problem. Comput. Intell. Neurosci. 2016, 2016, 8–18. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Bian, Z.; Liu, X. Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing–tabu search algorithm to solve the symmetrical traveling salesman problem. Appl. Soft Comput. 2016, 49, 937–952. [Google Scholar] [CrossRef]
- Ezugwu, A.E.S.; Adewumi, A.O.; Frîncu, M.E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem. Expert Syst. Appl. 2017, 77, 189–210. [Google Scholar] [CrossRef]
- Behnck, L.P.; Doering, D.; Pereira, C.E.; Rettberg, A. A modified simulated annealing algorithm for SUAVs path planning. IFAC-PapersOnLine 2015, 48, 63–68. [Google Scholar] [CrossRef]
- Zhao, D.; Xiong, W.; Shu, Z. Simulated annealing with a hybrid local search for solving the traveling salesman problem. J. Comput. Theor. Nanosci. 2015, 12, 1165–1169. [Google Scholar] [CrossRef]
- Xu, D.; Weise, T.; Wu, Y.; Lassig, J.; Chiong, R. An investigation of hybrid tabu search for the traveling salesman problem. Bio-Inspired Comput. Theor. Appl. 2015, 562, 523–537. [Google Scholar]
- Archetti, C.; Guastaroba, G.; Speranza, M.G. An ILP-refined tabu search for the directed profitable rural postman problem. Discret. Appl. Math. 2014, 163, 3–16. [Google Scholar] [CrossRef]
- Chiang, H.-P.; Chou, Y.-H.; Chiu, C.-H.; Kuo, S.-Y.; Huang, Y.-M. A quantum-inspired Tabu search algorithm for solving combinatorial optimization problems. Soft Comput. 2014, 18, 1771–1781. [Google Scholar] [CrossRef]
- Min, H.; Dazhi, P.; Song, Y. An improved hybrid ant colony algorithm and its application in solving TSP. In Proceedings of the 2014 IEEE 7th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 20–21 December 2014; pp. 1534–1551. [Google Scholar]
- Mohsen, A.M. Annealing ant colony optimization with mutation operator for solving tsp. Comput. Intell. Neurosci. 2016, 2016, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Ding, R.; Zhang, Y.; Cong, M.; Wang, F.; Tang, G. An improved ant colony optimization (I-ACO) method for the quasi travelling salesman problem (Quasi-TSP). Int. J. Geogr. Inf. Sci. 2015, 29, 1534–1551. [Google Scholar] [CrossRef]
- El-Samak, A.F.; Ashour, W. Optimization of traveling salesman problem using affinity propagation clustering and genetic algorithm. J. Artif. Intell. Soft Comput. Res. 2015, 5, 239–245. [Google Scholar] [CrossRef]
- Rani, K.; Kumar, V. Solving travelling salesman problem using genetic algorithm based on heuristic crossover and mutation operator. Int. J. Res. Eng. Technol. 2014, 3, 27–34. [Google Scholar]
- Deng, Y.; Liu, Y.; Zhou, D. An improved genetic algorithm with initial population strategy for symmetric TSP. Math. Probl. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Wang, Y. The hybrid genetic algorithm with two local optimization strategies for traveling salesman problem. Comput. Ind. Eng. 2014, 70, 124–133. [Google Scholar] [CrossRef]
- Wang, J.; Ersoy, O.K.; He, M.; Wang, F. Multi-offspring genetic algorithm and its application to the traveling salesman problem. App. Soft Comput. 2016, 43, 415–423. [Google Scholar] [CrossRef]
- Changdar, C.; Mahapatra, G.S.; Pal, R.K. An efficient genetic algorithm for multi-objective solid travelling salesman problem under fuzziness. Swarm Evol. Comput. 2014, 15, 27–37. [Google Scholar] [CrossRef]
- Haroun, S.A.; Jamal, B.; Hicham, E.H. A Performance Comparison of GA and ACO Applied to TSP. Int. J. Comput. Appl. 2015, 117, 28–35. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming in problem Solving; Springer: Berlin, Germany, 2002; pp. 635–653. [Google Scholar]
- Ferreira, C. Automatically Defined Functions in Gene Expression Programming; Springer: Berlin, Germany, 2006; pp. 21–56. [Google Scholar]
- Ferreira, C. Genetic representation and genetic neutrality in gene expression programming. Adv. Complex Syst. 2002, 5, 389–408. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin, Germany, 2006. [Google Scholar]
- Wu, J.; Li, T.Y.; Jiang, Y.; Li, Z.L.; Liu, Y.Y. Gene Expression Programming Based on Diversified Development Strategy. J. Jilin Univ. Inf. Sci. Ed. 2010, 28, 396–403. [Google Scholar]
- Tang, C.; Zhang, T.; Zuo, J.; Rui, W.; Jia, X. Knowledge discovery based on Gene Expression Programming-History, achievements and future directions. Comput. Appl. 2004, 10, 7–10. [Google Scholar]
- Ferreira, C. Combinatorial Optimization by Gene Expression Programming: Inversion Revisited; Springer: Berlin, Germany, 2002; pp. 160–174. [Google Scholar]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. A dynamic multiarmed bandit-gene expression programming hyper-heuristic for combinatorial optimization problems. IEEE Trans. Cybern. 2015, 45, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing; Springer: Berlin, Germany, 1987; pp. 7–15. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Reinelt, G. TSPLIB-A traveling salesman problem library. ORSA J. Comput. 1991, 3, 376–384. [Google Scholar] [CrossRef]
- Discrete and Combinatorial Optimization—IWR, Heidelberg. Available online: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ (accessed on 21 November 2018).
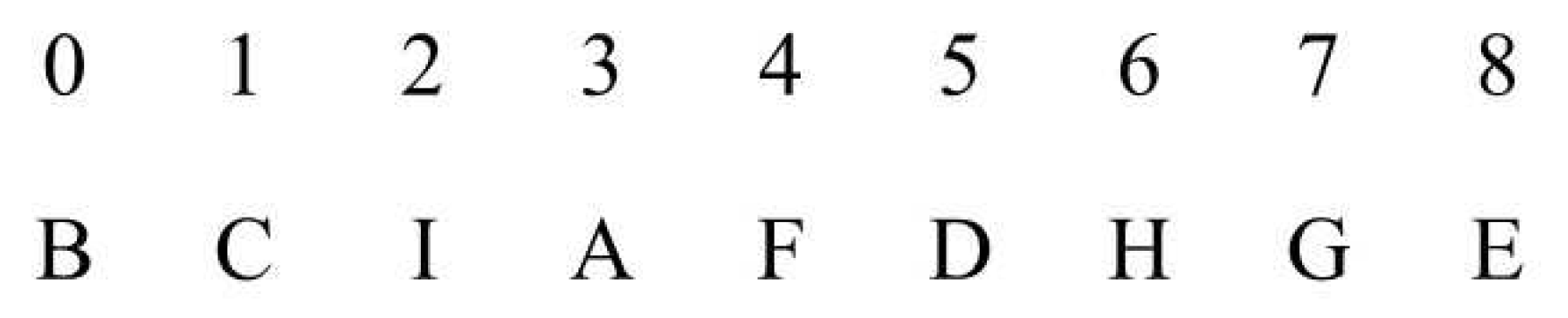
| Instance | Cities | Optimal Solution |
|---|---|---|
| fri26 | 26 | 937 |
| st70 | 70 | 675 |
| gr120 | 120 | 6942 |
| pcb442 | 442 | 50,778 |
| gr666 | 666 | 294,358 |
| rl1304 | 1304 | 252,948 |
| Parameter Item | Value |
|---|---|
| Initial temperature | 100 |
| Minimum temperature | |
| The probability of temperature drop | 0.98 |
| Population size | 500 |
| The number of runs | 10 |
| The number of generations | 1000 |
| IS Transposition rate | 0.3 |
| RIS Transposition rate | 0.3 |
| Gene Transposition rate | 0.1 |
| One-point recombination rate | 0.3 |
| Two-point recombination rate | 0.3 |
| Gene recombination rate | 0.1 |
| Instances | Optimal | Algorithm | Best | Worst | Average | Generations | Time (s) |
|---|---|---|---|---|---|---|---|
| fri26 | 937 | TSP-SAGEP | 937 | 971 | 941 | 150 | 7.0671 |
| GEP | 943 | 1132 | 961 | 800 | 8.1629 | ||
| st70 | 675 | TSP-SAGEP | 675 | 699 | 677 | 150 | 12.1135 |
| GEP | 698 | 822 | 710 | 800 | 14.0931 | ||
| gr120 | 6942 | TSP-SAGEP | 6942 | 7406 | 6995 | 200 | 19.4612 |
| GEP | 7147 | 10,035 | 7624 | 900 | 22.3573 | ||
| pcb442 | 50,778 | TSP-SAGEP | 50,811 | 52,147 | 50,878 | 300 | 51.0964 |
| GEP | 51,092 | 54,113 | 51,676 | 900 | 57.1428 | ||
| gr666 | 294,358 | TSP-SAGEP | 294,419 | 305,036 | 295,542 | 990 | 79.7853 |
| GEP | 310,982 | 410,368 | 328,459 | 990 | 85.1204 | ||
| rl1304 | 252,948 | TSP-SAGEP | 253,104 | 271,582 | 254,699 | 990 | 160.2458 |
| GEP | 281,296 | 334,871 | 290,611 | 990 | 165.5572 |
| Instances | Optimal | Algorithm | Best | Worst | Average | Rate | Time (s) |
|---|---|---|---|---|---|---|---|
| fri26 | 937 | TSP-SAGEP | 937 | 971 | 941 | 0 | 7.0671 |
| Ezugwu2017 | 937 | 1204 | 951 | 0 | 8.5247 | ||
| Mohsen2016 | 937 | 1299 | 955 | 0 | 8.5916 | ||
| Wang2016 | 937 | 1151 | 948 | 0 | 8.3103 | ||
| st70 | 675 | TSP-SAGEP | 675 | 699 | 677 | 0 | 12.1135 |
| Ezugwu2017 | 675 | 846 | 701 | 0 | 14.9045 | ||
| Mohsen2016 | 675 | 907 | 715 | 0 | 15.1037 | ||
| Wang2016 | 675 | 831 | 695 | 0 | 14.0985 | ||
| gr120 | 6942 | TSP-SAGEP | 6942 | 7406 | 6995 | 0 | 19.4612 |
| Ezugwu2017 | 6942 | 11,237 | 7786 | 0 | 25.3581 | ||
| Mohsen2016 | 6942 | 11,354 | 7801 | 0 | 27.0433 | ||
| Wang2016 | 6942 | 11,008 | 7655 | 0 | 23.6709 | ||
| pcb442 | 50,778 | TSP-SAGEP | 50,811 | 52,147 | 50,878 | 0.00065 | 51.0964 |
| Ezugwu2017 | 51,107 | 55,723 | 51,958 | 0.00644 | 61.0876 | ||
| Mohsen2016 | 51,143 | 56,098 | 52,044 | 0.00714 | 63.9011 | ||
| Wang2016 | 51,097 | 55,006 | 51,828 | 0.00624 | 59.4571 | ||
| gr666 | 294,358 | TSP-SAGEP | 294,419 | 305,036 | 295,542 | 0.00021 | 79.7853 |
| Ezugwu2017 | 311,855 | 417,702 | 331,024 | 0.05611 | 90.0014 | ||
| Mohsen2016 | 312,096 | 420,809 | 332,528 | 0.05684 | 92.0745 | ||
| Wang2016 | 311,003 | 411,984 | 329,199 | 0.05352 | 88.0163 | ||
| rl1304 | 252,948 | TSP-SAGEP | 253,104 | 271,582 | 25,4699 | 0.00062 | 160.2458 |
| Ezugwu2017 | 288,013 | 340,015 | 297,813 | 0.12175 | 169.0031 | ||
| Mohsen2016 | 290,057 | 341,298 | 299,305 | 0.12798 | 170.1165 | ||
| Wang2016 | 286,799 | 335,990 | 294,637 | 0.11803 | 167.9084 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, A.-H.; Zhu, L.-P.; Hu, B.; Deng, S.; Song, Y.; Qiu, H.; Pan, S. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information 2019, 10, 7. https://doi.org/10.3390/info10010007
Zhou A-H, Zhu L-P, Hu B, Deng S, Song Y, Qiu H, Pan S. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information. 2019; 10(1):7. https://doi.org/10.3390/info10010007
Chicago/Turabian StyleZhou, Ai-Hua, Li-Peng Zhu, Bin Hu, Song Deng, Yan Song, Hongbin Qiu, and Sen Pan. 2019. "Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming" Information 10, no. 1: 7. https://doi.org/10.3390/info10010007
APA StyleZhou, A.-H., Zhu, L.-P., Hu, B., Deng, S., Song, Y., Qiu, H., & Pan, S. (2019). Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information, 10(1), 7. https://doi.org/10.3390/info10010007




